Trend Test for Hydrological and Climatic Time Series Considering the Interaction of Trend and Autocorrelations
Abstract
:1. Introduction
2. Methods
2.1. Trend and Autocorrelations Analysis
2.1.1. MK Test and MMK Test
- (1)
- MK test
- (2)
- MMK test
2.1.2. Autocorrelations Test
- (1)
- Single-order autocorrelation test
- (2)
- Overall test for high-order autocorrelations
2.1.3. De-Trending Operation
2.1.4. OW Operation
2.2. Trend Tests Based on the MMK Test and OW Operation
2.2.1. Trend Test Based on the MMK Test
- Step 1 Input x0(t), and preset the significance level (α) and the maximum lag (Lmax = floor(n/4), where floor denotes the floor function) of autocorrelation coefficient in the order-by-order test;
- Step 2 Test the trend in x0(t) using Equations (1) and (2), and simultaneously test the global autocorrelations of x0(t) by Equations (5)~(8);
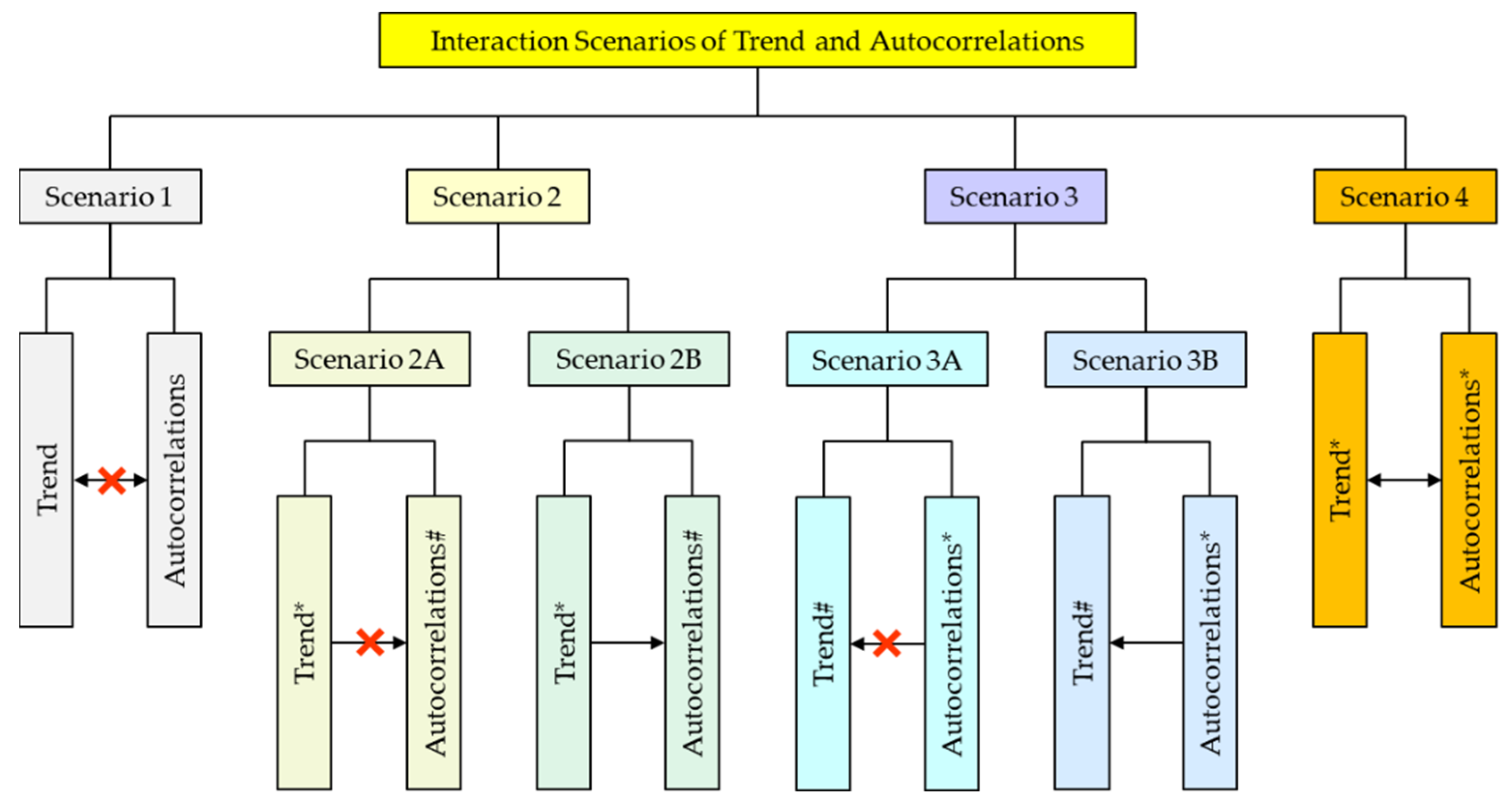
- Step 3 Output Result 1 if neither the trend nor the global autocorrelations are significant, output Result 2A if the trend is significant and the global autocorrelations are not significant, output Result 3A if the global autocorrelations are significant and the trend is not significant, and then terminate the trend test;
- Step 4 Conduct the de-trending operation for x0(t) using Equations (9)~(11), thus, generating the de-trended time series x1(t) if the trend and autocorrelations are significant;
- Step 5 Test the global autocorrelations of x1(t), output Result 2B if the global autocorrelations are not significant, and then terminate the trend test;
- Step 6 Test the autocorrelation coefficient ri (i = 1, …, Lmax) order by order if the global autocorrelations are significant, and then test the trend of x0(t) by Equations (3) and (4);
- Step 7 Output Result 3B if the trend is not significant; otherwise, output Result 4 and terminate the trend test.
2.2.2. Trend Test Based on the OW Operation
- Step 1 Input x0(t), α, the maximum number (Mmax = 1000) of simulations, the maximum number (Nmax = 10) of cycles for OW operation, and the increasing step (Δγ = 0.1) of variance of the Gaussian white noise;
- Steps 2~5 can be referred to the same steps in the trend test based on the MMK test;
- Step 6 Standardize x0(t) to generate the standardized time series x2(t) by Equation (12);
- Step 7 Generate a Gaussian white noise ε(t) with the variance of γ, and superimpose ε(t) on x2(t), thus, generating x3(t);
- Step 8 Conduct the de-trending operation for x3(t) using Equations (9)~(11), and thus, generating x4(t);
- Step 9 Test the global autocorrelations of x4(t), and then return to Step 7 if the global autocorrelations are significant and the current number (N) of cycles for the OW operation does not reach Nmax;
- Step 10 Increase γ in steps of Δγ, and then return to Step 7 if N is larger than Nmax and the global autocorrelations are still significant;
- Step 11 Test the trend of x3(t) if the global autocorrelations are not significant, and then record the current number (M) of simulations;
- Step 12 Accumulate for the number m1 if the trend is not significant; otherwise, accumulate for the number m2;
- Step 13 Return to Step 10 if M is not larger than Mmax; otherwise, calculate the percentages (f1 and f2) of m1 and m2 in M;
- Step 14 Output Result 3B if f1 is not smaller than f2; otherwise, output Result 4, and then terminate the trend test.
2.3. Simulation Experiments
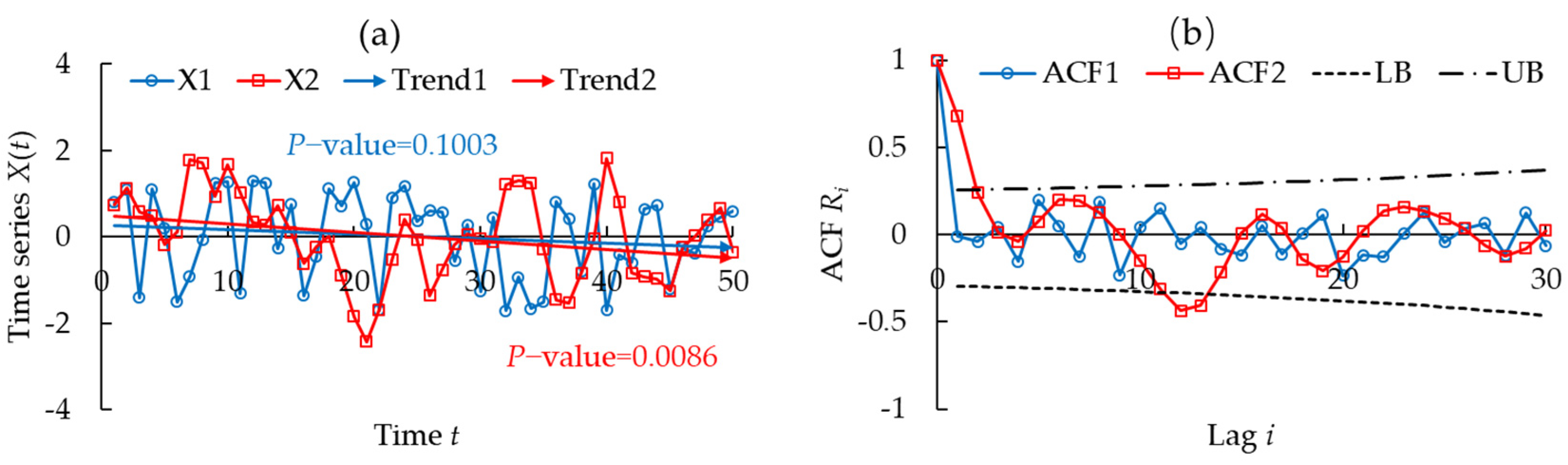
2.3.1. Generation of Sample Time Series
2.3.2. Introduction to Simulation Experiments
- (1)
- Simulation experiment 1
- (2)
- Simulation experiment 2
3. Application to STS
3.1. Preliminary Verification for Two Trend Test Methods
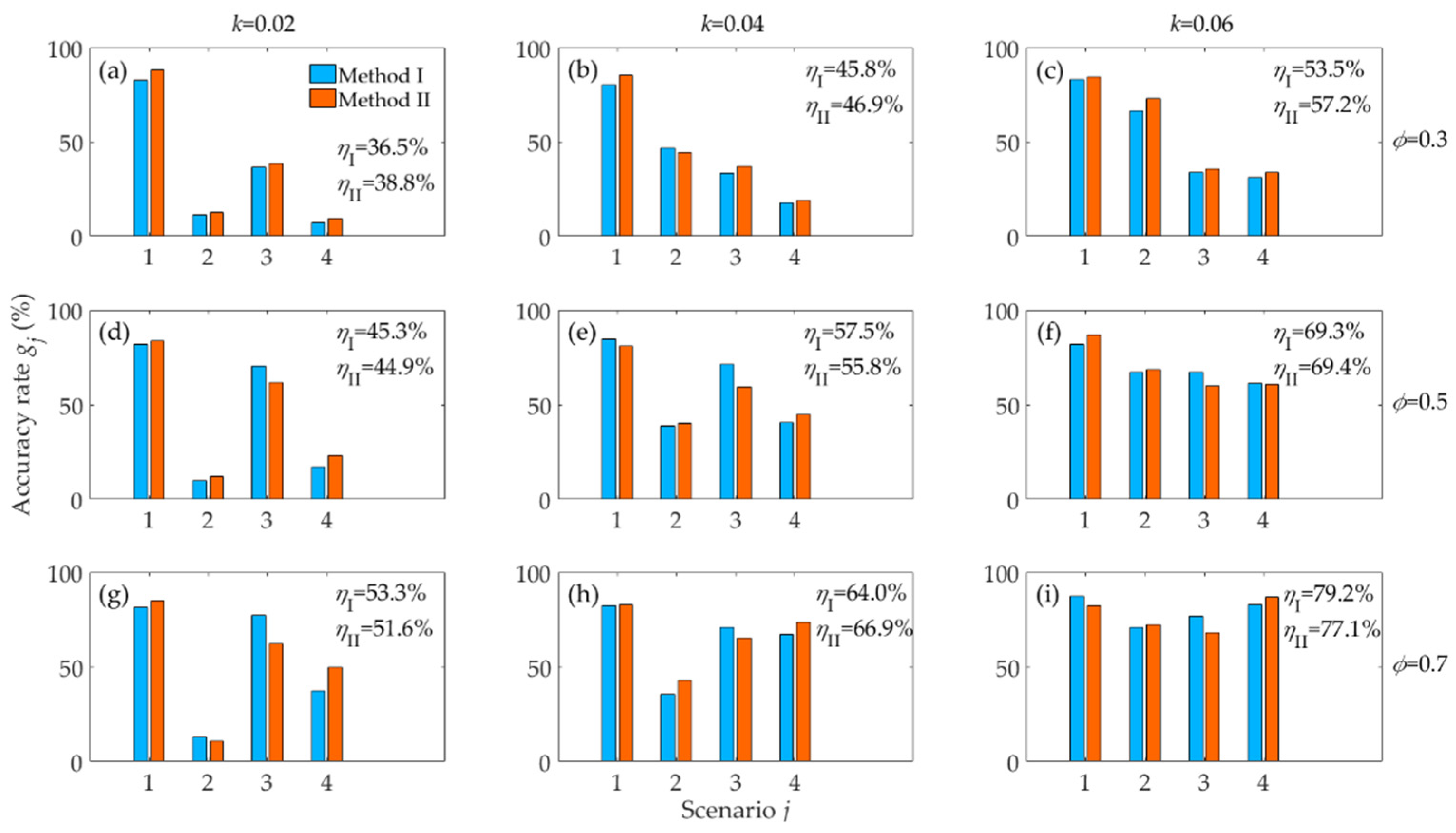
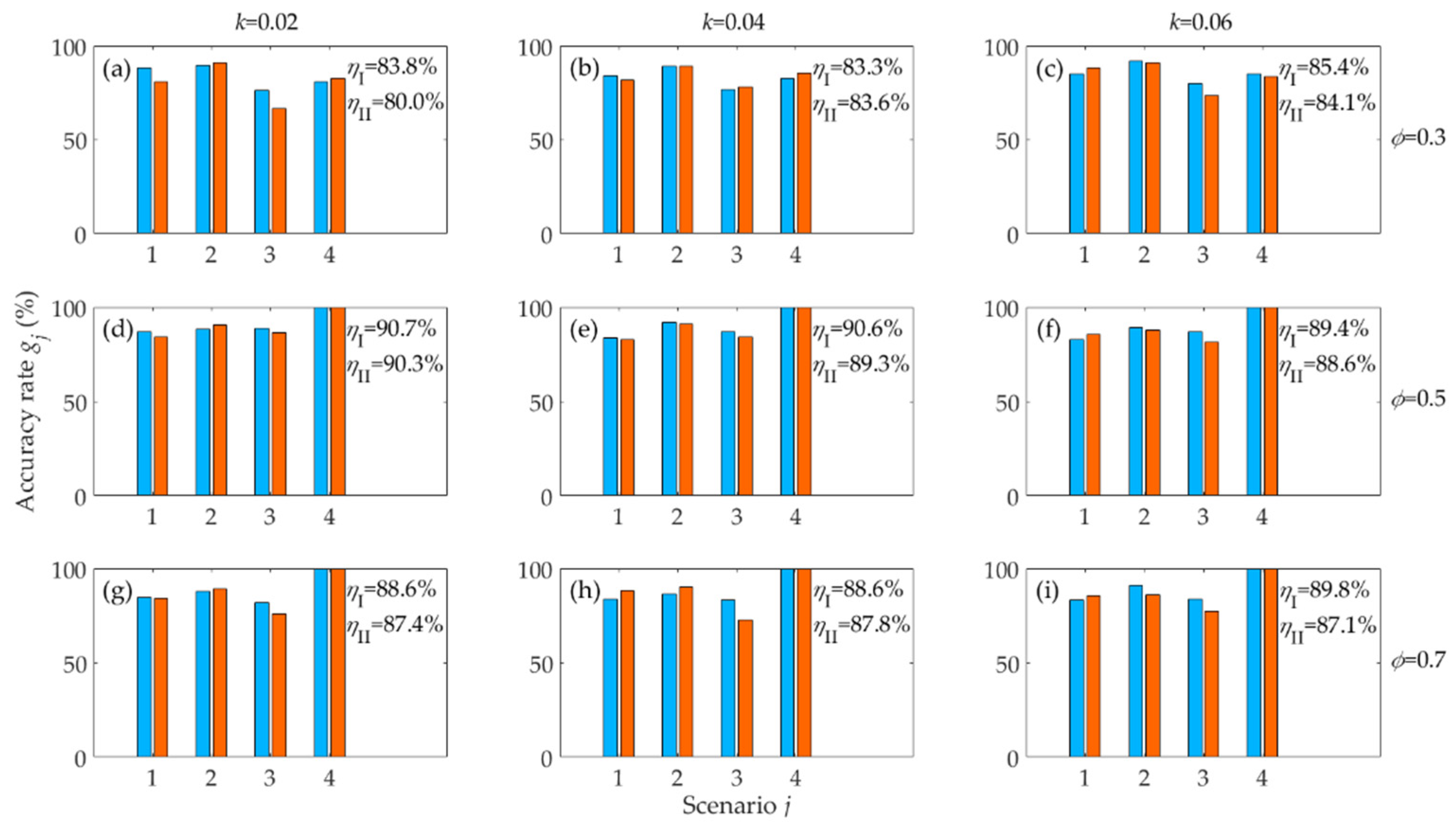
3.2. Results of Simulation Experiment 1
3.3. Results of Simulation Experiment 2
4. Application to HCTS
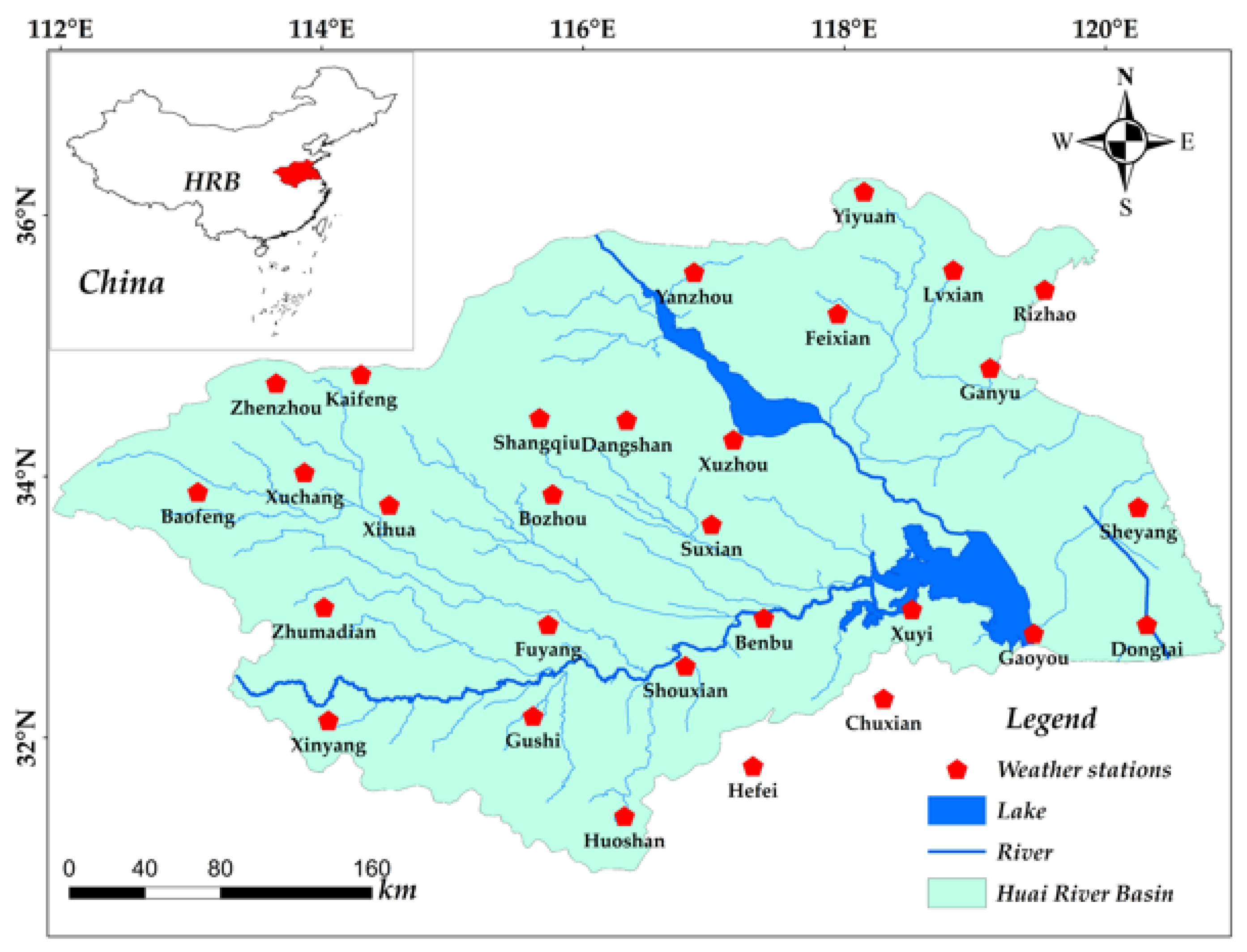
4.1. Study Area and Data
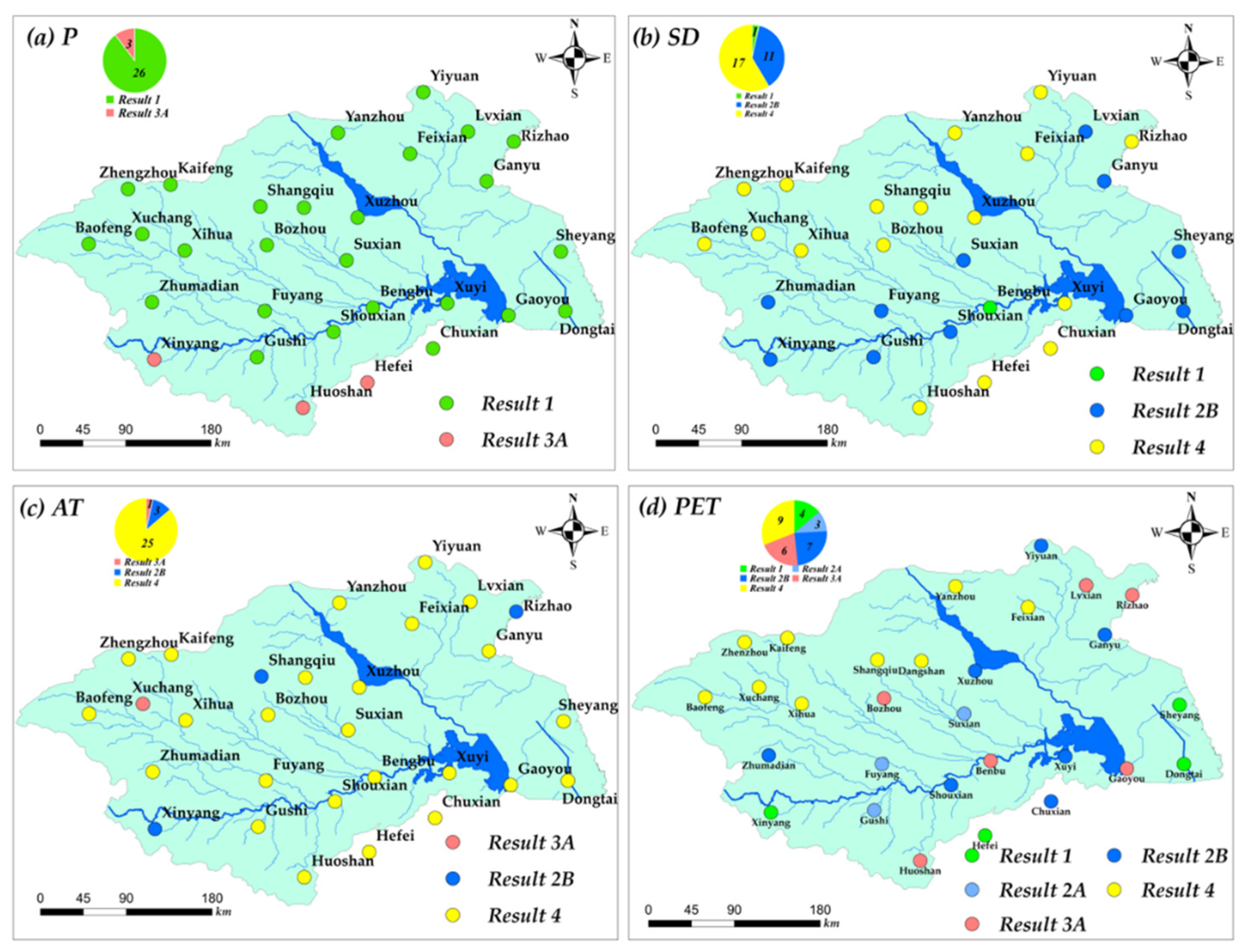
4.2. Trend Test Results of Six HCTSs
5. Discussion
5.1. Necessities and Effectiveness of the Outer Loop for the OW Operation
5.2. Impact of Significance Level on Trend Tests
5.3. Performances of the MMK Test and OW Operation
5.4. Recommendations and Limitations of This Study
6. Conclusions
- (1)
- Previous OW operations still face the risk of misjudging trends in the presence of significant autocorrelations. In order to improve the reliability of the trend test based on the OW operation, the proposed strategy of adding an outer loop to the trend test to calculate the occurrence frequency of significant and non-significant trends is necessary and effective.
- (2)
- Trend tests based on the MMK test and OW operations are similar in the accuracy of the trend tests. For long HCTSs with strong trends or autocorrelations, both tests can perform well and generate consistent trend test results in most cases. Nevertheless, when determining whether a significant trend in HCTS is a pseudo trend or not, the two tests may also produce opposite results in the existence of significant autocorrelations.
- (3)
- At a given significance level α, the accuracy rate of the trend test for an HCTS is always less than 1-α due to the distribution error of the test statistic, type II error in the hypothesis test, and error propagation in the joint test of trend and autocorrelations. With the significance level decreases, the accuracy rate of the trend test tends to decrease for short HCTSs and to increase for long HCTSs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
List of Abbreviations
| Abbreviation | Full Name |
| ACF | autocorrelation function |
| ARMA | autoregressive moving average |
| AT | average temperature |
| HCTS | hydrologic and climatic time series |
| HRB | Huaihe River basin |
| MK | Mann–Kendall |
| MMK | modified Mann–Kendall |
| RH | relative humidity |
| SD | sunshine duration |
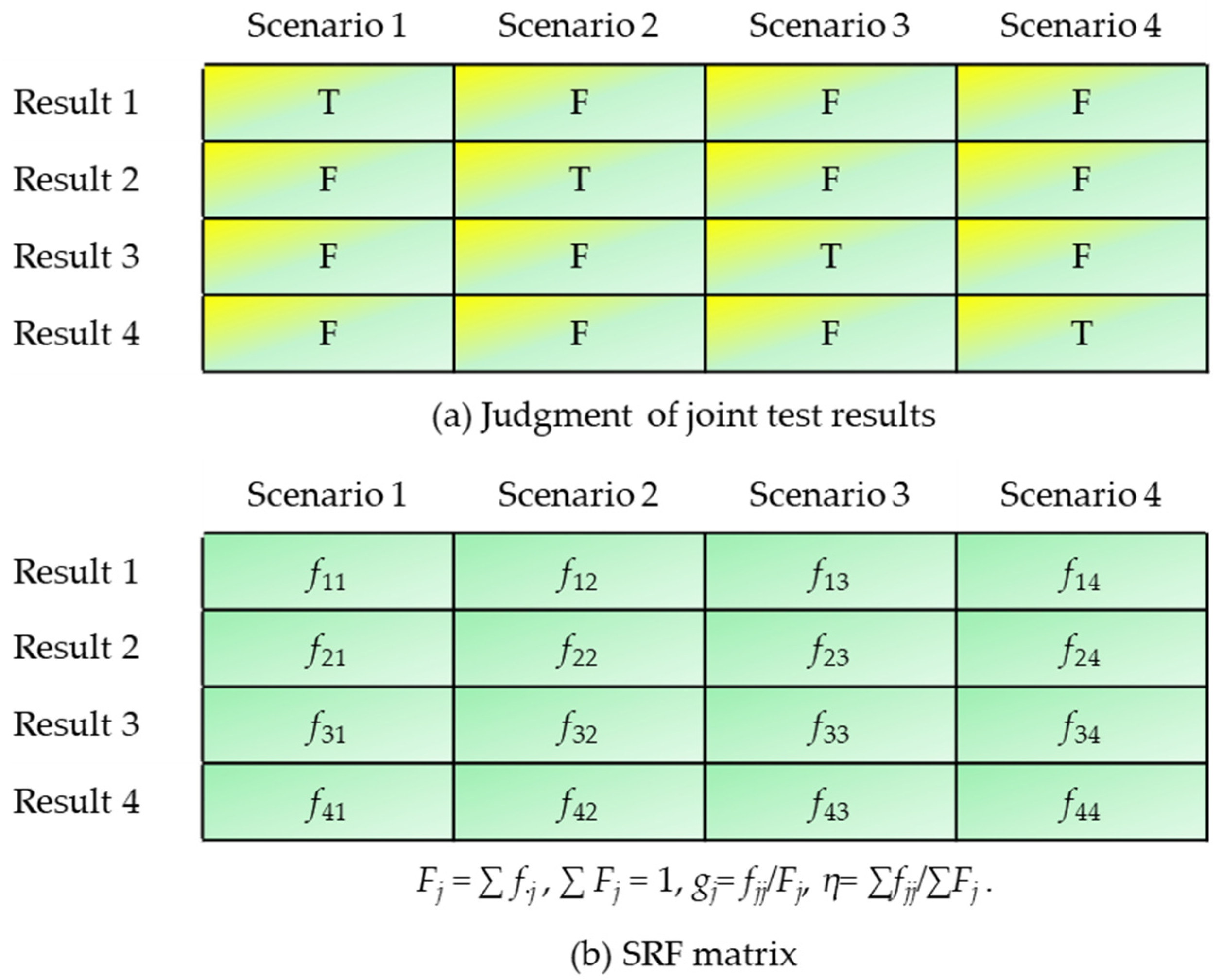
| SRF | scenario–result frequency |
| STS | sample time series |
| OW | over-whitening |
| PET | potential evapotranspiration |
| WS | wind speed |
Appendix A
| n | ϕ | k = 0.02 | k = 0.04 | k = 0.06 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 30 | 0.3 | 23.9 | 20.2 | 10.8 | 9.2 | 22.1 | 10.7 | 12.5 | 4.7 | 20.7 | 5.9 | 13.9 | 0.8 |
| 1.4 | 2.7 | 2.7 | 4.1 | 2.1 | 11.2 | 3.4 | 9.8 | 1.1 | 16.1 | 2.6 | 14.1 | ||
| 3.6 | 1.3 | 8.1 | 9.5 | 3.3 | 1.8 | 8.3 | 4.9 | 3.1 | 0.5 | 8.9 | 2.2 | ||
| 0.0 | 0.1 | 0.6 | 1.8 | 0.0 | 0.2 | 0.8 | 4.2 | 0.0 | 1.6 | 0.7 | 7.8 | ||
| 0.5 | 20.3 | 17.7 | 3.9 | 3.3 | 18.4 | 14.6 | 3.6 | 0.8 | 20.6 | 5.9 | 3.7 | 0.2 | |
| 1.0 | 2.3 | 2.2 | 5.0 | 0.8 | 10.7 | 2.0 | 6.8 | 0.9 | 16.6 | 2.5 | 7.1 | ||
| 3.4 | 2.9 | 18.1 | 13.7 | 2.5 | 1.6 | 18.1 | 7.4 | 3.5 | 1.2 | 16.1 | 2.9 | ||
| 0.1 | 0.0 | 1.5 | 4.6 | 0.0 | 0.8 | 1.6 | 10.3 | 0.1 | 1.0 | 1.7 | 16.0 | ||
| 0.7 | 20.9 | 18.5 | 1.0 | 0.2 | 21.5 | 13.7 | 1.0 | 0.1 | 19.8 | 5.1 | 1.1 | 0.1 | |
| 1.4 | 3.3 | 1.0 | 0.8 | 1.1 | 9.1 | 1.3 | 1.9 | 1.2 | 17.4 | 1.0 | 2.3 | ||
| 3.2 | 3.1 | 20.5 | 13.4 | 3.5 | 1.6 | 16.9 | 6.0 | 1.6 | 0.7 | 21.6 | 1.9 | ||
| 0.1 | 0.0 | 4.0 | 8.6 | 0.0 | 1.2 | 4.6 | 16.5 | 0.0 | 1.4 | 4.4 | 20.4 | ||
| 50 | 0.3 | 19.4 | 12.5 | 9.7 | 3.5 | 23.5 | 1.2 | 10.0 | 0.0 | 20.6 | 0.0 | 10.2 | 0.0 |
| 0.7 | 9.8 | 1.8 | 9.0 | 1.0 | 21.5 | 1.6 | 9.8 | 1.8 | 21.9 | 1.6 | 10.6 | ||
| 2.8 | 1.5 | 14.0 | 7.4 | 1.6 | 0.0 | 14.0 | 0.7 | 2.7 | 0.0 | 13.6 | 0.0 | ||
| 0.0 | 0.5 | 0.4 | 7.0 | 0.1 | 2.3 | 0.7 | 12.0 | 0.1 | 3.2 | 0.9 | 12.8 | ||
| 0.5 | 17.3 | 12.1 | 1.1 | 0.3 | 20.0 | 0.6 | 1.6 | 0.0 | 19.7 | 0.0 | 1.1 | 0.0 | |
| 1.1 | 10.9 | 0.3 | 1.7 | 0.9 | 22.5 | 0.6 | 1.6 | 0.9 | 22.2 | 0.7 | 2.3 | ||
| 4.2 | 2.0 | 22.1 | 8.6 | 1.9 | 0.2 | 19.1 | 0.2 | 2.3 | 0.0 | 23.0 | 0.0 | ||
| 0.0 | 0.7 | 2.8 | 14.8 | 0.0 | 2.7 | 2.8 | 25.3 | 0.1 | 2.9 | 3.3 | 21.5 | ||
| 0.7 | 20.9 | 11.5 | 0.0 | 0.0 | 20.5 | 0.7 | 0.2 | 0.0 | 18.6 | 0.0 | 0.0 | 0.0 | |
| 1.5 | 10.1 | 0.1 | 0.0 | 1.1 | 26.4 | 0.0 | 0.2 | 1.8 | 20.8 | 0.2 | 0.2 | ||
| 2.1 | 1.6 | 22.4 | 5.4 | 2.6 | 0.3 | 18.0 | 0.1 | 2.3 | 0.0 | 21.2 | 0.0 | ||
| 0.0 | 1.0 | 5.4 | 18.0 | 0.0 | 1.5 | 4.1 | 24.3 | 0.0 | 3.4 | 4.2 | 27.3 | ||
| 100 | 0.3 | 21.9 | 0.0 | 2.8 | 0.0 | 20.8 | 0.0 | 3.1 | 0.0 | 19.3 | 0.0 | 2.5 | 0.0 |
| 0.8 | 22.3 | 1.0 | 4.9 | 1.3 | 22.4 | 0.9 | 4.5 | 1.1 | 22.5 | 0.6 | 4.0 | ||
| 2.1 | 0.0 | 18.7 | 0.0 | 2.6 | 0.0 | 18.6 | 0.0 | 2.3 | 0.0 | 20.8 | 0.0 | ||
| 0.0 | 2.6 | 2.0 | 20.9 | 0.0 | 2.7 | 1.6 | 21.5 | 0.0 | 2.0 | 2.1 | 22.8 | ||
| 0.5 | 22.8 | 0.0 | 0.0 | 0.0 | 21.2 | 0.0 | 0.0 | 0.0 | 21.8 | 0.0 | 0.0 | 0.0 | |
| 1.0 | 23.0 | 0.0 | 0.1 | 1.5 | 23.1 | 0.0 | 0.1 | 1.7 | 21.9 | 0.0 | 0.0 | ||
| 2.5 | 0.0 | 20.3 | 0.0 | 2.6 | 0.0 | 21.6 | 0.0 | 2.8 | 0.0 | 22.4 | 0.0 | ||
| 0.0 | 3.1 | 2.6 | 24.6 | 0.0 | 2.0 | 3.2 | 24.7 | 0.0 | 2.7 | 3.4 | 23.3 | ||
| 0.7 | 19.6 | 0.0 | 0.0 | 0.0 | 21.8 | 0.0 | 0.0 | 0.0 | 20.4 | 0.0 | 0.0 | 0.0 | |
| 1.0 | 23.6 | 0.0 | 0.0 | 1.7 | 19.8 | 0.0 | 0.0 | 1.5 | 24.2 | 0.0 | 0.0 | ||
| 2.6 | 0.0 | 20.7 | 0.0 | 2.5 | 0.0 | 20.6 | 0.0 | 2.6 | 0.0 | 18.9 | 0.0 | ||
| 0.0 | 3.3 | 4.5 | 24.7 | 0.0 | 3.1 | 4.1 | 26.4 | 0.0 | 2.4 | 3.7 | 26.3 | ||
| n | ϕ | k = 0.02 | k = 0.04 | k = 0.06 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 30 | 0.3 | 25.0 | 18.1 | 11.0 | 10.7 | 22.0 | 12.3 | 12.3 | 4.2 | 20.7 | 5.4 | 11.8 | 1.5 |
| 1.0 | 3.0 | 1.8 | 3.9 | 1.5 | 11.3 | 1.7 | 11.3 | 1.0 | 19.7 | 2.4 | 13.5 | ||
| 2.3 | 2.4 | 8.3 | 9.2 | 2.2 | 1.3 | 8.8 | 5.0 | 2.8 | 0.7 | 8.3 | 1.7 | ||
| 0.0 | 0.3 | 0.5 | 2.5 | 0.1 | 0.4 | 0.8 | 4.8 | 0.0 | 1.1 | 0.9 | 8.5 | ||
| 0.5 | 21.7 | 19.2 | 4.5 | 2.4 | 19.3 | 12.8 | 4.1 | 1.3 | 22.9 | 6.3 | 4.2 | 0.1 | |
| 1.3 | 3.1 | 1.9 | 3.9 | 0.9 | 10.5 | 2.7 | 6.7 | 1.3 | 17.9 | 2.4 | 7.6 | ||
| 3.0 | 3.4 | 14.3 | 12.9 | 3.6 | 2.2 | 14.5 | 6.2 | 2.2 | 0.7 | 15.5 | 0.8 | ||
| 0.0 | 0.2 | 2.4 | 5.8 | 0.0 | 0.6 | 3.1 | 11.5 | 0.0 | 1.2 | 3.8 | 13.1 | ||
| 0.7 | 20.9 | 19.6 | 0.7 | 0.2 | 21.4 | 11.0 | 0.7 | 0.1 | 20.3 | 4.9 | 0.9 | 0.0 | |
| 1.1 | 2.8 | 1.6 | 2.1 | 0.7 | 9.9 | 1.3 | 3.5 | 0.9 | 17.6 | 1.5 | 2.4 | ||
| 2.6 | 3.0 | 15.4 | 10.3 | 3.7 | 1.5 | 16.4 | 3.2 | 3.4 | 0.2 | 18.4 | 0.7 | ||
| 0.0 | 0.1 | 7.1 | 12.5 | 0.0 | 0.7 | 6.7 | 19.2 | 0.1 | 1.7 | 6.2 | 20.8 | ||
| 50 | 0.3 | 22.1 | 12.4 | 8.3 | 2.4 | 20.7 | 1.0 | 8.3 | 0.0 | 20.7 | 0.0 | 9.9 | 0.0 |
| 1.1 | 11.1 | 1.8 | 7.9 | 1.6 | 22.1 | 2.0 | 11.7 | 1.0 | 20.2 | 1.2 | 12.9 | ||
| 2.8 | 1.2 | 13.6 | 4.5 | 2.9 | 0.1 | 12.6 | 0.0 | 2.4 | 0.0 | 13.9 | 0.0 | ||
| 0.1 | 1.0 | 1.7 | 8.0 | 0.0 | 2.5 | 1.1 | 13.4 | 0.0 | 2.8 | 1.4 | 13.6 | ||
| 0.5 | 20.3 | 11.2 | 1.1 | 0.3 | 22.3 | 0.9 | 1.2 | 0.0 | 21.4 | 0.0 | 0.8 | 0.0 | |
| 1.2 | 12.1 | 0.8 | 1.7 | 1.5 | 21.8 | 0.9 | 2.4 | 1.3 | 22.4 | 0.7 | 1.6 | ||
| 2.3 | 1.8 | 22.1 | 3.4 | 2.9 | 0.0 | 18.7 | 0.0 | 2.4 | 0.0 | 17.7 | 0.0 | ||
| 0.0 | 0.7 | 3.9 | 17.1 | 0.1 | 2.5 | 3.8 | 21.0 | 0.0 | 3.0 | 4.1 | 24.6 | ||
| 0.7 | 20.9 | 13.3 | 0.0 | 0.0 | 22.0 | 0.6 | 0.0 | 0.0 | 22.4 | 0.0 | 0.0 | 0.0 | |
| 1.6 | 11.5 | 0.0 | 0.3 | 1.3 | 21.6 | 0.2 | 0.1 | 1.5 | 21.1 | 0.0 | 0.2 | ||
| 2.6 | 1.0 | 17.2 | 3.2 | 2.3 | 0.0 | 20.0 | 0.0 | 2.3 | 0.0 | 15.5 | 0.0 | ||
| 0.0 | 0.6 | 8.6 | 19.2 | 0.0 | 2.0 | 7.2 | 22.7 | 0.0 | 3.1 | 7.0 | 26.9 | ||
| 100 | 0.3 | 19.9 | 0.0 | 4.0 | 0.0 | 18.6 | 0.0 | 3.3 | 0.0 | 22.3 | 0.0 | 2.9 | 0.0 |
| 1.6 | 21.8 | 1.5 | 4.2 | 1.6 | 21.9 | 0.7 | 3.9 | 0.9 | 22.6 | 0.8 | 4.0 | ||
| 3.0 | 0.0 | 18.0 | 0.0 | 2.6 | 0.0 | 20.4 | 0.0 | 2.1 | 0.0 | 18.5 | 0.0 | ||
| 0.1 | 2.1 | 3.5 | 20.3 | 0.0 | 2.6 | 1.7 | 22.7 | 0.0 | 2.3 | 2.9 | 20.7 | ||
| 0.5 | 23.0 | 0.0 | 0.0 | 0.0 | 20.2 | 0.0 | 0.0 | 0.0 | 21.6 | 0.0 | 0.0 | 0.0 | |
| 1.4 | 22.7 | 0.0 | 0.0 | 1.3 | 22.1 | 0.0 | 0.1 | 1.7 | 22.6 | 0.0 | 0.0 | ||
| 2.9 | 0.0 | 19.7 | 0.0 | 2.9 | 0.0 | 22.1 | 0.0 | 1.9 | 0.0 | 20.4 | 0.0 | ||
| 0.0 | 2.3 | 3.1 | 24.9 | 0.0 | 2.2 | 4.2 | 24.9 | 0.0 | 3.1 | 4.7 | 24.0 | ||
| 0.7 | 19.4 | 0.0 | 0.0 | 0.0 | 21.8 | 0.0 | 0.0 | 0.0 | 20.2 | 0.0 | 0.0 | 0.0 | |
| 1.0 | 25.0 | 0.0 | 0.0 | 1.2 | 23.4 | 0.0 | 0.0 | 1.1 | 22.0 | 0.0 | 0.0 | ||
| 2.6 | 0.0 | 18.5 | 0.0 | 1.7 | 0.0 | 18.1 | 0.0 | 2.3 | 0.0 | 20.3 | 0.0 | ||
| 0.1 | 3.0 | 5.9 | 24.5 | 0.0 | 2.5 | 6.8 | 24.5 | 0.0 | 3.6 | 5.9 | 24.6 | ||
References
- Dey, P.; Mishra, A. Separating the impacts of climate change and human activities on streamflow: A review of methodologies and critical assumption. J. Hydrol. 2017, 548, 278–290. [Google Scholar] [CrossRef]
- IPCC. Summary for Policymakers of Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Rising, J.A.; Taylor, C.; Ives, M.C.; Ward, R.E.T. Challenges and innovations in the economic evaluation of the risks of climate change. Ecol. Econ. 2022, 197, 107437. [Google Scholar] [CrossRef]
- Bose-O’Reilly, S.; Edlinger, M.; Lagally, L.; Lehmann, H.; Lob-Corzilius, T.; Schneider, M.; Schorlemmer, J.; van den Hazel, P.; Schoierer, J. Health effects of climate change-Are they sufficiently addressed in pediatric settings in Germany to meet parents’ needs? J. Clim. Change Health 2022, 6, 100129. [Google Scholar] [CrossRef]
- Wang, H.; You, Q.; Liu, G.; Wu, F. Climatology and trend of tourism climate index over China during 1979–2020. Atmos. Res. 2022, 227, 106321. [Google Scholar] [CrossRef]
- Turner, W.C.; Périquet, S.; Goelst, C.E.; Vera, K.B.; Cameron, E.Z.; Alexander, K.A.; Belant, J.L.; Cloete, C.C.; du Preez, P.; Getz, W.M.; et al. Africa’s drylands in a changing world: Challenges for wildlife conservation under climate and land-use changes in the Greater Etosha Landscape. Glob. Ecol. Conserv. 2022, 38, e02221. [Google Scholar] [CrossRef]
- Şen, Z. Hydrological trend analysis with innovative and over-whitening procedures. Hydrol. Sci. J. 2017, 62, 294–305. [Google Scholar] [CrossRef]
- Dang, C.; Zhang, H.; Singh, V.P.; Zhi, T.; Zhang, J.; Ding, H. A statistical approach for reconstructing natural streamflow series based on streamflow variation identification. Hydrol. Res. 2021, 52, 1100–1115. [Google Scholar] [CrossRef]
- Mudelsee, M. Trend analysis of climate time series: A review of methods. Earth Sci. Rev. 2019, 190, 310–322. [Google Scholar] [CrossRef]
- Almazroui, M.; Şen, Z. Trend Analyses Methodologies in Hydro-meteorological Records. Earth Syst. Environ. 2020, 4, 713–738. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall test for autocorrelation data. J. Hydrol. 1998, 201, 182–196. [Google Scholar] [CrossRef]
- O’ Brien, N.L.; Burn, D.H.; Annable, W.K.; Thompson, P.J. Trend detection in the presence of positive and negative serial correlation: A comparison of Block Maxima and Peaks-Over-threshold data. Water Resour. Res. 2021, 57, e2020WR028886. [Google Scholar]
- Mann, H.B. Non-parametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Measures; Charles Griffin: London, UK, 1975. [Google Scholar]
- Wang, F.; Huang, G.H.; Cheng, G.H.; Li, Y.P. Impacts of climate variations on non-stationarity of streamflow over Canada. Environ. Res. 2021, 197, 111118. [Google Scholar] [CrossRef] [PubMed]
- Von Storch, V.H. Misuses of Statistical Analysis in Climate Research. In Analysis of Climate Variability: Applications of Statistical Techniques; von Storch, H., Navarra, A., Eds.; Springer: Berlin, Germany, 1995; pp. 11–26. [Google Scholar]
- Yue, S.; Wang, C.Y. Applicability of prewhitening to eliminate the influence of serial correlation on the Mann-Kendall test. Water Resour. Res. 2002, 38, 4-1–4-7. [Google Scholar] [CrossRef]
- Noguchi, K.; Gel, Y.R.; Duguay, C.R. Bootstrap-based tests for trends in hydrological time series, with application to ice phenology data. J. Hydrol. 2011, 410, 150–161. [Google Scholar] [CrossRef]
- Hamed, K.H. Exact distribution of the Mann-Kendall trend test statistic for persistent data. J. Hydrol. 2009, 365, 86–94. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, S.; Huang, S.; Fang, H.; Ding, M.; Huang, C.; Shen, T. Local trend analysis method of hydrological time series based on piecewise linear representation and hypothesis test. J. Clean. Prod. 2022, 339, 130695. [Google Scholar] [CrossRef]
- Mullick Md, R.A.; Nur, R.M.; Alam Md, J.; Ashraful Islam, K.M. Observed trends in temperature and rainfall in Bangladesh using pre-whitening approach. Glob. Planet. Change 2019, 172, 104–113. [Google Scholar] [CrossRef]
- Xu, X.; Tang, Q. Spatiotemporal variations in damages to cropland from agrometeorological disasters in mainland China during 1978–2018. Sci. Total Environ. 2021, 785, 147247. [Google Scholar] [CrossRef] [PubMed]
- Datta, P.; Das, S. Analysis of long-term precipitation changes in West Bengal, India: An approach to detect monotonic trends influenced by autocorrelations. Dyn. Atmos. Ocean. 2019, 88, 101118. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, S.; Fang, H.; Ding, M.; Liu, D. A study on the precipitation concentration in a Chinese region and its relationship with teleconnections indices. J. Hydrol. 2022, 612, 128203. [Google Scholar] [CrossRef]
- Hassani, H. A note on the sum of the sample autocorrelation function. Phys. A 2010, 389, 1601–1606. [Google Scholar] [CrossRef]
- Box, G.E.P.; Pierce, D.A. Distribution of residual autocorrelations in autoregressive-integrated moving average time series models. J. Am. Stat. Assoc. 1970, 65, 1509–1526. [Google Scholar] [CrossRef]
- Ljung, G.M.; Box, G.E.P. On a measure of lack of fit in time series models. Boimetrika 1978, 65, 297–303. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, S.; Fang, H.; Wang, J. Global autocorrelation test based on the Monte Carlo method and impacts of eliminating nonstationary components on the global autocorrelation test. Stoch. Environ. Res. Risk Assess. 2020, 34, 1645–1658. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper No. 56; Food and Agriculture Organization: Rome, Italy, 1998. [Google Scholar]
- Bürger, G. On trend detection. Hydrol. Process. 2017, 31, 4039–4042. [Google Scholar] [CrossRef]
- Doan, A.E. Type I and Type II Error. In Encyclopedia of Social Measurement; Kempf-Leonard, K., Ed.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 883–888. [Google Scholar]
- Liu, Z.; Wu, G. Quantifying the precipitation-temperature relationship in China during 1961–2018. Int. J. Climatol. 2022, 42, 2656–2669. [Google Scholar] [CrossRef]
- Li, M.; Chu, R.; Shen, S.; Md Towfiqul Islam, A.Z. Dynamic analysis of pan evaporation variations in the Huai River Basin, a climate transition zone in eastern China. Sci. Total Environ. 2018, 625, 496–509. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, T.; Li, Z.; Li, C.; Li, Z.; Ying, K.; Shi, C.; Jiang, L.; Zhang, W. Evaluation of Surface Relative Humidity in China from the CRA-40 and Current Reanalyses. Adv. Atmos. Sci. 2021, 38, 1958–1976. [Google Scholar] [CrossRef]
- Chauhan, A.; Singh, S.; Maurya, R.K.S.; Rani, A.; Danodia, A. Spatio-temporal and trend analysis of rain days having different intensity from 1901-2020 at regional scale in Haryana, India. Results Geophys. Sci. 2022, 10, 100041. [Google Scholar] [CrossRef]
- Mateus, C.; Potito, A. Long-term trends in daily extreme air temperature indices in Ireland from 1885 to 2018. Weather. Clim. Extrem. 2022, 36, 100464. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G.; Lombardo, F. Untenable nonstationarity: An assessment of the fitness for purpose of trend tests in hydrology. Adv. Water Resour. 2018, 111, 132–155. [Google Scholar] [CrossRef]
- Xie, Y.; Huang, Q.; Chang, J.; Liu, S.; Wang, Y. Period analysis of hydrologic series through moving-window correlation analysis method. J. Hydrol. 2016, 538, 278–292. [Google Scholar] [CrossRef]
- Ghaderpour, E. Least-squares wavelet and cross-wavelet analyses of VLBI baseline length and temperature time series: Fortaleza-Hartebeesthoek-Westford-Wettzell. Publ. Astron. Soc. Pac. 2021, 133, 014502. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Vujadinovic, T.; Hassan, Q.K. Application of the Least-Squares Wavelet software in hydrology: Athabasca River Basin. J. Hydrol. Reg. Stud. 2021, 36, 100847. [Google Scholar] [CrossRef]


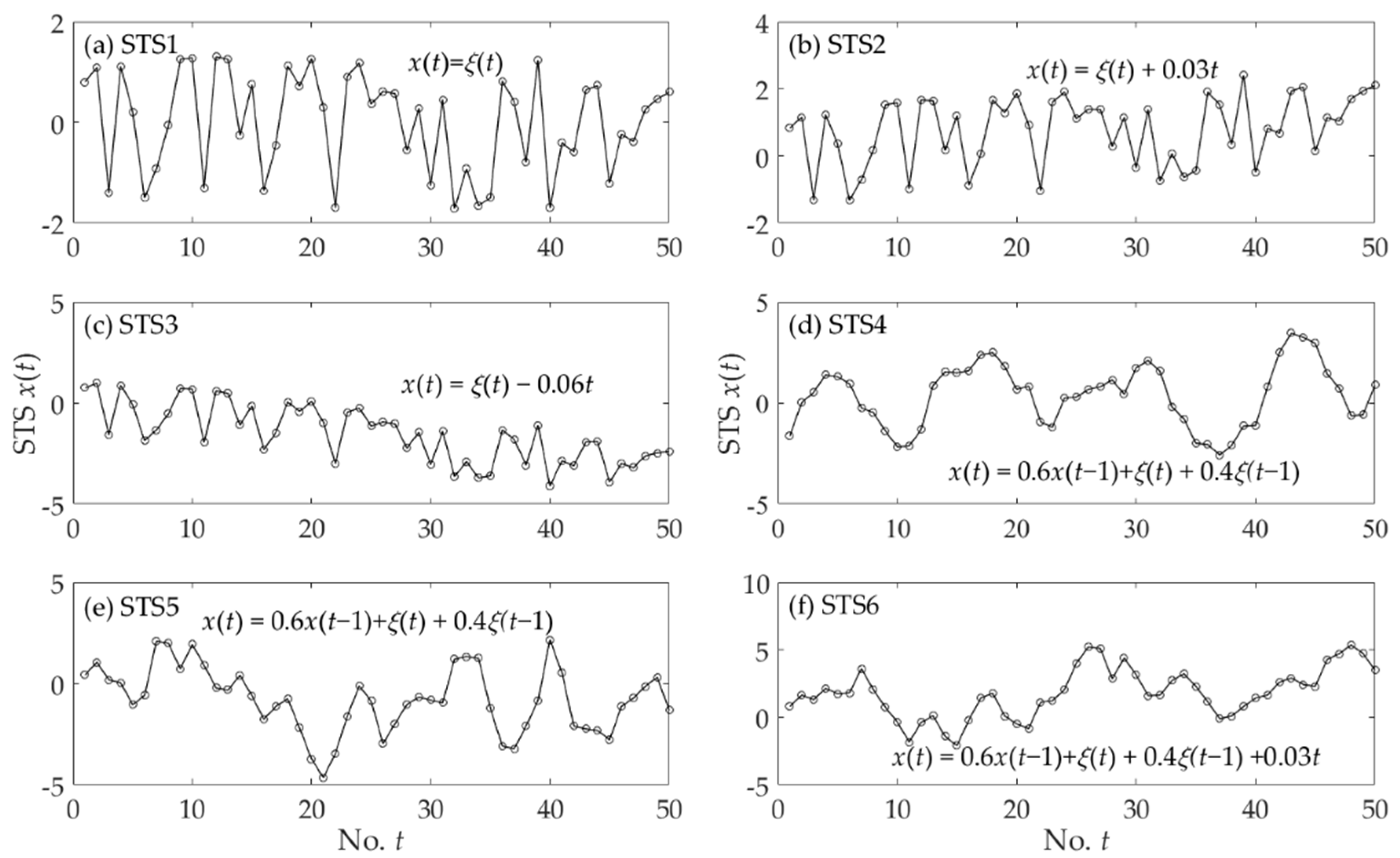


| STS | STS1 | STS2 | STS3 | STS4 | STS5 | STS6 |
|---|---|---|---|---|---|---|
| Result I | 1 | 2A | 2B | 3A | 3B | 4 |
| Result II | 1 | 2A | 2B | 3A | 3B | 4 |
| kI | 0 | 0.019 | −0.071 | 0 | 0 | 0.060 |
| kII | 0 | 0.019 | −0.071 | 0 | 0 | 0.059 |
| γa | 0 | 0 | 0 | 0 | 0.66 | 0.75 |
| f1 (%) | 0 | 0 | 0 | 0 | 66.0 | 13.2 |
| f2 (%) | 0 | 0 | 0 | 0 | 34.0 | 86.8 |
| N | MMK Test | OW Operation | ||||
|---|---|---|---|---|---|---|
| α = 10% | α = 5% | α = 1% | α = 10% | α = 5% | α = 1% | |
| 30 | 58.7 | 57.8 | 48.2 | 59.3 | 59.4 | 51.4 |
| 50 | 76.3 | 81.9 | 78.8 | 76.7 | 80.8 | 78.0 |
| 100 | 83.0 | 88.8 | 95.3 | 81.1 | 87.7 | 93.0 |
| N | f(TI&TII) | f(TI&FII) | f(FI&TII) | f(FI&FII) | f(TI) | f(TII) | f(TI&TII or FI&FII) | ra |
|---|---|---|---|---|---|---|---|---|
| 30 | 56.6 | 1.2 | 2.8 | 39.4 | 57.8 | 59.4 | 96.0 | 59.0 |
| 50 | 79.9 | 2.0 | 0.9 | 17.2 | 81.9 | 80.8 | 97.1 | 82.3 |
| 100 | 87.6 | 1.2 | 0.1 | 11.1 | 88.8 | 87.7 | 98.7 | 88.8 |
| No. | Station Name | SD (h/a) | AT (°C/a) | PET (mm/a) | |||
|---|---|---|---|---|---|---|---|
| kI | kII | kI | kII | kI | kII | ||
| 1 | Huoshan | −0.02 | −0.02 | 0.02 | 0.02 | 0.00 | 0.00 |
| 2 | Hefei | −0.02 | −0.03 | 0.02 | 0.02 | 0.00 | 0.00 |
| 3 | Xinyang | −0.03 | −0.03 | 0.03 | 0.03 | 0.00 | 0.00 |
| 4 | Gushi | −0.02 | −0.02 | 0.02 | 0.02 | −1.07 | −1.07 |
| 5 | Chuxian | −0.03 | −0.03 | 0.02 | 0.02 | −2.14 | −2.14 |
| 6 | Shouxian | −0.02 | −0.02 | 0.02 | 0.02 | −1.39 | −1.39 |
| 7 | Gaoyou | −0.01 | −0.01 | 0.04 | 0.04 | 0.00 | 0.00 |
| 8 | Fuyang | −0.03 | −0.03 | 0.02 | 0.02 | −0.95 | −0.95 |
| 9 | Dongtai | −0.01 | −0.01 | 0.03 | 0.03 | 0.00 | 0.00 |
| 10 | Bengbu | 0.00 | 0.00 | 0.02 | 0.02 | 0.00 | 0.00 |
| 11 | Xuyi | −0.03 | −0.02 | 0.02 | 0.02 | −1.75 | −1.75 |
| 12 | Zhumadian | −0.03 | −0.03 | 0.02 | 0.02 | −1.94 | −1.94 |
| 13 | Suxian | −0.02 | −0.02 | 0.03 | 0.03 | −0.95 | −0.95 |
| 14 | Sheyang | −0.01 | −0.01 | 0.03 | 0.03 | 0.00 | 0.00 |
| 15 | Xihua | −0.03 | −0.03 | 0.03 | 0.03 | −3.38 | −2.94 |
| 16 | Bozhou | −0.03 | −0.03 | 0.03 | 0.03 | 0.00 | 0.00 |
| 17 | Baofeng | −0.03 | −0.03 | 0.02 | 0.02 | −3.00 | −2.97 |
| 18 | Xuchang | −0.03 | −0.03 | 0.00 | 0.00 | −1.84 | −1.97 |
| 19 | Xuzhou | −0.02 | −0.01 | 0.03 | 0.03 | −1.63 | −1.63 |
| 20 | Dangshan | −0.02 | −0.02 | 0.02 | 0.02 | −2.44 | −2.38 |
| 21 | Shangqiu | −0.04 | −0.04 | 0.02 | 0.02 | −3.50 | −3.47 |
| 22 | Zhengzhou | −0.03 | −0.03 | 0.04 | 0.04 | −2.35 | −2.49 |
| 23 | Kaifeng | −0.03 | −0.03 | 0.04 | 0.04 | −1.50 | −1.48 |
| 24 | Ganyu | −0.02 | −0.02 | 0.03 | 0.03 | −1.00 | −1.00 |
| 25 | Feixian | −0.03 | −0.03 | 0.03 | 0.03 | −2.58 | −2.59 |
| 26 | Rizhao | −0.02 | −0.02 | 0.03 | 0.03 | 0.00 | 0.00 |
| 27 | Yanzhou | −0.02 | −0.02 | 0.02 | 0.02 | −2.64 | −2.61 |
| 28 | Lvxian | −0.03 | −0.03 | 0.03 | 0.03 | 0.00 | 0.00 |
| 29 | Yiyuan | −0.03 | −0.03 | 0.03 | 0.03 | −1.45 | −1.45 |
| HCTS | Station No. | No. 1 | No. 2 | No. 3 | No. 4 | No. 5 | No. 6 | No. 7 | No. 8 | No. 9 | No. 10 | No. 11 | No. 12 | No. 13 | No. 14 | No. 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WS | kI((m/s)/a) | 0.00 | 0.00 | 0.00 | −0.03 | −0.02 | −0.02 | −0.02 | 0.00 | −0.01 | 0.00 | −0.03 | −0.02 | −0.01 | −0.01 | −0.03 |
| kII ((m/s)/a) | 0.00 | 0.00 | 0.00 | −0.03 | −0.02 | −0.02 | −0.02 | −0.01 | −0.01 | 0.00 | −0.03 | −0.02 | −0.01 | −0.01 | −0.03 | |
| γa | 0.00 | 0.00 | 0.00 | 0.30 | 0.36 | 0.50 | 0.33 | 0.86 | 0.75 | 0.00 | 0.12 | 0.50 | 0.35 | 0.49 | 0.35 | |
| f1 (%) | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 7.8 | 0.7 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| f2 (%) | 0.0 | 0.0 | 0.0 | 100.0 | 100.0 | 100.0 | 100.0 | 92.2 | 99.3 | 0.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | |
| Station No. | No. 16 | No. 17 | No. 18 | No. 19 | No. 20 | No. 21 | No. 22 | No. 23 | No. 24 | No. 25 | No. 26 | No. 27 | No. 28 | No. 29 | ||
| kI((m/s)/a) | 0.00 | −0.02 | 0.00 | −0.03 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.01 | −0.02 | −0.01 | −0.01 | ||
| kII ((m/s)/a) | 0.00 | −0.02 | 0.00 | −0.03 | −0.02 | −0.03 | −0.02 | −0.03 | −0.02 | −0.02 | −0.02 | −0.02 | −0.01 | −0.01 | ||
| γa | 0.00 | 0.21 | 0.00 | 0.11 | 0.59 | 0.24 | 0.19 | 0.38 | 0.16 | 0.10 | 0.86 | 0.54 | 0.25 | 0.32 | ||
| f1 (%) | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 5.1 | 0.0 | 0.0 | 0.0 | ||
| f2 (%) | 0.0 | 100.0 | 0.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 94.9 | 100.0 | 100.0 | 100.0 | ||
| Station No. | No. 1 | No. 2 | No. 3 | No. 4 | No. 5 | No. 6 | No. 7 | No. 8 | No. 9 | No. 10 | No. 11 | No. 12 | No. 13 | No. 14 | No. 15 | |
| RH | kI (%/a) | −0.03 | −0.04 | −0.10 | −0.08 | 0.00 | 0.00 | −0.16 | 0.00 | −0.03 | 0.00 | 0.00 | −0.05 | 0.00 | 0.00 | 0.00 |
| kII (%/a) | 0.00 | −0.04 | −0.10 | −0.08 | 0.00 | 0.00 | −0.16 | 0.00 | 0.00 | 0.00 | −0.05 | 0.00 | 0.00 | 0.00 | −0.07 | |
| γa | 0.11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.15 | 0.00 | 0.29 | 0.00 | 0.23 | 0.10 | 0.00 | 0.00 | 0.22 | |
| f1 (%) | 52.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 65.4 | 0.0 | 19.2 | 51.7 | 0.0 | 0.0 | 15.2 | |
| f2 (%) | 47.8 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 34.6 | 0.0 | 80.8 | 48.3 | 0.0 | 0.0 | 84.8 | |
| Station No. | No. 16 | No. 17 | No. 18 | No. 19 | No. 20 | No. 21 | No. 22 | No. 23 | No. 24 | No. 25 | No. 26 | No. 27 | No. 28 | No. 29 | ||
| kI (%/a) | 0.00 | 0.00 | 0.00 | −0.04 | 0.00 | 0.00 | 0.00 | 0.00 | −0.04 | 0.00 | −0.07 | 0.08 | 0.00 | 0.00 | ||
| kII (%/a) | −0.06 | 0.00 | 0.00 | −0.04 | 0.06 | 0.00 | −0.12 | −0.15 | −0.04 | 0.00 | −0.07 | 0.08 | −0.05 | 0.00 | ||
| γa | 0.18 | 0.00 | 0.00 | 0.10 | 0.22 | 0.00 | 0.41 | 0.33 | 0.00 | 0.00 | 0.10 | 0.00 | 0.15 | 0.00 | ||
| f1 (%) | 37.3 | 0.0 | 0.0 | 37.7 | 36.4 | 0.0 | 2.3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 18.6 | 0.0 | ||
| f2 (%) | 62.7 | 0.0 | 0.0 | 62.3 | 63.6 | 0.0 | 97.7 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 81.4 | 0.0 |
| HCTS | P | SD | AT | WS | RH | PET |
|---|---|---|---|---|---|---|
| Result I | 1 | 2B | 4 | 4 | 3A | 2B |
| Result II | 1 | 2B | 4 | 4 | 3A | 2B |
| kI | 0.00 | −0.02 | 0.03 | −0.02 | 0.00 | −1.26 |
| kII | 0.00 | −0.02 | 0.03 | −0.02 | 0.00 | −1.26 |
| γa | 0.00 | 0.00 | 0.10 | 0.20 | 0.00 | 0.00 |
| f1 (%) | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| f2 (%) | 0.0 | 0.0 | 100.0 | 100.0 | 0.0 | 0.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Xie, Y.; Fang, H.; Du, H.; Xu, P. Trend Test for Hydrological and Climatic Time Series Considering the Interaction of Trend and Autocorrelations. Water 2022, 14, 3006. https://doi.org/10.3390/w14193006
Liu S, Xie Y, Fang H, Du H, Xu P. Trend Test for Hydrological and Climatic Time Series Considering the Interaction of Trend and Autocorrelations. Water. 2022; 14(19):3006. https://doi.org/10.3390/w14193006
Chicago/Turabian StyleLiu, Saiyan, Yangyang Xie, Hongyuan Fang, Huihua Du, and Pengcheng Xu. 2022. "Trend Test for Hydrological and Climatic Time Series Considering the Interaction of Trend and Autocorrelations" Water 14, no. 19: 3006. https://doi.org/10.3390/w14193006
APA StyleLiu, S., Xie, Y., Fang, H., Du, H., & Xu, P. (2022). Trend Test for Hydrological and Climatic Time Series Considering the Interaction of Trend and Autocorrelations. Water, 14(19), 3006. https://doi.org/10.3390/w14193006






