Water Hammer Simulation Using Simplified Convolution-Based Unsteady Friction Model
Abstract
:1. Introduction
2. Basic Equations
3. Modelling Wall Shear Stress
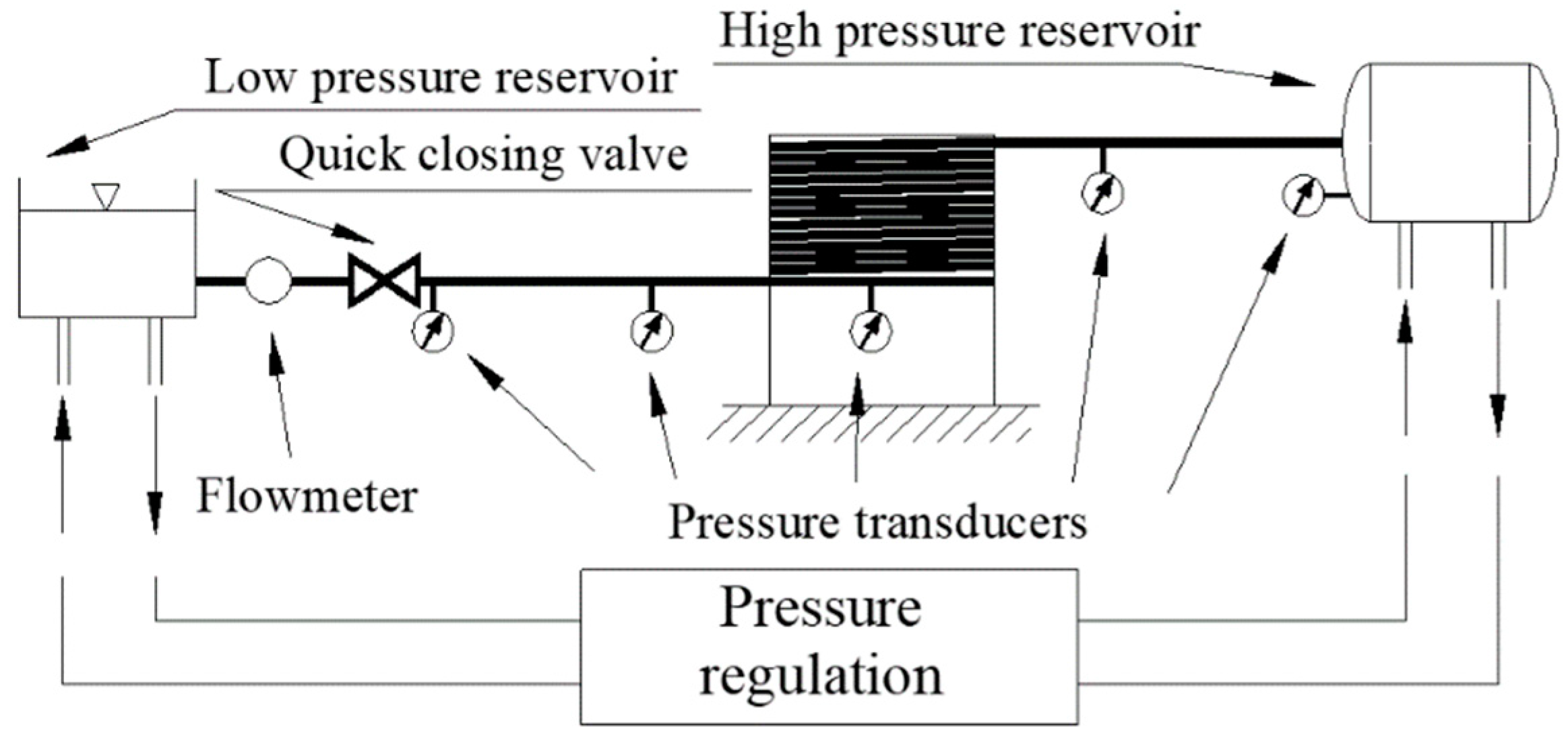
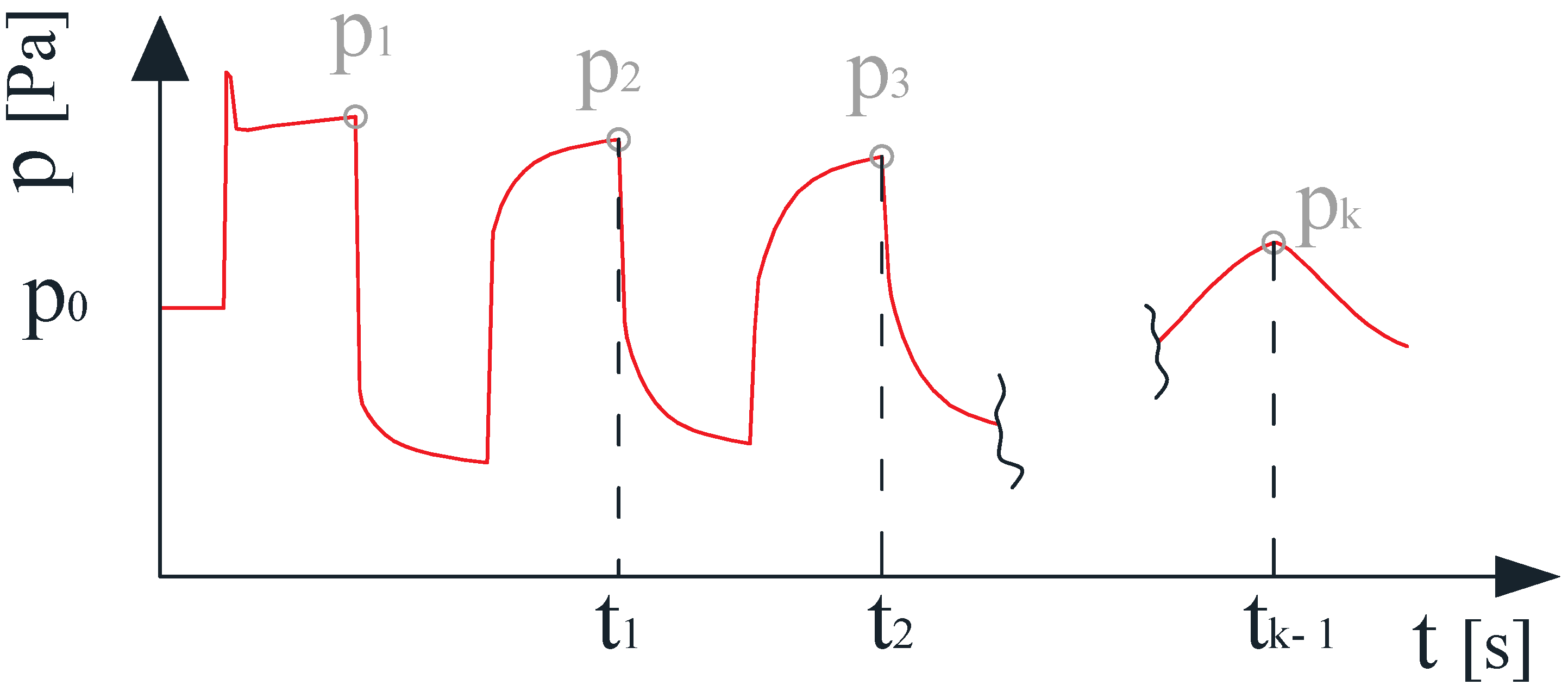
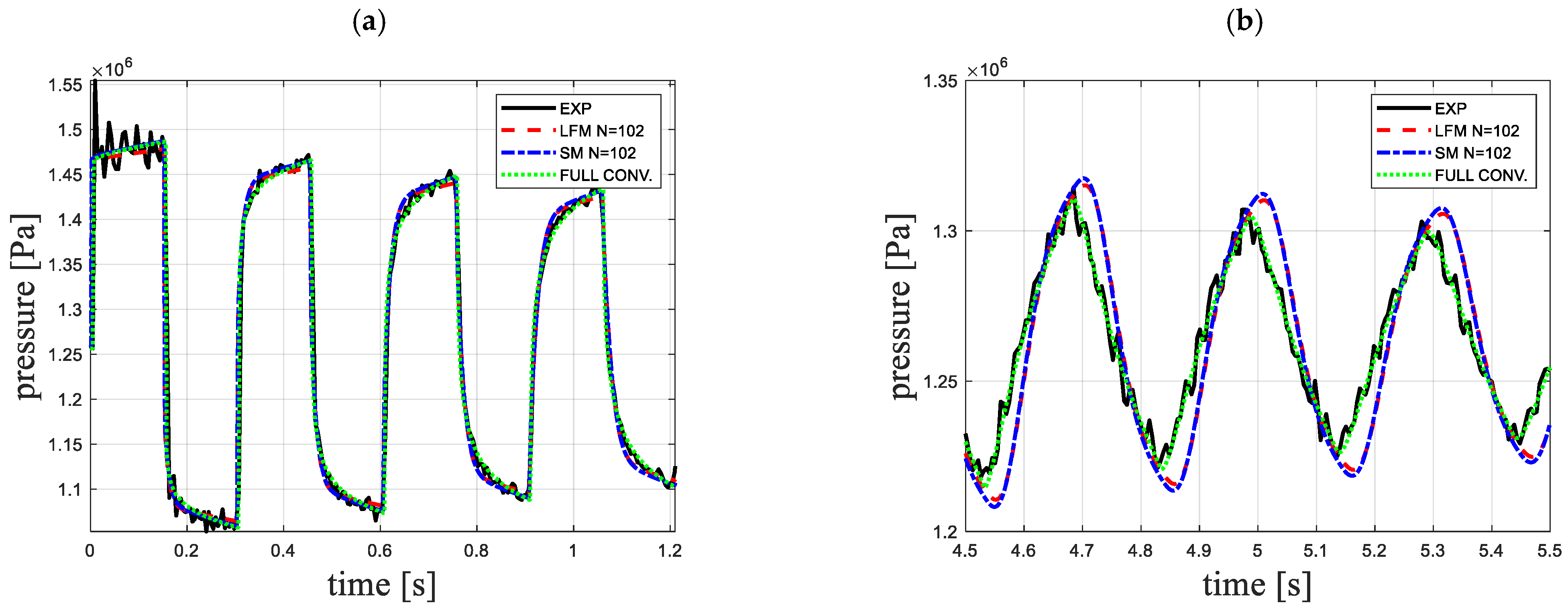
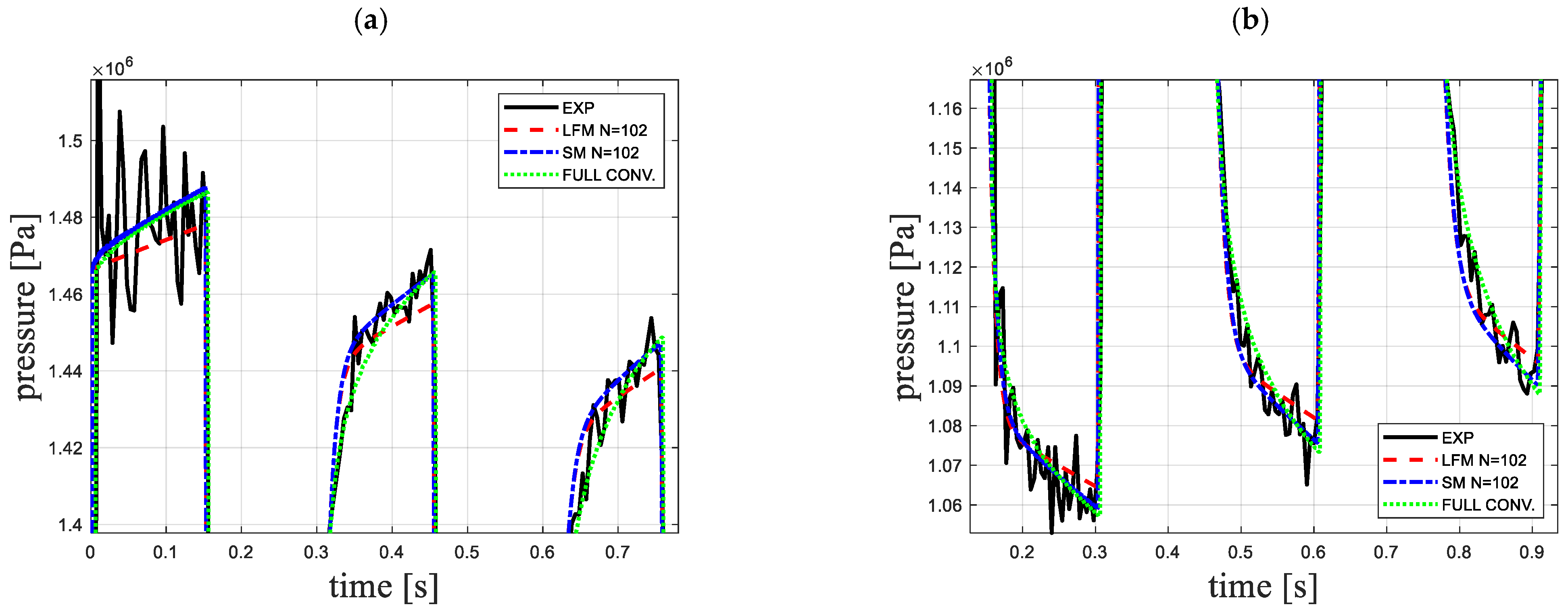
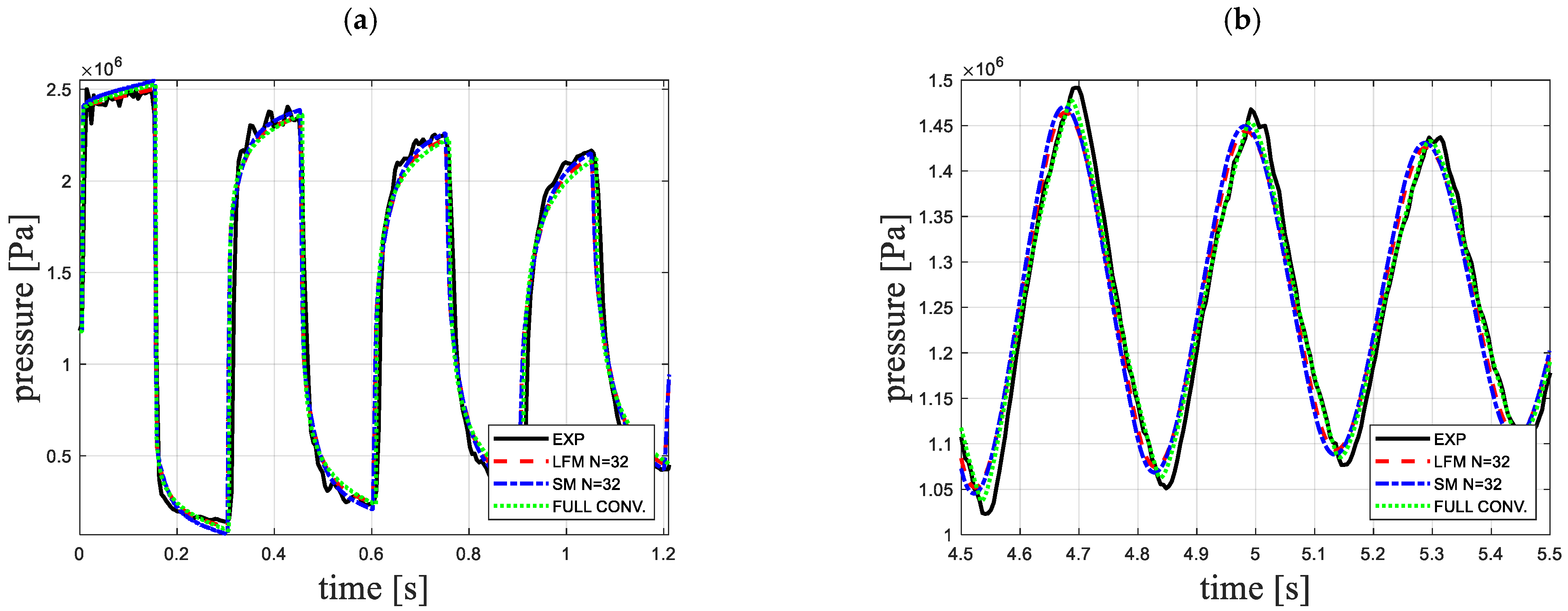
4. Analysis of the Results
- -
- Use of simplified weighting functions, as shown in this paper, built from only two exponential terms, guarantees the results of a high agreement with the experimental results;
- -
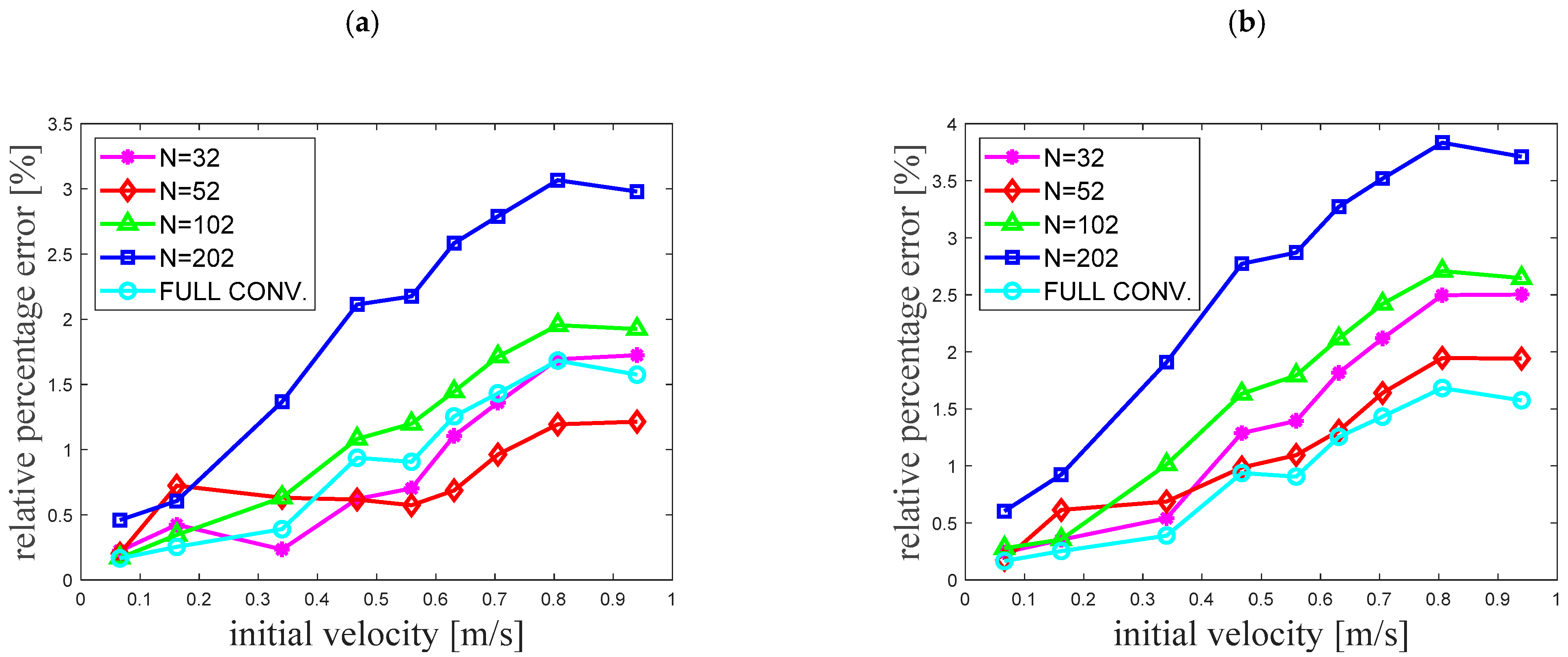
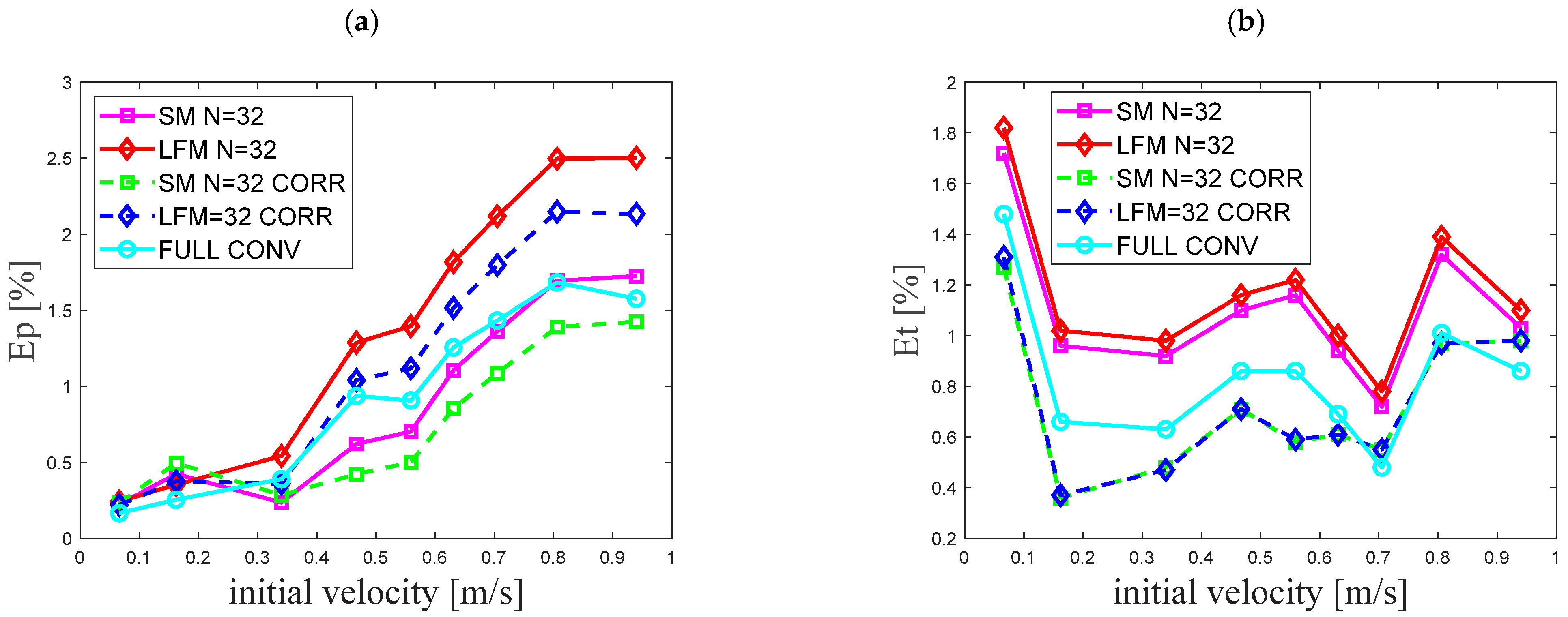
- Division of the pipeline along its length into 52 computational reaches guarantees the results with the lowest Ep errors;
- -
- The smallest errors of parameter Et representing the time compliance of the simulated amplitudes were obtained using the largest division, i.e., 202 elements. It should be noted, however, that the application of a simple correction in the form of a slight increase (decrease) in the value of the pressure wave speed c significantly reduces this error.
- -
- Necessity to use a constant time step (in a way, it is also a disadvantage of the characteristics method);
- -
- Necessity of one-time analytical calculation of appropriate values of the weighting function coefficients (from the formulas presented in the Appendix A);
- -
- Owing to the filtering of the upper range of the weighting function (from 103 to ∞), this method can only be used for modelling water hammer. Thus, preliminary analyses showed that it is not suitable for modelling typically unidirectional flows (accelerated and delayed).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ai, Bi and Ci | unsteady friction coefficients (-) |
| c | pressure wave speed (m/s) |
| D | pipe internal diameter (m) |
| Ep and Et | pressure and time compliance parameters (%) |
| e | pipe-wall thickness (m) |
| f | transient friction factor (-) |
| fq | Darcy–Weisbach friction factor (-) |
| g | acceleration due to gravity (m/s2) |
| j | imaginary unit (-) |
| k | empirical unsteady friction coefficient of the IAB model (-) |
| L | pipe length (m) |
| mi and ni | frictional weighting function coefficients (-) |
| N | number of computational reaches (-) |
| p | pressure (Pa) |
| pR | reservoir pressure (Pa) |
| R | pipe internal radius (m) |
| Re0 | initial Reynolds number (-) |
| s | Laplace parameter (1/s) |
| T | temperature in Celsius degrees (°C) |
| t | time (s) |
| u | dummy variable (s) |
| Wh | water hammer number (-) |
| w | weighting function of unsteady friction (-) |
| v | average flow velocity (m/s) |
| v0 | initial liquid velocity (m/s) |
| x | space coordinate (m) |
| yi | time dependent historical velocity effect (m/s) |
| Δt | numerical time step (s) |
| Δ | dimensionless time step (-) |
| Δx | numerical spatial step (m) |
| Δv | velocity change at the valve (m/s) |
| ε | pipe-wall roughness (m) |
| η | correction factor of unsteady friction (-) |
| κn | nth zeros of the Bessel function of type J2 (-) |
| μ | dynamic viscosity (Pa·s) |
| second viscosity coefficient (Pa·s) | |
| ν | kinematic viscosity of liquid (m2/s) |
| ρ | liquid density (kg/m3) |
| τ | wall shear stress (Pa) |
| Acronyms | |
| CBM | convolution-based model |
| CFM | Courant–Friedrichs–Lewy condition |
| CORR | corrected |
| EXP | experimental |
| FULL CONV | ineffective solution of the convolutional integral |
| HDPE | high-density polyethylene |
| IAB | instantaneous acceleration-based model |
| LFM | lumped friction method |
| MOC | method of characteristics |
| PVC | polyvinyl chloride |
| SM | standard method |
Appendix A. Estimation of the Weighting Function Coefficients
- (a)
- m1 calculation when :
- (b)
- m2 calculation when :
- (c)
- n1 calculation when :
- (d)
- n2 calculation when :
- (a)
- For laminar flow when :
- (b)
- For turbulent flow (Re > 2320):
- ●
- when calculated velocity is in range −10−5 < v < 10−5, assume v = −10−5 if it has a minus sign and v = 10−5 when it has a positive sign (to avoid division by zero);
- ●
- select optimal number of grid points through the pipe axis; it should generally not exceed N = 52;
- ●
- set yi(t) = 0 as an initial condition (for steady flow).
References
- Pothof, I.; Karney, B. Guidelines for Transient Analysis in Water Transmission and Distribution Systems. In Water Supply System Analysis—Selected Topics; IntechOpen: London, UK, 2012. [Google Scholar] [CrossRef] [Green Version]
- Jansson, M.; Andersson, M.; Karlsson, M. High-speed imaging of water hammer cavitation in oil–hydraulic pipe flow. Fluids 2022, 7, 102. [Google Scholar] [CrossRef]
- Mousavifard, M.; Norooz, R. Numerical analysis of transient cavitating pipe flow by Quasi 2D and 1D models. J. Hydraul. Res. 2022, 60, 295–310. [Google Scholar] [CrossRef]
- Warda, H.A.; Wahba, E.M.; Salah El-Din, M. Computational Fluid Dynamics (CFD) simulation of liquid column separation in pipe transients. Alex. Eng. J. 2020, 59, 3451–3462. [Google Scholar] [CrossRef]
- Zhou, L.; Li, Y.; Zhao, Y.; Ou, C.; Zhao, Y. An accurate and efficient scheme involving unsteady friction for transient pipe flow. J. Hydroinform. 2021, 23, 879–896. [Google Scholar] [CrossRef]
- Andrade, D.M.; Rachid, F.B.F. A versatile friction model for Newtonian liquids flowing under unsteady regimes in pipes. Meccanica 2022, 57, 43–72. [Google Scholar] [CrossRef]
- Guerrero, B.; Lambert, M.F.; Chin, R.C. Extension of the 1D Unsteady Friction Model for Rapidly Accelerating and Decelerating Turbulent Pipe Flows. J. Hydraul. Eng. 2022, 148, 04022014. [Google Scholar] [CrossRef]
- Santos, J.D.B.; Anjos, G.R.; Savi, M.A. An investigation of fluid-structure interaction in pipe conveying flow using reduced-order models. Meccanica 2022. [Google Scholar] [CrossRef]
- Cherian, R.M.; Sajikumar, N.; Sumam, K.S. Influence of Fluid–Structure Interaction on Pressure Fluctuations in Transient Flow. J. Pipeline Syst. Eng. Pract. 2021, 12, 04021002. [Google Scholar] [CrossRef]
- Henclik, S. Application of the shock response spectrum method to severity assessment of water hammer loads. Mech. Syst. Signal Process. 2021, 157, 107649. [Google Scholar] [CrossRef]
- Daily, J.W.; Hankey, W.L.; Olive, R.W.; Jordaan, J.M. Resistance coefficients for accelerated and decelerated flows through smooth tubes and orifices. Trans. ASME 1956, 78, 1071–1077. [Google Scholar] [CrossRef]
- Carstens, M.R.; Roller, J.E. Boundary-shear stress in unsteady turbulent pipe flow. J. Hydraul. Div. ASCE 1959, 95, 67–813. [Google Scholar] [CrossRef]
- Safwat, H.H.; van den Polder, J. Experimental and analytic data correlation study of water column separation. J. Fluids Eng. 1973, 95, 91–97. [Google Scholar] [CrossRef]
- Brunone, B.; Golia, U.M.; Greco, M. Some remarks on the momentum equations for fast transients. In Proceedings of the Hydraulic Transients with Column Separation (9th and Last Round Table of the IAHR Group), IAHR, Valencia, Spain, 4–6 September 1991; pp. 201–209. [Google Scholar]
- Vítkovský, J.; Lambert, M.; Simpson, A.; Bergant, A. Advances in unsteady friction modelling in transient pipe flow. In Proceedings of the 8th International Conference on Pressure Surges, The Hague, The Netherlands, 12–14 April 2000; pp. 471–482. [Google Scholar]
- Ramos, H.; Covas, D.; Borga, A.; Loureiro, D. Surge damping analysis in pipe systems: Modelling and experiments. J. Hydraul. Res. 2004, 42, 413–425. [Google Scholar] [CrossRef]
- Reddy, H.P.; Silva-Araya, W.F.; Chaudhry, M.H. Estimation of decay coefficients for unsteady friction for instantaneous, acceleration-based models. J. Hydraul. Eng. 2012, 138, 260–271. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, Z.; Deng, J.; Guo, X.; Lu, L. Unsteady friction model modified with compression–expansion effects in transient pipe flow. J. Water Supply Res. Technol.-Aqua 2022, 71, 330–344. [Google Scholar] [CrossRef]
- Hu, Y.; Zhou, L.; Pan, T.; Fang, H.; Li, Y.; Liu, D. Godunov-type solutions for free surface transient flow in pipeline incorporating unsteady friction. J. Water Supply: Res. Technol.-Aqua 2022, 71, 546–562. [Google Scholar] [CrossRef]
- Pan, T.; Zhou, L.; Ou, C.; Wang, P.; Liu, D. Smoothed particle hydrodynamics with unsteady friction model for water hammer pipe flow. J. Hydraul. Eng. 2022, 148, 04021057. [Google Scholar] [CrossRef]
- Zhou, L.; Li, Y.; Karney, B.; Cheng, Y. Godunov-type solutions for transient pipe flow implicitly incorporating Brunone unsteady friction. J. Hydraul. Eng. 2021, 147, 04021021. [Google Scholar] [CrossRef]
- Abdeldayem, O.M.; Ferràs, D.; van der Zwan, S.; Kennedy, M. Analysis of unsteady friction models used in engineering software for water hammer analysis: Implementation Case in WANDA. Water 2021, 13, 495. [Google Scholar] [CrossRef]
- Wan, W.; Mehmood, K. Instantaneous acceleration-based modeling of pumping systems response under transient events. Int. J. Mech. Sci. 2022, 224, 107354. [Google Scholar] [CrossRef]
- Zielke, W. Frequency-dependent friction in transient pipe flow. J. ASME 1968, 90, 109–115. [Google Scholar] [CrossRef]
- Trikha, A.K. An efficient method for simulating frequency-dependent friction in transient liquid flow. J. Fluids Eng. ASME 1975, 97, 97–105. [Google Scholar] [CrossRef]
- Kagawa, T.; Lee, I.; Kitagawa, A.; Takenaka, T. High speed and accurate computing method of frequency-dependent friction in laminar pipe flow for characteristics method. Trans. Jpn. Soc. Mech. Eng. Part A 1983, 49, 2638–2644. [Google Scholar] [CrossRef]
- Schohl, G.A. Improved approximate method for simulating frequency—Dependent friction in transient laminar flow. J. Fluids Eng. ASME 1993, 115, 420–424. [Google Scholar] [CrossRef]
- Urbanowicz, K. Fast and accurate modelling of frictional transient pipe flow. Z. Angew. Math. Mech. 2018, 98, 802–823. [Google Scholar] [CrossRef]
- Adamkowski, A.; Lewandowski, M. Experimental examination of unsteady friction models for transient pipe flow simulation. J. Fluids Eng. 2006, 128, 1351–1363. [Google Scholar] [CrossRef]
- Vardy, A.E.; Brown, J.M.B. Transient turbulent friction in smooth pipe flows. J. Sound Vib. 2003, 259, 1011–1036. [Google Scholar] [CrossRef]
- Urbanowicz, K. Modern modeling of water hammer. Pol. Marit. Res. 2017, 24, 68–77. [Google Scholar] [CrossRef]
- Johnston, D.N. Efficient methods for numerical modelling of laminar friction in fluid lines. J. Dyn. Syst. Meas. Control ASME 2006, 128, 829–834. [Google Scholar] [CrossRef]
- Wylie, E.B.; Streeter, V.L.; Suo, L. Fluid Transients in Systems; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Bergant, A.; Simpson, A.R.; Vítkovský, J.P. Developments in unsteady pipe flow friction modelling. J. Hydraul. Res. 2001, 39, 249–257. [Google Scholar] [CrossRef] [Green Version]
- Vítkovský, J.P.; Bergant, A.; Simpson, A.R.; Lambert, M.F. Systematic evaluation of one-dimensional unsteady friction models in simple pipelines. J. Hydraul. Eng. 2006, 132, 696–708. [Google Scholar] [CrossRef] [Green Version]
- Zielke, W. Frequency-Dependent Friction in Transient Pipe Flow. Doctoral Thesis, University of Michigan, Ann Arbor, MI, USA, 1966. [Google Scholar]
- Zarzycki, Z. On weighting function for wall shear stress during unsteady turbulent pipe flow. In Proceedings of the 8th International Conference on Pressure Surges, BHR Group, The Hague, The Netherlands, 12–14 April 2000; pp. 529–543. [Google Scholar]
- Vardy, A.E.; Brown, J.M.B. Transient turbulent flow in fully-rough pipes. J. Sound Vib. 2004, 270, 233–257. [Google Scholar] [CrossRef]
- Urbanowicz, K.; Bergant, A.; Karadzić, U.; Jing, H.; Kodura, A. Numerical investigation of the cavitating flow for constant water hammer number. J. Phys. Conf. Ser. 2021, 1736, 012040. [Google Scholar] [CrossRef]
- Vardy, A.E.; Brown, J.M.B. Evaluation of unsteady wall shear stress by Zielke’s method. J. Hydraul. Eng. 2010, 136, 453–456. [Google Scholar] [CrossRef]
- Xu, Y.; Jiao, Z.; Zhao, L. Fast meshless solution with lumped friction for water hammer. In Proceedings of the BATH/ASME 2020 Symposium on Fluid Power and Motion Control, Virtual, 9–11 September 2020. FPMC2020-2789, V001T01A043. [Google Scholar] [CrossRef]
- Urbanowicz, K. Analytical expressions for effective weighting functions used during simulations of water hammer. J. Theor. Appl. Mech. 2017, 55, 1029–1040. [Google Scholar] [CrossRef] [Green Version]
- Bergant, A.; Karadžić, U.; Vítkovský, J.P.; Vušanović, I.; Simpson, A.R. A discrete gas cavity model that considers the frictional effects of unsteady pipe flow. Stroj. Vestn.-J. Mech. Eng. 2005, 51, 692–710. [Google Scholar]
- Adamkowski, A.; Henclik, S.; Janicki, W.; Lewandowski, M. The influence of pipeline supports stiffness onto the water hammer run. Eur. J. Mech. B/Fluids 2016, 61, 297–303. [Google Scholar] [CrossRef] [Green Version]
- Henclik, S. Numerical modeling of water hammer with fluid–structure interaction in a pipeline with viscoelastic supports. J. Fluids Struct. 2018, 76, 469–487. [Google Scholar] [CrossRef]
- Holmboe, E.L. Viscous Distortion in Wave Propagation as Applied to Waterhammer and Short Pulses. Doctoral Thesis, Carnegie Institute of Technology, Pittsburgh, PA, USA, 1964. [Google Scholar]
- Covas, D. Inverse Transient Analysis for Leak Detection and Calibration of Water Pipe Systems Modelling Special Dynamic Effects. Doctoral Thesis, Imperial College London (University of London), London, UK, 2003. [Google Scholar]

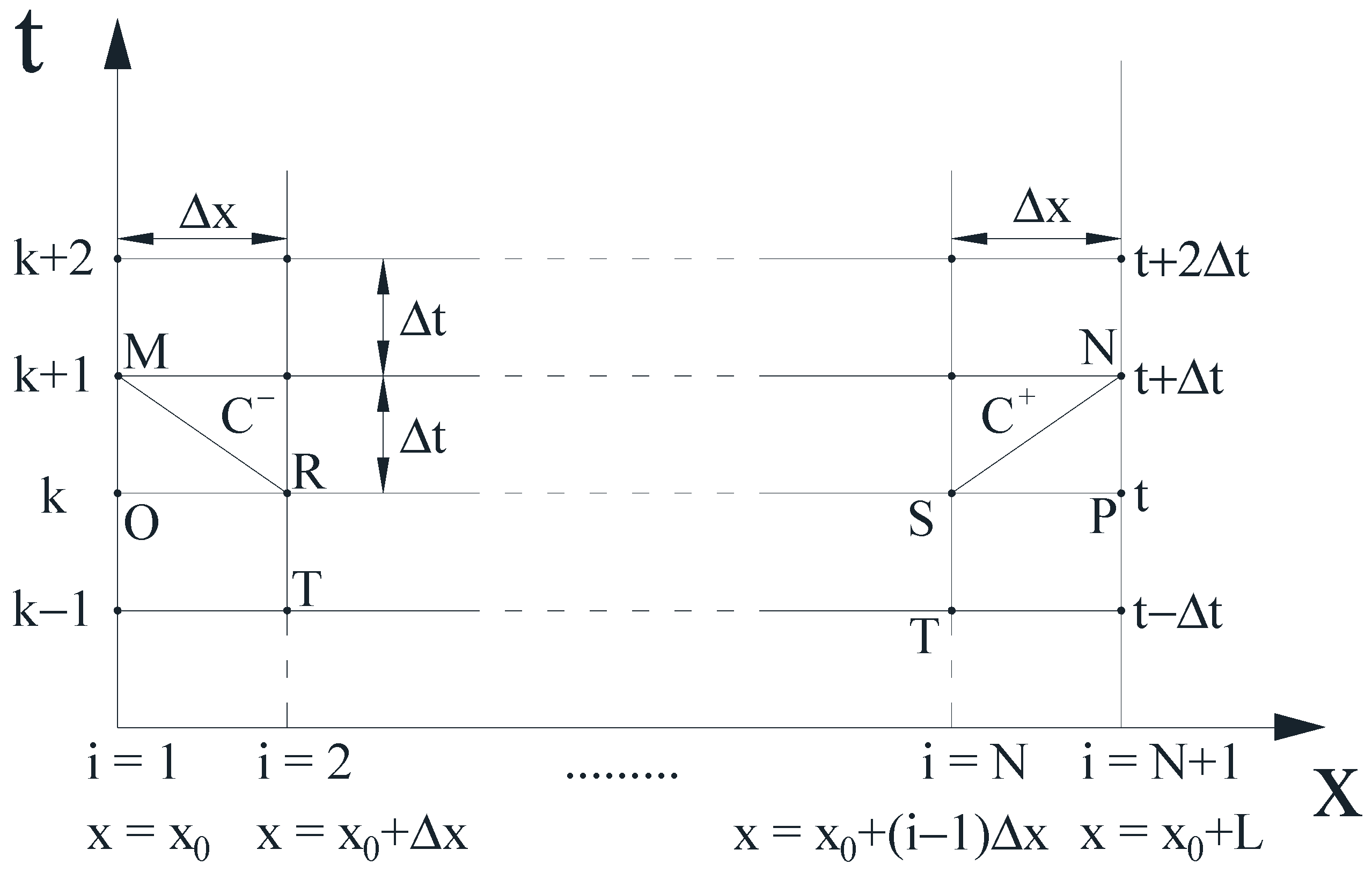



| 98.11 | 0.016 | 0.001 | 0.003 | 22.6 | 9.493·10−7 | 997.65 |
| Case | v0 [m/s] | Re0 [−] | pR [Pa] | c [m/s] |
|---|---|---|---|---|
| 01 | 0.066 | 1100 | 1.265·106 | 1300 |
| 02 | 0.162 | 2750 | 1.264·106 | 1300 |
| 03 | 0.340 | 5750 | 1.265·106 | 1300 |
| 04 | 0.467 | 7900 | 1.253·106 | 1305 |
| 05 | 0.559 | 9400 | 1.264·106 | 1300 |
| 06 | 0.631 | 10,650 | 1.264·106 | 1303 |
| 07 | 0.705 | 11,900 | 1.263·106 | 1300 |
| 08 | 0.806 | 13,600 | 1.263·106 | 1300 |
| 09 | 0.940 | 15,850 | 1.264·106 | 1300 |
| Case | Velocity [m/s] | SM—Standard Method | LFM—Lumped Friction Method | Full Conv. | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N = 32 | N = 52 | N = 102 | N = 202 | N = 32 | N = 52 | N = 102 | N = 202 | |||
| 01 | 0.066 | 1.72 | 1.59 | 1.49 | 1.49 | 1.82 | 1.66 | 1.54 | 1.53 | 1.48 |
| 02 | 0.162 | 0.96 | 0.82 | 0.70 | 0.70 | 1.02 | 0.87 | 0.75 | 0.75 | 0.66 |
| 03 | 0.340 | 0.92 | 0.78 | 0.67 | 0.66 | 0.98 | 0.84 | 0.73 | 0.72 | 0.63 |
| 04 | 0.467 | 1.10 | 0.97 | 0.86 | 0.85 | 1.16 | 1.02 | 0.91 | 0.90 | 0.86 |
| 05 | 0.559 | 1.16 | 1.03 | 0.93 | 0.91 | 1.22 | 1.09 | 0.98 | 0.97 | 0.86 |
| 06 | 0.631 | 0.94 | 0.81 | 0.71 | 0.69 | 1.00 | 0.87 | 0.77 | 0.75 | 0.69 |
| 07 | 0.705 | 0.72 | 0.61 | 0.50 | 0.48 | 0.78 | 0.65 | 0.56 | 0.54 | 0.48 |
| 08 | 0.806 | 1.32 | 1.21 | 1.11 | 1.09 | 1.39 | 1.26 | 1.16 | 1.14 | 1.01 |
| 09 | 0.940 | 1.03 | 0.92 | 0.82 | 0.80 | 1.10 | 0.98 | 0.88 | 0.85 | 0.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urbanowicz, K.; Bergant, A.; Stosiak, M.; Deptuła, A.; Karpenko, M.; Kubrak, M.; Kodura, A. Water Hammer Simulation Using Simplified Convolution-Based Unsteady Friction Model. Water 2022, 14, 3151. https://doi.org/10.3390/w14193151
Urbanowicz K, Bergant A, Stosiak M, Deptuła A, Karpenko M, Kubrak M, Kodura A. Water Hammer Simulation Using Simplified Convolution-Based Unsteady Friction Model. Water. 2022; 14(19):3151. https://doi.org/10.3390/w14193151
Chicago/Turabian StyleUrbanowicz, Kamil, Anton Bergant, Michał Stosiak, Adam Deptuła, Mykola Karpenko, Michał Kubrak, and Apoloniusz Kodura. 2022. "Water Hammer Simulation Using Simplified Convolution-Based Unsteady Friction Model" Water 14, no. 19: 3151. https://doi.org/10.3390/w14193151
APA StyleUrbanowicz, K., Bergant, A., Stosiak, M., Deptuła, A., Karpenko, M., Kubrak, M., & Kodura, A. (2022). Water Hammer Simulation Using Simplified Convolution-Based Unsteady Friction Model. Water, 14(19), 3151. https://doi.org/10.3390/w14193151












