Analysis of the Runoff Component Variation Mechanisms in the Cold Region of Northeastern China under Climate Change
Abstract
:1. Introduction
2. Materials and Methods
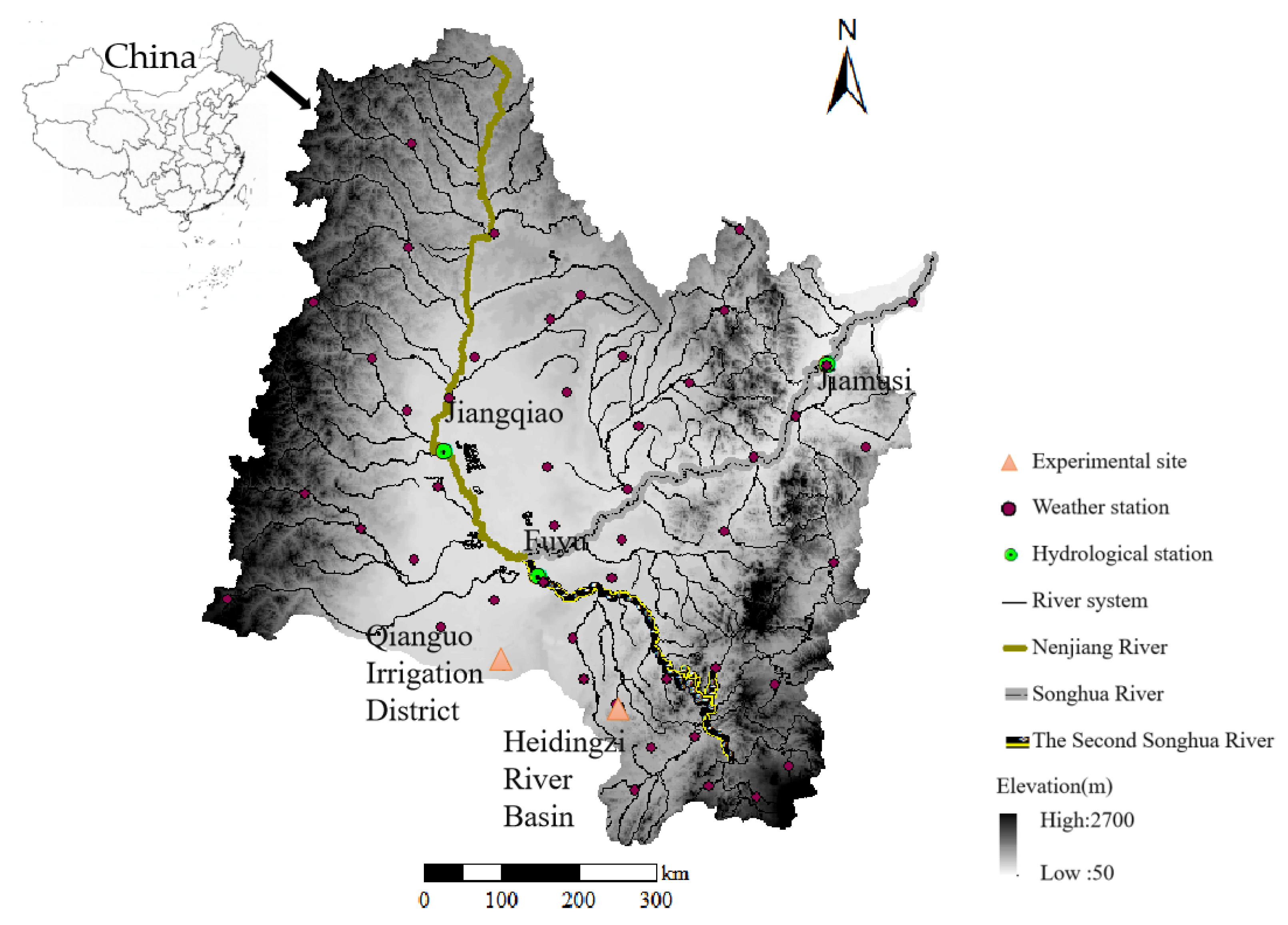
2.1. Study Area
2.2. Data Collection
2.3. Research Method
2.3.1. Principles of the WEP-N Model Hydrological Cycle
2.3.2. Multifactor Attribution Analysis
3. Results and Discussion
3.1. Model Calibration and Validation
3.2. Influence of Climate Change and Water Use on the Annual Runoff Variation in the SRB
3.3. Effect of Climate Change on Production Flow Variation during Different Periods in the SRB
3.3.1. Production Flow Variation during Different Periods
3.3.2. Production Flow Component Variation during Freezing Period
3.3.3. Production Flow Component Variation during the Thawing Period
3.3.4. Variations in Production Flow Components during the Non-Freeze-Thaw Period
3.4. Effects of Climate Change on Groundwater Recharge
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oyler, J.W.; Dobrowski, S.Z.; Ballantyne, A.P.; Klene, A.E.; Running, S.W. Artificial amplification of warming trends across the mountains of the western United States. Geophys. Res. Lett. 2015, 42, 153–161. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Li, H.; Duan, Z.; Ren, Z.; Meng, X.; Pan, X. Modelling glacier variation and its impact on water resource in the Urumqi Glacier No. 1 in Central Asia. Sci. Total Environ. 2018, 644, 1160–1170. [Google Scholar] [CrossRef]
- Yang, D.; Ye, B.; Kane, D.L. Streamflow changes over Siberian Yenisei River Basin. J. Hydrol. 2004, 296, 59–80. [Google Scholar] [CrossRef]
- Yang, W.; Jin, F.; Si, Y.; Li, Z. Runoff change controlled by combined effects of multiple environmental factors in a headwater catchment with cold and arid climate in northwest China. Sci. Total Environ. 2021, 756, 143995. [Google Scholar] [CrossRef]
- Li, B.; Chen, Y.; Chen, Z.; Li, W. Trends in runoff versus climate change in typical rivers in the arid region of northwest China. Quat. Int. 2012, 282, 87–95. [Google Scholar] [CrossRef]
- Pan, C.G.; Kamp, U.; Munkhjargal, M.; Halvorson, S.J.; Dashtseren, A.; Walther, M. An estimated contribution of glacier runoff to Mongolia’s Upper Khovd River Basin in the Altai Mountains. Mt. Res. Dev. 2019, 39, R12–R20. [Google Scholar] [CrossRef] [Green Version]
- Tang, Q.; Oki, T. Historical and future changes in streamflow and continental runoff. In Terrestrial Water Cycle and Climate Change: Natural and Human-Induced Impacts; John Wiley & Sons: Hoboken, NJ, USA, 2016; Volume 221, pp. 17–37. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, S.; Xu, J.; Shangguan, D. Glacier change and glacier runoff variation in the Tuotuo River basin, the source region of Yangtze River in western China. Environ. Geol. 2008, 56, 59–68. [Google Scholar] [CrossRef]
- Shiyin, L.; Yong, Z.; Yingsong, Z.; Yongjian, D. Estimation of glacier runoff and future trends in the Yangtze River source region, China. J. Glaciol. 2009, 55, 353–362. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Weng, B.; Man, Z.; Yu, Z.; Zhao, J. Analyzing the contributions of climate change and human activities on runoff in the Northeast Tibet Plateau. J. Hydrol. Reg. Stud. 2020, 27, 100639. [Google Scholar] [CrossRef]
- Rakhimova, M.; Liu, T.; Bissenbayeva, S.; Mukanov, Y.; Gafforov, K.S.; Bekpergenova, Z.; Gulakhmadov, A. Assessment of the impacts of climate change and human activities on runoff using climate elasticity method and general circulation model (GCM) in the Buqtyrma River Basin, Kazakhstan. Sustainability 2020, 12, 4968. [Google Scholar] [CrossRef]
- Qiu, L.; Peng, D.; Xu, Z.; Liu, W. Identification of the impacts of climate changes and human activities on runoff in the upper and middle reaches of the Heihe River basin, China. J. Water Clim. Chang. 2016, 7, 251–262. [Google Scholar] [CrossRef]
- Thompson, L.G.; Brecher, H.H.; Mosley-Thompson, E.; Hardy, D.R.; Mark, B.G. Glacier loss on Kilimanjaro continues unabated. Proc. Natl. Acad. Sci. USA 2009, 106, 19770–19775. [Google Scholar] [CrossRef] [Green Version]
- Otte, I.; Detsch, F.; Mwangomo, E.; Hemp, A.; Appelhans, T.; Nauss, T. Multidecadal trends and interannual variability of rainfall as observed from five lowland stations at Mt. Kilimanjaro, Tanzania. J. Hydrol. Meteorol. 2017, 18, 349–361. [Google Scholar] [CrossRef]
- Hemp, A. Climate change-driven forest fires marginalize the impact of ice cap wasting on Kilimanjaro. Glob. Chang. Biol. 2005, 11, 1013–1023. [Google Scholar] [CrossRef]
- Bozkurt, D.; Rojas, M.; Boisier, J.P.; Valdivieso, J. Climate change impacts on hydroclimatic regimes and extremes over Andean basins in central Chile. Hydrol. Earth Syst. Sci. Discuss. 2017, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Crespo, P.J.; Feyen, J.; Buytaert, W.; Bücker, A.; Breuer, L.; Frede, H.; Ramírez, M. Identifying controls of the rainfall–runoff response of small catchments in the tropical Andes (Ecuador). J. Hydrol. 2011, 407, 164–174. [Google Scholar] [CrossRef]
- St. Jacques, J.M.; Sauchyn, D.J.; Zhao, Y. Northern Rocky Mountain streamflow records: Global warming trends, human impacts or natural variability? Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Arrigoni, A.S.; Greenwood, M.C.; Moore, J.N. Relative impact of anthropogenic modifications versus climate change on the natural flow regimes of rivers in the Northern Rocky Mountains, United States. Water Resour. Res. 2010, 46, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Miao, C.; Yang, L.; Liu, B.; Gao, Y.; Li, S. Streamflow changes and its influencing factors in the mainstream of the Songhua River basin, Northeast China over the past 50 years. Environ. Earth Sci. 2011, 63, 489–499. [Google Scholar] [CrossRef]
- Chu, H.; Wei, J.; Qiu, J.; Li, Q.; Wang, G. Identification of the impact of climate change and human activities on rainfall-runoff relationship variation in the Three-River Headwaters region. Ecol. Indic. 2019, 106, 105516. [Google Scholar] [CrossRef]
- Meng, F.; Su, F.; Yang, D.; Tong, K.; Hao, Z. Impacts of recent climate change on the hydrology in the source region of the Yellow River Basin. J. Hydrol. Reg. Stud. 2016, 6, 66–81. [Google Scholar] [CrossRef] [Green Version]
- Song, C.; Wang, G.; Sun, X.; Hu, Z. River runoff components change variably and respond differently to climate change in the Eurasian Arctic and Qinghai-Tibet Plateau permafrost regions. J. Hydrol. 2021, 601, 126653. [Google Scholar] [CrossRef]
- Li, J.; Zhou, Z.; Wang, H.; Liu, J.; Jia, Y.; Hu, P.; Xu, C. Development of WEP-COR model to simulate land surface water and energy budgets in a cold region. Hydrol. Res. 2019, 50, 99–116. [Google Scholar] [CrossRef]
- Burn, D.H.; Elnur, M. Detection of hydrologic trends and variability. J. Hydrol. 2002, 255, 107–122. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. Appl. Statist. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Liu, J.J.; Zhou, Z.H.; Jia, Y.W.; Wang, H. A new method to quantitatively separate the effects of multi-factors on the water cycle evolution. J. Hydraul. Eng. 2014, 45, 658–665. [Google Scholar] [CrossRef]
- Liu, S.; Zhou, Z.; Liu, J.; Wang, K.; Li, J.; Wang, P.; Xie, X.; Jia, Y.; Wang, H. Simulation of water and nitrogen movement mechanism in cold regions during freeze-thaw period based on a distributed nonpoint source pollution model closely coupled water, heat, and nitrogen processes at the watershed scale. Environ. Sci. Pollut. Res. Int. 2022. [CrossRef]
- Flerchinger, G.N.; Saxton, K.E. Simultaneous heat and water model of a freezing snow-residue-soil system I. Theory and development. Trans. ASAE. 1989, 32, 573–576. [Google Scholar] [CrossRef]
- Hock, R. A distributed temperature-index ice-and snowmelt model including potential direct solar radiation. J. Glaciol. 1999, 45, 101–111. [Google Scholar] [CrossRef]
- Monteith, J.L. Principles of Environmental Physics; Edward Arnold: London, UK, 1973; Volume 214. [Google Scholar]
- Jia, Y.; Tamai, N. Integrated analysis of water and heat balances in Tokyo metropolis with a distributed model. J. Jpn. Soc. Hydrol. Water Resour. 1998, 11, 150–163. [Google Scholar] [CrossRef]
- Jia, Y.; Wang, H.; Zhou, Z.H.; Qiu, Y.Q.; Luo, X.Y.; Wang, J.H.; Yan, D.H.; Qin, D.Y. Development of the WEP-L distributed hydrological model and dynamic assessment of water resources in the Yellow River basin. J. Hydrol. 2006, 331, 606–629. [Google Scholar] [CrossRef]
- Zaradny, H. Groundwater Flow in Saturated and Unsaturated Soil; A. A. Balkema Uitgevers: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Hubbert, M.K. Darcy’s law and the field equations of the flow of underground fluids. Trans. AIME. 1956, 207, 222–239. [Google Scholar] [CrossRef]
- Ponce, V.M. Diffusion wave modeling of catchment dynamics. J. Hydraul. Eng. 1986, 112, 716–727. [Google Scholar] [CrossRef]
- Shang, S. Numerical simulation of soil moisture and thermal regime in winter. Irrig. Drain. 1997, 16, 12–17. (In Chinese) [Google Scholar]
- Wang, S.; Prasher, S.O.; Patel, R.M.; Yang, C.; Kim, S.; Madani, A.; Macdonald, P.M.; Robertson, S.D. Fate and transport of nitrogen compounds in a cold region soil using DRAINMOD. Comput. Electron. Agric. 2006, 53, 113–121. [Google Scholar] [CrossRef]
- Wang, A.W.; Xie, Z.H.; Feng, X.; Tian, X.; Qin, P. A soil water and heat transfer model including changes in soil frost and thaw fronts. Sci. China Earth Sci. 2014, 57, 1325–1339. [Google Scholar] [CrossRef]
- Lei, Z.D.; Yang, S.X.; Xie, C.S. Soil Hydrodynamics; Tsinghua University Press: Beijing, China, 1988; pp. 8–12. (In Chinese) [Google Scholar]
- Hansson, K.; Šimůnek, J.; Mizoguchi, M.; Lundin, L.C.; Van Genuchten, M.T. Water flow and heat transport in frozen soil: Numerical solution and freeze-thaw applications. Vadose Zone J. 2004, 3, 692–704. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Tian, F.; Yang, L.; Hu, H. Exploring the spatial variability of contributions from climate variation and change in catchment properties to streamflow decrease in a mesoscale basin by three different methods. J. Hydrol. 2014, 508, 170–180. [Google Scholar] [CrossRef]
- Falkenmark, M.; Widstrand, C. Population and water resources: A delicate balance. Popul. Bull. 1992, 47, 1–36. [Google Scholar] [PubMed]
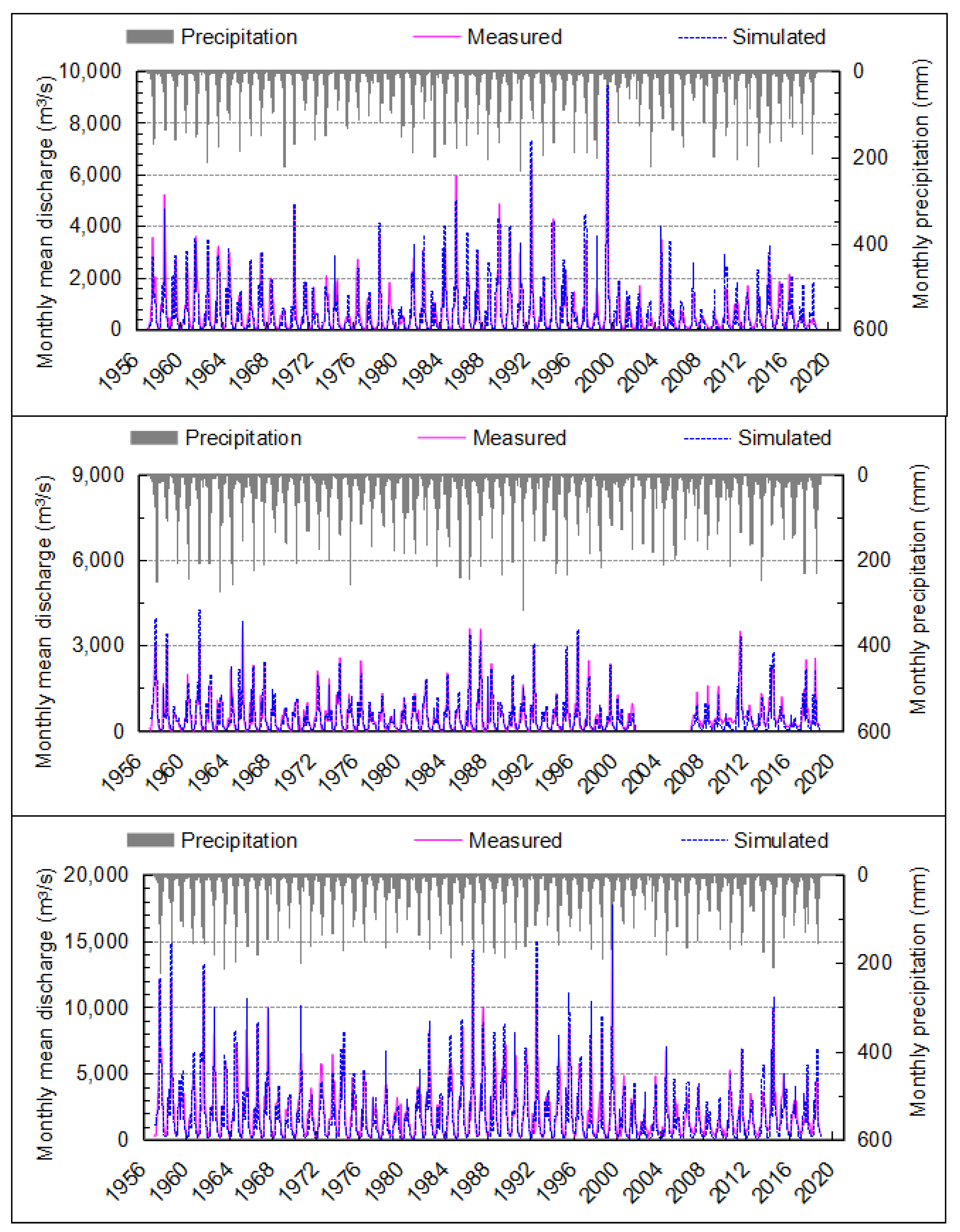

| Hydrological Site | NSE | RE/% | ||
|---|---|---|---|---|
| 1956–1990 | 1991–2018 | 1956–1990 | 1991–2018 | |
| Jiangqiao | 0.80 | 0.77 | 4.98 | 4.85 |
| Fuyu | 0.86 | 0.73 | 4.26 | −0.41 |
| Jiamusi | 0.81 | 0.76 | 4.51 | 0.83 |
| Scenario | Description |
|---|---|
| BS | Base scenario |
| BSW | Change base period water use data to that of the change period |
| BSM | Change base period meteorological data to that of the change period |
| BSWM | Change base period water use and meteorological data to those of the change period |
| Period | Temperature (°C) | Precipitation (mm) | Water Use (Billion m3) |
|---|---|---|---|
| Base | 2.5 | 540.2 | 19.2 |
| Change | 3.8 | 514.2 | 27.7 |
| Variation | 1.3 | 26.0 | 8.5 |
| Item | Annual Runoff | |
|---|---|---|
| BS | 73.7 billion m3 | |
| BSWM | 52.9 billion m3 | |
| BSWM-BS | −20.7 billion m3 | |
| Rate of change | −28.2% | |
| Contribution rate | Water use | 23.0% |
| Climate change | 77.0% | |
| Scenario | Description |
|---|---|
| BS | Base scenario |
| BST | Change base period air temperature to that of the change period |
| BSP | Change base period precipitation data to that of the change period |
| BSTP | Change base period air temperature and precipitation data to those of the change period |
| Item | Annual Production Flow | |||
|---|---|---|---|---|
| Production Flow | Surface Flow | Soil Flow | Base Flow | |
| BS | 160.2 mm | 131.2 mm | 2.8 mm | 26.2 mm |
| BSTP | 133.3 mm | 114.5 mm | 2.2 mm | 16.6 mm |
| BSTP-BS | −26.9 mm | −16.7 mm | −0.6 mm | −9.6 mm |
| Rate of change | −16.8% | −12.7% | −21.4% | −36.6% |
| 100.0% | 62.1% | 2.2% | 35.7% | |
| Period | Meteorological Factor | Whole Year | Freezing Period | Thawing Period | Non-Freeze-Thaw Period |
|---|---|---|---|---|---|
| Base | Precipitation (mm) | 540.1 | 23.6 | 71.5 | 445.0 |
| Temperature (°C) | 2.5 | −14.9 | 4.2 | 15.5 | |
| Change | Precipitation (mm) | 519.3 | 29.5 | 86.5 | 403.3 |
| Temperature (°C) | 3.9 | −13.8 | 5.8 | 16.9 | |
| Variation | Precipitation (mm) | −20.8 | 6.0 | 15.0 | −41.7 |
| Temperature (°C) | 1.3 | 1.1 | 1.6 | 1.4 |
| Item | Production Flow during Different Periods of Year | |||
|---|---|---|---|---|
| Whole Year | Freezing Period | Thawing Period | Non-Freeze-Thaw Period | |
| BS | 160.2 mm | 7.4 mm | 37.2 mm | 115.6 mm |
| BSTP | 133.3 mm | 7.7 mm | 31.8 mm | 93.8 mm |
| BSTP-BS | −27.0 mm | 0.3 mm | −5.5 mm | −21.8 mm |
| 100.0% | −1.1% | 20.4% | 80.7% | |
| Item | Production Flow during Freezing Period | |||
|---|---|---|---|---|
| Total Production Flow | Surface Flow | Soil Flow | Base Flow | |
| BS | 7.4 mm | 0.4 mm | 0.1 mm | 6.9 mm |
| BSTP | 8.4 mm | 0.8 mm | 0.1 mm | 7.5 mm |
| BSTP-BS | 1.0 mm | 0.4 mm | 0.0 mm | 0.6 mm |
| Rate of change | 13.9% | 99.3% | 31.2% | 8.5% |
| 100.0% | 40.0% | 0% | 60% | |
| Item | Production Flow during Thawing Period | |||
|---|---|---|---|---|
| Total Production Flow | Surface Flow | Soil Flow | BASE flow | |
| BS | 37.2 mm | 31.7 mm | 1.0 mm | 4.6 mm |
| BSTP | 31.8 mm | 28.1 mm | 1.1 mm | 4.9 mm |
| BSTP-BS | −3.2 mm | −3.6 mm | 0.1 mm | 0.3 mm |
| Rate of change | −8.4% | −11.4% | 10.0% | 6.5% |
| 100.0% | 112.5% | −3.1% | −9.4% | |
| Item | Production Flow during Non-Freeze-Thaw Period | |||
|---|---|---|---|---|
| Total Production Flow | Surface Flow | Soil Flow | Base Flow | |
| BS | 115.6 mm | 99.1 mm | 1.7 mm | 14.8 mm |
| BSTP | 97.9 mm | 87.6 mm | 1.5 mm | 8.8 mm |
| BSTP-BS | −17.7 mm | −11.5 mm | −0.2 mm | −6.0 mm |
| Rate of change | −15.3% | −11.6% | −11.8% | −40.5% |
| 100.0% | 65.0% | 1.1% | 33.9% | |
| Item | Groundwater Recharge during Different Periods | ||
|---|---|---|---|
| Freezing Period | Thawing Period | Non-Freeze-Thaw Period | |
| BS | 6.1 mm | 12.2 mm | 37.1 mm |
| BSTP | 6.7 mm | 12.7 mm | 27.9 mm |
| BSTP-BS | 0.6 mm | 0.5 mm | −9.2 mm |
| Rate of change | 9.2% | 4.1% | −24.8% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Zhou, Z.; Liu, J.; Li, J.; Wang, P.; Li, C.; Xie, X.; Jia, Y.; Wang, H. Analysis of the Runoff Component Variation Mechanisms in the Cold Region of Northeastern China under Climate Change. Water 2022, 14, 3170. https://doi.org/10.3390/w14193170
Liu S, Zhou Z, Liu J, Li J, Wang P, Li C, Xie X, Jia Y, Wang H. Analysis of the Runoff Component Variation Mechanisms in the Cold Region of Northeastern China under Climate Change. Water. 2022; 14(19):3170. https://doi.org/10.3390/w14193170
Chicago/Turabian StyleLiu, Shuiqing, Zuhao Zhou, Jiajia Liu, Jia Li, Pengxiang Wang, Cuimei Li, Xinmin Xie, Yangwen Jia, and Hao Wang. 2022. "Analysis of the Runoff Component Variation Mechanisms in the Cold Region of Northeastern China under Climate Change" Water 14, no. 19: 3170. https://doi.org/10.3390/w14193170
APA StyleLiu, S., Zhou, Z., Liu, J., Li, J., Wang, P., Li, C., Xie, X., Jia, Y., & Wang, H. (2022). Analysis of the Runoff Component Variation Mechanisms in the Cold Region of Northeastern China under Climate Change. Water, 14(19), 3170. https://doi.org/10.3390/w14193170







