A Multi-Model Multi-Scale Approach to Estimate the Impact of the 2007 Large-Scale Forest Fires in Peloponnese, Greece
Abstract
:1. Introduction
2. Materials and Methods
2.1. Hydrological Modelling
2.1.1. The Soil and Water Assessment Tool (SWAT)
2.1.2. HEC-HMS
2.1.3. SCS-CN Method
2.1.4. Suite of GR Hydrological Models
2.2. The Testing Framework
2.3. Description of the Study Area
2.4. Data Used
3. Results
3.1. Modelling of Daily Streamflow
3.1.1. SWAT—Pre-Fire Period
3.1.2. SWAT—Post Fire Period
3.1.3. Suite of GR Hydrological Models
3.2. Modelling of Flood Events
3.2.1. General
3.2.2. Calibration and Verification of the Model in Pre-Fire Conditions
3.2.3. On Floods in Post-Fire Conditions
Flood Event in November 2007
Flood Event in 9 January 2009–18 January 2009
Flood Event in 14 October 2009–17 October 2009
Flood Event in 5 February 2012–10 February 2012
3.3. Comparing Results at the Two Timescales
4. Discussion
5. Conclusions
- For both the daily and hourly time steps, there was a significant increase in the Curve Number after the fire was found.
- For daily streamflow, the SWAT model gave low values of the Nash–Sutcliffe efficiency when applied to the post-fire period, after it had been calibrated and verified for the pre-fire period. However, an increase in the Curve Number by approximately 20% clearly improved the NSE for the post-fire period. The Curve Number showed a decreasing trend with respect to time after the fire, which is consistent with the presumed regeneration of the vegetation. It appeared that, when used without recalibration after the fire, the SWAT model underestimates the daily streamflow by approximately 22% on average.
- For the hourly time step study using the HEC-HMS model, the threshold of the Curve Number in burnt areas was set to 95. The results showed that for a period of approximately three years after the fire, the Curve Number was still 95 in the burnt areas during the flood events, with a slow decrease rate after the third year. However, until the fifth year, the Curve Number still remained above 90. The model underestimated the peak flow in the basin by 35–70% (60 m3/s to 300 m3/s in absolute values), whereas the model proved capable of simulating the post-fire flood events in a satisfactory way if the modeller has knowledge about the change in Curve Number due to fire.
- The linear trend lines of the Curve Number in burnt areas with respect to time for the two-timescales show the same slope but different intercepts, with the latter being larger for the hourly scale. This implies that the magnitude of the Curve Number is systematically higher in the case of the hourly time step, but its rate of temporal decrease is timescale-independent.
- Past findings suggest that the hydrologic effects of a forest fire can be highly variable and difficulties in the model were verified in this study; specifically, in the first year after the fire, which was particularly dry, all models faced difficulties, which revealed that a unique model structure, such as that of the selected models, may not be sufficient.
- The lumped models employed in this work for daily simulations (GR Suite) showed very high performance with respect to the accuracy of prediction of the observed streamflow. Their credibility in predicting post-fire hydrological variables other than runoff was found to be considerably enhanced by employing parameter constraints in calibration. In this work, the use of the pre-fire value of parameter X1 (runoff production store capacity) as the upper bound in post-fire calibration proved particularly useful for a realistic simulation of internal model variables, such as actual evapotranspiration and percolation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rycroft, H.B. A Note on the Immediate Effects of Veldburning on Stormflow in a Jonkershoek Stream Catchment. J. S. Afr. For. Assoc. 1947, 15, 80–88. [Google Scholar] [CrossRef]
- Colman, C.A. Fire and water in southern California’s mountains. Calif. For. Range Exp. Stn. Misc. Pap. 1953, 3, 1–8. [Google Scholar]
- Lavabre, J.; Torres, D.S.; Cernesson, F. Changes in the hydrological response of a small Mediterranean basin a year after a wildfire. J. Hydrol. 1993, 142, 273–299. [Google Scholar] [CrossRef]
- Townsend, S.A.; Douglas, M.M. The effect of three fire regimes on stream water quality, water yield and export coefficients in a tropical savanna (northern Australia). J. Hydrol. 2000, 229, 118–137. [Google Scholar] [CrossRef]
- Pierson, F.B.; Robichaud, P.R.; Spaeth, K.E. Spatial and temporal effects of wildfire on the hydrology of a steep rangeland watershed. Hydrol. Process. 2001, 15, 2905–2916. [Google Scholar] [CrossRef]
- Springer, E.P.; Hawkins, R.H. Curve number and peakflow responses following the Cerro Grande fire on a small watershed. In Proceedings of the Watershed Management Conference “Managing Watersheds for Human and Natural Impacts Engineering, Ecological and Economic Challenges”, Williamsburg, VA, USA, 19–22 July 2005. [Google Scholar]
- Shakesby, R.A.; Doerr, S.H. Wildfire as a hydrological and geomorphological agent. Earth-Sci. Rev. 2006, 74, 269–307. [Google Scholar] [CrossRef]
- Lane, P.N.; Sheridan, G.J.; Noske, P.J. Changes in sediment loads and discharge from small mountain catchments following wildfire in south eastern Australia. J. Hydrol. 2006, 331, 495–510. [Google Scholar] [CrossRef]
- Moody, J.A.; Martin, D.A. Initial hydrologic and geomorphic response following a wildfire in the Colorado Front Range. Earth Surf. Process. Landf. 2001, 26, 1049–1070. [Google Scholar] [CrossRef]
- Moody, J.A.; Martin, D.A.; Haire, S.L.; Kinner, D.A. Linking runoff response to burn severity after a wildfire. Hydrol. Process. 2008, 22, 2063–2074. [Google Scholar] [CrossRef]
- Stoof, C.R.; Vervoort, R.W.; Iwema, J.; van den Elsen, E.; Ferreira, A.J.D.; Ritsema, C.J. Hydrological response of a small catchment burned by experimental fire. Hydrol. Earth Syst. Sci. 2012, 16, 267–285. [Google Scholar] [CrossRef] [Green Version]
- Scott, D.F.; Van Wyk, D.B. The effects of wildfire on soil wettability and hydrological behaviour of an afforested catchment. J. Hydrol. 1990, 121, 239–256. [Google Scholar] [CrossRef]
- Scott, D.F. The hydrological effects of fire in South African mountain catchments. J. Hydrol. 1993, 150, 409–432. [Google Scholar] [CrossRef] [Green Version]
- Soler, M.; Sala, M.; Gallart, F. Post fire evolution of runoff and erosion during an eighteen month period. Soil erosion and degradation as a consequence of forest fires. In Soil Degradation and Desertification in Mediterranean Environments; Sala, M., Rubio, J.L., Eds.; Geoforma Ediciones: Logroño, Spain, 1994; pp. 149–161. [Google Scholar]
- Soto, B.; Basanta, R.; Benito, E.; Perez, R.; Diaz-Fierros, F. Runoff and erosion from burnt soils in northwest Spain. Soil Erosion as a consequence of forest fires. In Soil Degradation and Desertification in Mediterranean Environments; Sala, M., Rubio, J.L., Eds.; Geoforma Ediciones: Logroño, Spain, 1994; pp. 91–98. [Google Scholar]
- Mayor, A.G.; Bautista, S.; Llovet, J.; Bellot, J. Post-fire hydrological and erosional responses of a Mediterranean landscape: Seven years of catchment-scale dynamics. Catena 2007, 71, 68–75. [Google Scholar] [CrossRef]
- Bart, R.; Hope, A. Streamflow response to fire in large catchments of a Mediterranean-climate region using paired-catchment experiments. J. Hydrol. 2010, 388, 370–378. [Google Scholar] [CrossRef]
- Inbar, M.; Tamir, M.; Wittenberg, L. Runoff and erosion processes after a forest fire in Mount Carmel, a Mediterranean area. Geomorphol. 1998, 24, 17–33. [Google Scholar] [CrossRef]
- Rulli, M.C.; Rosso, R. Hydrologic response of upland catchments to wildfires. Adv. Water Resour. 2007, 30, 2072–2086. [Google Scholar] [CrossRef]
- Cerrelli, G.A. FIRE HYDRO, a simplified method for predicting peak discharges to assist in the design of flood protection measures for western wildfires. In Proceedings of the Watershed Management Conference “Managing Watersheds for Human and Natural Impacts Engineering, Ecological and Economic Challenges”, Williamsburg, VA, USA, 19–22 July 2005. [Google Scholar]
- Feikema, P.M.; Sherwin, C.B.; Lane, P.N. Influence of climate, fire severity and forest mortality on predictions of long term streamflow: Potential effect of the 2009 wildfire on Melbourne’s water supply catchments. J. Hydrol. 2013, 488, 1–16. [Google Scholar] [CrossRef]
- Batelis, S.C.; Nalbantis, I. Potential effects of forest fires on streamflow in the Enipeas river basin, Thessaly, Greece. Environ. Process. 2014, 1, 73–85. [Google Scholar] [CrossRef] [Green Version]
- Versini, P.A.; Velasco, M.; Cabello, A.; Sempere-Torres, D. Hydrological impact of forest fires and climate change in a Mediterranean basin. Nat. Hazards 2013, 66, 609–628. [Google Scholar] [CrossRef]
- Earles, T.A.; Wright, K.R.; Brown, C.; Langan, T.E. Los Alamos forest fire impact modelling. J. Am. Water Resour. Assoc. 2004, 40, 371–384. [Google Scholar] [CrossRef]
- Goodrich, D.C.; Canfield, H.E.; Burns, I.S.; Semmens, D.J.; Miller, S.N.; Hernandez, M.; Levick, L.R.; Guertin, D.P.; Kepner, W.G. Rapid post-fire hydrologic watershed assessment using the AGWA GIS-based hydrologic modeling tool. In Proceedings of the Watershed Management Conference “Managing Watersheds for Human and Natural Impacts Engineering, Ecological and Economic Challenges”, Williamsburg, VA, USA, 19–22 July 2005. [Google Scholar]
- Cydzik, K.; Hogue, T.S. Modeling Postfire Response and Recovery using the Hydrologic Engineering Center Hydrologic Modeling System (HEC-HMS). J. Am. Water Resour. Assoc. 2009, 45, 702–714. [Google Scholar] [CrossRef]
- Nalbantis, I.; Lymperopoulos, S. Assessment of flood frequency after forest fires in small ungauged basins based on uncertain measurements. Hydrol. Sci. J. 2012, 57, 52–72. [Google Scholar] [CrossRef]
- Papathanasiou, C.; Alonistioti, D.; Kasella, A.; Makropoulos, C.; Mimikou, M. The impact of forest fires on the vulnerability of peri-urban catchments to flood events (The case of the Eastern Attica Region). Glob. NEST 2012, 14, 294–302. [Google Scholar]
- Papathanasiou, C.; Makropoulos, C.; Mimikou, M. Hydrological modelling for flood forecasting: Calibrating the post-fire initial conditions. J. Hydrol. 2015, 529, 1838–1850. [Google Scholar] [CrossRef]
- McLin, S.G.; Springer, E.P.; Lane, L.J. Predicting floodplain boundary changes following the Cerro Grande wildfire. Hydrol. Process. 2001, 15, 2967–2980. [Google Scholar] [CrossRef]
- Havel, A.; Tasdighi, A.; Arabi, M. Assessing the hydrologic response to wildfires in mountainous regions. Hydrol. Earth Syst. Sci. 2017, 22, 2527–2550. [Google Scholar] [CrossRef] [Green Version]
- NRCS. Hydrologic Soil Cover Complexes. In National Engineering Manual; USDA Natural Resources Conservation Service; NRCS: Washington, DC, USA, 2004; Chapter 9; p. 210-VI-NEH. [Google Scholar]
- Bertalanffy Von, L. General Systems Theory; Braziller: New York, NY, USA, 1962. [Google Scholar]
- Beven, K.J.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Arnold, J.G.; Williams, J.R.; Srinivasan, R.; King, K.W. SWAT: Soil and Water Assessment Tool; US Department of Agriculture, Agricultural Research Service: Temple, TX, USA, 1999.
- Neitsch, S.L.; Arnold, J.G.; Williams, J.R. Soil and Water Assessment Tool User’s Manual; US Department of Agriculture, Agricultural Research Service: Temple, TX, USA, 1999.
- Neitsch, S.L.; Arnold, J.G.; Kiniry, G.R.; Williams, J.R. Soil and Water Assessment Theoretical Tool Documentation; US Department of Agriculture, Agricultural Research Service: Temple, TX, USA, 2005.
- Bladon, K.D.; Silins, U.; Emelko, M.B.; Flannigan, M.; Dupont, D.; Robinne, F.; Wang, X.; Parisien, M.A.; Stone, M.; Thompson, D.K.; et al. Assessing the Impact of Active Land Management in Mitigating Wildfire Threat to Source Water Supply Quality; AGU Fall Meeting Abstracts: Washington, DC, USA, 2014; Volume 1, p. 4. [Google Scholar]
- Havel, A. Hydrologic and Hydraulic Response to Wildfires in the Upper Cache la Poudre Watershed Using a SWAT and HEC-RAS Model Cascade. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 2016. [Google Scholar]
- Liu, J.; Paul, S.; Manguerra, H. ArcSWAT Modeling Analysis for Post-Wildfire Logging Impacts on Sediment and Water Yields at Salmon-Challis National Forest, Idaho, USA. In Proceedings of the Watershed Management 2015 Symposium, Reston, VA, USA, 5–7 August 2015; pp. 240–250. [Google Scholar]
- Narsimlu, B.; Gosain, A.K.; Chahar, B.R.; Singh, S.K.; Srivastava, P.K. SWAT model calibration and uncertainty analysis for streamflow prediction in the Kunwari River Basin, India, using sequential uncertainty fitting. Environ. Process. 2015, 2, 79–95. [Google Scholar] [CrossRef]
- Putz, G.; Burke, J.M.; Smith, D.W.; Chanasyk, D.S.; Prepas, E.E.; Mapfumo, E. Modelling the effects of boreal forest landscape management upon streamflow and water quality: Basic concepts and considerations. J. Environ. Eng. Sci. 2003, 2, S87–S101. [Google Scholar] [CrossRef]
- Stengel, V.G. Comparing Simulated Hydrologic Response Before and After the 2011 Bastrop Complex Wildfire. Ph.D. Thesis, Texas State University, San Marcos, TX, USA, 2014. [Google Scholar]
- Watson, F.G. Large Scale, Long Term, Physically Based Modelling of the Effects of Land Cover Change on Forest Water Yield. Ph.D. Thesis, University of Melbourne, Melbourne, Australia, 1999. [Google Scholar]
- Goswami, M.; O’Connor, K.M.; Bhattarai, K.P. Development of regionalisation procedures using a multi-model approach for flow simulation in an ungauged catchment. J. Hydrol. 2007, 333, 517–531. [Google Scholar] [CrossRef]
- Sivapalan, M.; Takeuchi, K.; Franks, S.W.; Gupta, V.K.; Karambiri, H.; Lakshmi, V.; Liang, X.; McDonnell, J.J.; Mendiondo, E.M.; O’Connell, P.E.; et al. IAHS Decade on Predictions in Ungauged Basins (PUB), 2003–2012: Shaping an exciting future for the hydrological sciences. Hydrol. Sci. J. 2003, 48, 857–880. [Google Scholar] [CrossRef] [Green Version]
- Watson, F.G.; Vertessy, R.A.; Grayson, R.B. Large-scale modelling of forest hydrological processes and their long-term effect on water yield. Hydrol. Process. 1999, 13, 689–700. [Google Scholar] [CrossRef]
- Lane, P.N.; Feikema, P.M.; Sherwin, C.B.; Peel, M.C.; Freebairn, A.C. Modelling the long term water yield impact of wildfire and other forest disturbance in Eucalypt forests. Environ. Model. Softw. 2010, 25, 467–478. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Y.; Vaze, J.; Lane, P.; Xu, S. Improving runoff estimates using remote sensing vegetation data for bushfire impacted catchments. Agr. For. Meteorol. 2013, 182, 332–341. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Y.; Vaze, J.; Lane, P.; Xu, S. Impact of bushfire and climate variability on streamflow from forested catchments in southeast Australia. Hydrol. Sci. J. 2015, 60, 1340–1360. [Google Scholar] [CrossRef] [Green Version]
- US Army Corps of Engineers Hydrologic Engineering Center. Hydrologic Modeling System. In HEC-HMS User’s Manual; Hydrologic Engineering Center: Davis, CA, USA, 2015. [Google Scholar]
- DeBano, L.F. The role of fire and soil heating on water repellency in wildland environments: A review. J. Hydrol. 2000, 231, 195–206. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Le Moine, N. Le Bassin Versant de Surface vu Par le Souterrain: Une Voie D’amélioration des Performances et du Réalisme des Modèles Pluie-débit? Ph.D. Thesis, University Paris 6, Paris, France, 2008. [Google Scholar]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Mathevet, T.; Andréassian, V. A downward structural sensitivity analysis of hydrological models to improve low-flow simulation. J. Hydrol. 2011, 411, 66–76. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- WWF. Ecological Assessment of the Wildfires of August 2007 in the Peloponnese; World Wide Fund: Greece, Athens, 2007. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from ambient air temperature. Am. Soc. Agric. Eng. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Roy, D.P.; Boschetti, L.; Trigg, S.N. Remote sensing of fire severity: Assessing the performance of the normalized burn ratio. IEEE Geosci. Remote Sens. Lett. 2006, 3, 112–116. [Google Scholar] [CrossRef] [Green Version]
- Escuin, S.; Navarro, R.; Fernandez, P. Fire severity assessment by using NBR (Normalized Burn Ratio) and NDVI (Normalized Difference Vegetation Index) derived from LANDSAT TM/ETM images. Int. J. Remote Sens. 2008, 29, 1053–1073. [Google Scholar] [CrossRef]
- Keeley, J.E. Fire intensity, fire severity and burn severity: A brief review and suggested usage. Int. J. Wildland Fire 2009, 18, 116–126. [Google Scholar] [CrossRef]
- Saxe, S.; Hogue, T.S.; Hay, L. Characterization and evaluation of controls on post-fire streamflow response across western US watersheds. Hydrol. Earth Syst. Sci. 2018, 22, 1221–1237. [Google Scholar] [CrossRef] [Green Version]
- Michel, C. Hydrologie appliquée aux petits bassins ruraux. In Hydrology Handbook; Cemagref: Anthony, France, 1991. (In French) [Google Scholar]
- Montanari, A.; Young, G.; Savenije, H.H.G.; Hughes, D.; Wagener, T.; Ren, L.L.; Koutsoyiannis, D.; Cudennec, C.; Toth, E.; Grimaldi, S.; et al. “Panta Rhei—Everything flows”: Change in hydrology and society—The IAHS scientific decade 2013–2022. Hydrol. Sci. J. 2013, 58, 1256–1275. [Google Scholar] [CrossRef]
- Wagener, T.; Gupta, H.V. Model identification for hydrological forecasting under uncertainty. Stoch. Environ. Res. Risk Assess. 2005, 19, 378–387. [Google Scholar] [CrossRef]
- Box, G.E. Science and statistics. J. Am. Stat. Assoc. 1976, 71, 791–799. [Google Scholar] [CrossRef]
- BAER. Burned Area Emergency Rehabilitation Plan for Cerro Grande Fire; US Forest Service: Los Alamos, NM, USA, 2000.
- Fortesa, J.; Latron, J.; García-Comendador, J.; Tomàs-Burguera, M.; Company, J.; Calsamiglia, A.; Estrany, J. Multiple temporal scales assessment in the hydrological response of small mediterranean-climate catchments. Water 2020, 12, 299. [Google Scholar] [CrossRef] [Green Version]
- Cao, L.; Elliot, W.; Long, J.W. Spatial simulation of forest road effects on hydrology and soil erosion after a wildfire. Hydrol. Process. 2021, 35, e14139. [Google Scholar] [CrossRef]
- Balocchi, F.; Rivera, D.; Arumi, J.L.; Morgenstern, U.; White, D.A.; Silberstein, R.P.; Ramírez de Arellano, P. An Analysis of the Effects of Large Wildfires on the Hydrology of Three Small Catchments in Central Chile Using Tritium-Based Measurements and Hydrological Metrics. Hydrology 2022, 9, 45. [Google Scholar] [CrossRef]
- Ruíz-García, V.H.; Borja de la Rosa, M.A.; Gómez-Díaz, J.D.; Asensio-Grima, C.; Matías-Ramos, M.; Monterroso-Rivas, A.I. Forest Fires, Land Use Changes and Their Impact on Hydrological Balance in Temperate Forests of Central Mexico. Water 2022, 14, 383. [Google Scholar] [CrossRef]
- Onyutha, C.; Willems, P. Investigation of flow-rainfall co-variation for catchments selected based on the two main sources of River Nile. Stoch. Environ. Res. Risk Assess. 2018, 32, 623–641. [Google Scholar] [CrossRef]
- Bergström, S. Development and application of a conceptual runoff model for Scandinavian catchments. In SMHI RHO 7; SMHI: Norrköping, Sweden, 1976. [Google Scholar]
- Burnash, R.J.C. The NWS River forecast system-catchment modeling. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Littleton, CO, USA, 1995; pp. 311–366. [Google Scholar]
- Boughton, W. The Australian water balance model. Environ. Model. Softw. 2004, 19, 943–956. [Google Scholar] [CrossRef]
- Onyutha, C. Hydrological Model Supported by a Step-Wise Calibration against Sub-Flows and Validation of Extreme Flow Events. Water 2019, 11, 244. [Google Scholar] [CrossRef] [Green Version]
- Waseem, M.; Mani, N.; Andiego, G.; Usman, M. A review of criteria of fit for hydrological models. Int. Res. J. Eng. Technol. (IRJET) 2017, 4, 1765–1772. [Google Scholar]
- Althoff, D.; Rodrigues, L.N. Goodness-of-fit criteria for hydrological models: Model calibration and performance assessment. J. Hydrol. 2021, 600, 126674. [Google Scholar] [CrossRef]
- Onyutha, C. A hydrological model skill score and revised R-squared. Hydrol. Res. 2022, 53, 51–64. [Google Scholar] [CrossRef]
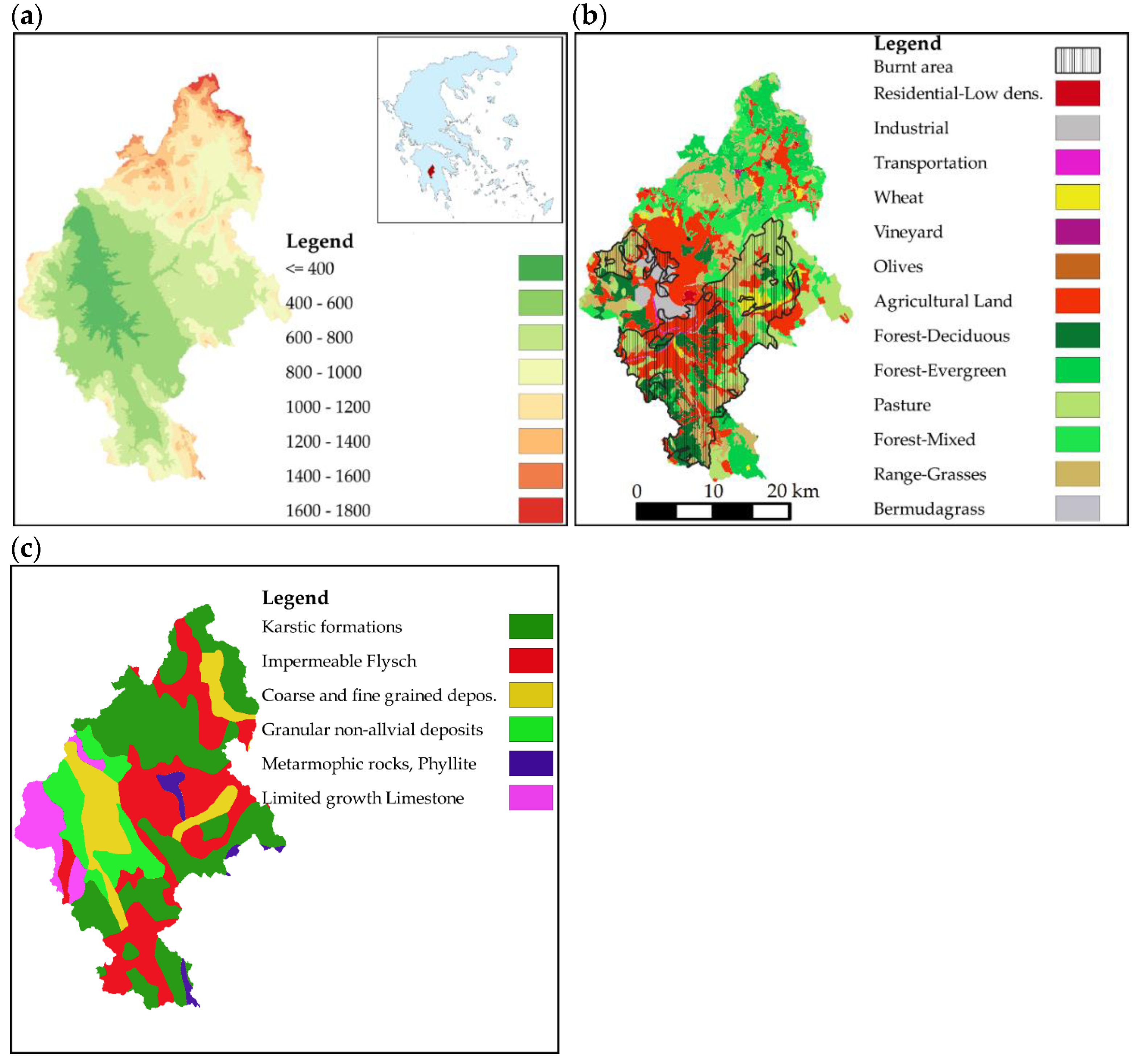









| Soil Type | Hydrologic Soil Group | Percentage of Area (%) |
|---|---|---|
| Karstic formations | A | 39.1 |
| Limited growth limestone | B | 6.8 |
| Flysch | D | 29.1 |
| Metamorphic rocks | C | 2.0 |
| Granular non-alluvial deposits | B | 10.4 |
| Coarse and fine-grained deposits of pebbles, gravel and sand | B | 12.6 |
| SWAT Land Use | Land Use | Hydrologic Soil Group | |||
|---|---|---|---|---|---|
| A | B | C | D | ||
| PAST | Pasture | 33 | 50 | - | 71 |
| UIDU | Urban Industrial | 71 | 78 | - | 89 |
| AGRL | Generic agriculture | 38 | 63 | - | 74 |
| FRSD | Deciduous Forest | 28 | 50 | - | 71 |
| FRSE | Evergreen Forest | 28 | 50 | - | 71 |
| FRST | Mixed Forest | 28 | 50 | - | 71 |
| RNGE | Grasslands/Herbaceous | 38 | 61 | - | 76 |
| Burnt areas | 36.3 | 59.7 | - | 72.8 | |
| Hydrological Year | Annual Mean of Daily Observed Flow Rate (m3/s) | Annual Mean of Daily Simulated Flow Rate (m3/s) | Percentage Error in Annual Mean of Mean Daily Flow Rate (%) | Post Fire NSE | Change of CNII (%) | New * NSE |
|---|---|---|---|---|---|---|
| 2007–08 | 1.39 | 2.56 | 81.36 | 0.429 | - | - |
| 2008–09 | 8.22 | 6.58 | −21.94 | 0.420 | 19.77 | 0.507 |
| 2009–10 | 8.86 | 8.65 | −5.98 | 0.423 | 0.00 | 0.423 |
| 2010–11 | 5.14 | 5.08 | −5.27 | 0.710 | 9.10 | 0.728 |
| 2011–12 | 9.21 | 8.17 | −15.33 | 0.779 | 9.07 | 0.798 |
| 2012–13 | 15.55 | 13.60 | −15.82 | 0.681 | 9.21 | 0.690 |
| Year | GR4J | GR5J | GR6J | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NSE Pre-Fire * | NSE Post-Fire ** | NSE Post-Fire *** | NSE Pre-Fire * | NSE Post-Fire ** | NSE Post-Fire *** | NSE Pre-Fire * | NSE Post-Fire ** | NSE Post-Fire *** | |
| 2007–2008 | 0.76 | 0.94 | 0.93 | 0.68 | 0.93 | 0.93 | 0.83 | 0.84 | 0.84 |
| 2008–2009 | 0.69 | 0.82 | 0.81 | 0.68 | 0.78 | 0.78 | 0.67 | 0.83 | 0.83 |
| 2009–2010 | 0.76 | 0.83 | 0.83 | 0.68 | 0.81 | 0.81 | 0.78 | 0.85 | 0.85 |
| 2010–2011 | 0.89 | 0.90 | 0.90 | 0.88 | 0.89 | 0.88 | 0.87 | 0.92 | 0.91 |
| 2011–2012 | 0.88 | 0.90 | 0.88 | 0.86 | 0.89 | 0.87 | 0.89 | 0.85 | 0.85 |
| 2012–2013 | 0.69 | 0.78 | 0.74 | 0.62 | 0.78 | 0.72 | 0.74 | 0.79 | 0.75 |
| Flood Event | Time lag tlag (h) | Correlation Coefficient | Flood Event | Time lag tlag (h) | Correlation Coefficient |
|---|---|---|---|---|---|
| Post-fire | Pre-fire | ||||
| 2012–2013 | 11 | 0.625 | 2005–06 | 10 | 0.656 |
| 2011–2012 | 24 | 0.645 | 2004–05 | 14 | 0.656 |
| 2010–2011 | 11 | 0.782 | 2003–04 | 9 | 0.768 |
| 2009–2010 | 12 | 0.488 | 2002–03 | 11 | 0.783 |
| 2008–2009 | 8 | 0.719 | 2000–01 | 12 | 0.645 |
| Quantity | Calibration Events | |||||
|---|---|---|---|---|---|---|
| 2000–2001 | 2003–2004 | |||||
| Observed | Simulated | Error (%) | Observed | Simulated | Error (%) | |
| Peak flow (m3/s) | 80.4 | 79.3 | 1.4 | 137.8 | 127.1 | 7.8 |
| Volume (m3) | 5267.1 | 6450.7 | −22.5 | 11,223.5 | 10,392.5 | 7.4 |
| Verification Events | ||||||
| 2002–2003 | 2004–2005 | |||||
| Observed | Simulated | Error (%) | Observed | Simulated | Error (%) | |
| Peak flow (m3/s) | 463.4 | 474.5 | −2.4 | 209.1 | 202.7 | 3.1 |
| Volume (m3) | 35,239.9 | 40,823.8 | −15.8 | 24,311.1 | 24,247.6 | 0.3 |
| November 2007 | Observed | Simulated with CNIIPreFire = 68.6 (Error %) | Simulated with CNIIburnt = 95 (Error %) | 9 January 2009–18 January 2009 | Observed | Simulated with CNIIPreFire = 68.6 (Error %) | Simulated with CNIIburnt = 95 (Error %) |
| Peak flow (m3/s) | 633.7 | 334.8 (47.2) | 566.2 (10.7) | Peak flow (m3/s) | 225.1 | 144.3 (35.9) | 225.7 (−0.2) |
| Volume (m3) | - | - | - | Volume (m3) | 14,332.2 | 13,780.4 (3.9) | 21,197.5 (−47.9) |
| 14 October 2009–17 October 2009 | Observed | Simulated with CNIIPreFire = 68.6 (Error %) | Simulated with CNIIburnt = 95 (Error %) | 5 February 2012–10 February 2012 | Observed | Simulated with CNIIPreFire = 68.6 (Error %) | Simulated with CNIIburnt = 95 (Error %) |
| Peak flow (m3/s) | 170.5 | 51.1 (70) | 133.7 (21.6) | Peak flow (m3/s) | 197.6 | 124.4 (37) | 197.6 (0.0) |
| Volume (m3) | 4262.6 | 2817.5 (33.9) | 7651.8 (−79.5) | Volume (m3) | 21,104.7 | 14,323.9 (32.1) | 23,159.5 (−9.7) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Batelis, S.C.; Nalbantis, I. A Multi-Model Multi-Scale Approach to Estimate the Impact of the 2007 Large-Scale Forest Fires in Peloponnese, Greece. Water 2022, 14, 3348. https://doi.org/10.3390/w14203348
Batelis SC, Nalbantis I. A Multi-Model Multi-Scale Approach to Estimate the Impact of the 2007 Large-Scale Forest Fires in Peloponnese, Greece. Water. 2022; 14(20):3348. https://doi.org/10.3390/w14203348
Chicago/Turabian StyleBatelis, Stamatis C., and Ioannis Nalbantis. 2022. "A Multi-Model Multi-Scale Approach to Estimate the Impact of the 2007 Large-Scale Forest Fires in Peloponnese, Greece" Water 14, no. 20: 3348. https://doi.org/10.3390/w14203348
APA StyleBatelis, S. C., & Nalbantis, I. (2022). A Multi-Model Multi-Scale Approach to Estimate the Impact of the 2007 Large-Scale Forest Fires in Peloponnese, Greece. Water, 14(20), 3348. https://doi.org/10.3390/w14203348






