Developments of Dynamic Shoreline Planform of Crenulate-Shaped Bay by a Novel Evolution Formulation
Abstract
:1. Introduction
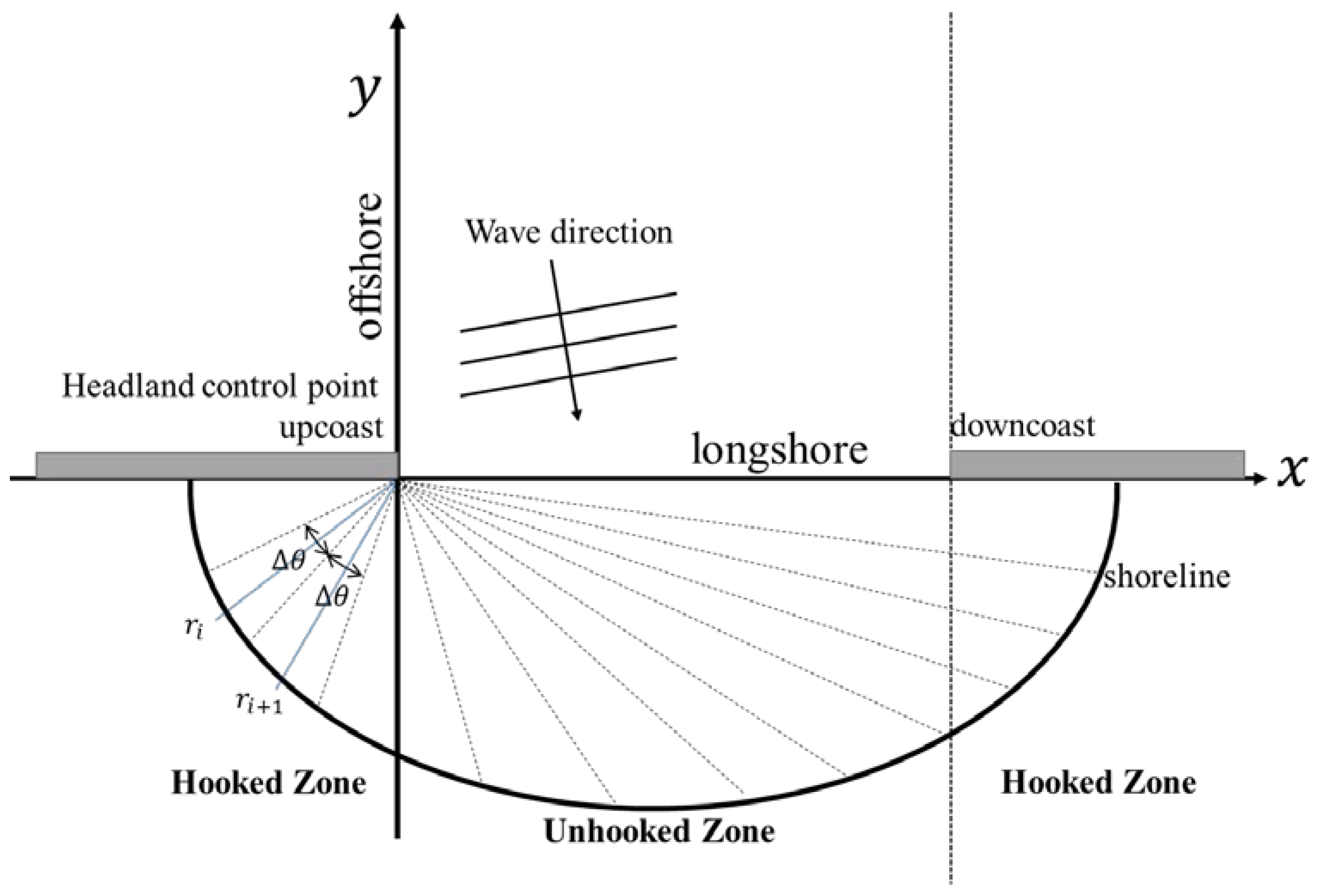
2. Evolution Formulation for Dynamic Shoreline Planform
3. Verification for the Consistency and the Stability of the Proposed Model
4. Numerical Validation and Comparisons
4.1. Case 1
4.2. Case 2
4.3. Case 3
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Özölçer, İ.H.; Kömürcü, M.İ.; Birben, A.R.; Yüksek, Ö.; Karasu, S. Effects of T-shape groin parameters on beach accretion. Ocean Eng. 2006, 33, 382–403. [Google Scholar] [CrossRef]
- Putro, A.H.S.; Lee, J.L. Analysis of longshore drift patterns on the littoral system of nusa dua beach in bali, indonesia. J. Mar. Sci. Eng. 2020, 8, 749. [Google Scholar] [CrossRef]
- Liang, T.-Y.; Chang, C.-H.; Hsiao, S.-C.; Huang, W.-P.; Chang, T.-Y.; Guo, W.-D.; Liu, C.-H.; Ho, J.-Y.; Chen, W.-B. On-Site Investigations of Coastal Erosion and Accretion for the Northeast of Taiwan. J. Mar. Sci. Eng. 2022, 10, 282. [Google Scholar] [CrossRef]
- Penney, W.G.; Price, A.T.; Martin, J.; Moyce, W.; Penney, W.G.; Price, A.; Thornhill, C. Part I. The diffraction theory of sea waves and the shelter afforded by breakwaters. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1952, 244, 236–253. [Google Scholar]
- Coastal Engineering Research Center. Shore Protection Manual; Department of the Army, Waterways Experiment Station, Corps of Engineers: Vicksburg MI, USA, 1984. [Google Scholar]
- Dally, W.R.; Pope, J. Detached Breakwaters for Shore Protection; Coastal Engineering Research Center: Vicksburg MI, USA, 1986. [Google Scholar]
- Mizutani, N.; Mostafa, A.M.; Iwata, K. Nonlinear regular wave, submerged breakwater and seabed dynamic interaction. Coast. Eng. 1998, 33, 177–202. [Google Scholar] [CrossRef]
- Laustrup, C.; Madsen, H.T. Design of breakwaters and beach nourishment. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994. [Google Scholar]
- Zhu, J.; Cai, F.; Shi, F.; Qi, H.; Lei, G.; Liu, J.; Cao, H.; Zheng, J. Beach response to breakwater layouts of drainage pipe outlets during beach nourishment. Estuar. Coast. Shelf Sci. 2019, 228, 106354. [Google Scholar] [CrossRef]
- Hsu, J.R.; Silvester, R.; Xia, Y.-M. Applications of headland control. J. Waterw. Port Coast. Ocean. Eng. 1989, 115, 299–310. [Google Scholar] [CrossRef]
- Hsu, J.R.C.; Evans, C. Parabolic Bay Shapes and Applications. Proc. Inst. Civ. Eng. 1989, 87, 557–570. [Google Scholar] [CrossRef]
- González, M.; Medina, R. On the application of static equilibrium bay formulations to natural and man-made beaches. Coast. Eng. 2001, 43, 209–225. [Google Scholar] [CrossRef]
- Iglesias, G.; Diz-Lois, G.; Pinto, F.T. Artificial Intelligence and headland-bay beaches. Coast. Eng. 2010, 57, 176–183. [Google Scholar] [CrossRef]
- Hsu, J.R.C.; Yu, M.J.; Lee, F.C.; Benedet, L. Static bay beach concept for scientists and engineers: A review. Coast. Eng. 2010, 57, 76–91. [Google Scholar] [CrossRef]
- Raabe, A.L.A.; Klein, A.H.d.F.; González, M.; Medina, R. MEPBAY and SMC: Software tools to support different operational levels of headland-bay beach in coastal engineering projects. Coast. Eng. 2010, 57, 213–226. [Google Scholar] [CrossRef]
- Hanson, H. GENESIS: A generalized shoreline change numerical model. J. Coast. Res. 1989, 5, 1–27. [Google Scholar]
- Gainza, J.; González, E.M.; Medina, R. A process based shape equation for a static equilibrium beach planform. Coast. Eng. 2018, 136, 119–129. [Google Scholar] [CrossRef]
- Pelnard-Considère, R. Essai de theorie de l’evolution des formes de rivage en plages de sable et de galets. J. De L’hydraulique 1957, 4, 289–298. [Google Scholar]
- Frey, A.E.; Connell, K.J.; Hanson, H.; Larson, M.; Thomas, R.C.; Munger, S.; Zundel, A. GenCade Version 1 Model Theory and User’s Guide; Engineer Research and Development Center: Vicksburg, MI, USA, 2012. [Google Scholar]
- Weesakul, S.; Rasmeemasmuang, T.; Tasaduak, S.; Thaicharoen, C. Numerical modeling of crenulate bay shapes. Coast. Eng. 2010, 57, 184–193. [Google Scholar] [CrossRef]
- Kaergaard, K.; Fredsoe, J. A numerical shoreline model for shorelines with large curvature. Coast. Eng. 2013, 74, 19–32. [Google Scholar] [CrossRef]
- Davidson, M.A.; Splinter, K.D.; Turner, I.L. A simple equilibrium model for predicting shoreline change. Coast. Eng. 2013, 73, 191–202. [Google Scholar] [CrossRef]
- Elshinnawy, A.I.; Medina, R.; González, M. Dynamic equilibrium planform of embayed beaches: Part 1. A new model and its verification. Coast. Eng. 2018, 135, 112–122. [Google Scholar] [CrossRef]
- Elshinnawy, A.I.; Medina, R.; González, M. Dynamic equilibrium planform of embayed beaches: Part 2. Design procedure and engineering applications. Coast. Eng. 2018, 135, 123–137. [Google Scholar] [CrossRef]
- Kristensen, S.E.; Drønen, N.; Deigaard, R.; Fredsoe, J. Hybrid morphological modelling of shoreline response to a detached breakwater. Coast. Eng. 2013, 71, 13–27. [Google Scholar] [CrossRef]
- Sato, S.; Ijima, T.; Tanaka, N. A study of critical depth and mode of sand movement using radioactive glass sand. Coast. Eng. Proc. 1962, 1, 18. [Google Scholar] [CrossRef]
- Komar, P.D.; Inman, D.L. Longshore sand transport on beaches. J. Geophys. Res. 1970, 75, 5914–5927. [Google Scholar] [CrossRef]
- Kraus, N.C.; Harikai, S. Numerical model of the shoreline change at Oarai Beach. Coast. Eng. 1983, 7, 1–28. [Google Scholar] [CrossRef]
- Hsu, T.-W.; Wen, C.-C. A parabolic equation extended to account for rapidly varying topography. Ocean. Eng. 2001, 28, 1479–1498. [Google Scholar] [CrossRef]
- Hsu, T.-W.; Wen, C.-C. On radiation boundary conditions and wave transformation across the surf zone. China Ocean Eng. 2001, 15, 395–406. [Google Scholar]
- Khoa, V. Experimentation on Bayed Beaches between Headlands for Small Wave Angle. M. Eng. Thesis No. WM-95 1995, 10. [Google Scholar]
- Eliot, M. Coastal Sediments, Beaches and Other Soft Shores. Coast Adapt Information Manual 8; National Climate Change Adaptation Research Facility: Gold Coast, Australia, 2016. [Google Scholar]













| Physical Parameters | Case B [20] |
|---|---|
| Incident wave angle (degree) | 25 |
| Wave height (cm) | 4.3 |
| Wave period (s) | 2.0 |
| Water depth at generator (cm) | 20 |
| Median grain size, (mm) | 0.3 |
| Initial beach slope | 1.4 |
| Running time (hr) | 38 |
| m = 109 | m = 179 | |||||
|---|---|---|---|---|---|---|
| Retreats | Advance | Retreats | Advance | |||
| 1.00 | −1048.4 | 1052.3 | 4.0% | −1049.7 | 1051.9 | 2.2% |
| 0.10 | −1048.4 | 1052.3 | 3.9% | −1049.7 | 1051.8 | 2.1% |
| 0.01 | −1048.3 | 1052.3 | 4.0% | −1049.7 | 1051.8 | 2.1% |
| m = 229 | Weesaukl et al., (2010) m = 229 | |||||
| retreats | advance | retreats | advance | |||
| 1.00 | −1049.6 | 1052.2 | 2.6% | −1067.3 | 1070.4 | 3.1% |
| 0.10 | −1049.6 | 1052.1 | 2.5% | −1067.2 | 1070.9 | 3.7% |
| 0.01 | −1049.6 | 1052.1 | 2.5% | −1067.3 | 1070.4 | 3.1% |
| ) | ||||||
| a1 | a2 | a3 | a4 | a5 | ||
|---|---|---|---|---|---|---|
| −110.751 | 511.919 | −902.138 | 543.411 | −92.390 | 2.31% | |
| −76.843 | 566.496 | −957.309 | 511.249 | −93.516 | 2.26% | |
| −64.301 | 616.012 | −958.011 | 471.467 | −115.137 | 2.25% | |
| −55.081 | 669.763 | −957.503 | 434.192 | −141.290 | 2.21% | |
| () | ||||||
| S = 50 | |||||
|---|---|---|---|---|---|
| m | L | 180 | 200 | 220 | |
| 109 | 1 | 0.003% | 0.004% | 0.006% | |
| 0.1 | 0.003% | 0.003% | 0.006% | ||
| 0.01 | 0.004% | 0.005% | 0.006% | ||
| 179 | 1 | 0.003% | 0.001% | 0.002% | |
| 0.1 | 0.002% | 0.001% | 0.002% | ||
| 0.01 | 0.001% | 0.002% | 0.002% | ||
| 229 | 1 | 0.001% | 0.002% | 0.002% | |
| 0.1 | 0.001% | 0.001% | 0.002% | ||
| 0.01 | 0.002% | 0.001% | 0.002% | ||
| S = 60 | |||||
| m | L | 180 | 200 | 220 | |
| 109 | 1 | 0.006% | 0.007% | 0.009% | |
| 0.1 | 0.007% | 0.007% | 0.009% | ||
| 0.01 | 0.007% | 0.009% | 0.008% | ||
| 179 | 1 | 0.004% | 0.005% | 0.003% | |
| 0.1 | 0.004% | 0.006% | 0.004% | ||
| 0.01 | 0.004% | 0.005% | 0.003% | ||
| 229 | 1 | 0.002% | 0.002% | 0.002% | |
| 0.1 | 0.002% | 0.003% | 0.003% | ||
| 0.01 | 0.003% | 0.002% | 0.003% | ||
| S = 70 | |||||
| m | L | 180 | 200 | 220 | |
| 109 | 1 | 0.009% | 0.009% | 0.012% | |
| 0.1 | 0.009% | 0.009% | 0.011% | ||
| 0.01 | 0.008% | 0.008% | 0.010% | ||
| 179 | 1 | 0.005% | 0.005% | 0.004% | |
| 0.1 | 0.006% | 0.006% | 0.003% | ||
| 0.01 | 0.005% | 0.005% | 0.004% | ||
| 229 | 1 | 0.003% | 0.003% | 0.003% | |
| 0.1 | 0.003% | 0.002% | 0.003% | ||
| 0.01 | 0.003% | 0.003% | 0.001% | ||
| Location | Yuguang Island | ||
|---|---|---|---|
| Model setting | [k1,k2,Ds,tanb] | [0.77, 0.38, 1.41, 1/60] | |
| Simulated time | 20 years | ||
| Wave average (2000–2021) | Height(H) | Period(T) | Direction |
| 0.66 m | 5.5 s | SW | |
| shoreline advance (+) | 110580.85 m2 | shoreline retreats (-) | 8183.34 |
| supplementary term q | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, H.-C.; Hsu, T.-W.; Fan, C.-M. Developments of Dynamic Shoreline Planform of Crenulate-Shaped Bay by a Novel Evolution Formulation. Water 2022, 14, 3504. https://doi.org/10.3390/w14213504
Tao H-C, Hsu T-W, Fan C-M. Developments of Dynamic Shoreline Planform of Crenulate-Shaped Bay by a Novel Evolution Formulation. Water. 2022; 14(21):3504. https://doi.org/10.3390/w14213504
Chicago/Turabian StyleTao, Hung-Cheng, Tai-Wen Hsu, and Chia-Ming Fan. 2022. "Developments of Dynamic Shoreline Planform of Crenulate-Shaped Bay by a Novel Evolution Formulation" Water 14, no. 21: 3504. https://doi.org/10.3390/w14213504








