A 3D Fully Non-Hydrostatic Model for Free-Surface Flows with Complex Immersed Boundaries
Abstract
1. Introduction
2. Numerical Model
2.1. Governing Equations
2.2. Numerical Solution by FDM
2.3. Numerical Solution with FDM and VOS-Based Immersed Boundary Method
2.4. Volume Fraction Transport Equation
2.5. Solution Procedure
- Propose the initial and the boundary conditions for a given time-step and use the VOF reconstruction method via Equation (23) to compute a cell-center estimate of the volume fraction and free-surface position.
- Solve the , and using Equations (10)–(12) via FDM.
- Solve the right-hand side D of pressure Poisson equation (Equation 16) using iterative method to obtain the pressure, Pn+1/2 based on point-successive over relaxation iteration.
- Solve the velocity, u, v, and w using Equations (7)–(9) via a split operating step FDM.
- Using the via Equation (20) to calculate the forcing function, , , and in Equations (7)–(9) include the effect of immersed body.
- In the fractional time-step, the values of velocities, forcing functions, and pressure variables calculated from the previous time-step were used to resolve the steps 1 to 5 to obtain new values. The above numerical procedure was reiterated until the prescribed time was reached.
3. Results and Discussion
3.1. Dam-Break Flow Passing a Cylinder
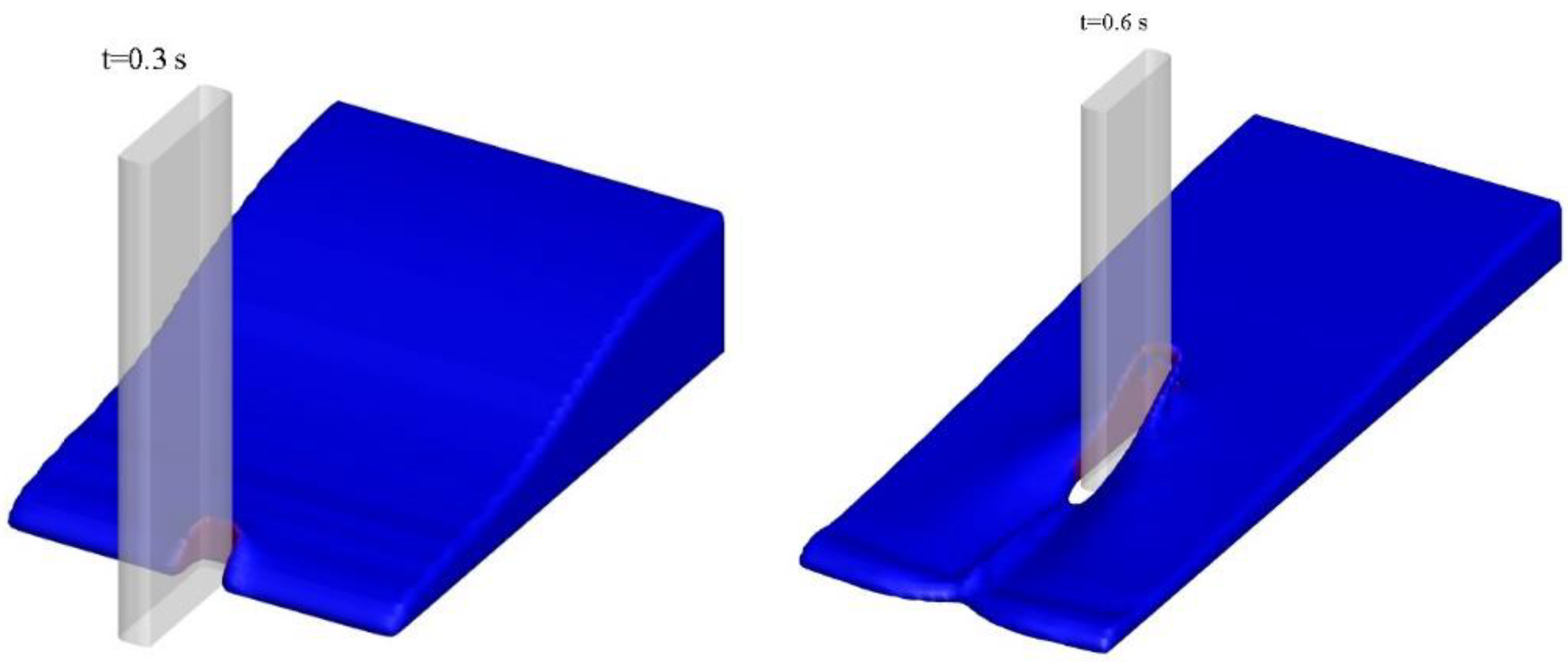
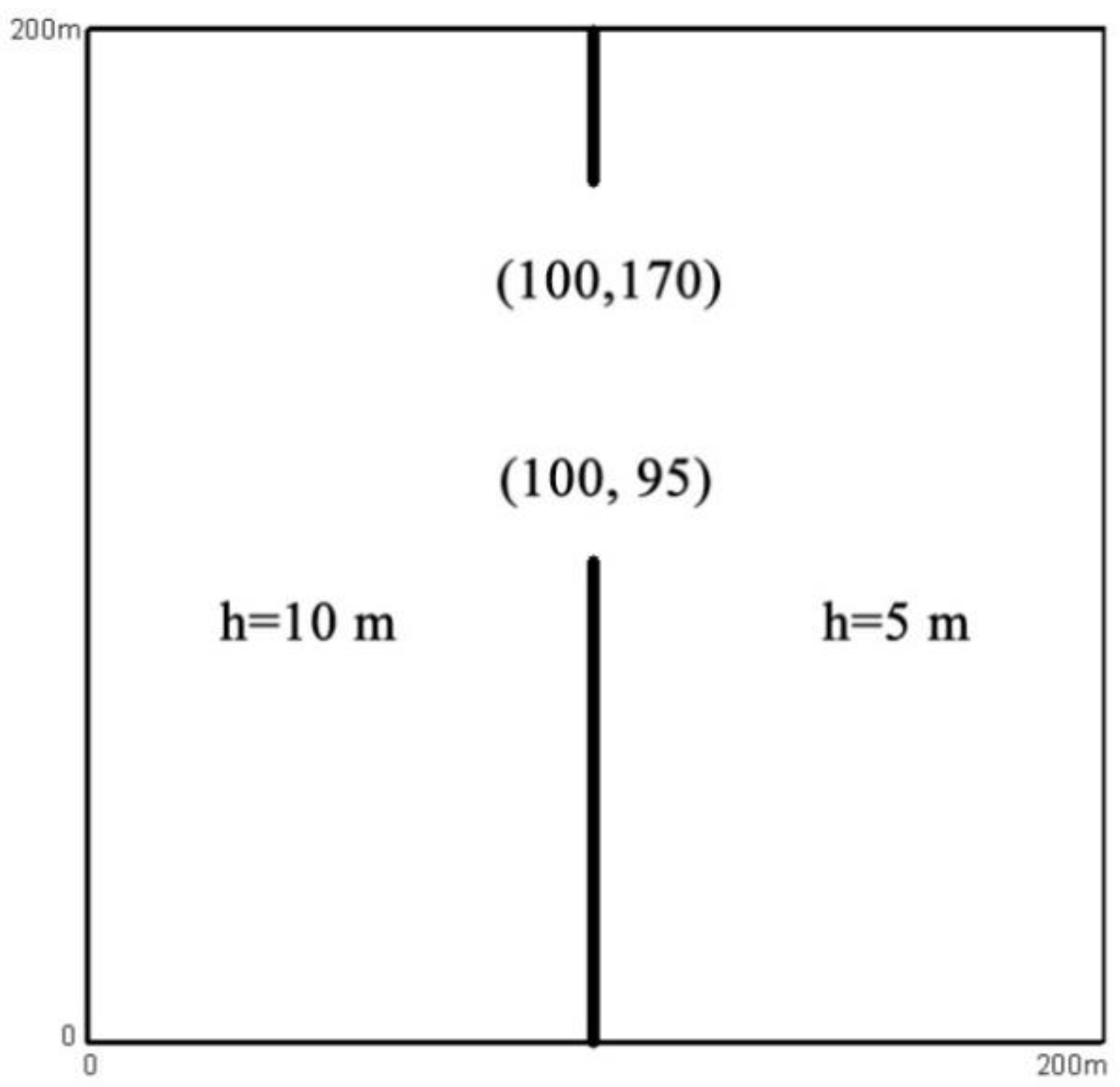
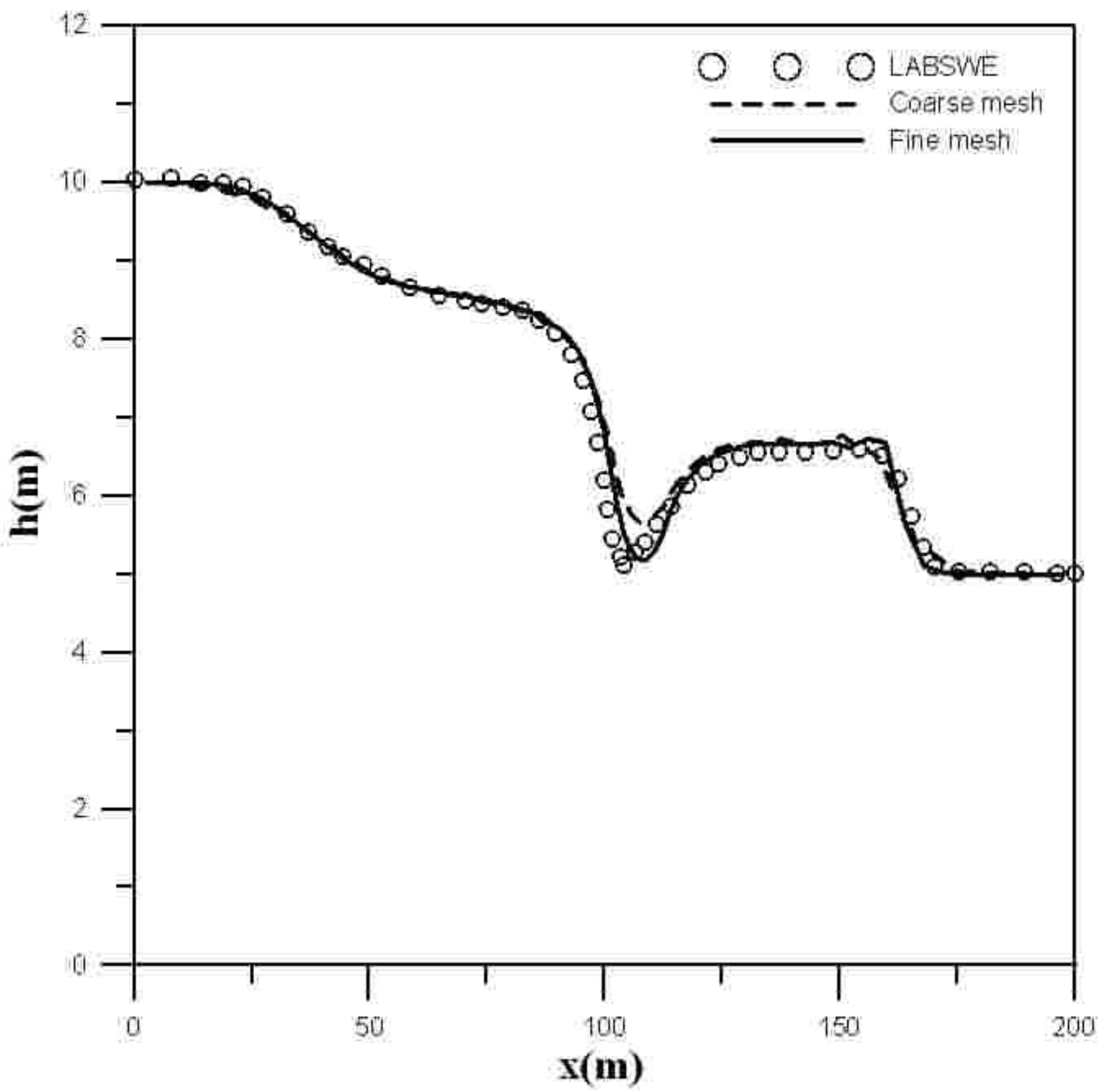
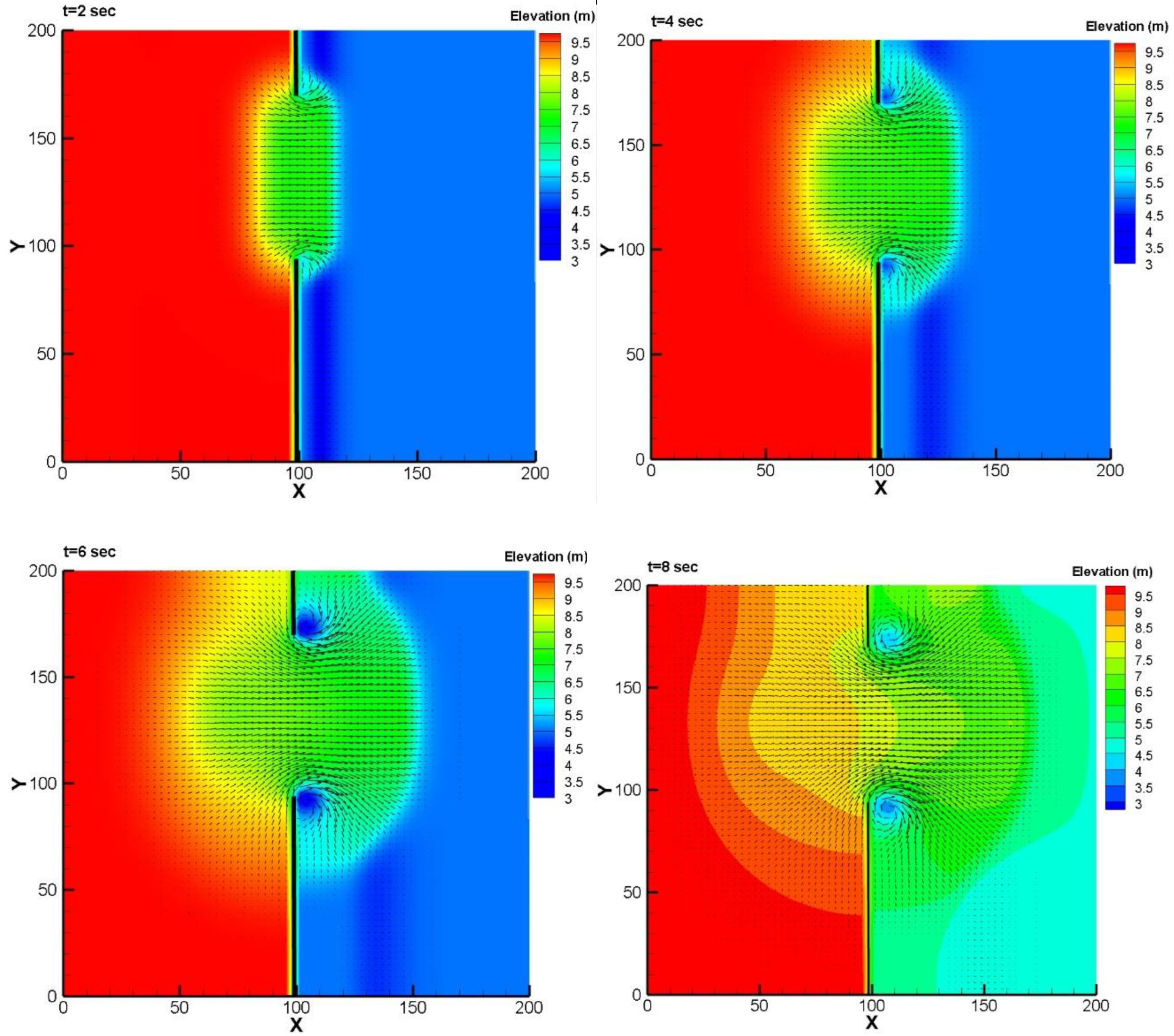
3.2. Partial Dam-Break Flow
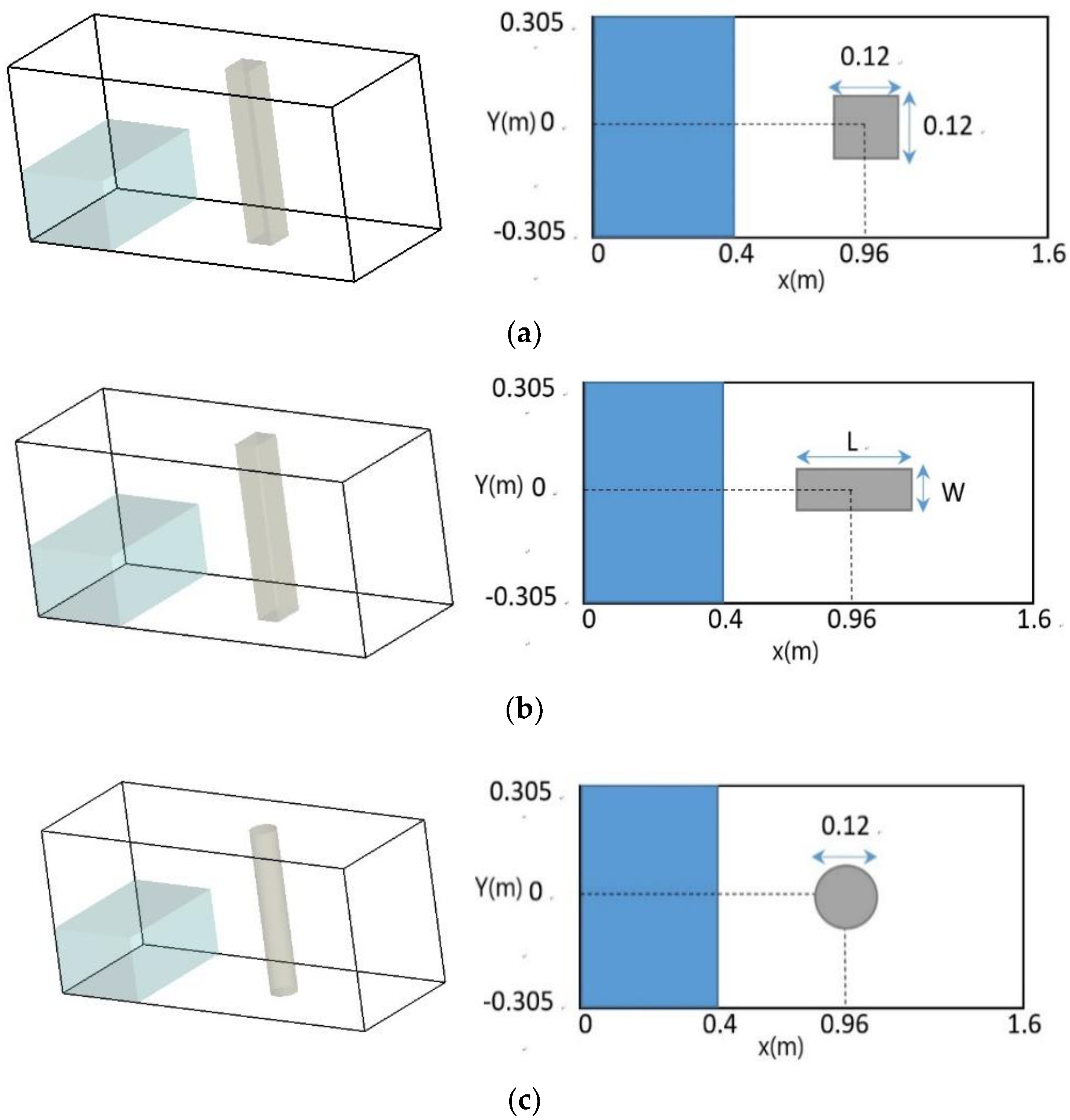
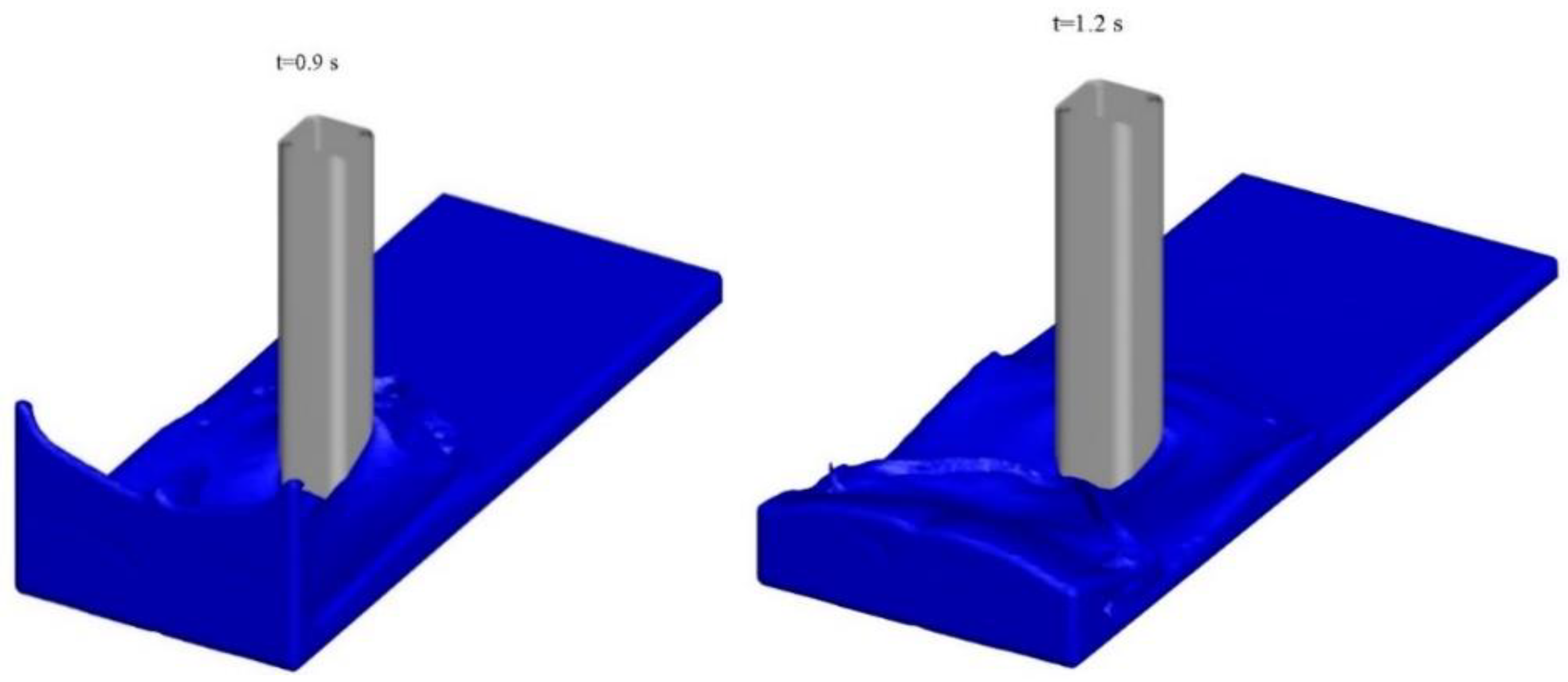
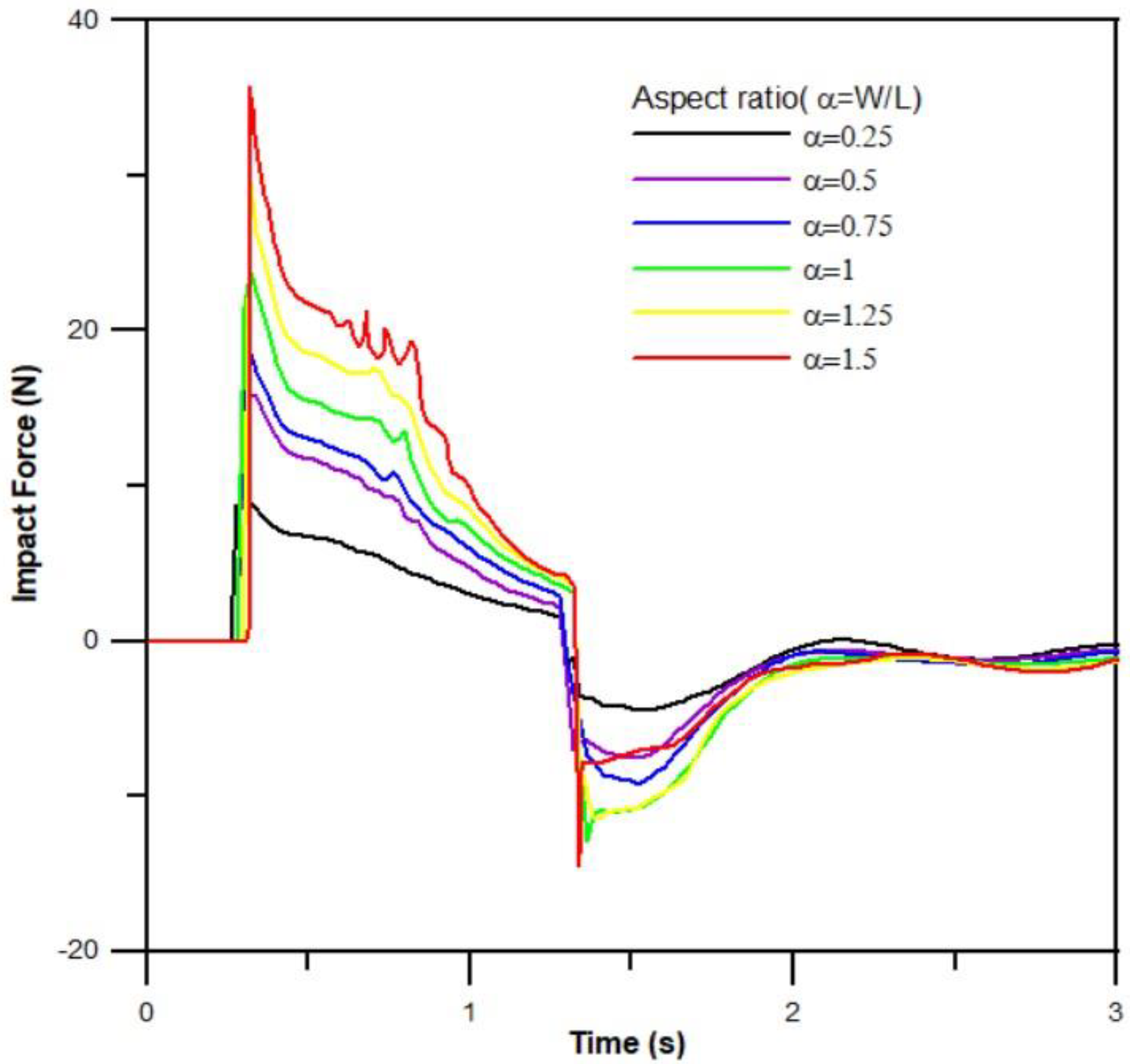
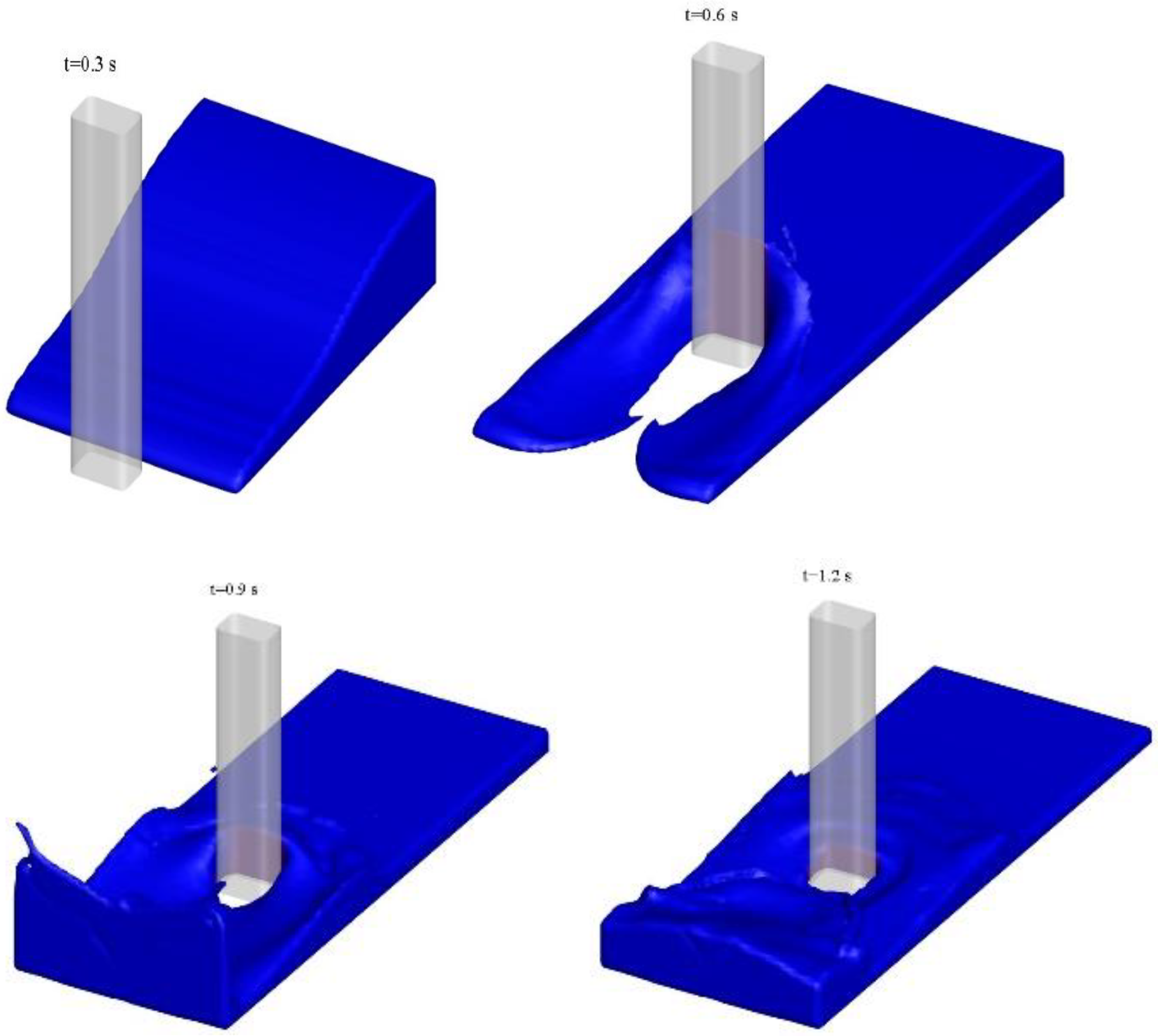
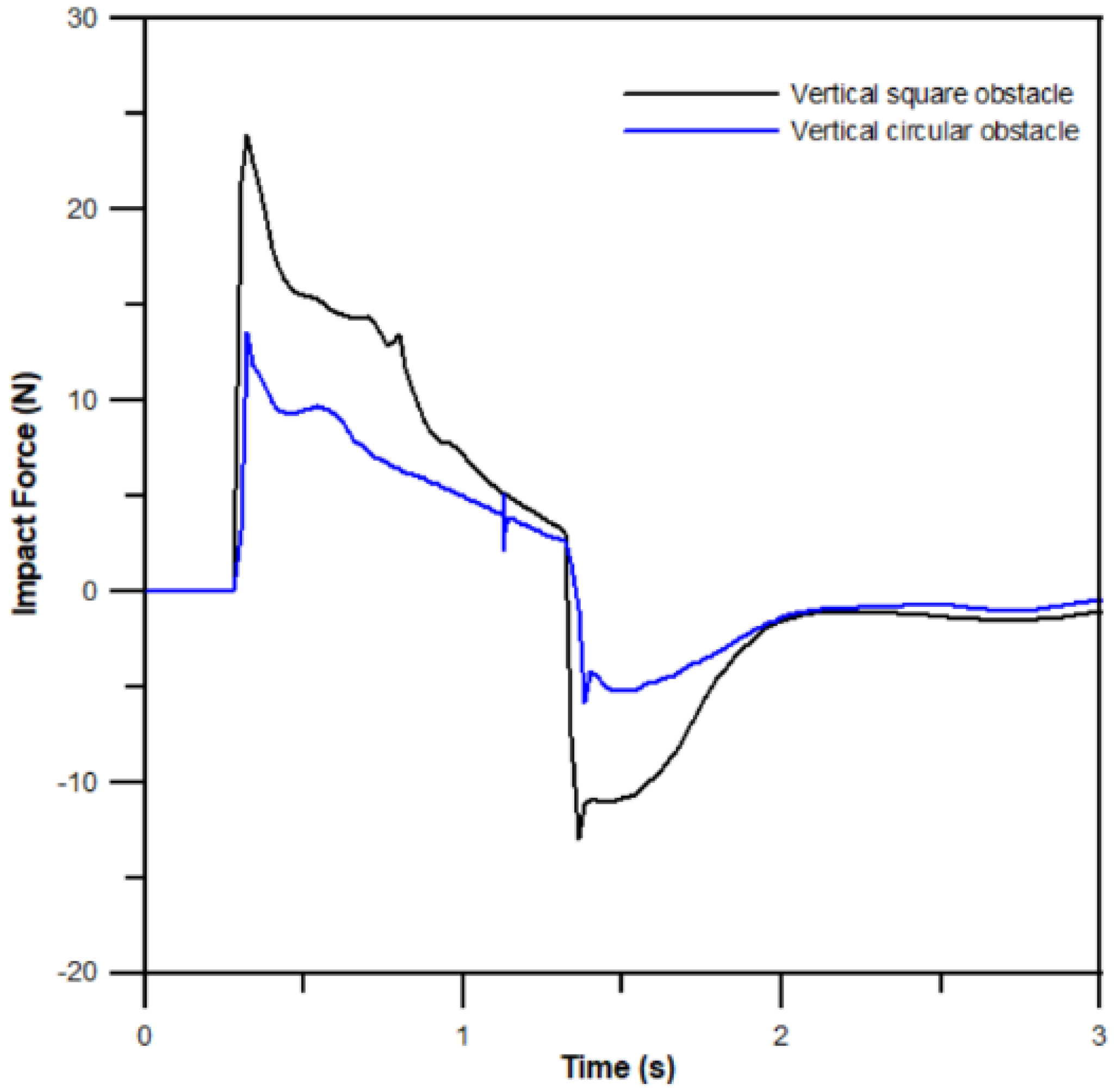
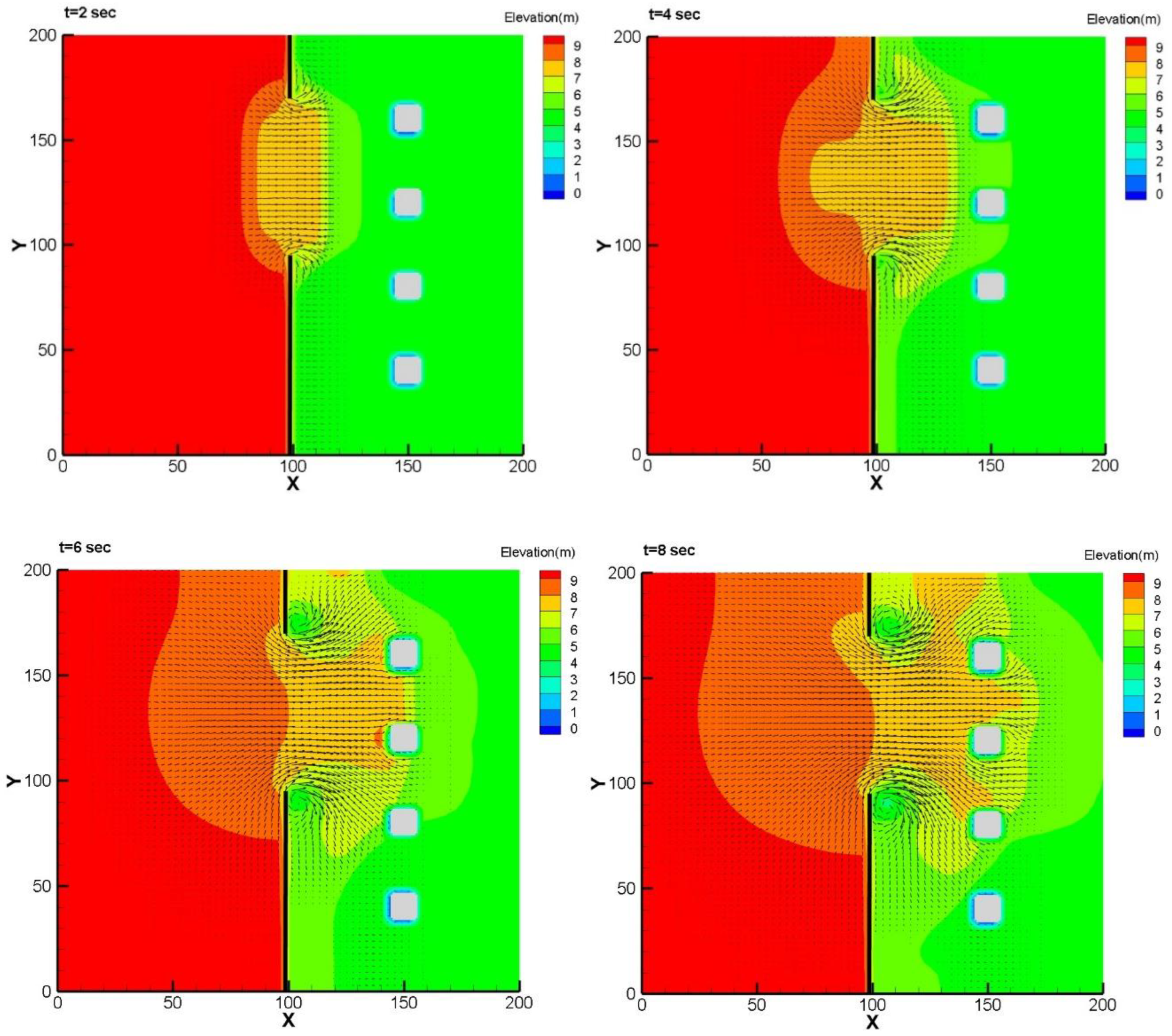
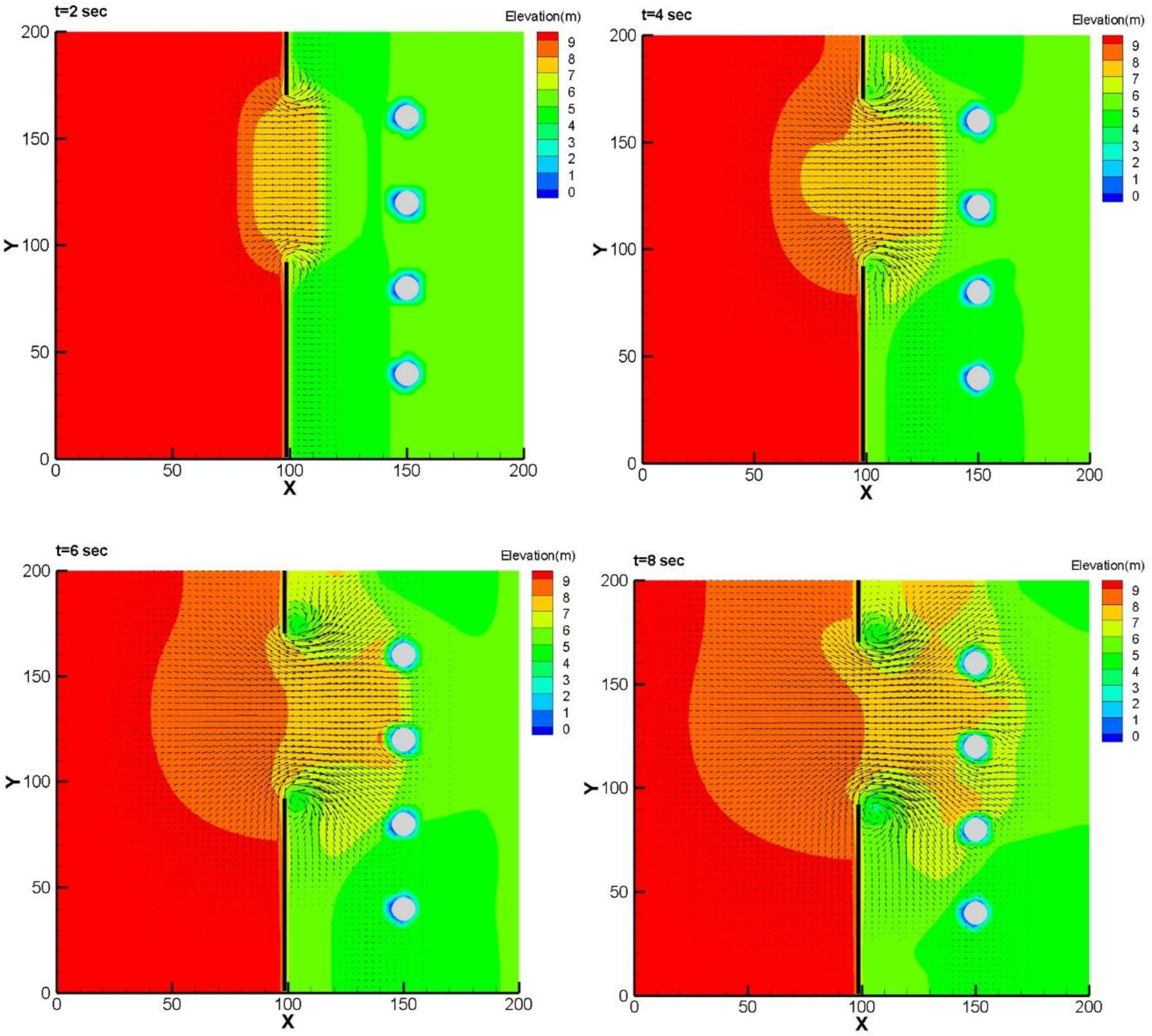
3.3. Dam-Break Surge Passing Four Aligned Square or Circular Cylinders
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Biscarini, C.; Francesco, S.D.; Manciola, P. CFD modelling approach for dam break flow studies. Hydrol. Earth Syst. Sci. 2010, 14, 705–718. [Google Scholar] [CrossRef]
- Akoz, M.S.; Kirkgoz, M.S.; Oner, A.A. Experimental and numerical modeling of a sluice gate flow. J. Hydr. Res. 2009, 47, 161–176. [Google Scholar] [CrossRef]
- Istrati, D.; Hasanpour, A. Numerical investigation of dam break-induced extreme flooding of bridge superstructures. In Proceedings of the 3rd International Conference on Natural Hazards & Infrastructure, Athens, Greece, 5–7 July 2022. [Google Scholar]
- Tsai, Y.S.; Lo, D.C. A ghost-cell immersed boundary method for wave-structure interaction using a two-phase flow model. Water 2020, 12, 3346. [Google Scholar] [CrossRef]
- Xiang, T.; Istrati, D.; Yim, S.C.; Buckle, I.G. Tsunami loads on a representative coastal bridge deck: Experimental study and validation of design equations. J. Water Port Coast. Ocean Eng. 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Hasanpour, A.; Istrati, D. Extreme storm wave impact on elevated coastal buildings. In Proceedings of the 3rd International Conference on Natural Hazards & Infrastructure, Athens, Greece, 5–7 July 2022. [Google Scholar]
- Azadbakht, M. Tsunami and hurricane wave loads on bridge superstructures. Ph.D. Thesis, Oregon State University, Corvallis, OR, USA, 2013. [Google Scholar]
- Xiang, T.; Istrati, D. Assessment of extreme wave impact on coastal decks with different geometries via the arbitrary Lagrangian-Eulerian method. J. Mar. Sci. Eng. 2021, 9, 1342. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.G. Tsunami Loads on Straight and Skewed Bridges—Part 2: Numerical Investigation and Design Recommendations; Oregon Department of Transportation: Salem, OR, USA, 2021. [Google Scholar]
- Hasanpour, A.; Istrati, D. Reducing extreme flooding loads on essential facilities via elevated structures. In Proceedings of the ASCE Lifelines Conference, Virtual, 31 January–11 February 2022. [Google Scholar]
- Elliot, R.C.; Chaudhry, M.H. A wave propagation model for two-dimensional dam-break flows. J. Hydr. Res. 1992, 30, 467–483. [Google Scholar] [CrossRef]
- Molls, T.; Chaudhry, M.H. Depth-averaged open-channel flow model. J. Hydr. Engrg. 1995, 121, 453–464. [Google Scholar] [CrossRef]
- Sanders, B.F. Non-reflecting boundary flux function for finite volume shallow-water models. Adv. Water Resour. 2001, 25, 195–202. [Google Scholar] [CrossRef]
- Rao, V.S.; Latha, G. A slope modification method for shallow water equations. Int. J. Numer. Meth. Fluids 1992, 14, 189–196. [Google Scholar] [CrossRef]
- Fraccarollo, L.; Toro, E.F. Experimental and numerical assessment of the shallow water model for two-dimensional dam-break type problems. J. Hydr. Res. 1995, 33, 843–864. [Google Scholar] [CrossRef]
- Wang, J.S.; He, Y.S.; Ni, H.G. Two-dimensional free surface flow in branch channels by a finite-volume TVD scheme. Adv. Water Resour. 2003, 26, 623–633. [Google Scholar] [CrossRef]
- Caleffi, V.; Valiani, A.; Bernini, A. High-order balanced CWENO scheme for movable bed shallow water equations. Adv. Water Resour. 2007, 30, 730–741. [Google Scholar] [CrossRef]
- Nujic, M. Efficient implementation of non-oscillatory schemes for the computation of free-surface flows. J. Hydr. Res. 1995, 3, 101–111. [Google Scholar] [CrossRef]
- Savic, L.J.; Holly, F.M., Jr. Dambreak flood waves computed by modified Godunov method. J. Hydr. Res. 1993, 1, 187–204. [Google Scholar] [CrossRef]
- Glaister, P. Approximate Rieman solutions of shallow water equations. J. Hydr. Res. 1988, 26, 293–306. [Google Scholar] [CrossRef]
- Harten, A. High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 1983, 49, 357–393. [Google Scholar] [CrossRef]
- Yang, J.Y.; Hsu, C.A.; Chang, S.H. Computations of free surface flows, part 2: 2D unsteady bore diffraction. J. Hydr. Res. 1993, 31, 403–412. [Google Scholar] [CrossRef]
- Yee, H.C. Construction of explicit and implicit symmetric TVD schemes and their applications. J. Comput. Phys. 1987, 68, 151–179. [Google Scholar] [CrossRef]
- Yang, H.Q.; Przekwas, A.J. A comparative study of advanced shock-capturing schemes applied to Burger’s equation. J. Comput. Phys. 1992, 102, 139–159. [Google Scholar] [CrossRef]
- Jeng, Y.N.; Payne, U.J. An adaptive TVD limiter. J. Comput. Phys. 1995, 118, 229–241. [Google Scholar] [CrossRef]
- Wang, J.S.; Ni, H.G.; He, Y.S. Finite-difference TVD scheme for computation of dam-break problems. J. Hydr. Engrg. ASCE 2000, 126, 253–262. [Google Scholar] [CrossRef]
- Harten, A.; Engquist, B.; Osher, S.; Chakravarthy, S.R. Uniformly high-order accurate essentially non-oscillatory schemes, III. J. Comput. Phys. 1987, 71, 231–275. [Google Scholar] [CrossRef]
- Liu, X.-D.; Osher, S.; Chan, T. Weighted essentially non-oscillatory schemes. J. Comput. Phys. 1994, 115, 200–212. [Google Scholar] [CrossRef]
- Jiang, G.-S.; Shu, C.-W. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Qiu, J.; Shu, C.-W. On the construction, comparison, and local characteristic decomposition for high-order central WENO schemes. J. Comput. Phys. 2002, 183, 187–209. [Google Scholar] [CrossRef]
- Wei, Z.; Dalrymple, R.A. Numerical study on mitigating tsunami force on bridges by an SPH model. J. Ocean Eng. Mar. Energy 2016, 2, 365–380. [Google Scholar] [CrossRef]
- Sarfaraz, M.; Pak, A. SPH numerical simulation of tsunami wave forces impinged on bridge superstructures. Coastal Eng. 2017, 121, 145–157. [Google Scholar] [CrossRef]
- Hasanpour, A.; Istrati, D.; Buckle, I. Coupled SPH–FEM modeling of tsunami-borne large debris flow and impact on coastal structures. J. Mar. Sci. Eng. 2021, 9, 1068. [Google Scholar] [CrossRef]
- Hasanpour, A.; Istrati, D.; Buckle, I.G. Multi-physics modeling of tsunami debris impact on bridge decks. In Proceedings of the 3rd International Conference on Natural Hazards & Infrastructure, Athens, Greece, 5–7 July 2022. [Google Scholar]
- Chen, X. A fully hydrodynamic model for three-dimensional, free-surface flows. Int. J. Numer. Meth. Fluids 2003, 42, 929–952. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Lo, D.C. A novel volume-of-solid-based immersed-boundary method for viscous flow with a moving rigid boundary. Numer. Heat Transf. B Fundam. 2015, 68, 115–140. [Google Scholar] [CrossRef]
- Chorin, A.J. A numerical method for solving incompressible viscous flow problem. J. Comput. Phys. 1967, 2, 12–26. [Google Scholar] [CrossRef]
- Weymouth, G.D.; Yue, D.K.-P. Conservative Volume-of-Fluid method for free-surface simulations on Cartesian-grids. J. Comput. Phys. 2010, 229, 2853–2865. [Google Scholar] [CrossRef]
- Raad, P.E.; Bidoae, R. The three-dimensional Eulerian–Lagrangian marker and micro cell method for the simulation of free surface flows. J. Comput. Phys. 2005, 203, 668–699. [Google Scholar] [CrossRef]
- Xie, Z.; Stoesser, T.; Xia, J. Simulation of three-dimensional free-surface dam-break flows over a cuboid, cylinder, and sphere. J. Hydraul. Eng. 2021, 147, 06021009. [Google Scholar] [CrossRef]
- Fennema, R.J.; Chaudhry, M.H. Explicit methods for two-dimensional unsteady free-surface flow. J. Hydr. Engrg. 1990, 116, 1013–1034. [Google Scholar] [CrossRef]
- Frandsen, J.B. Free-Surface Lattice Boltzmann Modeling in Single Phase Flows. In Advanced Numerical Models for Simulating Tsunami Waves and Runup; Liu, P., Yeh, H., Synolakis, C., Eds.; World Scientific: Singapore, 2008; Volume 10. [Google Scholar]








| Δt (s) | Grid Size (m) | ||
|---|---|---|---|
| 0.02 | 0.01 | 0.005 | |
| 0.001 | 48 | 156 | 508 |
| 0.0005 | 75 | 226 | 711 |
| 0.00025 | 105 | 306 | 938 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lo, D.-C.; Tsai, Y.-S. A 3D Fully Non-Hydrostatic Model for Free-Surface Flows with Complex Immersed Boundaries. Water 2022, 14, 3803. https://doi.org/10.3390/w14233803
Lo D-C, Tsai Y-S. A 3D Fully Non-Hydrostatic Model for Free-Surface Flows with Complex Immersed Boundaries. Water. 2022; 14(23):3803. https://doi.org/10.3390/w14233803
Chicago/Turabian StyleLo, Der-Chang, and Yuan-Shiang Tsai. 2022. "A 3D Fully Non-Hydrostatic Model for Free-Surface Flows with Complex Immersed Boundaries" Water 14, no. 23: 3803. https://doi.org/10.3390/w14233803
APA StyleLo, D.-C., & Tsai, Y.-S. (2022). A 3D Fully Non-Hydrostatic Model for Free-Surface Flows with Complex Immersed Boundaries. Water, 14(23), 3803. https://doi.org/10.3390/w14233803







