Structural Failure of the Cohesive Core of Rockfill Dams: An Experimental Research Using Sand-Bentonite Mixtures
Abstract
:1. Introduction
2. Methodology
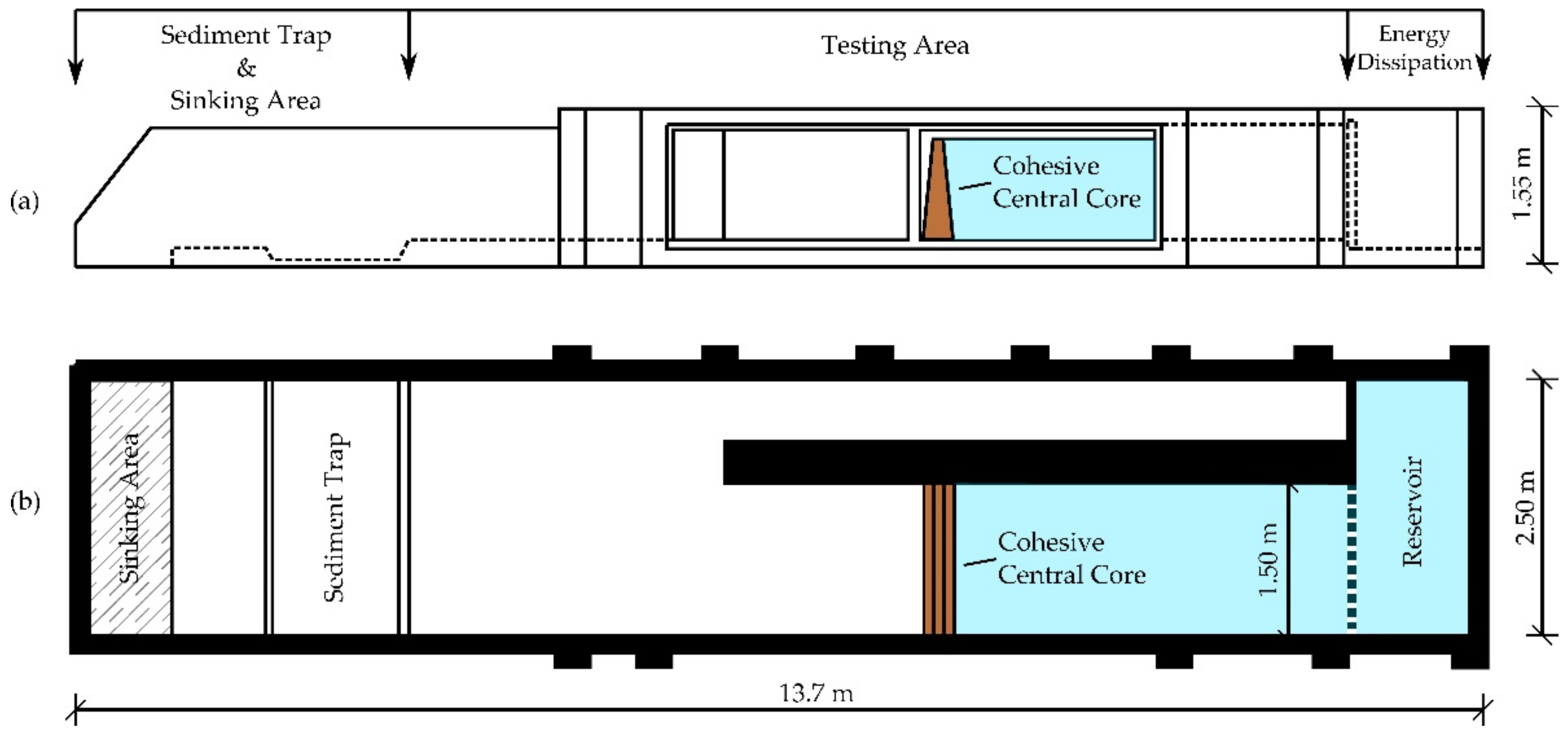
2.1. Facilities and Instrumentation
2.2. Materials and Geotechnical Characterization
2.2.1. Raw Materials
2.2.2. Soil Mixtures
2.2.3. Testing
2.3. Onsite Soil Mix Procedure
2.3.1. Theoretical Approach
2.3.2. Practical Approach
- Fill a bucket with sand in its initial state (moistured) and weigh it;
- Perform ten measurements with the SM150T moisture sensor and the HH150 meter (Mineral Mode). Use the average value as representative moisture;
- Place this sand inside the concrete mixer and again weigh the bucket to calculate the exact amount of sand used;
- Perform the previous steps until the total mass ranges from 90 to 110 kg;
- Average the moisture content of each bucket and use this value as a representative of the total amount of sand mass placed inside the concrete mixer;
- Open a bentonite bag and perform ten measurements with the SM150T moisture sensor and the HH150 meter (Coir Mode). Use the average value as representative moisture content;
- Use Equation (3) to calculate the mass of bentonite in its initial state to add to the mixture. Place the correct amount of bentonite inside the concrete mixer;
- Start the concrete mixer and let the sand and bentonite mix with the initial moisture contents;
- Use Equation (5) to calculate the initial moisture content of a sand-bentonite mixture, and Equation (7) to calculate the mass of water to add to obtain the desired moisture.
- Add water using a sprinkler while the concrete mixer is working (Figure 2a). As the moisture content increases, the sand-bentonite mixture tends to stick to the mixer walls. In these situations, stop the mixer and use a shovel to remove the mixture from the walls. Restart and stop the number of times necessary to finish adding the total amount of water.
- Once finished, dump the mixture into a trolley and finalize the moisture homogenization with a hoe (Figure 2b).
2.4. Construction of the Physical Models
- Drawing of the cohesive core cross-section on both flume walls;
- Once the cross-section was drawn, steel L profiles were stuck to the walls using silicone. L profiles were placed in such a way that one of the faces was in contact with the flume wall and the other with the cohesive core. The main edge should be aligned with the drawn cross-section. The inner part of the L profiles faced the cohesive core (Figure 3a), so in the end, the visible faces were used as a guide for cutting the excess material (Figure 3b).
- Placement of the formwork to compact the cohesive soil. Two parallel wooden panels 1.49 m long and 0.5 m wide (Figure 3c,d) were placed outside the metallic L profiles and adjusted as much as possible considering the dimensions of the compaction hammer. These two parallel panels were connected by four 5 mm steel threaded bars located near the corners. The distance between panels was fixed using nuts threaded in the 5 mm bars, one inside and two outside the formwork. This prevented both panels from moving during compaction.
- The cohesive core was compacted by layers with depths ranging from 0.05 m to 0.10 m before the compaction. The compaction hammer was an iron prism with two parallel square faces and four rectangular faces 0.095 m long and 0.05 m wide. In one of the four rectangular faces a corrugated steel bar 0.015 m in diameter and 0.77 m long was welded for handling purposes. Compaction was performed by lifting the compaction hammer by approximately 0.2 m and letting it fall freely the number of times needed to reach the desired density. Density was controlled using the Geotester Pocket Penetrometer and the Humboldt H-4212MH Pocket Shear Vane Tester.
- Once the crest elevation was reached, the excess material from the crest was cut with a rectangular trowel using the formwork as reference (Figure 3e). Then, remove the formwork and the 5 mm steel threaded bars from inside the cohesive core. The hole formed by removing these bars was refilled with the cohesive material. The excess material from the downstream face was cut with an artisanal blade roughly as wide as the flume using the previously installed metallic L profiles as a guide (Figure 3b).
- After cutting the excess material, the crest and downstream face were protected with an industrial vaseline (B-2 from Tecmasol) using a rectangular trowel (Figure 3f). This protective grease had a double purpose: to avoid drying of the cohesive material, and to avoid disintegration/precipitation when in contact with water (this phenomenon was observed in a previous trial).
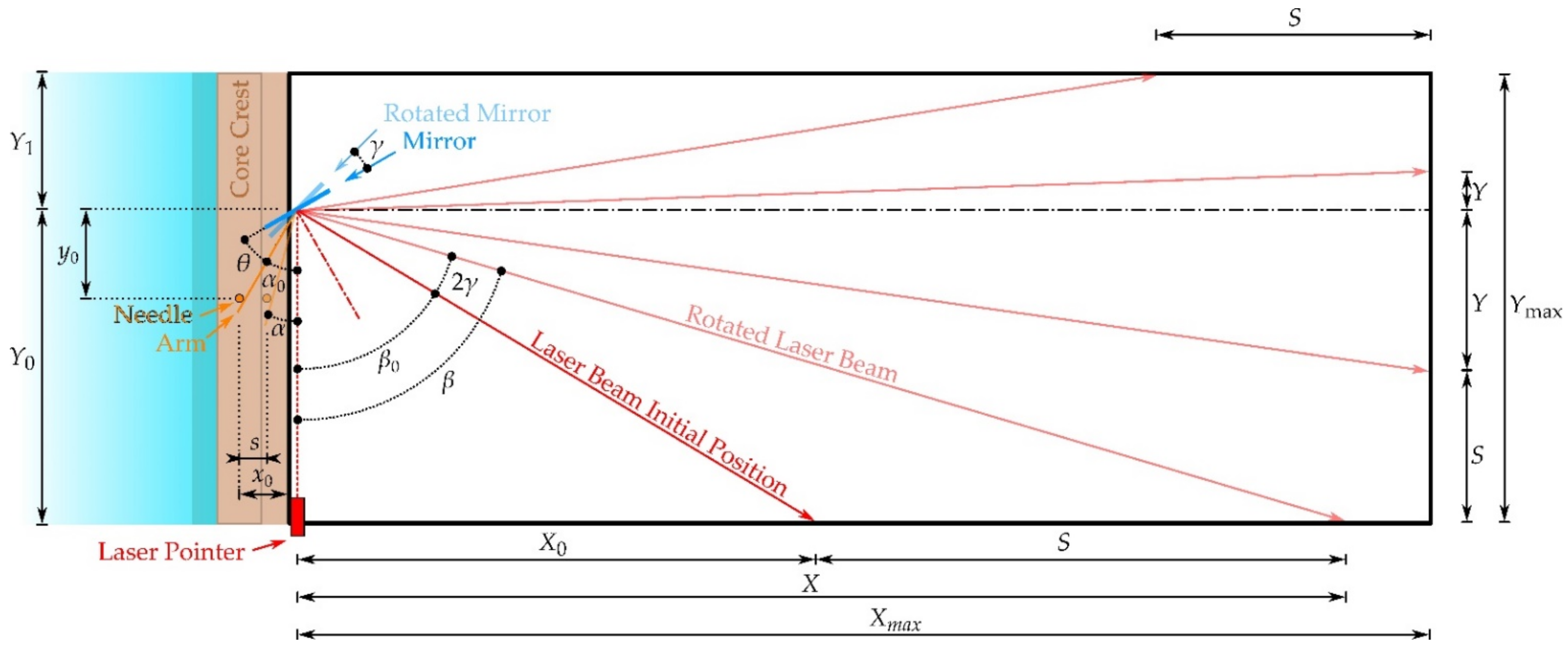
2.5. Measuring the Displacements of the Cohesive Core
2.6. Testing Procedure
2.7. Laboratory Experimental Tests
3. Results
3.1. Validation of the Onsite Soil Mix Procedure
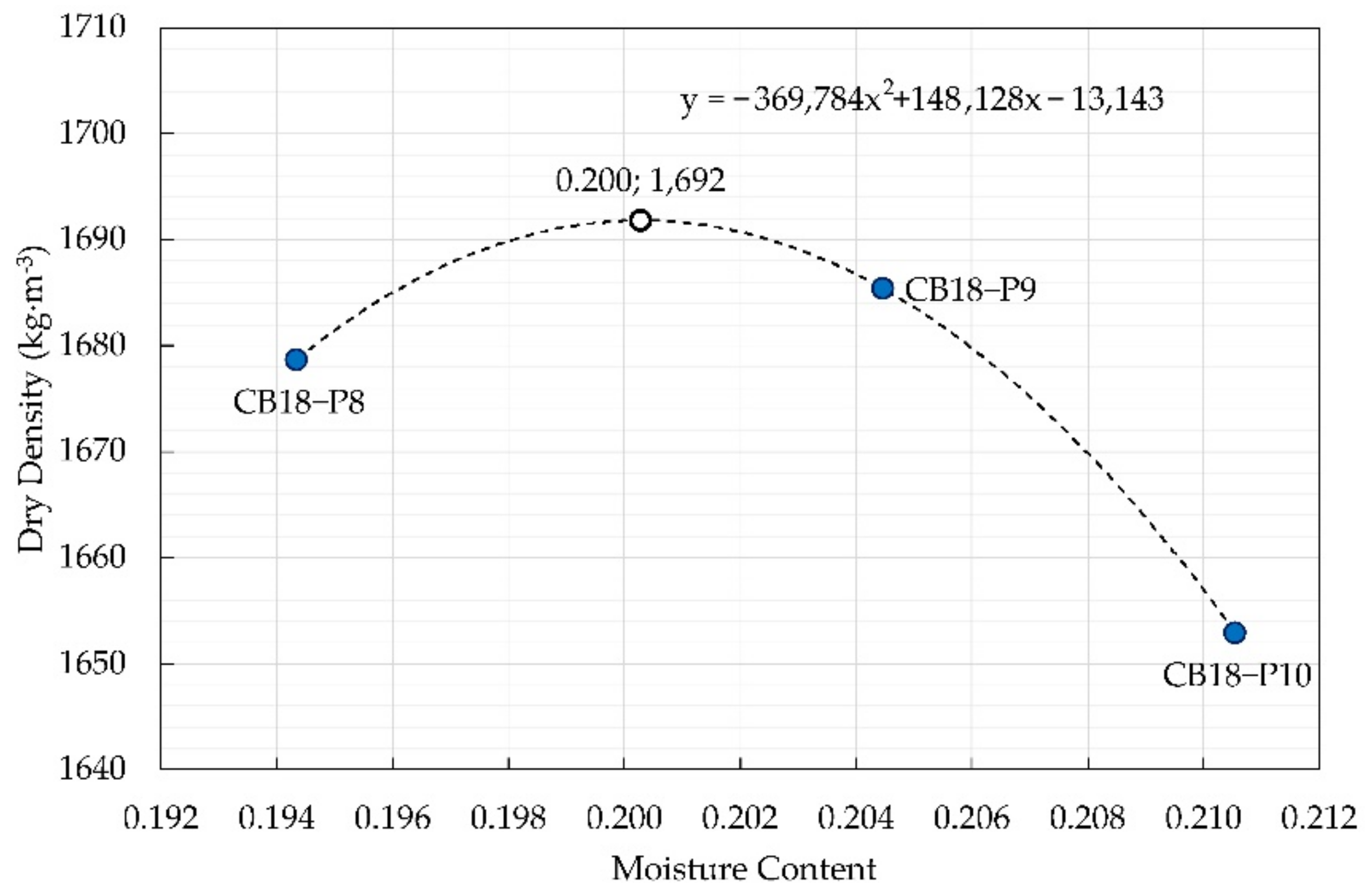
3.2. Compaction Tests
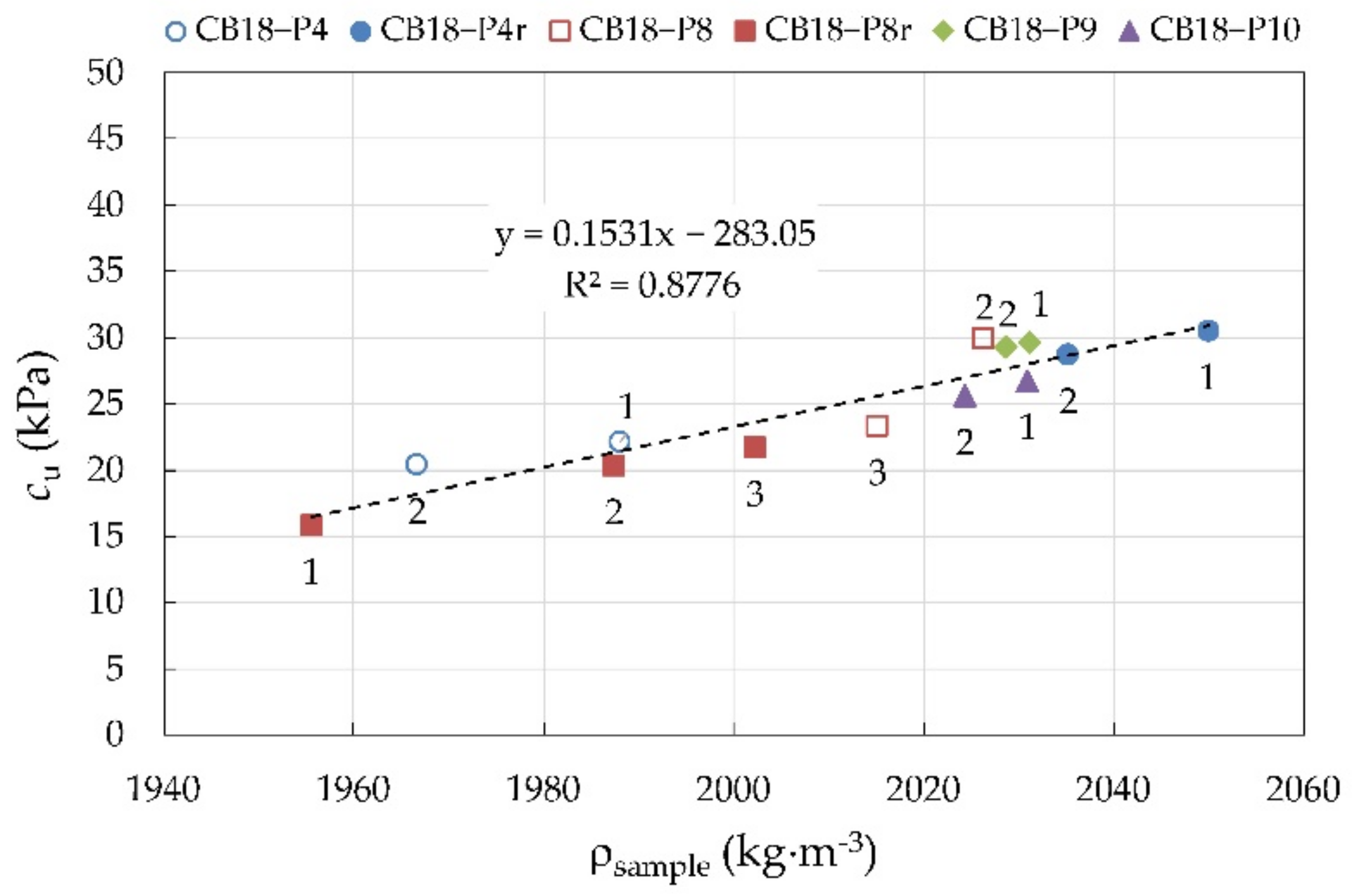
3.3. Undrained Unconfined Shear Strength
3.4. Undrained Direct Shear Strength
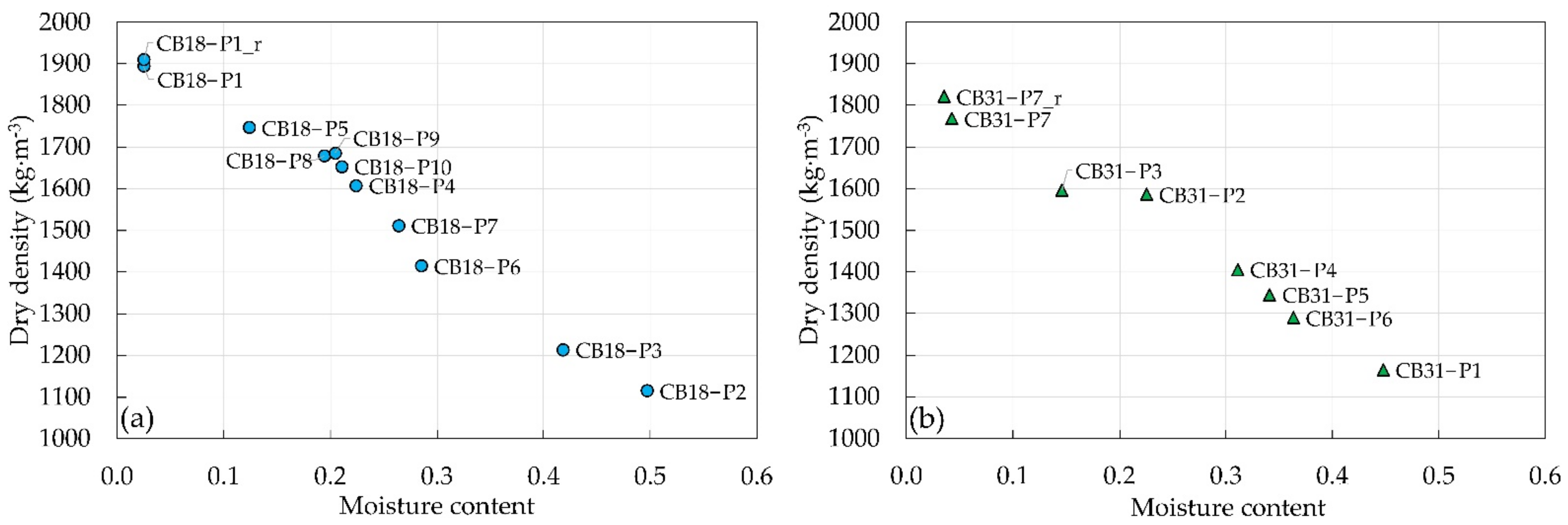
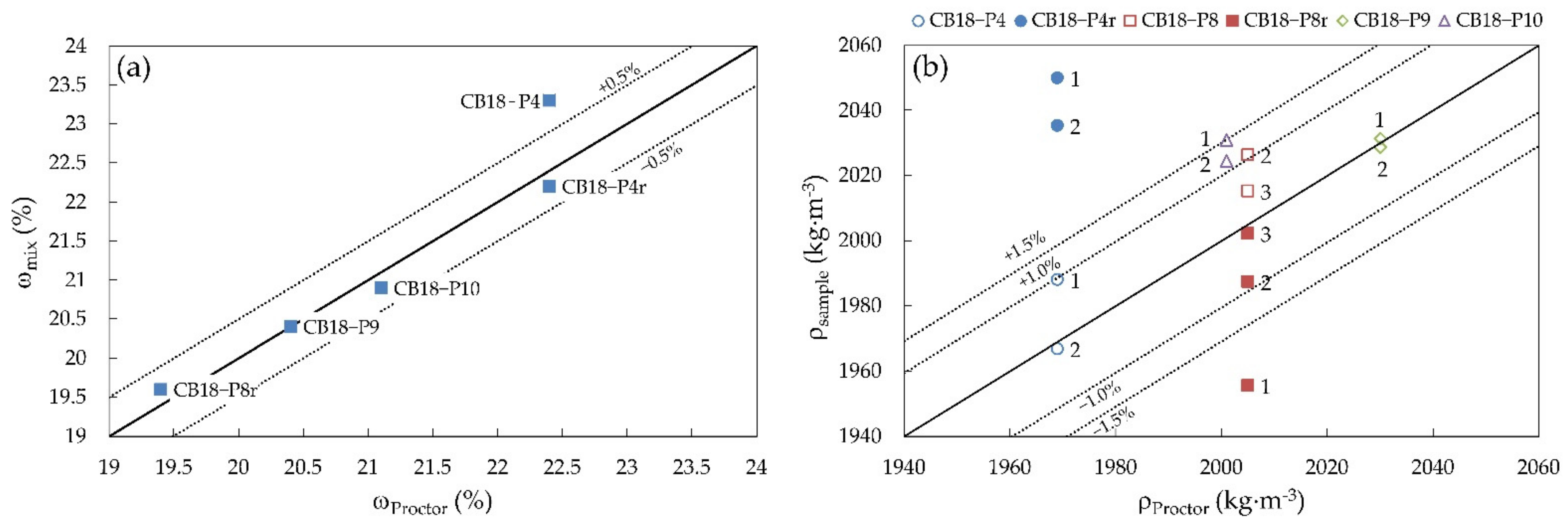
3.5. Cohesive Central Cores Density as Built
3.6. The Reservoir Level and the Displacements of the Cohesive Core
3.7. The Mechanics of Failure
4. Discussion
4.1. Compaction Tests
4.2. Tools for the Control of Compacticion of the Physical Models
4.2.1. Penetrometer Measurements
4.2.2. Shear Vane Measurements
4.3. Undrained Unconfined Shear Strength
4.4. Undrained Direct Shear Strength
4.5. Displacements of the Cohesive Core
4.6. Size and Geometry of the Breach
4.7. Methodological Considerations
4.8. Time to Failure
5. Conclusions
- The unconfined shear strength (cu) of the compacted sand-bentonite mixtures was both density and time-dependent. It grew with the increase in both of these variables. Regarding time, these compacted samples reached their maximum strength before 7 days of curation and were around 60% stronger than the samples tested after 1 day of curation. No differences were observed between 7 and 28 days of curation.
- The elastic modulus (Eu) obtained from the unconfined Simple Compression Tests was also time-dependent. Its value increased 59% on average from 3.9 MPa ± 0.8 MPa (one standard deviation) in samples tested after 1 day of curation to 6.3 MPa ± 0.8 MPa after 7 days of curation. No differences were observed between 7 and 28 days of curation.
- The cohesive central cores were extremely sensitive to small oscillations of the reservoir level. Even risings of just a few millimeters produced displacement of the crest in the downstream direction.
- The cohesive cores behaved as rigid bodies, like concrete slabs with three fixed sides and one free. Cracks formed on the downstream face developed until three independent blocks were formed, two of them rotating around the ‘vertical’ axes located in the lateral walls of the breach and one around the ‘horizontal’ axis located at the base of the breach.
- The shape and dimensions of the breach formed on the cohesive cores had roughly the same shape and dimensions as the unprotected area.
- The objective behind testing two different widths was to see how this change could affect the depth of the breach, as it would be expected that wider unprotections would result in the collapse of the core for a lower depth. For the conditions of this set of tests and its limitations, we cannot state that a wider unprotection of the cohesive core results in less deep breaches.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| cp | Soil strength to penetration measured with the Geotester Pocket Penetrometer kit (fundamental units M·L−1·T−2) |
| cu | Unconfined shear strength calculated from the Simple Compression Test (fundamental units M·L−1·T−2) |
| cuu | Cohesion of the compacted soil samples obtained from the unconsolidated undrained direct shear strength (fundamental units M·L−1·T−2) |
| Cu | Coefficient of uniformity, the ratio D60/D10 (dimensionless) |
| D10 | Sieve size passing 10% of the particles (fundamental units L) |
| D50 | Sieve size passing 50% of the particles (fundamental units L) |
| D60 | Sieve size passing 60% of the particles (fundamental units L) |
| Eu | Elastic modulus calculated from the Unconfined Simple Compression Tests (fundamental units M·L−1·T−2) |
| H | Cohesive core height (fundamental units L) |
| Hr | Reservoir water elevation from the flume base (fundamental units L) |
| Ib | Width of the cohesive core base (fundamental units L) |
| Ic | Width of the cohesive core crest (fundamental units L) |
| MAIN | Main Laboratory Experiments |
| pS:B | Sand-bentonite proportion in weight (dimensionless) |
| PRELIM | Preliminary Laboratory Experiments |
| qu | Unconfined compressive strength obtained from the Simple Compression Test (fundamental units M·L−1·T−2) |
| s | Real displacements along the flume longitudinal axis (fundamental units L) |
| su | Undrained shear strength measured with the Humboldt H-4212MH Pocket Shear Vane Tester (fundamental units M·L−1·T−2) |
| S | Amplified displacements along the flume walls (fundamental units L) |
| tfailure | Time for the failure of the compacted soil samples (fundamental units T) |
| w’ | Width of the cohesive core unprotected area (fundamental length L) |
| W | Generic apparent/moistured mass of a given amount of soil (fundamental units M) |
| WB | Apparent/moistured mass of bentonite (fundamental units M) |
| WB,d | Mass of dry bentonite (fundamental units M) |
| Wd | Generic mass of a dry amount of soil (fundamental units M) |
| WH2O,add | Mass of water to add to a given sand-bentonite mixture to reach the mixture desired moisture content (ωgoal) (dimensionless) |
| WS | Apparent/moistured mass of sand (fundamental units M) |
| WS,d | Mass of dry sand (fundamental units M) |
| x0 | Distance along the flume longitudinal axis between the initial position of the needle and the laser pointer (fundamental units L) |
| X0 | Distance along the flume’s right wall between the laser pointer and the initial position of the projected laser beam point (fundamental units L) |
| α | Angle of the original laser beam direction (perpendicular to the flume) with the new position of the rotating mirror’s arm (degrees) |
| α0 | Angle of the original laser beam direction (perpendicular to the flume) with the initial position of the mirror’s arm on which the needle leans on (degrees) |
| β | Angle of the original laser beam direction (perpendicular to the flume) with the projected laser beam direction after rotation (degrees) |
| β0 | Angle of the original laser beam direction (perpendicular to the flume) with the projected laser beam direction before any rotation (degrees) |
| ϕuu | Friction angle of the compacted soil samples obtained from the unconsolidated undrained direct shear strength (degrees) |
| γ | Mirror’s rotation angle (dimensionless) |
| εfailure | Strain/deformation for the failure of the compacted soil samples (dimensionless) |
| ρ | Aparent/moistened density of the compacted soil samples (fundamental units M·L−3) |
| ρd | Dry density of the compacted soil samples (fundamental units M·L−3) |
| ρProctor | Apparent/moistened density of the soil mixtures compacted within the Standard Proctor compaction tests campaign (fundamental units M·L−3) |
| ρsample | Apparent/moistened density of a given sample of compacted soil (fundamental units M·L−3) |
| τmax | Maximum shear stress ined from the unconsolidated undrained Direct Shear strength (fundamental units M·L−1·T−2) |
| ω | Moisture content (dimensionless) |
| ωadd | Laking moisture content, i.e., the difference between the desired moisture content (ωgoal) and the sand-bentonite mixture initial moisture content (ωSB,i) (dimensionless) |
| ωB | Bentonite’s moisture content (dimensionless) |
| ωgoal | Desired moisture content for a given sand-bentonite mixture (dimensionless) |
| ωmix | Moisture content of the soil mixtures before compaction (dimensionless) |
| ωProctor | Moisture content of the soil mixtures compacted within the Standard Proctor compaction tests campaign (dimensionless) |
| ωS | Sand’s moisture content (dimensionless) |
| ωsample | Moisture content of a given sample of compacted soil (dimensionless) |
| ωSB,i | Initial moisture content of a sand-bentonite mixture resulting from mixing the sand and the bentonite with their natural moisture contents in a given proportion pS:B (dimensionless) |
Appendix A

Appendix B
| Time (s) | Test Time (hh:mm:ss) | Displacement s (mm) | Time (s) | Test Time (hh:mm:ss) | Displacement s (mm) |
|---|---|---|---|---|---|
| 3571 | 13:05:05 | 0.0 | 4713 | 13:24:07 | 5.7 |
| 3592 | 13:05:26 | 0.1 | 4717 | 13:24:11 | 5.7 |
| 3594 | 13:05:28 | 0.2 | 4718 | 13:24:12 | 5.9 |
| 3595 | 13:05:29 | 0.3 | 4726 | 13:24:20 | 6.1 |
| 3596 | 13:05:30 | 0.4 | 4736 | 13:24:30 | 6.4 |
| 3597 | 13:05:31 | 0.8 | 4756 | 13:24:50 | 6.6 |
| 3598 | 13:05:32 | 1.1 | 4794 | 13:25:28 | 7.1 |
| 3599 | 13:05:33 | 1.9 | 4848 | 13:26:22 | 7.3 |
| 3613 | 13:05:47 | 1.9 | 4914 | 13:27:28 | 7.6 |
| 3704 | 13:07:18 | 1.9 | 4984 | 13:28:38 | 7.8 |
| 4598 | 13:22:12 | 1.9 | 5070 | 13:30:04 | 8.1 |
| 4670 | 13:23:24 | 1.9 | 5185 | 13:31:59 | 8.5 |
| 4674 | 13:23:28 | 2.0 | 5695 | 13:40:29 | 8.6 |
| 4675 | 13:23:29 | 2.1 | 5799 | 13:42:13 | 9.9 |
| 4677 | 13:23:31 | 2.2 | 5911 | 13:44:05 | 10.2 |
| 4678 | 13:23:32 | 2.3 | 5944 | 13:44:38 | 10.5 |
| 4680 | 13:23:34 | 2.7 | 5974 | 13:45:08 | 10.8 |
| 4681 | 13:23:35 | 2.8 | 5986 | 13:45:20 | 10.9 |
| 4682 | 13:23:36 | 2.9 | 6018 | 13:45:52 | 11.1 |
| 4683 | 13:23:37 | 3.0 | 6354 | 13:51:28 | 11.2 |
| 4684 | 13:23:38 | 3.1 | 6386 | 13:52:00 | 11.4 |
| 4686 | 13:23:40 | 3.2 | 6440 | 13:52:54 | 11.7 |
| 4688 | 13:23:42 | 3.3 | 6495 | 13:53:49 | 12.0 |
| 4689 | 13:23:43 | 3.4 | 6531 | 13:54:25 | 12.1 |
| 4690 | 13:23:44 | 3.5 | 6555 | 13:54:49 | 12.3 |
| 4694 | 13:23:48 | 3.8 | 6703 | 13:57:17 | 12.3 |
| 4697 | 13:23:51 | 4.3 | 6846 | 13:59:40 | 13.2 |
| 4698 | 13:23:52 | 4.6 | 6848 | 13:59:42 | 13.4 |
| 4699 | 13:23:53 | 4.9 | 6849 | 13:59:43 | 13.6 |
| 4701 | 13:23:55 | 5.0 | 6850 | 13:59:44 | 14.5 |
| 4703 | 13:23:57 | 5.1 | 6852 | 13:59:46 | 15.1 |
| 4705 | 13:23:59 | 5.2 | 6853 | 13:59:47 | 16.6 |
| 4707 | 13:24:01 | 5.4 | 6854 | 13:59:48 | 17.8 |
| 4710 | 13:24:04 | 5.6 | 6855 | 13:59:49 | 19.3 |
| Time (s) | Test Time (hh:mm:ss) | Displacement s (mm) | Time (s) | Test Time (hh:mm:ss) | Displacement s (mm) |
|---|---|---|---|---|---|
| 2508 | 13:10:00 | 0.0 | 3763 | 13:30:55 | 8.3 |
| 2585 | 13:11:17 | 1.3 | 3882 | 13:32:54 | 8.6 |
| 2611 | 13:11:43 | 4.1 | 3934 | 13:33:46 | 9.1 |
| 2614 | 13:11:46 | 4.2 | 3959 | 13:34:11 | 9.2 |
| 2616 | 13:11:48 | 4.3 | 3961 | 13:34:13 | 9.3 |
| 2621 | 13:11:53 | 5.3 | 4559 | 13:44:11 | 9.3 |
| 2622 | 13:11:54 | 5.4 | 4630 | 13:45:22 | 9.4 |
| 2624 | 13:11:56 | 5.8 | 4633 | 13:45:25 | 10.0 |
| 2625 | 13:11:57 | 6.5 | 4634 | 13:45:26 | 10.6 |
| 2627 | 13:11:59 | NA | 4636 | 13:45:28 | 11.3 |
| 2637 | 13:12:09 | 6.5 | 4637 | 13:45:29 | 11.4 |
| 2727 | 13:13:39 | 6.5 | 4638 | 13:45:30 | 11.8 |
| 2921 | 13:16:53 | 6.5 | 4639 | 13:45:31 | 12.0 |
| 2924 | 13:16:56 | 6.8 | 4641 | 13:45:33 | 12.1 |
| 2970 | 13:17:42 | 7.0 | 4643 | 13:45:35 | 13.9 |
| 3012 | 13:18:24 | 7.3 | 4644 | 13:45:36 | 16.1 |
| 3053 | 13:19:05 | 7.5 | 4646 | 13:45:38 | 17.9 |
| 3071 | 13:19:23 | 7.6 | 4647 | 13:45:39 | 19.4 |
| 3093 | 13:19:45 | 7.8 | 4649 | 13:45:41 | 20.5 |
| 3560 | 13:27:32 | 7.8 | 4650 | 13:45:42 | 21.0 |
| 3627 | 13:28:39 | 7.8 |
| Time (s) | Test Time (hh:mm:ss) | Displacement s (mm) | Time (s) | Test Time (hh:mm:ss) | Displacement s (mm) |
|---|---|---|---|---|---|
| 9 | 12:40:00 | 0.5 | 3409 | 13:36:40 | 5.3 |
| 309 | 12:45:00 | 0.5 | 3699 | 13:41:30 | 5.5 |
| 3284 | 13:34:35 | 0.5 | 3754 | 13:42:25 | 5.8 |
| 3287 | 13:34:38 | 0.5 | 3959 | 13:45:50 | 6.0 |
| 3289 | 13:34:40 | 1.0 | 4270 | 13:51:01 | 6.3 |
| 3290 | 13:34:41 | 2.0 | 4309 | 13:51:40 | 6.3 |
| 3292 | 13:34:43 | 3.0 | 4465 | 13:54:16 | 17.3 |
| 3296 | 13:34:47 | 3.5 | 4466 | 13:54:17 | 19.5 |
| 3299 | 13:34:50 | 4.0 | 4467 | 13:54:18 | 20.3 |
| 3302 | 13:34:53 | 4.3 | 4468 | 13:54:19 | 21.5 |
| 3309 | 13:35:00 | 4.5 | 4469 | 13:54:20 | 23.5 |
| 3311 | 13:35:02 | 4.8 | 4470 | 13:54:21 | 24.8 |
| 3312 | 13:35:03 | 5.0 | 4471 | 13:54:22 | 26.0 |
| 3319 | 13:35:10 | 5.0 | 4472 | 13:54:23 | 27.5 |
References
- Hansen, D.; Zhao, W.Z.; Han, S.Y. Hydraulic Performance and Stability of Coarse Rockfill Deposits. Proc. Inst. Civ. Eng.-Water Manag.-Water Manag. 2005, 158, 163–175. [Google Scholar] [CrossRef]
- Costa, J.E.; Schuster, R.L. The Formation and Failure of Natural Dams. Geol. Soc. Am. Bull. 1988, 100, 1054–1068. [Google Scholar] [CrossRef]
- Gregoretti, C.; Maltauro, A.; Lanzoni, S. Laboratory Experiments on the Failure of Coarse Homogeneous Sediment Natural Dams on a Sloping Bed. J. Hydraul. Eng. 2010, 136, 868–879. [Google Scholar] [CrossRef] [Green Version]
- Wishart, J.S. Overtopping Breaching of Rock-Avalanche Dams; University of Canterbury, Upper Riccarton: Christchurch, New Zealand, 2007. [Google Scholar]
- Foster, M.; Fell, R.; Spannagle, M. The Statistics of Embankment Dam Failures and Accidents. Can. Geotech. J. 2000, 37, 1000–1024. [Google Scholar] [CrossRef]
- Ergun, S. Fluid Flow through Packed Columns. Chem. Eng. Prog 1952, 48, 89–94. [Google Scholar]
- Ferdos, F.; Yang, J.; Wörman, A. Characterization of Hydraulic Behaviours of Coarse Rock Materials in a Large Permeameter. J. Geosci. Environ. Prot. 2013, 1, 1–6. [Google Scholar] [CrossRef]
- Ferdos, F.; Worman, A.; Ekstrom, I. Hydraulic Conductivity of Coarse Rockfill Used in Hydraulic Structures. Transp. Porous Media 2015, 108, 367–391. [Google Scholar] [CrossRef]
- Li, B.; Garga, V.K. Theoretical Solution for Seepage Flow in Overtopped Rockfill. J. Hydraul. Eng. 1998, 124, 213–217. [Google Scholar] [CrossRef]
- Li, B.; Garga, V.K.; Davies, M.H. Relationships for Non-Darcy Flow in Rockfill. J. Hydraul. Eng. 1998, 124, 206–212. [Google Scholar] [CrossRef]
- Monteiro-Alves, R.; Toledo, M.Á.; Morán, R. Characterization of the Overtopping Flow through the Downstream Shell of Rockfill Dams. J. Hydraul. Eng. 2019, 145, 04019015.1–04019015.17. [Google Scholar] [CrossRef]
- Monteiro-Alves, R. Erratum for “Characterization of the Overtopping Flow through the Downstream Shell of Rockfill Dams” by Ricardo Monteiro-Alves, Miguel Á. Toledo, and Rafael Morán. J. Hydraul. Eng. 2020, 146, 08220004–1. [Google Scholar] [CrossRef]
- Morteza, S.; Reza, S.M.; Habibollah, B. Concept of Hydraulic Porosity and Experimental Investigation in Nonlinear Flow Analysis through Rubble-Mound Breakwaters. J. Hydrol. (Amst.) 2014, 508, 266–272. [Google Scholar] [CrossRef]
- Salahi, M.-B.; Sedghi-Asl, M.; Parvizi, M. Nonlinear Flow through a Packed-Column Experiment. J. Hydrol. Eng. 2015, 20, 04015003:1–9. [Google Scholar] [CrossRef]
- Sedghi-Asl, M.; Rahimi, H.; Farhoudi, J.; Hoorfar, A.; Hartmann, S. One-Dimensional Fully Developed Turbulent Flow through Coarse Porous Medium. J. Hydrol. Eng. 2014, 19, 1491–1496. [Google Scholar] [CrossRef]
- Soualmia, A.; Jouini, M.; Masbernat, L.; Dartus, D. An Analytical Model for Water Profile Calculations in Free Surface Flows through Rockfills. J. Theor. Appl. Mech. 2015, 53, 209–215. [Google Scholar] [CrossRef] [Green Version]
- Stephenson, D.J. Rockfill in Hydraulic Engineering; Elsevier: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Venkataraman, P.; Rama Mohan Rao, P. Darcian, Transitional, and Turbulent Flow through Porous Media. J. Hydraul. Eng. 1998, 124, 840–846. [Google Scholar] [CrossRef]
- Hansen, D.; Roshanfekr, A. Use of Index Gradients and Default Tailwater Depth as Aids to Hydraulic Modeling of Flow-through Rockfill Dams. J. Hydraul. Eng. 2012, 138, 726–735. [Google Scholar] [CrossRef]
- Hansen, D.; Roshanfekr, A. Assessment of Potential for Seepage-Induced Unraveling Failure of Flow-through Rockfill Dams. Int. J. Geomech. 2012, 12, 560–573. [Google Scholar] [CrossRef]
- Parkin, A.K. Bulletin No. 7: Rockfill Dams with Inbuilt Spillways-Stability Characteristics; Water Research Foundation of Australis: Sydney, Australia, 1963. [Google Scholar]
- Toledo, M.Á. Presas de Escollera Sometidas a Sobrevertido. Estudio Del Movimiento Del Agua a Traves de La Escollera y de La Estabilidad Frente al Deslizamiento En Masa; Universidad Politécnica de Madrid: Madrid, Spain, 1997. [Google Scholar]
- Alves, R.M.; Toledo, M.Á.; Morán, R. Overflow for the Complete Failure of the Downstream Shell of a Rockfill Dam. In Proceedings of the 2nd International Seminar on Dam Protection against Overtopping, Fort Collins, CO, USA, 7–9 September 2016; Colorado State University, Libraries: Fort Collins, CO, USA, 2016. [Google Scholar]
- Javadi, N.; Mahdi, T.F. Experimental Investigation into Rockfill Dam Failure Initiation by Overtopping. Nat. Hazards 2014, 74, 623–637. [Google Scholar] [CrossRef]
- Morán, R.; Alves, R.; Toledo, M.Á.; Larese, A.; Salazar, F.; Rossi, R. Procedimiento de Diseño de Protecciones Tipo Repié para Evitar la Rotura por Deslizamiento en Masa de Presas de Escollera Sometidas a Percolaciones Extremas. In Proceedings of the III Jornadas de Ingeniería del Agua. La protección contra los riesgos hídricos, Valencia, Spain, 23–24 October 2013; Universitat Politècnica de València: Valencia, Spain, 2013. [Google Scholar]
- Larese, A.; Rossi, R.; Oñate, E.; Toledo, M.Á.; Morán, R.; Campos, H. Numerical and Experimental Study of Overtopping and Failure of Rockfill Dams. Int. J. Geomech. 2015, 15, 04014060. [Google Scholar] [CrossRef]
- Monteiro-Alves, R.; Toledo, M.Á.; Moran, R.; Balairón, L. Failure of the Downstream Shoulder of Rockfill Dams Due to Overtopping or Throughflow. Water 2022, 14, 1624. [Google Scholar] [CrossRef]
- Powledge, G.R.; Ralston, D.C.; Miller, P.; Chen, Y.H.; Clopper, P.E.; Temple, D.M. Mechanics of Overflow Erosion on Embankments. II: Hydraulic and Design Considerations. J. Hydraul. Eng. 1989, 115, 1056–1075. [Google Scholar] [CrossRef]
- Toledo, M.Á.; Alves, R.M.; Morán, R. Structural Failure of the Clay Core or the Upstream Face of Rockfill Dams in Overtopping Scenario. In Proceedings of the Dam Protections against Overtopping and Accidental Leakage; Toledo, M.Á., Morán, R., Oñate, E., Eds.; CRC Press/Balkema: EH Leiden, The Netherlands, 2015; pp. 101–109. [Google Scholar]
- Mohamed, M.; Samuels, P. Improving the Accuracy of Prediction of Breach Formation through Embankment Dams and Flood Embankments. In Proceedings of the River Flow 2002-International Conference on Fluvial Hydraulics, Louvain-la-Neuve, Belgium, 4–6 September 2002; Bousmar, D., Zech, Y., Eds.; Balkema: Louvain-la-Neuve, Belgium, 2002; Volume 2002. [Google Scholar]
- Ricoy, L.F.; Toledo, M.Á.; Morán, R. A Model for the Analysis of the Structural Failure of the Clay Core in Rockfill Dams Due to Overtopping. In Proceedings of the Protections 2016: 2nd International Seminar on Dam Protection Against Overtopping, Fort Collins, CO, USA, 7–9 September 2016; Colorado State University: Fort Collins, CO, USA, 2017. [Google Scholar]
- Monteiro Alves, R.M. Proceso de Rotura de Las Presas de Escollera Por Sobrevertido. Ph. D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2021. [Google Scholar]
- Wu, W. Simplified Physically Based Model of Earthen Embankment Breaching. J. Hydraul. Eng. 2013, 139, 837–851. [Google Scholar] [CrossRef]
- Franca, M.J.; Almeida, A.B. A Computational Model of Rockfill Dam Breaching Caused by Overtopping (RoDaB). J. Hydraul. Res. 2004, 42, 197–206. [Google Scholar] [CrossRef]
- USDA WinDAM C Software. Available online: http://go.usa.gov/cupCF (accessed on 30 August 2022).
- Wu, W. Introduction to DLBreach—A Simplified Physically-Based Dam/Levee Breach Model. (Version 2016.4); Clarkson University: Potsdam, NY, USA, 2016. [Google Scholar]
- Wu, W. Inputs and Outputs of DLBreach—A Simplified Physically-Based Dam/Levee Breach Model. (Version 2016.4); Clarkson University: Potsdam, NY, USA, 2016. [Google Scholar]
- Morris, M. Breaching of Earth Embankments and Dams; The Open University: Milton Keynes, UK, 2011. [Google Scholar]
- Hassan, M. EMBREA Web a Tool for the Simulation of Breach through Dams and Embankments. In Proceedings of the ICOLD Symposium on Sustainable Development of Dams and River Basins & APG Symposium on Water and Dams, New Delhi, India, 24–27 February 2021. [Google Scholar]
- Robinson, K.M.; Hanson, G.J. A Deterministic Headcut Advance Model. Trans. ASAE 1994, 37, 1437–1443. [Google Scholar] [CrossRef]
- Hanson, G.; Robinson, K.M.; Cook, K.R. Prediction of Headcut Migration Using a Deterministic Approach. Trans. ASAE 2001, 44, 525. [Google Scholar] [CrossRef]
- Hanson, G.J.; Cook, K.R.; Britton, S.L. Evaluating Erosion Widening and Headcut Migration Rates for Embankment Overtopping Tests. In Proceedings of the 2003 ASAE Annual Meeting, Las Vegas, NV, USA, 27–30 July 2003; p. 032067. [Google Scholar]
- Zhang, J.; Li, Y.; Xuan, G.; Wang, X.; Li, J. Overtopping Breaching of Cohesive Homogeneous Earth Dam with Different Cohesive Strength. Sci. China Ser. E Technol. Sci. 2009, 52, 3024–3029. [Google Scholar] [CrossRef]
- Yu, M.H.; Wei, H.Y.; Liang, Y.J.; Zhao, Y. Investigation of Non-Cohesive Levee Breach by Overtopping Flow. J. Hydrodyn. 2013, 25, 572–579. [Google Scholar] [CrossRef]
- Zhong, Q.M.; Chen, S.S.; Deng, Z. Numerical Model for Homogeneous Cohesive Dam Breaching Due to Overtopping Failure. J. Mt. Sci. 2017, 14, 571–580. [Google Scholar] [CrossRef]
- Hanson, G.J.; Cook, K.R.; Hunt, S.L. Physical Modeling of Overtopping Erosion and Breach Formation of Cohesive Embankments. Trans. ASAE 2005, 48, 1783–1794. [Google Scholar] [CrossRef]
- Wang, Z.; Bowles, D.S. Three-Dimensional Non-Cohesive Earthen Dam Breach Model. Part 1: Theory and Methodology. Adv. Water Resour. 2006, 29, 1528–1545. [Google Scholar] [CrossRef]
- Jiang, X.; Wei, Y.; Wu, L.; Hu, K.; Zhu, Z.; Zou, Z.; Xiao, W. Laboratory Experiments on Failure Characteristics of Non-Cohesive Sediment Natural Dam in Progressive Failure Mode. Env. Earth Sci. 2019, 78, 538. [Google Scholar] [CrossRef]
- Rahman, A.; Nistor, I.; Infante, J.A. The Effect of the Non-Cohesive Homogenous Embankment Geometry on the Breach Outflow and Erosion Rates during Overtopping. Proc. Annu. Conf.-Can. Soc. Civ. Eng. 2019, 2019, HYD005-1–HYD005-10. [Google Scholar]
- Wahl, T.L. Erosion Testing of Zoned Rockfill Embankments. Hydraulic Laboratory Report HL-2019-01; U.S. Nuclear Regulatory Commission: Washington, DC, USA, 2019. [Google Scholar]
- Lee, P.Y.; Suedkamp, R.J. Characteristics of Irregularly Shaped Compaction Curves of Soils. Highw. Res. Rec. 1972, 381, 1–9. [Google Scholar]
- Proia, R.; Croce, P.; Modoni, G. Experimental Investigation of Compacted Sand-Bentonite Mixtures. Procedia. Eng. 2016, 158, 51–56. [Google Scholar] [CrossRef]








| Sample 1 | Sample 2 | Sample 3 | |||
|---|---|---|---|---|---|
| Size (mm) | Passing (%) | Size (mm) | Passing (%) | Size (mm) | Passing (%) |
| 12.50 | 100.00 | 6.3 | 100 | 6.3 | 100 |
| 10.00 | 100.00 | 5 | 99.9 | 5 | 99.8 |
| 5.00 | 99.00 | 2 | 89.7 | 2 | 87.3 |
| 2.00 | 85.00 | 1 | 69.9 | 1 | 61.3 |
| 0.40 | 21.00 | 0.63 | 49.7 | 0.63 | 42.3 |
| 0.08 | 2.30 | 0.4 | 31.4 | 0.4 | 25 |
| 0.2 | 13.7 | 0.2 | 9.6 | ||
| 0.125 | 8.7 | 0.125 | 5.9 | ||
| 0.1047 | 6.9 | 0.1053 | 4.7 | ||
| 0.08 | 6.7 | 0.08 | 4.6 | ||
| 0.063 | 6.2 | 0.063 | 4.3 | ||
| 0.08 | 5.2 | 0.08 | 3.8 | ||
| 0.0625 | 4.2 | 0.0627 | 2.9 | ||
| 0.0551 | 2.7 | 0.0552 | 2.0 | ||
| 0.0395 | 1.5 | 0.0393 | 1.5 | ||
| 0.028 | 1.1 | 0.0281 | 0.9 | ||
| 0.0198 | 1.0 | 0.02 | 0.5 | ||
| 0.0145 | 0.9 | 0.0147 | 0.00 | ||
| 0.0103 | 0.6 | ||||
| 0.0073 | 0.5 | ||||
| 0.0052 | 0.5 | ||||
| 0.0036 | 0.4 | ||||
| 0.0026 | 0.3 | ||||
| 0.0015 | 0.1 | ||||
| Chemical Component | Percentage |
|---|---|
| SiO2 | 64.2% |
| Al2O3 | 12.1% |
| Fe2O3 | 2.6% |
| TiO2 | 0.5% |
| MgO | 8.5% |
| CaO | 1.2% |
| Na2O | 2.3% |
| K2O | 0.8% |
| Mixture | CB (%) | ω (%) | Std. Proctor | Simple Compression | Direct Shear |
|---|---|---|---|---|---|
| CB18-P1 | 18 | 2.5 | Yes | ||
| CB18-P2 | 18 | 49.7 | Yes | ||
| CB18-P3 | 18 | 41.8 | Yes | ||
| CB18-P4 | 18 | 22.4 | Yes | Yes | Yes |
| CB18-P5 | 18 | 12.4 | Yes | ||
| CB18-P6 | 18 | 28.5 | Yes | ||
| CB18-P7 | 18 | 26.4 | Yes | ||
| CB18-P8 * | 18 | 19.4 | Yes | Yes | Yes |
| CB18-P9 | 18 | 20.4 | Yes | Yes | Yes |
| CB18-P10 | 18 | 21.1 | Yes | Yes | Yes |
| CB31-P1 | 31 | 44.8 | Yes | ||
| CB31-P2 | 31 | 22.5 | Yes | ||
| CB31-P3 | 31 | 14.6 | Yes | ||
| CB31-P4 | 31 | 31.1 | Yes | ||
| CB31-P5 | 31 | 34.1 | Yes | ||
| CB31-P6 | 31 | 36.3 | Yes | ||
| CB31-P7 | 31 | 3.9 | Yes |
| Test | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | Symbol | PRELIM1 | PRELIM2 | MAIN1 | MAIN2 | MAIN3 | MAIN3+ |
| Core height (m) | H | 1 | 0.94 | 1 | 1 | 1 | ≈0.6 |
| Crest width (m) | lc | 0.15 | 0.12 | 0.06 | 0.06 | 0.06 | ≈0.076 |
| Base width (m) | lb | 0.5 | 0.45 | 0.1 | 0.1 | 0.1 | 0.1 |
| Reservoir level (m) | Hr | ≈1.05 | ≈0.94 | ≈1 | ≈1 | ≈1 | ≈0.68 * |
| Unprotection width (m) | w′ | 0.52 | 0.52 | 0.52 | 0.52 | 1.40 | 1.40 |
| Mixture | CB (%) | ω (%) | ρd (kg·m−3) | ρ (kg·m−3) |
|---|---|---|---|---|
| CB18-P1 * | 18 | 2.5 | 1902 | 1950 |
| CB18-P5 | 18 | 12.4 | 1747 | 1963 |
| CB18-P8 | 18 | 19.4 | 1679 | 2005 |
| CB18-P9 | 18 | 20.4 | 1685 | 2030 |
| CB18-P10 | 18 | 21.1 | 1653 | 2001 |
| CB18-P4 | 18 | 22.4 | 1608 | 1969 |
| CB18-P7 | 18 | 26.4 | 1512 | 1911 |
| CB18-P6 | 18 | 28.5 | 1414 | 1818 |
| CB18-P3 | 18 | 41.8 | 1214 | 1722 |
| CB18-P2 | 18 | 49.7 | 1116 | 1670 |
| CB31-P7 * | 31 | 3.9 | 1795 | 1864 |
| CB31-P3 | 31 | 14.6 | 1597 | 1830 |
| CB31-P2 | 31 | 22.5 | 1586 | 1944 |
| CB31-P4 | 31 | 31.1 | 1406 | 1843 |
| CB31-P5 | 31 | 34.1 | 1345 | 1804 |
| CB31-P6 | 31 | 36.3 | 1290 | 1758 |
| CB31-P1 | 31 | 44.8 | 1165 | 1687 |
| Mixture | Sample | ωProctor (%) | ωmix (%) | ωsample (%) | ρProctor (kg·m−3) | ρsample (kg·m−3) | cu (kPa) | εfailure (%) | tfailure (s) |
|---|---|---|---|---|---|---|---|---|---|
| CB18-P4 | 1 | 22.4 | 23.3 | 22.3 | 1969 | 1988 | 22.13 | 5.33 | 240 |
| 2 | 22.4 | 1967 | 20.38 | 5.33 | 240 | ||||
| CB18-P4r | 1 | 22.4 | 22.2 | 18.6 | 1969 | 2050 | 30.50 | 4.67 | 210 |
| 2 | 19.7 | 2035 | 28.71 | 6.67 | 300 | ||||
| CB18-P8 | 1 | 19.4 | NA | 20.0 | 2005 | NA | 29.33 | 4.67 | 210 |
| 2 | 19.8 | 2026 | 29.91 | 4.67 | 210 | ||||
| 3 | 19.6 | 2015 | 23.30 | 5.33 | 240 | ||||
| CB18-P8r | 1 | 19.4 | 19.6 | 23.6 | 2005 | 1956 | 15.74 | 7.33 | 330 |
| 2 | 21.8 | 1987 | 20.30 | 7.33 | 330 | ||||
| 3 | 21.1 | 2002 | 21.66 | 7.33 | 330 | ||||
| CB18-P9 | 1 | 20.4 | 20.4 | 19.5 | 2030 | 2031 | 29.65 | 6.00 | 270 |
| 2 | 19.4 | 2029 | 29.32 | 5.33 | 240 | ||||
| CB18-P10 | 1 | 21.1 | 20.9 | 20.5 | 2001 | 2031 | 26.70 | 7.33 | 330 |
| 2 | 20.2 | 2024 | 25.59 | 5.33 | 240 |
| Mixture | Sample | ωProctor (%) | ωmix (%) | ωsample (%) | ρProctor (kg·m−3) | ρsample (kg·m−3) | cu (kPa) | εfailure (%) | tfailure (s) |
|---|---|---|---|---|---|---|---|---|---|
| CB18-P8 (7 days) | 1 | 19.4 | 19.7 | 19.2 | 2005 | 2020 | 39.52 | 2.67 | 120 |
| 2 | 19.6 | 2015 | 37.47 | 3.33 | 150 | ||||
| 3 | 18.6 | 2027 | 41.92 | 2.67 | 120 | ||||
| CB18-P8 (28 days) | 1 | 19.4 | 20.0 | 18.8 | 2005 | 2041 | 38.98 | 4.00 | 180 |
| 2 | 18.6 | 2042 | 40.16 | 4.00 | 180 | ||||
| 3 | 18.7 | 2032 | 40.72 | 2.67 | 120 |
| Mixture | Sample | ωProctor | ωsample | ρProctor | ρsample | τmax | cuu | ϕuu |
|---|---|---|---|---|---|---|---|---|
| (%) | (%) | (kg·m−3) | (kg·m−3) | (kPa) | (kPa) | (°) | ||
| CB18-P4 | 1 | 22.4 | 22.6 | 1969 | 1954 | 42.87 | 42.16 | 16.1 |
| 2 | 22.7 | 1949 | 45.05 | |||||
| 3 | 25.8 | 1994 | 31.02 | |||||
| 3r | 25.8 | 1947 | 31.54 | |||||
| CB18-P8 | 1 | 19.4 | 19.8 | 2005 | 2005 | 32.88 | 30.61 | 50.2 |
| 2 | 19.8 | 2005 | 43.85 | |||||
| 3 | 19.8 | 2005 | 54.06 | |||||
| CB18-P9 | 1 | 20.4 | 20.5 | 2030 | 2025 | 37.85 | 36.98 | 35.3 |
| 2 | 20.7 | 2030 | 45.59 | |||||
| 3 | 20.2 | 2030 | 50.47 | |||||
| CB18-P10 | 1 | 21.1 | 21.0 | 2001 | 2002 | 23.33 | 23.36 | 52.8 |
| 2 | 21.5 | 2000 | 42.34 | |||||
| 3 | 21.5 | 2000 | 47.22 | |||||
| 3r | 21.2 | 2000 | 47.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monteiro-Alves, R.; Moran, R.; Toledo, M.Á.; Peraita, J. Structural Failure of the Cohesive Core of Rockfill Dams: An Experimental Research Using Sand-Bentonite Mixtures. Water 2022, 14, 3966. https://doi.org/10.3390/w14233966
Monteiro-Alves R, Moran R, Toledo MÁ, Peraita J. Structural Failure of the Cohesive Core of Rockfill Dams: An Experimental Research Using Sand-Bentonite Mixtures. Water. 2022; 14(23):3966. https://doi.org/10.3390/w14233966
Chicago/Turabian StyleMonteiro-Alves, Ricardo, Rafael Moran, Miguel Á. Toledo, and Javier Peraita. 2022. "Structural Failure of the Cohesive Core of Rockfill Dams: An Experimental Research Using Sand-Bentonite Mixtures" Water 14, no. 23: 3966. https://doi.org/10.3390/w14233966
APA StyleMonteiro-Alves, R., Moran, R., Toledo, M. Á., & Peraita, J. (2022). Structural Failure of the Cohesive Core of Rockfill Dams: An Experimental Research Using Sand-Bentonite Mixtures. Water, 14(23), 3966. https://doi.org/10.3390/w14233966










