The Stability Analysis of Tension-Leg Platforms under Marine Environmental Loads via Altering the Connection Angle of Tension Legs
Abstract
1. Introduction
2. Model Establishment and Calculation
2.1. Model Parameters
2.2. Environment Loads
2.2.1. Hydrodynamic Load
2.2.2. Wind Load
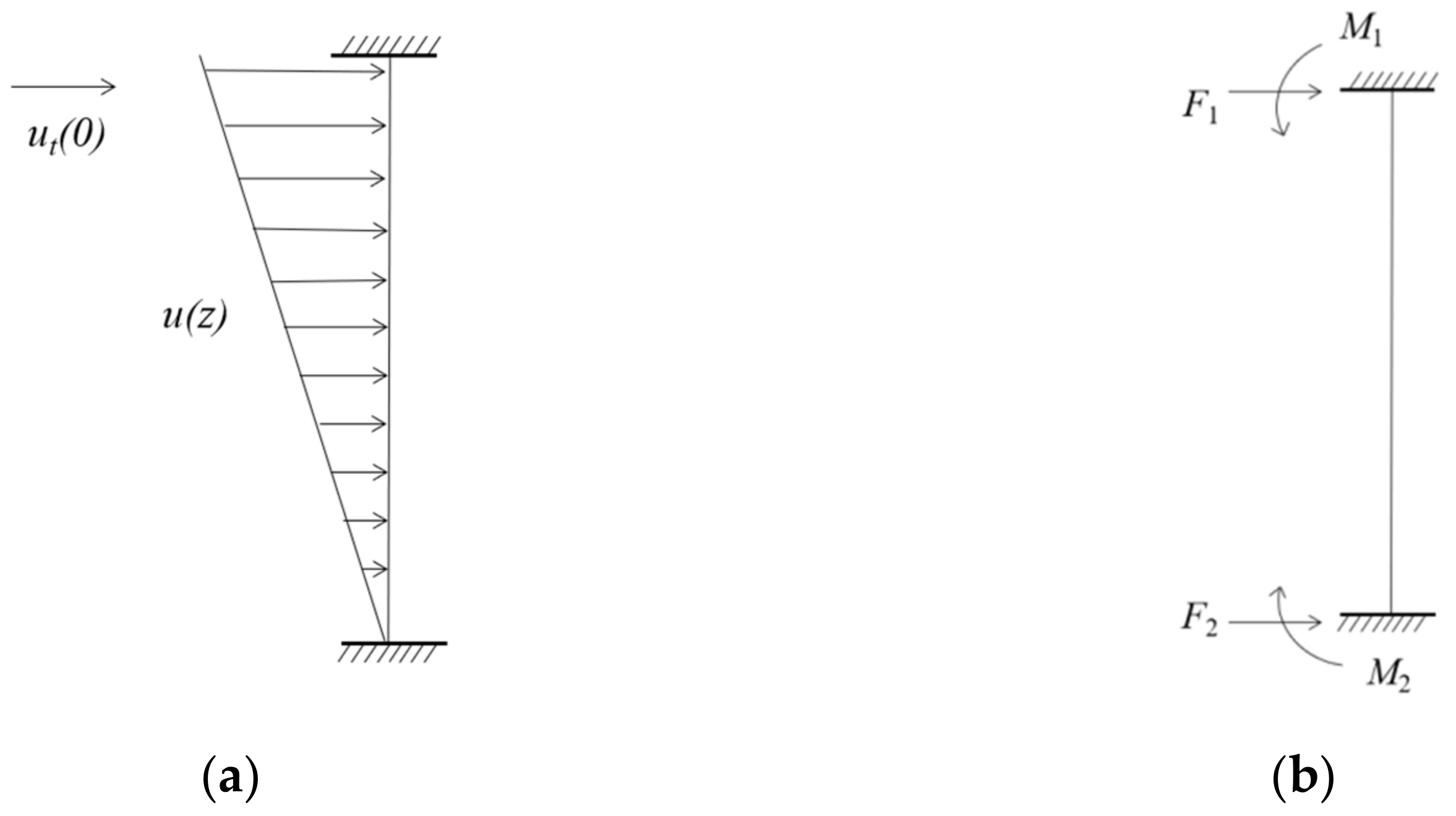
2.2.3. Current Load
2.3. Mooring Load
2.4. Dynamic Equation of the Platform
2.5. Finite Element Model of the Platform
3. Results and Discussion
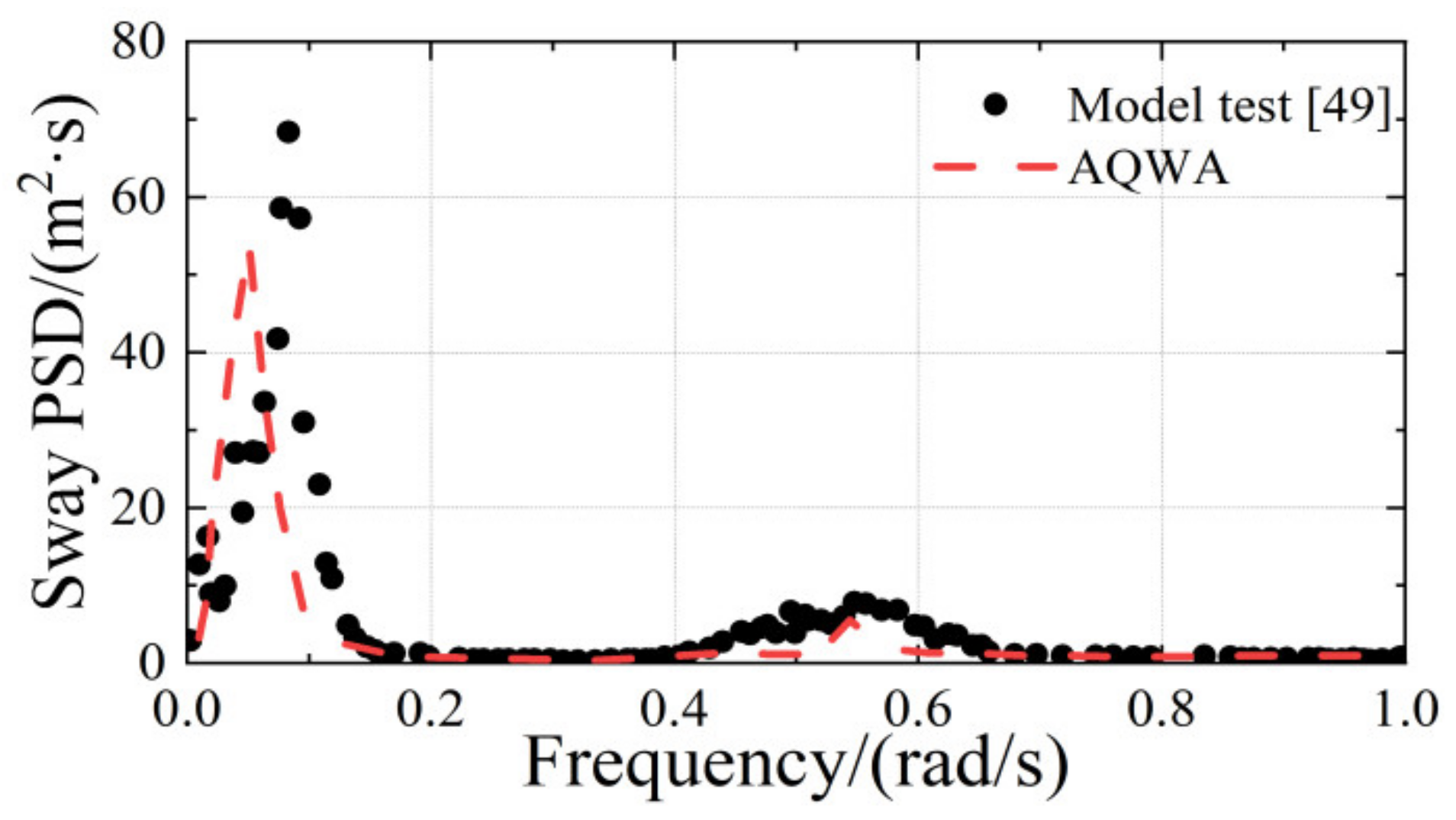
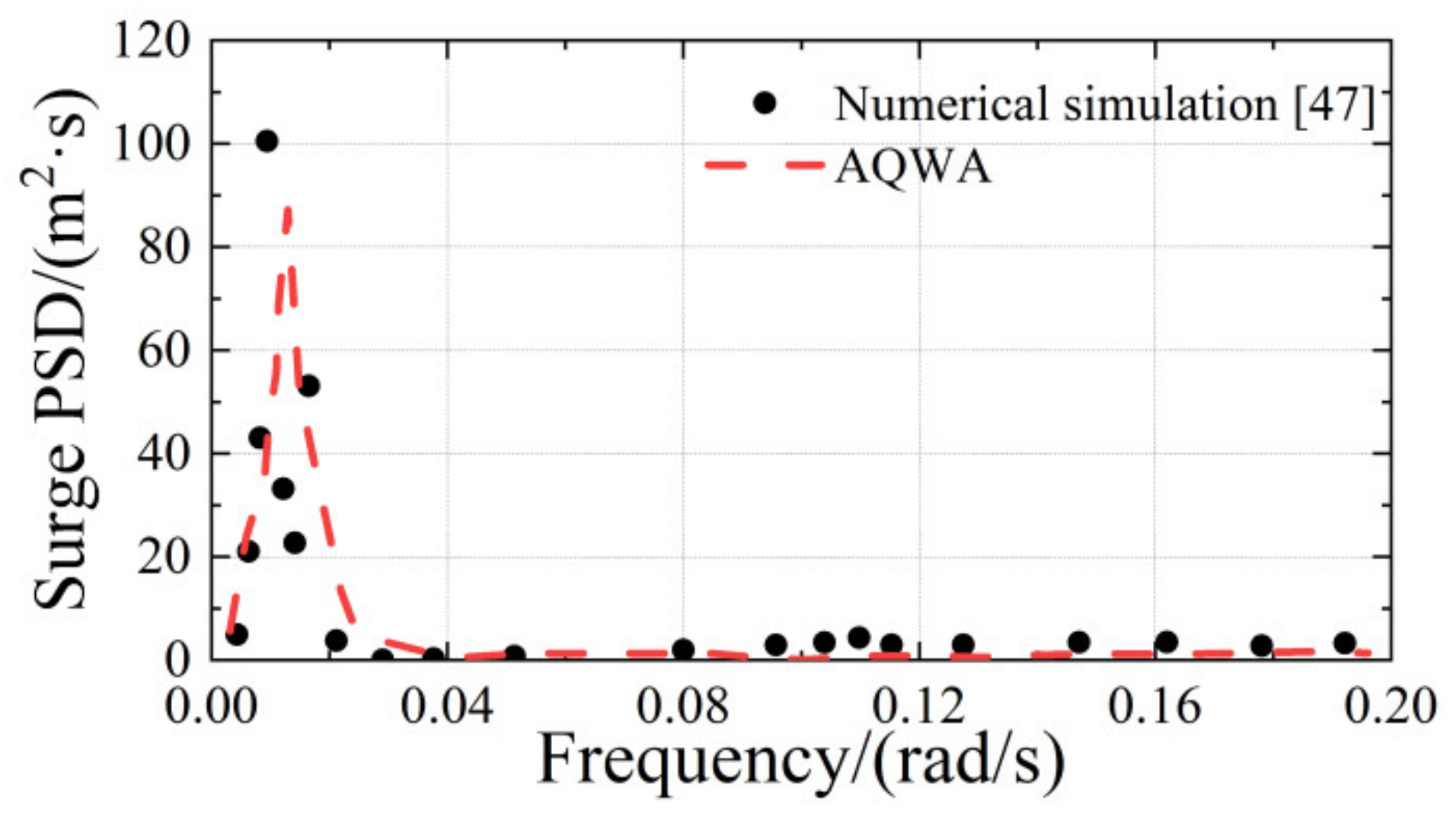
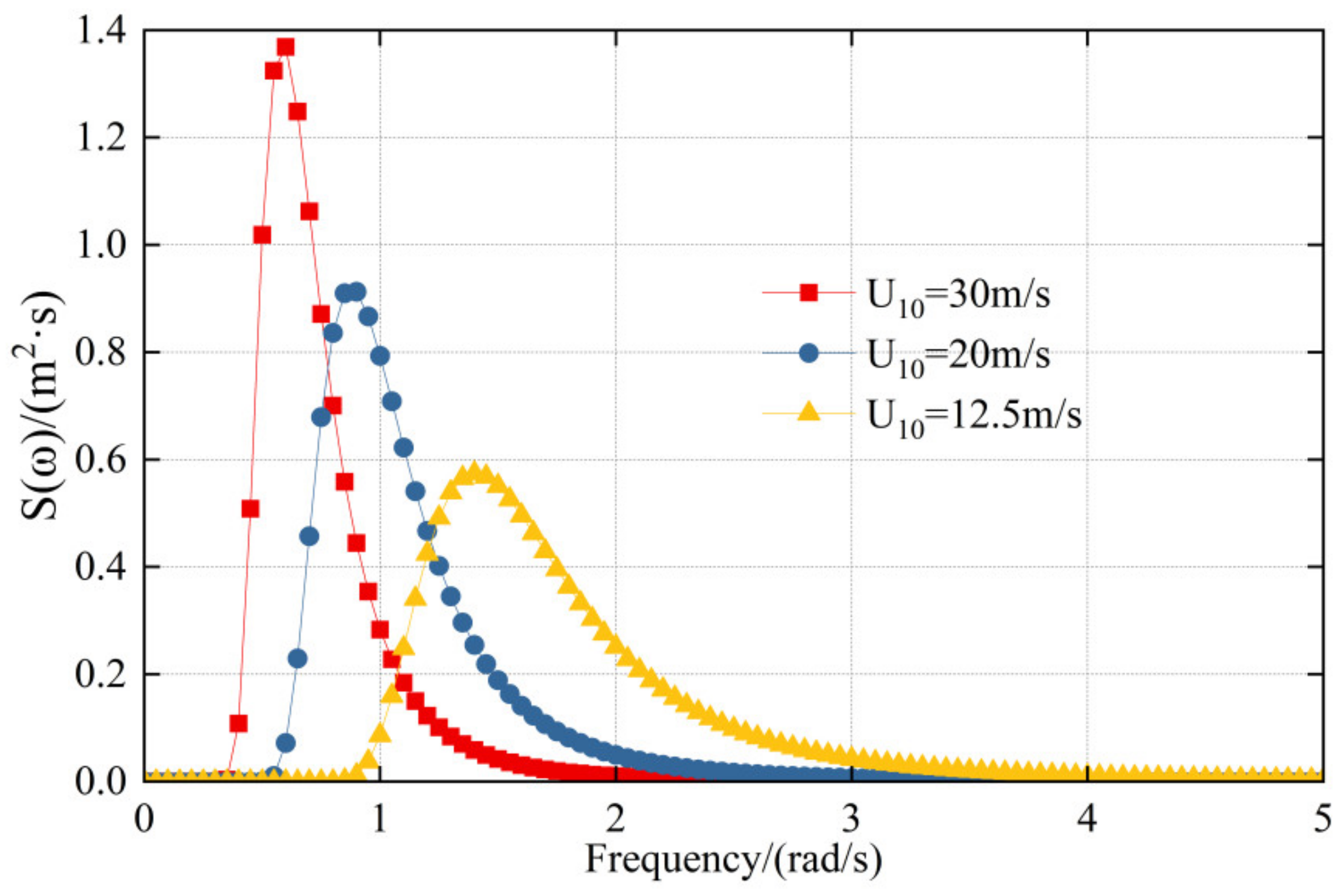
3.1. Comparative Analysis of PSD
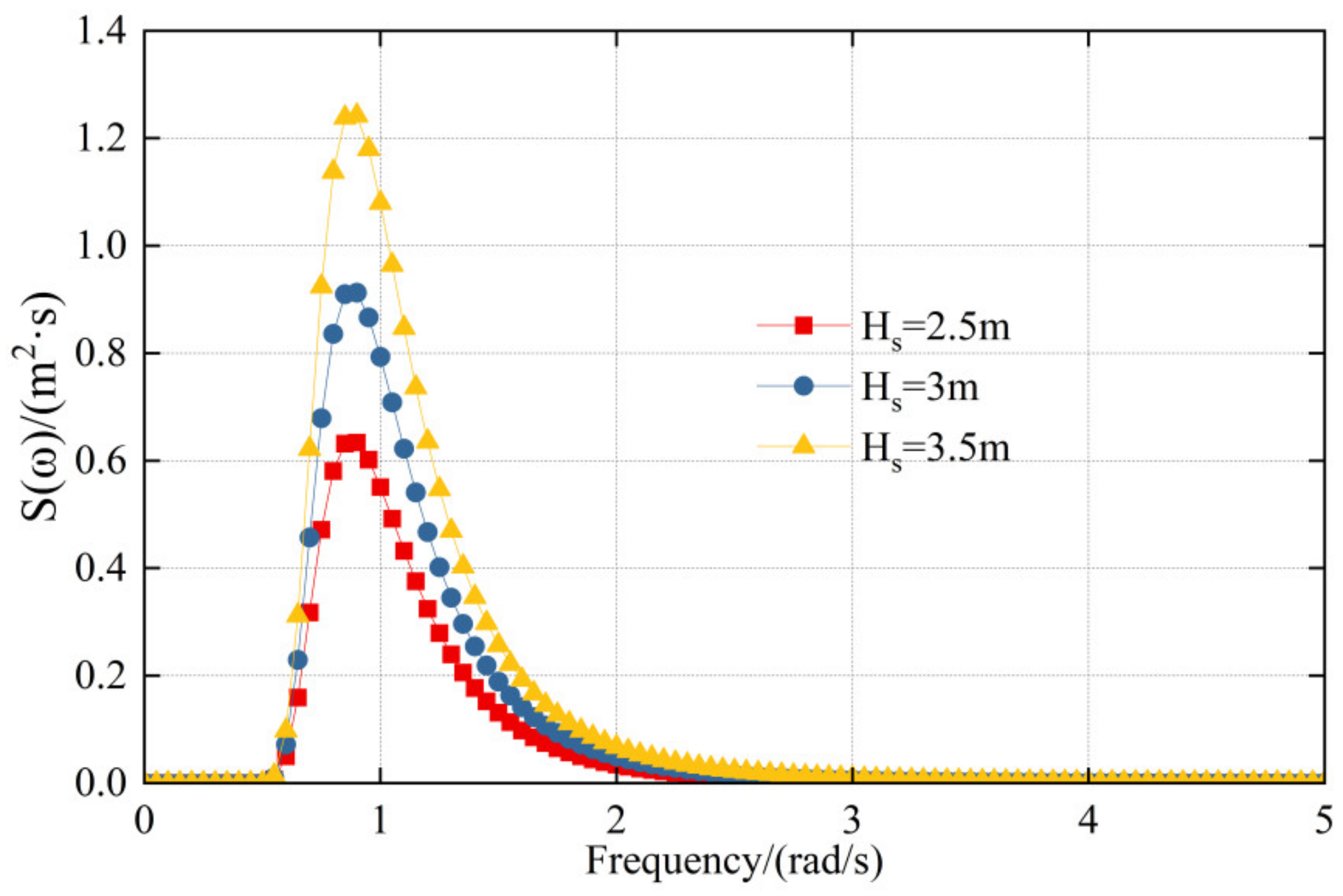
3.2. Environmental Conditions
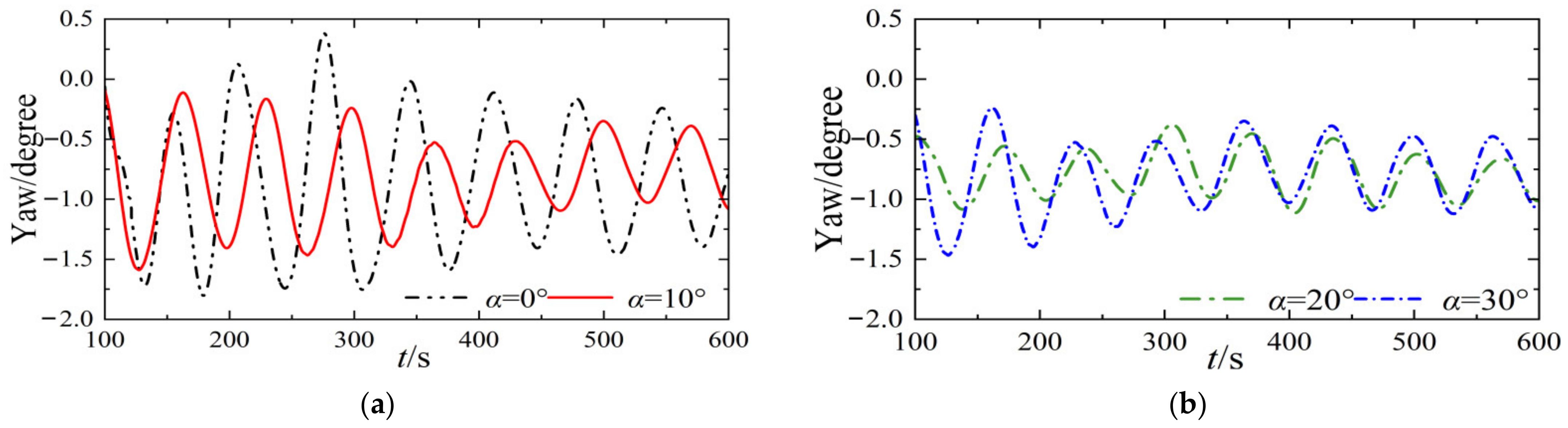
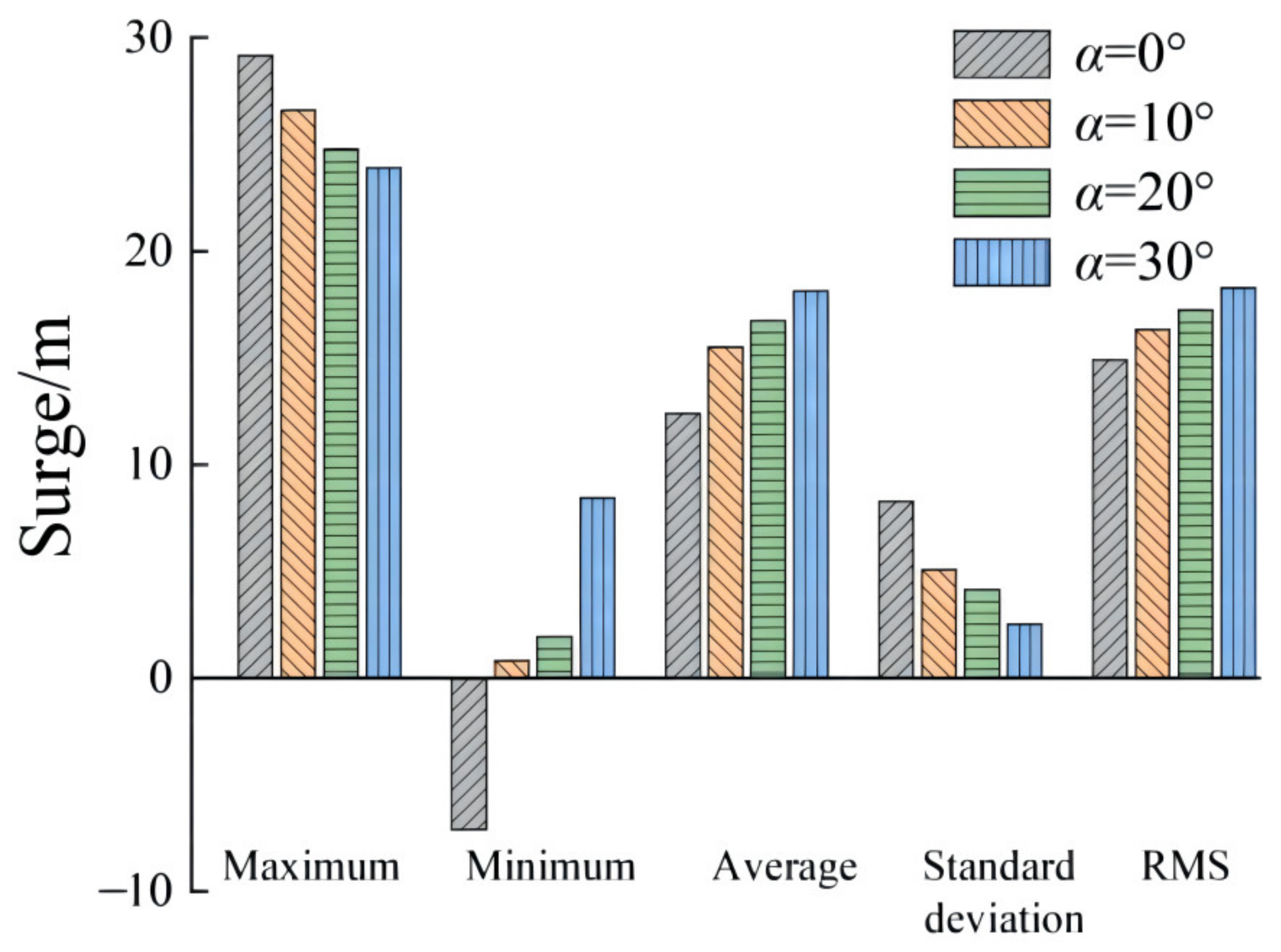
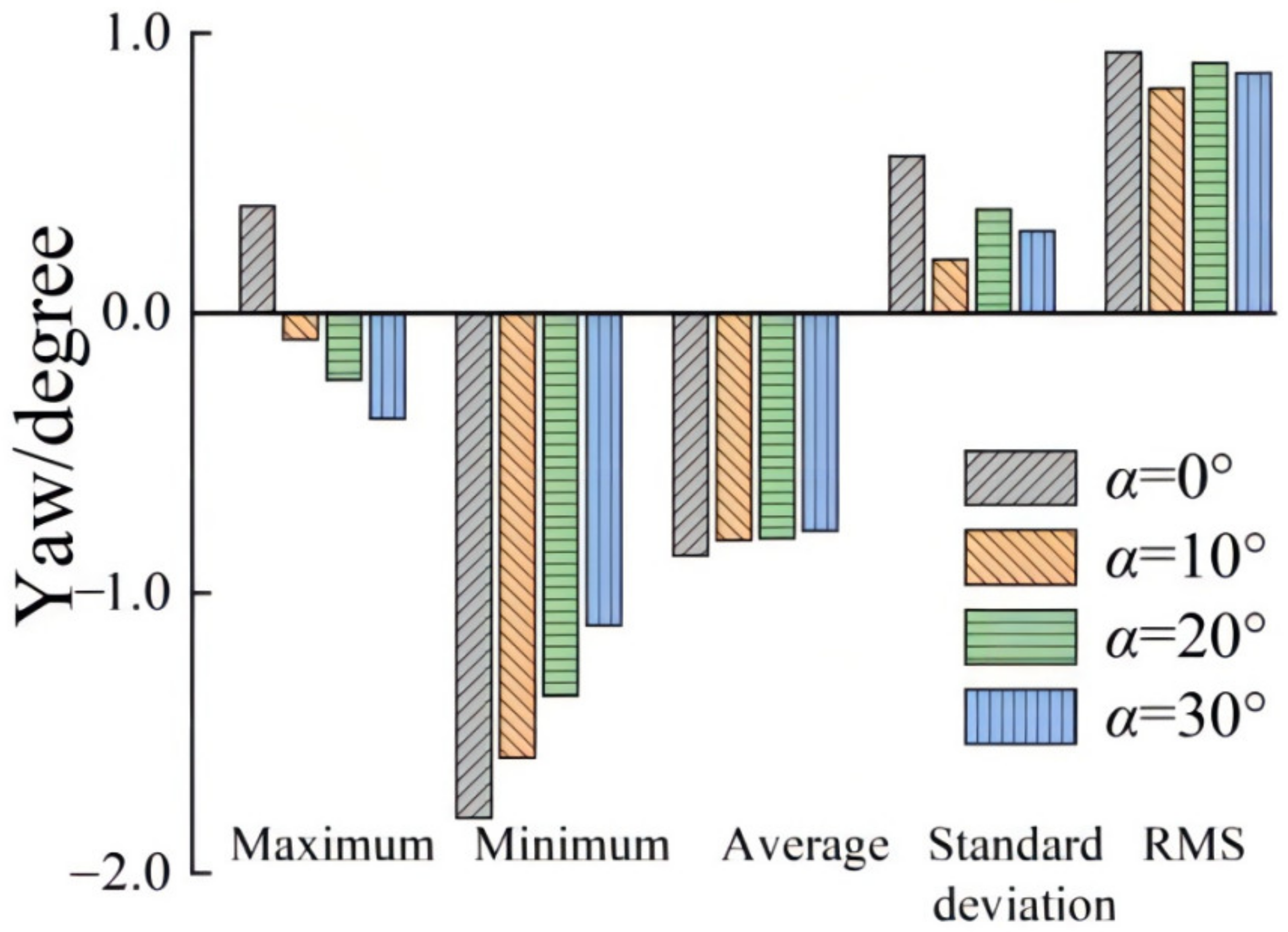
3.3. The Influence of the Mooring Connection Angle
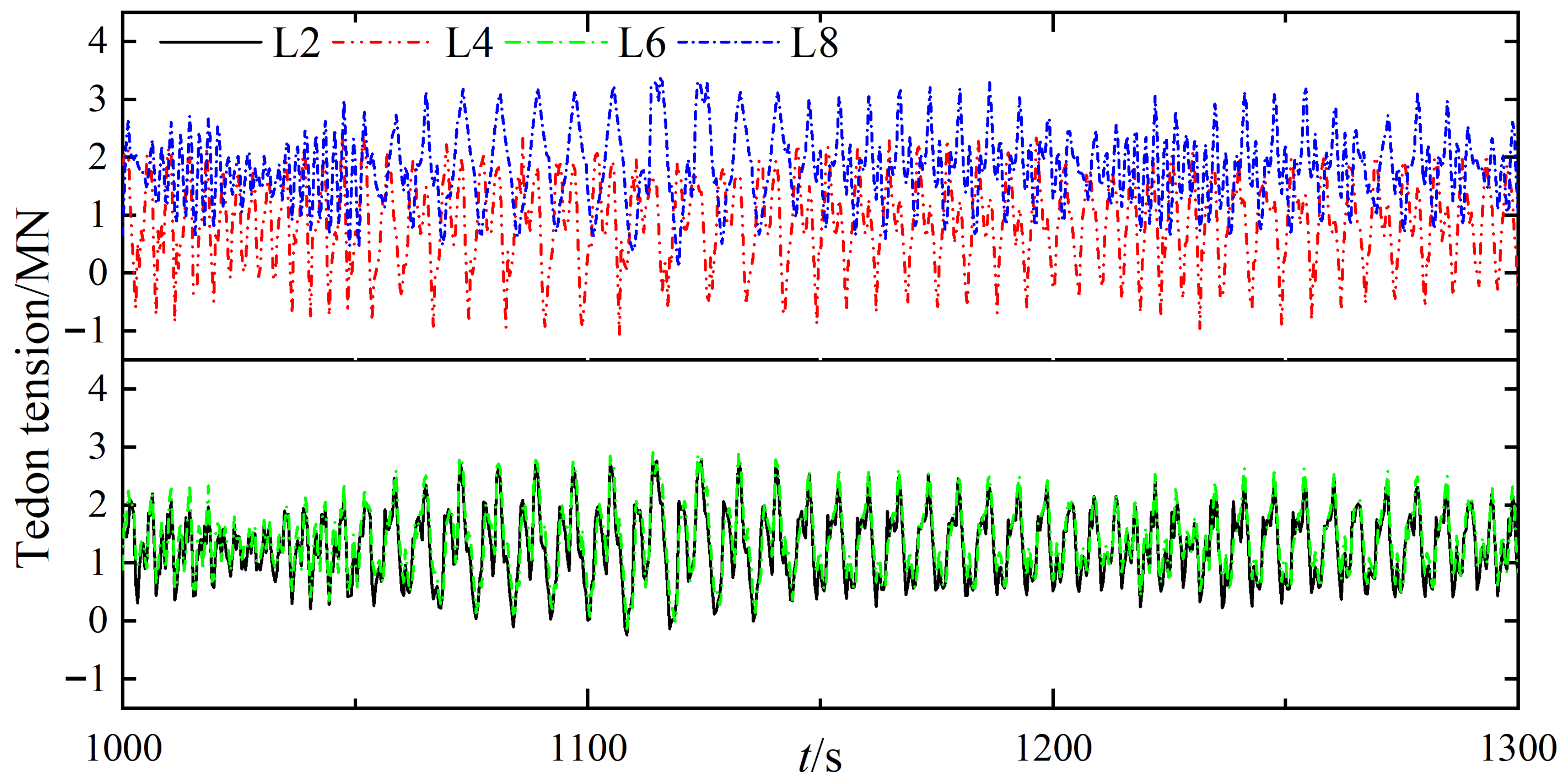
3.4. Tension under Different Environmental Loads
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Heronemus, W.E. Pollution-Free Energy From Offshore Winds. In Proceedings of the 8th Annual Conference of the Marine Technology Society, Washington, DC, USA, 11–13 September 1972. [Google Scholar]
- Huang, Y.; Cheng, P.; Wan, D. Numerical Analysis of a Floating Offshore Wind Turbine by Coupled Aero-Hydrodynamic Simulation. J. Mar. Sci. Appl. 2019, 18, 82–92. [Google Scholar] [CrossRef]
- Possner, A.; Caldeira, K. Geophysical potential for wind energy over the open oceans. Proc. Natl. Acad. Sci. USA 2017, 114, 11338–11343. [Google Scholar] [CrossRef] [PubMed]
- Koo, B.J.; Goupee, A.J.; Kimball, R.W.; Lambrakos, K.F. Model Tests for a Floating Wind Turbine on Three Different Floaters. J. Offshore Mech. Arct. Eng. 2014, 136, 1–11. [Google Scholar] [CrossRef]
- Tang, T.; Hu, J.; Liu, L. Study on the Dynamic Response for Floating Foundation of Offshore Wind Turbine. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; Volume 6, pp. 19–24. [Google Scholar]
- Guedon, S.; Weller, S. Study of a Floating Foundation for Wind Turbines. J. Offshore Mech. Arct. Eng. 2013, 135, 75–88. [Google Scholar] [CrossRef]
- Sethuraman, L.; Venugopal, V. Hydrodynamic response of a stepped-spar floating wind turbine: Numerical modelling and tank testing. Renew. Energy 2013, 52, 160–174. [Google Scholar] [CrossRef]
- Wang, H.F.; Fan, Y.H. Preliminary Design of Offshore Wind Turbine Tension Leg Platform In the South China Sea. J. Eng. Sci. Technol. Rev. 2013, 6, 88–92. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.G. Effect of fluid-structure interaction on connection forces in bridges due to tsunami loads. In Proceedings of the 30th US-Japan Bridge Engineering Workshop, Washington, DC, USA, 21–23 October 2014. [Google Scholar]
- Anagnostopoulos, S.A. Dynamic response of offshore platforms to extreme waves including fluid-structure interaction. Eng. Struct. 1982, 4, 179–185. [Google Scholar] [CrossRef]
- Choi, S.J.; Lee, K.H.; Gudmestad, O.T. The effect of dynamic amplification due to a structure’s vibration on breaking wave impact. Ocean Eng. 2015, 96, 8–20. [Google Scholar] [CrossRef]
- Mercier, J.A. A Method for Computing Float-Platform Motions in Waves. J. Hydronautics 1970, 4, 98–104. [Google Scholar] [CrossRef]
- Mekha, B.B.; Johnson, C.P.; Roesset, J.M. Effects of different wave free surface approximations on the response of a TLP in deep water. In Proceedings of the Fourth International Offshore and Polar Engineering Conference, Osaka, Japan, 10–15 April 1994; pp. 105–115. [Google Scholar]
- Kim, C.H.; Kim, M.H.; Liu, Y.H.; Zhao, C.T. Time Domain Simulation of Non-Linear Response of a Coupled TLP System. In Proceedings of the Fourth International Offshore and Polar Engineering Conference, Osaka, Japan, 10–15 April 1994; Volume 4, pp. 88–96. [Google Scholar]
- Jain, A.K. Nonlinear coupled response of offshore tension leg platforms to regular wave forces. Ocean Eng. 1997, 24, 577–592. [Google Scholar] [CrossRef]
- Zeng, X.H.; Li, X.W.; Liu, Y.; Wu, Y.X. Nonlinear Dynamic Responses of Tension Leg Platform with Slack-Taut Tether. China Ocean Eng. 2009, 23, 37–48. [Google Scholar]
- Horoub, M.M. Dynamic Analysis of a Tension Leg Platforms (TLPs) Inspired by Parallel Robotic Manipulators. IEEE Access 2020, 8, 35222–35230. [Google Scholar] [CrossRef]
- Pakozdi, C.; Kendon, T.E.; Stansberg, C.T. Breaking wave impact on a platform column: An introductory CFD study. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; Volume 44335, pp. 645–654. [Google Scholar]
- Xiang, T.; Istrati, D. Assessment of Extreme Wave Impact on Coastal Decks with Different Geometries via the Arbitrary Lagrangian-Eulerian Method. J. Mar. Sci. Eng. 2021, 9, 1342. [Google Scholar] [CrossRef]
- Pan, K.; IJzermans, R.H.A.; Jones, B.D.; Thyagarajan, A.; van Beest, B.W.H.; Williams, J.R. Application of the SPH method to solitary wave impact on an offshore platform. Comput. Part. Mech. 2015, 3, 155–166. [Google Scholar] [CrossRef]
- Canelas, R.; Ferreira, R.M.; Crespo, A.; Domínguez, J.M. A generalized SPH-DEM discretization for the modelling of complex multiphasic free surface flows. In Proceedings of the 8th International Spheric Workshop, Trondheim, Norway, 4–6 June 2013. [Google Scholar]
- Jonkman, J.; Larsen, T.; Hansen, A.; Nygaard, T.; Maus, K.; Karimirad, M.; Gao, Z.; Moan, T.; Fylling, I. Offshore code comparison collarboration within IEA wind task 23: Phase IV results regarding floating wind turbine modeling. In Proceedings of the European Wind Energy Conference (EWEC), Warsaw, Poland, 20–23 April 2010. [Google Scholar]
- Shen, M.; Hu, Z.; Liu, G. Dynamic response and viscous effect analysis of a TLP-type floating wind turbine using a coupled aero-hydro-mooring dynamic code. Renew. Energy 2016, 99, 800–812. [Google Scholar] [CrossRef]
- Li, L.; Hu, Z.; Wang, J.; Ma, Y. Development and Validation of an Aero-hydro Simulation Code for Offshore Floating Wind Turbine. J. Ocean Wind Energy 2015, 2, 1–11. [Google Scholar]
- Uzunoglu, E.; Soares, C.G. A system for the hydrodynamic design of tension leg platforms of floating wind turbine. Ocean Eng. 2019, 171, 78–92. [Google Scholar] [CrossRef]
- Cheng, P.; Huang, Y.; Wan, D. A numerical model for fully coupled aero-hydrodynamic analysis of floating offshore wind turbine. Ocean Eng. 2019, 173, 183–196. [Google Scholar] [CrossRef]
- Mohammad, R.T.; Rahim, S. Perturbation nonlinear response of tension leg platform under regular wave excitation. J. Mar. Sci. Technol. 2018, 23, 132–140. [Google Scholar]
- Luo, M.; Koh, C.G.; Lee, W.X.; Lin, P.; Reeve, D.E. Experimental study of freak wave impacts on a tension-leg platform. Mar. Struct. 2020, 74, 102821. [Google Scholar] [CrossRef]
- Kiamini, S.; Jalilvand, A.; Mobayen, S. LMI-based robust control of floating tension-leg platforms with uncertainties and time-delays in offshore wind turbines via T-S fuzzy approach. Ocean Eng. 2018, 154, 367–374. [Google Scholar] [CrossRef]
- Madsen, F.J.; Nielsen, T.R.L.; Kim, T.; Bredmose, H.; Pegalajar-Jurado, A.; Mikkelsen, R.F.; Lomholt, A.K.; Borg, M.; Mirzaei, M.; Shin, P. Experimental analysis of the scaled DTU10MW TLP floating wind turbine with different control strategies. Renew. Energy 2020, 155, 330–346. [Google Scholar] [CrossRef]
- Chow, J.H.; Ng, E.Y.; Narasimalu, S. Numerical study of the dynamic response of a wind turbine on a tension leg platform with a coupled partitioned six degree-of-freedom rigid body motion solve. Ocean Eng. 2019, 172, 575–582. [Google Scholar] [CrossRef]
- Yang, Y.; Bashir, M.; Wang, J.; Michailides, C.; Loughney, S.; Armin, M.; Hernández, S.; Urbano, J.; Li, C. Wind-wave coupling effects on the fatigue damage of tendons for a 10 MW multi-body floating wind turbine. Ocean Eng. 2020, 217, 107909. [Google Scholar] [CrossRef]
- Sun, J.; Hu, S.L.J.; Li, H. Laplace domain method for computing the transient response of floating structures to irregular waves. Ocean Eng. 2020, 203, 107200. [Google Scholar] [CrossRef]
- Dai, J.; Hu, W.; Yang, X.; Yang, S. Modeling and investigation of load and motion characteristics of offshore floating wind turbines. Ocean Eng. 2018, 159, 187–200. [Google Scholar] [CrossRef]
- Rao, D.S.B.; Selvam, R.P.; Srinivasan, N. Hydrodynamic Analysis of Tension Based Tension Leg Platform. In Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012; pp. 201–207. [Google Scholar]
- Adam, F.; Myland, T.; Dahlhaus, F.; Großmann, J. Scale tests of the GICON®-TLP for Wind Turbines. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; p. V09AT09A011. [Google Scholar]
- Han, Y.; Le, C.; Ding, H.; Cheng, Z.; Zhang, P. Stability and dynamic response analysis of a submerged tension leg platform for offshore wind turbines. Ocean Eng. 2017, 129, 68–82. [Google Scholar] [CrossRef]
- Ma, Z.; Ren, N.; Wang, Y.; Wang, S.; Shi, W.; Zhai, G. A Comprehensive Study on the Serbuoys Offshore Wind Tension Leg Platform Coupling Dynamic Response under Typical Operational Conditions. Energies 2019, 12, 2067. [Google Scholar] [CrossRef]
- Ren, N.; Ma, Z.; Shan, B. Experimental and numerical study of dynamic responses of a new combined TLP type floating wind turbine and a wave energy converter under operational conditions. Renew. Energy 2020, 151, 966–974. [Google Scholar] [CrossRef]
- Van der Meer, J.W.; Briganti, R.; Zanuttigh, B.; Wang, B. Wave transmission and reflection at low-crested structures: Design formulae, oblique wave attack and spectral change. Coast. Eng. 2005, 52, 915–929. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.G. Tsunami Loads on Straight and Skewed Bridges—Part 2: Numerical Investigation and Design Recommendations (No. FHWA-OR-RD-21-13); Oregon Department of Transportation: Salem, OR, USA, 2021. [Google Scholar]
- Matha, D. Model Development and Loads Analysis of an Offshore Wind Turbine on a Tension Leg Platform with a Comparison to Other Floating Turbine Concepts: April 2009; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2010.
- Taylor, R.E.; Jefferys, E.R. Variability of hydrodynamic load predictions for a tension leg platform. Ocean Eng. 1986, 13, 449–490. [Google Scholar] [CrossRef]
- Zhou, B.Z.; Wu, G.X. Resonance of a tension leg platform exited by third-harmonic force in nonlinear regular waves. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 373, 20140105. [Google Scholar] [CrossRef][Green Version]
- Kaushik, M. Theoretical and Experimental Aerodynamics; Springer: Singapore, 2019; pp. 107–126. [Google Scholar]
- API RP 2SK. Recommended Practice for Design and Analysis of Stationkeeping for Floating Structures; American Petroleum Institute: Washington, DC, USA, 2005; Volume 10, p. 59. [Google Scholar]
- Gu, J.Y.; Yang, J.M.; Lv, H.N. Studies of TLP Dynamic Response Under Wind, Waves and Current. China Ocean. Eng. 2012, 26, 363–378. [Google Scholar] [CrossRef]
- Offshore Standard DNV-OS-J101; Design of Offshore Wind Turbine Structures; Det Norske Veritas: Bærum, Norway, 2004.
- API RP2A WSD. Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms—Working Stress Design; American Petroleum Institute: Washington, DC, USA, 2000. [Google Scholar]
- Ding, Q.; Li, C.; Yu, N.; Hao, W.; Ji, J. Numerical and experimental investigation into the dynamic response of a floating wind turbine spar array platform. J. Mech. Sci. Technol. 2018, 32, 1106–1116. [Google Scholar] [CrossRef]
- Watanabe, E.; Utsunomiya, T.; Kubota, A. Analysis of wave-drift damping of a VLFS with shallow draft. Mar. Struct. 2000, 13, 383–397. [Google Scholar] [CrossRef]
- Senjanović, I.; Hadžić, N.; Tomić, M. On the linear stiffness of tension leg platforms. Sustain. Mar. Trans. Exp. Sea Res. 2011, 108, 1081–1088. [Google Scholar]
- Brown, D.T.; Mavrakos, S. Comparative study on mooring line dynamic loading. Mar. Struct. 1999, 12, 131–151. [Google Scholar] [CrossRef]
- Newman, J.N. Wave-drift damping of floating bodies. J. Fluid Mech. 1993, 249, 241–259. [Google Scholar] [CrossRef]
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: New York, NY, USA, 1990. [Google Scholar]
- Gu, J.Y.; Yang, J.M.; Lv, H.N. Numerical Simulations and Model Tests of the Mooring Characteristic of A Tension Leg Platform Under Random Waves. China Ocean Eng. 2013, 27, 563–578. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, J.; He, Y. Preliminary Design of a Multi-Column TLP Foundation for a 5-MW Offshore Wind Turbine. Energies 2012, 5, 3874–3891. [Google Scholar] [CrossRef]









| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Column spacing | 86.25 m | Total pretension | 14 × 103 kN |
| Column radius | 8.44 m | Inner diameter of tension leg | 0.3436 m |
| Column length | 67.5 m | Outside diameter of tension leg | 0.8 m |
| Floating box width | 7.50 m | Tendon length | 415.0 m |
| Floating box height | 10.50 m | Kxx | 1.501 × 109 kN·m−1 |
| Displacement | 54.5 × 106 kg | Kzz | 0.813 × 106 kN·m−1 |
| Total mass | 40.5 × 106 kg | Dry weight | 1575.9 kg·m−1 |
| Ixx | 82.37 × 109 kg·m2 | Wet weight | 240.5 kg·m−1 |
| Iyy | 82.37 × 109 kg·m2 | Tendon’s equivalent stiffness | 2.28 × 107 kN |
| Izz | 98.07 × 109 kg·m2 | Area of contour vertical to current | 5.019 × 103 m2 |
| Center of gravity | 38.0 m | Area of contour vertical to wind | 2.194 × 103 m2 |
| Draft | 35.00 m |
| Surge | Sway | Heave | Roll | Pitch | Yaw | |
|---|---|---|---|---|---|---|
| (rad·s−1) | 0.0612 | 0.0612 | 3.488 | 3.401 | 3.401 | 0.0764 |
| Operating Cases | Load | Hs (m) | Tm (s) | γ | U (m·s−1) | Vt(0) (m·s−1) |
|---|---|---|---|---|---|---|
| C0 | Environmental loads | 2.5 | 5.4 | 1 | 12.5 | 1.08 |
| C1 | Wind | - | - | - | 20 | - |
| C2 | Wave | 3 | 8.7 | 1 | - | - |
| C3 | Current | - | - | - | - | 1.08 |
| C4 | C1 + C2 + C3 | 3 | 8.7 | 1 | 20 | 1.08 |
| Angle | α = 0° | α = 10° | α = 20° | α = 30° | |
|---|---|---|---|---|---|
| DoF | |||||
| Surge | Maximum value | 29.1523 | 26.5868 | 24.7605 | 23.9051 |
| Minimum value | −7.1160 | 0.8314 | 1.9338 | 8.4415 | |
| Average | 12.4023 | 15.5085 | 16.7358 | 18.1114 | |
| Standard deviation | 8.2605 | 5.0815 | 4.1396 | 2.5211 | |
| Root mean square | 14.8965 | 16.3179 | 17.2390 | 18.2856 | |
| Pitch | Maximum value | 0.0761 | 0.0549 | 0.0581 | 0.0278 |
| Minimum value | −0.1839 | −0.1693 | −0.1411 | −0.0990 | |
| Average | −0.0652 | −0.0494 | −0.0475 | −0.0208 | |
| Standard deviation | 0.0526 | 0.0642 | 0.0517 | 0.0225 | |
| Root mean square | 0.0708 | 0.0915 | 0.0715 | 0.0306 | |
| Yaw | Maximum value | 0.3804 | −0.0940 | −0.2403 | −0.3778 |
| Minimum value | −1.8028 | −1.5896 | −1.3665 | −1.1153 | |
| Average | −0.8671 | −0.8121 | −0.8050 | −0.7787 | |
| Standard deviation | 0.5595 | 0.1917 | 0.3694 | 0.2915 | |
| Root mean square | 0.9319 | 0.8019 | 0.8922 | 0.8561 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Wei, N.; Yao, W. The Stability Analysis of Tension-Leg Platforms under Marine Environmental Loads via Altering the Connection Angle of Tension Legs. Water 2022, 14, 283. https://doi.org/10.3390/w14030283
Xu X, Wei N, Yao W. The Stability Analysis of Tension-Leg Platforms under Marine Environmental Loads via Altering the Connection Angle of Tension Legs. Water. 2022; 14(3):283. https://doi.org/10.3390/w14030283
Chicago/Turabian StyleXu, Xu, Naying Wei, and Wenjuan Yao. 2022. "The Stability Analysis of Tension-Leg Platforms under Marine Environmental Loads via Altering the Connection Angle of Tension Legs" Water 14, no. 3: 283. https://doi.org/10.3390/w14030283
APA StyleXu, X., Wei, N., & Yao, W. (2022). The Stability Analysis of Tension-Leg Platforms under Marine Environmental Loads via Altering the Connection Angle of Tension Legs. Water, 14(3), 283. https://doi.org/10.3390/w14030283





