Influence of Negatively Buoyant Jets on a Strongly Curved Open-Channel Flow Using RANS Models with Experimental Data
Abstract
:1. Introduction
2. Methodology
2.1. Experimental Setup and Flow Configuration
2.2. Experimental Methods
2.3. Numerical Methods and Turbulence Models
2.3.1. Numerical Models
2.3.2. The Standard k-ε Model
2.3.3. The Non-Linear k-ε Model (Shih Quadratic k-ε)
2.3.4. The k-ω SST (Shear Stress Transport) Model
2.4. Boundary Conditions and Model Setup
3. Results and Analysis
3.1. Model Evaluation
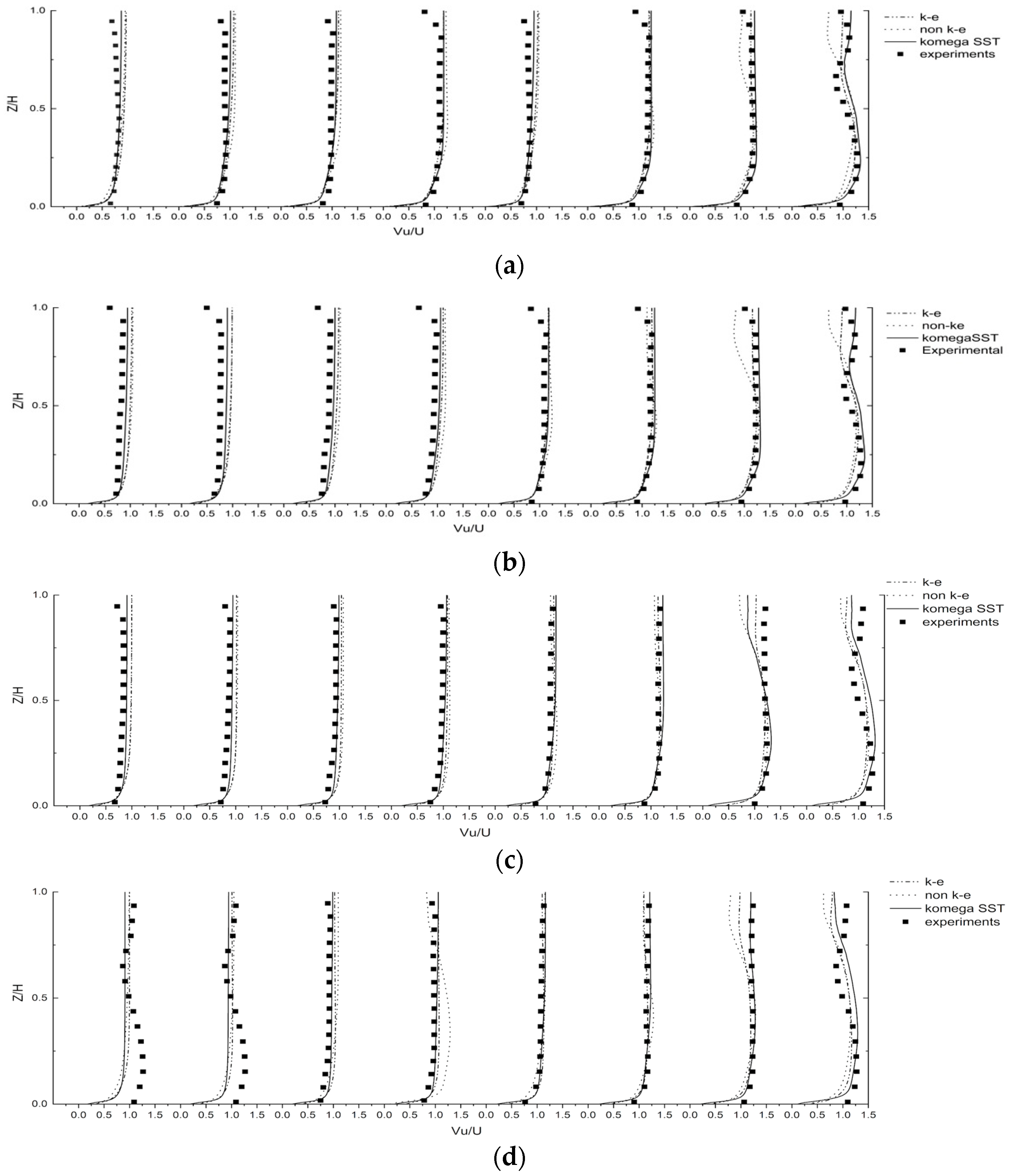
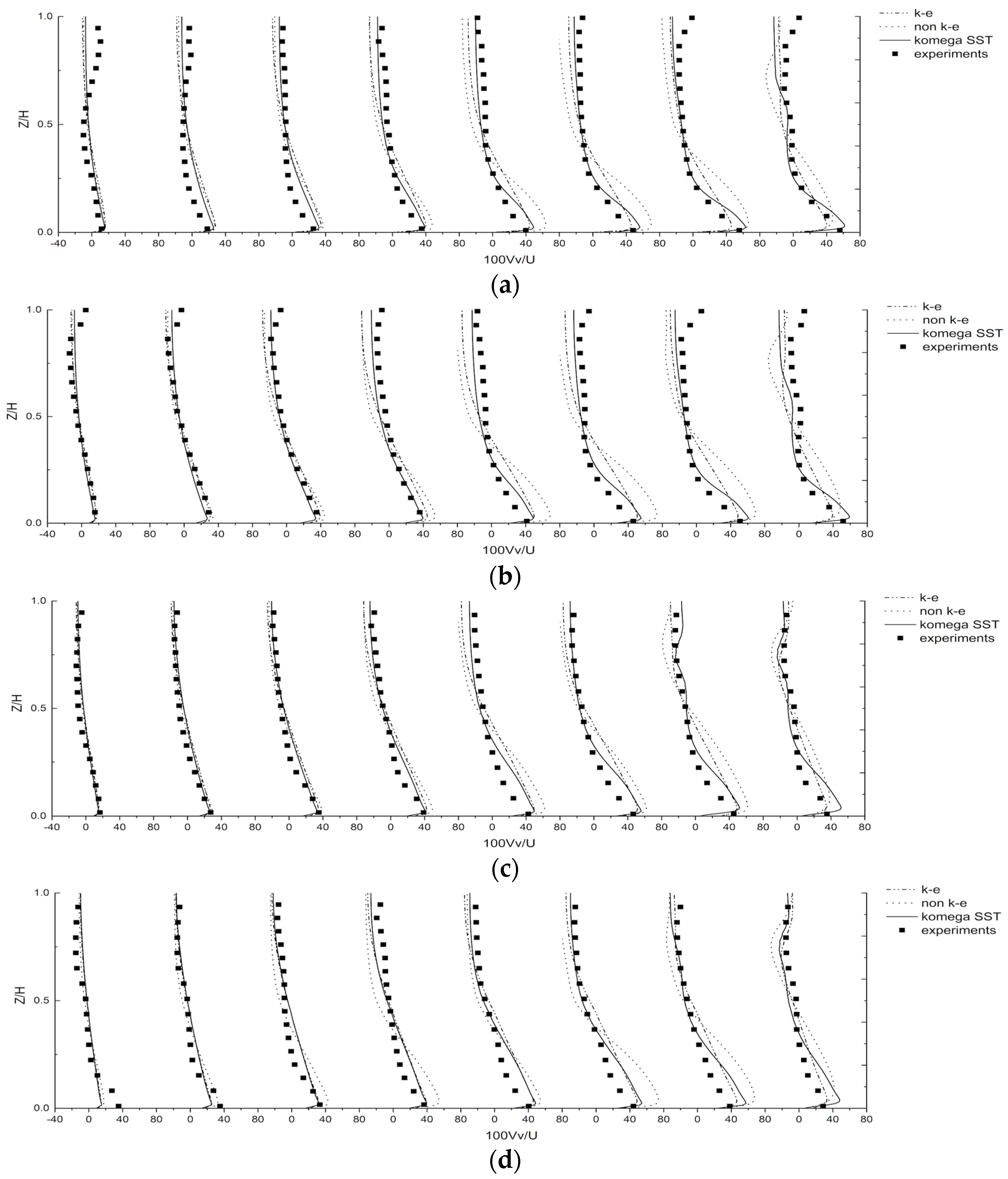
3.2. Velocity Distribution
3.3. Secondary Flow Pattern
4. Discussion
5. Conclusions
- With all the applied turbulence models, the streamwise velocities were all well predicted for the lower salinity cases. Discrepancies were found near the water’s surface at the outer bank region due to the inability of resolving the outer bank cell numerically. Reasonable agreement was obtained concerning the transverse velocities between the numerical results and the measured data. The major computational differences were observed with the vertical velocity component. Overall, the k-ω SST model exhibited the best performance in the present study. The computational errors can be attributed to the use of the isotropic eddy viscosity and the rigid-lid free surface assumption.
- The velocity patterns in all three directions were influenced by the effect of secondary flow, which was attained in the channel bend by the experimental data and numerical simulations.
- The overall shapes of streamlines at each salinity case are different from each other because of the interaction between the jet mixing behavior and the secondary flow in the channel bend.
- The presence of negatively buoyant jets disturbed the development of the outer bank cell, and the influence was attenuated as salinity increased.
- In the inner bank region, flow separation was strengthened by the participation of the negatively buoyant jets.
- High positive streamwise vorticity cores, which represent the main circulation, were found at the inner bank, and they were pushed towards the inner bank wall as salinity increased.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chang, Y.C. Lateral Mixing in Meandering Channels; University of Iowa: Iowa City, IA, USA, 1971. [Google Scholar]
- Kashyap, S.; Constantinescu, G.; Rennie, C.D.; Post, G.; Townsend, R. Influence of channel aspect ratio and curvature on flow, secondary circulation, and bed shear stress in a rectangular channel bend. J. Hydraul. Eng. 2012, 138, 1045–1059. [Google Scholar] [CrossRef]
- Ye, J.; McCorquodale, J.A. Simulation of curved open channel flows by 3D hydrodynamic model. J. Hydraul. Eng. 1998, 124, 687–698. [Google Scholar] [CrossRef]
- Choi, Y.; Stewar, J.P.; Graves, R.W. Empirical Model for Basin Effects Accounts for Basin Depth and Source Location. BSSA 2005, 95, 1412–1427. [Google Scholar] [CrossRef]
- Song, G.C.; Seo, I.W.; Kim, Y.D. Analysis of secondary current effect in the modeling of shallow flow in open channels. Adv. Water Resour. 2012, 41, 29–48. [Google Scholar] [CrossRef]
- Rozovskii, I. Flow of Water in Bends of Open Channels; Academy of Sciences of the Ukrainian SSR; Israel Program for Scientific Translations: Jerusalem, Israel, 1961. [Google Scholar]
- Leppold, L.B.; Bagnold, R.A.; Wolman, M.G.; Brush, L.M., Jr. Flow Resistance in Sinuous or Irregular Channels: U.S. Geological Survey Professional Paper 282-D; U.S. Government Printing Office: Washington, DC, USA, 1960; pp. D111–D134.
- Ottevanger, W.; Blanckaert, K.; Uijttewaal, W.S.J. Processes governing the flow redistribution in sharp river bends. Geomorphology 2012, 163, 45–55. [Google Scholar] [CrossRef] [Green Version]
- Ottevanger, W.; Blanckaert, K.; Uijttewaal, W.S.J. A Parameter Study on Bank Shear Stresses in Curved Open Channel Flow by Means of Large-Eddy Simulation. In Proceedings of the 7th IAHR Symp. on River, Coastal and Estuarine Morphodynamics, International Association for Hydro-Environment Engineering and Research, Madrid, Spain, 6–8 September 2011; pp. 1917–1927. [Google Scholar]
- Engelund, F.; Skovgaard, O. On the origin of meandering and braiding in alluvial streams. J. Fluid Mech. 1973, 57, 289–302. [Google Scholar] [CrossRef]
- Ikeda, S.; Yamasaka, M.; Chiyoda, M. Bed topography and sorting in bends. J. Hydraul. Eng. 1987, 113, 190–204. [Google Scholar] [CrossRef]
- Jamieson, G.P.; Rennie, C.D. Spatial variability of three dimensional Reynolds stresses in a developing channel bend. Earth Surf. Processes Landf. 2010, 35, 1029–1043. [Google Scholar] [CrossRef]
- Zeng, J.; Constantinescu, G.; Blanckaert, K.; Weber, L. Flow and bathymetry in sharp open-channel bends: Experiments and predictions. Water Resour. Res. 2008, 44, W09401-n/a. [Google Scholar] [CrossRef]
- Kalkwijk, J.T.; De Vriend, H.J. Computation of the flow in shallow river bends. J. Hydraul. Res. 1980, 18, 327–342. [Google Scholar] [CrossRef] [Green Version]
- Kasvi, E.; Laamanen, L.; Lotsari, E.; Alho, P. Flow Patterns and Morphological Changes in a Sandy Meander Bend during a Flood-Spatially and Temporally Intensive ADCP Measurement Approach. Water 2017, 9, 106. [Google Scholar] [CrossRef] [Green Version]
- Tchobanoglous, G. Wastewater Engineering: Treatment Disposal Reuse, 2nd ed.; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Cheng, G.C.; Farokhi, S. On turbulent flows dominated by curvature effects. J. Fluid Engrg. ASME 1992, 114, 52–57. [Google Scholar] [CrossRef]
- de Vriend, H. Velocity redistribution in curved rectangular channels. J. Fluid Mech. 1980, 107, 423–439. [Google Scholar] [CrossRef]
- Duan, J.G.; Julien, P.Y. Julien Numerical simulation of the inception of channel meandering. Earth Surf. Process. Landf. 2005, 30, 1093–1110. [Google Scholar] [CrossRef]
- Odgaard, A.J.; Bergs, M.A. Flow processes in a curved alluvial channel. Water Resour. Res. 1988, 24, 45–56. [Google Scholar] [CrossRef]
- Booij, R. Measurements and large eddy simulations of the flows in some curved flumes. J. Turbul. 2003, 4, 008. [Google Scholar] [CrossRef]
- Blanckaert, K.; De Vriend, H.J. Secondary flow in sharp open-channel bends. J. Fluid Mech. 2004, 498, 353–380. [Google Scholar] [CrossRef] [Green Version]
- Blanckaert, K. Flow separation at convex banks in open channels. J. Fluid Mech. 2015, 779, 432–467. [Google Scholar] [CrossRef]
- Blanckaert, K. Saturation of curvature-induced secondary flow, energy losses, and turbulence in sharp open-channel bends: Laboratory experiments, analysis, and modeling. J. Geophys. Res. 2009, 114, 432–467. [Google Scholar] [CrossRef] [Green Version]
- Blanckaert, K.; Graf, W.H. Momentum Transport in Sharp Open-Channel Bends. J. Hydraul. Eng. 2004, 130, 186–198. [Google Scholar] [CrossRef]
- Patankar, S.V.; Pratap, V.S.; Spalding, D.B. Prediction of turbulent flow in curved pipes. J. Fluid Mech. 1975, 67, 583–595. [Google Scholar] [CrossRef] [Green Version]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in 3-D parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Leschziner, M.A.; Rodi, W. Calculation of strongly curved open channel flow. J. Hydraul. Div. 1979, 105, 1297–1314. [Google Scholar] [CrossRef]
- Demuren, A.O.; Rodi, W. Calculation of flow and pollutant dispersion in meandering channels. J. Fluid Mech. 1986, 172, 63–92. [Google Scholar] [CrossRef]
- Cokljat, D.; Younis, B.A. Second-Order closure study of open-channel flows. J. Hydraul. Eng. 1995, 121, 94–107. [Google Scholar] [CrossRef]
- Ruther, N.; Olsen, N.R.B. Three-Dimensional modeling of sediment transport in a narrow 90° channel bend. J. Hydraul. Eng. 2005, 131, 917–920. [Google Scholar] [CrossRef]
- Khosronejad, A.; Rennie, C.D.; Salehi Neyshabouri, A.A.; Townsend, R.D. 3D Numerical Modeling of Flow and Sediment Transport in laboratory channel bends. J. Hydraul. Eng. (ASCE) 2007, 133, 1123–1134. [Google Scholar] [CrossRef]
- Zhiyin, Y. Large-Eddy simulation: Past, present and the future. Chin. J. Aeronaut. 2015, 28, 11–24. [Google Scholar] [CrossRef] [Green Version]
- Shaheed, R.; Mohammadian, A.; Yan, X. A Review of Numerical Simulations of Secondary Flows in River Bends. Water 2021, 13, 884. [Google Scholar] [CrossRef]
- van Balen, W.; Blanckaert, K.; Uijttewaal, W.S.J. Analysis of the role of turbulence in curved open-channel flow at different water depths by means of experiments, LES and RANS. J. Turbul. 2010, 11, N12. [Google Scholar] [CrossRef]
- Van Balen, W.; Uijttewaal, W.S.J.; Blanckaer, K. Large-Eddy Simulation of a Mildly Curved Open-Channel Flow. J. Fluid Mech. 2009, 630, 413–442. [Google Scholar] [CrossRef] [Green Version]
- Van Balen, W.; Uijttewaal, W.S.J.; Blanckaert, K. Large-Eddy Simulation of a Curved Open-Channel Flow over Topography. Phys. Fluids 2010, 22, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Constantinescu, G.; Kashyap, S.; Tokyay, T.; Rennie, C.D.; Townsend, R.D. Hydrodynamic Processes and Sediment Erosion Mechanisms in an Open Channel Bend of Strong Curvature with Deformed Bathymetry. J. Geophys. Res. Earth Surf. 2013, 118, 480–496. [Google Scholar] [CrossRef]
- Mete, K.; Constantinescu, G.; Blanckaert, K. Hydrodynamic Processes, Sediment Erosion Mechanisms, and Reynolds-Number-Induced Scale Effects in an Open Channel Bend of Strong Curvature with Flat Bathymetry. J. Geophys. Res. Earth Surf. 2013, 118, 2308–2324. [Google Scholar]
- Adrian, R.; Westerweel, J. Particle Image Velocimetry; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- Yan, X.; Mohammadian, A. Numerical modeling of vertical buoy- ant jets subjected to lateral confinement. J. Hydraul. Eng. 2017, 143, 04017016. [Google Scholar] [CrossRef] [Green Version]

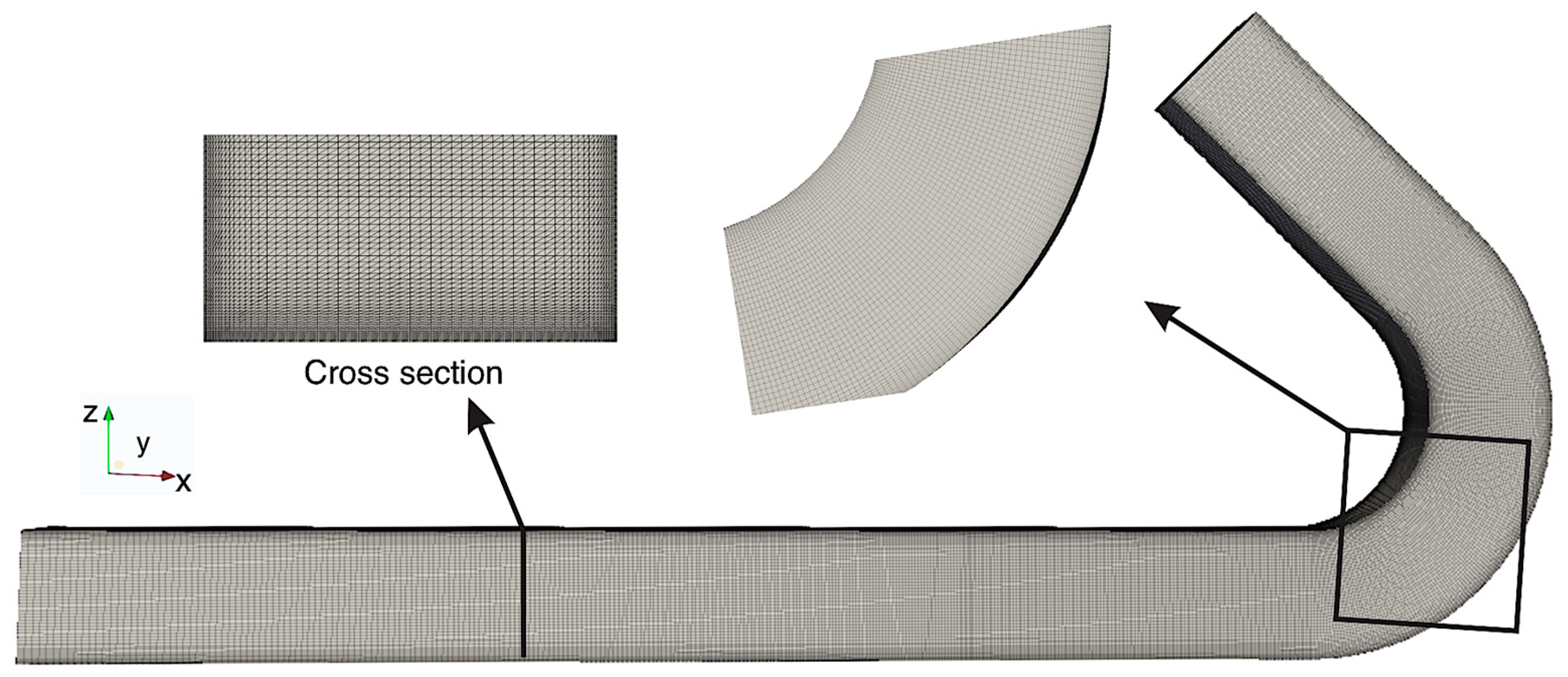


| Q (l/s) | V (m/s) | H (m) | R (m) | B (m) | Re | Fr | R/B | B/H |
|---|---|---|---|---|---|---|---|---|
| 2 | 0.1 | 0.1 | 0.3 | 0.2 | 22,400 | 0.22 | 1.5 | 2 |
| Run | Salinity | Simulation Type | Density Difference |
|---|---|---|---|
| No-1 | No jet | k-ε | - |
| S3.5-1 | S3.5 | k-ε | 3 |
| S10-1 | S10 | k-ε | 8 |
| S16.5-1 | S16.5 | k-ε | 13 |
| No-2 | No jet | Non-linear k-ε | - |
| S3.5-2 | S3.5 | Non-linear k-ε | 3 |
| S10-2 | S10 | Non-linear k-ε | 8 |
| S16.5-2 | S16.5 | Non-linear k-ε | 13 |
| No-3 | No jet | k-ω SST | - |
| S3.5-3 | S3.5 | k-ω SST | 3 |
| S10-3 | S10 | k-ω SST | 8 |
| S16.5-3 | S16.5 | k-ω SST | 13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Mohammadian, A.; Rennie, C.D. Influence of Negatively Buoyant Jets on a Strongly Curved Open-Channel Flow Using RANS Models with Experimental Data. Water 2022, 14, 347. https://doi.org/10.3390/w14030347
Wang X, Mohammadian A, Rennie CD. Influence of Negatively Buoyant Jets on a Strongly Curved Open-Channel Flow Using RANS Models with Experimental Data. Water. 2022; 14(3):347. https://doi.org/10.3390/w14030347
Chicago/Turabian StyleWang, Xueming, Abdolmajid Mohammadian, and Colin D. Rennie. 2022. "Influence of Negatively Buoyant Jets on a Strongly Curved Open-Channel Flow Using RANS Models with Experimental Data" Water 14, no. 3: 347. https://doi.org/10.3390/w14030347
APA StyleWang, X., Mohammadian, A., & Rennie, C. D. (2022). Influence of Negatively Buoyant Jets on a Strongly Curved Open-Channel Flow Using RANS Models with Experimental Data. Water, 14(3), 347. https://doi.org/10.3390/w14030347







