Numerical Study of the Emission of Acoustic Energy of Single Collapsing Vapor Bubble Near a Rigid Wall
Abstract
:1. Introduction
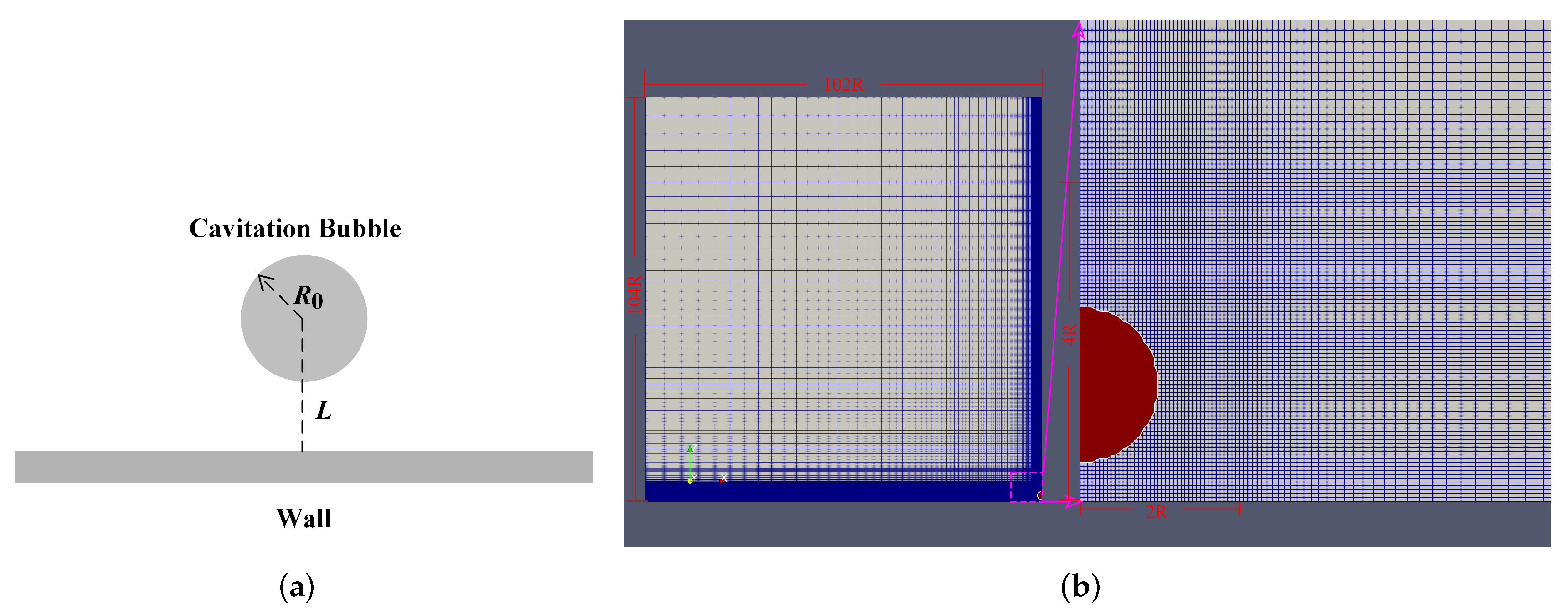
2. Numerical Modeling
2.1. Governing Equations
2.2. Numerical Implementation
3. Validation and Results
3.1. Validation
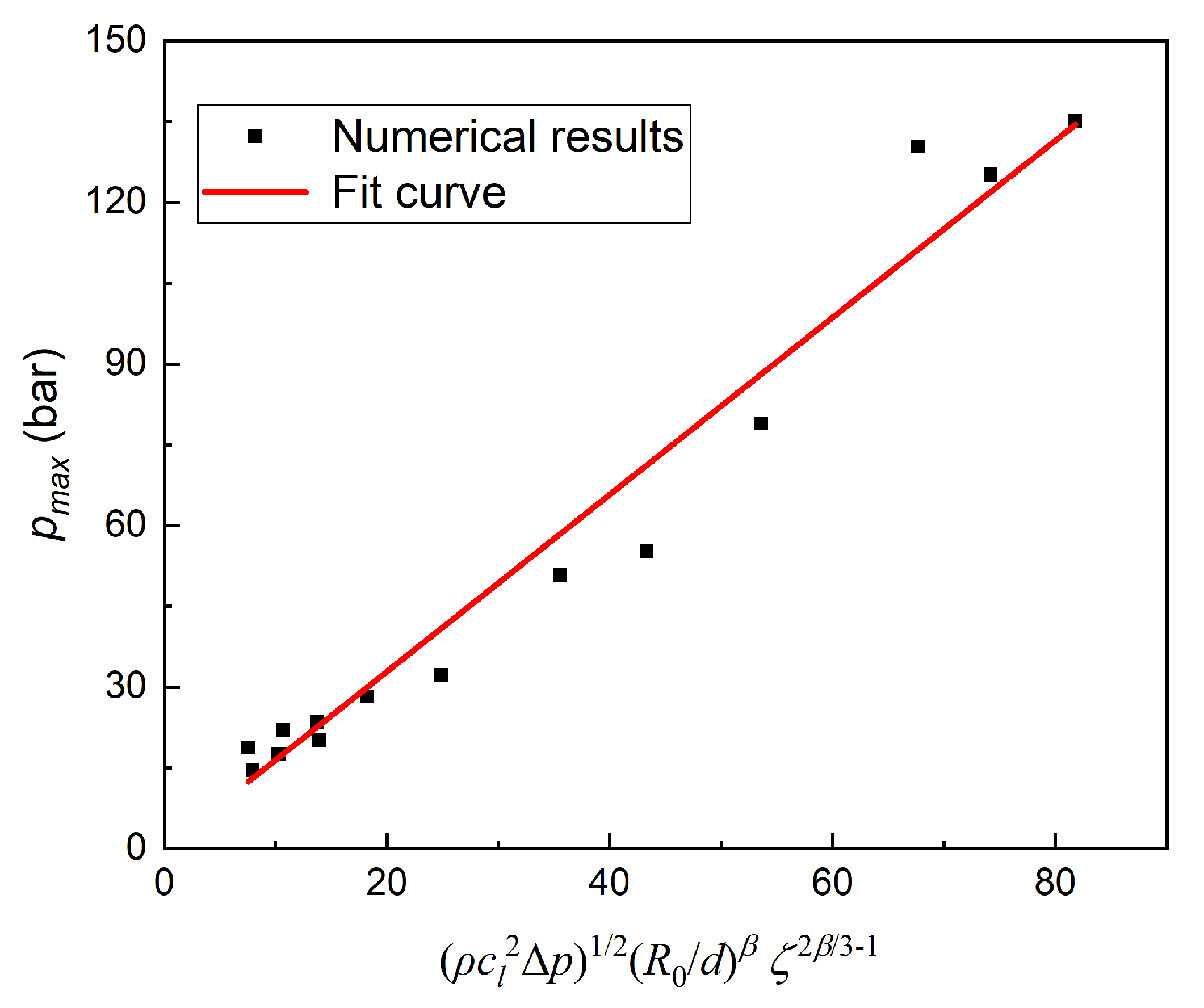
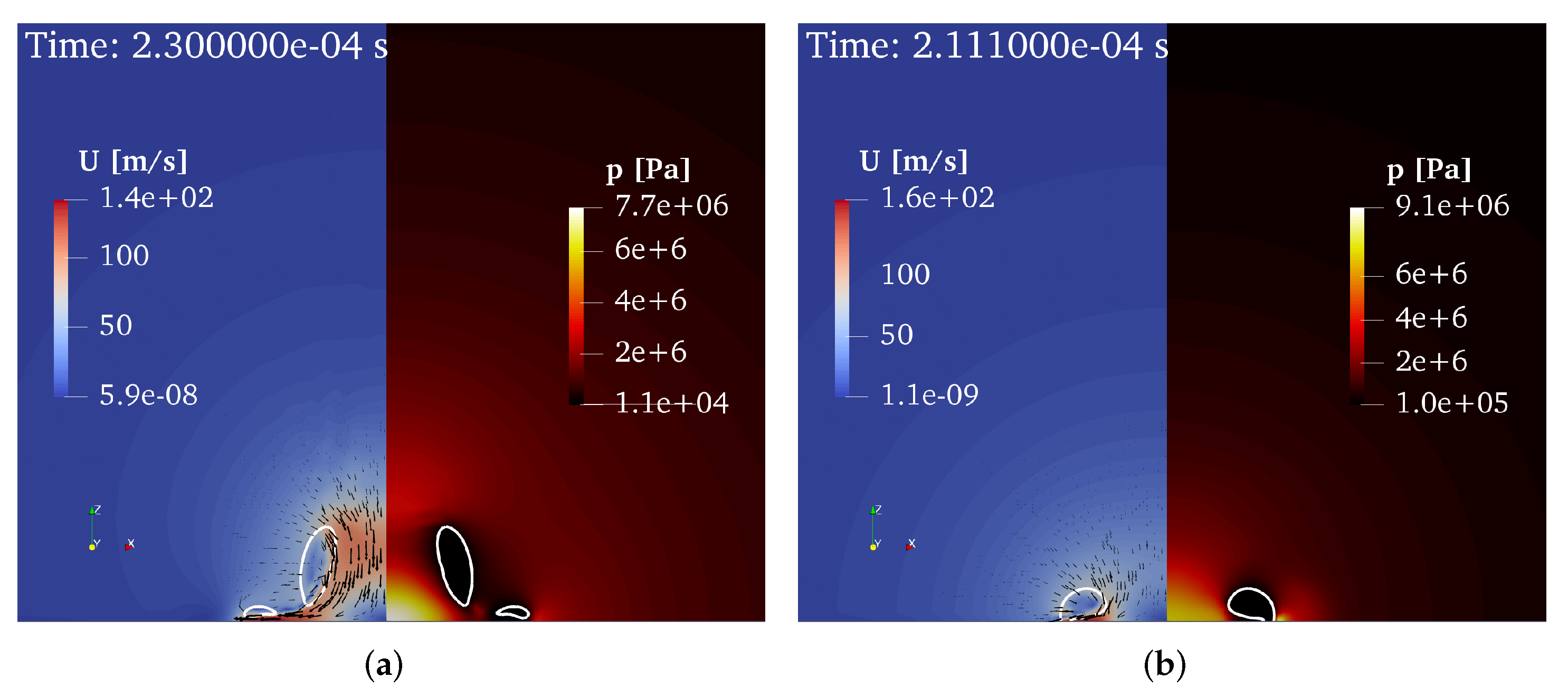
3.2. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gohil, P.P.; Saini, R. Coalesced effect of cavitation and silt erosion in hydro turbines—A review. Renew. Sustain. Energy Rev. 2014, 33, 280–289. [Google Scholar] [CrossRef]
- Arndt, R.E. Some remarks on hydrofoil cavitation. J. Hydrodyn. Ser. B 2012, 24, 305–314. [Google Scholar] [CrossRef]
- Escaler, X.; Egusquiza, E.; Farhat, M.; Avellan, F.; Coussirat, M. Detection of cavitation in hydraulic turbines. Mech. Syst. Signal Process. 2006, 20, 983–1007. [Google Scholar] [CrossRef] [Green Version]
- Avellan, F. Introduction to Cavitation in Hydraulic Machinery; Technical Report; Politehnica University of Timișoara: Timișoara, Romania, 2004. [Google Scholar]
- Dorji, U.; Ghomashchi, R. Hydro turbine failure mechanisms: An overview. Eng. Fail. Anal. 2014, 44, 136–147. [Google Scholar] [CrossRef]
- Neopane, H.P.; Cervantes, M. Sediment erosion in hydraulic turbines. Glob. J. Res. Eng. 2011, 11, 16–26. [Google Scholar]
- Brennen, C.E. Cavitation and Bubble Dynamics; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Franc, J.P.; Michel, J.M. Fundamentals of Cavitation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 76. [Google Scholar]
- Kornfeld, M.; Suvorov, L. On the destructive action of cavitation. J. Appl. Phys. 1944, 15, 495–506. [Google Scholar] [CrossRef]
- van Rijsbergen, M.; Foeth, E.J.; Fitzsimmons, P.; Boorsma, A. High-speed video observations and acoustic-impact measurements on a NACA 0015 foil. In Proceedings of the 8th International Symposium on Cavitation, Singapore, 13–16 August 2012; pp. 958–964. [Google Scholar]
- Pfitsch, W.; Gowing, S.; Fry, D.; Donnelly, M.; Jessup, S. Development of measurement techniques for studying propeller erosion damage in severe wake fields. In Proceedings of the 7th International Symposium on Cavitation, Ann Arbor, MI, USA, 16–20 August 2009. [Google Scholar]
- Cao, Y.; Peng, X.; Yan, K.; Xu, L.; Shu, L. A qualitative study on the relationship between cavitation structure and erosion region around a 3d twisted hydrofoil by painting method. In Proceedings of the Fifth International Symposium on Marine Propulsors, Espoo, Finland, 12–15 June 2017. [Google Scholar]
- Arabnejad, M.H.; Svennberg, U.; Bensow, R.E. Numerical assessment of cavitation erosion risk using incompressible simulation of cavitating flows. Wear 2021, 464, 203529. [Google Scholar] [CrossRef]
- Berchiche, N.; Grekula, M.; Bark, G. Concept of Focusing of Collapse Energy–Application to Cavitation Observations. In Proceedings of the 5th International Symposium on Cavitation (CAV 2003), Osaka, Japan, 1–4 November 2003; pp. 1–4. [Google Scholar]
- Dular, M.; Coutier-Delgosha, O. Numerical modelling of cavitation erosion. Int. J. Numer. Methods Fluids 2009, 61, 1388–1410. [Google Scholar] [CrossRef]
- Peters, A.; Sagar, H.; Lantermann, U.; el Moctar, O. Numerical modelling and prediction of cavitation erosion. Wear 2015, 338, 189–201. [Google Scholar] [CrossRef]
- Peters, A.; Lantermann, U.; el Moctar, O. Numerical prediction of cavitation erosion on a ship propeller in model-and full-scale. Wear 2018, 408–409, 1–12. [Google Scholar] [CrossRef]
- Patella, R.F.; Reboud, J.L.; Briançon-Marjollet, L. A phenomenological and numerical model for scaling the flow agressiveness in cavitation erosion. In Cavitation Erosion Workshop; Val de Reuil, France, 2004; Available online: https://slideplayer.com/amp/12767153/ (accessed on 10 December 2021).
- Patella, R.F.; Archer, A.; Flageul, C. Numerical and experimental investigations on cavitation erosion. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2012; Volume 15, p. 022013. [Google Scholar]
- Fortes-Patella, R.; Challier, G.; Reboud, J.L.; Archer, A. Energy balance in cavitation erosion: From bubble collapse to indentation of material surface. J. Fluids Eng. 2013, 135, 011303. [Google Scholar] [CrossRef]
- Hammitt, F.G. Observations on cavitation damage in a flowing system. J. Basic Eng. 1963, 85, 347–356. [Google Scholar] [CrossRef]
- Schenke, S.; van Terwisga, T.J. An energy conservative method to predict the erosive aggressiveness of collapsing cavitating structures and cavitating flows from numerical simulations. Int. J. Multiph. Flow 2019, 111, 200–218. [Google Scholar] [CrossRef] [Green Version]
- Melissaris, T.; Bulten, N.; van Terwisga, T.J. On the applicability of cavitation erosion risk models with a URANS solver. J. Fluids Eng. 2019, 141, 101104. [Google Scholar] [CrossRef] [Green Version]
- Philipp, A.; Lauterborn, W. Cavitation erosion by single laser-produced bubbles. J. Fluid Mech. 1998, 361, 75–116. [Google Scholar] [CrossRef]
- Shima, A.; Takayama, K.; Tomita, Y.; Ohsawa, N. Mechanism of impact pressure generation from spark-generated bubble collapse near a wall. Aiaa J. 1983, 21, 55–59. [Google Scholar] [CrossRef]
- Tomita, Y.; Shima, A. Mechanisms of impulsive pressure generation and damage pit formation by bubble collapse. J. Fluid Mech. 1986, 169, 535–564. [Google Scholar] [CrossRef]
- Vokurka, K. Significant intervals of energy transforms in bubbles freely oscillating in liquids. J. Hydrodyn. 2017, 29, 217–225. [Google Scholar]
- Tian, Z.L.; Liu, Y.L.; Zhang, A.M.; Tao, L. Energy dissipation of pulsating bubbles in compressible fluids using the Eulerian finite-element method. Ocean Eng. 2010, 196, 106714. [Google Scholar] [CrossRef]
- Tinguely, M.; Obreschkow, D.; Kobel, P.; Dorsaz, N.; De Bosset, A.; Farhat, M. Energy partition at the collapse of spherical cavitation bubbles. Phys. Rev. E 2012, 86, 046315. [Google Scholar] [CrossRef] [Green Version]
- Schenke, S.; Melissaris, T.; Van Terwisga, T. On the relevance of kinematics for cavitation implosion loads. Phys. Fluids 2019, 31, 052102. [Google Scholar] [CrossRef]
- Cole, R. Underwater Explosions; Princeton University Press: Princeton, NJ, USA, 1948. [Google Scholar]
- Wang, Q. Local energy of a bubble system and its loss due to acoustic radiation. J. Fluid Mech. 2016, 797, 201–230. [Google Scholar] [CrossRef] [Green Version]
- Christian, C.M. Modeling Laser-Generated Cavitation Bubbles. Master’s Thesis, Pennsylvania State University, College of Engineering, University Park, PA, USA, 2012. [Google Scholar]
- Zeng, Q.; Gonzalez-Avila, S.R.; Dijkink, R.; Koukouvinis, P.; Gavaises, M.; Ohl, C.D. Wall shear stress from jetting cavitation bubbles. J. Fluid Mech. 2018, 846, 341–355. [Google Scholar] [CrossRef] [Green Version]
- Aganin, A.; Ganiev, O.; Davletshin, A.; Ukrainskii, L. Evaluation of Thermal and Acoustic Energy during Collapse of Cavitation Bubbles. J. Mach. Manuf. Reliab. 2020, 49, 367–373. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Koch, M.; Lechner, C.; Reuter, F.; Köhler, K.; Mettin, R.; Lauterborn, W. Numerical modeling of laser generated cavitation bubbles with the finite volume and volume of fluid method, using OpenFOAM. Comput. Fluids 2016, 126, 71–90. [Google Scholar] [CrossRef]
- Lechner, C.; Koch, M.; Lauterborn, W.; Mettin, R. Pressure and tension waves from bubble collapse near a solid boundary: A numerical approach. J. Acoust. Soc. Am. 2017, 142, 3649–3659. [Google Scholar] [CrossRef] [PubMed]
- Schnerr, G.H.; Sezal, I.H.; Schmidt, S.J. Numerical investigation of three-dimensional cloud cavitation with special emphasis on collapse induced shock dynamics. Phys. Fluids 2008, 20, 040703. [Google Scholar] [CrossRef]
- Antoine, C. Tension des vapeurs: Nouvelle relation entre les tension et les temperatures. Comptes Rendus 1888, 107, 681–684. [Google Scholar]
- Rayleigh, L. On the pressure developed in a liquid during the collapse of a spherical cavity. Phil. Mag. 1917, 34, 94–98. [Google Scholar] [CrossRef]
- Yin, J.; Zhang, Y.; Zhu, J.; Lv, L.; Tian, L. An experimental and numerical study on the dynamical behaviors of the rebound cavitation bubble near the solid wall. Int. J. Heat Mass Transf. 2021, 177, 121525. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.; Deng, J. Numerical study of the collapse of multiple bubbles and the energy conversion during bubble collapse. Water 2019, 11, 247. [Google Scholar] [CrossRef] [Green Version]
- Supponen, O.; Obreschkow, D.; Kobel, P.; Tinguely, M.; Dorsaz, N.; Farhat, M. Shock waves from nonspherical cavitation bubbles. Phys. Rev. Fluids 2017, 2, 093601. [Google Scholar] [CrossRef] [Green Version]
- Vogel, A.; Lauterborn, W. Acoustic transient generation by laser-produced cavitation bubbles near solid boundaries. J. Acoust. Soc. Am. 1988, 84, 719–731. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, H.; Chen, L.; Liang, X. Numerical Study of the Emission of Acoustic Energy of Single Collapsing Vapor Bubble Near a Rigid Wall. Water 2022, 14, 455. https://doi.org/10.3390/w14030455
Duan H, Chen L, Liang X. Numerical Study of the Emission of Acoustic Energy of Single Collapsing Vapor Bubble Near a Rigid Wall. Water. 2022; 14(3):455. https://doi.org/10.3390/w14030455
Chicago/Turabian StyleDuan, Hangbo, Linya Chen, and Xiaoyu Liang. 2022. "Numerical Study of the Emission of Acoustic Energy of Single Collapsing Vapor Bubble Near a Rigid Wall" Water 14, no. 3: 455. https://doi.org/10.3390/w14030455
APA StyleDuan, H., Chen, L., & Liang, X. (2022). Numerical Study of the Emission of Acoustic Energy of Single Collapsing Vapor Bubble Near a Rigid Wall. Water, 14(3), 455. https://doi.org/10.3390/w14030455





