7.1. Interfering Factors
Previous studies showed that radon anomalies are not only affected by tectonic activities, but also affected by meteorological conditions such as air temperature, air pressure and precipitation. [
4,
7,
42,
43,
44,
45,
46]. In this study, we collected atmospheric pressure (PRS), air temperature (T) and precipitation (PR) data of each station, and the missing data was supplemented by the monitoring data of nearby stations. We calculate the wavelet coherence (WTC) of atmospheric pressure, temperature and precipitation on radon concentration, and calculate the correlation between pressure, temperature and precipitation and raw radon data, low-frequency data and high-frequency data.
As shown in
Figure 7, in the results of wavelet coherence in the whole observation time, the three WTC images of each station are similar. This may be due to the similar seasonal cycle period of air pressure, temperature and precipitation. Radon and air pressure, air temperature and precipitation of MD, CN, TC, LD and ML stations have coherence within the band of 1 year in the whole period; PRS, T and PR of CN and TC stations showed coherence with radon in some time periods. CN station showed correlation before September 1994 (about day No.500), and TC station showed a high coherence for a 1 year band in May 1993 to March 1994 and 1995 to 1996. The PRS, T and PR at NJ, LC and SM stations do not show correlation with radon within the band of 1 year. There was a correlation between radon and T and between radon and PR of ML station within the band of a half year in June 1994 to July 1995. For other bands, there are sporadic correlations in each station’s results, but the duration is short, mostly within 100 days.
In addition, we also calculated the correlation coefficients of air pressure, precipitation and temperature to the original radon data, high-frequency information data and low-frequency information data. The formula is as follows:
where
is correlation coefficients,
is the number of data,
and
mean the ith data of x and y respectively, and
and
mean the average value of x and y respectively. The calculation results are shown in
Table 9. There are nine results for each station. For the correlation coefficient, less than 0.3 is considered as no correlation, and 0.3 to 0.8 is considered as a weak correlation [
47]. The results of the correlation coefficient show that PRS, T and PR have no significant correlation with radon.
The calculation results for R at each station show that radon concentration has no certain correlation with PR, while it can be seen from WTC that except for LD and ML stations, radon and PR of other stations have correlation only for part of the time or no correlation, which is similar to the result for R. We speculate that this may be related to the well depth. For deep groundwater, the response of groundwater dynamics to the infiltration recharge of precipitation is delayed, and precipitation signals may be smoothed, resulting in that the correlation between the two cannot be identified.
According to Feng’s study [
48], the increase in air pressure will make the degassing effect worse and reduce the radon concentration in water, but the influence of air pressure on radon concentration in deep groundwater is small. That may be why the relationship between air pressure and radon concentration is not obvious in our calculation results.
The formula for radon dissolution is as follows [
49]:
where S is the solubility of radon and the T is the temperature. We can see that the increase in temperature will increase the solubility of radon, thus increasing the concentration of radon in water. However, there is no obvious correlation in R results, and there is even a negative correlation between temperature and radon concentration in NJ and MD.
According to the calculation results of WTC, meteorological factors have a certain impact (mainly periodic) on radon concentrations in water, which is consistent with the previous research conclusions. It is worth noting that in the results of WTC, there is a stable strong correlation (mainly periodic) between water radon concentration and meteorological factors in two stations (LD and ML); however, the calculation results of R show that there is no strong correlation between meteorological factors and water radon in eight stations. Overall, meteorological factors did not cause short-term radon concentration changes.
7.2. Possible Explanations for Different Anomaly Characteristics
In the results, we summarized three kinds of anomaly characteristics, namely sudden jump anomalies, fluctuation anomalies and persistent anomalies. Previous studies showed that radon concentrations in water are closely related to the state of the seismogenic system [
4,
5,
50]. Therefore, if we regard the rock rupture as an “avalanche point” of the complex system of block motion on a micro level, the anomalies in AR-1 may indicate the micro fracturing process of rocks near the monitoring well. From the physical meaning of the index, the AR-1′s sudden jump anomaly indicates that the recovery speed of the system suddenly decreases and approaches the “avalanche point” in a certain moment within WL (10 days). Fluctuation anomalies in AR-1 mean that the state of the system changes sharply over a period of time. Persistent anomalies in AR-1 mean that the state of the system’s recovery speed keeps slowing down over a period, which is a typical sign of CSD in other studies. For variance, sudden jump anomalies mean that the sample data has changed greatly at a certain moment within 10 days. Fluctuation anomalies represent multiple numerical mutations with an interval of about 10 days over a period of time. Persistent anomalies indicate that the sample data are in a state of large fluctuation ranges for a period of time. The three types of anomaly characteristics may be caused by different water radon anomaly mechanisms.
Zhang et al. proposed that as an important carrier of radon migration, groundwater flow anomalies have an important impact on radon [
7]. The precursory mechanism of water radon anomalies may be closely related to the change in permeability during earthquake preparation. In the process of earthquake preparation, the accumulation of stress and strain may cause changes in crustal permeability [
51]. The continuous accumulation process constantly disrupts the mechanical balance between particles, moving each other, changes the porosity and groundwater flow, and finally leads to “avalanches” and forms new pore channels. In this process, the radon concentration in water changes continuously, which may provide an explanation for the persistent anomaly.
According to the theory of the “strong body earthquake-generating model” [
52], when the crustal deformation process outside the nucleation area continues to develop, it may lead to frequent rock micro fractures for a period of time, resulting in frequent changes in hydrogeological conditions and radon concentrations, manifested by irregular and frequent fluctuations over a short time, forming fluctuation anomalies, until the rock mass in the nucleation area suddenly breaks when the pressure reaches the threshold, forming an earthquake. The frequent rock micro fracturing in this process may provide an explanation for the sudden jump anomalies and fluctuation anomalies.
In addition, the main anomaly characteristics in the results of different stations are different. Binda et al. revealed that the response of hydrogeochemistry to seismic activity is closely related to hydrogeological conditions. This indicates that different hydrogeological conditions may lead to different responses [
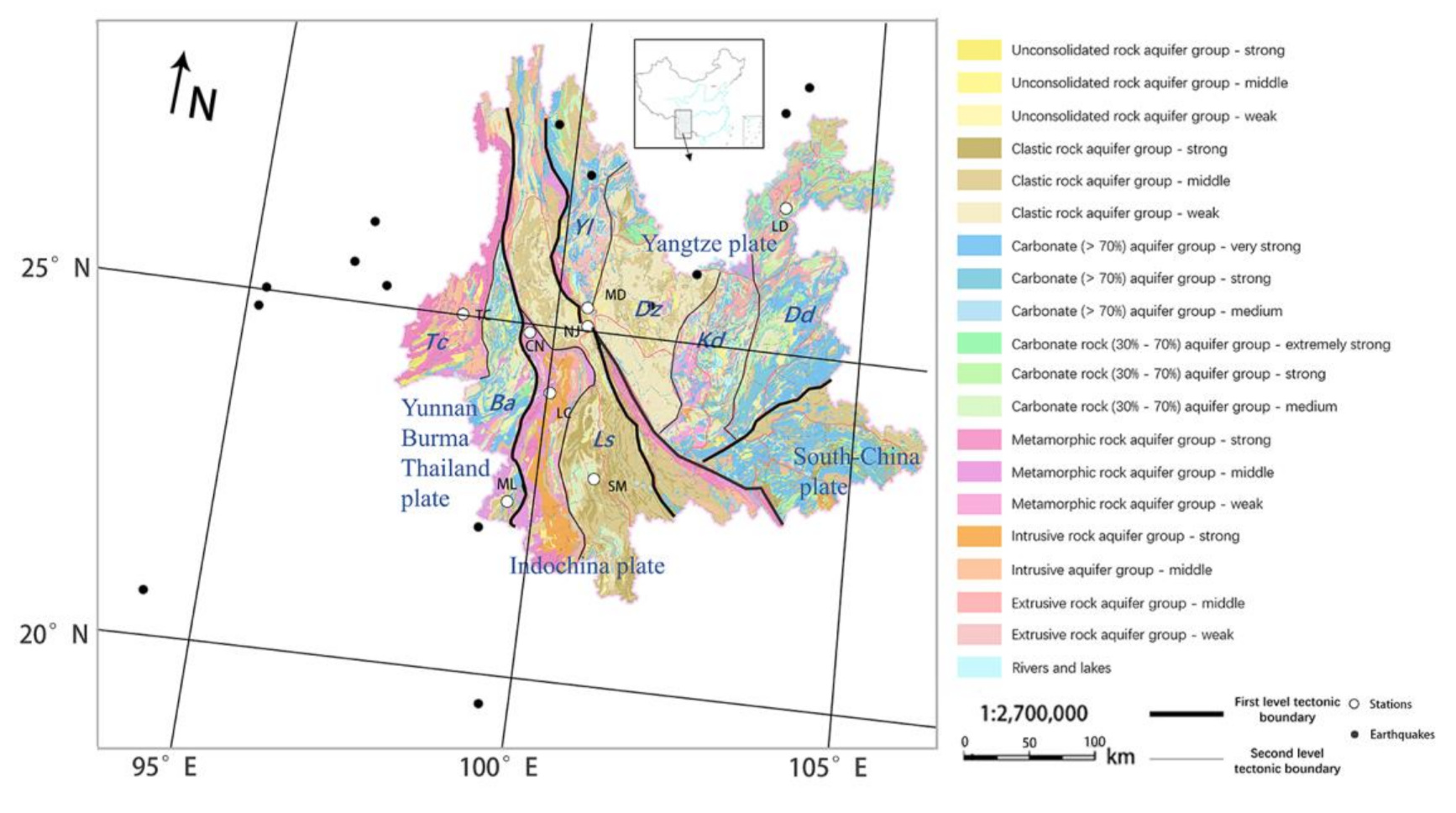
53]. In the present study, in the high-frequency results of MD and LD, AR-1 mainly shows the sudden jump anomalies. MD is a thermal water well with a shallow well depth and LD is a spring. In terms of lithology, MD and LD are in sedimentary rocks with significant karstification that may lead to a good hydraulic connection among aquifers. It is possible that the mixing between shallow groundwater and deep fluid or gas will occur occasionally during earthquake preparation, thus causing a sudden jump anomaly. In contrast, high-frequency results of AR-1 in TC and LC mainly presented with fluctuation anomalies. The formation lithologies of TC and LC are magmatic rocks, and the well depth is relatively deep and groundwater is fissure water. We speculate that the change in groundwater radon concentration in the wells mostly result from the release of rock micro fracturing caused by crustal stress due to the poor hydraulic connection and relatively stable conditions. The relatively stable conditions may amplify the slight fluctuations of radon concentration in groundwater, making fluctuation anomalies the main anomaly feature of AR-1 at these two stations. On the whole, different hydrogeological conditions, along with regional stress and strain changes, could result in different responses of aquifers and the associated different anomalies in water radon concentration at each station, requiring further study.
7.3. Temporal and Spatial Characteristics of Radon Anomalies
7.3.1. Relationship between Epicenter Distance and Anomaly Occurrence Time at Each Station
Some previous studies suggest that there may be a spatio-temporal relationship between the occurrence of earthquakes and precursors. In the present study, we conducted the statistical analyses on the occurrence time of each earthquake and earthquake precursory anomalies, and calculated the time of precursory anomalies ahead of the earthquakes (
Table 3,
Table 4,
Table 6 and
Table 7). Then, we plotted the diagram of precursory time and epicentral distance to investigate the possible relationship between them. When we take the single station as the research object, most R
2 of the results are less than 0.1, reflecting that there is no certain linear correlation between the precursory time and epicentral distance. Considering that there may be too little data at a single station that may result in a great uncertainty of results, we drew a scatter diagram with all the stations’ data (
Figure 8). Whether it is high-frequency or low-frequency data, or AR-1 or variance, the data points in the figures are randomly and irregularly distributed. R
2 of the correlation showed in the figures is far less than 0.1, indicating that there is almost no linear relationship between precursory time and epicentral distance.
When we chose the earthquakes with the epicentral distance less than 300 km, the associated calculation results showed that the R
2 of correlation between the epicentral distance and precursory time of variance (L), AR-1 (L) and variance (H) ranges from 0.051 to 0.245 (
Figure 9), indicating that there may be a very weak or no positive correlation. However, the R
2 of the epicentral distance and precursory time of AR-1 (H) is close to 0.5, showing an obvious positive correlation. This may indicate that within 300 km, the larger the epicenter distance is, the earlier the occurrence time of water radon precursor anomalies. This conclusion is consistent with that of some previous studies.
In some areas, there is also a positive correlation between the time of radon anomalies and the epicentral distance. According to the calculation results of the previous empirical formula (1), the seismogenic range of the M 5.7 earthquake is about 300 km. Considering that there is a high frequency of earthquakes with M 5–6 in the study area, we speculate that this phenomenon may be closely related to the earthquake preparation process. According to Mei’s “strong body earthquake generating model”, when the earthquake begins to prepare, a large number of small fractures will appear in the edge area with low fracturing strength, which leads to the earliest abnormal radon concentrations in peripheral groundwater. With the accumulation of stress, the fracturing gradually migrates to the epicenter, finally forming a phenomenon that the abnormal time is proportional to the epicenter distance. This may provide an explanation for such correlations.
7.3.2. Relationship between Epicentral Distance and Anomaly Time of Three Large Earthquakes
Taking the Lijiang, Wuding and Menglian earthquakes as the research objects, the relationship between the epicentral distance of eight stations and the anomaly days before the earthquake is calculated. The results show that only in the case of high-frequency information AR-1, there is a weak positive correlation between the epicentral distance of the LJ earthquake and the precursory time; that is, the precursory anomaly appears earlier with the increase in epicentral distance. In other results, R
2 values are less than 0.3, indicating that there is very weak or no significant correlation between them (
Figure 10).
The above results may indicate that there may be no universal law in the temporal and spatial relationship of earthquake precursors. It may be related to the earthquake preparation process and the hydrogeological conditions around the monitoring stations. For the Lijiang earthquake, many studies have proposed that its seismogenic process conforms to the “strong body earthquake-generating model”. This is consistent with our results. There are different results for other earthquakes, which may be due to different seismogenic modes and hydrogeological conditions of stations.
We speculate that the water radon anomaly at each monitoring point is not the response of the critical point of the whole seismogenic system, but the “critical point” of each small system. The criticalities of these small systems are related to the critical state of the whole regional seismogenic system, but they cannot accurately indicate the critical state of the whole system. For the application of self-organized critical states of complex dynamic systems in earthquake preparation, we may need to find an index that can effectively indicate the whole regional crustal movements from spatial observations.