Assessing Performances of Multivariate Data Assimilation Algorithms with SMOS, SMAP, and GRACE Observations for Improved Soil Moisture and Groundwater Analyses
Abstract
:1. Introduction
2. Model, Study Area, and Data
2.1. Model Configurations
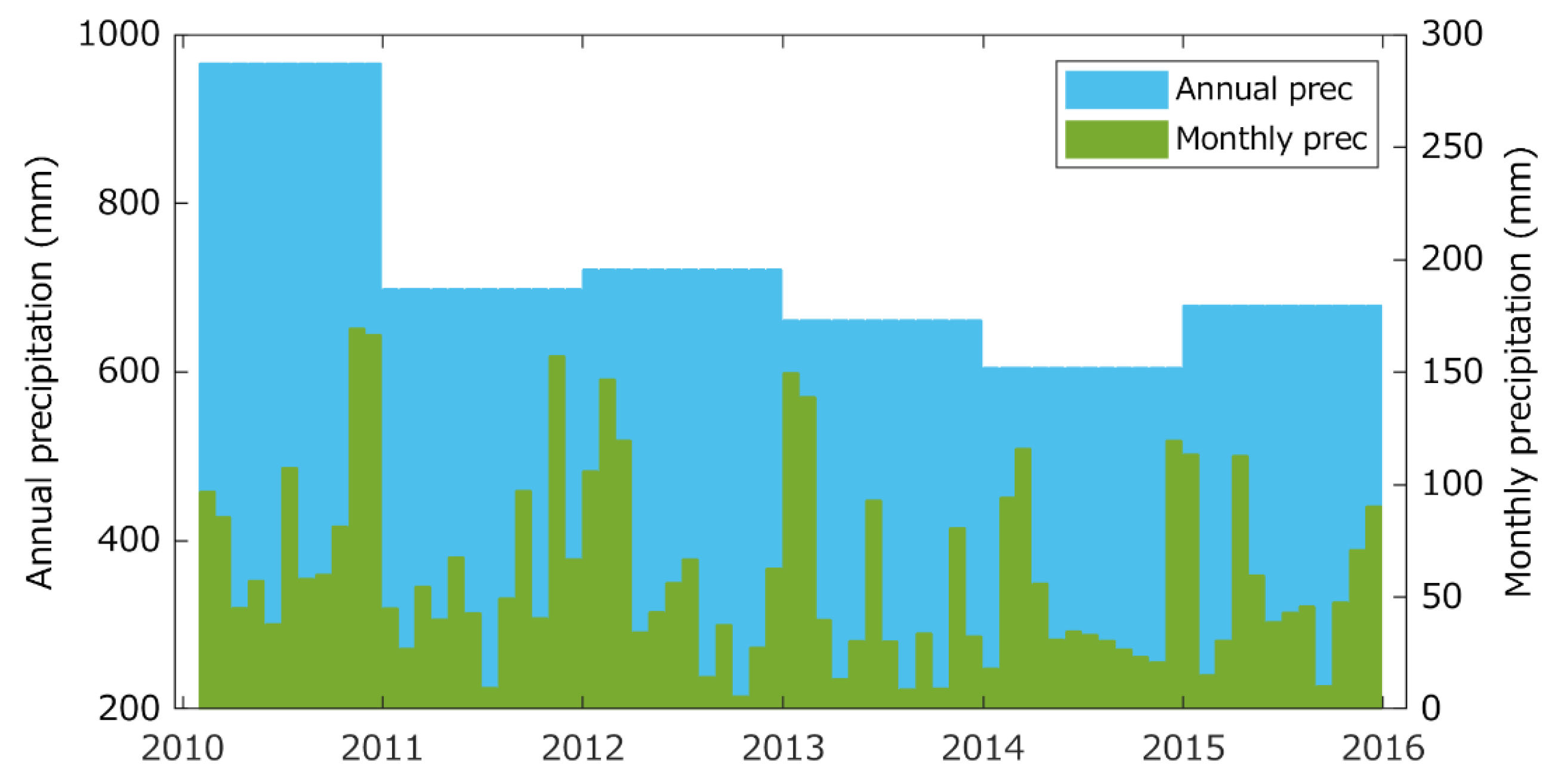
2.2. Study Area and In Situ Data
2.3. Satellite Soil Moisture Data
2.4. GRACE Data
3. Methodology
3.1. Implementation of Multivariate DA
3.2. Ensemble Kalman Smoother (EnKS)
3.3. Particle Smoother (PS)
3.4. Ensemble Gaussian Particle Smoother (EnGPS)
3.5. Evolutionary Smoother (EvS)
4. Results
4.1. Initial Comparison
4.2. Multivariate DA Impacts on SM and TWS Estimates
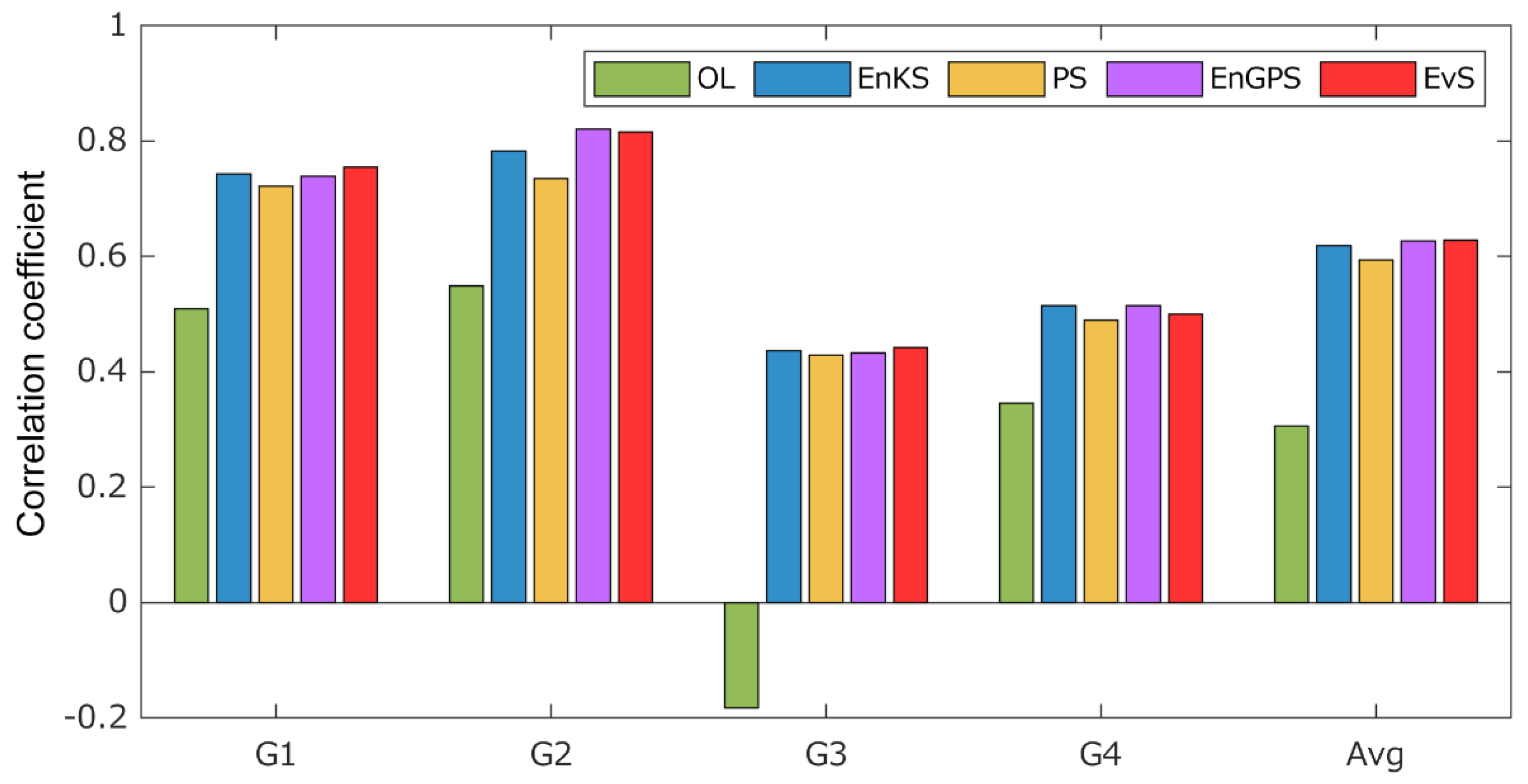
4.3. Error Characteristics of DA Systems
4.4. Validation with In Situ Data
4.4.1. Soil Moisture
4.4.2. Groundwater Storage
5. Discussion
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Ensemble Kalman Smoother (EnKS)
Appendix B. Particle Smoother (PS)
Appendix C. Ensemble Gaussian Particle Smoother (EnGPS)
Appendix D. Evolutionary Smoother (EvS)
References
- Pitman, A.J. The Evolution of, and Revolution in, Land Surface Schemes Designed for Climate Models. Int. J. Climatol. 2003, 23, 479–510. [Google Scholar] [CrossRef]
- Moradkhani, H. Hydrologic Remote Sensing and Land Surface Data Assimilation. Sensors 2008, 8, 2986–3004. [Google Scholar] [CrossRef] [PubMed]
- Reichle, R.H. Data Assimilation Methods in the Earth Sciences. Adv. Water Resour. 2008, 31, 1411–1418. [Google Scholar] [CrossRef]
- Yin, W.; Han, S.-C.; Zheng, W.; Yeo, I.-Y.; Hu, L.; Tangdamrongsub, N.; Ghobadi-Far, K. Improved Water Storage Estimates within the North China Plain by Assimilating GRACE Data into the CABLE Model. J. Hydrol. 2020, 590, 125348. [Google Scholar] [CrossRef]
- Yan, H.; Moradkhani, H. Combined Assimilation of Streamflow and Satellite Soil Moisture with the Particle Filter and Geostatistical Modeling. Adv. Water Resour. 2016, 94, 364–378. [Google Scholar] [CrossRef] [Green Version]
- Tian, S.; Tregoning, P.; Renzullo, L.J.; van Dijk, A.I.J.M.; Walker, J.P.; Pauwels, V.R.N.; Allgeyer, S. Improved Water Balance Component Estimates through Joint Assimilation of GRACE Water Storage and SMOS Soil Moisture Retrievals. Water Resour. Res. 2017, 53, 1820–1840. [Google Scholar] [CrossRef]
- Sabater, J.M.; Rüdiger, C.; Calvet, J.-C.; Fritz, N.; Jarlan, L.; Kerr, Y. Joint Assimilation of Surface Soil Moisture and LAI Observations into a Land Surface Model. Agric. For. Meteorol. 2008, 148, 1362–1373. [Google Scholar] [CrossRef] [Green Version]
- Montzka, C.; Pauwels, V.R.N.; Franssen, H.-J.H.; Han, X.; Vereecken, H. Multivariate and Multiscale Data Assimilation in Terrestrial Systems: A Review. Sensors 2012, 12, 16291–16333. [Google Scholar] [CrossRef] [Green Version]
- Girotto, M.; Reichle, R.H.; Rodell, M.; Liu, Q.; Mahanama, S.; De Lannoy, G.J.M. Multi-Sensor Assimilation of SMOS Brightness Temperature and GRACE Terrestrial Water Storage Observations for Soil Moisture and Shallow Groundwater Estimation. Remote Sens. Environ. 2019, 227, 12–27. [Google Scholar] [CrossRef]
- Tangdamrongsub, N.; Han, S.-C.; Yeo, I.-Y.; Dong, J.; Steele-Dunne, S.C.; Willgoose, G.; Walker, J.P. Multivariate Data Assimilation of GRACE, SMOS, SMAP Measurements for Improved Regional Soil Moisture and Groundwater Storage Estimates. Adv. Water Resour. 2020, 135, 103477. [Google Scholar] [CrossRef]
- Reichle, R.H.; McLaughlin, D.B.; Entekhabi, D. Hydrologic Data Assimilation with the Ensemble Kalman Filter. Mon. Weather Rev. 2002, 130, 103–114. [Google Scholar] [CrossRef] [Green Version]
- Evensen, G. The Ensemble Kalman Filter: Theoretical Formulation and Practical Implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Ott, E.; Hunt, B.R.; Szunyogh, I.; Zimin, A.V.; Kostelich, E.J.; Corazza, M.; Kalnay, E.; Patil, D.J.; Yorke, J.A. A Local Ensemble Kalman Filter for Atmospheric Data Assimilation. Tellus Dyn. Meteorol. Oceanogr. 2004, 56, 415–428. [Google Scholar] [CrossRef]
- Krymskaya, M.V.; Hanea, R.G.; Verlaan, M. An Iterative Ensemble Kalman Filter for Reservoir Engineering Applications. Comput. Geosci. 2009, 13, 235–244. [Google Scholar] [CrossRef] [Green Version]
- Weerts, A.H.; El Serafy, G.Y.H. Particle Filtering and Ensemble Kalman Filtering for State Updating with Hydrological Conceptual Rainfall-Runoff Models. Water Resour. Res. 2006, 42, W09403. [Google Scholar] [CrossRef] [Green Version]
- Moradkhani, H.; Hsu, K.-L.; Gupta, H.; Sorooshian, S. Uncertainty Assessment of Hydrologic Model States and Parameters: Sequential Data Assimilation Using the Particle Filter. Water Resour. Res. 2005, 41, W05012. [Google Scholar] [CrossRef] [Green Version]
- Dumedah, G. Formulation of the Evolutionary-Based Data Assimilation, and Its Implementation in Hydrological Forecasting. Water Resour. Manag. 2012, 26, 3853–3870. [Google Scholar] [CrossRef]
- Chemin, Y.; Honda, K. Spatiotemporal Fusion of Rice Actual Evapotranspiration With Genetic Algorithms and an Agrohydrological Model. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3462–3469. [Google Scholar] [CrossRef]
- Ines, A.V.M.; Mohanty, B.P. Near-Surface Soil Moisture Assimilation for Quantifying Effective Soil Hydraulic Properties Using Genetic Algorithms: 2. Using Airborne Remote Sensing during SGP97 and SMEX02. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef] [Green Version]
- Dumedah, G.; Coulibaly, P. Evaluating Forecasting Performance for Data Assimilation Methods: The Ensemble Kalman Filter, the Particle Filter, and the Evolutionary-Based Assimilation. Adv. Water Resour. 2013, 60, 47–63. [Google Scholar] [CrossRef]
- Tangdamrongsub, N.; Han, S.-C.; Yeo, I.-Y. Enhancement of Water Storage Estimates Using GRACE Data Assimilation with Particle Filter Framework. In Proceedings of the 22nd International Congress on Modelling and Simulation (MODSIM), Hobart, TAS, Australia, 5 December 2017; pp. 1041–1047. [Google Scholar]
- Decker, M. Development and Evaluation of a New Soil Moisture and Runoff Parameterization for the CABLE LSM Including Subgrid-Scale Processes. J. Adv. Model. Earth Syst. 2015, 7, 1788–1809. [Google Scholar] [CrossRef]
- Kowalczyk, E.A.; Wang, Y.P.; Law, R.M.; Davies, H.L.; McGregor, J.L.; Abramowitz, G.S. The CSIRO Atmosphere Biosphere Land Exchange (CABLE) Model for Use in Climate Models and as an Offline Model; CSIRO Marine and Atmospheric Research: Aspendale, Australia, 2006; ISBN 978-1-921232-30-5. [Google Scholar]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-SatellitE Retrievals for GPM (IMERG); Algorithm Theoretical Basis Document (ATBD)Version 06; NASAGSFC: Greenbelt, MD, USA, 2019.
- Tangdamrongsub, N.; Han, S.-C.; Decker, M.; Yeo, I.-Y.; Kim, H. On the Use of the GRACE Normal Equation of Inter-Satellite Tracking Data for Estimation of Soil Moisture and Groundwater in Australia. Hydrol. Earth Syst. Sci. 2018, 22, 1811–1829. [Google Scholar] [CrossRef] [Green Version]
- Rüdiger, C.; Hancock, G.; Hemakumara, H.M.; Jacobs, B.; Kalma, J.D.; Martinez, C.; Thyer, M.; Walker, J.P.; Wells, T.; Willgoose, G.R. Goulburn River Experimental Catchment Data Set. Water Resour. Res. 2007, 43, W10403. [Google Scholar] [CrossRef] [Green Version]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Bitar, A.A.; Cabot, F.; Gruhier, C.; Juglea, S.E.; et al. The SMOS Soil Moisture Retrieval Algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Bitar, A.A.; Mialon, A.; Kerr, Y.H.; Cabot, F.; Richaume, P.; Jacquette, E.; Quesney, A.; Mahmoodi, A.; Tarot, S.; Parrens, M.; et al. The Global SMOS Level 3 Daily Soil Moisture and Brightness Temperature Maps. Earth Syst. Sci. Data 2017, 9, 293–315. [Google Scholar] [CrossRef] [Green Version]
- Crow, W.T.; Koster, R.D.; Reichle, R.H.; Sharif, H.O. Relevance of Time-Varying and Time-Invariant Retrieval Error Sources on the Utility of Spaceborne Soil Moisture Products. Geophys. Res. Lett. 2005, 32, L24405. [Google Scholar] [CrossRef] [Green Version]
- Reichle, R.H.; Koster, R.D. Bias Reduction in Short Records of Satellite Soil Moisture. Geophys. Res. Lett. 2004, 31, L19501. [Google Scholar] [CrossRef] [Green Version]
- Lievens, H.; Tomer, S.K.; Al Bitar, A.; De Lannoy, G.J.M.; Drusch, M.; Dumedah, G.; Hendricks Franssen, H.-J.; Kerr, Y.H.; Martens, B.; Pan, M.; et al. SMOS Soil Moisture Assimilation for Improved Hydrologic Simulation in the Murray Darling Basin, Australia. Remote Sens. Environ. 2015, 168, 146–162. [Google Scholar] [CrossRef]
- Colliander, A.; Jackson, T.J.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.B.; Cosh, M.H.; Dunbar, R.S.; Dang, L.; Pashaian, L.; et al. Validation of SMAP Surface Soil Moisture Products with Core Validation Sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-Resolution CSR GRACE RL05 Mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE Measurements of Mass Variability in the Earth System. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Flechtner, F.; Neumayer, K.-H.; Dahle, C.; Dobslaw, H.; Fagiolini, E.; Raimondo, J.-C.; Güntner, A. What Can Be Expected from the GRACE-FO Laser Ranging Interferometer for Earth Science Applications? In Remote Sensing and Water Resources; Cazenave, A., Champollion, N., Benveniste, J., Chen, J., Eds.; Space Sciences Series of ISSI; Springer International Publishing: Cham, Switzerland, 2016; pp. 263–280. ISBN 978-3-319-32449-4. [Google Scholar]
- Wahr, J.; Swenson, S.; Velicogna, I. Accuracy of GRACE Mass Estimates. Geophys. Res. Lett. 2006, 33, L06401. [Google Scholar] [CrossRef] [Green Version]
- Jarque, C.M.; Bera, A.K. Efficient Tests for Normality, Homoscedasticity and Serial Independence of Regression Residuals. Econ. Lett. 1980, 6, 255–259. [Google Scholar] [CrossRef]
- Entekhabi, D.; Reichle, R.H.; Koster, R.D.; Crow, W.T. Performance Metrics for Soil Moisture Retrievals and Application Requirements. J. Hydrometeorol. 2010, 11, 832–840. [Google Scholar] [CrossRef]
- Decker, M.; Or, D.; Pitman, A.; Ukkola, A. New Turbulent Resistance Parameterization for Soil Evaporation Based on a Pore-Scale Model: Impact on Surface Fluxes in CABLE. J. Adv. Model. Earth Syst. 2017, 9, 220–238. [Google Scholar] [CrossRef] [Green Version]
- Steiger, J.H. Tests for Comparing Elements of a Correlation Matrix. Psychol. Bull. 1980, 87, 245–251. [Google Scholar] [CrossRef]
- Al-Khaldi, M.M.; Johnson, J.T. Soil Moisture Retrievals Using CYGNSS Data in a Time-Series Ratio Method: Progress Update and Error Analysis. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Teixeira da Encarnação, J.; Arnold, D.; Bezděk, A.; Dahle, C.; Doornbos, E.; van den IJssel, J.; Jäggi, A.; Mayer-Gürr, T.; Sebera, J.; Visser, P.; et al. Gravity Field Models Derived from Swarm GPS Data. Earth Planets Space 2016, 68, 127. [Google Scholar] [CrossRef] [Green Version]
- Plaza Guingla, D.A.; De Keyser, R.; De Lannoy, G.J.M.; Giustarini, L.; Matgen, P.; Pauwels, V.R.N. Improving Particle Filters in Rainfall-Runoff Models: Application of the Resample-Move Step and the Ensemble Gaussian Particle Filter. Water Resour. Res. 2013, 49, 4005–4021. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]








| EnKS | PS | EnGPS | EvS | |
|---|---|---|---|---|
| Sample size | N | N | N | 2N |
| Error distribution | Gaussian | No restriction | No restriction | No restriction |
| Evaluation approach | Kalman gain function | Likelihood function | Likelihood function and proposal distribution | Cost functions |
| Updating approach | Applying Kalman gain function | Resampling particles based on the likelihood function | Resampling particles based on EnKS posterior estimates | Natural selection (crossover, mutation) through the iteration process |
| Posterior estimation | Mean of ensemble members | The weighted mean of ensemble members | The weighted mean of ensemble members | Mean of ensemble members or only selecting optimal members |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tangdamrongsub, N.; Dong, J.; Shellito, P. Assessing Performances of Multivariate Data Assimilation Algorithms with SMOS, SMAP, and GRACE Observations for Improved Soil Moisture and Groundwater Analyses. Water 2022, 14, 621. https://doi.org/10.3390/w14040621
Tangdamrongsub N, Dong J, Shellito P. Assessing Performances of Multivariate Data Assimilation Algorithms with SMOS, SMAP, and GRACE Observations for Improved Soil Moisture and Groundwater Analyses. Water. 2022; 14(4):621. https://doi.org/10.3390/w14040621
Chicago/Turabian StyleTangdamrongsub, Natthachet, Jianzhi Dong, and Peter Shellito. 2022. "Assessing Performances of Multivariate Data Assimilation Algorithms with SMOS, SMAP, and GRACE Observations for Improved Soil Moisture and Groundwater Analyses" Water 14, no. 4: 621. https://doi.org/10.3390/w14040621
APA StyleTangdamrongsub, N., Dong, J., & Shellito, P. (2022). Assessing Performances of Multivariate Data Assimilation Algorithms with SMOS, SMAP, and GRACE Observations for Improved Soil Moisture and Groundwater Analyses. Water, 14(4), 621. https://doi.org/10.3390/w14040621







