Regional Flood Frequency Analysis for Sustainable Water Resources Management of Genale–Dawa River Basin, Ethiopia
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Study Area
2.2. Screening, Sources, and Analysis of Data
2.3. Hydrological Regionalization
2.4. Discordancy Measure
2.5. Tests for Homogeneity of Stations and Regions
2.5.1. Conventional Homogeneity Test
2.5.2. L-moment-Based Homogeneity Testing
2.6. Delineation of Homogeneous Regions
2.7. Selection of Regional Distribution
3. Results and Discussion
3.1. Identification of a Homogeneous Region
3.2. Discordancy Measure
3.3. Test for Regional Homogeneity
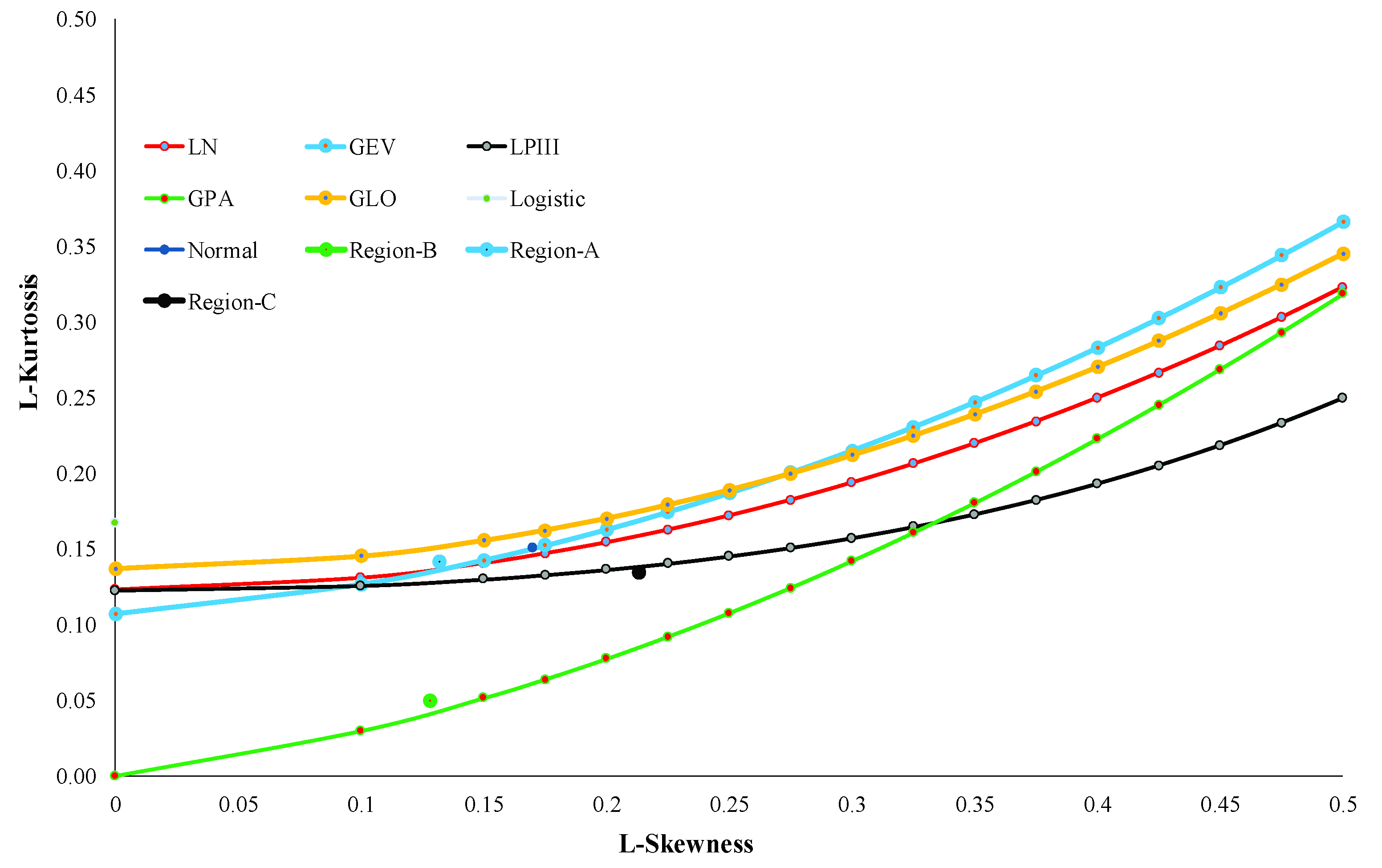
3.4. Demarcation of Homogeneous Regions
3.5. Selection of Best Fit Distribution
3.6. Performance Evaluation of Regional Flood Frequency Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stedinger, J.R.; Griffis, V. Flood Frequency Analysis in the United States. J. Hydrol. Eng. 2008, 13, 199–204. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: New York, NY, USA, 1997. [Google Scholar]
- Kochanek, K.; Strupczewski, W.G.; Bogdanowicz, E. On seasonal approach to flood frequency modelling. Part II: Flood frequency analysis of Polish rivers. Hydrol. Process. 2012, 26, 717–730. [Google Scholar] [CrossRef]
- Schendel, T.; Thongwichian, R. Considering historical flood events in flood frequency analysis: Is it worth the effort? Adv. Water Resour. 2017, 105, 144–153. [Google Scholar] [CrossRef]
- Blöschl, G.; Bierkens, M.F.P.; Chambel, A.; Cudennec, C.; Destouni, G.; Fiori, A.; Kirchner, J.W.; McDonnell, J.J.; Savenije, H.H.G.; Sivapalan, M.; et al. Twenty-three unsolved problems in hydrology (UPH)—A community perspective. Hydrol. Sci. J. 2019, 64, 1141–1158. [Google Scholar] [CrossRef]
- Machado, M.J.; Botero, B.A.; López, J.; Francés, F.; Díez-Herrero, A.; Benito, G. Flood frequency analysis of historical flood data under stationary and non-stationary modelling. Hydrol. Earth Syst. Sci. 2015, 19, 2561–2576. [Google Scholar] [CrossRef]
- Lee, D.-H.; Kim, N.W. Regional Flood Frequency Analysis for a Poorly Gauged Basin Using the Simulated Flood Data and L-Moment Method. Water 2019, 11, 1717. [Google Scholar] [CrossRef]
- Hassan, B.G.H.; Ping, F. Formation of Homogenous Regions for Luanhe Basin—By Using L-Moments and Cluster Techniques. Int. J. Environ. Sci. Dev. 2012, 3, 205–210. [Google Scholar] [CrossRef]
- Javeed, Y.; Apoorva, K.V. Flow Regionalization Under Limited Data Availability—Application of IHACRES in the Western Ghats. Aquat. Procedia 2015, 4, 933–941. [Google Scholar] [CrossRef]
- Hailegeorgis, T.T.; Alfredsen, K. Regional flood frequency analysis and prediction in ungauged basins including estimation of major uncertainties for mid-Norway. J. Hydrol. Reg. Stud. 2017, 9, 104–126. [Google Scholar] [CrossRef]
- Lilienthal, J.; Fried, R.; Schumann, A. Homogeneity testing for skewed and cross-correlated data in regional flood frequency analysis. J. Hydrol. 2018, 556, 557–571. [Google Scholar] [CrossRef]
- Nathanael, J.; Smithers, J.; Horan, M. Assessing the performance of regional flood frequency analysis methods in South Africa. Water SA 2018, 44, 387–398. [Google Scholar] [CrossRef]
- Tanaka, T.; Tachikawa, Y.; Iachikawa, Y.; Yorozu, K. Impact assessment of upstream flooding on extreme flood frequency analysis by incorporating a flood-inundation model for flood risk assessment. J. Hydrol. 2017, 554, 370–382. [Google Scholar] [CrossRef]
- Cassalho, F.; Beskow, S.; de Mello, C.R.; de Moura, M.M. Regional flood frequency analysis using L-moments for geographically defined regions: An assessment in Brazil. J. Flood Risk Manag. 2018, 12, e12453. [Google Scholar] [CrossRef]
- Ekeu-wei, I.T. Evaluation of Hydrological Data Collection Challenges and Flood Estimation Uncertainties in Nigeria. Environ. Nat. Resour. Res. 2018, 8, 44. [Google Scholar] [CrossRef]
- Malekinezhad, H.; Nachtnebel, H.P.; Klik, A. Regionalization approach for extreme flood analysis using L-moments. J. Agric. Sci. Technol. 2011, 13, 1183–1196. [Google Scholar]
- Komi, K.; Amisigo, B.; Diekkrüger, B.; Hountondji, F. Regional Flood Frequency Analysis in the Volta River Basin, West Africa. Hydrology 2016, 3, 5. [Google Scholar] [CrossRef]
- Ahn, J.; Cho, W.; Kim, T.; Shin, H.; Heo, J.H. Flood frequency analysis for the annual peak flows simulated by an event-based rainfall-runoff model in an urban drainage basin. Water 2014, 6, 3841–3863. [Google Scholar] [CrossRef]
- Abida, H.; Ellouze, M. Probability distribution of flood flows in Tunisia. Hydrol. Earth Syst. Sci. 2008, 12, 703–714. [Google Scholar] [CrossRef]
- Zhang, Q.; Gu, X.; Singh, V.P.; Sun, P.; Chen, X.; Kong, D. Magnitude, frequency and timing of floods in the Tarim River basin, China: Changes, causes and implications. Glob. Planet. Chang. 2017, 139, 44–55. [Google Scholar] [CrossRef]
- Ibeje, A.O.; Ekwueme, B.N. Regional Flood Frequency Analysis using Dimensionless Index Flood Method. Civ. Eng. J. 2020, 6, 2425–2436. [Google Scholar] [CrossRef]
- Seckin, N.; Haktanir, T.; Yurtal, R. Flood frequency analysis of Turkey using L-moments method. Hydrol. Process. 2011, 25, 3499–3505. [Google Scholar] [CrossRef]
- Hassan, B.G.H.; Ping, F. Regional Rainfall Frequency Analysis for the Luanhe Basin—By Using L-moments and Cluster Techniques. APCBEE Procedia 2012, 1, 126–135. [Google Scholar] [CrossRef]
- Gebregiorgis, A.S.; Moges, S.A.; Awulachew, S.B. Basin Regionalization for the Purpose of Water Resource Development in a Limited Data Situation: Case of Blue Nile River Basin, Ethiopia. J. Hydrol. Eng. 2013, 18, 1349–1359. [Google Scholar] [CrossRef]
- Wiltshire, S.E. Grouping basins for regional flood frequency analysis. Hydrol. Sci. J. 1985, 30, 151–159. [Google Scholar] [CrossRef][Green Version]
- Ahn, K.-H.; Palmer, R. Regional Flood Frequency Analysis Using Spatial Proximity and Basin Characteristics. J. Hydrol. 2016, 540, 329–338. [Google Scholar] [CrossRef]
- Bogdanowicz, E.; Kochanek, K.; Strupczewski, W.G. The weighted function method: A handy tool for flood frequency analysis or just a curiosity? J. Hydrol. 2018, 559, 209–221. [Google Scholar] [CrossRef]
- Cassalho, F.; Beskow, S.; Vargas, M.M.; de Moura, M.M.; Ávila, L.F.; de Mello, C.R. Hydrological regionalization of maximum stream flows using an approach based on L-moments. RBRH 2017, 22, 2318–2331. [Google Scholar] [CrossRef]
- Wu, Y.; Lall, U.; Lima, C.H.R.; Zhong, P. Local and regional flood frequency analysis based on hierarchical Bayesian model: Application to annual maximum streamflow for the Huaihe River basin. Hydrol. Earth Syst. Sci. Discuss. 2018, 12, 253–262. [Google Scholar] [CrossRef]
- Odry, J.; Arnaud, P. Comparison of Flood Frequency Analysis Methods for Ungauged Catchments in France. Geosciences 2017, 7, 88. [Google Scholar] [CrossRef]
- Cassalho, F.; Beskow, S.; de Mello, C.R.; de Moura, M.M.; Kerstner, L.; Ávila, L.F. At-Site Flood Frequency Analysis Coupled with Multiparameter Probability Distributions. Water Resour. Manag. 2018, 32, 285–300. [Google Scholar] [CrossRef]
- Burn, D.H. Evaluation of Regional Flood Frequency Analysis with a Region of Influence Approach Evaluation of Regional Flood Frequency Analysis with a Region of Influence Approach. Water Resour. Res. 1990, 26, 2257–2265. [Google Scholar] [CrossRef]
- Hussain, Z.; Pasha, G.R. Regional flood frequency analysis of the seven sites of Punjab, Pakistan, using L-moments. Water Resour. Manag. 2009, 23, 1917–1933. [Google Scholar] [CrossRef]
- Kyselý, J.; Picek, J. Regional growth curves and improved design value estimates of extreme precipitation events in the Czech Republic. Clim. Res. 2007, 33, 243–255. [Google Scholar] [CrossRef]
- Nobert, J.; Mugo, M.; Gadain, H. Estimation of design floods in ungauged catchments using a regional index flood method. A case study of Lake Victoria Basin in Kenya. Phys. Chem. Earth 2014, 67–69, 4–11. [Google Scholar] [CrossRef]
- Noto, L.V.; La Loggia, G. Use of L-Moments Approach for Regional Flood Frequency Analysis in Sicily, Italy. Water Resour. Manag. 2009, 23, 2207–2229. [Google Scholar] [CrossRef]
- Parida, B.P.; Kachroo, R.K.; Shrestha, D.B. Regional Flood Frequency Analysis of Mahi-Sabarmati Basin (Subzone 3-a) using Index Flood Procedure with L-Moments. Water Resour. Manag. 1998, 12, 1–12. [Google Scholar] [CrossRef]
- Peel, M.C.; Vogel, R.M.; Mcmahon, T.A. The utility of L-moment ratio diagrams for selecting a regional probability distribution. Hydrol. Sci. Bull. 2001, 46, 147–155. [Google Scholar] [CrossRef]
- Yang, T.; Xu, C.; Shao, Q.; Chen, X. Regional flood frequency and spatial patterns analysis in the Pearl River Delta region using L-moments approach. Stoch. Environ. Res. Risk Assess. 2010, 24, 165–182. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Some Statistics Useful in Regional Frequency Analysis. Water Resour. Res. 1993, 29, 271–281. [Google Scholar] [CrossRef]
- Drissia, T.K.; Jothiprakash, V.; Anitha, A.B. Flood Frequency Analysis Using L Moments: A Comparison between At-Site and Regional Approach. Water Resour. Manag. 2019, 33, 1013–1037. [Google Scholar] [CrossRef]
- Kumar, R.; Goel, N.K.; Chatterjee, C.; Nayak, P.C. Regional Flood Frequency Analysis using Soft Computing Techniques. Water Resour. Manag. 2015, 29, 1965–1978. [Google Scholar] [CrossRef]
- Hussain, Z. Application of the Regional Flood Frequency Analysis to the Upper and Lower Basins of the Indus River, Pakistan. Water Resour. Manag. 2011, 25, 2797–2822. [Google Scholar] [CrossRef]
- Atiem, I.A.; Harmanciŏlu, N.B. Assessment of Regional Floods Using L-Moments Approach: The Case of The River Nile. Water Resour. Manag. 2006, 20, 723–747. [Google Scholar] [CrossRef]
- Seckin, N.; Yurtal, R.; Haktanir, T. Regional flood frequency analysis for gauged and ungauged cathments of seyhan river basin in Turkey. J. Eng. Res. 2014, 2, 48–71. [Google Scholar]
- Eregno, F.E. Regional Flood Frequency Analysis Using L-Moment in the Tributaries of Upper Blue Nile River, South Western. Merit Res. J. 2014, 2, 12–21. [Google Scholar]
- Kar, K.K.; Yang, S.-K.; Lee, J.-H.; Khadim, F.K. Regional frequency analysis for consecutive hour rainfall using L-moments approach in Jeju Island, Korea. Geoenviron. Disasters 2017, 4, 18. [Google Scholar] [CrossRef]
- Castellarin, A.; Burn, D.H.; Brath, A. Homogeneity testing: How homogeneous do heterogeneous cross-correlated regions seem? J. Hydrol. 2008, 360, 67–76. [Google Scholar] [CrossRef]
- Zhang, Z.; Stadnyk, T.A. Investigation of Attributes for Identifying Homogeneous Flood Regions for Regional Flood Frequency Analysis in Canada. Water 2020, 12, 2570. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Y.; Ren, J. The Coupling Effect of Flood Discharge and Storm Surge on Extreme Flood Stages: A Case Study in the Pearl River Delta, South China. Int. J. Disaster Risk Sci. 2021, 12, 495–509. [Google Scholar] [CrossRef]
- Arnaud, P.; Cantet, P.; Odry, J. Uncertainties of flood frequency estimation approaches based on continuous simulation using data resampling. J. Hydrol. 2017, 554, 360–369. [Google Scholar] [CrossRef]
- Saf, B. Regional Flood Frequency Analysis Using L-Moments for the West Mediterranean Region of Turkey. Water Resour. Manag. 2009, 23, 531–551. [Google Scholar] [CrossRef]
- Khan, B.; Iqbal, M.J.; Yosufzai, M.A.K. Flood risk assessment of river Indus of Pakistan. Arab. J. Geosci. 2011, 4, 115–122. [Google Scholar] [CrossRef]
- Gebrehiwot, S.G.; Ilstedt, U.; Gärdenas, A.I.; Bishop, K. Hydrological characterization of watersheds in the Blue Nile Basin, Ethiopia. Hydrol. Earth Syst. Sci. 2011, 15, 11–20. [Google Scholar] [CrossRef]
- Hailegeorgis, T.T.; Abdella, Y.S.; Alfredsen, K.; Kolberg, S. Evaluation of Regionalization Methods for Hourly Continuous Streamflow Simulation Using Distributed Models in Boreal Catchments. J. Hydrol. Eng. 2015, 20, 04015028. [Google Scholar] [CrossRef]
- Zhou, R.D.; Donnelly, R.C.; Judge, D.G. On the relationship between the 10,000 year flood and probable maximum flood. In Proceedings of the HydroVision International Conference, Denver, CO, USA, 12–14 July 2008; pp. 1–16. [Google Scholar]
- Rao, A.R.; Srinivas, V.V. Regionalization of Watersheds: An Approach Based on Cluster Analysis; Springer: Dordrecht, The Netherlands, 2008; ISBN 9781402068515. [Google Scholar]
- Sine, A.; Ayalew, S. Identification and Delineation of Hydrological Homogeneous Regions—The Case of Blue Nile River Basin. In Proceedings of the Lake Abaya Research Symposium 2004; Volume 4, pp. 59–72. Available online: https://www.uni-siegen.de/zew/publikationen/fwu_water_resources/volume0405/preface.pdf (accessed on 19 December 2021).
- Abida, H.; Ellouze, M. Hydrological Delineation of Homogeneous Regions in Tunisia. Water Resour. Manag. 2006, 20, 961–962. [Google Scholar] [CrossRef]
- Kachroo, R.K.; Mkhandi, S.H.; Parida, B.P. Flood frequency analysis of southern Africa: I. Delineation of homogeneous regions. Hydrol. Sci. J. 2000, 45, 437–447. [Google Scholar] [CrossRef]
- Rao, A.R.; Hamed, K.H. Flood Frequency Analysis; CRC Press: Washington, DC, USA, 2000. [Google Scholar]
- Silva, A.T.; Naghettini, M.; Portela, M.M. On some aspects of peaks-over-threshold modeling of floods under nonstationarity using climate covariates. Stoch. Environ. Res. Risk Assess. 2014, 28, 1587–1599. [Google Scholar] [CrossRef]
- Lim, Y.H. Regional Flood Frequency Analysis of the Red River Basin Using L-moments Approach. In Proceedings of the World Environmental and Water Resources Congress 2007; American Society of Civil Engineers: Reston, VA, USA, 2007; Volume 1, pp. 1–10. [Google Scholar]
- Halbert, K.; Nguyen, C.C.; Payrastre, O.; Gaume, E. Reducing uncertainty in flood frequency analyses: A comparison of local and regional approaches involving information on extreme historical floods. J. Hydrol. 2016, 541 Pt A, 90–98. [Google Scholar] [CrossRef]
- Kjeldsen, T.R.; Smithers, J.C.; Schulze, R.E. Flood frequency analysis at ungauged sites in the KwaZulu-Natal province, South Africa. Water SA 2001, 27, 315–324. [Google Scholar] [CrossRef]
- Lin, G.; Chen, L. Identification of homogeneous regions for regional frequency analysis using the self-organizing map. J. Hydrol. 2006, 324, 1–9. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.; Xiong, F. An Entropy-Based Generalized Gamma Distribution for Flood Frequency Analysis. Entropy 2017, 19, 239. [Google Scholar] [CrossRef]
- Smith, A.; Sampson, C.; Bates, P. Regional flood frequency analysis at the global scale. Water Resour. Res. 2015, 51, 539–553. [Google Scholar] [CrossRef]
- Samantaray, S.; Sahoo, A. Estimation of flood frequency using statistical method: Mahanadi River basin, India. H2Open J. 2020, 3, 189–207. [Google Scholar] [CrossRef]
- Lima, C.H.R.; Lall, U.; Troy, T.; Devineni, N. A hierarchical Bayesian GEV model for improving local and regional flood quantile estimates. J. Hydrol. 2016, 541 Pt B, 816–823. [Google Scholar] [CrossRef]
- England, J.F.; Jarrett, R.D.; Salas, J.D. Data-based comparisons of moments estimators using historical and paleoflood data. J. Hydrol. 2003, 278, 172–196. [Google Scholar] [CrossRef]
- Chen, Y.D.; Huang, G.; Shao, Q.; Xu, C.-Y. Regional analysis of low flow using L-moments for Dongjiang basin, South China. Hydrol. Sci. J. 2006, 51, 1051–1064. [Google Scholar] [CrossRef]
- Rahman, A.S.; Rahman, A.; Zaman, M.A.; Haddad, K.; Ahsan, A.; Imteaz, M. A study on selection of probability distributions for at-site flood frequency analysis in Australia. Nat. Hazards 2013, 69, 1803–1813. [Google Scholar] [CrossRef]
- Coast, G.; Rahman, A.; Haddad, K.; Kuczera, G. Features of Regional Flood Frequency Estimation (RFFE) Model in Australian Rainfall and Runoff. In Proceedings of the 21st International Congress on Modelling and Simulation, Gold Coast, Australia, 29 November–4 December 2015; pp. 2207–2213. [Google Scholar]
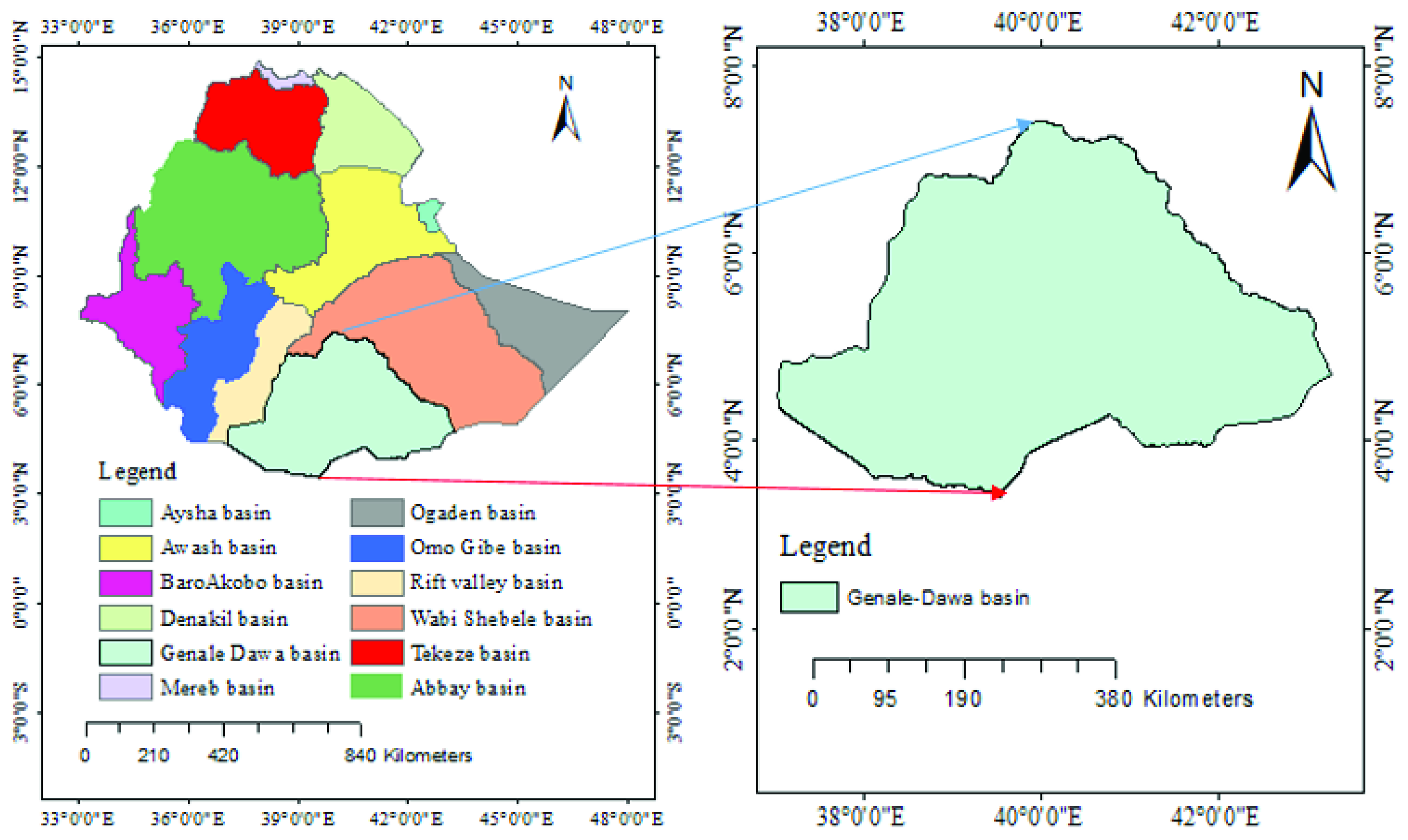




| River | Location | Coordinate | Area (Km2) | Record Period | Time | |
|---|---|---|---|---|---|---|
| Latitude | Longitude | (Years) | ||||
| Dawa | Melka Guba | 4°52′ | 39°19′ | 19,611 | 1986–2015 | 30 |
| Dawa | Near Digatty | 4°17′ | 39°20′ | 12,710 | 1997–2015 | 19 |
| Awatta | Near Odo Shakiso | 5°54′ | 38°56′ | 1611 | 1997–2014 | 18 |
| Genale | Chinamasa | 5°31′ | 39°41′ | 10,574 | 1985–2008 | 24 |
| Genale | Halwey | 4°26′ | 41°50′ | 54,093 | 1985–2009 | 25 |
| Genale | Kolle Bridge | 4°32′ | 41°45′ | 83,219 | 1998–2008 | 13 |
| Halgol | Near Gom-Goma | 6°20′ | 39°50′ | 160 | 1990–2008 | 19 |
| Mormora | Near Megado | 5°41′ | 38°48′ | 1375 | 1985–2015 | 31 |
| Shaya | Near Robe | 7°10′ | 39°58′ | 433.8 | 1985–2014 | 30 |
| Togona | Shallo Village | 7°0′ | 39°58′ | 336.2 | 1985–2008 | 24 |
| Weyib | Near Agarfa | 7°12′ | 39°48′ | 7719 | 1985–2008 | 24 |
| Weyib | Alemkerem | 6°59′ | 40°58′ | 3576.9 | 1990–2009 | 20 |
| Weyib | Near Denbel | 7°2′ | 40°48′ | 1215 | 1986–2008 | 23 |
| Weyib | Sofumer | 6°54′ | 40°50′ | 3792.7 | 1990–2010 | 21 |
| Welmel | Melka Amana | 6°14′ | 39°46′ | 1048 | 1990–2009 | 20 |
| Yadot | Near Dello Mena | 6°25′ | 39°51′ | 531 | 1990–2008 | 19 |
| Group Name | Station Name | Best Fit Distribution |
|---|---|---|
| Region-A | Chinamasa | GEV |
| Kolle Bridge | GEV | |
| Halwey | GEV | |
| Melka Amana | GEV | |
| Gom-Goma | GEV | |
| Dello Mena | GEV | |
| Region-B | Melka Guba | LPIII |
| Megado | LPIII | |
| Digatty | LPIII | |
| Odo Shakiso | LPIII | |
| Region-C | Robe | GPA |
| Agarfa | GPA | |
| Shallo Village | GPA | |
| Alemkerem | GPA | |
| Denbel | GPA | |
| Sofumer | GPA |
| Name of Station | LCv | LCs | LCk | Cv | Cs | Ck | Di |
|---|---|---|---|---|---|---|---|
| Region-A | |||||||
| Chinamasa | 0.1999 | 0.0467 | 0.1142 | 0.3767 | 0.7377 | 1.3105 | 1.0313 |
| Kolle Bridge | 0.1386 | 0.0221 | 0.1017 | 0.2409 | 0.2473 | −0.1652 | 1.1287 |
| Halwey | 0.2008 | 0.0893 | 0.0106 | 0.3457 | 0.3285 | −1.2458 | 1.3149 |
| Melka Amana | 0.2079 | −0.0830 | −0.0070 | 0.3559 | −0.2569 | −1.1165 | 0.856 |
| Gom-Goma | 0.2575 | 0.0757 | 0.0285 | 0.4281 | 0.2689 | −0.8923 | 0.9737 |
| Dello Mena | 0.2399 | −0.0462 | −0.0420 | 0.4025 | −0.1339 | −1.3512 | 0.6953 |
| CC | 0.1977 | 0.1814 | |||||
| Region-B | |||||||
| Melka Guba | 0.2205 | 0.0750 | 0.0376 | 0.3900 | 0.3613 | −0.5180 | 0.9999 |
| Megado | 0.2014 | 0.1444 | −0.0181 | 0.3537 | 0.4413 | −1.2430 | 0.9999 |
| Digatty | 0.1571 | 0.2078 | 0.2027 | 0.2891 | 0.9800 | 0.5214 | 0.9999 |
| Odo Shakiso | 0.1420 | 0.1718 | 0.2330 | 0.3117 | 0.2892 | −1.1837 | 0.9999 |
| CC | 0.2043 | 0.1332 | |||||
| Region-C | |||||||
| Robe | 0.1467 | 0.1152 | 0.1015 | 0.2864 | 0.3858 | −0.5594 | 1.3966 |
| Agarfa | 0.2463 | 0.0904 | −0.0704 | 0.4151 | 0.1876 | −1.4661 | 1.5528 |
| Shallo Village | 0.1440 | 0.0074 | 0.0706 | 0.2424 | −0.0296 | −0.9363 | 0.6659 |
| Alemkerem | 0.1202 | −0.2746 | 0.1009 | 0.2109 | −0.9492 | 0.1508 | 0.5846 |
| Denbel | 0.1458 | −0.0479 | −0.0317 | 0.2303 | −0.2159 | −1.0681 | 0.5881 |
| Sofumer | 0.1458 | −0.1523 | −0.0428 | 0.2521 | −0.4272 | −1.2117 | 1.2120 |
| CC | 0.2806 | 0.2714 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mengistu, T.D.; Feyissa, T.A.; Chung, I.-M.; Chang, S.W.; Yesuf, M.B.; Alemayehu, E. Regional Flood Frequency Analysis for Sustainable Water Resources Management of Genale–Dawa River Basin, Ethiopia. Water 2022, 14, 637. https://doi.org/10.3390/w14040637
Mengistu TD, Feyissa TA, Chung I-M, Chang SW, Yesuf MB, Alemayehu E. Regional Flood Frequency Analysis for Sustainable Water Resources Management of Genale–Dawa River Basin, Ethiopia. Water. 2022; 14(4):637. https://doi.org/10.3390/w14040637
Chicago/Turabian StyleMengistu, Tarekegn Dejen, Tolera Abdisa Feyissa, Il-Moon Chung, Sun Woo Chang, Mamuye Busier Yesuf, and Esayas Alemayehu. 2022. "Regional Flood Frequency Analysis for Sustainable Water Resources Management of Genale–Dawa River Basin, Ethiopia" Water 14, no. 4: 637. https://doi.org/10.3390/w14040637
APA StyleMengistu, T. D., Feyissa, T. A., Chung, I.-M., Chang, S. W., Yesuf, M. B., & Alemayehu, E. (2022). Regional Flood Frequency Analysis for Sustainable Water Resources Management of Genale–Dawa River Basin, Ethiopia. Water, 14(4), 637. https://doi.org/10.3390/w14040637









