Experimental Study of Forces Influencing Vertical Breakwater under Extreme Waves
Abstract
:1. Introduction
2. Experimental Setup
3. Numerical Simulation
4. Results and Discussion
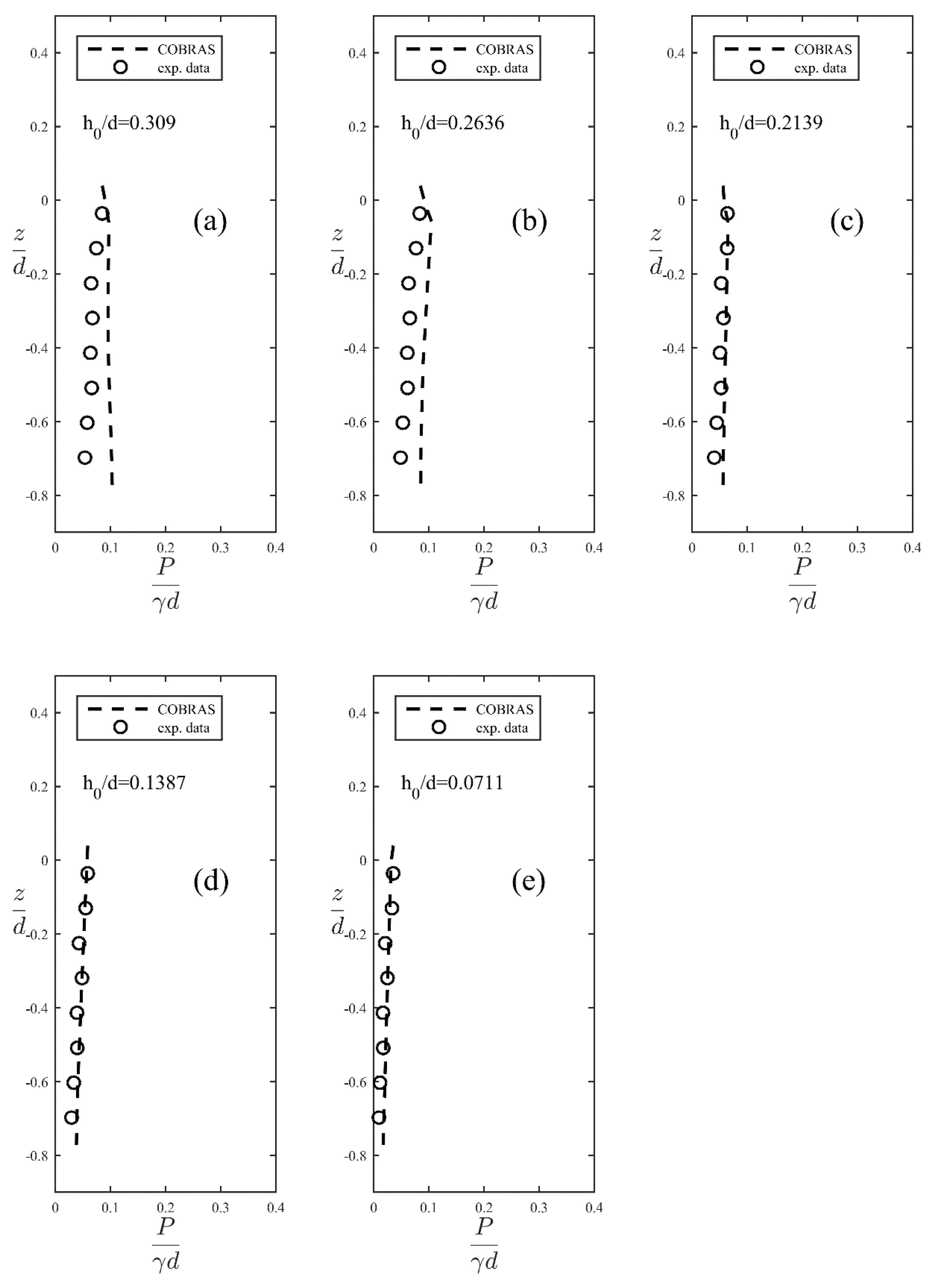
4.1. Dynamic Wave Pressure
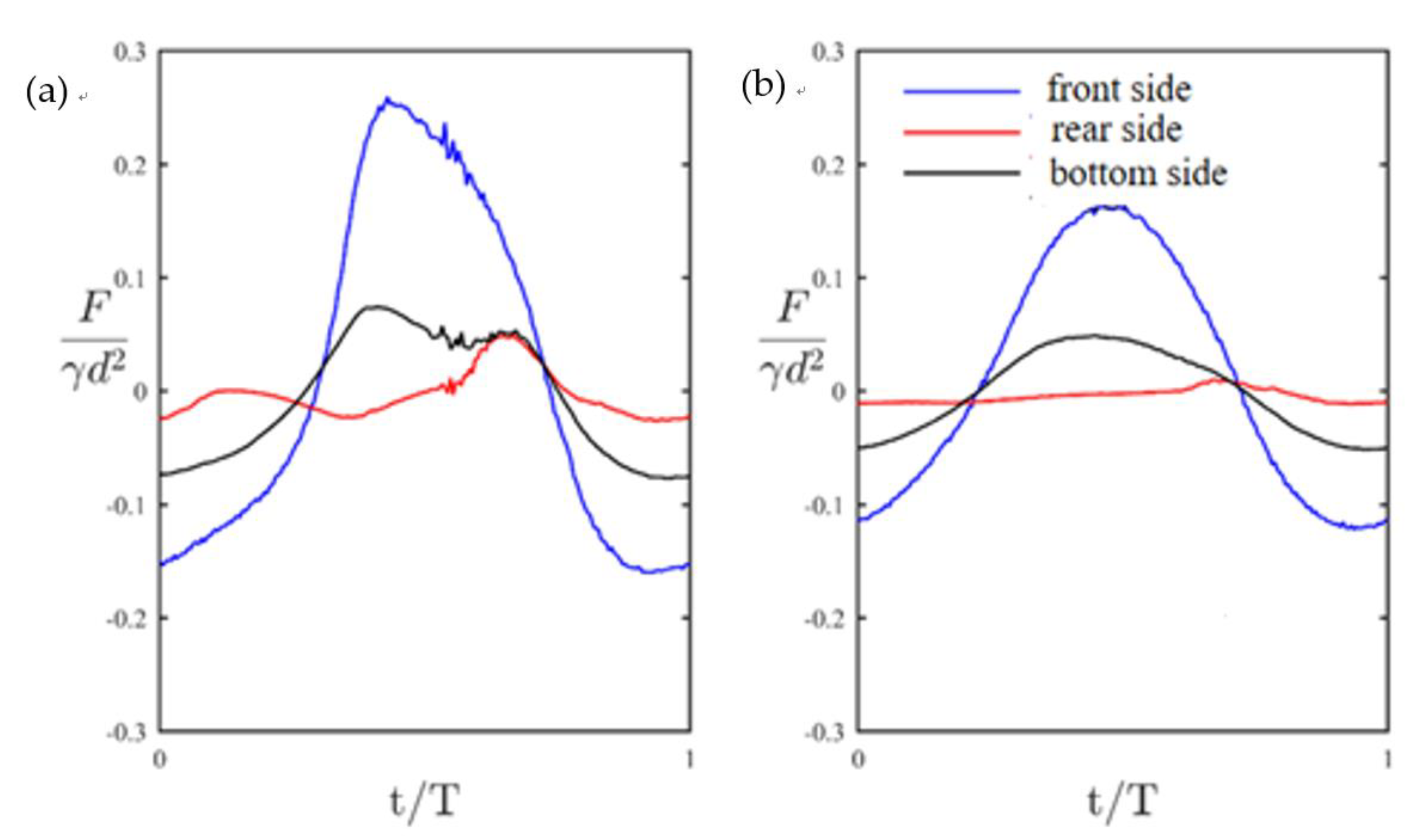
4.2. The Variation of Wave Force
4.3. Simplified Equations for Calculating Horizontal Forces and Uplifting Force
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Allsop, N.; McKenna, J.; Vicinanza, D.; Wittaker, T. New Design Methods for Wave Impact Loading on Vertical Breakwaters and Seawalls. Coast. Eng. Proc. 1996, 1. [Google Scholar] [CrossRef]
- Bullock, G.; Obhrai, C.; Peregrine, D.; Bredmose, H. Violent breaking wave impacts. Part 1: Results from large-scale regular wave tests on vertical and sloping walls. Coast. Eng. 2007, 54, 602–617. [Google Scholar] [CrossRef]
- Cuomo, G.; Allsop, W.; Bruce, T.; Pearson, J. Breaking wave loads at vertical seawalls and breakwaters. Coast. Eng. 2010, 57, 424–439. [Google Scholar] [CrossRef] [Green Version]
- Oumeraci, H.; Kortenhaus, A.; Allsop, N.W.H.; De Groot, M.B.; Crouch, R.S.; Vrijling, J.K.; Voortman, H.G. Probabilistic Design Tools for Vertical Breakwater; Balkema: Rotterdam, The Netherland, 2001. [Google Scholar]
- Jensen, O.J. A Monograph on Rubble Mound Breakwaters; Danish Hydraulic Institute: Horsrolm, Denmark, 1984. [Google Scholar]
- Pedersen, J.; Burcharth, H.F. Wave Forces on Crown Walls. In Coastal Engineering 1992; Edge, B.L., Ed.; ASCE: New York, NY, USA, 1992; pp. 1489–1502. [Google Scholar]
- Takahashi, S.; Tanimoto, K.; Miyanaga, S. Uplift Wave Forces Due to Compression of Enclosed Air Layer and Their Similitude Law. Coast. Eng. Jpn. 1985, 28, 191–206. [Google Scholar] [CrossRef]
- Takahashi, S.; Tanimoto, K.; Simosako, K. A proposal of impulsive pressure coefficient for the design of composite breakwaters. In Proceedings of the International Conference Hydro-Technical Engineering for Port and Harbor Construction (Hydro-Port 94), Yokosuka, Japan, 19–21 October 1994; pp. 489–504. [Google Scholar]
- Martin, F.L.; Losada, M.A.; Medina, R. Wave loads on rubble mound breakwater crown walls. Coast. Eng. 1999, 37, 149–174. [Google Scholar] [CrossRef]
- Tabet-Aoul, E.H.; Ambert, E. Tentative new formula for maximum horizontal wave forces acting on perforated caisson. J. Waterw. Port Coast. Ocean. Eng. 2003, 129, 34–40. [Google Scholar] [CrossRef]
- Arnason, H.; Petroff, C.; Yeh, H. Tsunami Bore Impingement onto a Vertical Column. J. Disaster Res. 2009, 4, 391–403. [Google Scholar] [CrossRef]
- Robertson, I.; Paczkowski, K.; Riggs, H.R.; Mohamed, A. Tsunami bore forces on walls. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; pp. 395–403. [Google Scholar]
- Attary, N.; Van De Lindt, J.W.; Unnikrishnan, V.U.; Barbosa, A.R.; Cox, D.T. Methodology for Development of Physics-Based Tsunami Fragilities. J. Struct. Eng. 2017, 143, 04016223. [Google Scholar] [CrossRef]
- Petrone, C.; Rossetto, T.; Goda, K. Fragility assessment of a RC structure under tsunami actions via nonlinear static and dynamic analyses. Eng. Struct. 2017, 136, 36–53. [Google Scholar] [CrossRef] [Green Version]
- Alam, M.S.; Winter, A.O.; Galant, G.; Shekhar, K.; Barbosa, A.R.; Motley, M.R.; Eberhard, M.O.; Cox, D.T.; Arduino, P.; Lomonaco, P. Tsunami-Like Wave-Induced Lateral and Uplift Pressures and Forces on an Elevated Coastal Structure. J. Waterw. Port Coastal Ocean Eng. 2020, 146, 04020008. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H. On particle-based simulation of a dam break over a wet bed. J. Hydraul. Res. 2010, 48, 238–249. [Google Scholar] [CrossRef]
- Yim, S.C.; Wei, Y.; Azadbakht, M.; Nimmala, S.; Potisuk, T. Case Study for Tsunami Design of Coastal Infrastructure: Spencer Creek Bridge, Oregon. J. Bridg. Eng. 2015, 20, 05014008. [Google Scholar] [CrossRef]
- Yeh, H.; Barbosa, A.; Ko, H.; Cawley, J.G. Tsunami Loadings on Structures: Review and Analysis. Coast. Eng. Proc. 2014, 1, 4. [Google Scholar] [CrossRef] [Green Version]
- Kato, T.; Terada, Y.; Ito, K.; Hattori, R.; Abe, T.; Miyake, T.; Koshimura, S.; Nagai, T. Tsunami due to the 2004 September 5th off the Kii peninsula earthquake, Japan, recorded by a new GPS buoy. Earth Planets Space 2005, 57, 297–301. [Google Scholar] [CrossRef] [Green Version]
- Hsiao, S.-C.; Lin, T.-C. Tsunami-like solitary waves impinging and overtopping an impermeable seawall: Experiment and RANS modeling. Coast. Eng. 2010, 57, 1–18. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P.L.-F. A numerical study of breaking waves in the surf zone. J. Fluid Mech. 1998, 359, 239–264. [Google Scholar] [CrossRef]
- Lin, P.Z.; Liu, P.L.F. Turbulence transport, vorticity dynamics, and solute mixing under plunging breaking waves in surf zone. J. Geophys. Res. 1998, 103, 15677–15694. [Google Scholar] [CrossRef]
- Losada, I.J.; Lara, J.L.; Guanche, R.; Gonzalez-Ondina, J.M. Numerical analysis of wave overtopping of rubble mound breakwaters. Coast. Eng. 2008, 55, 47–62. [Google Scholar] [CrossRef]
- Shakibaeinia, A.; Jin, Y.-C. A mesh-free particle model for simulation of mobile-bed dam break. Adv. Water Resour. 2011, 34, 794–807. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Teng, B. Numerical and simplified methods for the calculation of the total horizontal wave force on a perforated caisson with a top cover. Coast. Eng. 2007, 54, 67–75. [Google Scholar] [CrossRef]
- Goda, Y. Random Seas and Maritime Structures; World Scientific Publishing Company: Tokyo, Japan, 1985. [Google Scholar]
- Oumeraci, H.; Kortenhaus, A. Analysis of the dynamic response of caisson breakwaters. Coast. Eng. 1994, 22, 159–183. [Google Scholar] [CrossRef]
- Van der Meer, J.W.; Allsop, N.; Bruce, T.; De Rouck, J.; Kortenhaus, A.; Pullen, T.; Schüttrumpf, H.; Troch, P.; Zanuttigh, B. EurOtop: Manual on Wave Overtopping of Sea Defences and Related Sturctures: An Overtopping Manual Largely Based on European Research, but for Worlwide Application, 2nd ed. 2018. Available online: www.overtopping-manual.com (accessed on 19 January 2022).
- Ting, F.C.; Kirby, J.T. Observation of undertow and turbulence in a laboratory surf zone. Coast. Eng. 1994, 24, 51–80. [Google Scholar] [CrossRef]
- Shih, T.-H.; Zhu, J.; Lumley, J.L. Calculation of Wall-Bounded Complex Flows and Free Shear Flows. Int. J. Numer. Methods Fluids 1996, 23, 1133–1144. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P.L.-F. Internal wave-maker for Navier–Stokes equations models. J. Waterw. Port Coast. Ocean. Eng. 1999, 125, 207–217. [Google Scholar] [CrossRef]
- Tsai, C.P.; Lee, T.L.; Yeh, P.O. Forces on breakwaters by standing waves with water overtopping. Int. J. Offshore Polar Eng. 1999, 3, 182–187. [Google Scholar]

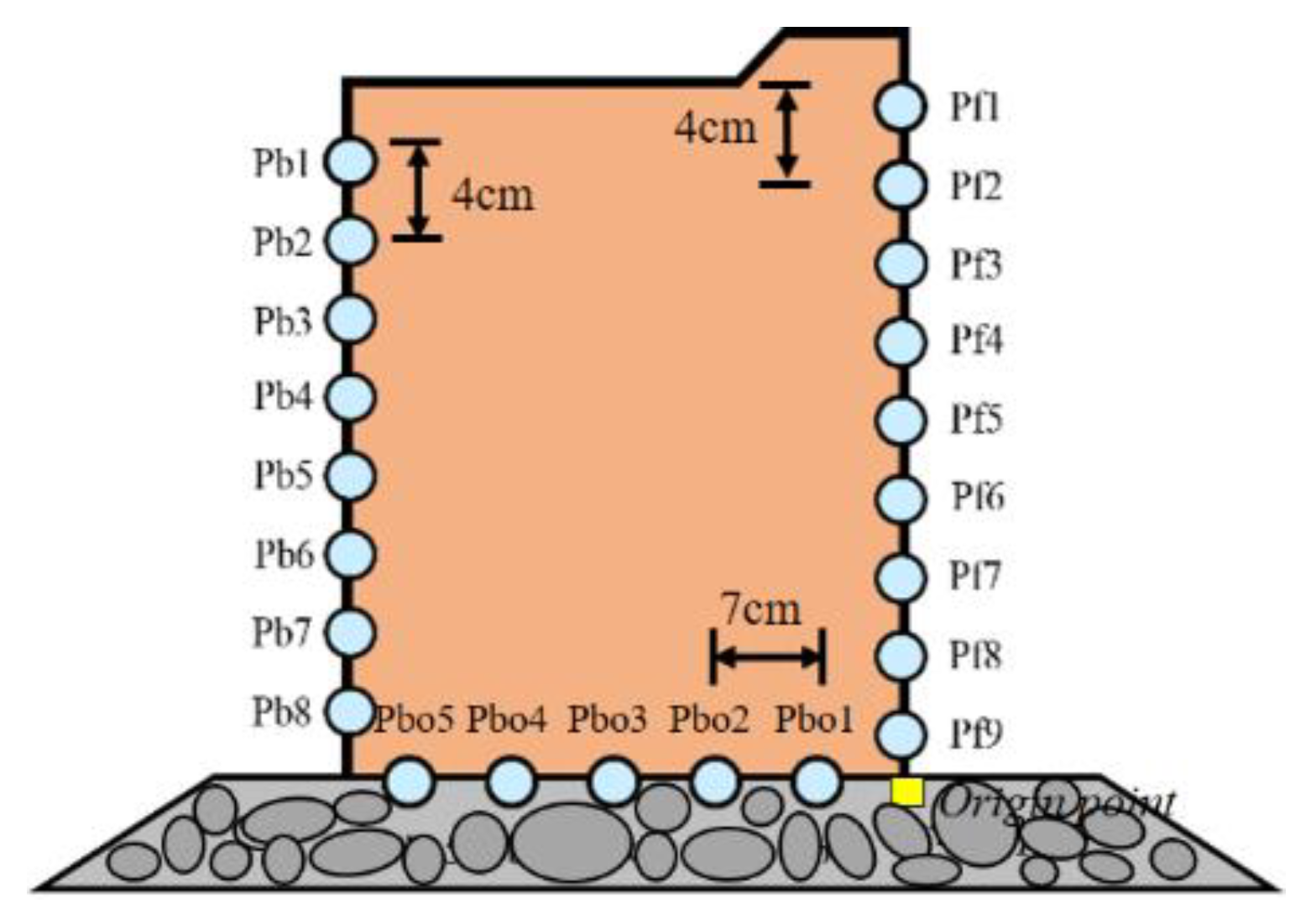
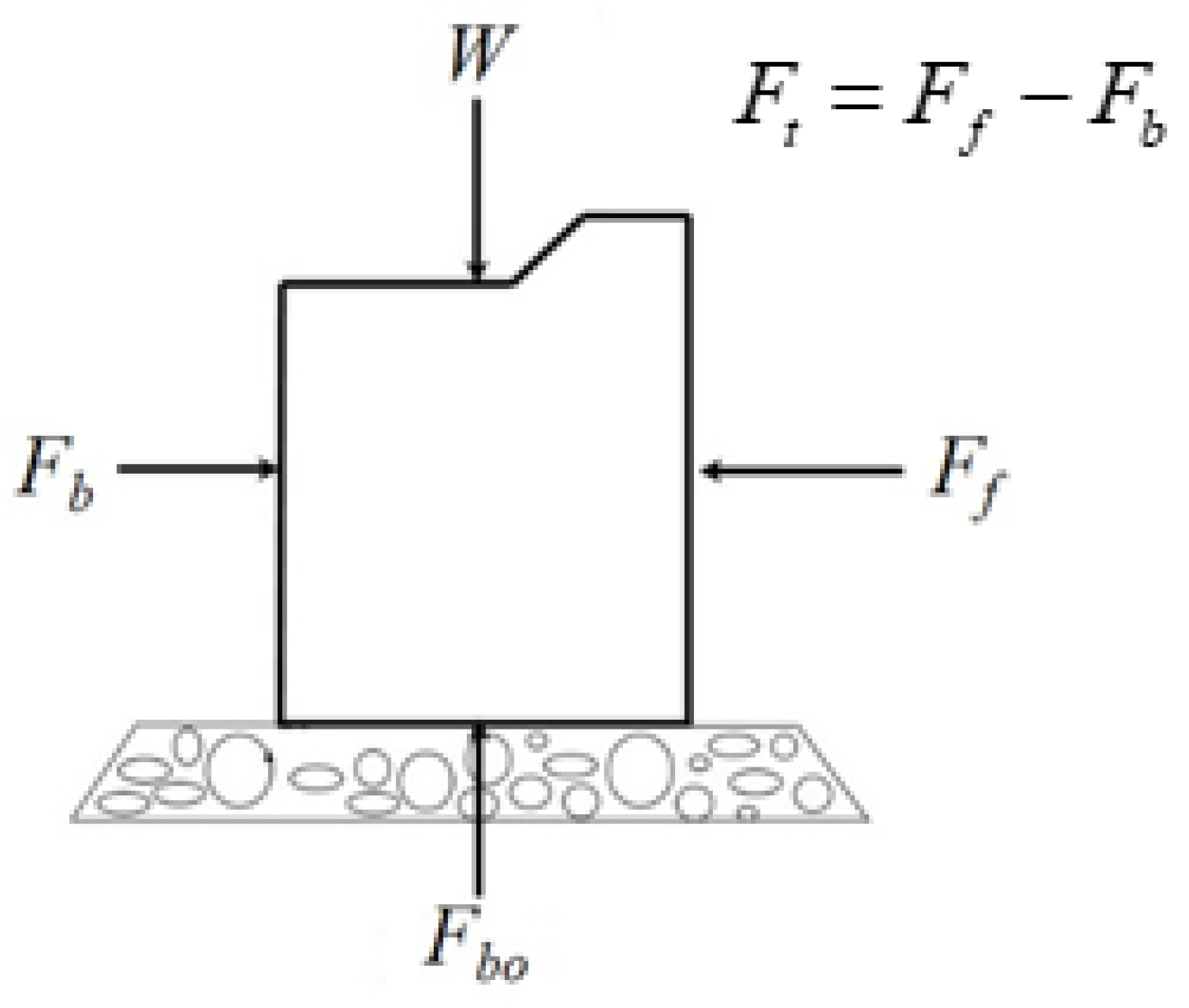
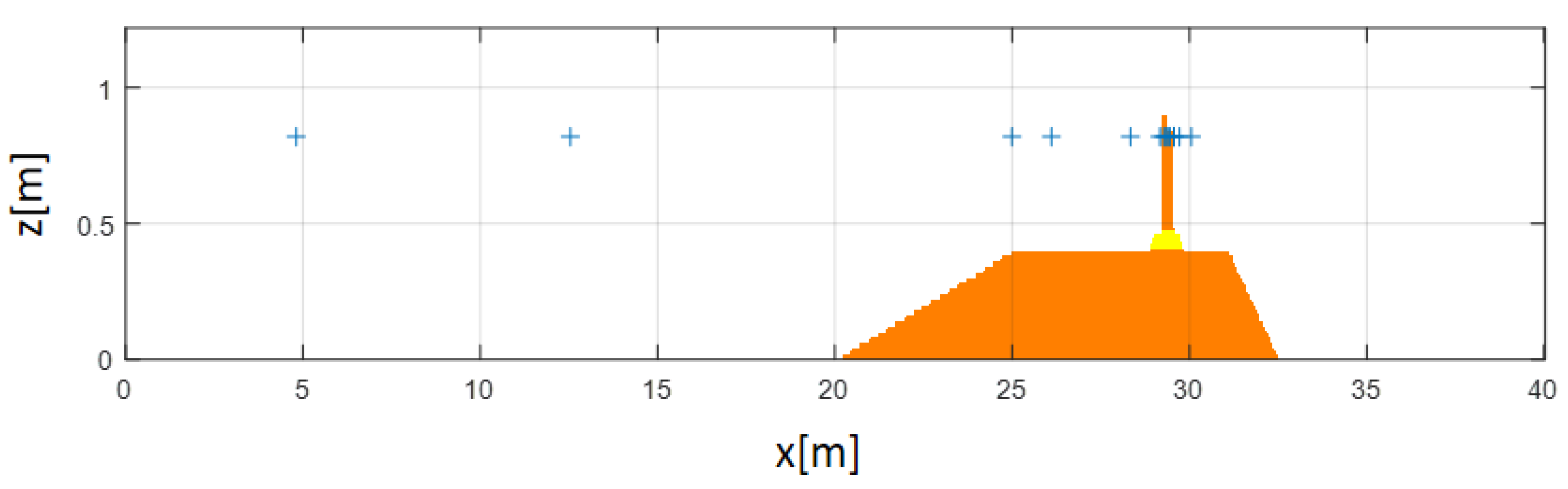
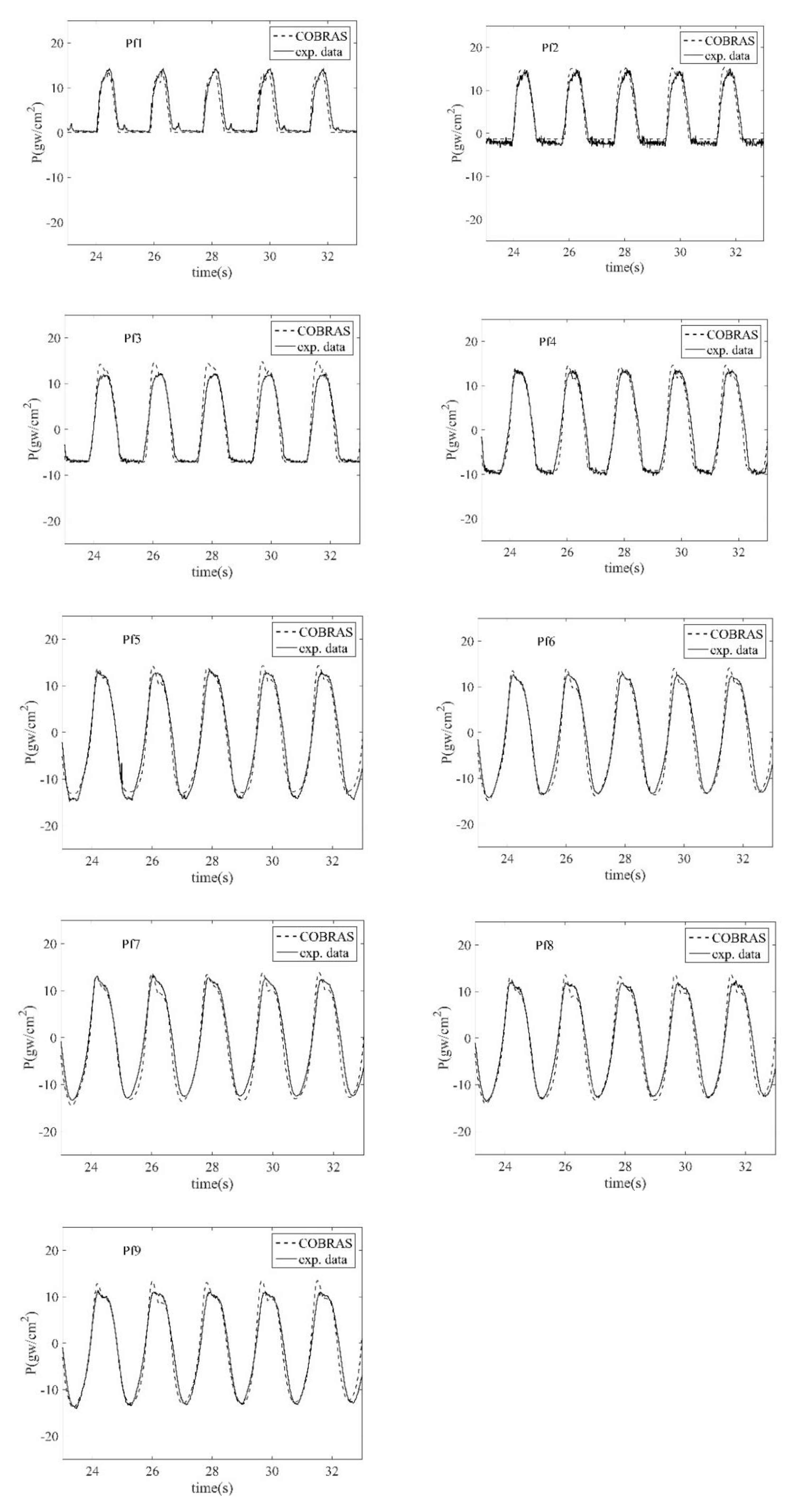
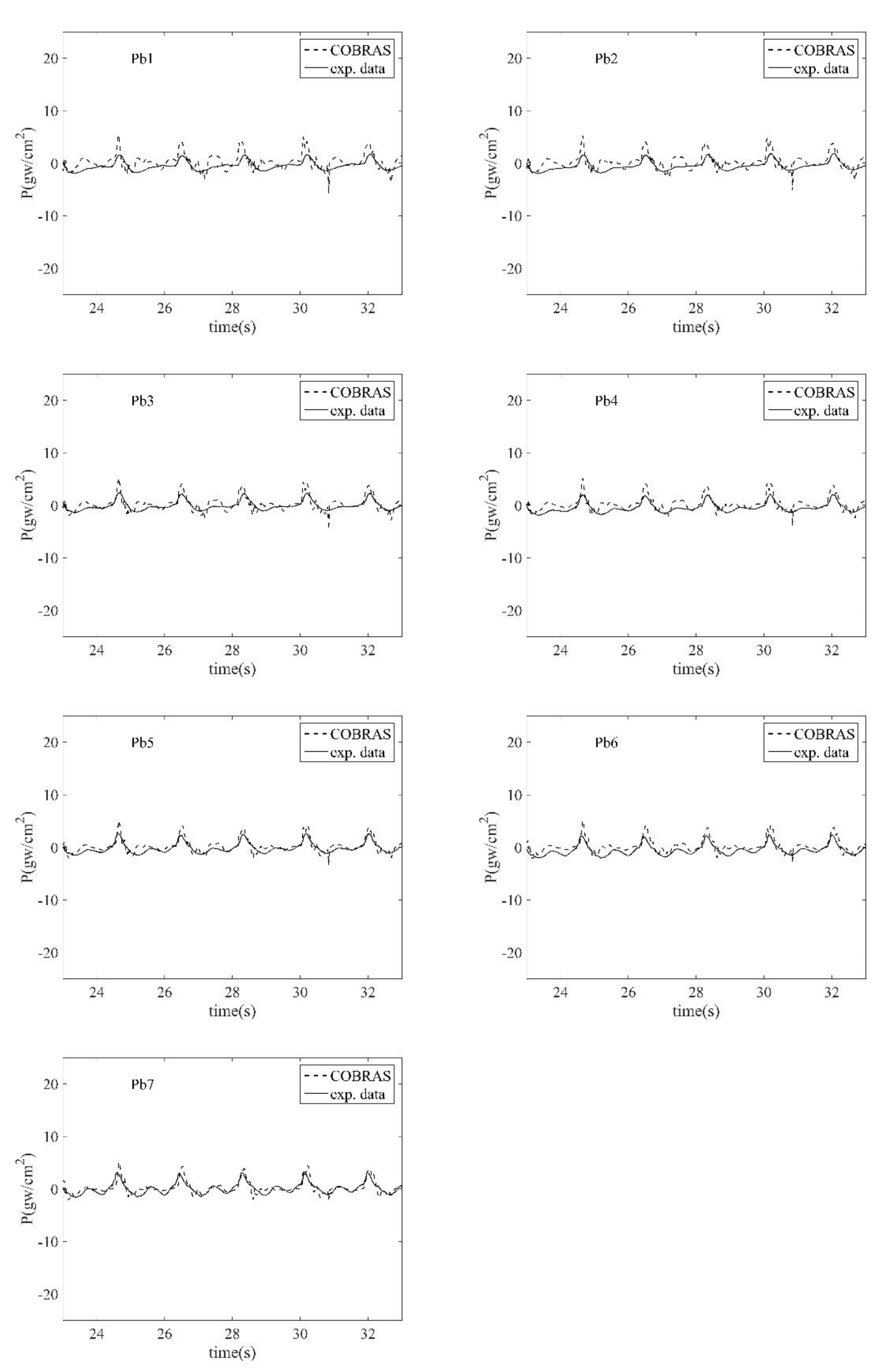

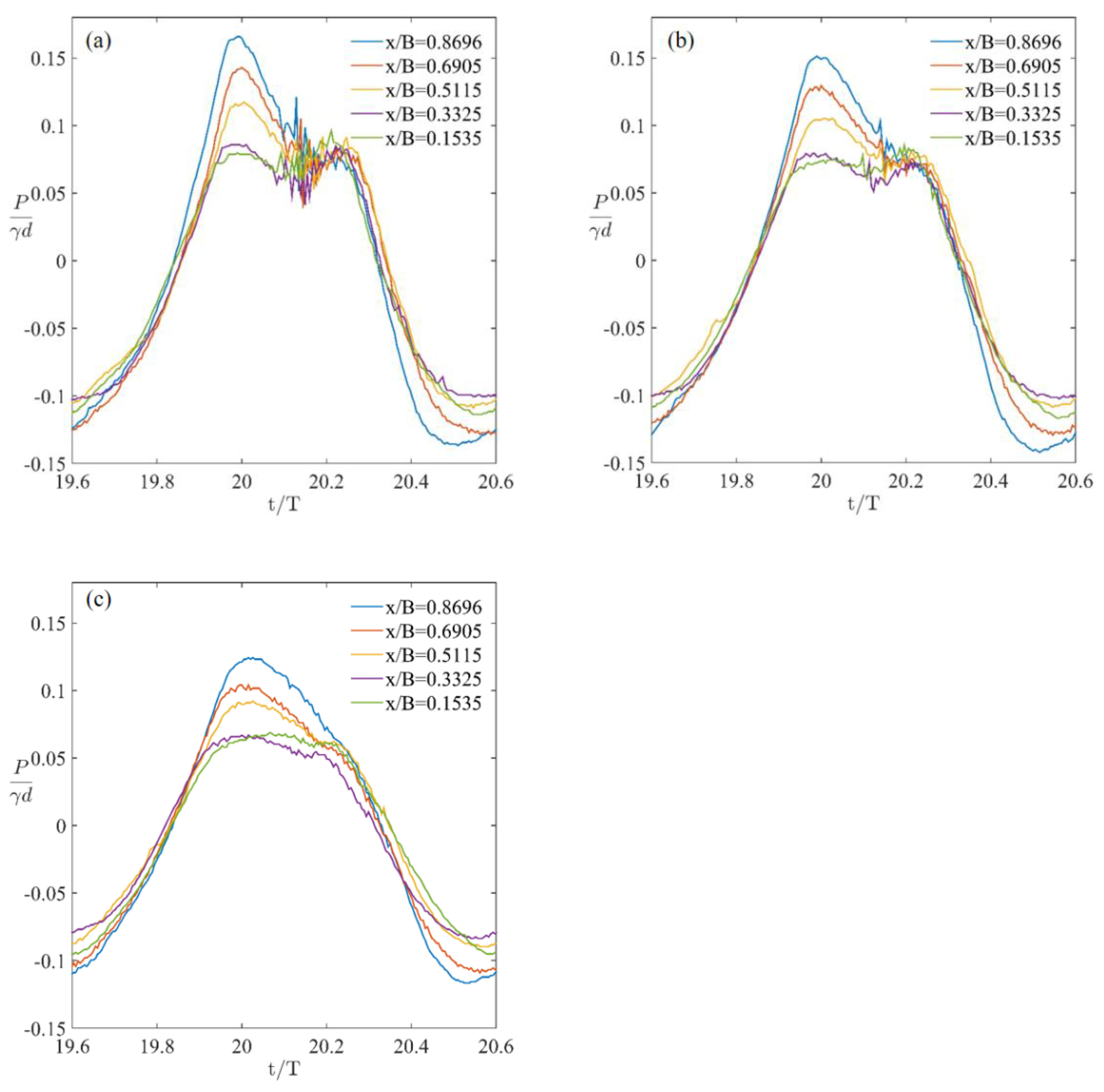
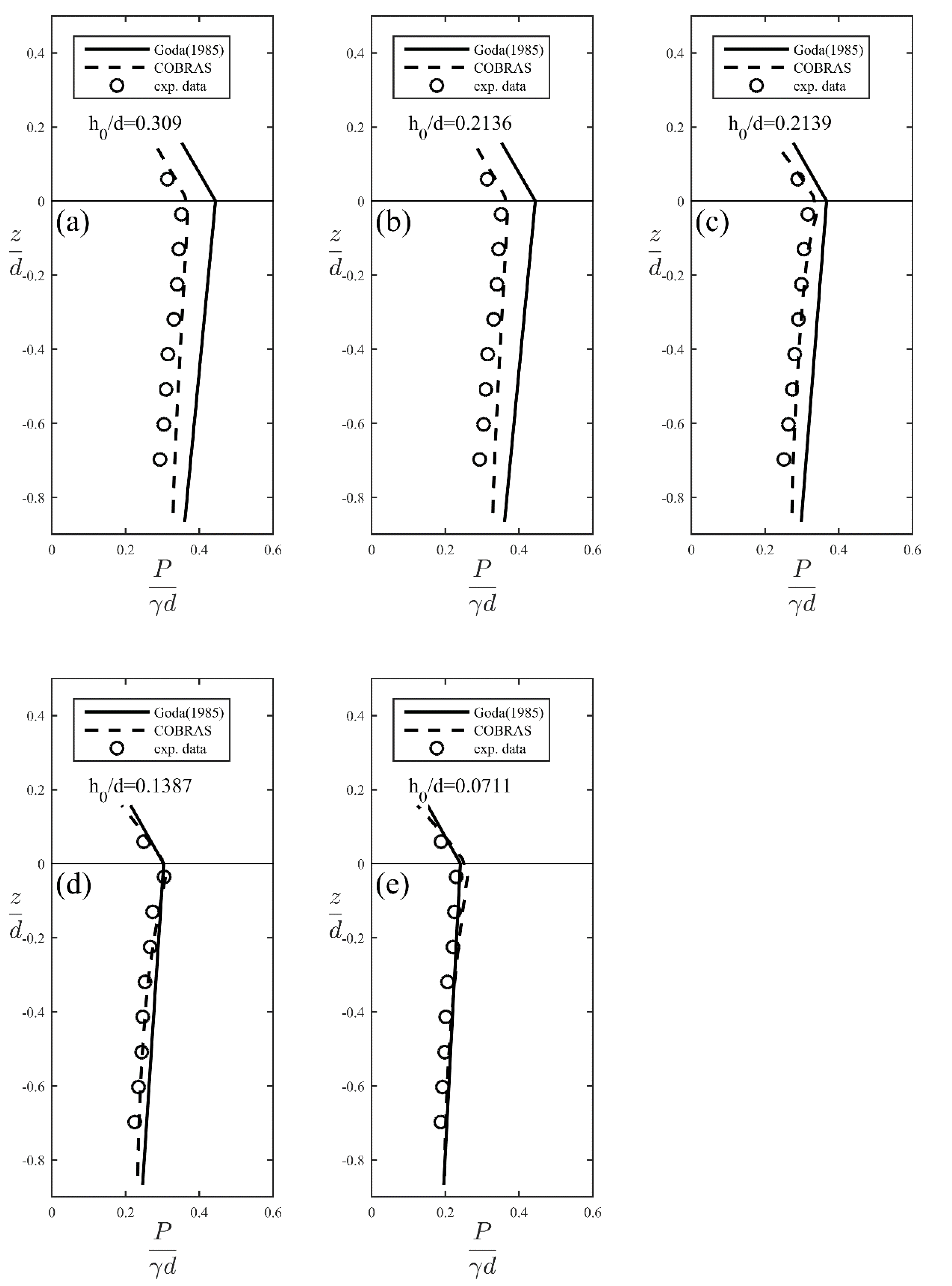
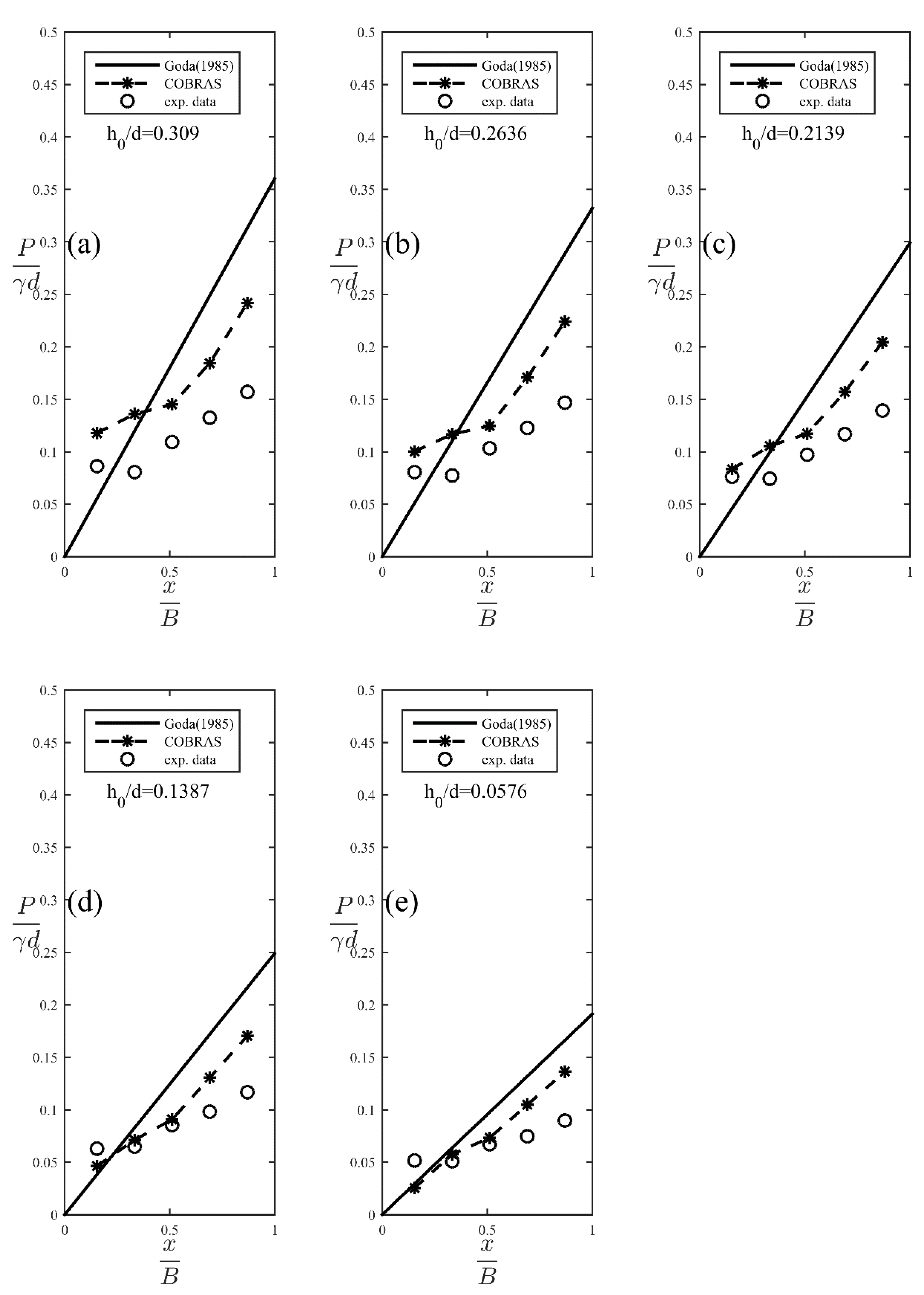


| Case No. | Wave Height (cm) | Mean Wave Height (cm) | CV | Wave Period (s) | Mean Wave Period (s) | CV | Water Depth (cm) |
|---|---|---|---|---|---|---|---|
| 1 | 22.45 | 22.54 | 1.08% | 1.94 | 1.94 | 0.21% | 82.3 |
| 22.35 | 1.94 | ||||||
| 22.81 | 1.93 | ||||||
| 2 | 21.34 | 21.17 | 0.86% | 1.94 | 1.94 | 0.32% | |
| 21.19 | 1.94 | ||||||
| 20.98 | 1.93 | ||||||
| 3 | 18.80 | 18.69 | 0.76% | 1.94 | 1.94 | 0.21% | |
| 18.53 | 1.94 | ||||||
| 18.74 | 1.94 | ||||||
| 4 | 15.29 | 15.43 | 1.47% | 1.94 | 1.94 | 0.10% | |
| 15.30 | 1.94 | ||||||
| 15.69 | 1.94 | ||||||
| 5 | 11.74 | 12.01 | 2.35% | 1.94 | 1.94 | 0.21% | |
| 11.98 | 1.94 | ||||||
| 12.30 | 1.93 | ||||||
| 6 | 22.29 | 22.41 | 1.54% | 1.85 | 1.84 | 0.29% | |
| 22.15 | 1.84 | ||||||
| 22.80 | 1.85 | ||||||
| 7 | 21.07 | 21.02 | 0.20% | 1.84 | 1.85 | 0.44% | |
| 21.00 | 1.85 | ||||||
| 21.00 | 1.85 | ||||||
| 8 | 18.43 | 18.38 | 0.96% | 1.84 | 1.85 | 0.53% | |
| 18.53 | 1.85 | ||||||
| 18.19 | 1.85 | ||||||
| 9 | 15.76 | 15.52 | 1.38% | 1.86 | 1.85 | 0.49% | |
| 15.43 | 1.84 | ||||||
| 15.36 | 1.85 | ||||||
| 10 | 12.27 | 12.37 | 2.08% | 1.86 | 1.85 | 0.25% | |
| 12.19 | 1.85 | ||||||
| 12.67 | 1.86 | ||||||
| 11 | 22.05 | 22.33 | 1.23% | 1.75 | 1.75 | 0.13% | |
| 22.60 | 1.75 | ||||||
| 22.35 | 1.75 | ||||||
| 12 | 21.02 | 20.87 | 0.62% | 1.75 | 1.76 | 0.54% | |
| 20.80 | 1.77 | ||||||
| 20.80 | 1.75 | ||||||
| 13 | 18.10 | 18.21 | 1.59% | 1.75 | 1.76 | 0.50% | |
| 18.53 | 1.77 | ||||||
| 17.98 | 1.76 | ||||||
| 14 | 15.44 | 15.50 | 0.77% | 1.76 | 1.76 | 0.17% | |
| 15.43 | 1.75 | ||||||
| 15.64 | 1.76 | ||||||
| 15 | 12.28 | 12.29 | 1.30% | 1.77 | 1.76 | 0.26% | |
| 12.14 | 1.76 | ||||||
| 12.46 | 1.76 |
| Pressure Gauges | Distance from the Origin Point (m) |
|---|---|
| Pf1 | 0.390 |
| Pf2 | 0.350 |
| Pf3 | 0.310 |
| Pf4 | 0.270 |
| Pf5 | 0.230 |
| Pf6 | 0.190 |
| Pf7 | 0.150 |
| Pf8 | 0.110 |
| Pf9 | 0.070 |
| Pbo1 | 0.041 |
| Pbo2 | 0.111 |
| Pbo3 | 0.181 |
| Pbo4 | 0.251 |
| Pbo5 | 0.321 |
| Pb1 | 0.335 |
| Pb2 | 0.295 |
| Pb3 | 0.255 |
| Pb4 | 0.215 |
| Pb5 | 0.175 |
| Pb6 | 0.135 |
| Pb7 | 0.095 |
| Pb8 | 0.055 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsu, H.-C.; Chen, Y.-Y.; Chen, Y.-R.; Li, M.-S. Experimental Study of Forces Influencing Vertical Breakwater under Extreme Waves. Water 2022, 14, 657. https://doi.org/10.3390/w14040657
Hsu H-C, Chen Y-Y, Chen Y-R, Li M-S. Experimental Study of Forces Influencing Vertical Breakwater under Extreme Waves. Water. 2022; 14(4):657. https://doi.org/10.3390/w14040657
Chicago/Turabian StyleHsu, Hung-Chu, Yang-Yih Chen, Yi-Ru Chen, and Meng-Syue Li. 2022. "Experimental Study of Forces Influencing Vertical Breakwater under Extreme Waves" Water 14, no. 4: 657. https://doi.org/10.3390/w14040657
APA StyleHsu, H. -C., Chen, Y. -Y., Chen, Y. -R., & Li, M. -S. (2022). Experimental Study of Forces Influencing Vertical Breakwater under Extreme Waves. Water, 14(4), 657. https://doi.org/10.3390/w14040657







