A Technical Note on the Application of a Water Budget Model at Regional Scale: A Water Manager’s Approach towards a Sustainable Water Resources Management
Abstract
:1. Introduction
2. Materials and Methods
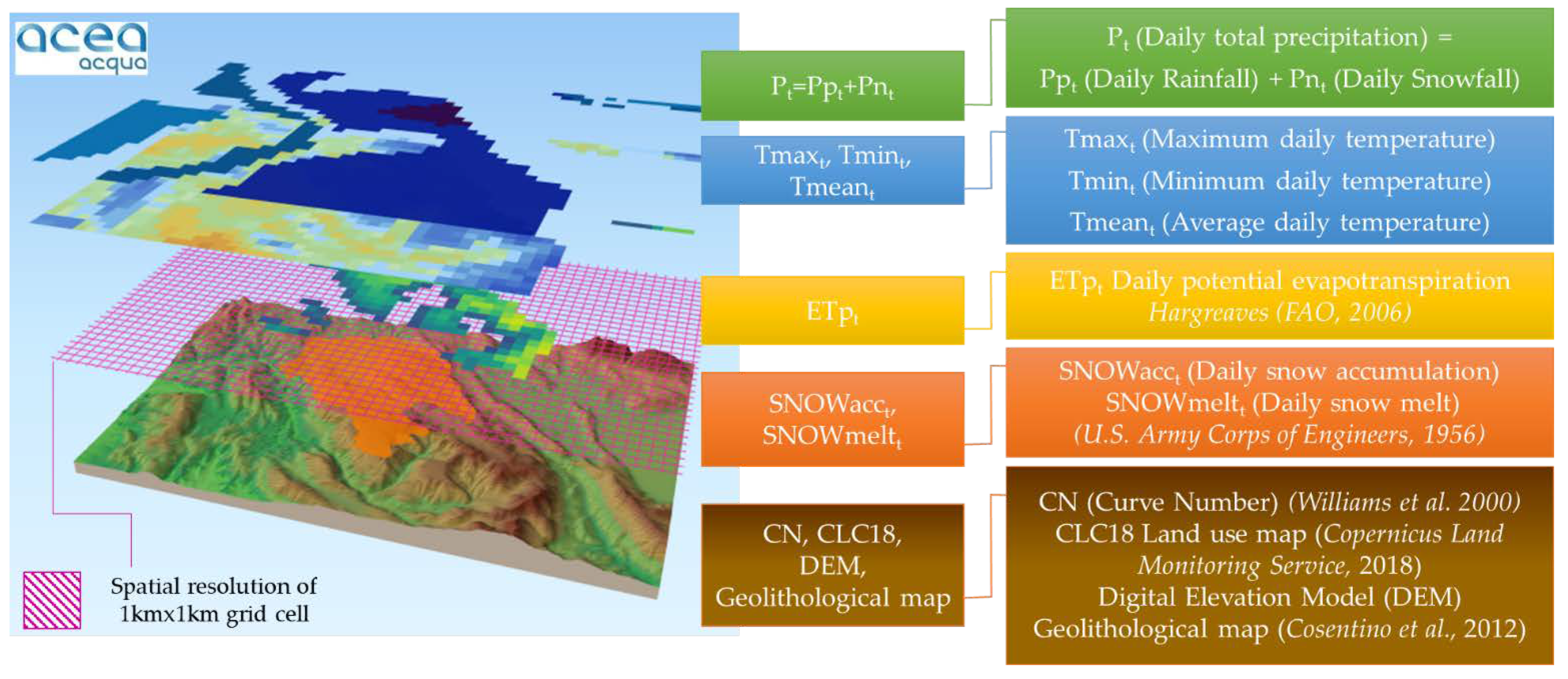
2.1. General Modelling Definitions
- IN represents the inflow of water (i.e., precipitation) into the control hydrological unit in a given ∆t;
- OUT represents the outflow (i.e., evapotranspiration, runoff, infiltration) from the control hydrological unit in a given ∆t;
- ΔS represents the change in storage within the hydrological control unit in a given ∆t (positive if the outflow is less than the inflow, and negative otherwise).
- Producing different water resource management scenarios in order to assess (ex ante) their potential impact on water use, demand, and availability;
- Learning (ex-post) from the effects of mitigation actions implemented in the past to counteract possible drought and water-scarcity events.
2.2. Framework of the Proposed Water Budget Model
- is the initial losses [mm], i.e., the fraction of precipitation intercepted by the vegetation, filling in the surface cavities, etc.; the surface runoff occurs only when the daily precipitation is greater than the intercepted fraction. is usually assumed to be 0.2;
- is the retention coefficient [mm]. is the function of several parameters representing the soil type and its saturation, land use, and slope.
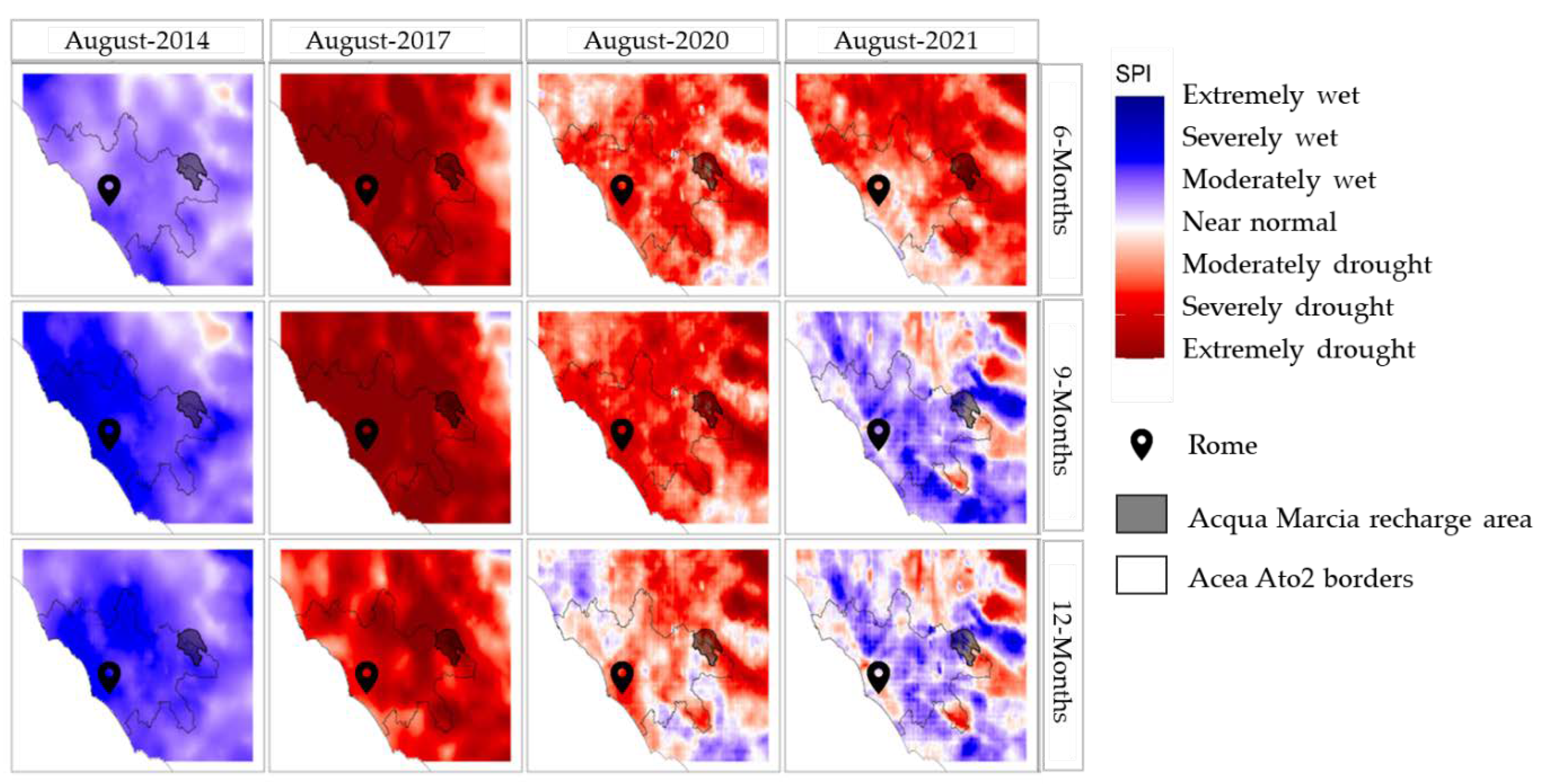
- 6 months, representing the precipitation between March and August (i.e., the cumulative precipitation of the spring–summer seasons);
- 9 months, representing the precipitation between December and August (i.e., the cumulative precipitation of the winter–spring–summer seasons);
- 12 months, corresponding to the cumulative precipitation during the entire hydrological year (September–August), therefore also finally including the autumn season’s precipitation.
2.3. Study Area
- (a)
- High springs, located at a water table level between 329 m and 326 m asl at the base of the hilly relief where the village of Agosta is settled;
- (b)
- Low springs, with a water table level between 324 m and 321 m asl, near the Marano Equo village;
- (c)
- Fiumetto plain springs, located between 322 and 321 m asl, within the Arsoli valley.
3. Application of the Methodology to the Case Study Acqua Marcia Springs
- Modest negative asymmetry in the distribution of the frequency values can be appreciated, and the mean value tends to be slightly lower than the 50th percentile;
- An appreciable range (slightly less than ±0.5) around the normalized mean value affected the frequency distribution. This implies that the infiltration rates representative of extremely dry (or wet) hydrological years can differ by up to approximately 50% from the long-term average condition;
- IN(A) values included in the lower tail of the frequency distribution are representative of the most-severe drought events of the last 30 years, which occurred in the second decade of the 2000s;
- IN(A) values included in the upper tail of the frequency distribution mainly occurred during the first decade of the 2000s;
- IN(A) values calculated for the last 20 years show a wide dispersion, including both the upper and the lower values of the whole sample.
- 2014, IN(A) > 75th percentile;
- 2017 and 2020, IN(A) < 25th percentile;
- 2021, 50th percentile < IN(A) < 75th percentile.
4. Discussion and Conclusions
- It is essential to implement studies with a long-term duration and a wide spatial perspective. In fact, in order to perform appropriate monitoring of water resources and in particular to intercept potential drought events in advance, it is necessary, on one hand, according to the traditional methodological approach, to determine the frequency, duration, and spatial domain over which the phenomena extend [44]; on the other hand, it must be considered that the climate processes tend to propagate through the hydrological cycle [22,24], gradually influencing the different components (i.e., precipitation, soil moisture, infiltration, groundwater recharge, and spring flows). In this regard, several authors ([23,45] among others) argue that the propagation of the drought signal reaches the groundwater components often slowly or not at all, but when this occurs, drought produces severe and long-lasting consequences.
- It is desirable that water managers, practitioners, and public authorities refer to the same robust and well-grounded methodologies, because relying on the same methodology allows readily monitoring and reliably quantifying the water resources’ status in an area.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- EU Commission. Guidance Document on the Application of Water Balances for Supporting the Implementation of the WFD. 2015. Available online: http://www.emwis.org/initiatives/pawa/background/guidance-document-application-water-balances-supporting-implementation-wfd (accessed on 3 October 2019).
- Borzì, I.; Bonaccorso, B.; Aronica, G.T. The Role of DEM Resolution and Evapotranspiration Assessment in Modeling Groundwater Resources Estimation: A Case Study in Sicily. Water 2020, 12, 2980. [Google Scholar] [CrossRef]
- Viaroli, S.; Mastrorillo, L.; Lotti, F.; Paolucci, V.; Mazza, R. The groundwater budget: A tool for preliminary estimation of the hydraulic connection between neighboring aquifers. J. Hydrol. 2018, 556, 72–86. [Google Scholar] [CrossRef]
- Preziosi, E.; Romano, E. Dall’analisi idrostrutturale allo studio modellistico di acquiferi regionali. Ital. J. Eng. Geol. Environ. 2009, 1, 183–198. [Google Scholar]
- Mineo, C.; Ridolfi, E.; Napolitano, F.; Russo, F. The areal reduction factor: A new analytical expression for the Lazio Region in central Italy. J. Hydrol. 2018, 560, 471–479. [Google Scholar] [CrossRef]
- Beven, K. Changing ideas in hydrology—The case of physically-based models. J. Hydrol. 1989, 105, 157–172. [Google Scholar] [CrossRef]
- Konikow, L.F.; Bredehoeft, J.D. Ground-water models cannot be validated. Adv. Water Resour. 1992, 15, 75–83. [Google Scholar] [CrossRef]
- Gondwe, B.R.; Merediz-Alonso, G.; Bauer-Gottwein, P. The influence of conceptual model uncertainty on management decisions for a groundwater-dependent ecosystem in karst. J. Hydrol. 2011, 400, 24–40. [Google Scholar] [CrossRef]
- Borzì, I.; Bonaccorso, B. Quantifying Groundwater Resources for Municipal Water Use in a Data-Scarce Region. Hydrology 2021, 8, 184. [Google Scholar] [CrossRef]
- Braca, G.; Bussettini, M.; Ducci, D.; Lastoria, B.; Mariani, S. Evaluation of national and regional groundwater resources under climate change scenarios using a GIS-based water budget procedure. Rend. Lincei. Sci. Fis. E Nat. 2019, 30, 109–123. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Seeking Parsimony in Hydrology and Water Resources Technology. In Proceedings of the European Geosciences Union General Assembly 2009, Vienna, Austria, 19–24 April 2009; Geophysical Research Abstracts: Vienna, Austria, 2009; Volume 11, p. 11469. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 4 February 2020).
- Slater, L.J.; Thirel, G.; Harrigan, S.; Delaigue, O.; Hurley, A.; Khouakhi, A.; Prosdocimi, I.; Vitolo, C.; Smith, K. Using R in hydrology: A review of recent developments and future directions. Hydrol. Earth Syst. Sci. 2019, 23, 2939–2963. [Google Scholar] [CrossRef] [Green Version]
- Van Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Vorobevskii, I.; Kronenberg, R.; Bernhofer, C. Global BROOK90 R package: An automatic framework to simulate the water balance at any location. Water 2020, 12, 2037. [Google Scholar] [CrossRef]
- Li, X.; Vernon, C.R.; Hejazi, M.I.; Link, R.P.; Feng, L.; Liu, Y.; Rauchenstein, L.T. Xanthos–a global hydrologic model. J. Open Res. Softw. 2017, 5, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Rossi, M.; Donnini, M. Estimation of regional scale effective infiltration using an open source hydrogeological balance model and free/open data. Environ. Model. Softw. 2018, 104, 153–170. [Google Scholar] [CrossRef]
- Zini, L.; Calligaris, C.; Treu, F.; Zavagno, E.; Iervolino, D.; Lippi, F. Groundwater sustainability in the Friuli Plain. Acqua Mundi 2013, 4, 41–54. [Google Scholar]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Chow, V.T. Handbook of Applied Hydrology; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Panagoulia, D.; Dimou, G. Sensitivities of groundwater-streamflow interaction to global climate change. Hydrol. Sci. J. 1996, 41, 781–796. [Google Scholar] [CrossRef] [Green Version]
- Mineo, C.; Passaretti, S.; Varriale, A. Drought risk analysis and spring discharge forecasting: A coupled method for an optimal fresh water management, ICNAAM 2020. In Proceedings of the 18th International Conference of Numerical Analysis and Applied Mathematics, Rhodes, Greece, 17–23 September 2020. [Google Scholar]
- Van Loon, A.F. Hydrological drought explained. Wiley Interdisciplinary Reviews. Water 2015, 2, 359–392. [Google Scholar]
- Changnon, S.A., Jr. Detecting Drought Conditions in Illinois; Circular 169; Illinois State Water Survey: Champaign, IL, USA, 1987. [Google Scholar]
- Mariani, S.; Braca, G.; Romano, E.; Lastoria, B.; Bussettini, M. Linee Guida Sugli Indicatori di Siccità e Scarsità Idrica da Utilizzare Nelle Attività Degli Osservatori Permanenti per gli Utilizzi idrici—Stato Attuale e Prospettive Future; Technical Report. 2018. Available online: http://www.isprambiente.gov.it/files2018/notizie/LineeGuidaPubblicazioneFinaleL6WP1_concopertina.pdf (accessed on 18 April 2019).
- Peres, D.J.; Modica, R.; Cancelliere, A. Assessing future impacts of climate change on water supply system performance: Application to the Pozzillo Reservoir in Sicily, Italy. Water 2019, 11, 2531. [Google Scholar] [CrossRef] [Green Version]
- Sappa, G.; De Filippi, F.M.; Iacurto, S.; Grelle, G. Evaluation of minimum karst spring discharge using a simple rainfall-input model: The case study of Capodacqua di Spigno Spring (Central Italy). Water 2019, 11, 807. [Google Scholar] [CrossRef] [Green Version]
- Mineo, C.; Passaretti, S.; Varriale, A.; Cosentino, C. A grid based model for a continuous time evaluation of water balance: A water manager’s perspective on the estimation of the status of water resources, IDRA2020. In Proceedings of the XXXVII Convegno Nazionale di Idraulica e Costruzioni Idrauliche, Reggio Calabria, Italy, 14–16 June 2021. [Google Scholar]
- Williams, J.R.; Arnold, J.G.; Srinivasan, R. The APEX Model; BRC Report No. 00–06; Blackland Research and Extension Center, Texas Agricultural Experiment Station; Texas A & M University System: Temple, TX, USA, 2000. [Google Scholar]
- U.S. Army Corps of Engineers. Snow Hydrology; North Pacific Division: Portland, OR, USA, 1956.
- Percopo, C.; Brandolin, D.; Canepa, M.; Capodaglio, P.; Cipriano, G.; Gafà, R.; Iervolino, D.; Marcaccio, M.; Mazzola, M.; Mottola, A.; et al. Criteri tecnici per l’analisi dello stato quantitativo e il monitoraggio dei corpi idrici sotterranei. ISPRA Man. E Linee Guid. 2017, 157, 1–108. [Google Scholar]
- Food and Agricolture Organization (FAO). Crop Evapotranspiration (guidelines for computing crop water requirements). FAO Irrig. Drain. 2006, 56, 1–300. [Google Scholar]
- USDA SCS (Soil Conservation Service). Section 4, Hydrology. In SCS National Engineering Handbook; USDA: Washington, DC, USA, 1972. [Google Scholar]
- Cover, C.L. Copernicus Land Monitoring Service. European Environment Agency (EEA); European Union. Available online: https://land.copernicus.eu/pan-european/corine-land-cover/clc2018 (accessed on 14 June 2018).
- Cosentino, D.; Pasquali, V. Carta Geologica Informatizzata Della Regione Lazio; Università degli Studi Roma Tre—Dipartimento di Scienze Geologiche, Regione Lazio—Agenzia Regionale Parchi—Area Difesa del Suolo: Roma, Italy, 2012. [Google Scholar]
- Williams, J.R.; Singh, V. The EPIC model. Computer models of watershed hydrology. Water Resour. Publ. Highl. Ranch Colo. 1995, 25, 909–1000. [Google Scholar]
- Mineo, C.; Moccia, B.; Lombardo, F.; Russo, F.; Napolitano, F. 2019 Preliminary analysis about the effects on the SPI values computed from different best-fit probability models in two Italian regions. In Proceedings of the International Conference on Urban Drainage Modelling, Palermo, Italy, 23–26 September 2018; Mannina, G., Ginebra, S., Eds.; Springer International Publishing: New York, NY, USA, 2019; pp. 958–962. [Google Scholar] [CrossRef]
- Romano, E.; Del Bon, A.; Petrangeli, A.B.; Preziosi, E. Generating synthetic time series of springs discharge in relation to standardized precipitation indices. Case study in Central Italy. J. Hydrol. 2013, 507, 86–99. [Google Scholar] [CrossRef]
- Fiorillo, F. Spring hydrographs as indicators of droughts in a karst environment. J. Hydrol. 2009, 373, 290–301. [Google Scholar] [CrossRef]
- Boni, C.F.; Bono, P.; Capelli, G. Schema idrogeologico dell’Italia centrale: Carta Idrogeologica dell’Italia centrale (Scala 1:500.000), Carta Idrologica dell’Italia centrale (Scala 1:500.000), Carta dei Bilanci Idrogeologici e delle Risorse Idriche sotterranee (Scala 1:000.000). Mem. Soc. Geol. Ital. 1986, 35, 991–1012. [Google Scholar]
- Braca, G.; Bussettini, M.; Lastoria, B.; Mariani, S.; Piva, F. Il Bilancio Idrologico Gis BAsed a scala Nazionale su Griglia regolare—BIGBANG: Metodologia e stime. Rapporto sulla disponibilità naturale della risorsa idrica. Rapp. ISPRA 2021, 339, 1–181. [Google Scholar]
- Scanlon, B.R.; Healy, R.W.; Cook, P.G. Choosing appropriate techniques for quantifying groundwater recharge. Hydrogeol. J. 2002, 10, 18–39. [Google Scholar] [CrossRef]
- Romano, N.; Palladino, M.; Chirico, G.B. Parameterization of a bucket model for soil-vegetation atmosphere modelling under seasonal climatic regimes. Hydrol. Earth Syst. Sci. 2011, 15, 3877–3893. [Google Scholar] [CrossRef] [Green Version]
- Romano, E.; Guyennon, N.; Duro, A.; Giordano, R.; Petrangeli, A.B.; Portoghese, I.; Salerno, F. A Stakeholder Oriented Modelling Framework for the Early Detection of Shortage in Water Supply Systems. Water 2018, 10, 762. [Google Scholar] [CrossRef] [Green Version]
- Stockinger, M.P.; Bogena, H.R.; Lücke, A.; Diekkrüger, B.; Cornelissen, T.; Vereecken, H. Tracer sampling frequency influences estimates of young water fraction and streamwater transit time distribution. J. Hydrol. 2016, 541, 952–964. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Passaretti, S.; Mineo, C.; Varriale, A.; Cosentino, C. A Technical Note on the Application of a Water Budget Model at Regional Scale: A Water Manager’s Approach towards a Sustainable Water Resources Management. Water 2022, 14, 712. https://doi.org/10.3390/w14050712
Passaretti S, Mineo C, Varriale A, Cosentino C. A Technical Note on the Application of a Water Budget Model at Regional Scale: A Water Manager’s Approach towards a Sustainable Water Resources Management. Water. 2022; 14(5):712. https://doi.org/10.3390/w14050712
Chicago/Turabian StylePassaretti, Stefania, Claudio Mineo, Anna Varriale, and Claudio Cosentino. 2022. "A Technical Note on the Application of a Water Budget Model at Regional Scale: A Water Manager’s Approach towards a Sustainable Water Resources Management" Water 14, no. 5: 712. https://doi.org/10.3390/w14050712
APA StylePassaretti, S., Mineo, C., Varriale, A., & Cosentino, C. (2022). A Technical Note on the Application of a Water Budget Model at Regional Scale: A Water Manager’s Approach towards a Sustainable Water Resources Management. Water, 14(5), 712. https://doi.org/10.3390/w14050712





