Next Article in Journal
Understanding the Combined Effects of Land Cover, Precipitation and Catchment Size on Nitrogen and Discharge—A Case Study of the Mississippi River Basin
Previous Article in Journal
A Novel Calculation Method of Hydrodynamic Pressure Based on Polyhedron SBFEM and Its Application in Nonlinear Cross-Scale CFRD-Reservoir Systems
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 14
Issue 6
10.3390/w14060866
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Spatio-Temporal Characteristics of Drought and Its Relationship with El Niño-Southern Oscillation in the Songhua River Basin from 1960 to 2019

by
Lv Ren
1,2,* and
Xiaohua Dong
1,*
1
College of Hydraulic & Environmental Engineering, China Three Gorges University, Yichang 443000, China
2
China Renewable Energy Engineering Institute, Beijing 100120, China
*
Authors to whom correspondence should be addressed.
Water 2022, 14(6), 866; https://doi.org/10.3390/w14060866
Submission received: 27 January 2022 / Revised: 2 March 2022 / Accepted: 9 March 2022 / Published: 10 March 2022
(This article belongs to the Section Hydrology)
Browse Figures
Versions Notes

Abstract

:
Drought is a severe natural hazard all over the world, resulting in enormous losses in many aspects, especially in agriculture. It is essential to analyze the spatio-temporal variation of drought and its relationships with the El Niño-Southern Oscillation under a background of global climate change for better drought prevention. The Songhua River Basin (SHRB), which is an important food base in northeastern China that suffered a severe drought in 2020, was chosen as the research site. The standardized precipitation evapotranspiration index (SPEI) was chosen as the drought index to analyze the spatio-temporal variation of droughts in the SHRB by linear regression analysis and T-test using the meteorological data from 1960 to 2019. The cross-wavelet analysis was adopted to reveal the relationship between the SPEI and El Niño-Southern Oscillation indexes (the Niño 1+2 SST Index (SST1), Niño 3 SST Index (SST2), Niño 3.4 SST Index (SST3), Niño 4 SST Index (SST4), and Southern Oscillation Index (SOI)). The results reveal that the changing trends of yearly, spring, summer, autumn, and winter precipitation were 0.56, 1.47 (p < 0.05), 0.13, 0.04, and 0.16 (p < 0.05) mm/a, respectively; the precipitations were higher in the southeastern regions and lower in the western regions, with extreme values of 831.62 mm and 381.69 mm, respectively. The SPEI was significantly increased (p < 0.05) with a gradient of 0.01/a on a yearly scale and were increased in all seasons (significant in winter (p < 0.05)). The drought probability on a yearly scale was dominated by summer and autumn. The SPEI was positively correlated with SST1, SST2, SST3, and SST4 in a different period with a different resonant period and was negatively correlated with the SOI with a short-term period for 3–4 years from 1986 to 1990 and a long-term period for 9–12 years from 1992 to 2010. These results could provide a scientific guide for drought prevention in the SHRB.

1. Introduction

Droughts are natural catastrophes that occur as a result of a long-term deficit of water [1,2]. They vary from floods and other natural disasters in that they normally develop slowly, which could affect local ecology, agriculture, and economic development [3,4,5]. In general, droughts can be separated into four categories by the formation stage of the drought: meteorological drought, hydrological drought, agricultural drought, and socioeconomic drought [6]. A long-term meteorological drought would result in a hydrological drought, a hydrological drought would result in a reduction of agricultural water consumption, lead to an agricultural drought, and finally result in the reduction in crop yields, further forming a socioeconomic drought [7,8,9].
In recent years, droughts have become a research hotspot all over the world, giving rise to many types of research about drought. The main tool to describe drought is the drought index, and the most used drought indexes are the standardized precipitation index (SPI) [10], the standardized precipitation evapotranspiration index (SPEI) [11], the Palmer drought index (PDSI) [12], and some other integrated indexes [13,14]. Compared to the SPI, the SPEI considers both the precipitation and potential evapotranspiration, which could describe drought by more characteristics. The SPEI has been widely used in previous studies. Tan et al. [15] used the SPEI to explore the drought variation in Ningxia province, China, and found that the annual SPEI decreased by 0.37/10a from 1972 to 2011. Bae et al. [16] calculated the SPEI for eight stations in South Korea and found that the SPEI increased significantly from 1981–1995 to 1996–2010. Jin et al. [17] used the SPEI as a tool to analyze the spatio-temporal variation of droughts in the Zoige Wetland, Southwest China, and found that the SPEI was decreased by 0.142/10a from 1961 to 2016. Many scholars investigated the variation of SPEI, and most of them obtained a decreased trend of SPEI, which indicated that the drought events mainly exhibited an increasing trend in most regions, which was also pronounced by Chen et al. [18]. It is important to evaluate the SPEI variation for better drought prevention, especially in agricultural regions.
Under the trend of global climate change, it is reported that a series of measures should be conducted to control the mean surface warming below 1.5 °C [19]. Under this condition, the occurrence and frequency of extreme rainfall events would be increased in the future [20]. However, drought is affected by many factors besides rainfall, and it is still unclear whether drought events would be more frequent and severe in the future [21]. Large-scale atmospheric circulation was the previous change index for climate change, and many climatic factors were affected by the large-scale atmospheric circulation [22,23,24]. Hence, many researchers investigate the relationships between these large-scale atmosphere circulations and drought. The El Niño-Southern Oscillation is one of the factors that most concerned previous researchers of drought. Mo and Schemm [25] used the meteorological data from 1915 to 2006 to reveal the relationship between the ENSO event and drought events, and the results showed that the cold ENSO events are more likely to initiate droughts. Wang and Kumar [26] assessed the relationship between precipitation, drought, and ENSO in the southwestern US, and the results revealed that the changes in ENSO could affect the characteristics of precipitation and further change the frequency and intensity of drought in these regions. Zhou et al. [27] evaluated the relationships between ENSO and droughts for 48 ecogeographical regions in China, and found that drought was strongly correlated with ENSO in most regions The correlation was highest in Jiangnan regions, and these correlations between agricultural drought and ENSO exist with a lag time. These previous studies all indicated that a correlation exists between ENSO and drought.
The Songhua River Basin (SHRB) is located in northeastern China, an important food production base of China. About 37% of the total area in the SHRB was agricultural land, and, as reported by the China Flood and Drought Disaster Prevention Bulletin [28], the agricultural land affected by drought within northeastern China was up to 4.3 × 104 km2 in 2020. Though the previous study carried out by Faiz et al. [29] has already analyzed the future SPEI changes under different emissions scenarios in the SHRB, it did not discuss the historical change trend in detail, nor discussed the correlation with ENSO. Under the background of global climate change, the change of drought in the SHRB is unclear. It is of significant importance to investigate the spatio-temporal variations of drought in the SHRB, for better agricultural drought prevention.
The aims of this study are: (1) analyze the spatio-temporal change trend of the precipitation in the SHRB on multiple time scales from 1960 to 2019; (2) analyze the temporal variation on multiple time scales from 1960 to 2019; (3) analyze the frequency changes of the drought events on multiple time scales from 1960 to 2019; (4) discuss the correlation between the SPEI and El Niño-Southern Oscillation indexes; (5) discuss the relationship between precipitation and SPEI; and (6) discuss the effect of drought on agriculture.

2. Study Area

The Songhua River Basin (SHRB) is located in northeastern China (Figure 1), with a range between 119°52″–132°31″ E and 41°42″–51°38″ N and an area of 5.55 × 105 km2. The elevation of the SHRB ranges from 5–2617 m, and the northwestern and southeastern SHRB are dominated by mountainous topography, while the plain is concentrated in the middle SHRB. The SHRB is located in the north temperate monsoon climate zone, the average annual temperature is 3–5 °C, which obviously varies within the year, the annual average precipitation is about 500 mm, and about 60–80% of the total annual precipitation is concentrated in the flood season (June–September). The spatio-temporal differences of precipitation and temperature in the SHRB are significant, which would result in the extreme climatic event.
The main land use within the SHRB is agricultural land and forest, with proportions of 37% and 39%, respectively, in 2015. The main crops within the SHRB are soybeans, corn, sorghum, and wheat. Its fertile soil makes it be an important crop base of China. During 2020, the agricultural land affected by drought within northeastern China measured up to 4.3 × 104 km2 [28]. With the prospect of significant climate change, the historical drought characteristic and its relationship with large-scale climatic indexes should be understood for better agriculture production and sustainability.

3. Data and Methods

3.1. Data

The daily weather data (including precipitation, temperature, solar radiation, sunshine duration, and wind speed) were obtained from the National Meteorological Science Data Center (https://data.cma.cn/, accessed on 4 March 2022), and the period for these data was 1960–2019. Weather data from 61 weather stations were used in this research, which were located within the SHRB or near the boundary of the SHRB. The distribution of these weather stations is shown in Figure 1. The El Niño-Southern Oscillation was represented by the Niño 1+2 SST Index (SST1), Niño 3 SST Index (SST2), Niño 3.4 SST Index (SST3), Niño 4 SST Index (SST4), and Southern Oscillation Index (SOI), which was released by the NOAA ESRL Physical Sciences Laboratory. The first four indexes are associated with El Niño, and the last one is associated with the Southern Oscillation. Series from 1960 to 2019 of these five indexes were obtained from the website (https://psl.noaa.gov/gcos_wgsp/, accessed on 4 March 2022) For a more detailed description of these indexes, refer to that website. The MEI index was obtained from https://psl.noaa.gov/enso/mei/ (accessed on 4 March 2022).

3.2. The Standardized Precipitation Evapotranspiration Index

The standardized precipitation evapotranspiration index (SPEI) is calculated using the precipitation and potential evapotranspiration (PET) [12]. Potential evapotranspiration (PET) is the amount of evaporation and transpiration that would occur if a sufficient water source were available. The calculation methods of the SPEI are as follows:
  • First, the PET was calculated using the Penman–Monteith model as shown below:
    E T 0 = 0.408 Δ ( R n − G ) + γ 900 T + 273 U 2 ( e s − e a ) Δ + γ ( 1 + 0.34 U 2 )
    where E T 0 is the reference crop evapotranspiration, mm / d ; R n is the net radiation on the canopy surface, MJ / ( m 2 · d ) ; G is the soil heat flux, MJ / ( m 2 · d ) ; T is the average temperature, °C; e s is the saturation vapor pressure, kPa ; e a is the actual vapor pressure, kPa ; Δ is the slope of the tangent line of the saturation vapor pressure—air temperature relationship curve at the temperature, kPa / °C; γ is the hygrometer constant, kPa / °C; and U 2 is the wind speed above the ground, m / s .
  • Then, the difference between the monthly precipitation and PET was calculated using the following equation:
    D i = P i − P E T i
    where D i is the difference between the precipitation and PET at the time i and P i and P E T i are the monthly precipitation and PET at the i time.
  • Next, the difference of the precipitation and evapotranspiration at different time scales was calculated using the equation mentioned below:
    D n k = ∑ i = 0 k − 1 ( P n − i − P E T n − i ) , n ≥ k
    where k is the time scale (1 month, 3 months, and 12 months) and n is the calculation frequency.
  • Next, the three-parameter log-logistic probability distribution was used to normalize the D series and to further calculate the SPEI. For each D value, the normalized value was calculated as follows:
    F ( x ) = [ 1 + ( α x − γ ) β ] − 1
    The parameters mentioned before were calculated with the following equations:
    α = ( ω 0 − 2 ω 1 ) β Γ ( 1 + 1 / β ) Γ ( 1 − 1 / β )
    β = 2 ω 1 − ω 0 6 ω 1 − ω 0 − 6 ω 2
    γ = ω 0 − α Γ ( 1 + 1 / β ) Γ ( 1 − 1 / β )
    where Γ is a factorial function and ω 0 ,   ω 1 ,   ω 2 is the probability-weighted moment of D data series:
    ω s = 1 N ∑ i = 1 N ( 1 − F i ) s D i
    F i = i − 0.35 N
    where N is the number of months in the calculation.
  • Finally, the cumulative probability density was standardized as follows:
    P = 1 − F ( x )
    When the cumulative probability P ≤ 0.5 :
    ω = − 2 ln ( P )
    SPEI = ω − c 0 + c 1 ω + c 2 ω 2 1 + d 1 ω + d 2 ω 2 + d 3 ω 3
    where the constants c 0 ,   c 1 ,   c 2 ,   d 1 ,   d 2 ,   d 3 were assigned the values of 2.515517, 0.802853, 0.010328, 1.432788, 0.189269, and 0.001308, respectively [30].
According to the previous studies [30,31], the standard of the ranges of the SPEI for each state of drought and wet is shown in Table 1.

3.3. Analysis Methods

In this study, the precipitation and SPEI were calculated on different time scales and interpolated within space by the inverse distance-weighted (IDW) method [32]. The trend analysis was performed on a basin scale. The linear regression analysis [33] was adopted to analyze the historical trend of precipitation and SPEI and the correlation between precipitation and SPEI in the SHRB, and the F-test [34] was adopted to test the significance of these trends and correlation. Besides, the modified Mann–Kendall test [35] was used to validate the trends of these variables, and the Z-value of the variable showed a significant trend (p < 0.05). The cross-wavelet analysis is widely used in identifying the historical correlation between different factors, especially the meteorological factors in hydrological fields [36,37,38]. In this study, it was adopted to analyze the relationships between the different El Niño-Southern Oscillation indexes and SPEI. A more detailed basic description of the cross-wavelet analysis can be referred in a previous study [39]. The cross-wavelet analysis in this paper was carried out in the Matlab 2019 software.

4. Results

4.1. Spatio-Temporal Distribution of Precipitation

Figure 2a and Figure 3a–d show the annual and seasonal precipitation variation in the SHRB. The average annual, spring, summer, autumn, and winter precipitation were 527 mm, 76 mm, 348 mm, 87 mm, and 14 mm, respectively. The average seasonal precipitation was ranked as summer > autumn > spring > winter, with about 66% of the total annual precipitation concentrated in summer. The changing trends of yearly, spring, summer, autumn, and winter precipitation were 0.56, 1.47 (p < 0.05), 0.13, 0.04, 0.16 (p < 0.05) mm/a, respectively, which indicates that the precipitation increased in these time scales. Their trend could also be validated by the results from Table 2. The Z-values of the spring and winter precipitation were 1.9 and 1.86, respectively, both significant at a confidence interval of 95% (Table 3) As shown in Table 4, the highest average monthly precipitation appeared in July, with a value of 146.08 mm, and the lowest average monthly precipitation appeared in January, with a value of 3.45 mm. The temporal variation was significant in different months. The monthly precipitation increased in all months except August and September, and the increase in precipitation was significant (p < 0.05) in February, March, May, November, and December. As to the results shown in Table 2, the July precipitation also showed a decreasing trend, and the increase in precipitation was significant (p < 0.05) only in June and December due to differences in the two methods. In summary, the precipitation increased in the SHRB at almost all temporal scales.
Figure 4 shows the spatial distribution of the yearly and seasonal precipitation. We can find that the spatial distribution characteristic of precipitation on a yearly scale and a monthly scale were similar. The precipitation in the SHRB was higher in the southeastern regions, with the highest value of 831.62 mm, and lower in the western regions, with the lowest value of 381.69 mm. The highest precipitations were 162.55, 502.07, 155.11, and 39.08 mm in spring, summer, autumn, and winter, respectively; and the lowest precipitations were 47.29, 273.39, 51.19, and 4.57 mm in spring, summer, autumn, and winter, respectively. The spatial difference was almost consistent during all seasons.

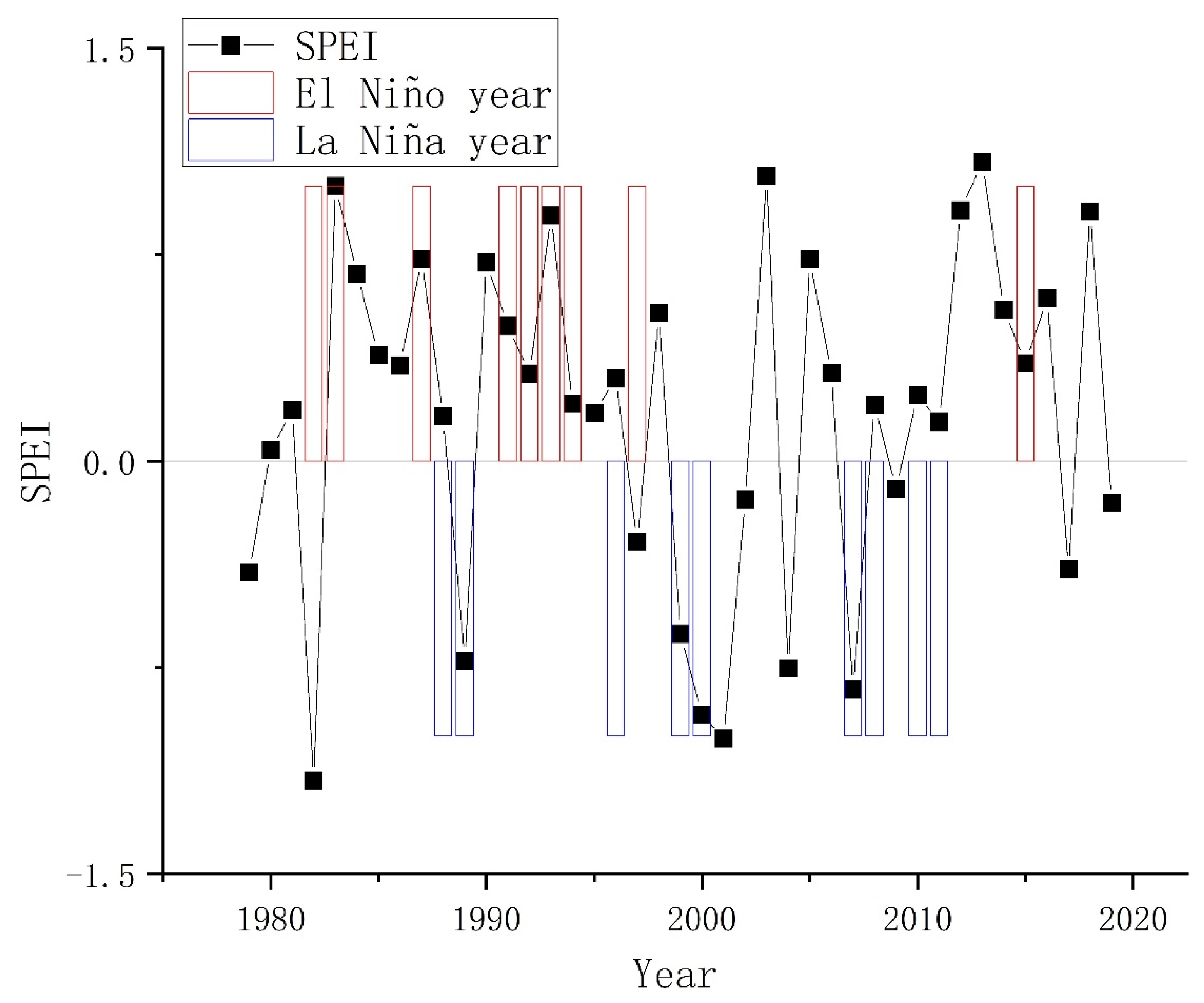
4.2. Temporal Variation of the SPEI

As shown in Figure 2, the trend of the annual SPEI significantly increased (p < 0.05) with a gradient of 0.01/a. From 1960 to 2019, there were 14a with a drought state. Among these drought years, about 29% were at a middle drought, and about 71% were at a slight drought. The most severe drought year was 1975, and the wettest year was 2013. For a seasonal scale (Figure 3e–h), the SPEI in the SHRB were increased in all seasons, with a significant increase in winter (p < 0.05). The changing trend of the SPEI in spring, summer, autumn, and winter was 0.009/a, 0.009/a, 0.003/a, and 0.001/a, respectively. As shown in Table 2, the trend of the SPEI was also significant on a yearly and seasonal scale when using the MMK method. The number of years that suffered a drought state in spring, summer, autumn, and winter was 12, 15, 15, and 17, respectively. The drought on a season scale was a little more frequent than on a yearly scale in summer, autumn, and winter. This indicated that the SHRB was more likely to suffer a drought in these three seasons, especially in winter. As shown in Table 2, the monthly SPEI increased in almost all months except March, with a gradient of −0.0009/a and was significantly increased (p < 0.01) in January, with a gradient of 0.02/a. However, in Table 3 the monthly SPEI significantly increased (p < 0.05) in January, February, May, June, October, and December, with Z-values of 1.98, 2.44, 1.74, 2.65, 1.75, and 1.68, respectively. The highest change trend in monthly SPEI was in December, with a value of 0.01/a. In summary, the SPEI increased in the SHRB on almost all temporal scales except in March. This indicated the SHRB had a wetting trend from 1960 to 2019.

4.3. Frequency of Drought Events with Different Time Scales

Figure 5 shows the statistic of the amount of drought months for each year. Severe drought occurred in 1966, 1967, 1982, 1989, and 2019, when six months of drought were experienced. The years without drought were 1986, 2013, and 2018. It is noteworthy that there was no drought in 2018, but drought occurred for six months in 2019. The overall trend of the drought months decreased, as shown in the slip 10a drought month line in Figure 5. The average drought months in a year before 1980 was about 3–4 months, but from 1980 to 2019, the average drought months in a year was about 2–3 months. Compared to the drought months in these two periods, the drought months in a year from 1980 to 2019 was less than that from 1960 to 1979.
Figure 6 shows the frequency of different states for each period from 1960 to 2019. The frequencies of drought, normal, and wet for all periods were 20–31%, 39–58%, and 20–32%, respectively. The frequency range of the drought and wet states were close in this period. The highest and lowest drought frequency happened in February (31%) and spring (20%), respectively. February was the only period that suffered extreme drought. The drought in each period were mainly classified into slight drought and middle drought, with frequencies of 10–25% and 3–14%, respectively. The highest and lowest wet frequencies happened in autumn (32%) and October (20%), respectively.
Figure 7 shows the spatial distribution of the drought probability. The drought probability varied from 25 to 39.99% within the SHRB on a yearly scale, and ranged from 27.12 to 40.68%, 23.73 to 40.68%, 27.12 to 38.98%, and 25.42 to 44.07% in spring, summer, autumn, and winter, respectively. The drought probability distribution on a yearly scale was similar to that in summer and autumn. The drought probability during these three periods was higher in the southern and mideastern regions and lower in the western regions. The drought probability in spring was higher in the midwestern regions and lower in the eastern and southern regions. As to winter, the drought probability was higher in the southwestern regions. These results may indicate that the drought probability on a yearly scale was dominated by summer and autumn.

4.4. Correlation between the SPEI and El Niño-Southern Oscillation Indexes

The XWT describes the link between the climate indexes and SPEI from time-frequency space by varying the power spectrum and phase structure (Figure 8). The colored stripes in these graphs depict the wavelet power spectrum, and a thick black contour represents the resonant period that passed a 95 percent significance test. The relative phase relationship is represented by arrows: “→” indicates that the variation of the climatic indexes and SPEI are positively correlated; “←” indicates that both of the factors are negatively correlated; “↓” indicates that the variation of SPEI lags behind that of the climatic indexes with one-fourth of the resonant period; and “↑” indicates that the variation of SPEI is ahead of the climatic index with one-fifth of the resonant period [40,41]. Only the resonant period inside the COI was examined in XWT, which was influenced by the edge effect.
As shown in Figure 8, the relationship between SPEI and SST1 and between SPEI and SST2 was similar. Two significant resonant periods exist between them: a short-term period for 2–4 years and 5–6 years occurred from 1982 to 1990 and from 1994 to 2002, respectively. From 1982 to 1990, the SPEI was positively correlated with SST1 and SST2 with a lead time, while from 1994 to 2002, the SPEI was positively correlated with SST1 and SST2 synchronously. There were two significant resonant periods between SPEI and SST3: a short-term period for 2–4 years from 1984 to 1992 and a long-term period for 9–10 years from 2000 to 2008. From 1984 to 1992, the SPEI was positively correlated with SST3 with a lead time, while from 2000 to 2008, the SPEI was positively correlated with SST3 synchronously. There were three significant resonant periods between SPEI and SST4: a short-term period for 2–4 years from 1982 to 1992 and long-term periods for 9–12 years and 13 years from 1994 to 2010 and from 1978 to 1986, respectively. From 1982 to 1992 and from 1982 to 1992, the SPEI was positively correlated with SST4 with a lead time, while from 1994 to 2010, the SPEI was positively correlated with SST4 synchronously. All in all, on the 95% confidence interval, the SPEI was positively correlated with the SST1, SST2, and SST3 from 1960 to 2019, while the relationship between the SPEI and the SST4 was negative before 1988 and positive after 1988.
There were two significant resonant periods between SPEI and SOI: a short-term period for 3–4 years from 1986 to 1990 and a long-term period for 9–12 years from 1992 to 2010. From 1986 to 1990, the SPEI was negatively correlated with SOI with a lag time, while from 1992–2010, the SPEI was negatively correlated with SOI synchronously. On the 95% confidence interval, the SPEI was negatively correlated with the SOI index, which is opposite to the correlation between SPEI and SST.

5. Discussion

5.1. Relationship between Precipitation and SPEI

A lack of precipitation is one of the most important driving factors in the formation of drought [42], which is easier to estimate compared to other driving factors, such as evapotranspiration, soil moisture content, etc. Drought mainly formed due to water deficit; among all driving factors, precipitation is the only water input source, and other factors are all consumed water resources. It is important to investigate the relationship between precipitation and SPEI for a better understanding of the effect of precipitation on drought [43,44].
In our research site, a linear regression analysis of the precipitation and SPEI was carried out on multiple time scales, including annual, seasonal, and monthly scales, using the data from 1960 to 2019. The results are shown in Figure 9 and Table 5. The precipitation was positively correlated with SPEI on all time scales. On a yearly scale, the precipitation was correlated with SPEI with an R-value of 0.31, which passed the confidence level of 99%. On a seasonal scale, the precipitation was correlated (p < 0.01) with SPEI with a R-values of 0.44, 0.79, and 0.66 in spring, summer, and autumn, respectively. As to winter, the precipitation had no correlation with SPEI, with a confidence level of 95%. However, among these yearly and seasonal scales, the changing trend of the SPEI response to the change of precipitation was largest, with a value of 0.022. As to the relationship in summer, the correlation between precipitation and SPEI was obvious, but the changing trend was the lowest, with a value of 0.008. The SPEI was calculated by the precipitation and potential evapotranspiration. This difference in change trend may be caused by the differences in the total precipitation and potential evapotranspiration value in each period. The higher value of precipitation in summer results in a high correlation and the higher value of potential evapotranspiration in summer results in a lower change trend in the response of SPEI to precipitation. This was also reflected in the relationship on a monthly scale; the precipitation and SPEI were correlated with SPEI (p < 0.01) on a monthly scale except for January, February, November, and December. The precipitation was correlated with SPEI in December (p < 0.05).
The water resource replenishment in a region is mainly from precipitation. The water is consumed for plant growth and human activities, mainly from surface runoff, reservoir, and soil moisture [45,46]. During spring, summer, and autumn, the precipitation was much higher than that during winter. The largest amount of water consumed in winter was mainly from the previous water storage in some low-precipitation periods [47], which resulted in the low correlation between precipitation and SPEI in winter. Besides this, the propagation time between precipitation to water use may also lead to an uncorrelation between precipitation and SPEI in some periods [8,48].

5.2. Effect of the El Niño-Southern Oscillation on Drought

In this study, the relationship between SPEI and some climatic indexes (SST1, SST2, SST3, SST4, and SOI) related to the El Niño-Southern Oscillation have been revealed. In our results, the SPEI was positively correlated with SST1, SST2, SST3, and SST4, in a different period with a different resonant period. Moreover, the SPEI was negatively correlated with the SOI for a short-term period of 3–4 years from 1986 to 1990 and a long-term period for 9–12 years from 1992 to 2010. In general, SST1, SST2, SST3, and SST4 almost all have a short-term period of 2–4 years with SPEI during the 1980s and a lead time exists in these correlations. The difference is mainly in the long-term resonant periods. These results reveal that if the El Niño index increased in the future, the SPEI would increase with some probability; while if the Southern Oscillation index increased in the future, the SPEI would decrease with some probability. A decrease in the El Niño index or an increase in the Southern Oscillation index could result in a drought event.
In other regions, researchers also investigated the relationship between ENSO and SPEI. Islam et al. [49] found that the SPEI was negatively correlated with ENSO from 1980 to 2017 in Bangladesh, but the correlation was not significant. Sun et al. [50] found that the SPEI was positively correlated with SSTA of the Nino3.4 region from 1961 to 2014 in Anhui province, China. Aryal and Zhu [51] investigated the relationship between drought and ENSO events in the US and found that drought was more likely to happen during the negative phase of the ENSO. Besides, there is also much literature about the relationship between the SPEI and ENSO [52,53,54]. They also obtain different conclusions about this topic in different regions. This shows that the effect of the El Niño-Southern Oscillation on SPEI is varied in different regions. Understanding the correlation between the El Niño-Southern Oscillation indexes and SPEI could promote drought prediction under a background of global climate change [54,55,56].
El Niño and La Niña are the two main results brought by the El Niño-Southern Oscillation, the temporal SPEI, and El Niño and La Niña years from 1979 to 2019 within the SHRB, as shown in Figure 10. It is obvious that the SPEI was higher during the El Niño years and lower during the La Niña years. This phenomenon was more significant before 2000, and less significant after 2000. During the La Niña years (2008, 2010, and 2011) there with a wet state and the values of SPEI were higher than 0. These results further proved that the El Niño-Southern Oscillation was an influencing factor for drought monitoring. Such research has also been conducted in other regions. Gao et al. [57] reported that the severe drought event in northern China in winter 2008–2009 was mainly influenced by La Niña and the Tibetan Plateau, Rodrigues et al. [58] revealed the reasons why the 2011–2012 La Niña caused a severe drought in the Brazilian northeast, and You et al. [59] found that La Niña could reduce the runoff and further increase the probability of drought events. These all have consistent results with our research that La Niña could increase the risk of drought. On the contrary, some research also has converse results that El Niño could also cause drought events in some regions [60,61]. The influence of the El Niño-Southern Oscillation on climate is complicated and varies in different regions, which need more investigation.

5.3. Effect of the Drought on Agriculture

Drought has resulted in much loss in the local economy, especially in agriculture [51]. Meteorological drought would propagate into hydrological drought and further propagated into agricultural drought, and finally, lead to a reduction in crops [9,62]. In China, many researchers have investigated crop reduction in drought. Li et al. [63] found that the SPEI on a different scale could affect the crop yields of wheat, maize, and cotton in Xinjiang, China. Zhang et al. [64] found that extreme drought could reduce maize yields with a high probability. Guo, Liu, Zhang, Wang, Wang, Wang, and Li [4] evaluated crop reduction under a background of different RCP scenarios and found that the maize yields would be decreased in northeast China. Jia et al. [65] and Wu et al. [66] found that the drought events would decrease the maize production in southwestern China, especially in the West Mountain area of Guizhou Province.
As reported by the China Flood and Drought Disaster Prevention Bulletin [28], the agricultural land affected by drought within northeastern China measured up to 4.3 × 104 km2 in 2020, which was almost all caused by the lack of precipitation. The SHRB is an important crop base of China. Though the historical trend of the precipitation and SPEI increased, the drought monitoring should also be concerned under a background of global warming. In this research, the relationship between the SPEI and El Niño-Southern Oscillation indexes was revealed. It would help in drought prevention in the SHRB, further reducing the loss in agriculture when drought occurs.

6. Conclusions

This paper analyzed the spatio-temporal variation of the precipitation and SPEI in the SHRB and the relationships between the SPEI and El Niño-Southern Oscillation indexes were revealed. The main conclusions were as follows:
  • The average annual, spring, summer, autumn, and winter precipitations were 527 mm, 76 mm, 348 mm, 87 mm, and 14 mm, respectively. About 66% of the total annual precipitation was concentrated in summer. The change trends of yearly, spring, summer, autumn, and winter precipitation were 0.56, 1.47 (p < 0.05), 0.13, 0.04, and 0.16 (p < 0.05) mm/a, respectively. The monthly precipitation increased in all months except August and September, and the increase in precipitation was significant (p < 0.05) in February, March, May, November, and December. The precipitation in the SHRB was higher in the southeastern regions, with the highest value of 831.62 mm, and was lower in the western regions, with the lowest value of 381.69 mm.
  • The trend of annual SPEI significantly increased (p < 0.05), with a gradient of 0.01/a. The SPEI in the SHRB increased in all seasons and were significant in winter (p < 0.05). The monthly SPEI increased in almost all months except March, with a gradient of −0.0009/a, and was significantly increased (p < 0.01) in January, with a gradient of 0.02/a. The SHRB had a wetting trend from 1960 to 2019.
  • Severe drought occurred in 1966, 1967, 1982, 1989, and 2019, when six months of draught were experienced. The years without drought were 1986, 2013, and 2018. The drought months in a year from 1980 to 2019 were less than those from 1960 to 1979. The frequencies of drought, normal, and wet for all periods ranged from 20 to 31%, 39 to 58%, and 20 to 32%, respectively. The drought probability distribution on the yearly scale was similar to that in summer and autumn, and the drought probability on a yearly scale was dominated by summer and autumn.
  • The SPEI was positively correlated with SST1, SST2, SST3, and SST4, in a different period with a different resonant period. Moreover, the SPEI was negatively correlated with the SOI for a short-term period of 3–4 years from 1986 to 1990 and for a long-term period of 9–12 years from 1992 to 2010. A decrease in the El Niño index or an increase in the Southern Oscillation index could result in a drought event.

Author Contributions

Conceptualization, L.R.; formal analysis, L.R.; investigation, L.R.; methodology, L.R.; supervision, X.D.; visualization, L.R.; writing—original draft, L.R.; writing—review and editing, X.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Scientific research project of Guizhou Water Resources Department: Study on Key Technologies of water regulating for fine quality production of characteristic crops in seasonal arid areas, the 2020 Opening fund from Hubei Key Laboratory of Intelligent Vision Based Monitoring for Hydroelectric Engineering (2020SDSJ03), the Construction fund for Hubei Key Laboratory of Intelligent Vision Based Monitoring for Hydroelectric Engineering (2019ZYYD007), the European Space Agency (ESA) and National Remote Sensing Center of China (58516), the National Natural Science Foundation of China (No. 52109058), the Power Construction Corporation of China (DJ-ZDZX-2016-02-09), and the Research Fund for Excellent Dissertation of China Three Gorges University (No. 2021BSPY003).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

This research was supported by the scientific research project of Guizhou Water Resources Department: Study on Key Technologies of water regulating for fine quality production of characteristic crops in seasonal arid areas.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Panagoulia, D.; Dimou, G. Definitions and effects of droughts. In Proceedings of the Conference on Mediterranean Water Policy: Building on Existing Experience, Mediterranean Water Network, Valencia, Spain, 23 April 1998; Volume 1, p. 11. Available online: https://www.researchgate.net/publication/273728913_definitions_and_effects_of_droughts (accessed on 4 March 2022).
  2. Panagoulia, D.; Dimou, G. Climatic instability and low-flow regimes. In Proceedings of the Water Resources Management under Drought or Water Shortage Conditions, EWRA 95 Symposium, Nicosia, Cyprus, 14–18 March 1995; Tsiourtis, N.X., Ed.; August Aimé Balkema: Amsterdam, The Netherlands, 1995; pp. 29–34. [Google Scholar]
  3. Chen, T.; Xia, G.; Liu, T.; Chen, W.; Chi, D. Assessment of drought impact on main cereal crops using a standardized precipitation evapotranspiration index in Liaoning Province, China. Sustainability 2016, 8, 1069. [Google Scholar] [CrossRef] [Green Version]
  4. Guo, E.; Liu, X.; Zhang, J.; Wang, Y.; Wang, C.; Wang, R.; Li, D. Assessing spatiotemporal variation of drought and its impact on maize yield in Northeast China. J. Hydrol. 2017, 553, 231–247. [Google Scholar] [CrossRef]
  5. Parsons, D.J.; Rey, D.; Tanguy, M.; Holman, I.P. Regional variations in the link between drought indices and reported agricultural impacts of drought. Agric. Syst. 2019, 173, 119–129. [Google Scholar] [CrossRef]
  6. Liu, X.; Pan, Y.; Zhu, X.; Yang, T.; Bai, J.; Sun, Z. Drought evolution and its impact on the crop yield in the North China Plain. J. Hydrol. 2018, 564, 984–996. [Google Scholar] [CrossRef]
  7. Espinosa, L.A.; Portela, M.M.; Rodrigues, R. Spatio-temporal variability of droughts over past 80 years in Madeira Island. J. Hydrol. -Reg. Stud. 2019, 25. [Google Scholar] [CrossRef]
  8. Li, Z.; Huang, S.; Zhou, S.; Leng, G.; Liu, D.; Huang, Q.; Wang, H.; Han, Z.; Liang, H. Clarifying the propagation dynamics from meteorological to hydrological drought induced by climate change and direct human activities. J. Hydrometeorol. 2021, 22, 2359–2378. [Google Scholar] [CrossRef]
  9. Ding, Y.; Gong, X.; Xing, Z.; Cai, H.; Zhou, Z.; Zhang, D.; Sun, P.; Shi, H. Attribution of meteorological, hydrological and agricultural drought propagation in different climatic regions of China. Agric. Water Manag. 2021, 255. [Google Scholar] [CrossRef]
  10. McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–183. [Google Scholar]
  11. Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
  12. Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965; Volume 30.
  13. Rajsekhar, D.; Singh, V.P.; Mishra, A.K. Multivariate drought index: An information theory based approach for integrated drought assessment. J. Hydrol. 2015, 526, 164–182. [Google Scholar] [CrossRef]
  14. Shah, D.; Mishra, V. Integrated Drought Index (IDI) for drought monitoring and assessment in India. Water Resour. Res. 2020, 56, e2019WR026284. [Google Scholar] [CrossRef]
  15. Tan, C.; Yang, J.; Li, M. Temporal-spatial variation of drought indicated by SPI and SPEI in Ningxia Hui Autonomous Region, China. Atmosphere 2015, 6, 1399–1421. [Google Scholar] [CrossRef] [Green Version]
  16. Bae, S.; Lee, S.-H.; Yoo, S.-H.; Kim, T. Analysis of drought intensity and trends using the modified SPEI in South Korea from 1981 to 2010. Water 2018, 10, 327. [Google Scholar] [CrossRef] [Green Version]
  17. Jin, X.; Qiang, H.; Zhao, L.; Jiang, S.; Cui, N.; Cao, Y.; Feng, Y. SPEI-based analysis of spatio-temporal variation characteristics for annual and seasonal drought in the Zoige Wetland, Southwest China from 1961 to 2016. Theor. Appl. Climatol. 2020, 139, 711–725. [Google Scholar] [CrossRef]
  18. Chen, H. and J. Sun, Changes in drought characteristics over china using the standardized precipitation evapotranspiration index. J. Clim. 2015, 28, 5430–5447. [Google Scholar] [CrossRef]
  19. Masson-Delmotte, V.; Zhai, P.; Pörtner, H.-O.; Roberts, D.; Skea, J.; Shukla, P.R.; Pirani, A.; Moufouma-Okia, W.; Péan, C.; Pidcock, R. Global warming of 1.5 °C; World Meteorological Organization: Geneva, Switzerland, 2018; Volume 1. [Google Scholar]
  20. Li, H.; Chen, H.; Wang, H.; Yu, E. Future precipitation changes over China under 1.5 C and 2.0 C global warming targets by using CORDEX regional climate models. Sci. Total Environ. 2018, 640, 543–554. [Google Scholar] [CrossRef]
  21. Mukherjee, S.; Mishra, A.; Trenberth, K.E. Climate change and drought: A perspective on drought indices. Curr. Clim. Chang. Rep. 2018, 4, 145–163. [Google Scholar] [CrossRef]
  22. Li, M.; Cao, F.; Wang, G.; Chai, X.; Zhang, L. Evolutional characteristics of regional meteorological drought and their linkages with southern oscillation index across the loess plateau of China during 1962–2017. Sustainability 2020, 12, 7237. [Google Scholar] [CrossRef]
  23. Du, Y.; Berndtsson, R.; An, D.; Zhang, L.; Yuan, F.; Hao, Z. Integrated large-scale circulation impact on rainy season precipitation in the source region of the Yangtze River. Int. J. Climatol. 2020, 40, 2285–2295. [Google Scholar] [CrossRef]
  24. Tong, S.; Li, X.; Zhang, J.; Bao, Y.; Bao, Y.; Na, L.; Si, A. Spatial and temporal variability in extreme temperature and precipitation events in Inner Mongolia (China) during 1960–2017. Sci. Total Environ. 2019, 649, 75–89. [Google Scholar] [CrossRef]
  25. Mo, K.C.; Schemm, J.E. Relationships between ENSO and drought over the southeastern United States. Geophys. Res. Lett. 2008, 35, 35. [Google Scholar] [CrossRef]
  26. Wang, H.; Kumar, A. Assessing the impact of ENSO on drought in the US Southwest with NCEP climate model simulations. J. Hydrol. 2015, 526, 30–41. [Google Scholar] [CrossRef]
  27. Zhou, L.; Wang, S.; Du, M.; Chen, Q.; He, C.; Zhang, J.; Zhu, Y.; Gong, Y. The influence of ENSO and MJO on drought in different ecological geographic regions in China. Remote Sens. 2021, 13, 875. [Google Scholar] [CrossRef]
  28. Compilation group of China Flood and Drought Disaster Prevention Bulletin. Summary of China Flood and Drought Disaster Prevention Bulletin 2020. China Flood Drought Manag. 2021, 31, 26–32. [Google Scholar] [CrossRef]
  29. Faiz, M.A.; Liu, D.; Fu, Q.; Baig, F.; Tahir, A.A.; Li, M.; Khan, M.I.; Shoaib, M.; Li, T.; Cui, S. Multi-index drought characteristics in Songhua River basin, Northeast China. Clim. Res. 2019, 78, 1–19. [Google Scholar] [CrossRef]
  30. An, Q.; He, H.; Gao, J.; Nie, Q.; Cui, Y.; Wei, C.; Xie, X. Analysis of temporal-spatial variation characteristics of drought: A case study from Xinjiang, China. Water 2020, 12, 741. [Google Scholar] [CrossRef] [Green Version]
  31. Huang, H.; Zhang, B.; Cui, Y.; Ma, S. Analysis on the characteristics of dry and wet periods in the yangtze river basin. Water 2020, 12, 2960. [Google Scholar] [CrossRef]
  32. Khorsandi, N.; Mahdian, M.H.; Pazira, E.; Nikkami, D.; Chamheidar, H. Comparison of different interpolation methods for investigating spatial variability of rainfall erosivity index. Pol. J. Environ. Stud. 2012, 21, 1659–1666. [Google Scholar]
  33. Weisberg, S. Applied Linear Regression; John Wiley & Sons: New York, NY, USA, 2005; Volume 528. [Google Scholar]
  34. Tiku, M. Tables of the power of the F-test. J. Am. Stat. Assoc. 1967, 62, 525–539. [Google Scholar] [CrossRef]
  35. Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
  36. Adamowski, J.F. Development of a short-term river flood forecasting method for snowmelt driven floods based on wavelet and cross-wavelet analysis. J. Hydrol. 2008, 353, 247–266. [Google Scholar] [CrossRef]
  37. Ghaderpour, E.; Vujadinovic, T.; Hassan, Q.K. Application of the least-squares wavelet software in hydrology: Athabasca River basin. J. Hydrol. Reg. Stud. 2021, 36, 100847. [Google Scholar] [CrossRef]
  38. Miao, J.; Liu, G.; Cao, B.; Hao, Y.; Chen, J.; Yeh, T.; Chyi, J. Identification of strong karst groundwater runoff belt by cross wavelet transform. Water Resour. Manag. 2014, 28, 2903–2916. [Google Scholar] [CrossRef]
  39. Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef] [Green Version]
  40. Bi, S.; Bi, S.; Lu, Y.; Qu, Y.; Zhao, F. Temporal and spatial characteristics of droughts and floods in northern China from 1644 to 1911. J. Earth Syst. Sci. 2019, 128, 98. [Google Scholar] [CrossRef] [Green Version]
  41. Du, C.; Chen, J.; Nie, T.; Dai, C. Spatial-temporal changes in meteorological and agricultural droughts in Northeast China: Change patterns, response relationships and causes. Nat. Hazards 2021, 110, 155–173. [Google Scholar] [CrossRef]
  42. Ndehedehe, C.E.; Ferreira, V.G.; Agutu, N.O.; Onojeghuo, A.O.; Okwuashi, O.; Kassahun, H.T.; Dewan, A. What if the rains do not come? J. Hydrol. 2021, 595, 126040. [Google Scholar] [CrossRef]
  43. Wang, L.N.; Zhu, Q.K.; Zhao, W.J.; Zhao, X.K. The drought trend and its relationship with rainfall intensity in the Loess Plateau of China. Nat. Hazards 2015, 77, 479–495. [Google Scholar] [CrossRef]
  44. Tang, H.; Wen, T.; Shi, P.; Qu, S.; Zhao, L.; Li, Q. Analysis of characteristics of hydrological and meteorological drought evolution in Southwest China. Water 2021, 13, 1846. [Google Scholar] [CrossRef]
  45. Liu, B.; Shao, M. Modeling soil-water dynamics and soil-water carrying capacity for vegetation on the Loess Plateau, China. Agric. Water Manag. 2015, 159, 176–184. [Google Scholar] [CrossRef]
  46. Fu, B.; Xu, P.; Wang, Y.; Yan, K.; Chaudhary, S. Assessment of the ecosystem services provided by ponds in hilly areas. Sci. Total Environ. 2018, 642, 979–987. [Google Scholar] [CrossRef]
  47. Ji, H.; Chen, S.; Pan, S.; Xu, C.; Jiang, C.; Fan, Y. Morphological variability of the active Yellow River mouth under the new regime of riverine delivery. J. Hydrol. 2018, 564, 329–341. [Google Scholar] [CrossRef]
  48. Apurv, T.; Sivapalan, M.; Cai, X. Understanding the role of climate characteristics in drought propagation. Water Resour. Res. 2017, 53, 9304–9329. [Google Scholar] [CrossRef] [Green Version]
  49. Islam, A.R.M.; Salam, R.; Yeasmin, N.; Kamruzzaman, M.; Shahid, S.; Fattah, M.; Uddin, A.; Shahariar, M.H.; Mondol, M.A.H.; Jhajharia, D. Spatiotemporal distribution of drought and its possible associations with ENSO indices in Bangladesh. Arab J. Geosci. 2021, 14, 2681. [Google Scholar] [CrossRef]
  50. Sun, P.; Zhang, Q.; Cheng, C.; Singh, V.P.; Shi, P. ENSO-induced drought hazards and wet spells and related agricultural losses across Anhui province, China. Nat. Hazards 2017, 89, 963–983. [Google Scholar] [CrossRef]
  51. Aryal, Y.; Zhu, J. Evaluating the performance of regional climate models to simulate the US drought and its connection with El Nino Southern Oscillation. Theor. Appl. Climatol. 2021, 145, 1259–1273. [Google Scholar] [CrossRef]
  52. Gupta, V.; Jain, M.K. Unravelling the teleconnections between ENSO and dry/wet conditions over India using nonlinear Granger causality. Atmos Res. 2021, 247, 105168. [Google Scholar] [CrossRef]
  53. Aryal, Y.; Zhu, J. Multimodel ensemble projection of meteorological drought scenarios and connection with climate based on spectral analysis. Int. J. Climatol. 2020, 40, 3360–3379. [Google Scholar] [CrossRef]
  54. Zhou, F.; Fang, K.; Zhang, F.; Dong, Z. Hydroclimate change encoded in tree rings of Fengshui woods in Southeastern China and its teleconnection with El Niño-Southern Oscillation. Water Resour. Res. 2020, 56, e2018WR024612. [Google Scholar] [CrossRef]
  55. Gong, X.; Du, S.; Li, F.; Ding, Y. Study on the spatial and temporal characteristics of mesoscale drought in china under future climate change scenarios. Water 2021, 13, 2761. [Google Scholar] [CrossRef]
  56. Woolway, R.I.; Kraemer, B.M.; Lenters, J.D.; Merchant, C.J.; O’Reilly, C.M.; Sharma, S. Global lake responses to climate change. Nat. Rev. Earth Environ. 2020, 1, 388–403. [Google Scholar] [CrossRef]
  57. Gao, H.; Yang, S. A severe drought event in northern China in winter 2008–2009 and the possible influences of La Nina and Tibetan Plateau. J. Geophys. Res. Atmos. 2009, 114, 114. [Google Scholar] [CrossRef]
  58. Rodrigues, R.R.; McPhaden, M.J. Why did the 2011–2012 La Nina cause a severe drought in the Brazilian Northeast? Geophys. Res. Lett. 2014, 41, 1012–1018. [Google Scholar] [CrossRef]
  59. You, Y.; Liu, J.; Zhang, Y.; Beck, H.E.; Gu, X.; Kong, D. Impacts of El Nino-southern oscillation on global runoff: Characteristic signatures and potential mechanisms. Hydrol. Process. 2021, 35, e14367. [Google Scholar] [CrossRef]
  60. Zhang, W.; Jin, F.-F.; Turner, A. Increasing autumn drought over southern China associated with ENSO regime shift. Geophys. Res. Lett. 2014, 41, 4020–4026. [Google Scholar] [CrossRef] [Green Version]
  61. Pan, X.; Chin, M.; Ichoku, C.M.; Field, R.D. Connecting Indonesian fires and drought with the type of El Nino and phase of the Indian Ocean Dipole during 1979–2016. J. Geophys. Res. Atmos. 2018, 123, 7974–7988. [Google Scholar] [CrossRef]
  62. Hamal, K.; Sharma, S.; Khadka, N.; Haile, G.G.; Joshi, B.B.; Xu, T.; Dawadi, B. Assessment of drought impacts on crop yields across Nepal during 1987–2017. Meteorol. Appl. 2020, 27, 27. [Google Scholar] [CrossRef]
  63. Li, H.; Li, Y.; Huang, G.; Sun, J. Probabilistic assessment of crop yield loss to drought time-scales in Xinjiang, China. Int. J. Climatol. 2021, 41, 4077–4094. [Google Scholar] [CrossRef]
  64. Zhang, Q.; Shi, R.; Singh, V.P.; Xu, C.-Y.; Yu, H.; Fan, K.; Wu, Z. Droughts across China: Drought factors, prediction and impacts. Sci. Total Environ. 2022, 803, 150018. [Google Scholar] [CrossRef]
  65. Jia, H.-C.; Pan, D.-H.; Li, J.; Zhang, W.-C.; Ghulam, R. Risk assessment of maize drought disaster in southwest China using the Environmental Policy Integrated Climate model. J. Mt. Sci. 2016, 13, 465–475. [Google Scholar] [CrossRef]
  66. Wu, L.; Feng, L.; Li, Y.; Wang, J.; Wu, L. A yield-related agricultural drought index reveals spatio-temporal characteristics of droughts in Southwestern China. Sustainability 2019, 11, 714. [Google Scholar] [CrossRef] [Green Version]
Water 14 00866 g001 550
Figure 1. Location and elevation distribution of the SHRB and the distribution of the weather stations used for this study.
Figure 1. Location and elevation distribution of the SHRB and the distribution of the weather stations used for this study.
Water 14 00866 g001
Water 14 00866 g002 550
Figure 2. Annual precipitation (a) and SPEI (b) within the SHRB from 1960 to 2019.
Figure 2. Annual precipitation (a) and SPEI (b) within the SHRB from 1960 to 2019.
Water 14 00866 g002
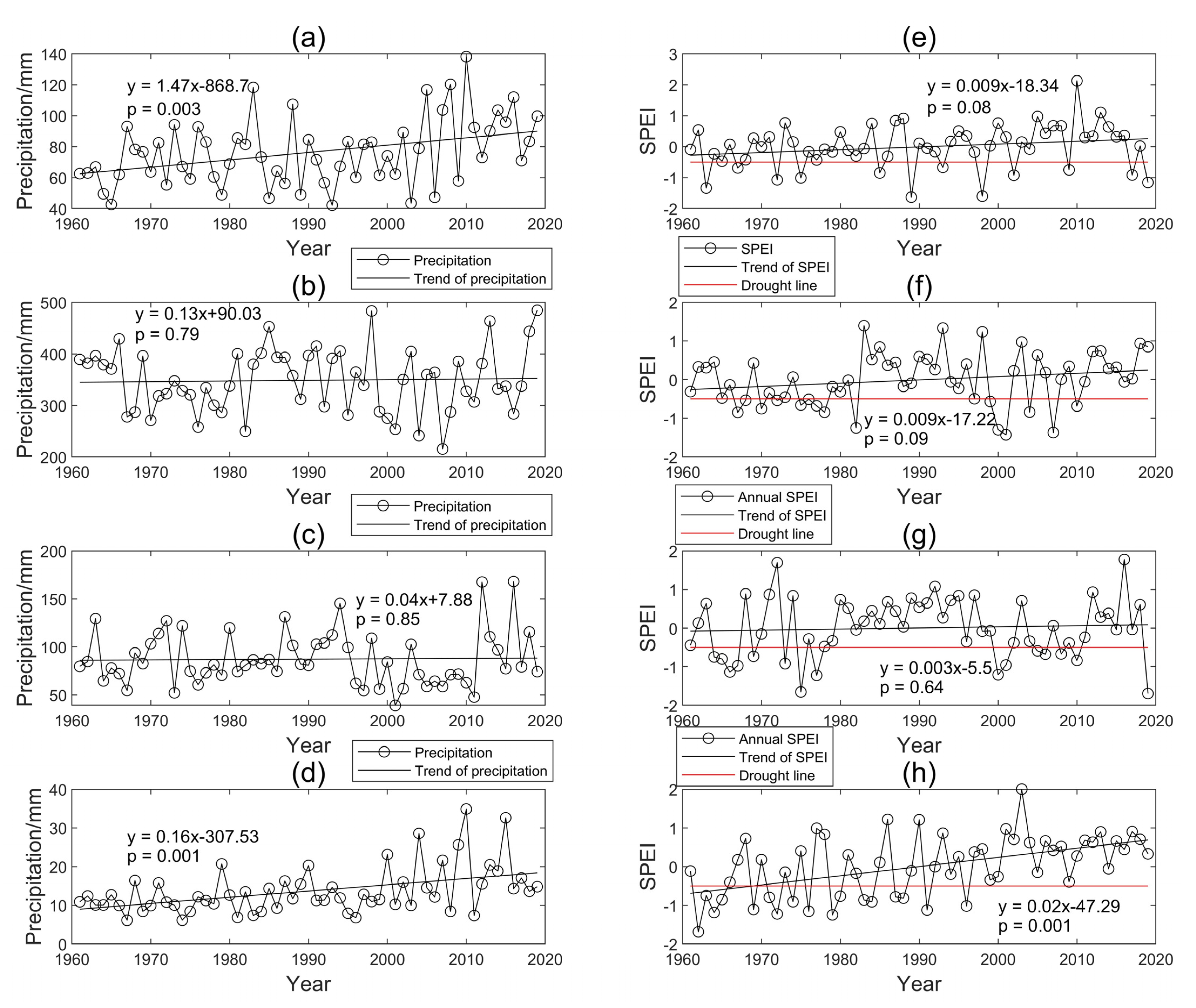
Water 14 00866 g003 550
Figure 3. Seasonal precipitation and SPEI series within the SHRB from 1960 to 2019. (a–d) show the precipitation series within the SHRB in spring, summer, autumn, and winter, respectively. (e–h) show the SPEI series within the SHRB in spring, summer, autumn, and winter, respectively.
Figure 3. Seasonal precipitation and SPEI series within the SHRB from 1960 to 2019. (a–d) show the precipitation series within the SHRB in spring, summer, autumn, and winter, respectively. (e–h) show the SPEI series within the SHRB in spring, summer, autumn, and winter, respectively.
Water 14 00866 g003
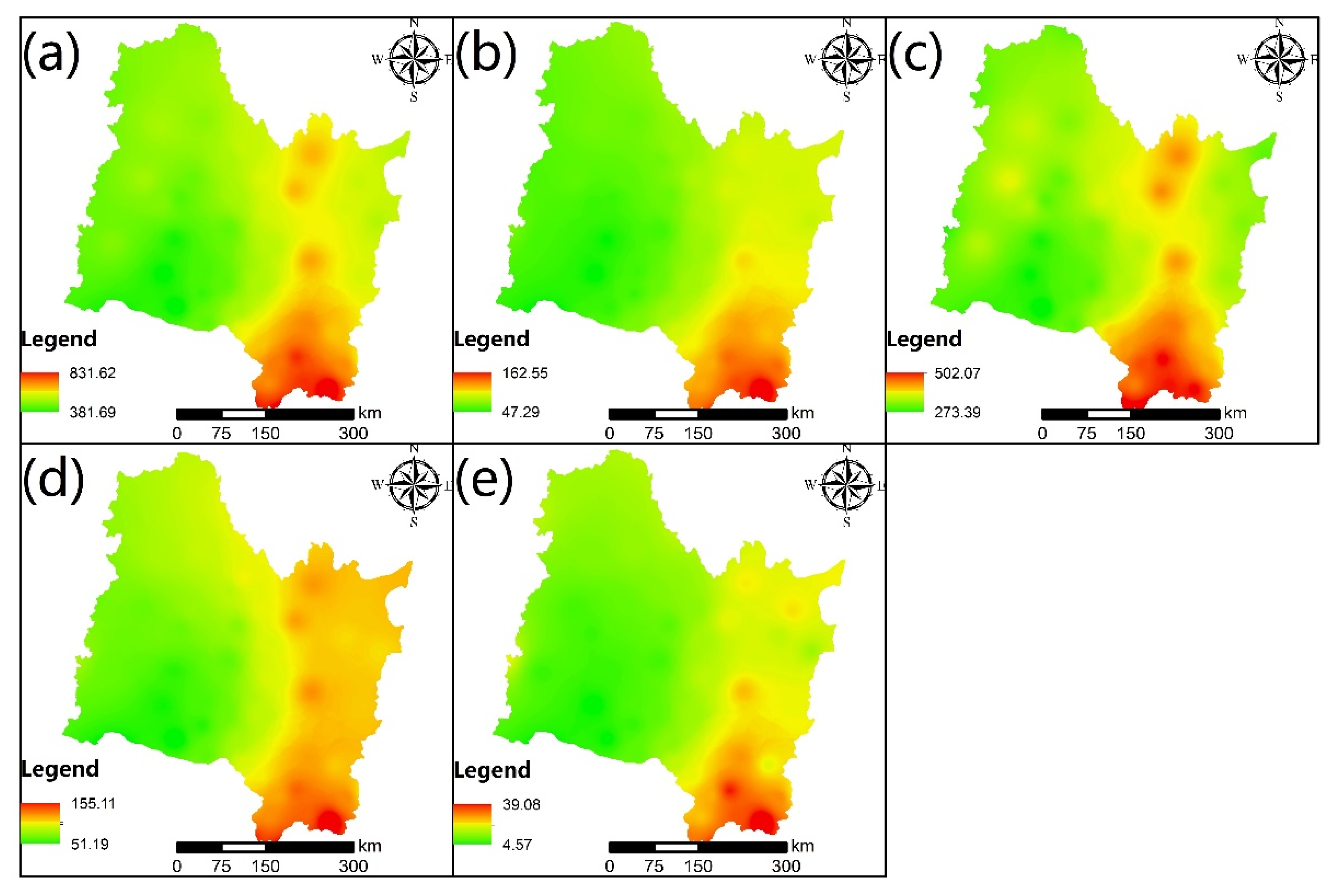
Water 14 00866 g004 550
Figure 4. Average yearly and seasonal precipitation distribution within the SHRB. The (a–e) represent the average yearly, spring, summer, autumn, and winter precipitation, respectively.
Figure 4. Average yearly and seasonal precipitation distribution within the SHRB. The (a–e) represent the average yearly, spring, summer, autumn, and winter precipitation, respectively.
Water 14 00866 g004
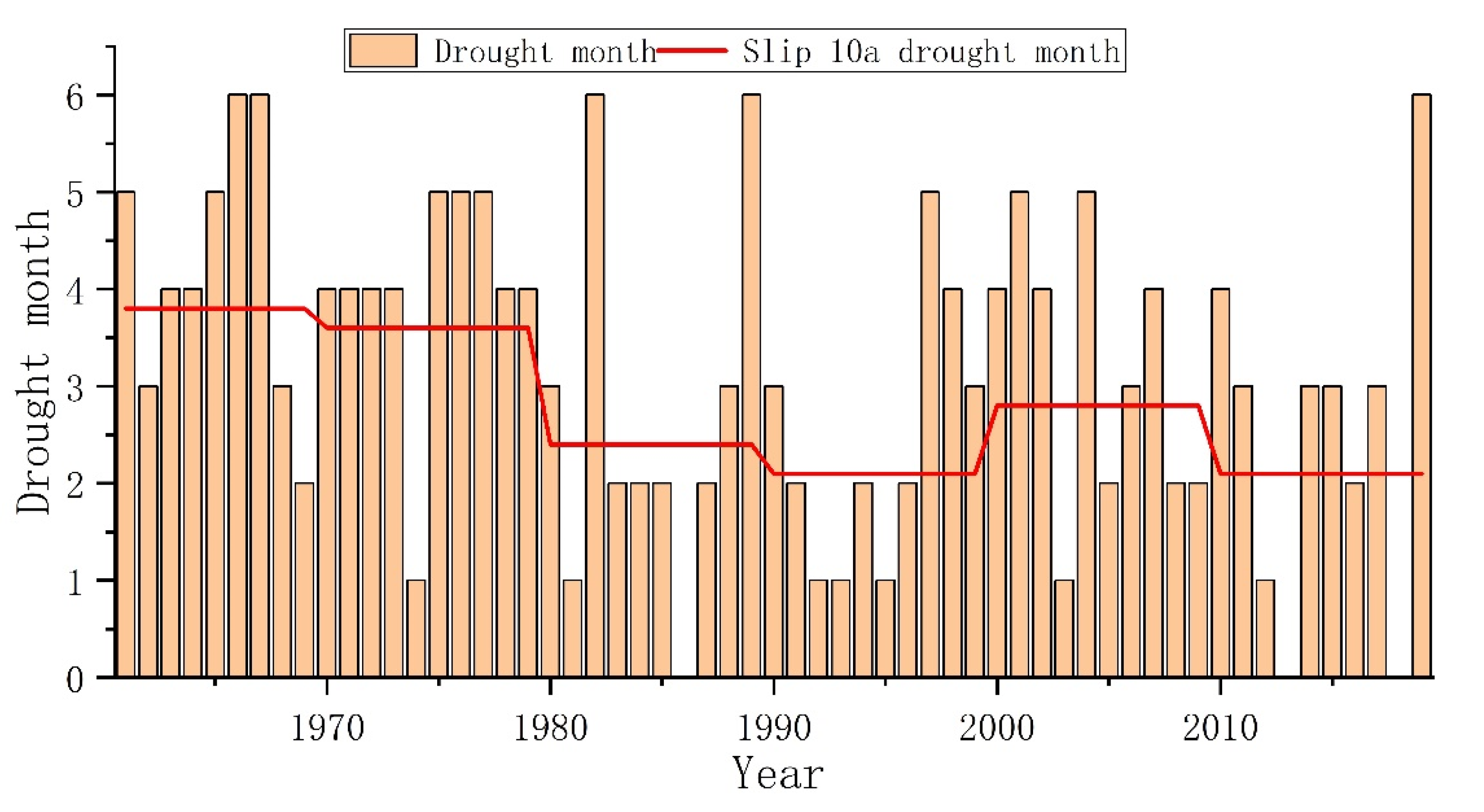
Water 14 00866 g005 550
Figure 5. Number of drought months in different years.
Figure 5. Number of drought months in different years.
Water 14 00866 g005
Water 14 00866 g006 550
Figure 6. The frequency of different states in different periods from 1960 to 2019. The Spr, Sum, Aut, and Win was represented the spring, summer, autumn, and winter, respectively.
Figure 6. The frequency of different states in different periods from 1960 to 2019. The Spr, Sum, Aut, and Win was represented the spring, summer, autumn, and winter, respectively.
Water 14 00866 g006
Water 14 00866 g007 550
Figure 7. Spatial distribution of the drought probability on different scales within the SHRB from 1960 to 2019. (a–e) show the drought probability on an annual, spring, summer, autumn, and winter scale, respectively.
Figure 7. Spatial distribution of the drought probability on different scales within the SHRB from 1960 to 2019. (a–e) show the drought probability on an annual, spring, summer, autumn, and winter scale, respectively.
Water 14 00866 g007
Water 14 00866 g008 550
Figure 8. Correlations between the climatic indexes and SPEI on a yearly scale. A bold black contour represents the 95 percent significance threshold against red noise; a thin black line represents the cone of influence (COI) and bold arrows reflect phase change.
Figure 8. Correlations between the climatic indexes and SPEI on a yearly scale. A bold black contour represents the 95 percent significance threshold against red noise; a thin black line represents the cone of influence (COI) and bold arrows reflect phase change.
Water 14 00866 g008
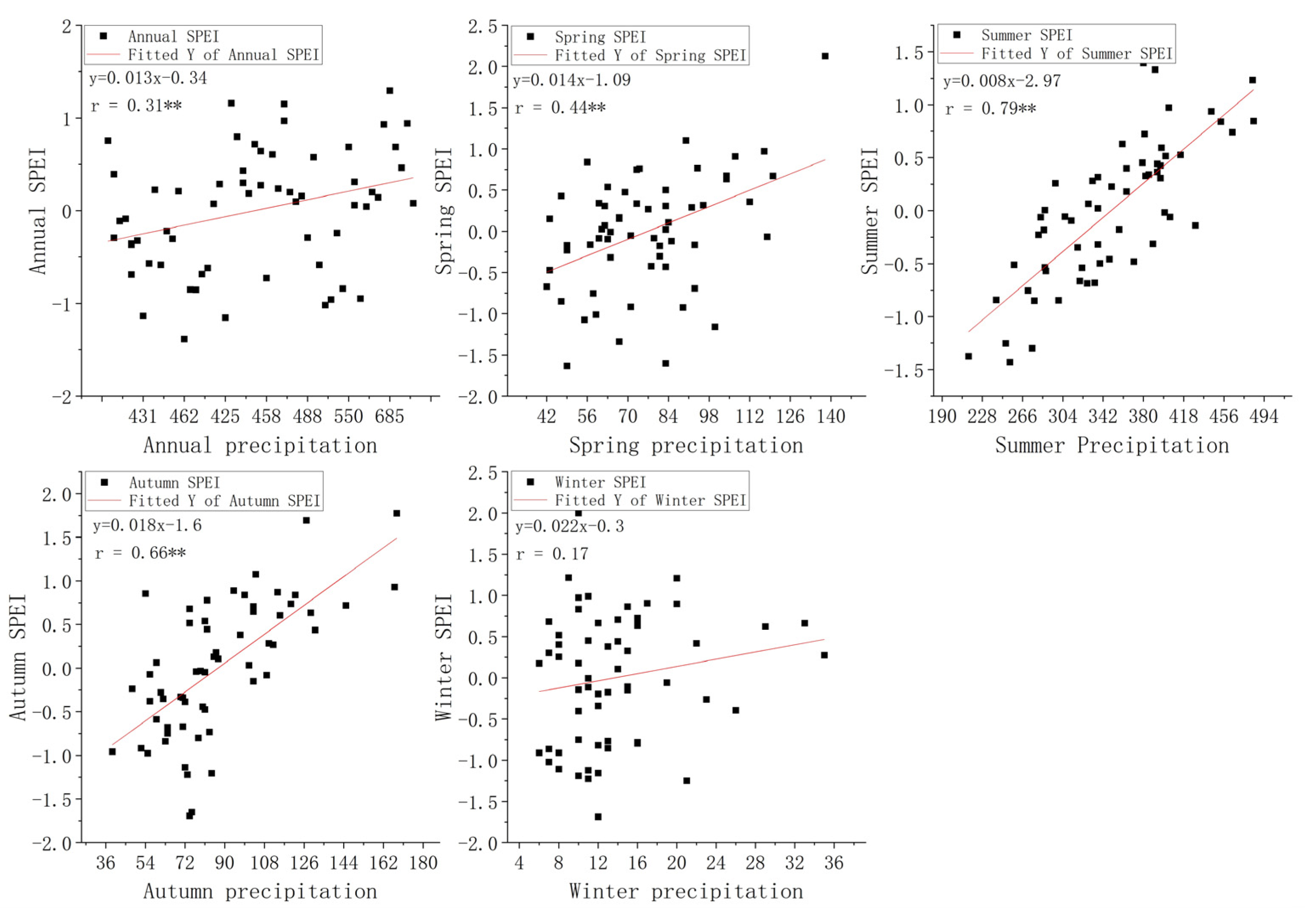
Water 14 00866 g009 550
Figure 9. Relationship between precipitation and SPEI on a yearly and seasonal scale. The symbols ** indicate the trend that has passed the 99% significance tests.
Figure 9. Relationship between precipitation and SPEI on a yearly and seasonal scale. The symbols ** indicate the trend that has passed the 99% significance tests.
Water 14 00866 g009
Water 14 00866 g010 550
Figure 10. The annual SPEI and El Niño and La Niña years from 1979 to 2019 within the SHRB.
Figure 10. The annual SPEI and El Niño and La Niña years from 1979 to 2019 within the SHRB.
Water 14 00866 g010
Table
Table 1. The index standard of the state of drought and wet and the range of the SPEI.
Table 1. The index standard of the state of drought and wet and the range of the SPEI.
The State of Drought and WetRange of the SPEI
Wet0.5 < SPEI
Normal−0.5 < SPEI ≤ 0.5
Slight drought−1.0 < SPEI ≤ −0.5
Middle drought−2.0 < SPEI ≤ −1.0
Extreme droughtSPEI ≤ −2.0
Table
Table 2. Statistics of the Z-value of the MMK test for precipitation and SPEI on yearly and seasonal scales.
Table 2. Statistics of the Z-value of the MMK test for precipitation and SPEI on yearly and seasonal scales.
Time PeriodZ-Value
PrecipitationSPEI
Spring1.9 *2.04 *
Summer0.11.82 *
Autumn−0.470.56 *
Winter1.86 *2.09 *
Annual0.821.65 *
The symbol of * indicates a trend that has passed the 95% significance test.
Table
Table 3. Z-values of the MMK test for precipitation and SPEI on a monthly scale.
Table 3. Z-values of the MMK test for precipitation and SPEI on a monthly scale.
Time PeriodZ-ValueTime PeriodZ-Value
PrecipitationSPEIPrecipitationSPEI
January0.881.98 *July−0.991.15
February0.792.44 *August−0.60.08
March1.53−0.45September−1.03−0.38
April0.670.89October1.241.75 *
May1.091.74 *November1.310.86
June2.15 *2.65 *December1.88 *1.68 *
The symbol of * indicates a trend that has passed the 95% significance test.
Table
Table 4. Monthly average precipitation and the trend of precipitation and SPEI within the SHRB.
Table 4. Monthly average precipitation and the trend of precipitation and SPEI within the SHRB.
MonthPrecipitationSPEIMonthPrecipitationSPEI
Mean ValueTrendTrendMean ValueTrendTrend
January3.450.02/a0.02/a **July146.080.3/a0.004/a
February4.140.04/a *0.009/aAugust115.96−0.07/a0.002/a
March8.910.08/a *−0.0009/aSeptember53.63−0.12/a0.0009/a
April21.980.02/a0.003/aOctober23.700.02/a0.006/a
May45.740.31/a *0.009/aNovember10.190.09/a *0.005/a
June87.580.38/a0.009/aDecember6.070.09/a *0.01/a
The symbol of * and ** indicates a trend that has passed the 95% and 99% significance test, respectively.
Table
Table 5. Correlation coefficient between precipitation and SPEI on a monthly scale.
Table 5. Correlation coefficient between precipitation and SPEI on a monthly scale.
MonthRMonthR
January0.008July0.71 **
February0.04August0.86 **
March0.44 **September0.76 **
April0.59 **October0.39 **
May0.67 **November0.05
June0.82 **December0.32 *
The symbols of * and ** indicate the trend that has passed the 95% and 99% significance tests, respectively.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Ren, L.; Dong, X. Spatio-Temporal Characteristics of Drought and Its Relationship with El Niño-Southern Oscillation in the Songhua River Basin from 1960 to 2019. Water 2022, 14, 866. https://doi.org/10.3390/w14060866

AMA Style

Ren L, Dong X. Spatio-Temporal Characteristics of Drought and Its Relationship with El Niño-Southern Oscillation in the Songhua River Basin from 1960 to 2019. Water. 2022; 14(6):866. https://doi.org/10.3390/w14060866

Chicago/Turabian Style

Ren, Lv, and Xiaohua Dong. 2022. "Spatio-Temporal Characteristics of Drought and Its Relationship with El Niño-Southern Oscillation in the Songhua River Basin from 1960 to 2019" Water 14, no. 6: 866. https://doi.org/10.3390/w14060866

APA Style

Ren, L., & Dong, X. (2022). Spatio-Temporal Characteristics of Drought and Its Relationship with El Niño-Southern Oscillation in the Songhua River Basin from 1960 to 2019. Water, 14(6), 866. https://doi.org/10.3390/w14060866

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop