Numerical Investigation on Solitary Wave Interaction with a Vertical Cylinder over a Viscous Mud Bed
Abstract
1. Introduction
2. Numerical Model
3. Validation Tests
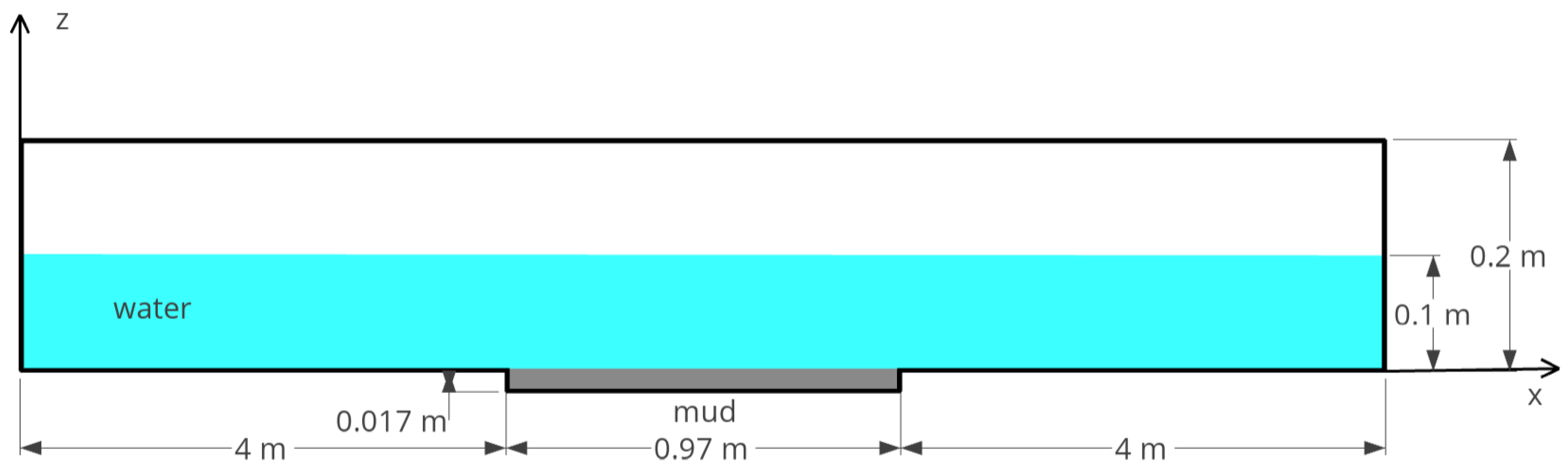
3.1. Solitary Wave Propagating over a Viscous Mud Bed
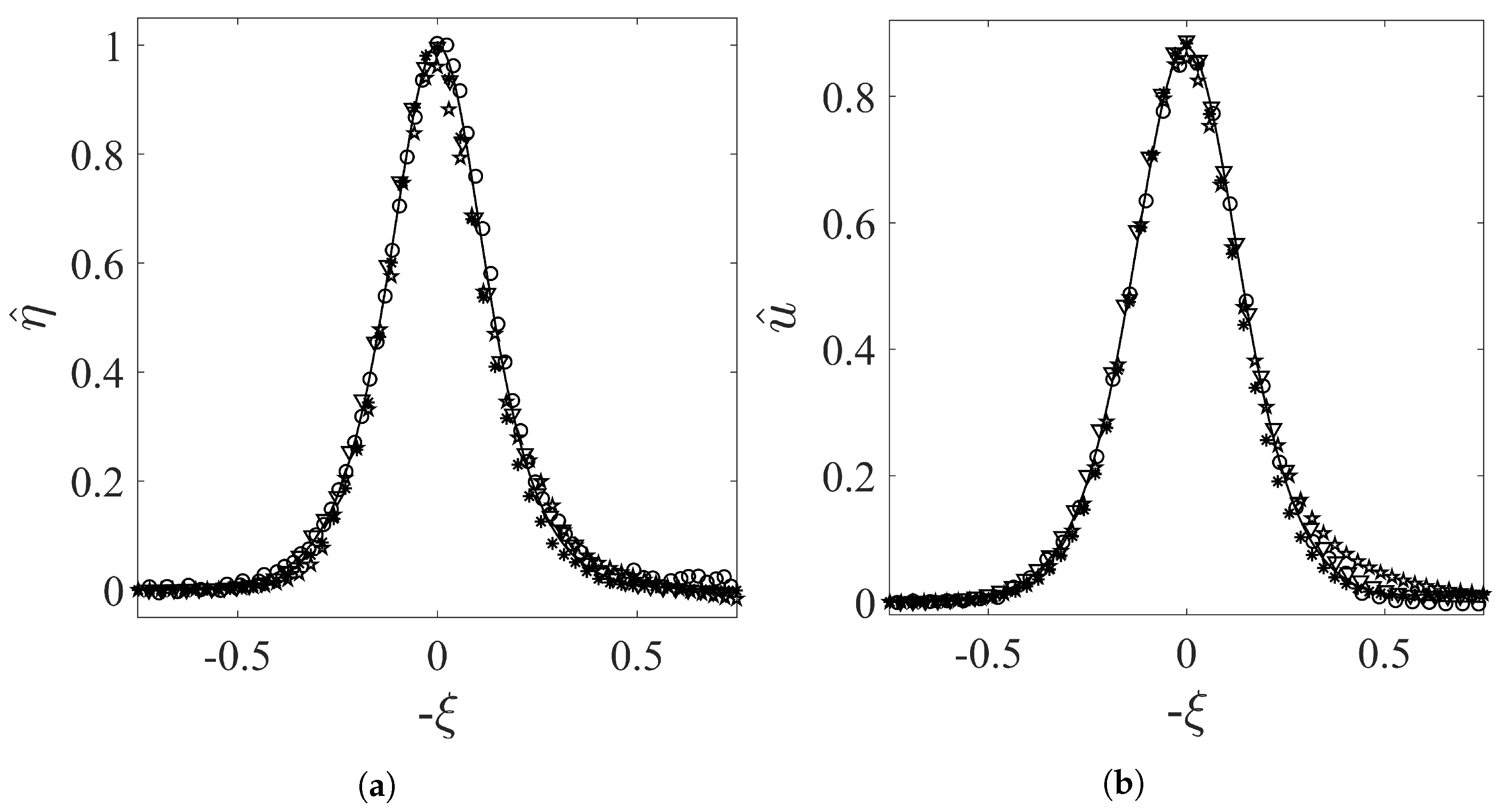
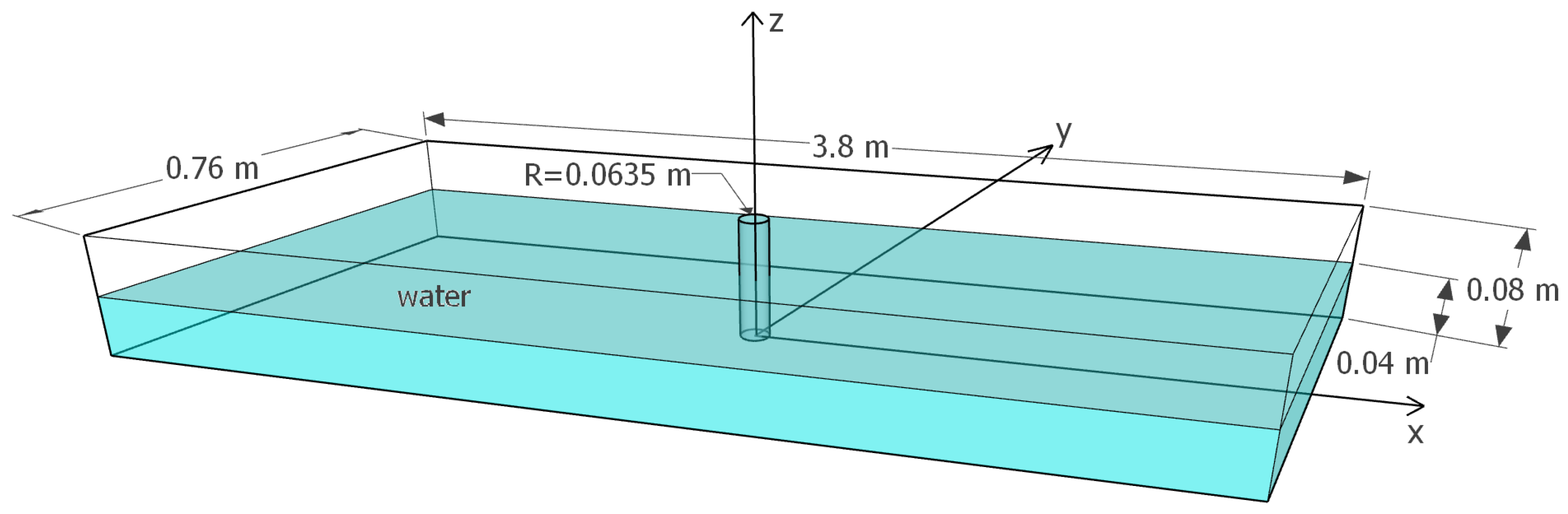
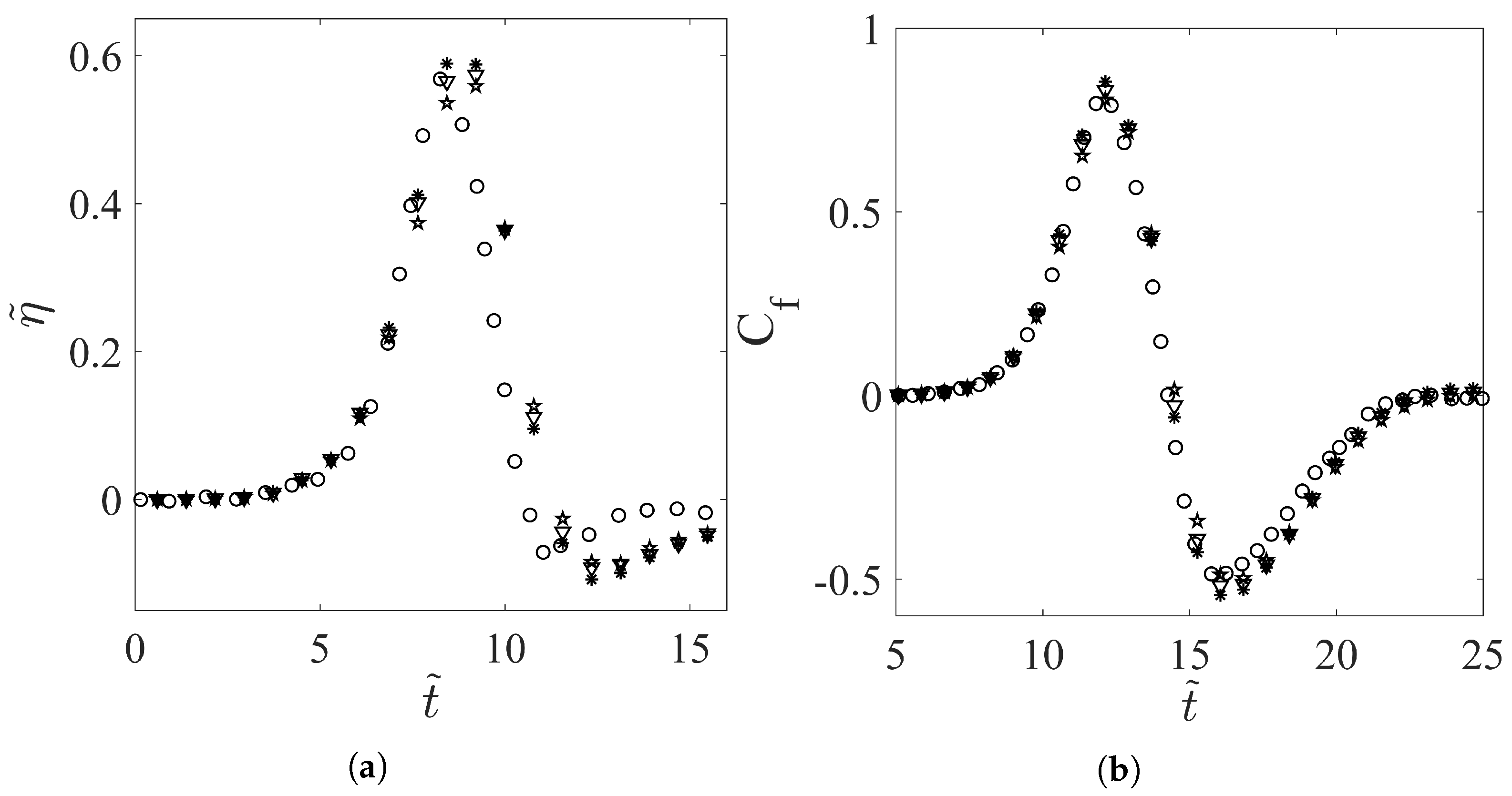
3.2. Solitary Wave Passing a Vertical Cylinder over a Rigid Bottom
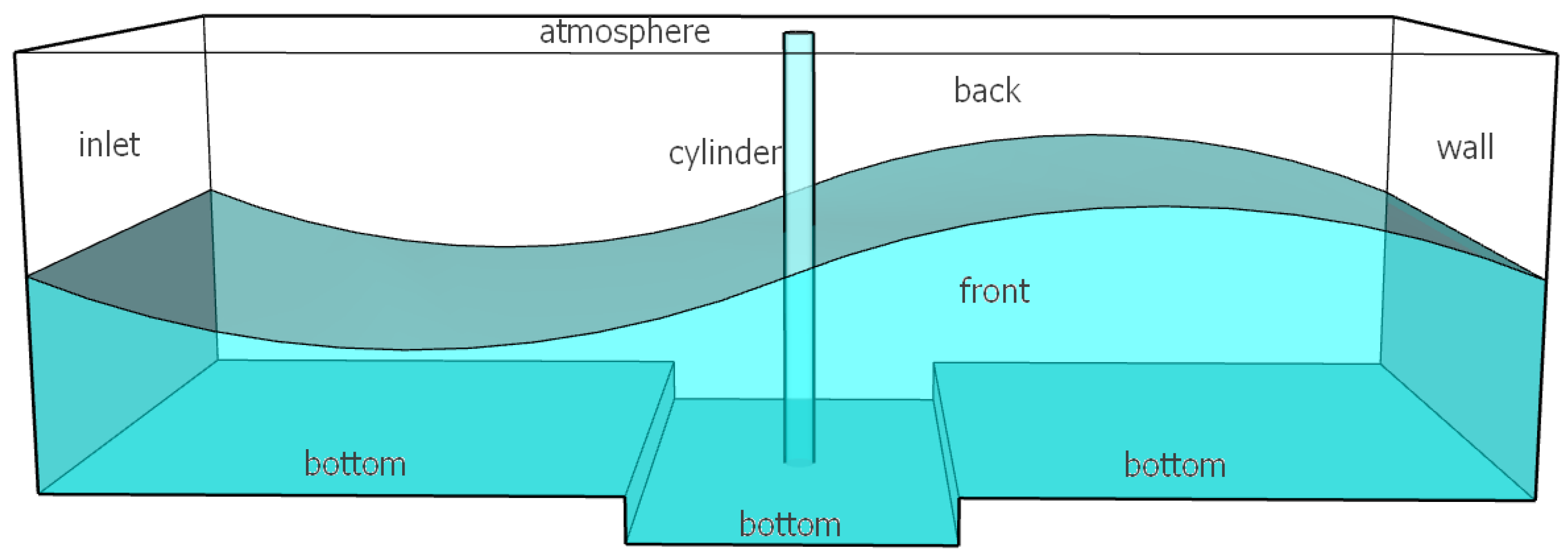
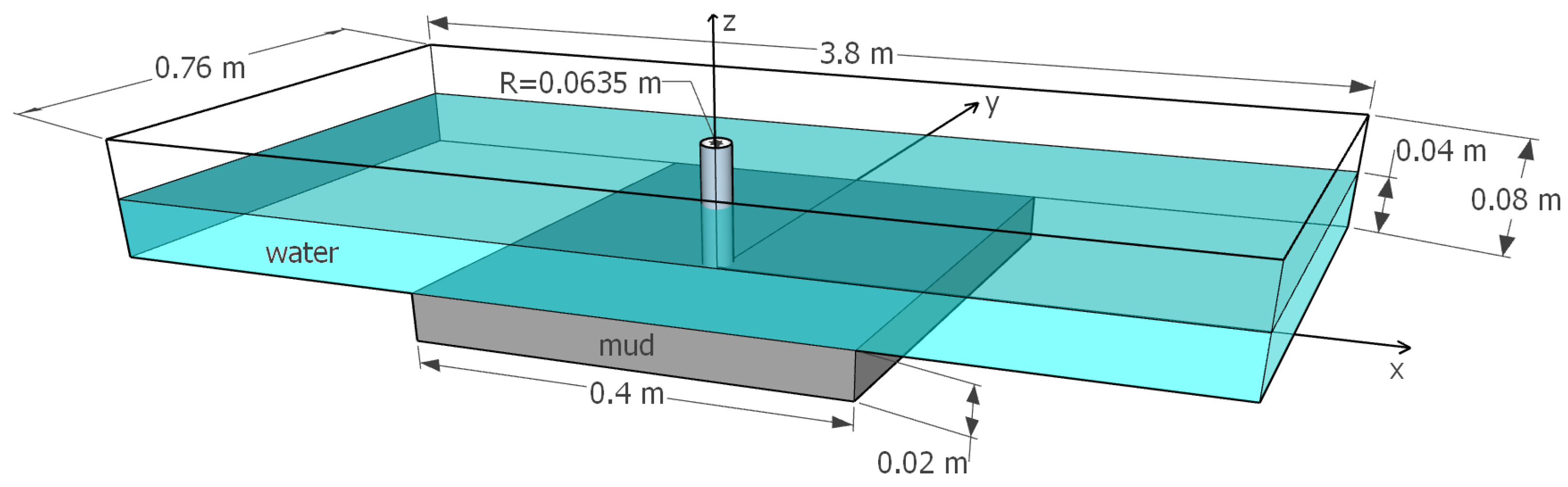
4. Setup of Numerical Investigation
4.1. Numerical Experiments
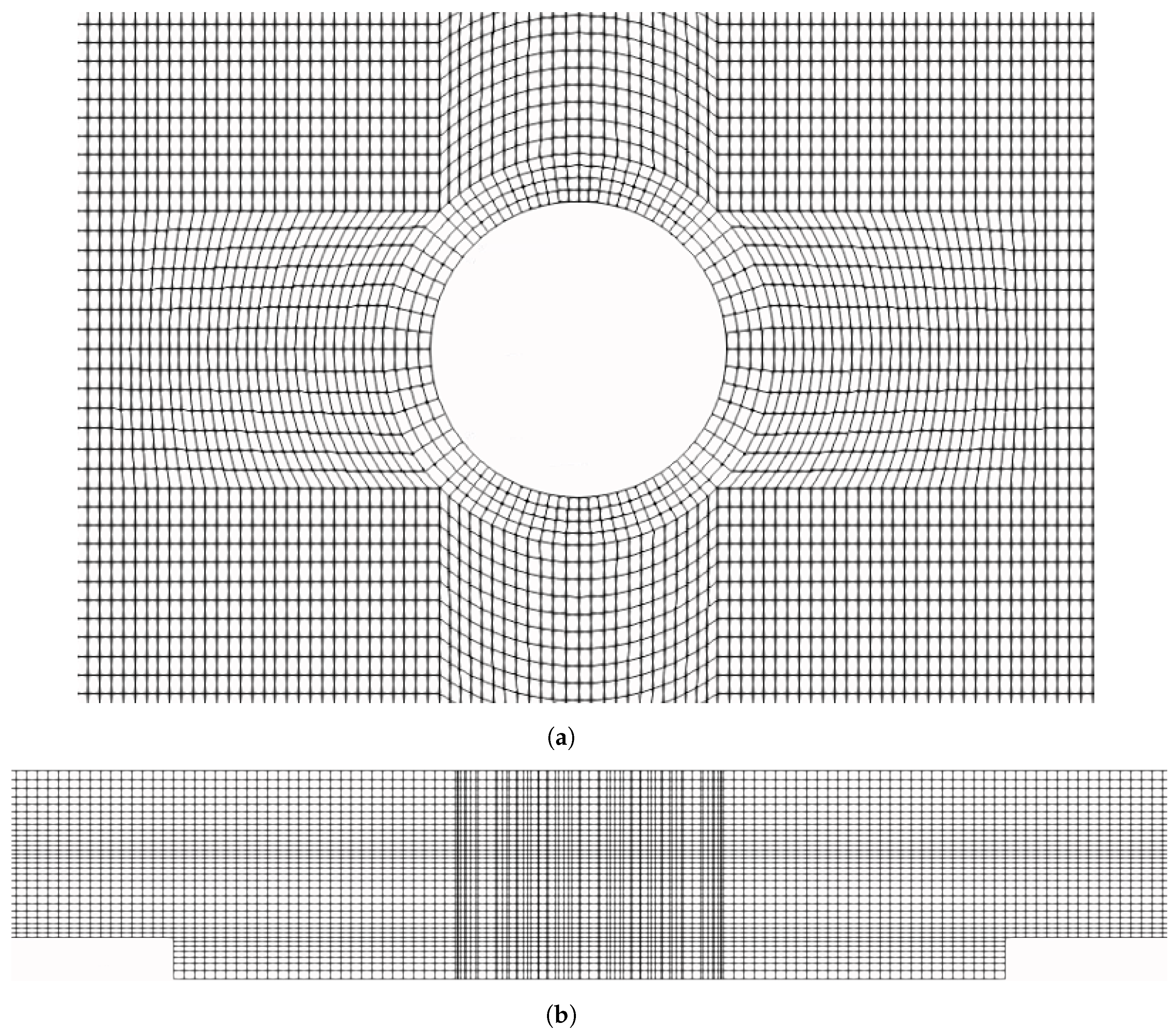
4.2. Mesh Configuration
5. Results
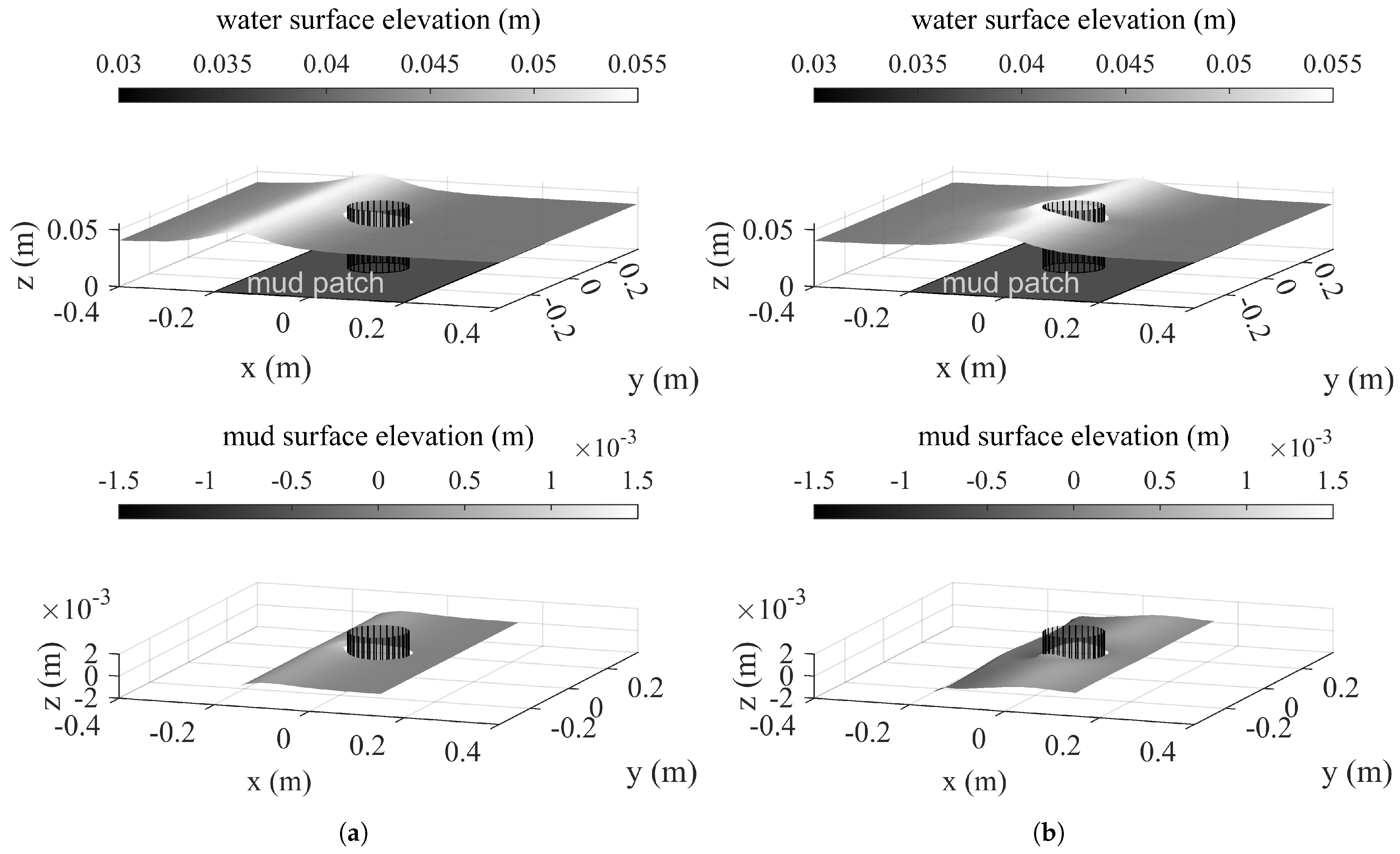
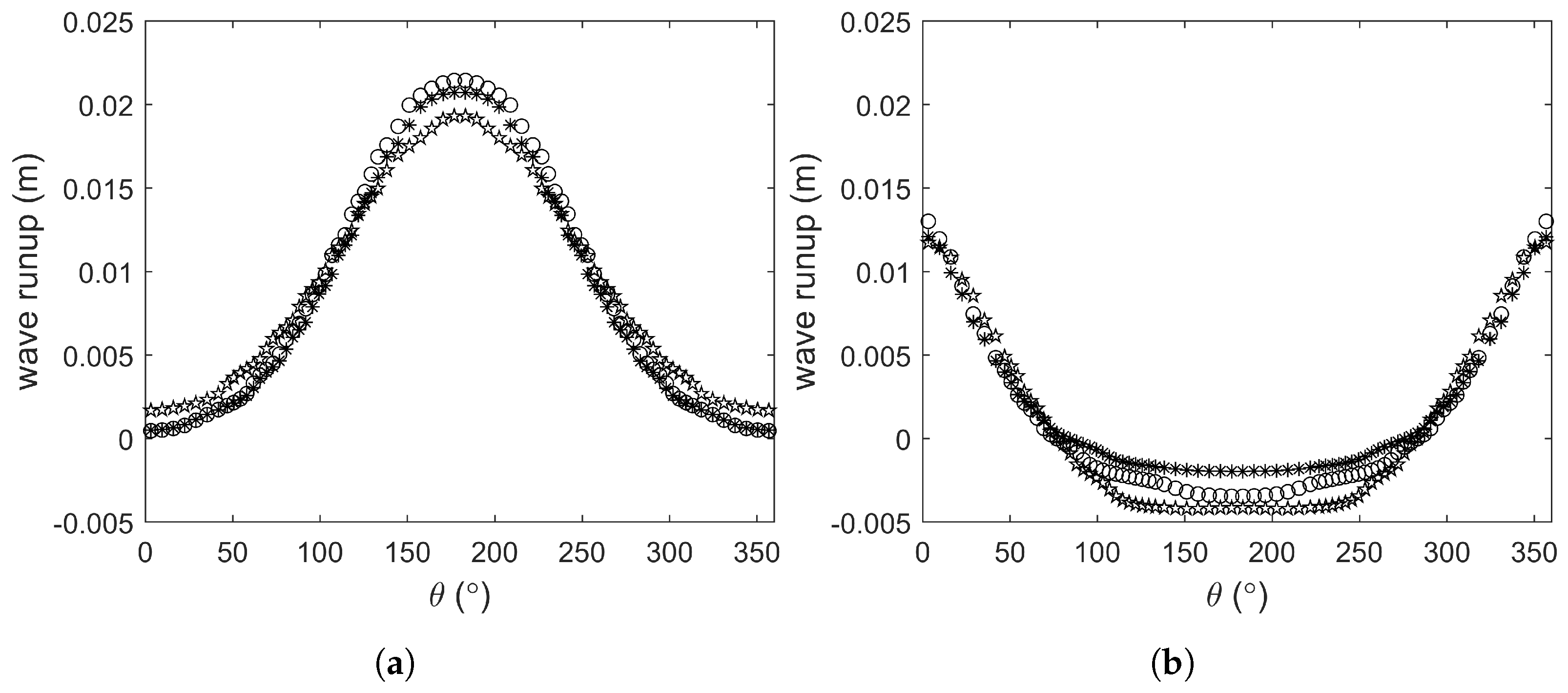
5.1. Water Surface and Mud Surface
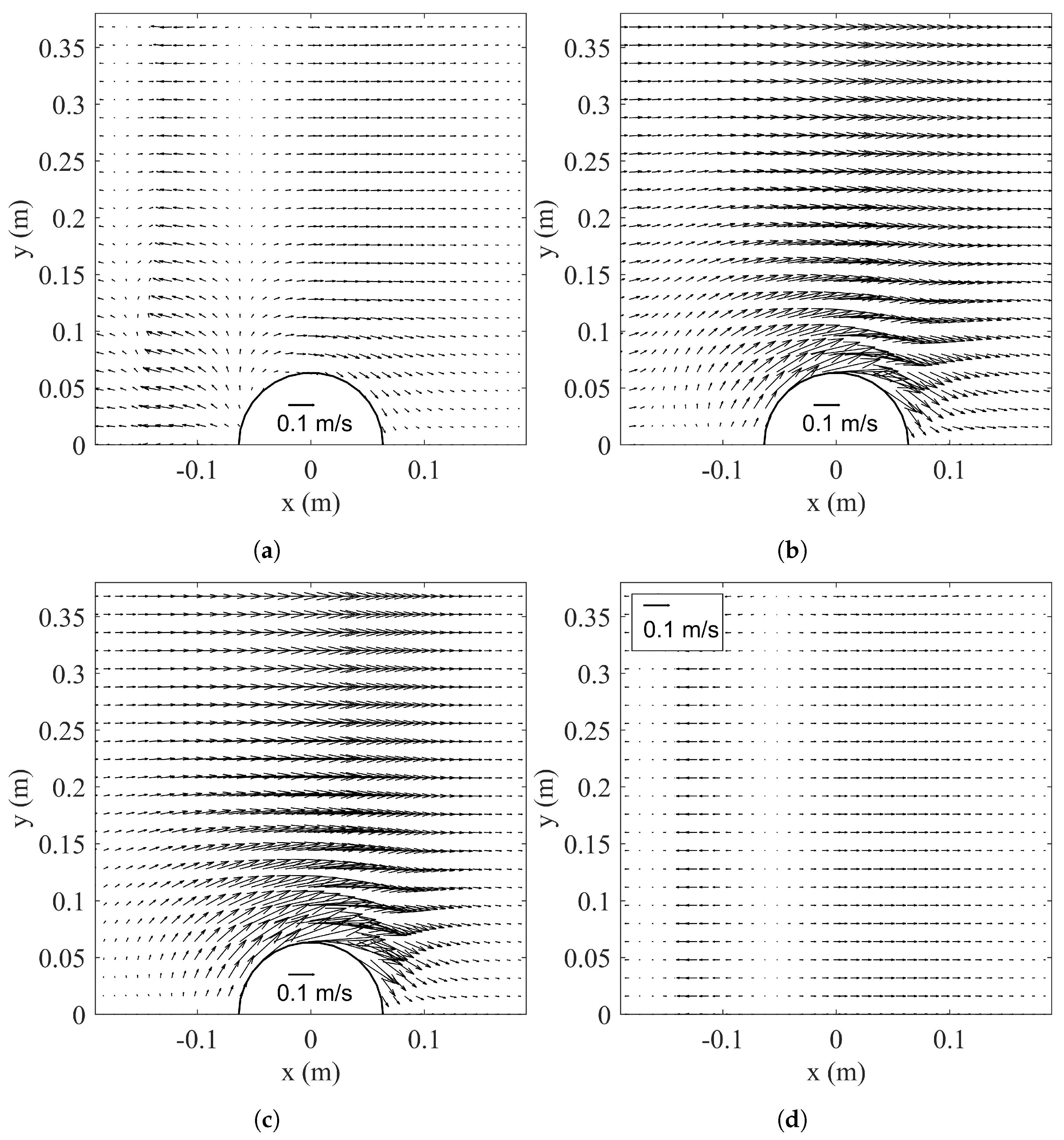
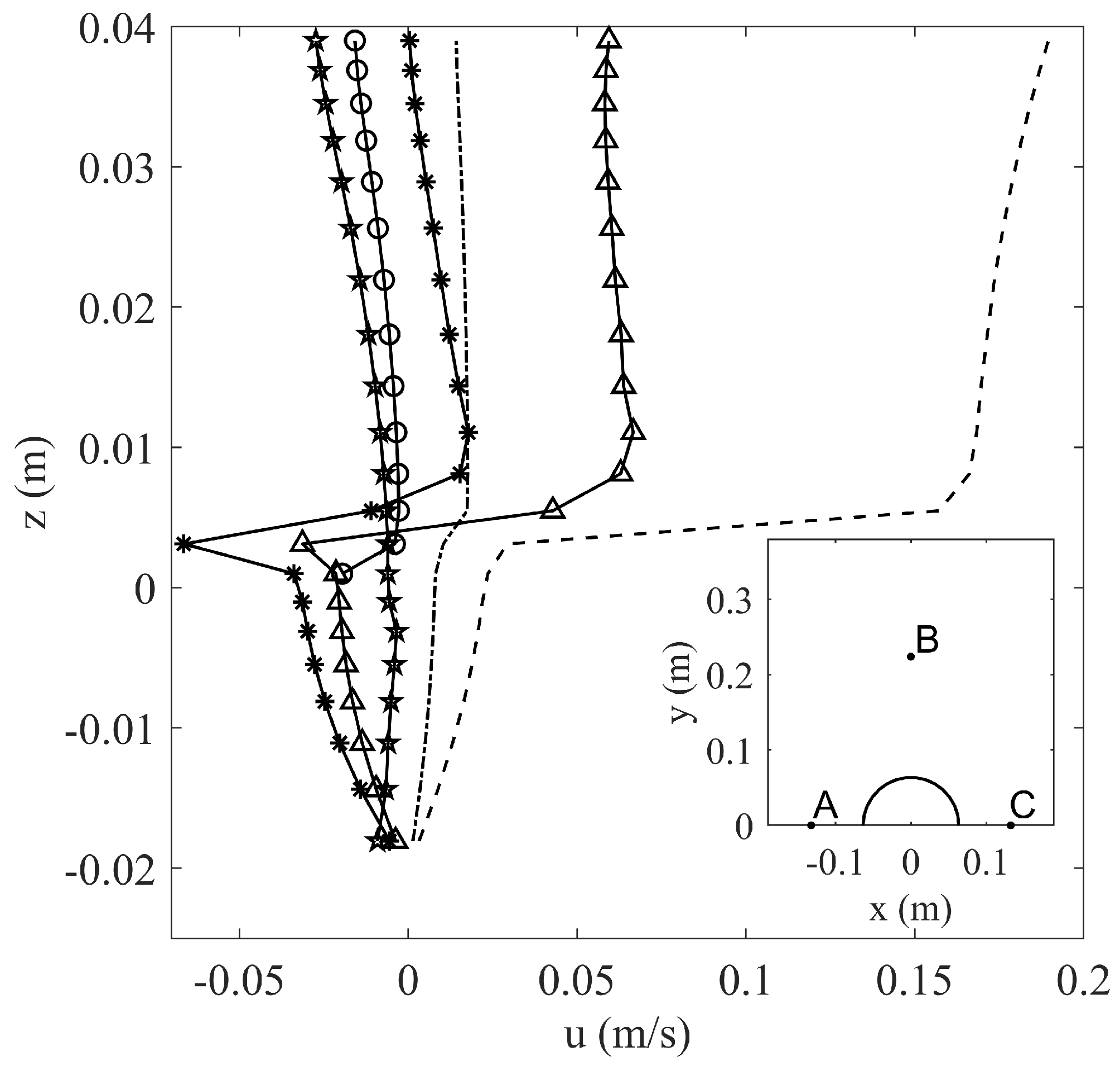
5.2. Velocity Field
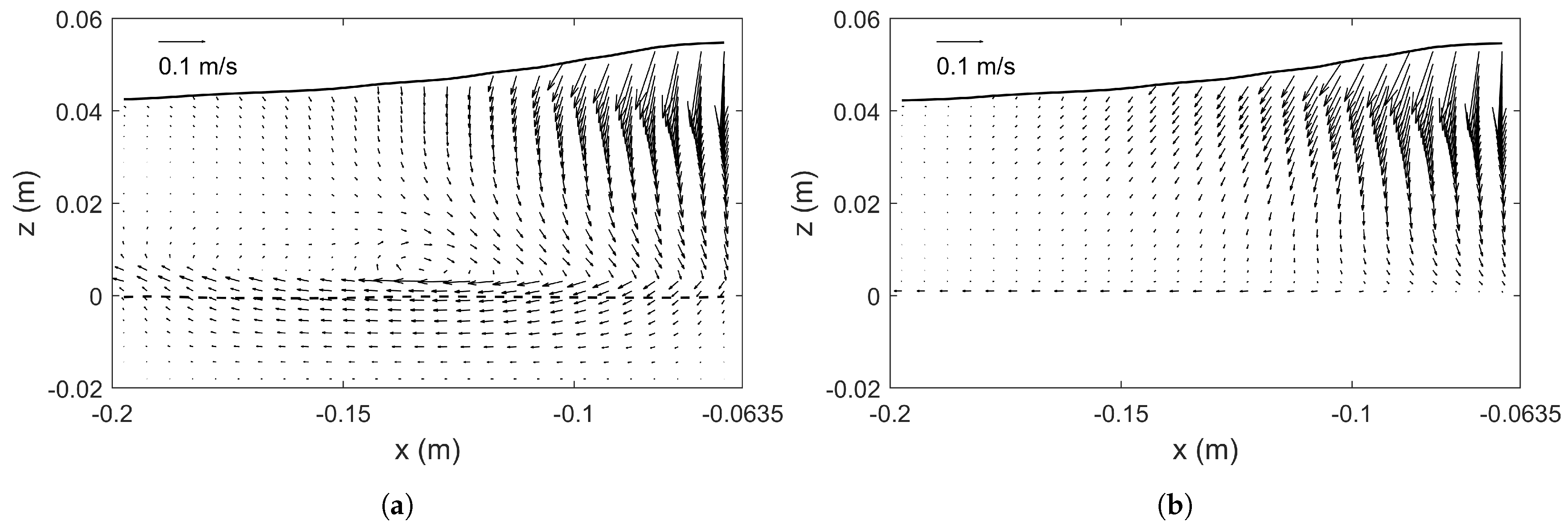
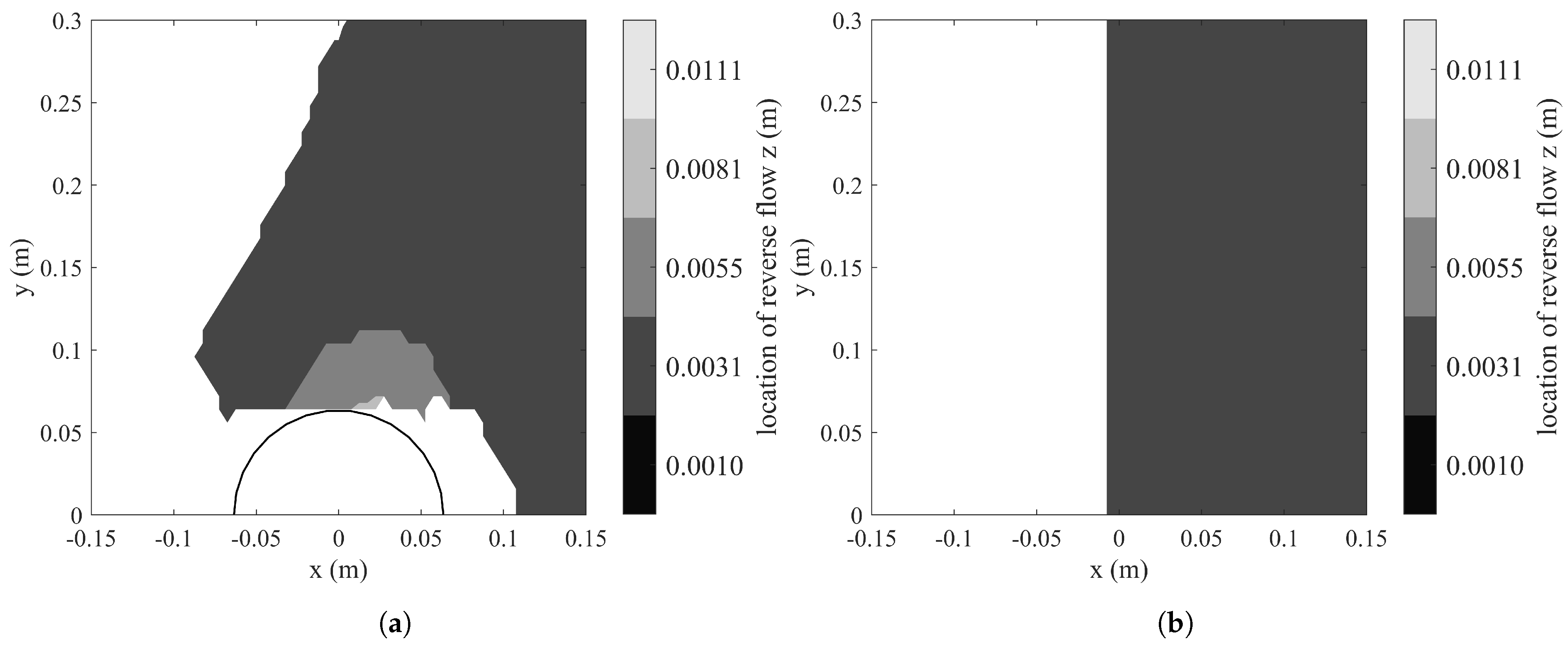
5.3. Flow Reversal
5.4. Mud Flow
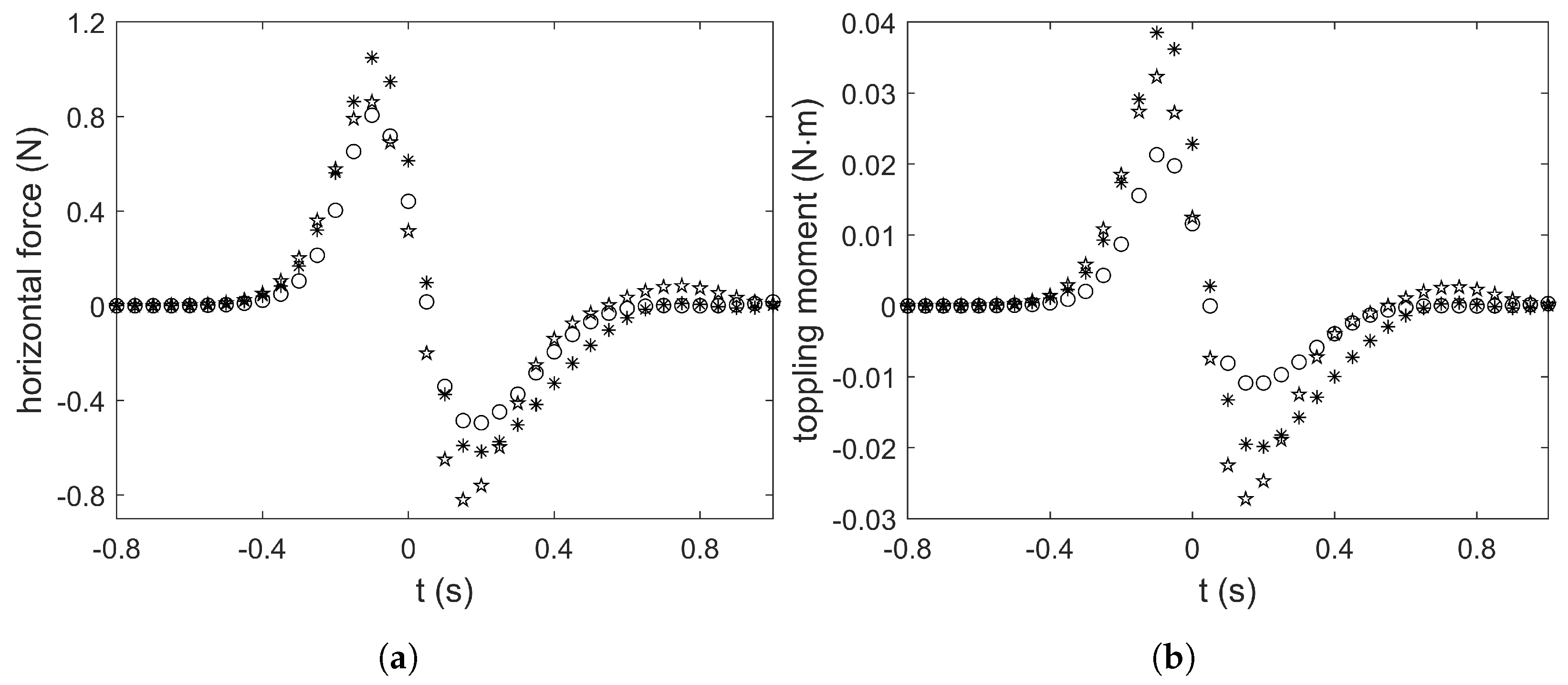
5.5. Forces and Moments
6. Concluding Remarks
- The mud surface deformation is one order of magnitude smaller than the water surface deformation and their deformation patterns are different.
- The scour pattern caused by a solitary wave on a viscous mud bed is different from that commonly observed on a sandy seabed and warrants future investigation.
- In contrast to existing theories assuming a water–solid boundary, the existence of a mud bed instead of a solid boundary appears to have increased the thickness of the water boundary layer near the water–mud interface. Subsequently, the water flow reversal phenomenon occurring inside the boundary layer became more prominent. A more elaborate boundary layer flow analysis is needed.
- The existence of a mud bed increases the total loading and the toppling moment on the cylinder due to wave-induced mud flow.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Correia, J.A.; Ferradosa, T.; Castro, J.M.; Fantuzzi, N.; De Jesus, A.M. Editorial: Renewable energy and oceanic structures: Part I. Proc. Inst. Civ. Eng. Marit. Eng. 2019, 172, 1–2. [Google Scholar] [CrossRef]
- Fazeres-Ferradosa, T.; Chambel, J.; Taveira-Pinto, F.; Rosa-Santos, P.; Taveira-Pinto, F.V.C.; Giannini, G.; Haerens, P. Scour protections for offshore foundations of marine energy harvesting technologies: A review. J. Mar. Sci. Eng. 2021, 9, 297. [Google Scholar] [CrossRef]
- Grimshaw, R. The solitary wave in water of variable depth. J. Fluid Mech. 1970, 42, 639–656. [Google Scholar] [CrossRef]
- Isaacson, M.D.S.Q. Solitary wave diffraction around large cylinder. J. Waterw. Port Coast. Ocean Eng. 1983, 109, 121–127. [Google Scholar] [CrossRef]
- Wang, K.H.; Wu, T.Y.; Yates, G.T. Three-dimensional scattering of solitary waves by vertical cylinder. J. Waterw. Port Coast. Ocean Eng. 1992, 118, 551–566. [Google Scholar] [CrossRef]
- Yates, G.T.; Wang, K.H. Solitary wave scattering by a vertical cylinder: Experimental study. In Proceedings of the 4th International Offshore and Polar Engineering Conference, Osaka, Japan, 10–15 April 1994. [Google Scholar]
- Tonkin, S.; Yeh, H.; Kato, F.; Sato, S. Tsunami scour around a cylinder. J. Fluid Mech. 2003, 496, 165–192. [Google Scholar] [CrossRef]
- Mo, W.; Irschik, K.; Oumeraci, H.; Liu, P.L.F. A 3D numerical model for computing non-breaking wave forces on slender piles. J. Eng. Math. 2007, 58, 19–30. [Google Scholar] [CrossRef]
- Lo, H.Y.; Liu, P.L.F. Solitary waves incident on a submerged horizontal plate. J. Waterw. Port Coast. Ocean Eng. 2014, 140, 04014009. [Google Scholar] [CrossRef]
- Pujara, N.; Liu, P.L.F.; Yeh, H. The swash of solitary waves on a plane beach: Flow evolution, bed shear stress and run-up. J. Fluid Mech. 2015, 779, 556–597. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R.; Baykal, C.; Sumer, B.M. Tsunami-induced scour around monopile foundations. Coast. Eng. 2017, 129, 36–49. [Google Scholar] [CrossRef]
- Larsen, B.E.; Arbøll, L.K.; Kristoffersen, S.F.; Carstensen, S.; Fuhrman, D.R. Experimental study of tsunami-induced scour around a monopile foundation. Coast. Eng. 2018, 138, 9–21. [Google Scholar] [CrossRef]
- Wu, T.R.; Lo, H.Y.; Tsai, Y.L.; Ko, L.H.; Chuang, M.H.; Liu, P.L.F. Solitary wave interacting with a submerged circular plate. J. Waterw. Port Coast. Ocean Eng. 2021, 147, 04020046. [Google Scholar] [CrossRef]
- Jamalabadi, M.Y.A.; Oveisi, M. Numerical simulation of interaction of a current with a circular cylinder near a rigid bed. J. Appl. Math. Phys. 2016, 4, 398–411. [Google Scholar] [CrossRef][Green Version]
- Li, J.; Fuhrman, D.R.; Kong, X.; Xie, M.; Yang, Y. Three-dimensional numerical simulation of wave-induced scour around a pile on a sloping beach. Ocean Eng. 2021, 233, 9–21. [Google Scholar] [CrossRef]
- Li, J.; Kong, X.; Yang, Y.; Deng, L.; Xiong, W. CFD investigations of tsunami-induced scour around bridge piers. Ocean Eng. 2022, 244, 110373. [Google Scholar] [CrossRef]
- Healy, T.; Wang, Y.; Healy, J.A. Muddy Coasts of the World: Processes, Deposits and Function, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Sumer, B.M.; Whitehouse, R.J.S.; Tørum, A. Scour around coastal structures: A summary of recent research. Coast. Eng. 2001, 44, 153–190. [Google Scholar] [CrossRef]
- Schindler, R.; Stripling, S.; Whitehouse, R.; Harris, J. The influence of physical cohesion on scour around a monopile. In Proceedings of the 8th International Conference on Scour and Erosion, Oxford, UK, 12–15 September 2016. [Google Scholar]
- Harris, J.M.; Whitehouse, R.J.S. Scour development around large-diameter monopiles in cohesive soils: Evidence from the field. J. Waterw. Port Coast. Ocean Eng. 2017, 143, 04017022. [Google Scholar] [CrossRef]
- Fazeres-Ferradosa, T.; Taveira-Pinto, F.; Rosa-Santos, P.; Chambel, J. A review of reliability analysis of offshore scour protections. Proc. Inst. Civ. Eng. Marit. Eng. 2019, 172, 104–117. [Google Scholar] [CrossRef]
- Porter, K.E.; Simons, R.; Harris, J.; Ferradosa, T.F. Scour development in complex sediment beds. Coast. Eng. Proc. 2012, 1, sediment.3. [Google Scholar] [CrossRef]
- Gade, H.G. Effects of a nonrigid, impermeable bottom on plane surface waves in shallow water. J. Mar. Res. 1958, 16, 61–81. [Google Scholar]
- Dalrymple, R.A.; Liu, P.L.F. Waves over soft muds: A two-layer fluid model. J. Phys. Oceanogr. 1978, 8, 1121–1131. [Google Scholar] [CrossRef]
- Jiang, L.; Zhao, Z. Viscous damping of solitary waves over fluid-mud seabeds. J. Waterw. Port Coast. Ocean Eng. 1989, 115, 345–362. [Google Scholar] [CrossRef]
- Liu, P.L.F.; Chan, I.C. On long-wave propagation over a fluid-mud seabed. J. Fluid Mech. 2007, 579, 467–480. [Google Scholar] [CrossRef]
- Park, Y.S.; Liu, P.L.F.; Clark, S.J. Viscous flows in a muddy seabed induced by a solitary wave. J. Fluid Mech. 2008, 598, 383–392. [Google Scholar] [CrossRef]
- Hsu, W.Y.; Hwung, H.H.; Hsu, T.J.; Torres-Freyermuth, A.; Yang, R.Y. An experimental and numerical investigation on wave-mud interactions. J. Geophys. Res. Ocean. 2013, 118, 1126–1141. [Google Scholar] [CrossRef]
- Guo, X.; Nian, T.; Wang, Z.; Zhao, W.; Fan, N.; Jiao, H. Low-temperature rheological behavior of submarine mudflows. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 04019043. [Google Scholar] [CrossRef]
- Guo, X.; Nian, T.; Zhao, W.; Gu, Z.; Liu, C.; Liu, X.; Jia, Y. Centrifuge experiment on the penetration test for evaluating undrained strength of deep-sea surface soils. Int. J. Min. Sci. Technol. 2021; in press. [Google Scholar] [CrossRef]
- Mei, C.C.; Liu, K.F. A Bingham-plastic model for a muddy seabed under long waves. J. Geophys. Res. Ocean. 1978, 92, 14581–14594. [Google Scholar] [CrossRef]
- Chan, I.C.; Liu, P.L.F. Responses of Bingham-plastic muddy seabed to a surface solitary wave. J. Fluid Mech. 2009, 618, 155–180. [Google Scholar] [CrossRef]
- Guo, X.; Nian, T.; Wang, D.; Gu, Z. Evaluation of undrained shear strength of surficial marine clays using ball penetration-based CFD modelling. Acta Geotech. 2021. [Google Scholar] [CrossRef]
- Mei, C.C.; Krotov, M.; Huang, Z.; Huhe, A. Short and long waves over a muddy seabed. J. Fluid Mech. 2010, 643, 33–58. [Google Scholar] [CrossRef]
- Oveisy, A.; Hall, K.; Soltanpour, M.; Shibayama, T. A two-dimensional horizontal wave propagation and mud mass transport model. Cont. Shelf Res. 2009, 29, 652–665. [Google Scholar] [CrossRef]
- Keulegan, G.H. Gradual damping of solitary waves. J. Res. Natl. Bur. Stand. 1948, 40, 487–498. [Google Scholar] [CrossRef]
- Liu, P.L.F.; Orfila, A. Viscous effects on transient long-wave propagation. J. Fluid Mech. 2004, 520, 83–92. [Google Scholar] [CrossRef]
- Liu, P.L.F.; Park, Y.S.; Cowen, E.A. Boundary layer flow and bed shear stress under a solitary wave. J. Fluid Mech. 2007, 574, 449–463. [Google Scholar] [CrossRef]
- Xu, K.; Milliman, J.D.; Li, A.; Liu, J.P.; Kao, S.J.; Wan, S. Yangtze- and Taiwan-derived sediments on the inner shelf of East China Sea. Cont. Shelf Res. 2009, 29, 2240–2256. [Google Scholar] [CrossRef]
- Huh, C.A.; Chen, W.; Hsu, F.H.; Su, C.C.; Chiu, J.K.; Lin, S.; Liu, C.S.; Huang, B.J. Modern (<100 years) sedimentation in the Taiwan Strait: Rates and source-to-sink pathways elucidated from radionuclides and particle size distribution. Cont. Shelf Res. 2011, 31, 47–63. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Higuera, P. olaFlow: CFD for Waves [Software]. 2017. Available online: https://doi.org/10.5281/zenodo.1297013 (accessed on 1 March 2022).
- Greenshields, C.J. OpenFOAM Programmer’s Guide; Technical Report Version 3.0.1; OpenFOAM Foundation Ltd.: London, UK, 2015. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Sarpkaya, T.; Isaacson, M.D.S.Q. Mechanics of Wave Forces on Offshore Structures, 1st ed.; Van Nostrand Reinhold: New York, NY, USA, 1981. [Google Scholar]




| Name | Test1 | Test2 | Test3 | Test4 |
|---|---|---|---|---|
| Incident wave | solitary wave () | solitary wave () | solitary wave () | solitary wave () |
| Cylinder | yes | yes | yes | no |
| Slot | yes | yes | no | yes |
| Material in slot | highly viscous Newtonian fluid | water | N/A | highly viscous Newtonian fluid |
| Name | Test1 | Test2 | Test3 | Test4 |
|---|---|---|---|---|
| Flume size | 3.80 m long, 0.76 m wide, 0.08 m high | same as test1 | same as test1 | same as test1 |
| Slot size | 0.40 m long, 0.76 m wide, 0.02 m high | same as test1 | N/A | same as test1 |
| Cylinder | radius 0.0635 m | same as test1 | same as test1 | N/A |
| Min. mesh | cm | same as test1 | same as test1 | same as test1 |
| cm for ; increases to cm at 1.9 m | same as test1 | same as test1 (w/o slot) | same as test1 (w/o cylinder) | |
| cm for rectangular cells; cm for curvilinear cells | same as test1 | same as test1 (w/o slot) | same as test1 (w/o cylinder) | |
| cm near the air–water and water–mud interfaces; increases to cm away from the interfaces | same as test1 | same as test1 (w/o slot) | same as test1 (w/o cylinder) | |
| Mesh near cylinder | 4 concentric layers from the cylinder; each layer consists of 76 curvilinear cells of roughly equal size as nearby rectangular cells | same as test1 | same as test1 (w/o slot) | same as test1 (w/o cylinder) |
| No. of cells | 1,609,884 | same as test1 | 1,557,468 | 1,628,110 |
| Name | Test1 | Test2 | Test3 |
|---|---|---|---|
| Total maximum positive force | N | N | N |
| Maximum positive force from to water surface | N | N | N |
| Maximum positive force from m to m | N | N | N/A |
| Total maximum negative force | N | N | N |
| Maximum negative force from to water surface | N | N | N |
| Maximum negative force from m to m | N | N | N/A |
| Name | Test1 | Test2 | Test3 |
|---|---|---|---|
| Total maximum positive moment about m | N·m | N·m | N/A |
| Maximum positive moment about m, calculated only from m to water surface | N·m | N·m | N·m |
| Total maximum negative moment about m | N·m | N·m | N/A |
| Maximum negative moment about m, calculated only from m to water surface | N·m | N·m | N·m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, R.; Lo, P.H.-Y. Numerical Investigation on Solitary Wave Interaction with a Vertical Cylinder over a Viscous Mud Bed. Water 2022, 14, 1135. https://doi.org/10.3390/w14071135
Guo R, Lo PH-Y. Numerical Investigation on Solitary Wave Interaction with a Vertical Cylinder over a Viscous Mud Bed. Water. 2022; 14(7):1135. https://doi.org/10.3390/w14071135
Chicago/Turabian StyleGuo, Ronglian, and Peter H.-Y. Lo. 2022. "Numerical Investigation on Solitary Wave Interaction with a Vertical Cylinder over a Viscous Mud Bed" Water 14, no. 7: 1135. https://doi.org/10.3390/w14071135
APA StyleGuo, R., & Lo, P. H.-Y. (2022). Numerical Investigation on Solitary Wave Interaction with a Vertical Cylinder over a Viscous Mud Bed. Water, 14(7), 1135. https://doi.org/10.3390/w14071135






