Abstract
This paper took the Foziling Reservoir in the Pi River Basin as an example, used an improved genetic algorithm to optimize the flood control dispatching during the flood process, and compared the results with the traditional genetic algorithm and the dispatching plan in the 2020 large-scale reservoir flood control operation plan. The results showed that, compared with the traditional genetic algorithm, the improved genetic algorithm saved the time for the model to determine the penalty coefficients and made the model application more convenient. At the same time, the design of the original scheduling scheme also has certain limitations. The scheduling results obtained by improving the genetic algorithm could occupy a small flood control capacity as much as possible under the premise of ensuring the safety of the reservoir itself and the downstream area.
1. Introduction
Reservoir flood control optimization dispatch is an important non-engineering flood control measure that can improve the flood control capacity of the reservoir, which plays a role in regulating flood peaks, storing floodwaters, reducing or even avoiding flood disasters [1]. In practice, the optimal operation model is generally constructed and solved based on certain optimization algorithms such as linear programming, nonlinear programming and dynamic programming [2,3,4] to realize the optimal operation of reservoir flood control.
With the progress of modern computer technology, a class of modern heuristic algorithms based on biology, physics and artificial intelligence [5,6,7,8] has been developed. The genetic algorithm (GA) is an important optimization algorithm in heuristic algorithms. It imitates the law of “survival of the fittest” in nature, uses a selection operation to eliminate individuals with low fitness according to the fitness of the generated individual, uses “crossover” and “mutation” operations to generate new populations, and finally gets feasible solutions that meet the requirements of decision makers with evolution from generation to generation. Compared with other optimization methods, such as linear programming and dynamic programming, the GA algorithm has the characteristics of strong adaptability, global optimization, self- adaptation, strong robustness, etc., so it is widely used in reservoir optimal scheduling and other fields [9,10,11].
Then, in order to improve the convergence speed of the genetic algorithm, Liu et al. [12] proposed an improved strategy which can comprehensively improve the computational efficiency of the genetic algorithm by studying the encoding method, constraint processing strategy and convergence of the genetic algorithm. Ahmed et al. [13] used the penalty function method to deal with constraints, that is, using the appropriate fitting function to distinguish between feasible and infeasible solutions satisfying the constraints, and obtained good convergence results. In order to solve the problem where the genetic algorithm converges to the local optimal solution, Wang [14] constructed a multi-objective reservoir optimal operation model, proposed an adaptive genetic algorithm and applied it to an example. The results showed that the genetic algorithm combined with adaptive mapping could make the optimization results closer to the frontier of the non-inferior solution of the model.
There are many constraints in the process of reservoir dispatching. The common processing method of the traditional GA algorithm is the penalty function method, which accelerates the screening by imposing penalties on the individual fitness of each generation that does not meet the constraints. However, the penalty coefficient of the penalty function is often difficult to determine, as the algorithm with the too small coefficient may converge to an infeasible solution, and the algorithm that is too large may fall into local convergence [12]. Therefore, this paper improves the traditional GA algorithm and uses prior knowledge to consider some constraints (such as water balance constraints and discharge capacity constraints) when generating the initial population, screens randomly generated genes, and keeps a series of qualified genes so as to avoid excessive or negative flow at adjacent times, thus reducing the number of penalty functions; At the same time, new individuals generated by crossover and variation in each generation are screened to ensure that genes on each chromosome meet the constraints to improve the efficiency of calculation.
As an important tributary of the middle reaches of the Huai River, the Pi River has a steep slope and rapid flow, and flood disasters have occurred frequently in its history. Since the founding of the People’s Republic of China, large floods occurred in 14 years, including 1951, 1953, 1954, 1956, 1964, 1969, 1975, 1984, 1991, 1996, 1999, 2003, 2005 and 2015, which brought serious flooding disasters to the middle and lower reaches of the river basin [15]. The Foziling Reservoir is located in the middle reaches of the Dongpi River in Huoshan County, Lu’ an City. It belongs to the Pi River system of the Huai River Basin and is the lowest level of the Dongpi River cascade reservoir group. The Foziling Reservoir is located in the northern edge of the northern subtropical zone, belonging to the East Asian monsoon humid climate zone. The reservoir basin is a deep mountain area of the Dabie Mountains, most of which are high mountains, and a rainy center is formed with the main peak of the Dabie Mountains as the center. The main river is 77 km with an average slope of 6.5 ‰. Precipitation is mainly concentrated in the flood season (May–September), during which the flood collection time is short, the fluctuation is fast, the flood peak flow is large, and the main inflow rivers are the Manshui River and the Huangwei River. According to the measured data from 1956 to 2010, the average annual rainfall is 1481 mm, the average annual inflow is 51.4 m3/s, the average annual inflow is 1.62 billion m3, and the average annual runoff depth is 880 mm. The historical highest reservoir water level is 130.64 m, and the corresponding reservoir capacity is 511 million m3.
In addition, the Foziling Reservoir is an important part of the Huai River treatment project and protects Huoshan County Town and Luan City downstream of the reservoir. The location of the Foziling Reservoir and its objects of protection is shown in Figure 1. Therefore, this paper took Foziling Reservoir in the Pi River Basin as the research object, took the maximum safe discharge and the maximum flood control capacity occupied by the reservoir as the control index, and used the July 1991 and June 1999 floods as an example to optimize the flood control operation of the reservoir through the improved genetic algorithm and the flood control optimization dispatching model. The results were compared with the traditional genetic algorithm and the scheduling plan of the Foziling Reservoir in the 2020 large-scale reservoir flood control operation plan (hereinafter referred to as the 2020 operation regulation) to verify the effectiveness and rationality of the improved genetic algorithm.
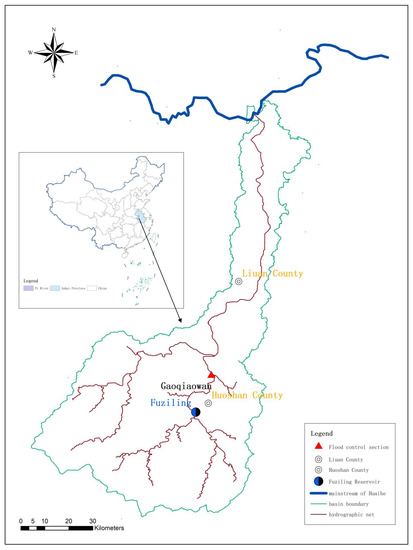
Figure 1.
Location of Foziling Reservoir and its protection objects.
2. Materials and Methods
2.1. Construction of Optimal Flood Control Dispatching Model
The prerequisite for the optimized flood control dispatching of reservoirs is to clarify whether there are flood control tasks downstream. If there is no protection object downstream, the reservoir only needs to be designed for its own safety, and the discharge can be based on its own discharge capacity; however, if there are important towns and other objects in the downstream that need to be protected, then the reservoir discharge cannot only be designed for its own discharge capacity. On this basis, the downstream protection objects need to be considered [16]. Only when the discharge flow of the reservoir is lower than the maximum safe discharge flow of the control section of the downstream protection object can the protection object be considered to be in a safe state. Therefore, when encountering a flood, the optimization objective is to occupy as little as possible of the flood control reservoir capacity under the premise of ensuring the safety of the reservoir itself and the protection objects downstream of the reservoir [17,18], that is, the maximum flood control safety guarantee criterion [19]. Under the circumstances, the reservoir has enough capacity to deal with the next possible flood. For the convenience of calculation, the scheduling process is discretized into moments and periods. At this time, the objective function is shown in the following formula:
where is the flood control storage capacity occupied by the reservoir at time , million m3.
In order to make the results of the model fit the actual situation, the following constraints need to be constructed to limit the solution process, so as to obtain a feasible solution that meets the requirements of decision makers.
- 1.
- Water level restriction
- 2.
- Discharge flow restriction
- 3.
- Water balance restriction
- 4.
- Relationship between water level and storage capacity, relationship between water level and discharge capacity
- 5.
- Amplitude constraints of discharge flow
- 6.
- Non-negative constraints.
The above variables such as water level, storage capacity, and discharge flow are not negative.
In Formulas (2)–(8), and are the flood limit water level of the reservoir, the design flood level, m; is the water level of the reservoir at time , m; is the discharge flow of the reservoir during the period, m3/s; is the maximum discharge capacity of the reservoir itself at each time period, including spillway steel pipe, spillway, etc., m3/s; is the safe discharge flow of the control section downstream of the reservoir, m3/s; is the inflow of the reservoir during the period, m3/s; is the time step; is the water level and storage capacity relation curve function of the reservoir at time ; is the function of the water level and discharge capacity of the reservoir at the end of the period; ΔQ is the variation range of reservoir discharge flow in adjacent periods.
2.2. Model Solving Method
In this paper, the improved GA algorithm is used to solve the model.
- 1.
- Population initialization
When generating the initial population, different coding strategies will affect the calculation accuracy of the algorithm and the time required to achieve convergence. For example, although the concept of binary code is clear, its output needs to be converted to a real number and is limited by the length of code, which often causes problems such as inadequate calculation accuracy and coding redundancy. Real value coding minimizes the problem of limited coding length and saves time for binary to real value conversion. Therefore, this paper uses real value coding to take the discharge flow rate of each period in the dispatching process as a decision variable, i.e., gene, so the length of coding is the number of decision variables.
where is the individuals in a population; is the gene on the chromosome; is the number of genes; is the population size.
The inflow process and starting water level of the reservoir are often known during operation, and the population initialization can be completed according to the following steps.
- (1)
- There are groups, and random outflow from 0 to are generated in each group;
- (2)
- According to the relationship between water level and storage capacity, water level and discharge capacity, the storage capacity and discharge capacity corresponding to at the current time are calculated;
- (3)
- According to Formula (10), the initial outflow is replaced, and the storage capacity at the next moment is calculated;
- (4)
- According to Formula (6), the corresponding to at is obtained. Repeat steps 2 and 3.
- 2.
- Construct penalty functions
There are three penalty functions, which are punish 1, which is imposed on the failure of reservoir water levels to return to flood limit levels at the end of the dispatching period, punish 2, which is imposed on reservoir water levels exceeding flood control high levels or below flood limit levels during the dispatching period, and punish 3 for the variation of discharge flow rates in adjacent periods of the reservoir, as detailed in Formulas (11)–(13).
where is the water level at the end of dispatching; and are the highest and lowest water levels that can be reached during dispatching.
- 3.
- Calculate population fitness
Fitness reflects the strengths and weaknesses of individuals in a population. The design and complexity of the fitness function will affect the convergence speed and robustness of the algorithm. In this paper, the fitness function consists of the objective function and the penalty function.
where is the fitness of the chromosome I; is the storage capacity corresponding to the largest gene on the chromosome I; , and are the penalty coefficients corresponding to each penalty function.
Since the objective function of this study is to minimize the flood reservoir capacity occupied in the process of dispatching, individuals with high fitness values are easy to be eliminated in the next genetic operation, and the lower the fitness value, the stronger the competitiveness of the individuals.
- 4.
- Genetic manipulation
Selection: This operation simulates the survival of the fittest in nature, ranks the individuals in the population according to the fitness value, selects the individuals with lower fitness in the population through the selection rate Ps and then selects the better ones from the remaining individuals to replace the eliminated ones again so as to ensure that the size of the population remains unchanged. At the same time, in order to avoid the gene of the best individual being destroyed due to crossover and mutation in the evolution process, the elite strategy is adopted, i.e., to preserve the best individual that has appeared so far in the evolution process and copy it to the next generation to replace the individual with high fitness value.
Crossover: In order to generate new individuals for the next generation and improve the search ability of the genetic algorithm, the selected individuals need to be crossed. The crossover operator includes single point crossover, multi-point crossover, uniform crossover, etc. In this paper, a single point crossover method is used to generate new individuals. That is to say, according to the crossover rate Pc, the paired chromosomes generate crossover sites and exchange gene fragments before or after the crossover sites of paired chromosomes, as shown in the following Figure 2.
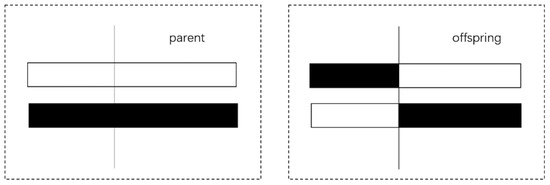
Figure 2.
Single point crossover.
Mutation: During the process of new population generation, some individual genes will be mutated, so it is necessary to mutate the crossed individuals according to the rate of mutation Pm. Among them, the individuals with good fitness value have little probability of mutation, so as to ensure that the effective genes on the chromosome will not be deleted as much as possible [20]. At the same time, with the increase of evolutionary generation, the range of mutation gradually decreases. In the early stage of evolution, the original gene is replaced by a randomly generated gene. In the later stage of evolution, the gene to be mutated is enlarged or reduced on a small scale to enable the algorithm to perform a local search.
After crossover and mutation, genes on each individual’s chromosome still need to be screened to satisfy the downstream safety discharge, reservoir discharge capacity and water balance constraints. The calculation steps of the genetic algorithm are shown in Figure 3.
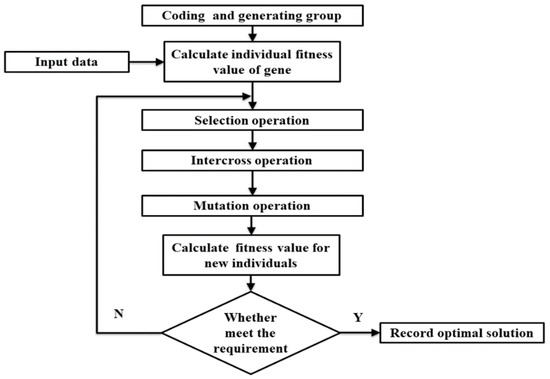
Figure 3.
The flowchart of the genetic algorithm.
- 5.
- Control Parameters
The control parameters are generally determined by experience. In order to make the calculation results close to the theoretical optimal solution and reduce the amount of calculation to improve the calculation efficiency, this paper makes several trial calculations based on experience. Finally, the initial population n, selection rate Ps, and crossover rate Pc is defined as 40, 40%, and 60%, respectively. The formula for calculating the mutation rate Pm is as follows. Selection of parameters can be seen in 4.3 Selection of control parameters.
where , , are respectively the fitness value of the individual I of the population, the current average fitness value and the minimum fitness value of the population.
3. Results
3.1. Overview of the Study Area
The Foziling Reservoir is located at the upper reaches of the east source of the Pi River, a tributary of the Huai River. The Manshui River and the Huangwei River run into the reservoir. It is a large (2) reservoir that focuses on flood control and takes irrigation, power generation, and shipping into account. It is rated to withstand a one in a thousand years flood. The dam site of the reservoir is in the southwest of Huoshan County, Anhui Province, with a control area of 1270 km2. The flood limit water level in the main flood season is 118.56 m, the design flood level is 125.65 m, and corresponding storage capacity is 262.02 × 106 m3, 397.80 × 106 m3, respectively. Reservoir flood discharge facilities are equipped with flood discharge steel pipes, spillways, etc. When the water level rises to the corresponding elevation, they undertake their discharge tasks respectively. The characteristic water level of the Foziling Reservoir is shown in Table 1.

Table 1.
Characteristic water level of Foziling Reservoir (m, based on the waste elevation of yellow river mouth).
The flood control standard of the downstream reservoir is once in 20 years, so the reservoir should play a flood control role. The reservoir protects important cities and towns such as Huoshan County (17 km downstream) and Luan City (60 km downstream), important infrastructure such as Hewu, Ningxi Railway, G35 and G42 Expressway downstream, and the 312 National Highway (65 km away from the reservoir), and protects about 1.3 million people and 720,000 mu of cultivated land. The corresponding control sections in Huoshan County and Luan City are the Gaoqiaowan Section and the Hengpaitou Section, respectively, and the corresponding maximum safe discharge is 3760 m3/s and 4770 m3/s.
In the 2020 operation regulation, when the water level of the Foziling Reservoir rises in flood season but does not exceed 123.08 m, the discharge flow of the reservoir is controlled within 3450 m3/s. If the water level continues to rise, then all flood discharge facilities will be opened to ensure the safety of the reservoir itself. Therefore, in this study, the maximum safe discharge flow of the reservoir is 3450 m3/s, which means that as long as the maximum discharge flow of the reservoir does not exceed 3450 m3/s, the downstream Huoshan County and Luan City will be protected in a safe state. Figure 4 and Figure 5 show the water level-reservoir capacity relation curve and water level-discharge capacity relation curve of the Foziling Reservoir.
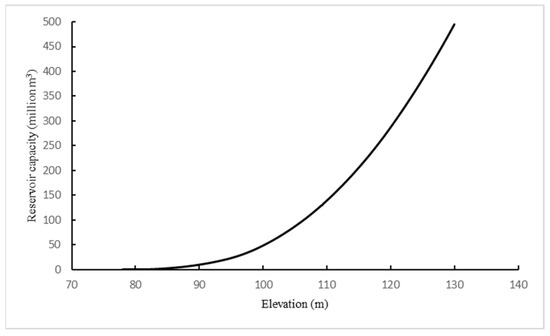
Figure 4.
Water level-reservoir capacity relationship.
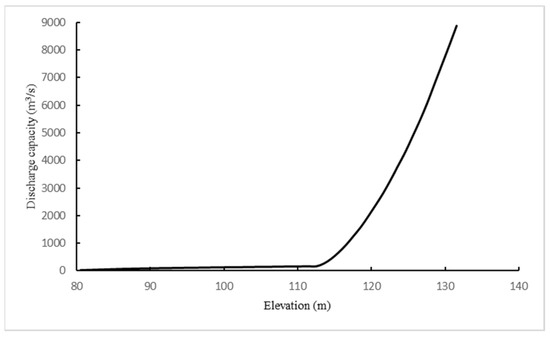
Figure 5.
Water level-discharge capacity relationship.
3.2. Application Results
3.2.1. Scheduling Rules of Optimization Algorithm
On the premise of ensuring the safety of downstream flood control, this paper takes the minimum flood control reservoir capacity of the Foziling Reservoir in the situation of a flood as the goal and considers the following principles:
From flood limit water level (118.56 m) in the main flood season, the water level during dispatching cannot exceed the designed flood level (125.65 m). After the end of the flood, the water level is required to fall back to the flood limit water level in order to cope with the next possible flood.
In order to ensure the flood control safety of Huoshan County and Luan City downstream of the reservoir, the maximum discharge flow of the reservoir cannot exceed 3450 m3/s during operation.
3.2.2. Optimization Results
The floods that occurred in the history of the Foziling Reservoir areselected as the input condition of the model for optimal flood control operation. Taking the floods of July 1991 and June 1999 as examples, the flood inflow process and reservoir regulation process are shown in Figure 6 and Figure 7.
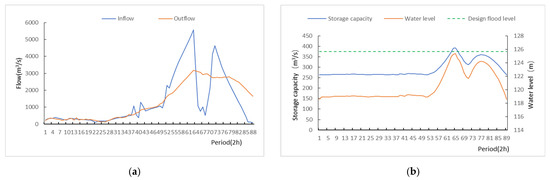
Figure 6.
Reservoir regulation process in July 1991 flood scenario: (a) Process of inflow and outflow in Foziling Reservoir; (b) Process of water level and storage capacity in Foziling Reservoir.
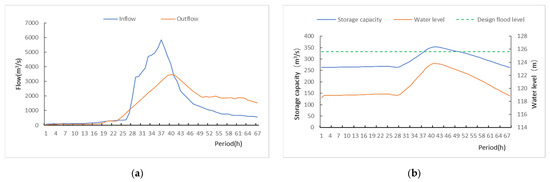
Figure 7.
Reservoir regulation process in the June 1999 flood scenario: (a) Process of inflow and outflow in the Foziling Reservoir; (b) Process of water level and storage capacity in the Foziling Reservoir.
The flood process is discretized, in which the flood dispatching process in July 1991 is divided into 88 periods, and the step length of each period is 2 h. The flood dispatching process in June 1999 is divided into 67 periods, and each time step is 1 h. It can be seen from Figure 6 and Figure 7 that the reservoir plays a full role in flood control. Through the reservoir storage, the discharge of the reservoir has never exceeded the maximum safe discharge of 3450 m3/s, and the downstream safety is guaranteed. At the same time, in these two floods, the highest water level of the reservoir did not reach the design flood level of 125.65 m, and both fell back to the flood limit water level at the end of the period. It can be considered that the safety of the reservoir is also guaranteed.
4. Discussion
4.1. Comparison between Improved Genetic Algorithm and 2020 Operation Regulation
In order to verify the rationality of the model, the results are compared with the 2020 operation regulation. The reservoir operation process is shown in Figure 8 and Figure 9.
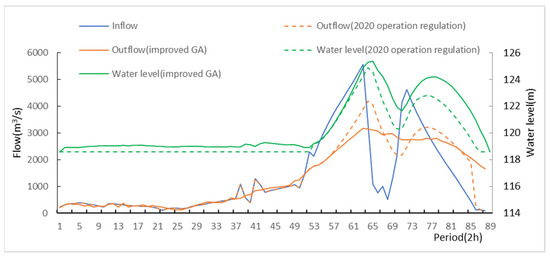
Figure 8.
Reservoir operation process based on 2020 operation regulation and improved genetic algorithm in July 1991 flood situation.
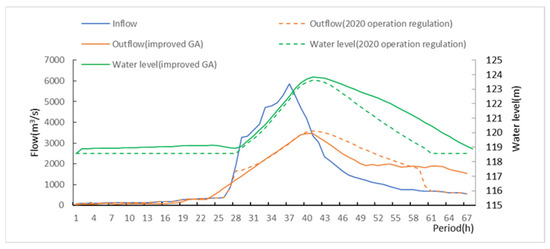
Figure 9.
Reservoir operation process based on 2020 operation regulation and improved genetic algorithm in June 1999 flood situation.
The optimal scheduling scheme in 2020 is shown in Table 2. When the flood occurred in July 1991, the reservoir water level was up to 124.86 m, which was lower than the design flood level of 125.65 m, and the reservoir capacity was 372.60 × 106 m3. However, since the 62nd period, the reservoir no longer guarantees the downstream safety. At this time, the reservoir flood discharge facilities are fully discharged, according to the discharge capacity, to ensure its own safety. At the 67th period, the water level is lower than 123.08 m, and the discharge is re-controlled within 3450 m3/s. In the flood scenario of June 1999, the reservoir water exceeded 123.08 m in the 39th period, and reached the highest level at 123.62 m in the 41st period. The corresponding reservoir capacity was 348.84 × 106 m3, and returned to below 123.08 m in the 45th period.

Table 2.
2020 operation regulation under ideal condition.
According to the 2020 regulation, under the ideal scenario, the downstream was in a dangerous state for 10 h when the flood occurred in July 1991, and the maximum discharge was 4187.92 m3/s. At the same time, the maximum water level of the reservoir was 124.86 m, and there was still 0.79 m space to be used from the designed flood level. When the reservoir suffered the flood in June 1999, the maximum storage capacity of the reservoir was 348.84 × 106 m3, the corresponding water level was 123.62 m, and the discharge was 3585.02 m3/s, which still exceeded the maximum safe discharge of 3450 m3/s, and the downstream control section of Gaoqiaowan was facing a flood risk for up to 6 h. Compared with the 2020 operation regulation, the flood control capacity occupied by the operation scheme under the improved genetic algorithm is 391.84 × 106 m3, 352.80 × 106 m3, and the corresponding water level is 125.36 m and 123.83 m, respectively. However, the downstream of the reservoir is always in a safe state. The reservoir occupied the flood control capacity as small as possible under the condition that its water level does not exceed the designed flood level and ensures the safety of the downstream. The operation scheme reduces the risk of flood control.
4.2. Comparison between Improved Genetic Algorithm and Traditional Genetic Algorithm
Compared with the improved genetic algorithm, the traditional genetic algorithm does not consider the constraint of the maximum discharge capacity of the reservoir when generating the initial population, but takes it into account in the penalty function. Therefore, the punish 4 should be added when the reservoir discharge exceeds the maximum discharge capacity of the reservoir.
The number of evolutions is set to 100,000 generations and both converge within 100,000 generations. Therefore, under different flood scenarios, the scheduling processes of the improved genetic algorithm and traditional genetic algorithm are shown in Figure 10 and Figure 11.
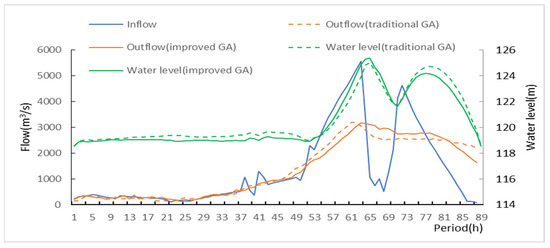
Figure 10.
Reservoir operation process based on traditional and improved genetic algorithm in the July 1991 flood situation.
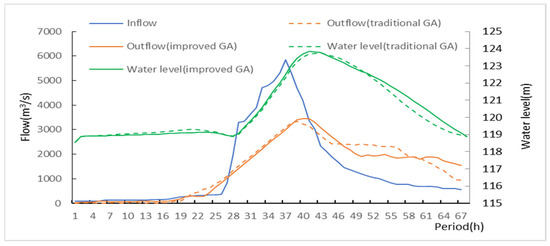
Figure 11.
Reservoir operation process based on traditional and improved genetic algorithm in June 1999 flood situation.
It can be seen from Figure 10 and Figure 11 that in the scheduling process based on the traditional genetic algorithm, when the flood occurred in July 1991, the maximum reservoir water level is 125.01 m, and the corresponding reservoir capacity is 375.46 m3. In the flood scenario of June 1999, the maximum water level is 123.74 m and the corresponding storage capacity is 351.04 m3. In the scheduling process based on the improved genetic algorithm, the highest reservoir water level under different flood scenarios are 125.36 m, 123.83 m, and the corresponding reservoir capacity is 391.84 × 106 m3, 352.80 × 106 m3. To explore the reason, the fitness value and its composition when the algorithms converge are counted, as shown in Table 3.

Table 3.
Attribute table of fitness value when genetic algorithms converge.
Table 3 shows that under two flood scenarios, the punish 4 (discharge capacity penalty value) is not completely removed according to the fitness value obtained by the traditional genetic algorithm, that is, the fitness value is composed of the maximum flood control capacity occupied by the reservoir and the discharge capacity penalty value. That is to say, there is an outflow greater than the discharge capacity in the scheduling process, which is not in line with the actual situation. Because the penalty coefficient is too small, the algorithm converges to an infeasible solution. Therefore, the more penalty functions, the more difficult it is to determine the coefficients of penalty functions. In this paper, the improved genetic algorithm not only improves the genetic operation, but also considers the discharge capacity constraint when generating new individuals, reduces the number of penalty functions, saves the time for determining the penalty coefficient, and makes the model application more convenient.
4.3. Selection of Control Parameters
The effects of initial population n, selection rate Ps, and crossover rate Pc on the fitness values are shown in the Figure 12, Figure 13 and Figure 14, where the fitness values are the average of the results obtained after 10 runs of the model.
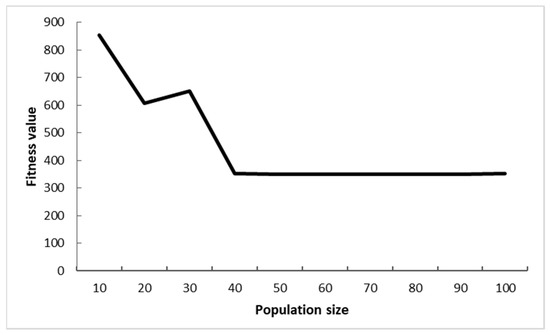
Figure 12.
Impact of population size on fitness value.
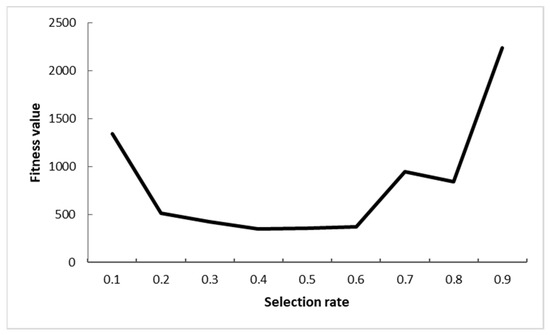
Figure 13.
Impact of selection rate Ps on fitness value.
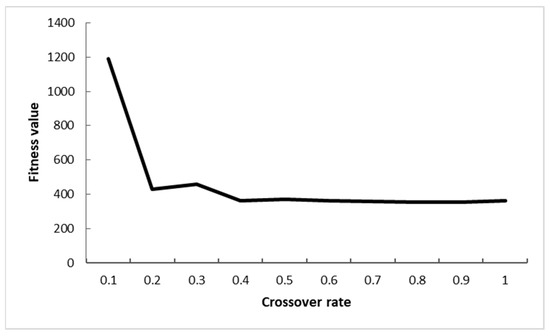
Figure 14.
Impact of crossover rate Pc on fitness value.
Figure 12 shows the effect of different initial population sizes on fitness values after 10,000 generations of evolution with experience-based selection rates Ps = 0.6 and Pc = 0.8. From the graph, it can be seen that the increase of initial population enriches the diversity of the population and the fitness values tend to be stable. When is small, although the calculation speed is improved, it is easy to cause close relatives to get married, and the fitness values are unsatisfactory due to insufficient initial samples. If the number of is too large, it will result in an increase in computational effort without a significant change in fitness values. To sum up, the initial population is set at 40.
Figure 13 shows the effect of selection rate Ps on fitness values when the number of evolutionary generations is 10,000, the initial population is 40, and the crossover rate is 0.8. Population diversity decreases with the decrease of Ps, which may lead to the loss of effective genes and the converging to an infeasible solution. If the level of Ps is too high, the evolutionary effect is not obvious, and the fitness value is not convergent at the end of evolution, so Ps = 0.4 is selected in this paper.
If the crossover rate Pc is too high, it is likely to destroy the individuals with good fitness values. If the Pc is too small, it will cause the generation of new individuals to be slow and the search will stall. This paper explores the effect of crossover Pc on fitness values based on 10,000 generations of evolution, initial population = 40 and selection rate Ps = 0.4. See Figure 14. Since the elite strategy is used to prevent gene destruction in good individuals to some extent, the fitness values do not fluctuate much with the increase of Pc, and the crossover rate Pc is finally set to 0.6.
5. Conclusions
In this paper, the improved genetic algorithm is used to optimize flood control operation. The results are compared with the schemes of the traditional genetic algorithm and reservoir operation regulation in 2020. The main conclusions are as follows.
The improved genetic algorithm can save time for determining the penalty coefficient and make the model application more convenient. The traditional genetic algorithm penalty function needs to consider the water level constraint, discharge amplitude constraint, discharge capacity constraint, etc., while the improved genetic algorithm considers the water balance constraint, maximum safety discharge constraint, non-negative constraint and discharge capacity constraint in the coding, which reduces the number of penalty functions and makes the penalty coefficient easy to determine to a certain extent.
Compared with the scheme based on the 2020 operation regulation, the optimization of the dispatching scheme by the improved genetic algorithm occupies the flood control storage as small as possible under the premise of ensuring the flood control safety of the reservoir itself and the downstream protection objects. Under different flood scenarios in July 1991 and June 1999, according to the scheme in the 2020 operation regulation, the downstream protection object is in danger for 10 h and 6 h, respectively. The improved genetic algorithm not only ensures the downstream safety, but also achieves the highest reservoir water levels of 125.36 m and 123.83 m, which are lower than the designed flood level of 125.65 m.
Author Contributions
Conceptualization, M.R.; methodology, M.R. and Q.Z.; software, Q.Z.; validation, Q.Z., Y.Y. and G.W.; formal analysis, Y.Y. and L.Z.; investigation, M.R. and G.W.; resources, M.R., W.X. and L.Z.; data curation, Q.Z. and Y.Y.; writing—original draft preparation, Q.Z.; writing—review and editing, M.R., G.W. and L.Z.; visualization, Q.Z. and Y.Y.; supervision, G.W. and W.X.; project administration, M.R. and G.W.; funding acquisition, M.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Plan Project of China, grant number 2018YFC1508003; the National Natural Science Foundation of China, grant number 51809281.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Luo, F. Analysis of joint flood control optimization dispatching of reservoir group. Nanfang Agric. Mach. 2017, 48, 176. [Google Scholar]
- Hu, Z. Review on Optimal Operation of Reservoir Groups. Sci. Technol. West China 2013, 12, 25–26. [Google Scholar]
- Lin, Y.; Wang, Y. The Summary of Research Development on the Optimal Scheduling of Multi-reservoir System. Agric. Technol. 2007, 4, 96–100. [Google Scholar]
- Yang, H. Review on Analysis Methods of Reservoir Group Optimal Operation System. Jilin Water Resour. 2009, 8, 49–52. [Google Scholar]
- Wardlaw, R.; Sharif, M. Evaluation of genetic algorithms for optimal reservoir system operation. J. Water Resour. Plan. Manag. 1999, 125, 25–33. [Google Scholar] [CrossRef]
- Hu, T. Research on the Artificial Neural Network Methodology for Multi-Reservoir Operating Rules. Adv. Water Sci. 1995, 6, 53–60. [Google Scholar]
- Brouwer, M.A.; Vandenbergh, P.J.; Aengevaeren, W.R. Use of multi-objective particle swarm optimization in water resources management. J. Water Resour. Plan. Manag. 2008, 134, 257–265. [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, L.; Dong, Z.; Xiao, J.; Li, Y.; Shi, R.; Liu, W. Optimal Operation of Flood Control for Reservoir Group Based on Improved Genetic Algorithm. Hydropower Energy Sci. 2018, 36, 59–62, 153. [Google Scholar]
- Ge, J.; Qiu, Y.; Wu, C.; Pu, G. Overview of genetic algorithm research. Appl. Res. Comput. 2008, 10, 2911–2916. [Google Scholar]
- Zhang, X.; Dong, Z.; Ma, H. Study on Optimization Operation of Xiaolangdi Reservoir Based on Improved Multi-objective Genetic Algorithm. Water Resour. Power 2018, 1, 65–68. [Google Scholar]
- Liu, P.; Guo, S.; Li, W.; Yi, S. A review of application of genetic algorithm to reservoir operation. Adv. Sci. Technol. Water Resour. Hydropower 2006, 26, 78–83. [Google Scholar]
- Ahmed, J.A.; Xue, X. Genetic Algorithm for Optimal Operation of Comprehensive Utilization Reservoir. Express Water Resour. Hydropower 2006, 3, 7–12, 15. [Google Scholar]
- Wang, B. Research on Improved Genetic Algorithm and Optimal Operation of Cascade Reservoirs. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2018. [Google Scholar]
- Zhang, Z.; Hu, Y.; He, X.; Xue, C.; Wang, F. Research on joint flood control operation in Pi River Basin of Huaihe Tributary. China Flood Control Drought Relief 2020, 30, 22–27. [Google Scholar]
- Lu, C.; Fang, S. Research on optimal operation of reservoir flood control based on genetic algorithm. China Water Transp. (Second. Half Mon.) 2016, 16, 110–111. [Google Scholar]
- Chen, F. Research and Application of Optimal Scheduling of Cascade Reservoirs in the Lower Reaches of Jinsha River. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2017. [Google Scholar]
- Ding, P. Research on Flood Control Operation Scheme Based on Expert Experience of Shitoukoumen Reservoir. Master’s Thesis, Dalian University of Technology, Dalian, China, 2020. [Google Scholar]
- Guo, S.; Chen, J.; Liu, P.; Li, Y. State of the-art review of joint operation for multi-reservoir systems. Adv. Water Sci. 2010, 21, 496–503. [Google Scholar]
- Lei, D. Research on Guxian Reservoir Optimal Operation Based on Improved Genetic Algorithm. Master’s Thesis, Zhengzhou University, Zhengzhou, China, 2017. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).