Analysis of Hydrologic Drought Frequency Using Multivariate Copulas in Shaying River Basin
Abstract
1. Introduction
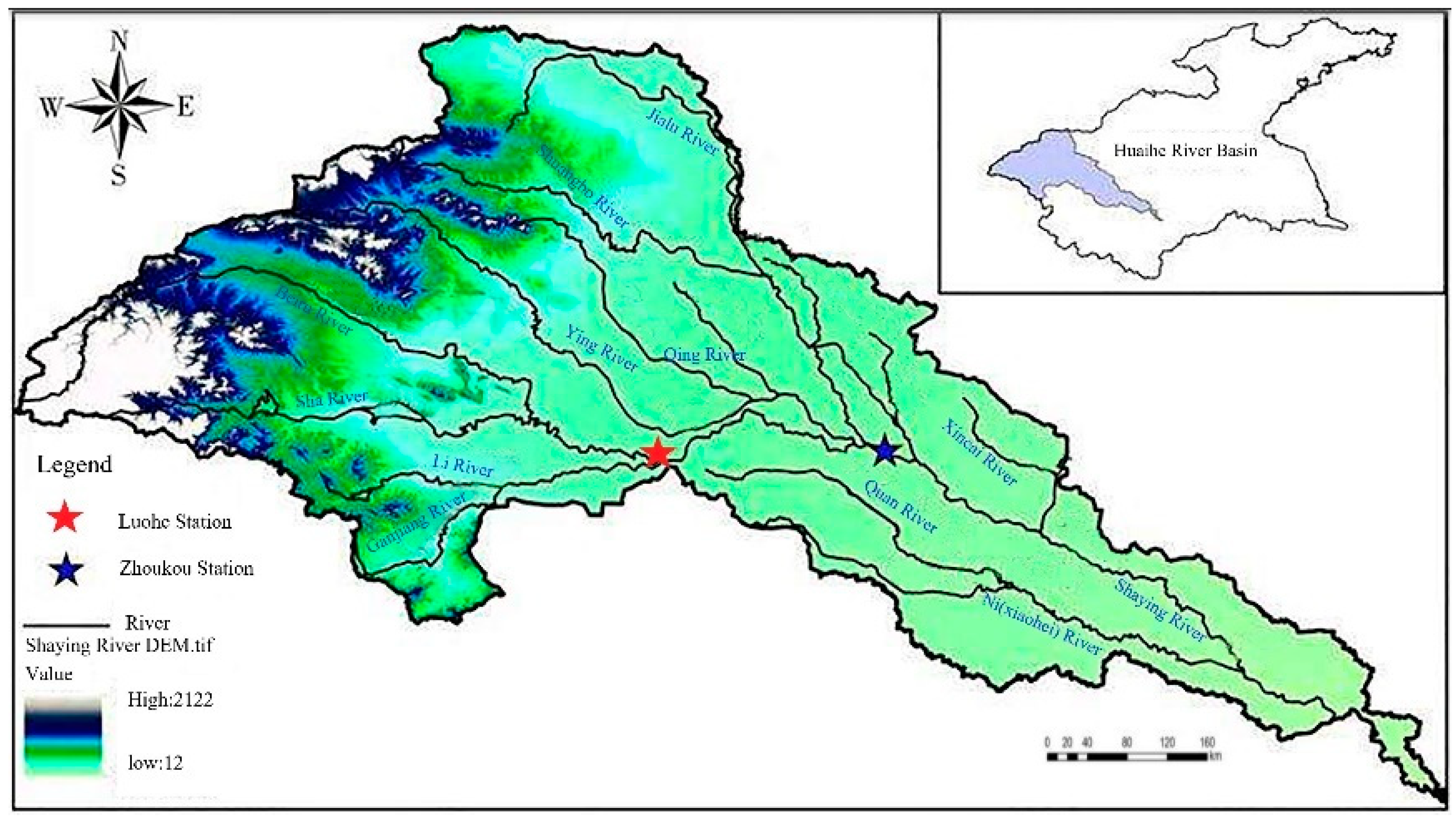
2. Study Area and Data
3. Methodology
3.1. Construction of the Copula-Based Joint Drought Deficit Index
3.1.1. Standardized Runoff Index (SRI)
3.1.2. Drought Characters Identification with Runs Theory
- (1)
- According to the SRI drought degree classification presented in Table 1, three given threshold degree of runs theory were defined (). When the monthly SRI values were below , the corresponding month was potentially identified as a drought event (e.g., the four drought events shown in Figure 3, including a, b, d, e, f).
- (2)
- For a drought event whose duration was only one month (e.g., a and f), if SRI < −1, this month was regarded as a single drought event (e.g., with a severity ), or else non-drought event in the month (e.g., f)
- (3)
- A drought event may contain a few consecutive months with negative SRI (e.g., b and its severity ).
- (4)
- If the duration of a drought event contained two branches, (e.g., d and e), and c is the interval between drought event d and e, and the duration of c was less than 6 months, in which , then drought d and e were still regarded as a single drought event, drought duration , the corresponding severity (shadow area in Figure 3) was defined as . Otherwise, e and d were recognized as two independent drought events.
- (5)
- P was the absolute value of minimum SRI value in a drought event (e.g., ).
3.2. Copula-Based Joint Distribution Function
3.3. Marginal Distribution
3.4. Return Period Estimation
4. Results and Discussion
4.1. Drought Characteristics Identification and Analysis
4.2. Univariate Marginal Distribution Selection
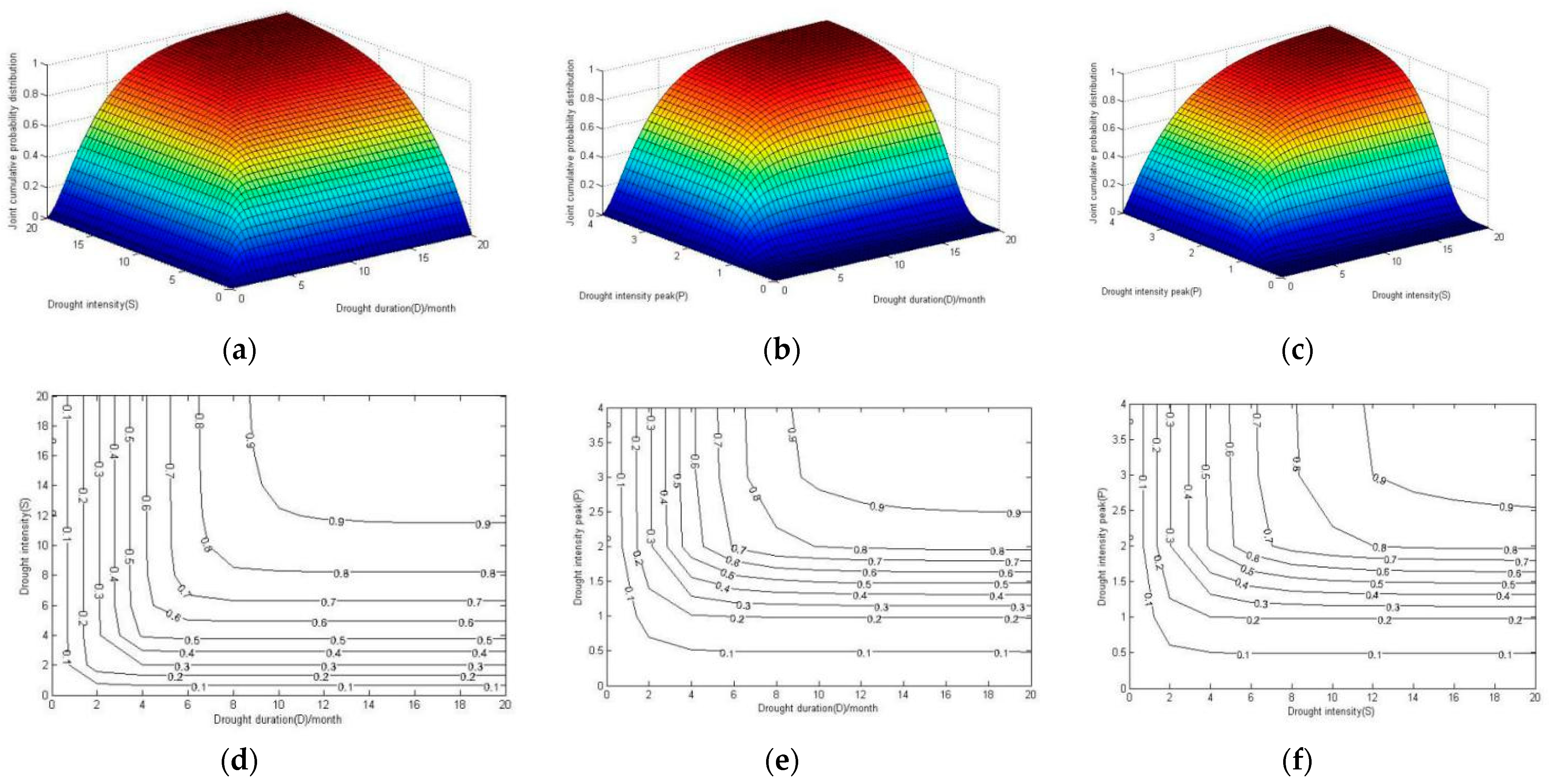
4.3. Bivariate and Trivariate Copula Joint Distribution Model of Drought
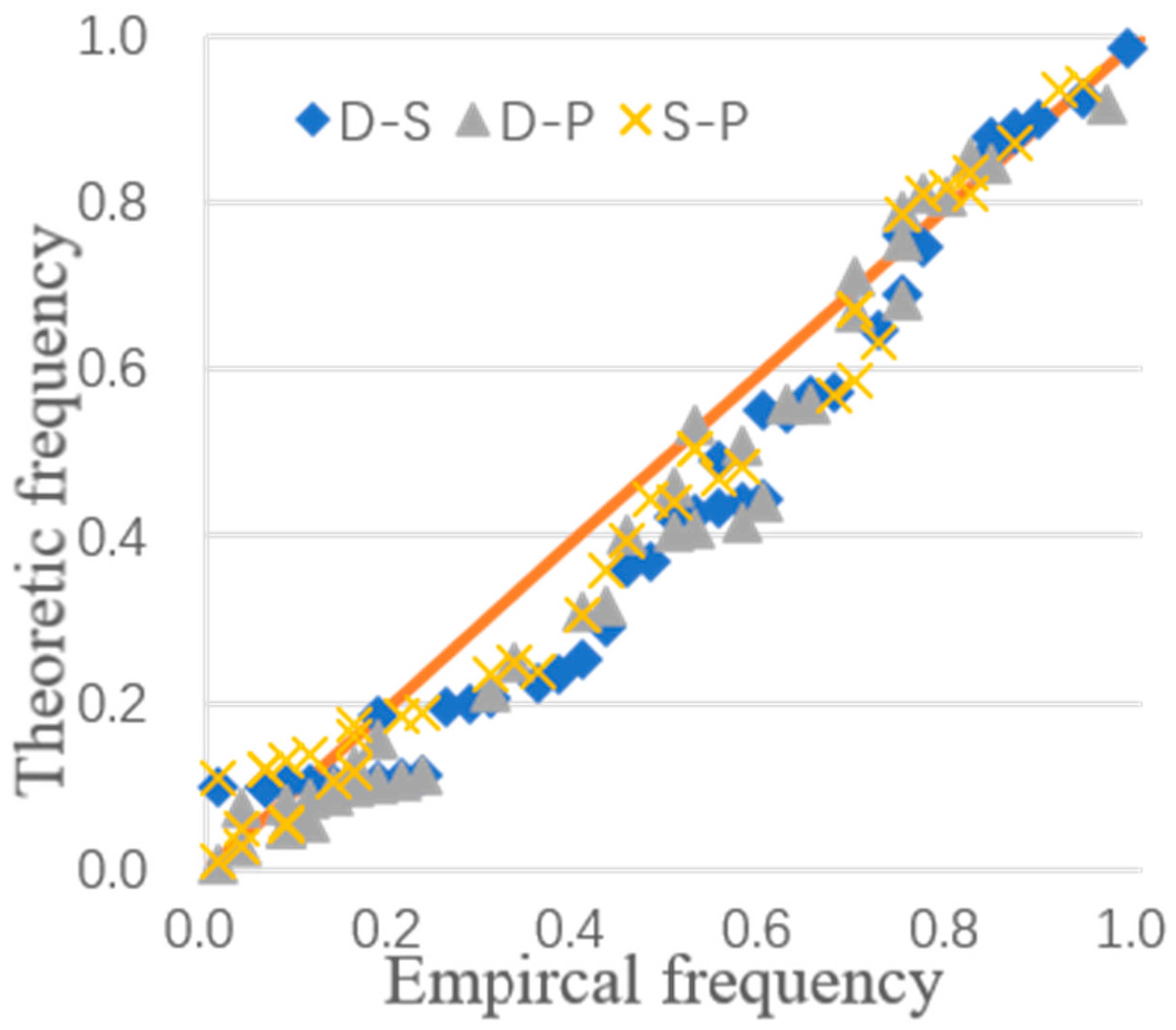
4.3.1. Bivariate Copula Model
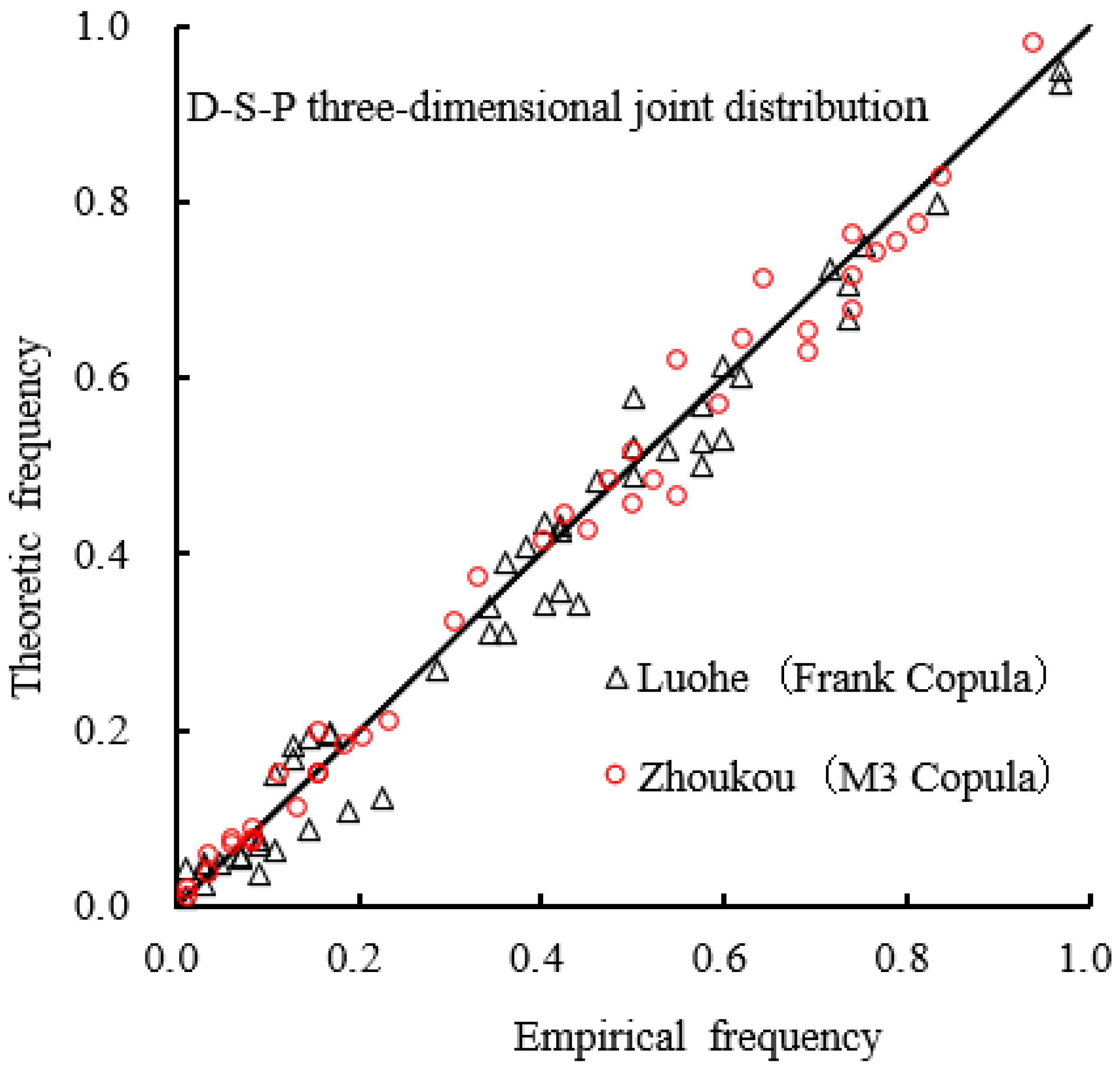
4.3.2. Trivariate Copula Function Model
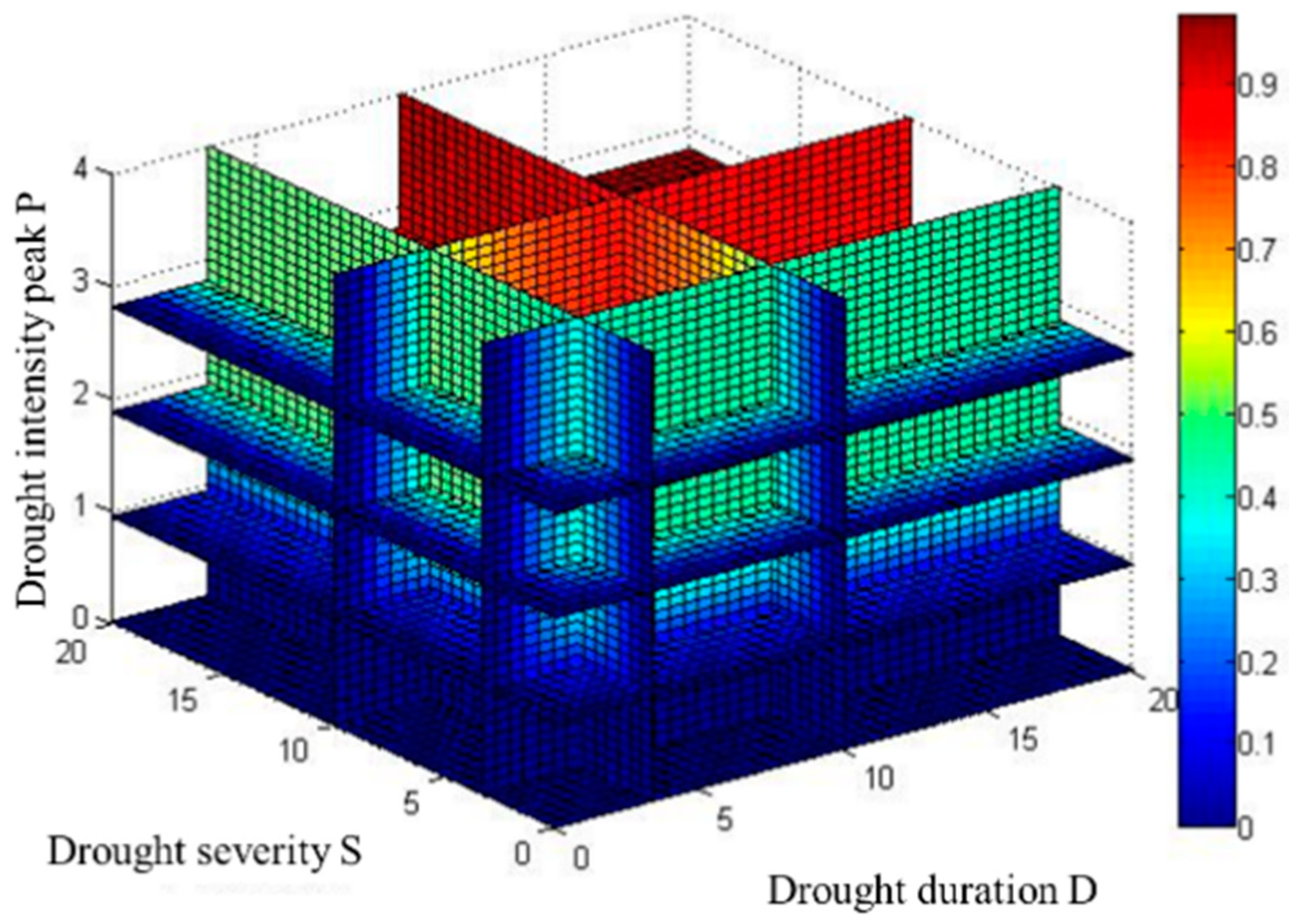
4.4. Drought Frequency Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sai, M.; Murthy, C.; Chandrasekar, K.; Jeyaseelan, A.; Diwakar, P.; Dadhwal, V. Agricultural drought: Assessment & monitoring. Mausam 2021, 67, 131–142. [Google Scholar]
- Du, C.; Chen, J.; Nie, T. Spatial–temporal changes in meteorological and agricultural droughts in Northeast China: Change patterns, response relationships and causes. Nat. Hazards 2021, 110, 155–173. [Google Scholar] [CrossRef]
- Wilhite, D.A. Drought as a Natural Hazard: Concepts and Definitions. In Drought: A Global Assessment; Routledge: London, UK, 2000; pp. 3–18. [Google Scholar]
- Yang, J. Comprehensive drought characteristics analysis based on a nonlinear multivariate drought index. J. Hydrol. 2017, 557, 651–667. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, Z.; Xu, L. Meteorological drought forecasting based on a statistical model with machine learning techniques in Shaanxi province, China. Sci. Total Environ. 2019, 665, 338–346. [Google Scholar] [CrossRef]
- Xu, K.; Yang, D.; Xu, X.; Lei, H. Copula based drought frequency analysis considering the spatio-temporal variability in Southwest China. J. Hydrol. 2015, 527, 630–640. [Google Scholar] [CrossRef]
- Li, F.; Li, H.; Lu, W. Meteorological drought monitoring in northeastern China using multiple indices. Water 2019, 11, 72. [Google Scholar] [CrossRef]
- Yevjevich, V. An objective approach to definitions and investigations of continental hydrologic droughts. J. Hydrol. 1969, 7, 353. [Google Scholar]
- Sen, Z. Run-sums of annual flow series. J. Hydrol. 1977, 35, 311–324. [Google Scholar] [CrossRef]
- Clausen, B.; Pearson, C. Susceptibility of water supply reservoirs to drought conditions. J. Hydrol. Eng. 1998, 3, 140–148. [Google Scholar]
- Salvadori, G.; De Michele, C. Multivariate real-time assessment of droughts via copula-based multi-site Hazard Trajectories and Fans. J. Hydrol. 2015, 526, 101–115. [Google Scholar] [CrossRef]
- Byzedi, M.; Saghafian, B.; Mohammadi, K.; Siosemarde, M. Regional analysis of streamflow drought: A case study in southwestern Iran. Environ. Earth Sci. 2014, 71, 2955–2972. [Google Scholar] [CrossRef][Green Version]
- Yu, J.; Kim, T.; Park, D. Future Hydrological Drought Risk Assessment Based on Nonstationary Joint Drought Management Index. Water 2019, 11, 532. [Google Scholar] [CrossRef]
- Li, M.; Li, J.; Feng, P.; Chen, L. Construction of time-dependent drought index under changing environment and its application. J. Hydraul. Eng. 2018, 49, 1386–1395. [Google Scholar]
- Tsakiris, G.; Kordalis, N.; Tigkas, D.; Tsakiris, V.; Vangelis, H. Analysing drought severity and areal extent by 2D Archimedean copulas. Water Resour. Manag. 2016, 30, 5723–5735. [Google Scholar] [CrossRef]
- Liu, X.; Wang, S.; Zhou, Y.; Wang, F.; Yang, G.; Liu, W. Spatial analysis of meteorological drought return periods in china using copulas. Nat. Hazards 2016, 80, 367–388. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Huang, Q.; Chen, Y. Spatio-temporal changes and frequency analysis of drought in the Wei River Basin, China. Water Resour. Manag. 2014, 28, 3095–3110. [Google Scholar] [CrossRef]
- Saghafian, B.; Sanginabadi, H. Multivariate groundwater drought analysis using copulas. Hydrol. Res. 2020, 51, 666–685. [Google Scholar] [CrossRef]
- Tosunoğlu, F.C. On of Joint modeling of drought characteristics derived from historical and synthetic rainfalls: Application of Generalized Linear Models and Copulas. J. Hydrol. Reg. Stud. 2017, 14, 167–181. [Google Scholar] [CrossRef]
- She, D.; Mishra, A.; Xia, J.; Zhang, L.; Zhang, X. Wet and dry spell analysis using copulas. Int. J. Hyperth. 2016, 36, 476–491. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Salvadori, G.; De Michele, C. Catchment compatibility via copulas: A non-parametric study of the dependence structures of hydrological responses. Water Resour. Res. 2016, 90, 116–133. [Google Scholar] [CrossRef]
- De Baets, B.; De Meyer, H. Cutting levels of the winning probability relation of random variables pairwisely coupled by a same Frank copula. Int. J. Approx. Reason. 2019, 112, 22–36. [Google Scholar] [CrossRef]
- Tosunoglu, F.; Can, I. Application of copulas for regional bivariate frequency analysis of meteorological droughts in Turkey. Nat. Hazards 2016, 82, 1457–1477. [Google Scholar] [CrossRef]
- Ayantobo, O.; Li, Y.; Song, S. Copula-based trivariate drought frequency analysis approach in seven climatic sub-regions of mainland China over 1961–2013. Theor. Appl. Climatol. 2019, 137, 2217–2237. [Google Scholar] [CrossRef]
- Chen, X.; Li, F.; Li, J.; Feng, P. Three-dimensional identification of hydrological drought and multivariate drought risk probability assessment in the Luanhe River basin, China. Theor. Appl. Climatol. 2019, 137, 3055–3076. [Google Scholar] [CrossRef]
- Kim, Y.; Chung, G.H. Hydrologic Risk Assessment of Future Extreme Drought in South Korea Using Bivariate Frequency Analysis. Water 2019, 11, 2052. [Google Scholar] [CrossRef]
- Majid, M.; Babak, A.; Hossein, R. New approach in bivariate drought duration and severity analysis. J. Hydrol. 2018, 559, 166–181. [Google Scholar]
- Xy, A.; Ypla, B.; Yrl, A. A MCMC-based maximum entropy copula method for bivariate drought risk analysis of the Amu Darya River Basin. J. Hydrol. 2020, 590, 125502. [Google Scholar]
- Sun, P.; Zhang, Q.; Song, C. Hydrological Drought Regimes of the Huai River Basin, China: Probabilistic Behavior, Causes and Implications. Water 2019, 11, 2390. [Google Scholar] [CrossRef]
- Sun, C.; Huang, G.; Fan, Y. Drought Occurring with Hot Extremes: Changes under Future Climate Change on Loess Plateau, China. Earth’s Future 2019, 7, 587–604. [Google Scholar] [CrossRef]
- Serinaldi, F. Copula-based mixed models for bivariate rainfall data: An empirical study in regression perspective. Stoch. Environ. Res. Risk Assess. 2009, 23, 677–693. [Google Scholar] [CrossRef]
- Song, S.; Singh, V. Meta-elliptical copulas for drought frequency analysis of periodic hydrologic data. Stoch. Environ. Res. Risk Assess. 2010, 24, 425–444. [Google Scholar] [CrossRef]
- Saghafian, B.; Mehdikhani, H. Drought characterization using a new copula based trivariate approach. Nat. Hazards 2014, 72, 1391–1407. [Google Scholar] [CrossRef]
- Song, S.; Singh, V. Frequency analysis of droughts using the Plackett copula and parameter estimation by genetic algorithm. Stoch. Environ. Res. Risk Assess. 2010, 24, 783–805. [Google Scholar] [CrossRef]
- Song, S.; Kang, Y. Pair-copula decomposition constructions for multivariate hydrological drought frequency analysis. In Proceedings of the 2011 International Symposium on Water Resource and Environmental Protection, Xi’an, China, 20–22 May 2011; Volume 4, pp. 2635–2638. [Google Scholar]
- Reddy, M.; Singh, V. Multivariate modeling of droughts using copulas and meta-heuristic methods. Stoch. Environ. Res. Risk Assess. 2014, 28, 475–489. [Google Scholar] [CrossRef]
- Hui, F.; Yusof, F.; Yusop, Z. Trivariate copula in drought analysis: A case study in peninsular Malaysia. Theor. Appl. Climatol. 2019, 138, 657–671. [Google Scholar]
- Dixit, S.; Jayakumar, K. A study on copula-based bivariate and trivariate drought assessment in Godavari River basin and the teleconnection of drought with large-scale climate indices. Theor. Appl. Climatol. 2021, 146, 1335–1353. [Google Scholar] [CrossRef]
- Stefanidis, S.; Dafis, S.; Stathis, D. Evaluation of regional climate models (RCMs) performance in simulating seasonal precipitation over Mountainous Central Pindus (Greece). Water 2020, 12, 2750. [Google Scholar] [CrossRef]
- Stefanidis, S.; Stathis, D. Spatial and temporal rainfall variability over the Mountainous Central Pindus (Greece). Climate 2018, 6, 75. [Google Scholar] [CrossRef]
- Ma, X.; Shi, P.; Wang, Z. Trend analysis of precipitation in upstream catchment of Shaying he river. Water Resour. Power 2013, 31, 7–11. [Google Scholar]
- Tao, J.; Sun, X.; Cao, Y.; Ling, M. Evaluation of water quality and its driving forces in the Shaying River Basin with the grey relational analysis based on combination weighting. Environ. Sci. Pollut. Res. 2022, 29, 18103–18115. [Google Scholar] [CrossRef]
- Li, H.; Qu, X.; Tao, J.; Hu, C.; Zuo, Q. The optimal allocation of water resources oriented to prioritizing ecological needs using multiple schemes in the Shaying River Basin (henan section), China. Water Supply 2022, 22, 1593–1610. [Google Scholar] [CrossRef]
- Nikravesh, G.; Aghababaei, M.; Nazari-Sharabian, M. Drought Frequency Analysis Based on the Development of a Two-Variate Standardized Index (Rainfall-Runoff). Water 2020, 12, 2599. [Google Scholar] [CrossRef]
- Kubiak-Wojcicka, K.; Juskiewicz, W. Relationships between meteorological and hydrological drought in a young-glacial zone (north-western Poland) based on Standardised Precipitation Index (SPI) and Standardized Runoff Index (SRI). Acta Montan. Slovaca 2020, 25, 517–531. [Google Scholar]
- Sun, X.; Li, Z.; Tian, Q. Assessment of hydrological drought based on nonstationary runoff data. Hydrol. Res. 2020, 51, 894–910. [Google Scholar] [CrossRef]
- Zuo, D.; Hou, W.; Yan, P. Research on drought in southwest China based on the theory of run and two-dimensional joint distribution theory. Acta Phys. Sin. 2014, 63, 230204. [Google Scholar]
- Wu, R.; Zhang, J.; Bao, Y.; Guo, E. Run Theory and Copula-Based Drought Risk Analysis for Songnen Grassland in Northeastern China. Sustainability 2019, 11, 6032. [Google Scholar] [CrossRef]
- Fuchs, S.; Mccord, Y.; Schmidt, K. Characterizations of Copulas Attaining the Bounds of Multivariate Kendall’s Tau. J. Optim. Theory Appl. 2018, 178, 424–438. [Google Scholar] [CrossRef]
- Vcelar, F.; Patikova, Z. A comparative study of Tarski’s fixed point theorems with the stress on commutative sets of L-fuzzy isotone maps with respect to transitivities. Fuzzy Sets Syst. 2020, 382, 29–56. [Google Scholar] [CrossRef]
- Großmaß, T. Copula and Tail Dependence. Master’s Thesis, Humboldt University, Berlin, Germany, 2007. [Google Scholar]
- Bardossy, A.; Pegram, G. Copula based multisite model for daily precipitation simulation. Hydrol. Earth Syst. Sci. 2009, 13, 2299–2314. [Google Scholar] [CrossRef]
- Fasano, G.; Franceschini, A. A multidimensional version of the Kolmogorov-Smirnov test. Mon. Not. R. A Stronomical Soc. 1987, 225, 155–170. [Google Scholar] [CrossRef]
- Abdi, H. Kendall Rank Correlation. In Encyclopedia of Measurement and Statistics; Salkind, N.J., Ed.; SAGE: Thousand Oaks, CA, USA, 2006. [Google Scholar]
- Ma, J.; Han, X. Spatial temporal variations of average temperature and extreme maximum temperature in Gansu Province. Yellow River 2014, 36, 35–38. [Google Scholar]
- Kim, J.; So, B.; Kwon, H. Estimation of return period and its uncertainty for the recent 2013–2015 drought in the Han River watershed in South Korea. Hydrol. Res. 2018, 49, 1313–1329. [Google Scholar] [CrossRef]
- Poulin, A.; Huard, D.; Favre, A.; Pugin, S. Importance of tail dependence in bivariate frequency analysis. J. Hydrol. Eng. 2007, 12, 394–403. [Google Scholar] [CrossRef]
- Francesco, S.; Brunella, B.; Antonino, C.; Salvatore, G. Probabilistic characterization of drought properties through copulas. Phys. Chem. Earth 2009, 34, 596–605. [Google Scholar]



| Degree | Classification | SRI |
|---|---|---|
| 1 | No drought | −0.5 < SRI |
| 2 | Mild drought | −1.0 < SRI ≤ −0.5 |
| 3 | Moderate drought | −1.5 < SRI ≤ −1.0 |
| 4 | Severe drought | −2.0 < SRI ≤ −1.5 |
| 5 | Extreme drought | SRI ≤ −2.0 |
| Period | Luohe Station | Zhoukou Station | ||||||
|---|---|---|---|---|---|---|---|---|
| Times | D (Months) | S | P | Times | D (Months) | S | P | |
| 1950s | 5 | 4.75 | 5.33 | 1.29 | 2 | 2.00 | 2.90 | 1.61 |
| 1960s | 9 | 4.43 | 5.24 | 1.52 | 8 | 3.13 | 3.46 | 1.33 |
| 1970s | 13 | 3.92 | 3.72 | 1.19 | 10 | 3.10 | 5.18 | 1.66 |
| 1980s | 7 | 5.29 | 4.48 | 1.40 | 8 | 3.88 | 4.07 | 1.36 |
| 1990s | 8 | 5.88 | 6.05 | 1.24 | 8 | 7.25 | 8.08 | 1.52 |
| 2000s | 9 | 4.88 | 4.55 | 1.44 | 5 | 4.00 | 5.12 | 1.53 |
| 1951–2008 | 51 | 4.78 | 4.79 | 1.35 | 41 | 4.17 | 5.09 | 1.50 |
| Maximum duration | 14 months | 19 months | ||||||
| Hydrological Station | Drought Characteristic Variable | Marginal Distribution Function | Parameters | ||
|---|---|---|---|---|---|
| Shape Parameter | Scale Parameter | Location Parameter | |||
| Luohe | D | Exponential | - | 3.83 | 0.43 |
| S | Log-normal | 0.85 | - | 1.08 | |
| P | Gamma | 10.14 | 0.13 | - | |
| Zhoukou | D | Gamma | 1.64 | 2.55 | - |
| S | Weibull | 1.08 | 5.26 | - | |
| P | Log-normal | 0.39 | - | 0.32 | |
| Hydrological Station | Drought Characteristic Variable | K–S Result | Correlation Coefficient τ | ||||
|---|---|---|---|---|---|---|---|
| Z | β | Critical Value Z (α = 0.05) | D–S | D–P | S–P | ||
| Luohe | D | 0.1625 | 0.14 | 0.191 | 0.8334 | 0.5241 | 0.5971 |
| S | 0.1532 | 0.17 | |||||
| P | 0.0537 | 0.99 | |||||
| Zhoukou | D | 0.1409 | 0.36 | 0.2076 | 0.8537 | 0.5300 | 0.66 |
| S | 0.1556 | 0.26 | |||||
| P | 0.0819 | 0.93 | |||||
| Copula Function | Variable | Luohe | Zhoukou | ||||
|---|---|---|---|---|---|---|---|
| θ | RMSE | AIC | θ | RMSE | AIC | ||
| Frank | D–S | 17.6 | 0.0768 | −259.75 | 19.82 | 0.0822 | −202.92 |
| D–P | 2.97 | 0.0681 | −272.06 | 5.84 | 0.0687 | −217.55 | |
| S–P | 5.08 | 0.0791 | −256.81 | 8.28 | 0.0555 | −235.03 | |
| Clayton | D–S | 3.28 | 0.0932 | −240 | 4.25 | 0.0956 | −190.52 |
| D–P | 0.59 | 0.078 | −258.24 | 1.2 | 0.0839 | −201.19 | |
| S–P | 1.03 | 0.0428 | −319.38 | 1.25 | 0.0842 | −200.95 | |
| Gumbel | D–S | 4.39 | 0.0842 | −250.44 | 4.85 | 0.0892 | −196.18 |
| D–P | 1.5 | 0.0664 | −274.63 | 1.91 | 0.0761 | −209.22 | |
| S–P | 1.9 | 0.0475 | −308.73 | 2.38 | 0.062 | −225.99 | |
| Joe | D–S | 5.98 | 0.0909 | −242.59 | 6.37 | 0.0992 | −187.47 |
| D–P | 1.81 | 0.0674 | −273.12 | 2.26 | 0.0856 | −199.54 | |
| S–P | 2.34 | 0.0545 | −294.81 | 3.1 | 0.0789 | −206.24 | |
| Symmetric Archimedean Copula | Asymmetric Archimedean Copula | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Hydrological Station | Copula Function | θ | RMSE | AIC | Copula Function | θ1 | θ2 | RMSE | AIC |
| Luohe | Frank | 5.38 | 0.0851 | −249.39 | M3 | 3.32 | 5.68 | 0.0971 | −235.85 |
| Clayton | 1.15 | 0.1061 | −226.81 | M4 | 1.01 | 1.98 | 0.0879 | −245.92 | |
| Gumbel | 1.94 | 0.0916 | −241.83 | M5 | 1.51 | 1.99 | 0.0999 | −232.99 | |
| Joe | 2.39 | 0.1058 | −227.14 | M12 | 1.91 | 2.83 | 0.1241 | −210.81 | |
| Zhoukou | Frank | 8.38 | 0.0819 | −203.13 | M3 | 6.31 | 9.84 | 0.0673 | −219.23 |
| Clayton | 1.48 | 0.1223 | −169.86 | M4 | 2.26 | 3.91 | 0.0834 | −201.66 | |
| Gumbel | 2.39 | 0.1772 | −139.89 | M5 | 2.13 | 2.95 | 0.0704 | −215.54 | |
| Joe | 2.97 | 0.1146 | −175.64 | M12 | 3.11 | 4.71 | 0.1027 | −184.66 | |
| Hydrometric Station | T | D | S | P | D–S | D–P | S–P | D–S–P | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Luohe | 2 | 2.40 | 2.54 | 1.20 | 1.87 | 2.15 | 1.54 | 2.84 | 1.83 | 2.21 | 1.52 | 2.33 |
| 5 | 6.30 | 5.55 | 1.59 | 4.27 | 6.03 | 3.38 | 9.57 | 3.71 | 7.66 | 2.92 | 6.99 | |
| 10 | 9.25 | 8.20 | 1.81 | 7.63 | 14.52 | 6.52 | 21.42 | 6.42 | 22.62 | 4.86 | 15.27 | |
| 20 | 12.20 | 11.27 | 2.01 | 13.43 | 39.18 | 12.82 | 45.51 | 11.55 | 74.32 | 8.40 | 33.33 | |
| 50 | 16.10 | 16.06 | 2.25 | 29.21 | 173.55 | 31.72 | 118.04 | 26.65 | 402.84 | 18.57 | 94.67 | |
| 100 | 19.05 | 20.33 | 2.42 | 54.57 | 596.86 | 63.22 | 239.12 | 51.69 | 1530.84 | 35.31 | 206.93 | |
| Zhoukou | 2 | 2.03 | 1.96 | 1.12 | 1.91 | 2.10 | 1.75 | 2.33 | 1.80 | 2.25 | 1.67 | 2.27 |
| 5 | 5.29 | 6.53 | 1.73 | 4.45 | 5.70 | 3.69 | 7.75 | 3.92 | 6.89 | 3.38 | 6.89 | |
| 10 | 7.46 | 9.80 | 2.10 | 8.09 | 13.10 | 6.50 | 21.67 | 6.91 | 18.11 | 5.61 | 17.83 | |
| 20 | 9.53 | 12.99 | 2.46 | 14.27 | 33.40 | 11.73 | 67.74 | 12.30 | 53.53 | 9.36 | 49.31 | |
| 50 | 12.19 | 17.12 | 2.92 | 30.54 | 137.82 | 26.92 | 351.18 | 27.63 | 262.62 | 19.97 | 251.50 | |
| 100 | 14.16 | 20.49 | 3.26 | 56.17 | 455.40 | 51.99 | 1305.76 | 52.77 | 952.37 | 37.00 | 960.36 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Cui, B.; Hao, X.; He, P.; Liu, L.; Song, Z. Analysis of Hydrologic Drought Frequency Using Multivariate Copulas in Shaying River Basin. Water 2022, 14, 1306. https://doi.org/10.3390/w14081306
Ma J, Cui B, Hao X, He P, Liu L, Song Z. Analysis of Hydrologic Drought Frequency Using Multivariate Copulas in Shaying River Basin. Water. 2022; 14(8):1306. https://doi.org/10.3390/w14081306
Chicago/Turabian StyleMa, Jianqin, Bifeng Cui, Xiuping Hao, Pengfei He, Lei Liu, and Zhirui Song. 2022. "Analysis of Hydrologic Drought Frequency Using Multivariate Copulas in Shaying River Basin" Water 14, no. 8: 1306. https://doi.org/10.3390/w14081306
APA StyleMa, J., Cui, B., Hao, X., He, P., Liu, L., & Song, Z. (2022). Analysis of Hydrologic Drought Frequency Using Multivariate Copulas in Shaying River Basin. Water, 14(8), 1306. https://doi.org/10.3390/w14081306






