Uncertainty Analysis for Image-Based Streamflow Measurement: The Influence of Ground Control Points
Abstract
:1. Introduction
2. Study Site and Measuring Instruments
2.1. Description of Study Site
2.2. Measuring Instruments
3. Methods: LSPIV Measurement and Uncertainty Assessment
3.1. LSPIV Measurement
3.1.1. Collinearity Equations
3.1.2. Image Matching
3.1.3. Surface Velocity and River Discharge
3.2. Uncertainty Assessment: Monte Carlo Simulations
4. Results and Discussion
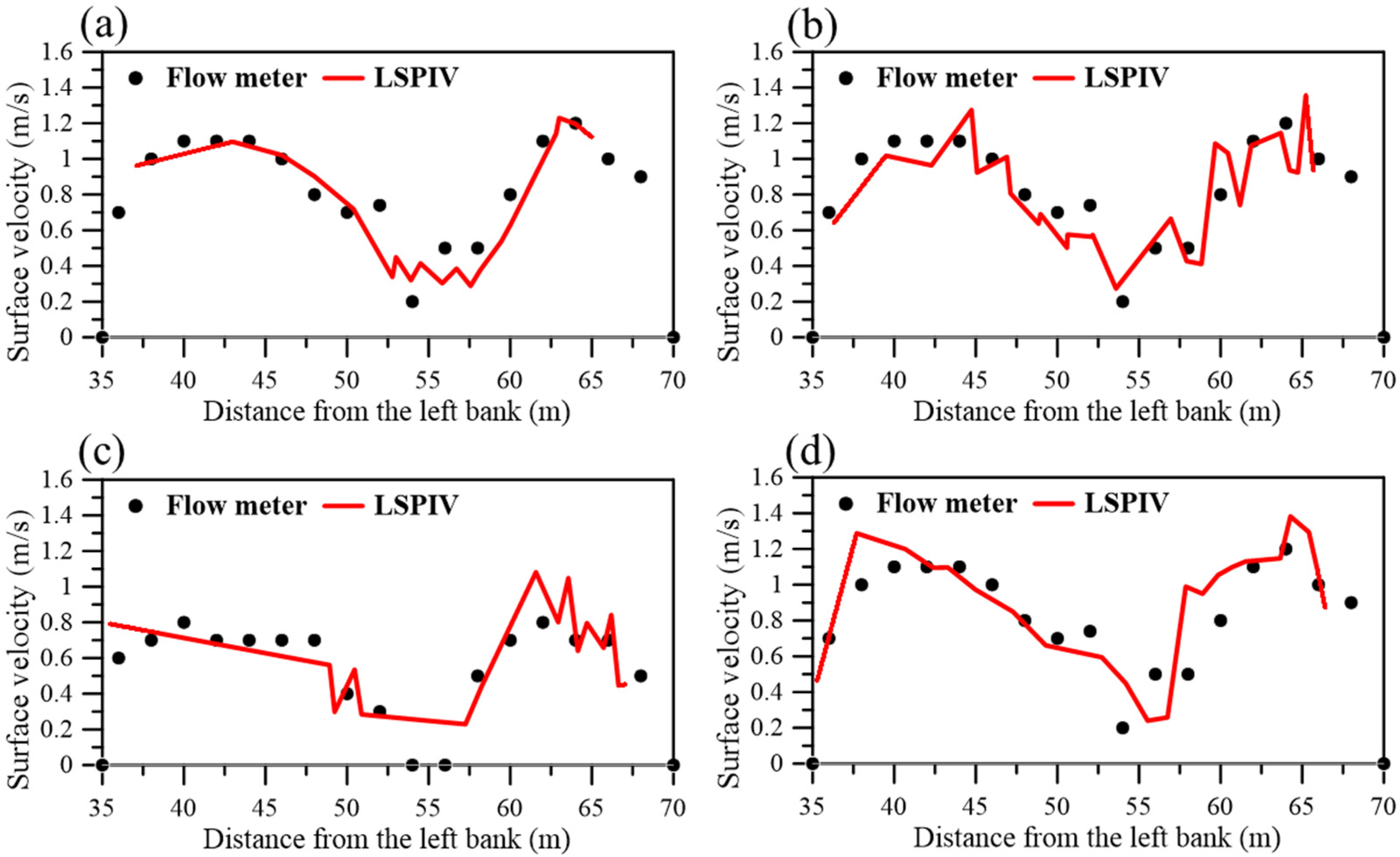
4.1. Streamflow Measurement Using LSPIV
4.2. Uncertainty in GCPs and Camera Parameters
- Near-field camera: Cu (normal), Cv (normal), f (log Pearson type III), Cx (beta), Cy (beta), Cz (log Pearson type III), θ (normal), β (normal), and τ (log Pearson type III);
- Far-field camera: Cu (log Pearson type III), Cv (normal), f (log Pearson type III), Cx (log Pearson type III), Cy (Weibull), Cz (log Pearson type III), θ (normal), β (normal), and τ (log Pearson type III).
4.3. Uncertainty in Streamflow Measurement: GCP Measurement Times
4.4. Uncertainty in Streamflow Measurement: GCP Measurement Accuracy
4.5. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter | Near-Field Camera | Far-Field Camera | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Beta | Gamma | Normal | Log Pearson III | Weibull | Beta | Gamma | Normal | Log Pearson III | Weibull | |
| Cu (Pixels) | 0.5064 | 0.4716 | 0.4454 | 0.4964 | 0.7246 | 0.4924 | 0.6789 | 0.4223 | 0.4151 | 0.7273 |
| Cv (Pixels) | 0.5715 | 0.5750 | 0.5064 | 0.5201 | 0.6487 | 0.5609 | 0.5482 | 0.4903 | 0.5005 | 0.6654 |
| f (m) | 6 × 10−5 | 12 × 10−5 | 15 × 10−5 | 5 × 10−5 | 35 × 10−5 | 15 × 10−5 | 27 × 10−5 | 45 × 10−5 | 11 × 10−5 | 76 × 10−5 |
| Cx (m) | 0.0013 | 0.0129 | 0.0042 | 0.0014 | 0.0059 | 0.0035 | 0.0042 | 0.0035 | 0.0022 | 0.018 |
| Cy (m) | 0.0134 | 0.0334 | 0.0306 | 0.0151 | 0.0269 | 0.0475 | 0.1521 | 0.1255 | 0.1131 | 0.0473 |
| Cz (m) | 0.0030 | 0.0072 | 0.0123 | 0.0027 | 0.0295 | 0.0034 | 0.0100 | 0.0130 | 0.0032 | 0.0320 |
| θ (Degrees) | 0.0289 | 0.0533 | 0.0167 | 0.0209 | 0.1611 | 0.0731 | 0.0659 | 0.0400 | 0.0460 | 0.2977 |
| β (Degrees) | 0.0460 | 0.0718 | 0.0195 | 0.2213 | 0.2115 | 0.0392 | 0.0266 | 0.0218 | 0.0256 | 0.1393 |
| τ (Degrees) | 0.0178 | 0.1120 | 0.0189 | 0.0176 | 0.1726 | 0.0670 | 0.0680 | 0.0714 | 0.0341 | 0.3639 |
References
- Kantoush, S.A.; Schleiss, A.J.; Sumi, T.; Murasaki, M. LSPIV implementation for environmental flow in various laboratory and field cases. J. Hydro-Environ. Res. 2011, 5, 263–276. [Google Scholar] [CrossRef] [Green Version]
- Tauro, F.; Tosi, F.; Mattoccia, S.; Toth, E.; Piscopia, R.; Grimaldi, S. Optical tracking velocimetry (OTV): Leveraging optical flow and trajectory-based filtering for surface streamflow observations. Remote Sens. 2018, 10, 2010. [Google Scholar] [CrossRef] [Green Version]
- Fujita, I.; Notoya, Y.; Tani, K.; Tateguchi, S. Efficient and accurate estimation of water surface velocity in STIV. Environ. Fluid Mech. 2019, 19, 1363–1378. [Google Scholar] [CrossRef] [Green Version]
- Koutalakis, P.; Tzoraki, O.; Zaimes, G. UAVs for hydrologic scopes: Application of a low-coast UAV to estimate surface water velocity for using three different image-based methods. Drones 2019, 3, 14. [Google Scholar] [CrossRef] [Green Version]
- Pumo, D.; Alongi, F.; Ciraolo, G.; Noto, L.V. Optical methods for river monitoring: A simulation-based approach for explore optical experimental setup for LSPIV. Water 2021, 13, 247. [Google Scholar] [CrossRef]
- Guillen, N.F.; Patalano, A.; Garcia, C.M.; Bertoni, J.C. Use of LSPIV in assessing urban flash flood vulnerability. Nat. Hazards 2017, 87, 383–394. [Google Scholar] [CrossRef]
- Muste, M.; Ho, H.C.; Kim, D. Consideration on direct stream flow measurements using video imagery: Outlook and research needs. J. Hydro-Environ. Res. 2011, 5, 289–300. [Google Scholar] [CrossRef]
- Pizarro, A.; Dal Sasso, S.F.; Perks, M.T.; Manfreda, S. Identifying the optimal spatial distribution of tracers for optical sensing of stream surface flow. Hydrol. Earth Syst. Sci. 2020, 24, 5173–5185. [Google Scholar] [CrossRef]
- Costa, J.; Cheng, R.; Haeni, F.; Melcher, N.; Spicer, K.; Hayes, E.; Plant, W.; Hayes, K.; Teague, C.; Barrick, D. Use of radars to monitor stream discharge by noncontact method. Water Resour. Res. 2006, 40, 14. [Google Scholar] [CrossRef]
- Lewis, Q.W.; Lindroch, E.M.; Rhoads, B.L. Integrating unmanned aerial systems and LSPIV for rapid, cost-effective stream gauging. J. Hydrol. 2018, 560, 230–246. [Google Scholar] [CrossRef]
- LeGrand, M.C.L.; Luce, J.J.; Metcalfe, R.A.; Buttle, J.M. Development of an inexpensive automated streamflow monitoring system. Hydrol. Process. 2020, 34, 3021–3023. [Google Scholar] [CrossRef]
- Dramais, G.; Le Coz, J.; Camenen, B.; Hauet, A. Advantages of a mobile LSPIV method for measuring flood discharges and improving stage-discharge curves. J. Hydro-Environ. Res. 2011, 5, 301–312. [Google Scholar] [CrossRef] [Green Version]
- Tauro, F.; Olivieri, G.; Petroselli, A.; Porfiri, M.; Grimaldi, S. Flow monitoring with a camera: A case study on a flood event in the Tiber River. Environ. Monit. Assess. 2016, 188, 118. [Google Scholar] [CrossRef]
- Dobson, D.W.; Holland, K.T.; Calantoni, J. Fast, large-scale, particle image velocimetry-based estimations of river surface velocity. Comput. Geosci. 2014, 70, 35–43. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Kinzel, P.J.; Nelson, J.M. Remote measurement of river discharge using thermal particle image velocimetry (PIV) and various sources of bathymetric information. J. Hydrol. 2017, 554, 490–506. [Google Scholar] [CrossRef]
- Huang, W.C.; Young, C.C.; Liu, W.C. Application of an automated discharge imaging system and LSPIV during typhoon events in Taiwan. Water 2018, 10, 280. [Google Scholar] [CrossRef] [Green Version]
- Schweitzer, S.A.; Cowen, E.A. Instantaneous river-wide water surface velocity field measurements at centimeter scales using infrared quantitative image velocimetry. Water Resour. Res. 2021, 57, e2020WR029279. [Google Scholar] [CrossRef]
- Creutin, J.; Muste, M.; Bradley, A.; Kim, S.; Kruger, A. River gauging using PIV techniques: A proof of concept experiment on the Iowa River. J. Hydrol. 2003, 277, 182–194. [Google Scholar] [CrossRef]
- Fujita, I.; Muste, M.; Kruger, A. Large-scale particle image velocimetry for flow analysis in hydraulic engineering applications. J. Hydraul. Res. 1998, 36, 397–414. [Google Scholar] [CrossRef]
- Jodeau, M.; Hauet, A.; Paquier, A.; Le Coz, J.; Dramais, G. Application and evaluation of LS-PIV technique for the monitoring river surface velocities in high flow conditions. Flow Meas. Instrum. 2008, 19, 117–127. [Google Scholar] [CrossRef]
- Muste, M.; Fujita, I.; Hauet, A. Large-scale particles image velocimetry for measurements in riverine environments. Water Resour. Res. 2008, 44, 2008WR006950. [Google Scholar] [CrossRef] [Green Version]
- Muste, M.; Hauet, A.; Fujita, I.; Legout, C.; Ho, H.C. Capabilities of Large-scale Particle Image Velocimetry to characterize shallow free-surface flows. Adv. Water Resour. 2014, 70, 160–171. [Google Scholar] [CrossRef]
- Fujita, I.; Kunita, Y. Application of aerial LSPIV to the 2002 flood of the Yodo River using a helicopter mounted high density video camera. J. Hydro-Environ. Res. 2011, 5, 323–331. [Google Scholar] [CrossRef]
- Bechle, A.; Wu, C.H.; Liu, W.C.; Kimura, N. Development and application of an automated river-estuary discharge imaging system. J. Hydraul. Eng. 2012, 138, 327–339. [Google Scholar] [CrossRef]
- Ran, Q.H.; Li, W.; Liao, Q.; Tang, H.L.; Wang, M.Y. Application of an automated LSPIV system in a mountainous stream for continuous flood flow measurements. Hydrol. Process. 2016, 30, 3014–3029. [Google Scholar] [CrossRef]
- Tauro, F.; Porfiri, M.; Grimaldi, S. Orienting the camera and firing lasers to enhance large scale particle image velocimetry for streamflow monitoring. Water Resour. Res. 2014, 50, 7470–7483. [Google Scholar] [CrossRef]
- Tauro, F.; Piscopia, R.; Grimaldi, S. Streamflow observations from cameras: Large-scale particle image velocimetry or particle tracking velocimetry? Water Resour. Res. 2017, 53, 10374–10394. [Google Scholar] [CrossRef] [Green Version]
- Yeh, M.T.; Chung, T.N.; Huang, Y.X.; Lai, C.W.; Juang, D.J. Applying adaptive LS-PIV with dynamically adjusting detection region approach on the surface velocity measurement of river flow. Comput. Electr. Eng. 2017, 74, 466–482. [Google Scholar] [CrossRef]
- Li, W.; Liao, Q.; Ran, Q. Stereo-imaging LSPIV (SI-LSPIV) for 3D water surface reconstruction and discharge measurement in mountain river flows. J. Hydrol. 2019, 578, 124099. [Google Scholar] [CrossRef]
- Zhu, X.; Kouyi, G.L. An analysis of LSPIV-based surface velocity measurement techniques for stormwater detention basin management. Water Resour. Res. 2019, 55, 888–903. [Google Scholar] [CrossRef]
- Naves, J.; Puertas, A.J.; Regueiro-Picallo, M.; Suarez, J. Using a 2D shallow water model to assess Large-Scale Particle Image Velocimetry (LSPIV) and Structure from Motion (SfM) techniques in a street-scale urban drainage physical model. J. Hydrol. 2019, 575, 54–65. [Google Scholar] [CrossRef]
- Naves, J.; Garcia, J.T.; Puertas, J.; Anta, J. Assessing different imaging velocimetry techniques to measure shallow runoff velocities during rain events using an urban drainage physical model. Hydrol. Earth Syst. Sci. 2021, 25, 885–900. [Google Scholar] [CrossRef]
- Liu, W.C.; Huang, W.C. Development of a three-axis accelerometer and large-scale particle image velocimetry (LSPIV) to enhance surface velocity measurements in rivers. Comput. Geosci. 2021, 155, 104866. [Google Scholar] [CrossRef]
- Le Coz, J.; Hauet, A.; Pierrefeu, G.; Dramais, G.; Camenen, B. Performance of imagine-based velocimetry (LSPIV) applied to flash-flood discharge measurements in Mediterranean rivers. J. Hydrol. 2010, 394, 542–552. [Google Scholar] [CrossRef] [Green Version]
- Tauro, F.; Pagano, C.; Phamduy, P.; Grimaldi, S.; Porfirim, M. Large-scale particle image velocimetry from an unmanned aerial vehicle. IEEE/ASME Trans. Mechatron. 2015, 20, 3269–3275. [Google Scholar] [CrossRef]
- Liu, W.C.; Lu, C.H.; Huang, W.C. Large-scale image velocimetry to measure streamflow from videos recorded from unmanned aerial vehicle and fixed imaging system. Remote Sens. 2021, 13, 2661. [Google Scholar] [CrossRef]
- Thielicke, W.; Stamhuis, E. PIVlab-Towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB. J. Open Source Softw. 2014, 2, e30. [Google Scholar] [CrossRef] [Green Version]
- Perks, M.T.; Russell, A.J.; Large, A.R.G. Technical note: Advances in flash flood monitoring using unmanned aerial vehicles (UAVs). Hydrol. Earth Syst. Sci. 2016, 20, 4005–4015. [Google Scholar] [CrossRef] [Green Version]
- Leitao, J.P.; Pena-Haro, S.; Luthi, B.; Scheidegger, A.; de Vitry, M.M. Urban overland runoff velocity measurement with consumer-grade surveillance cameras and surface structure image velocimetry. J. Hydrol. 2018, 565, 791–804. [Google Scholar] [CrossRef]
- Detert, M. How to avoid and correct biased riverine surface image velocimetry. Water Resour. Res. 2021, 57, e2020WR027833. [Google Scholar] [CrossRef]
- Rozos, E.; Dimitriadis, P.; Mazi, K.; Lykoudis, S.; Koussis, A. On the uncertainty of the image velocimetry method parameters. Hydrology 2020, 7, 65. [Google Scholar] [CrossRef]
- Le Coz, J.; Renard, B.; Vansuyt, V.; Jodeau, M.; Hauet, A. Estimating the uncertainty of video-based flow velocity and discharge measurements due to the conversion of field to image coordinates. Hydrol. Process. 2021, 35, e14169. [Google Scholar] [CrossRef]
- Jolley, M.J.; Russell, A.J.; Quinn, P.F.; Perks, M.T. Considerations when applying large-scale PIV and PTV for determining river flow velocity. Front. Water 2021, 3, 709268. [Google Scholar] [CrossRef]
- Meselhe, E.A.; Peeva, T.; Muste, M. Large scale particle image velocimetry for low velocity and shallow water flows. J. Hydraul. Eng. 2004, 130, 937–940. [Google Scholar] [CrossRef]
- Hauet, A.; Kruger, A.; Krajewski, W.F.; Bradley, A.; Muste, M.; Creutin, J.D. Experiment system for real-time discharge estimation using an imagine-based method. J. Hydrol. Eng. 2008, 13, 105–110. [Google Scholar] [CrossRef]
- Gharahjeh, S.; Aydin, I. Application of video imaginary techniques for low cost measurement of water surface velocity in open channel. Flow Meas. Instrum. 2016, 51, 79–94. [Google Scholar] [CrossRef]
- Wolf, P.; DeWitt, B. Elements of Photogrammetry: With Applications in GIS; McGraw-Hill: Boston, MA, USA, 2000. [Google Scholar]
- Wanek, J.M.; Wu, C.H. Automated trinocular stereo imaging system for three-dimensional surface wave measurements. Ocean Eng. 2006, 33, 723–747. [Google Scholar] [CrossRef]
- Le Coz, J.; Renard, B.; Bonnifait, L.; Branger, F.; Le Boursicaud, R. Combining hydraulic knowledge and uncertain gaugings in the estimation of hydrometric rating curves: A Bayesian approach. J. Hydrol. 2014, 509, 573–587. [Google Scholar] [CrossRef] [Green Version]
- Renard, B.; Garreta, V.; Lang, M. An application of Bayesian analysis and Markov chain Monte Carlo methods to the estimation of a regional trend in annual maxima. Water Resour. Res. 2006, 42, W12422. [Google Scholar] [CrossRef]
- Despax, A.; Perret, C.; Garcon, R.; Hauet, A.; Belleville, A.; Le Coz, J.; Favre, A.C. Considering sampling strategy and cross-section complexity for estimating the uncertainty of discharge measurement using velocity-area method. J. Hydrol. 2016, 533, 128–140. [Google Scholar] [CrossRef]
- Kiang, J.E.; Gazoorian, C.; McMillan, H.; Coxon, C.; Le Coz, J.; Westerberg, I.K.; Belleville, A.; Sevrez, D.; Sikorska, A.E.; Petersen-Øverleir, A.; et al. A comparison of methods for streamflow uncertainty estimation. Water Resour. Res. 2018, 54, 7149–7176. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.C.; Liu, H.M. Integrating hydrodynamic model and Monte Carlo simulation for predicting extreme water levels in a river system. Terr. Atmos. Ocean. Sci. 2019, 30, 589–604. [Google Scholar] [CrossRef] [Green Version]
- Schweitzer, S.A.; Cowen, E.A. A method for analysis of spatial uncertainty in image based surface velocimetry. Front. Water 2022, 4, 744278. [Google Scholar] [CrossRef]
- Fleit, G.; Baranya, S. An improved particle image velocimetry method for efficient flow analyses. Flow Meas. Instrum. 2019, 69, 101619. [Google Scholar] [CrossRef]












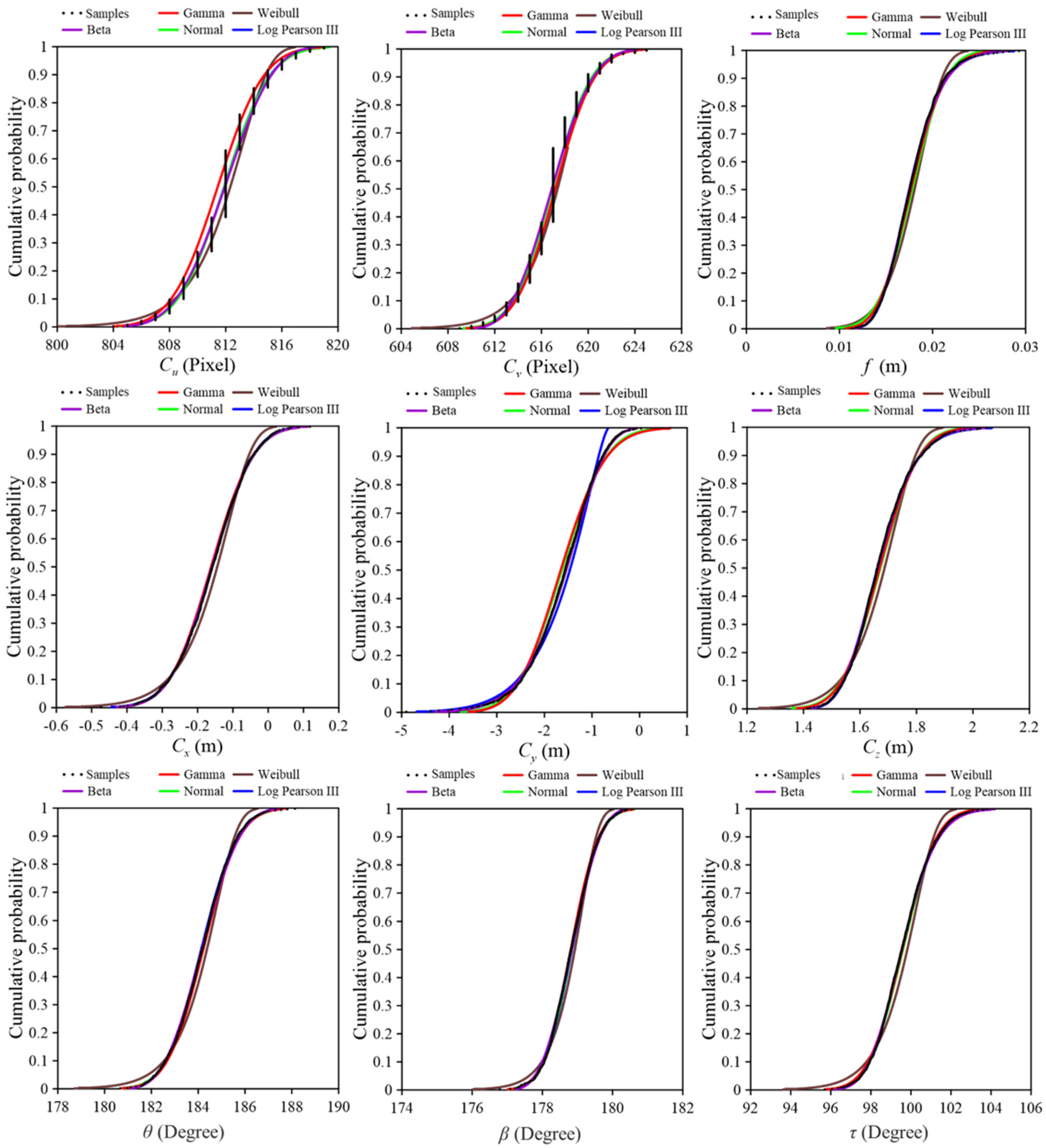



| Date/Camera | Cu (Pixels) | Cv (Pixels) | f (m) | Cx (m) | Cy (m) | Cz (m) | θ (Degrees) | β (Degrees) | τ (Degrees) | |
|---|---|---|---|---|---|---|---|---|---|---|
| 3 May 2020 | FF | 812 | 617 | 0.018 | −0.16 | −1.595 | 1.648 | 178.83 | 184.16 | 99.28 |
| NF | 812 | 617 | 0.015 | −0.261 | −0.629 | 1.064 | 168.15 | 186.42 | 111.77 | |
| 26 July 2020 | FF | 812 | 617 | 0.018 | −0.189 | −1.696 | 1.605 | 178.65 | 184.09 | 97.38 |
| NF | 812 | 617 | 0.014 | 0.070 | 0.410 | 0.778 | 175.92 | 178.02 | 110.72 | |
| 1 November 2020 | FF | 812 | 617 | 0.018 | −0.393 | −1.675 | 1.648 | 178.26 | 189.17 | 96.63 |
| NF | 812 | 617 | 0.017 | −0.145 | −0.634 | 1.133 | 160.76 | 184.64 | 115.46 | |
| 3 December 2020 | FF | 812 | 617 | 0.018 | 0.373 | −1.749 | 1.744 | 178.86 | 178.25 | 98.76 |
| NF | 812 | 617 | 0.012 | 0.017 | −0.080 | 1.132 | 176.70 | 184.84 | 112.26 | |
| Date | 3 May | 26 July | 1 November | 3 December |
|---|---|---|---|---|
| Max water depth (m) | 0.66 | 0.79 | 0.62 | 0.85 |
| VFM (m/s) | 0.528 | 0.750 | 0.554 | 0.829 |
| VLSPIV (m/s) | 0.485 | 0.665 | 0.492 | 0.758 |
| MAE (m/s) | 0.097 | 0.154 | 0.104 | 0.098 |
| RMSE (m/s) | 0.107 | 0.191 | 0.111 | 0.110 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.-C.; Huang, W.-C.; Young, C.-C. Uncertainty Analysis for Image-Based Streamflow Measurement: The Influence of Ground Control Points. Water 2023, 15, 123. https://doi.org/10.3390/w15010123
Liu W-C, Huang W-C, Young C-C. Uncertainty Analysis for Image-Based Streamflow Measurement: The Influence of Ground Control Points. Water. 2023; 15(1):123. https://doi.org/10.3390/w15010123
Chicago/Turabian StyleLiu, Wen-Cheng, Wei-Che Huang, and Chih-Chieh Young. 2023. "Uncertainty Analysis for Image-Based Streamflow Measurement: The Influence of Ground Control Points" Water 15, no. 1: 123. https://doi.org/10.3390/w15010123
APA StyleLiu, W.-C., Huang, W.-C., & Young, C.-C. (2023). Uncertainty Analysis for Image-Based Streamflow Measurement: The Influence of Ground Control Points. Water, 15(1), 123. https://doi.org/10.3390/w15010123









