Simultaneous Scheduling and Synthesis of Industrial Water Allocation Networks
Abstract
:1. Introduction
1.1. Sequential Methodology and Direct or Indirect Water Re-Use
1.2. Simultaneous Methodology and Indirect Water Re-Use
1.3. Simultaneous Methodology and Direct Water Re-Use
1.4. Problem Statement
- The production recipe representation using STN;
- Unit capacity and suitability of occurrence of tasks in each unit;
- Storage capacity for each material state;
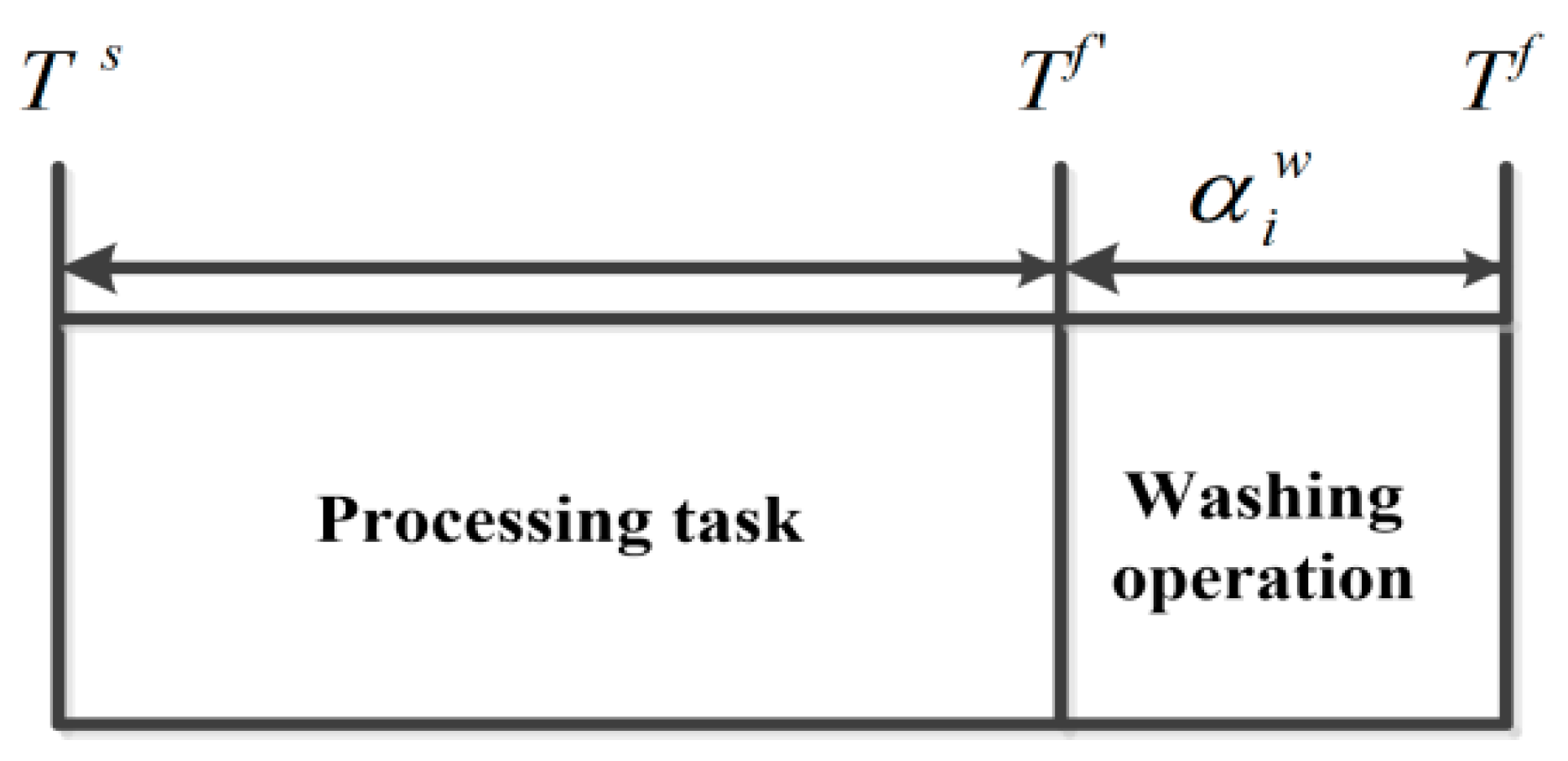
- Processing time for each task (variable or constant);
- Washing time in each unit;
- Contaminant mass load (constant or batch dependent);
- Maximum inlet and outlet concentration of each contaminant for different units;
- Different costs for products, fresh water and wastewater discharge;
- Scheduling time horizon;
- Maximum capacity of the central storage tank for water storage;
- Contaminant removal ratio and regenerator flow rate.
2. Mathematical Formulation
2.1. Production Scheduling Model
2.1.1. Handling Multiple States Having Different Processing Time Durations for the Same Task in a Processing Unit
2.1.2. Duration Constraints
2.1.3. Sequencing Constraints
2.1.4. Tightening Constraint
2.1.5. Storage Constraints
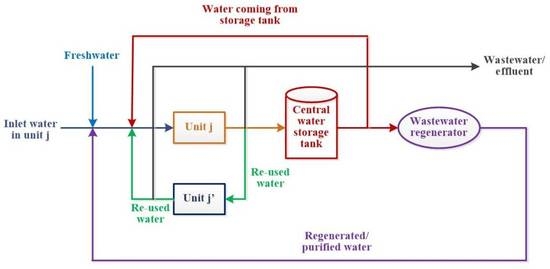
2.2. WAN Model
2.2.1. Mass Balance of Water around Washing Unit
2.2.2. Water Mass Balance around the Central Water Storage Tank
2.2.3. Water Mass Balance around Regeneration Unit
2.2.4. Sequencing Constraints for Water Reuse
2.2.5. Sequencing Constraints for Storage Tank
2.2.6. Sequencing Constraints Associated with Regeneration Unit
2.2.7. Scheduling Constraints for Washing
2.2.8. Modifications in the Scheduling Model
2.2.9. Objective Function
2.3. Important Contributions of the Proposed Work
- A unit-specific event-based production scheduling model has been adapted from the literature [19] with several modifications including: introducing a three-index finish time variable to handle different processing times for multiple states produced by a task, new constraints for avoiding real time storage violation when the same state is being produced and consumed in the same unit, modified sequencing constraints to handle the new definition of finish time of a task by combining the washing operation to occur at the same event after the task.
- In WAN, immediate washing is considered in the processing units after completion of the processing task i.e., the washing operation takes place without post processing unit wait policy.
- Central water storage tank and wastewater regenerator are incorporated in the water network synthesis to target minimum freshwater consumption.
- Sequential and simultaneous methodologies are compared for the integrated problem of water allocation network synthesis and batch scheduling.
- A preliminary analysis for two-objective optimization is presented where revenue is maximized, and the total water cost is minimized simultaneously using the weighted-sum method.
3. Computational Results and Discussion
3.1. Case Study 1
3.2. Case Study 2
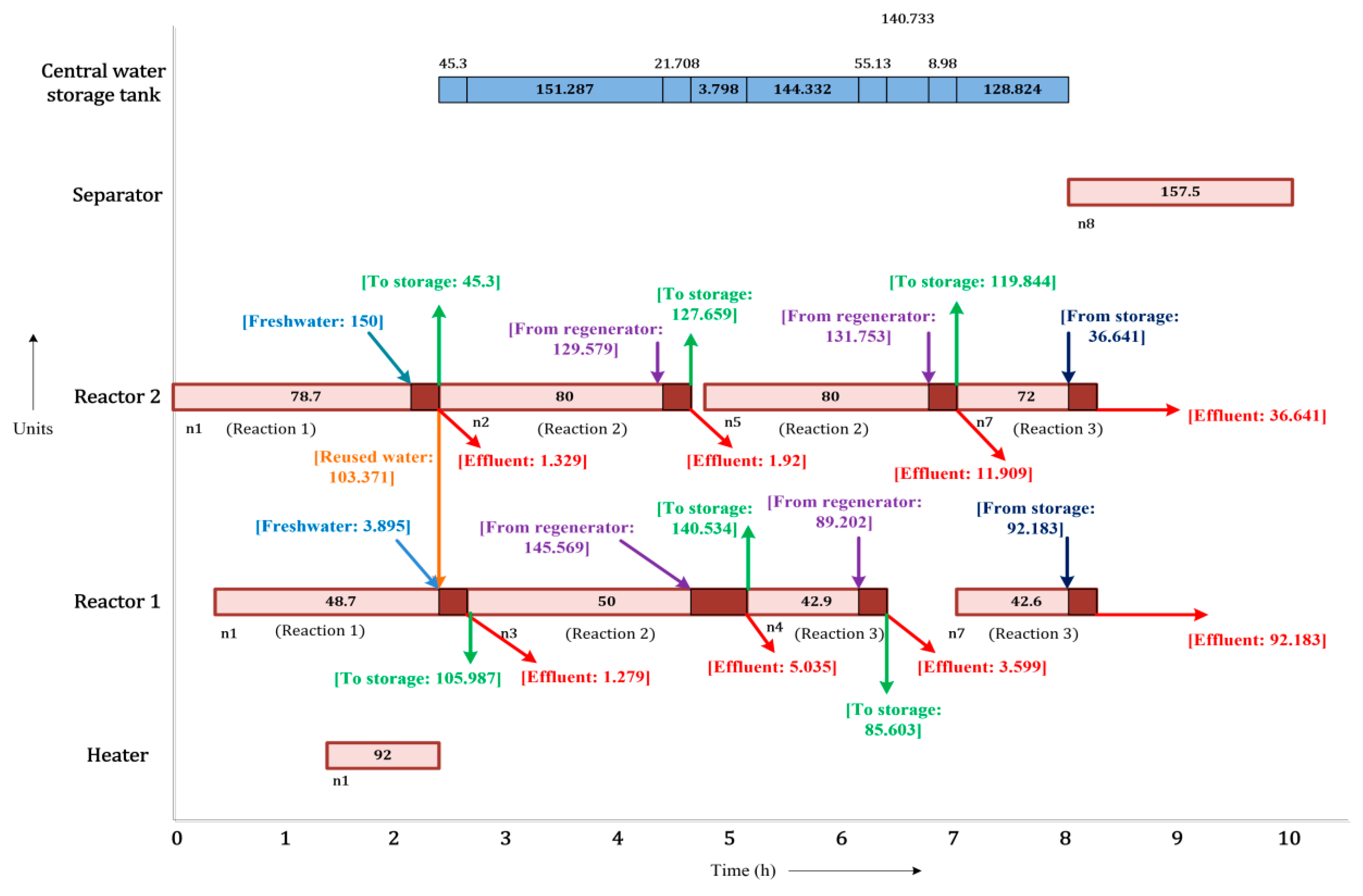
3.2.1. Limitations of the Literature Gantt Chart from Majozi and Gouws
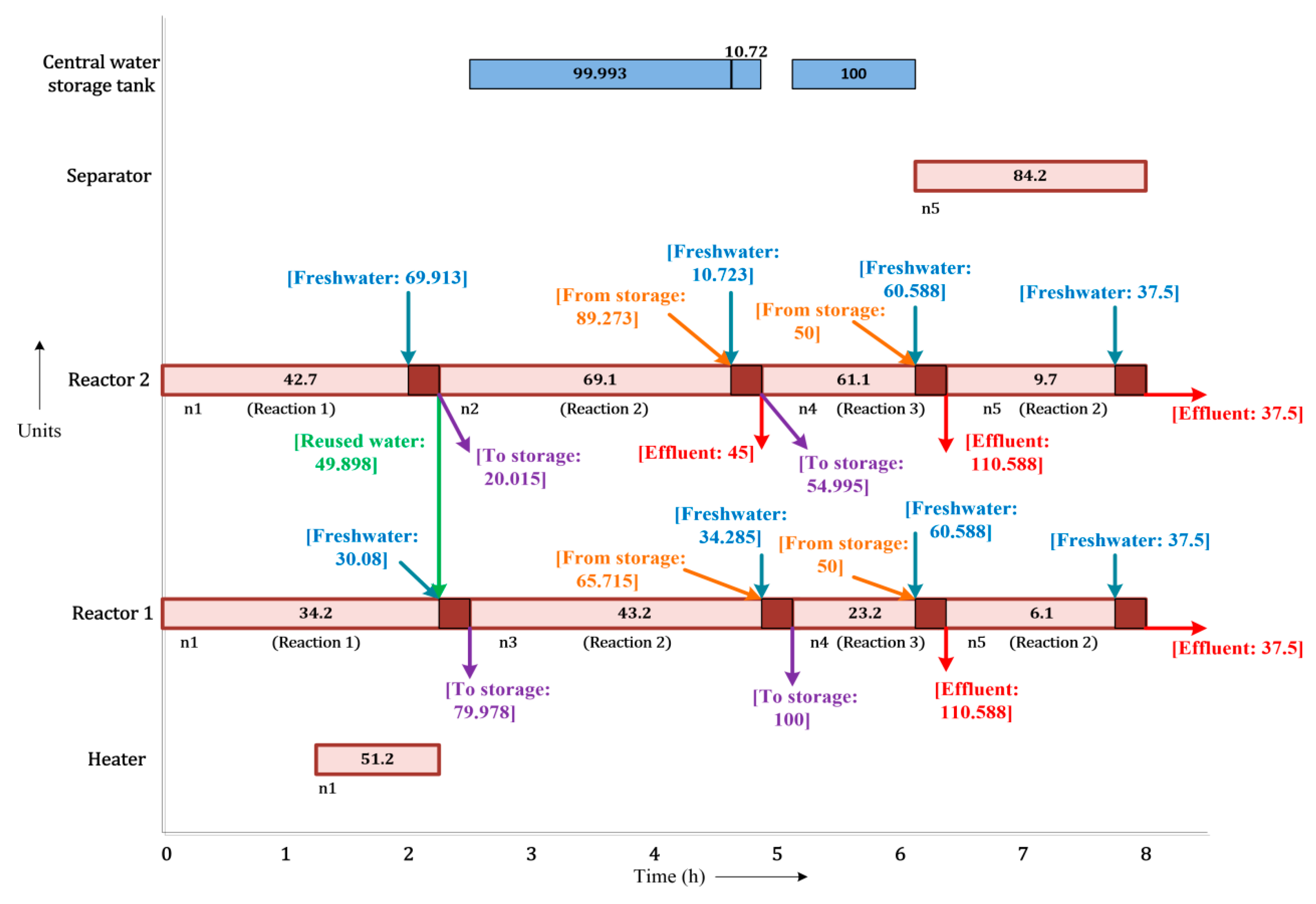
3.3. Case Study 3
3.3.1. Limitations of the Literature Gantt Chart from Adekola and Majozi
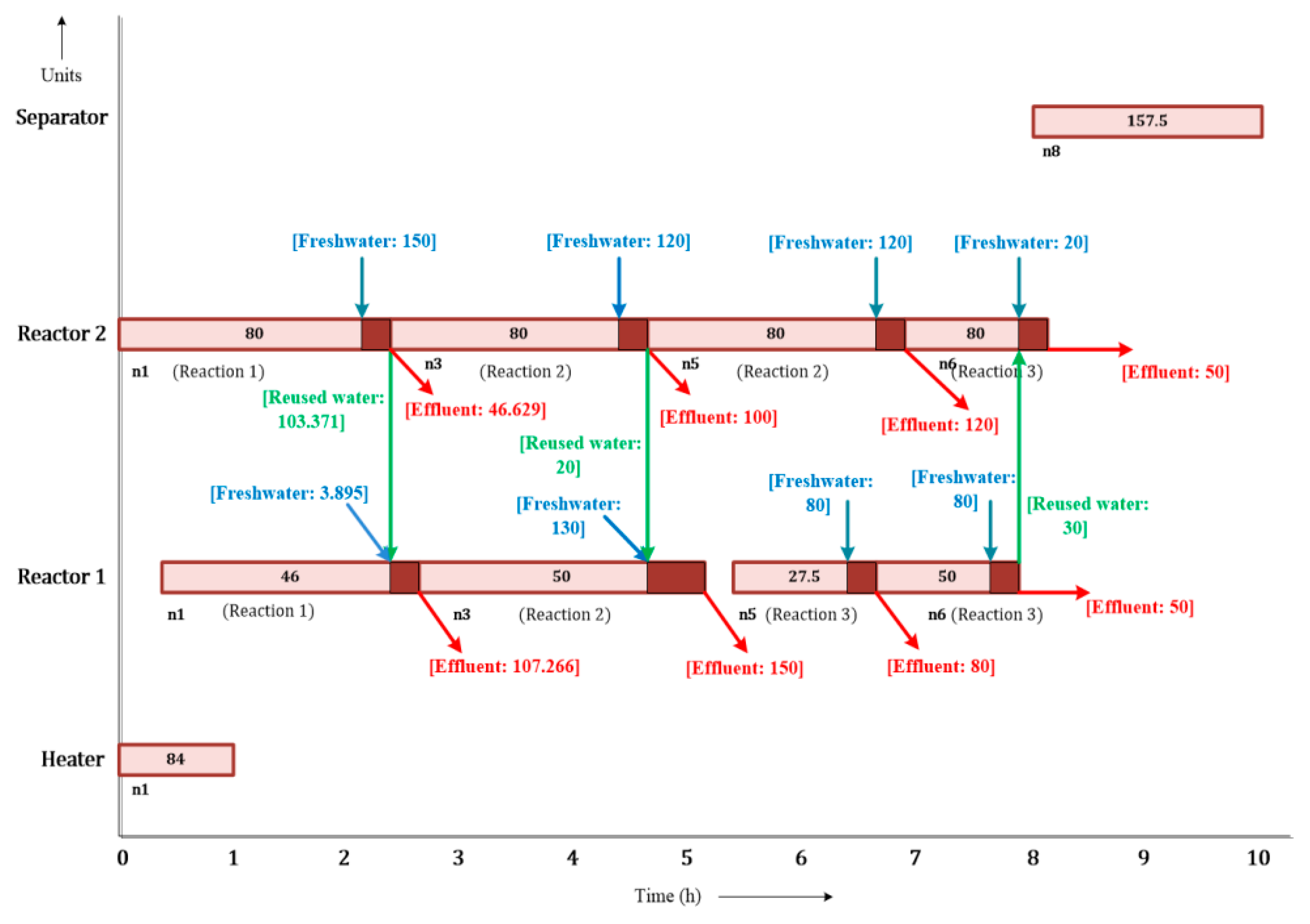
3.4. Case Study 4
3.4.1. Limitations of Literature Gantt Chart from Adekola and Majozi
- Contaminant mass balance for water reuse from mixer 1 to mixer 3: (375 + 225) × Cin = 375 × 0.04 + 225 × 0
- Hence, Cin = 0.025, which is greater than 0.014, the maximum allowed inlet concentration of shampoo in mixer 3.
- (114.4 + 218.9) × Cin = 114.4 × 0.06 + 218.9 × 0
- Hence, Cin = 0.0205, which is greater than 0.007, the maximum allowed inlet concentration of cream in mixer 2.
- Contaminant mass balance for water reuse from mixer 4 to mixer 1:
- (105.9 + 269.1) × Cin = 105.9 × 0.06 + 269.1 × 0
- Hence, Cin = 0.0169, which is greater than 0.0035, the maximum allowed inlet concentration of cream in mixer 1.
3.5. Two-Objective Optimization Using Weighted-Sum-Method
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Indices: | |
| i, i’ | tasks |
| j, j’ | units |
| n, n’ | events |
| s | states |
| c | contaminants |
| stt | storage tanks |
| Scheduling | |
| Sets: | |
| I | tasks |
| Ij | tasks that can be performed in unit j |
| IPC | tasks that produce and consumes same state |
| J | units |
| N | total number of event points |
| S | states |
| Sdfis | intermediates states with dedicated finite intermediate storage |
| SPC | states that are being produced and consumed in the same unit |
| C | contaminants species |
| Parameters | |
| minimum batch size of task i | |
| maximum batch size of task i | |
| αis | fixed term of processing time of task i for state s |
| largest fixed term of processing time of task i for state s | |
| βis | variable term of the processing time of task i for state s |
| H | short-term scheduling horizon |
| Ps | price of state s |
| Δn | limit on the maximum number of events over which a task is allowed to continue |
| M | large positive number in big-M constraints |
| Binary Variables | |
| w(i,n,n’) | binary variable for task i that starts at event n and ends at event n’ |
| Positive Variables | |
| Ts(i,n) | start time of task i at event n |
| Tf(i,n) | finish time of task i at event n |
| Tf(i,s,n) | finish time of task i for state s at event n |
| Water Allocation Network | |
| Parameters | |
| cost of fresh water | |
| cost of effluent water treatment | |
| mass load of contaminant c added from task i to the water stream | |
| maximum inlet water mass to task i | |
| maximum inlet concentration of contaminant c for task i | |
| maximum outlet concentration of contaminant c for task i | |
| time required for washing after task i | |
| initial amount of water in storage tank | |
| maximum storage capacity of the tank | |
| initial concentration of contaminant c in the storage vessel | |
| RRc | contaminant removal ratio |
| freg | regenerator flow rate |
| Binary Variables | |
| binary variable signifies the occurrence of washing task i at event n | |
| binary variable shows the transfer of water from task i to task i’ at event n | |
| binary variable shows the transfer of water to the storage tank from task i at event n | |
| binary variable shows the transfer of water from storage tank to task i at event n | |
| binary variable shows the transfer of water from storage tank to regenerator at event n | |
| binary variable shows the transfer of water from the regenerator to task i at event n | |
| Positive Variables | |
| mass of water consumed for washing unit for task i at the end of event n | |
| mass of water exiting after washing unit for task i at the end of event n | |
| mass of fresh water used for washing unit for task i at the end of event n | |
| mass of effluent water produced after washing the unit for task i at the end of event n | |
| mass of water recycled from task i to task i’ at event n | |
| mass of water to storage from task i at event n | |
| mass of water coming from storage to task i at event n | |
| mass of water coming to regenerator from storage at event n | |
| mass of water coming out from regenerator to task i at event n | |
| inlet concentration of contaminant c, entering task i at event n | |
| outlet concentration of contaminant c, exiting task i at event n | |
| inlet concentration of contaminant c, entering storage at event n | |
| outlet concentration of contaminant c, exiting from storage at event n | |
| outlet concentration of contaminant c, exiting from regenerator at event n | |
| inlet time of water used for task i, at event n | |
| outlet time of water used for task i, at event n | |
| water recycle time from task i to task i’, at event n | |
| inlet time of water in regenerator from storage tank at event n | |
| outlet time of water from regenerator to task i at event n |
Appendix A
Appendix A.1. Allocation Constraint
Appendix A.2. Capacity Constraint
Appendix A.3. Material Balance
Appendix A.4. Duration Constraint
Appendix A.5. Sequencing Constraint
Appendix A.6. Tightening Constraint
Appendix A.7. Storage Constraint
Appendix A.8. Bounds
Appendix B
| Tasks | i | Unit (j) | αi (h) | βi (h/kg) | (kg) | (kg) |
|---|---|---|---|---|---|---|
| Heating | 1 | Heater | 0.667 | 0.00667 | 0 | 100 |
| Reaction 1 | 2 | Reactor 1 | 1.334 | 0.02664 | 0 | 50 |
| 3 | Reactor 2 | 1.334 | 0.01665 | 0 | 80 | |
| Reaction 2 | 4 | Reactor 1 | 1.334 | 0.02664 | 0 | 50 |
| 5 | Reactor 2 | 1.334 | 0.01665 | 0 | 80 | |
| Reaction 3 | 6 | Reactor 1 | 0.667 | 0.01332 | 0 | 50 |
| 7 | Reactor 2 | 0.667 | 0.008325 | 0 | 80 | |
| Separation | 8 | Separator | 1.3342 | 0.00666 | 0 | 200 |
| State | Storage Capacities (kg) | Selling Price ($/kg) |
|---|---|---|
| S1 | UL | NA |
| S2 | UL | NA |
| S3 | UL | NA |
| S4 | 100 | NA |
| S5 | 200 | NA |
| S6 | 150 | NA |
| S7 | 200 | NA |
| S8 | UL | 10 |
| S9 | UL | 10 |
| Tasks | i | Unit (j) | Washing Time (h) | Max. Contaminant (ppm) | Max. Flow (t) | |
|---|---|---|---|---|---|---|
| Inlet | Outlet | |||||
| Heating | 1 | Heater | NA | NA | NA | NA |
| Reaction 1 | 2 | Reactor 1 | 0.2 | 250 | 600 | 80 |
| 3 | Reactor 2 | 0.2 | 250 | 600 | 80 | |
| Reaction 2 | 4 | Reactor 1 | 0.2 | 500 | 800 | 100 |
| 5 | Reactor 2 | 0.2 | 500 | 800 | 100 | |
| Reaction 3 | 6 | Reactor 1 | 0.2 | 400 | 850 | 120 |
| 7 | Reactor 2 | 0.2 | 400 | 850 | 120 | |
| Separation | 8 | Separator | NA | NA | NA | NA |
| Tasks | i | Unit (j) | αi (h) | (kg) | (kg) |
|---|---|---|---|---|---|
| Heating | 1 | Heater | 1 | 0 | 100 |
| Reaction 1 | 2 | Reactor 1 | 2 | 0 | 50 |
| 3 | Reactor 2 | 2 | 0 | 80 | |
| Reaction 2 | 4 | Reactor 1 | 2 | 0 | 50 |
| 5 | Reactor 2 | 2 | 0 | 80 | |
| Reaction 3 | 6 | Reactor 1 | 1 | 0 | 50 |
| 7 | Reactor 2 | 1 | 0 | 80 | |
| Separation | 8 | Separator | 1 for product 2 2 for int.AB | 0 | 200 |
| State | Storage Capacities (kg) | Selling Price (c.u./kg) |
|---|---|---|
| S1 | UL | NA |
| S2 | UL | NA |
| S3 | UL | NA |
| S4 | 100 | NA |
| S5 | 200 | NA |
| S6 | 150 | NA |
| S7 | 200 | NA |
| S8 | UL | 100 |
| S9 | UL | 100 |
| Task (Unit) | Max. Contaminant Concentration (g contaminant/kg water) | |||
|---|---|---|---|---|
| Contaminant 1 | Contaminant 2 | Contaminant 3 | ||
| Reaction 1 (Reactor 1) | Max inlet | 0.5 | 0.5 | 2.3 |
| Max outlet | 1 | 0.9 | 3 | |
| Reaction 2 (Reactor 1) | Max inlet | 0.01 | 0.05 | 0.3 |
| Max outlet | 0.2 | 0.1 | 1.2 | |
| Reaction 3 (Reactor 1) | Max inlet | 0.15 | 0.2 | 0.35 |
| Max outlet | 0.3 | 1 | 1.2 | |
| Reaction 1 (Reactor 2) | Max inlet | 0.05 | 0.2 | 0.05 |
| Max outlet | 0.1 | 1 | 12 | |
| Reaction 2 (Reactor 2) | Max inlet | 0.03 | 0.1 | 0.2 |
| Max outlet | 0.075 | 0.2 | 1 | |
| Reaction 3 (Reactor 2) | Max inlet | 0.3 | 0.6 | 1.5 |
| Max outlet | 2 | 1.5 | 2.5 | |
| Task (i) | Unit (j) | Mass Load (g) | ||
|---|---|---|---|---|
| Contaminant 1 | Contaminant 2 | Contaminant 3 | ||
| Reaction 1 | Reactor 1 | 4 | 80 | 10 |
| Reactor 2 | 15 | 24 | 358 | |
| Reaction 2 | Reactor 1 | 28.5 | 7.5 | 135 |
| Reactor 2 | 9 | 2 | 16 | |
| Reaction 3 | Reactor 1 | 15 | 80 | 85 |
| Reactor 2 | 22.5 | 45 | 36.5 | |
| Unit/Task | Duration of Washing (h) | ||
|---|---|---|---|
| Reaction 1 | Reaction 2 | Reaction 3 | |
| Reactor 1 | 0.25 | 0.5 | 0.25 |
| Reactor 2 | 0.3 | 0.25 | 0.25 |
| Contaminants | Removal Ratio, (RRc) |
|---|---|
| Contaminant 1 | 0.98 |
| Contaminant 2 | 0.97 |
| Contaminant 3 | 0.96 |
| Mixer | Product | No. of Batches | Time (h) |
|---|---|---|---|
| 1 | Shampoo | 2 | 7 |
| 2 | Deodorant | 3 | 5.5 |
| 3 | Lotion | 1 | 11 |
| 4 | Cream | 2 | 11 |
| Mixer | Contaminant | Residue Mass (kg) | Limiting Water (kg) | Maximum Outlet Contaminant Concentration (kg/kg) |
|---|---|---|---|---|
| 1 | Shampoo | 15 | 576.9 | 0.04 |
| 2 | Deodorant | 15 | 361.4 | 0.045 |
| 3 | Lotion | 30 | 697.6 | 0.05 |
| 4 | Cream | 70 | 1238.9 | 0.06 |
| Mixer | Shampoo (kg product/kg water) | Deodorant (kg product/kg water) | Lotion (kg product/kg water) | Cream (kg product/kg water) |
|---|---|---|---|---|
| 1 | 0.014 | 0 | 0.007 | 0.0035 |
| 2 | 0.014 | 0.0035 | 0.007 | 0.007 |
| 3 | 0.014 | 0 | 0.007 | 0.0035 |
| 4 | 0.014 | 0 | 0.007 | 0.0035 |
| Contaminant | Removal Ratio, (RRc) |
|---|---|
| Shampoo | 0.95 |
| Deodorant | 0.99 |
| Lotion | 0.96 |
| Creams | 0.98 |
References
- Halim, I.; Srinivasan, R. Sequential methodology for integrated optimization of energy and water use during batch process scheduling. Comput. Chem. Eng. 2011, 35, 1575–1597. [Google Scholar] [CrossRef]
- Ahmetovic, E.; Ibric, N.; Kravanja, Z.; Grossmann, I.E. Water and energy integration: A comprehensive literature review of non-isothermal water network synthesis. Comput. Chem. Eng. 2015, 82, 144–171. [Google Scholar] [CrossRef]
- Majozi, T. Wastewater minimisation using central reusable water storage in batch plants. Comput. Chem. Eng. 2005, 29, 1631–1646. [Google Scholar] [CrossRef]
- Cheng, K.F.; Chang, C.T. Integrated water network designs for batch processes. Ind. Eng. Chem. Res. 2007, 46, 1241–1253. [Google Scholar] [CrossRef]
- Chen, C.L.; Lee, J.Y.; Tang, J.W.; Ciou, Y.J. Synthesis of water-using network with central reusable storage in batch processes. Comput. Chem. Eng. 2009, 33, 267–276. [Google Scholar] [CrossRef]
- Gouws, J.F.; Majozi, T.; Gadalla, M. Flexible mass transfer model for water minimization in batch plants. Chem. Eng. Process. 2008, 47, 2323–2335. [Google Scholar] [CrossRef]
- Majozi, T.; Gouws, J.F. A mathematical optimisation approach for wastewater minimisation in multipurpose batch plants: Multiple contaminants. Comput. Chem. Eng. 2009, 33, 1826–1840. [Google Scholar] [CrossRef] [Green Version]
- Zhou, R.J.; Li, L.J.; Xiao, W.; Dong, H.G. Simultaneous optimization of batch process schedules and water-allocation network. Comput. Chem. Eng. 2009, 33, 1153–1168. [Google Scholar] [CrossRef]
- Ierapetritou, M.G.; Floudas, C.A. Effective continuous-time formulation for short-term scheduling: 1. Multipurpose batch processes, Ind. Eng. Chem. Res. 1998, 37, 4341–4359. [Google Scholar] [CrossRef]
- Li, L.J.; Zhou, R.J.; Dong, H.G. State-Time-Space Superstructure-Based MINLP Formulation for Batch Water-Allocation Network Design. Ind. Eng. Chem. Res. 2010, 49, 236–251. [Google Scholar] [CrossRef]
- Adekola, O.; Majozi, T. Wastewater minimization in multipurpose batch plants with a regeneration unit: Multiple contaminants. Comput. Chem. Eng. 2011, 35, 2824–2836. [Google Scholar] [CrossRef]
- Chaturvedi, N.D.; Manan, Z.A.; Alwi, S.R.W.; Bandyopadhyay, S. Effect of multiple water resources in a flexible-schedule batch water network. J. Clean. Prod. 2016, 125, 245–252. [Google Scholar] [CrossRef]
- Li, Z.; Majozi, T. Optimal design of batch water network with a flexible scheduling framework. Ind. Eng. Chem. Res. 2019, 58, 9500–9511. [Google Scholar] [CrossRef]
- Yang, F.; Fan, X.Y.; Jia, X.; Klemes, J.J.; Liu, Z.Y. An iterative design approach for water networks with multiple regeneration units. J. Clean. Prod. 2020, 271, 122483. [Google Scholar] [CrossRef]
- Li, Z.; Majozi, T. Synthesis of flexible batch water networks using dynamic programming. Ind. Eng. Chem. Res. 2020, 59, 13175–13189. [Google Scholar] [CrossRef]
- Chaturvedi, N.D.; Sinha, R.K. Simultaneous minimization of minimum resource and storage requirements in batch process. Comput. Aided Chem. Eng. 2021, 50, 1741–1746. [Google Scholar] [CrossRef]
- Gouws, J.F.; Majozi, T. Usage of inherent storage for minimization of wastewater in multipurpose batch plants. Chem. Eng. Sci. 2009, 64, 3545–3554. [Google Scholar] [CrossRef]
- Adekola, O.; Majozi, T. Wastewater minimization in batch plants with sequence dependent changeover. Comput. Chem. Eng. 2017, 97, 85–103. [Google Scholar] [CrossRef]
- Vooradi, R.; Shaik, M.A. Improved three-index unit-specific event-based model for short-term scheduling of batch plants. Comput. Chem. Eng. 2012, 43, 148–172. [Google Scholar] [CrossRef]
- Kondili, E.; Pantelides, C.C.; Sargent, R.W.H. A general algorithm for short-term Scheduling of batch operations-I. MILP formulation. Comput. Chem. Eng. 1993, 17, 211–227. [Google Scholar] [CrossRef]
- Chaturvedi, N.D.; Bandyopadhyay, S. Optimization of multiple freshwater resources in a flexible schedule batch water network. Ind. Eng. Chem. Res. 2014, 53, 5996–6005. [Google Scholar] [CrossRef]













| Without Central Storage Tank | With Central Storage Tank | |
|---|---|---|
| Total freshwater (t) | 370.392 | 341.176 |
| Cost of fresh water and effluent ($) | 740.784 | 682.42 |
| Net profit ($) | 529.644 | 588.076 |
| Binary variables | 180 | 234 |
| Continuous variables | 501 | 571 |
| No. of constraints | 1321 | 1390 |
| Without Central Storage Tank | With Central Storage Tank | |
|---|---|---|
| Total freshwater (t) | 269.362 | 242.5 |
| Cost of fresh water and effluent ($) | 538.724 | 485 |
| Net profit ($) | 711.798 | 765.522 |
| Binary variables | 250 | 310 |
| Continuous variables | 729 | 797 |
| No. of constraints | 1810 | 2419 |
| Proposed Work | Majozi and Gouws [7] | |
|---|---|---|
| Objective value ($) | 19,055.524 | 21,187.5 |
| Revenue from products ($) | 22,575 | 24,800 |
| Freshwater consumption (kg) | 703.895 | 722.5 |
| Total cost of freshwater and effluent ($) | 3519.475 | 3612.5 |
| Binary variables | 3088 | - |
| Continuous variables | 5300 | - |
| No. of Constraints | 16,301 | - |
| Using Storage Tank without a Regenerator | Using Storage Tank along with a Regenerator | |||
|---|---|---|---|---|
| Proposed Work | Adekola and Majozi [11] | Proposed Work | Adekola and Majozi [11] | |
| Objective value ($) | 19,955.524 | 20,180 | 21,805.524 | 21,129 |
| Revenue from products ($) | 22,575 | 22,575 | 22,575 | 23,137.5 |
| Freshwater consumption (kg) | 523.895 | 479 | 153.895 | 401.7 |
| Total cost of freshwater and effluent ($) | 2619.48 | 2395 | 769.475 | 2008.5 |
| Binary variables | 3906 | - | 4392 | 532 |
| Continuous variables | 6192 | - | 6528 | - |
| No. of constraints | 25,936 | - | 28,370 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chauhan, S.; Shaik, M.A. Simultaneous Scheduling and Synthesis of Industrial Water Allocation Networks. Water 2023, 15, 210. https://doi.org/10.3390/w15010210
Chauhan S, Shaik MA. Simultaneous Scheduling and Synthesis of Industrial Water Allocation Networks. Water. 2023; 15(1):210. https://doi.org/10.3390/w15010210
Chicago/Turabian StyleChauhan, Sudha, and Munawar A. Shaik. 2023. "Simultaneous Scheduling and Synthesis of Industrial Water Allocation Networks" Water 15, no. 1: 210. https://doi.org/10.3390/w15010210
APA StyleChauhan, S., & Shaik, M. A. (2023). Simultaneous Scheduling and Synthesis of Industrial Water Allocation Networks. Water, 15(1), 210. https://doi.org/10.3390/w15010210