Member Formation Methods Evaluation for a Storm Surge Ensemble Forecast System in Taiwan
Abstract
:1. Introduction
2. Materials and Methods
2.1. COMCOT-SS (Cornell Multi-Grid Coupled Tsunami Model—Storm Surge)
2.2. Parametric Wind and Pressure Fields
2.3. Computational Domain and Gauges
2.4. The Boundary Condition for Tides
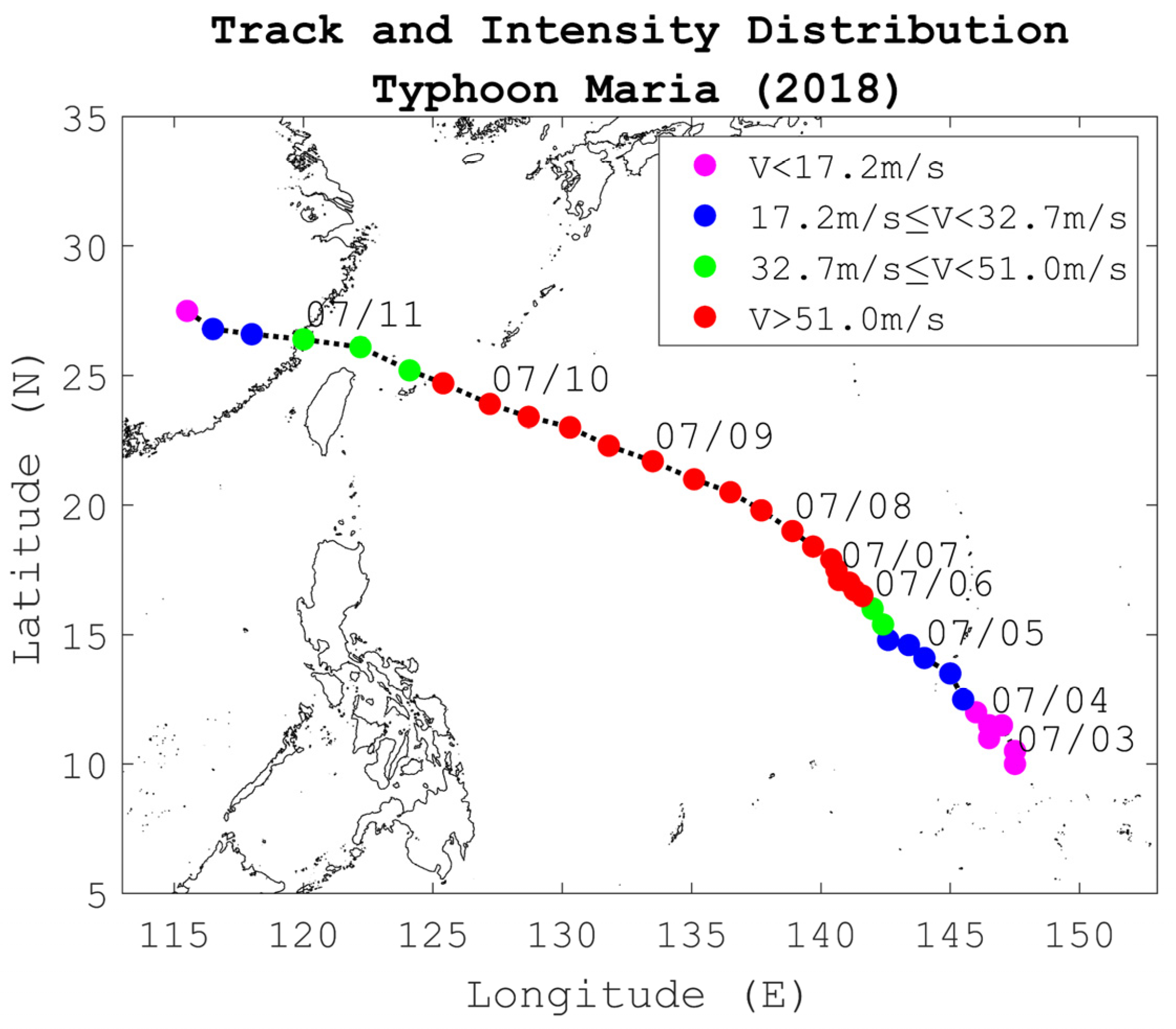
2.5. Ensemble Generation of Typhoon Tracks
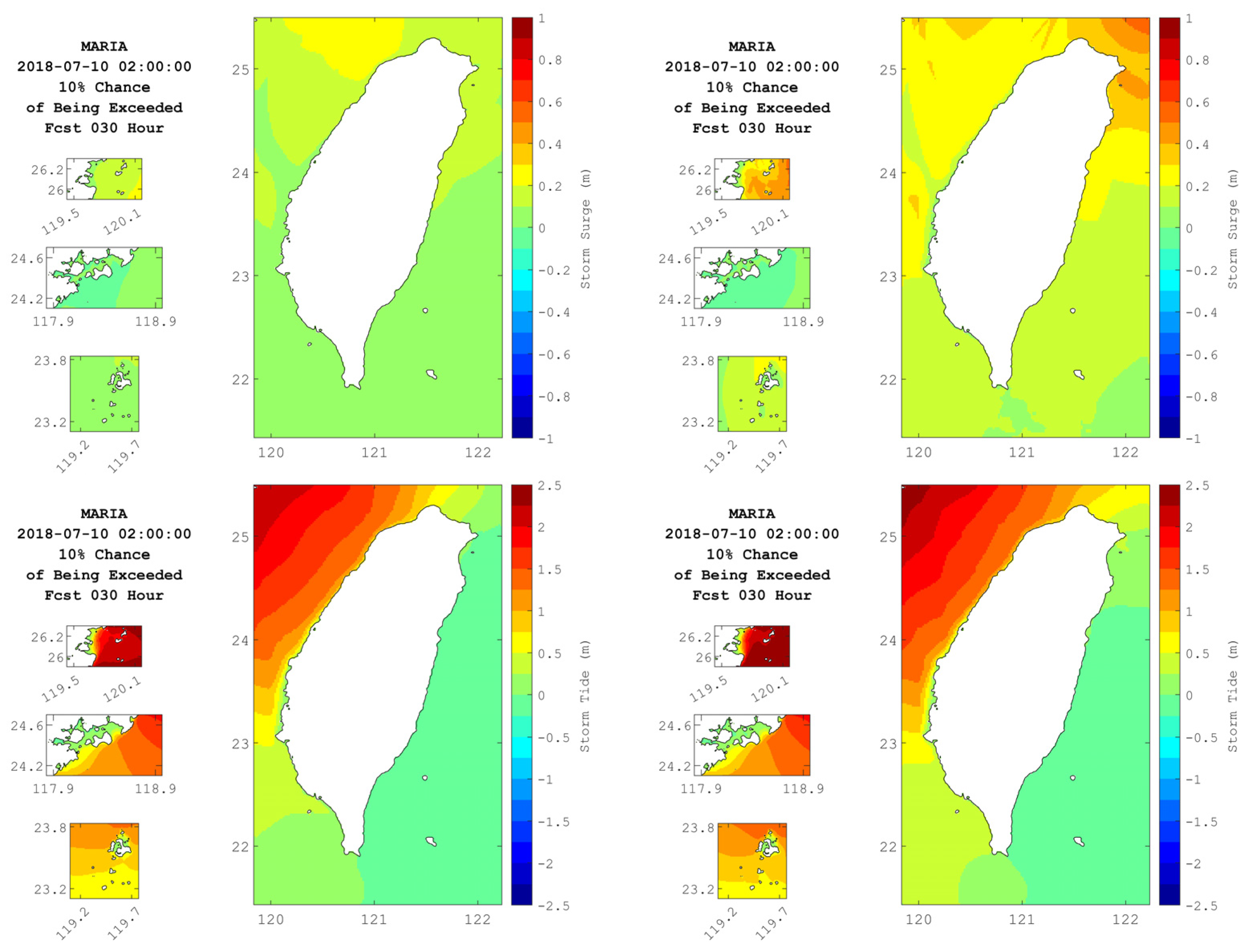
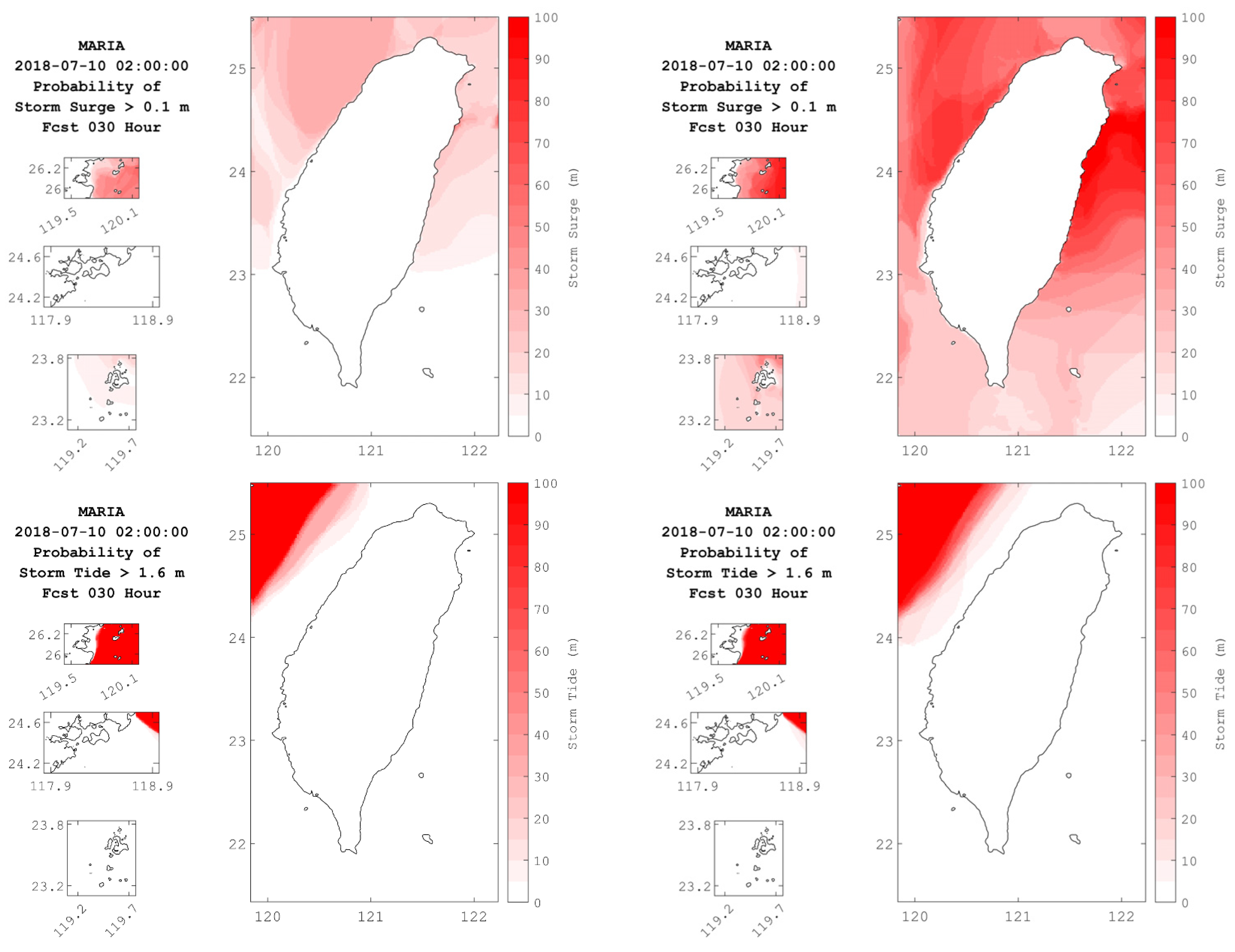
3. Results and Discussion
3.1. Calibration of the Storm Surge from the Deterministic Forecast and the Revised Track
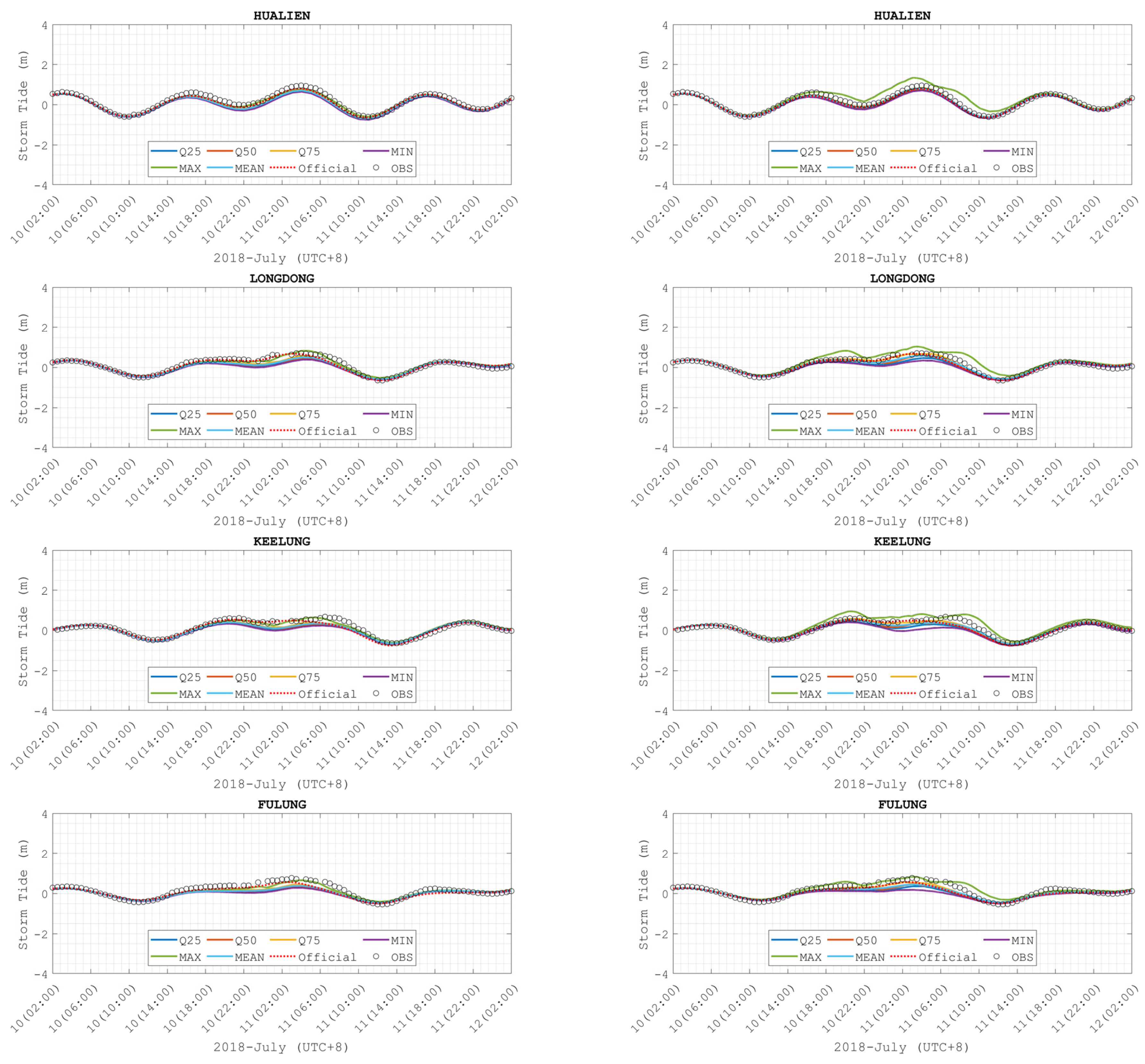
3.2. Surge Elevation from Ensemble Members at Gauges
3.3. Elevation Profiles from Ensemble Forecast System
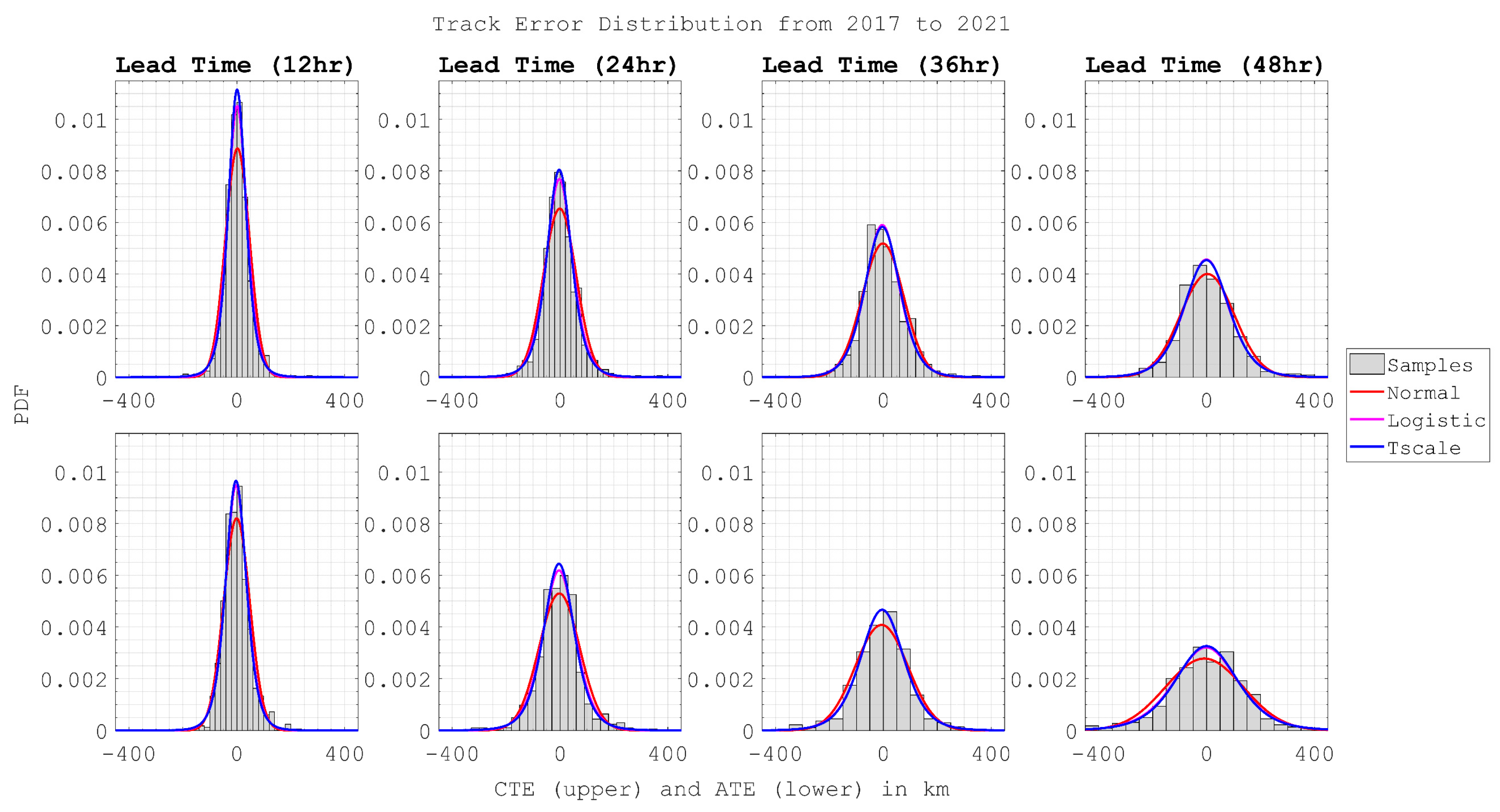
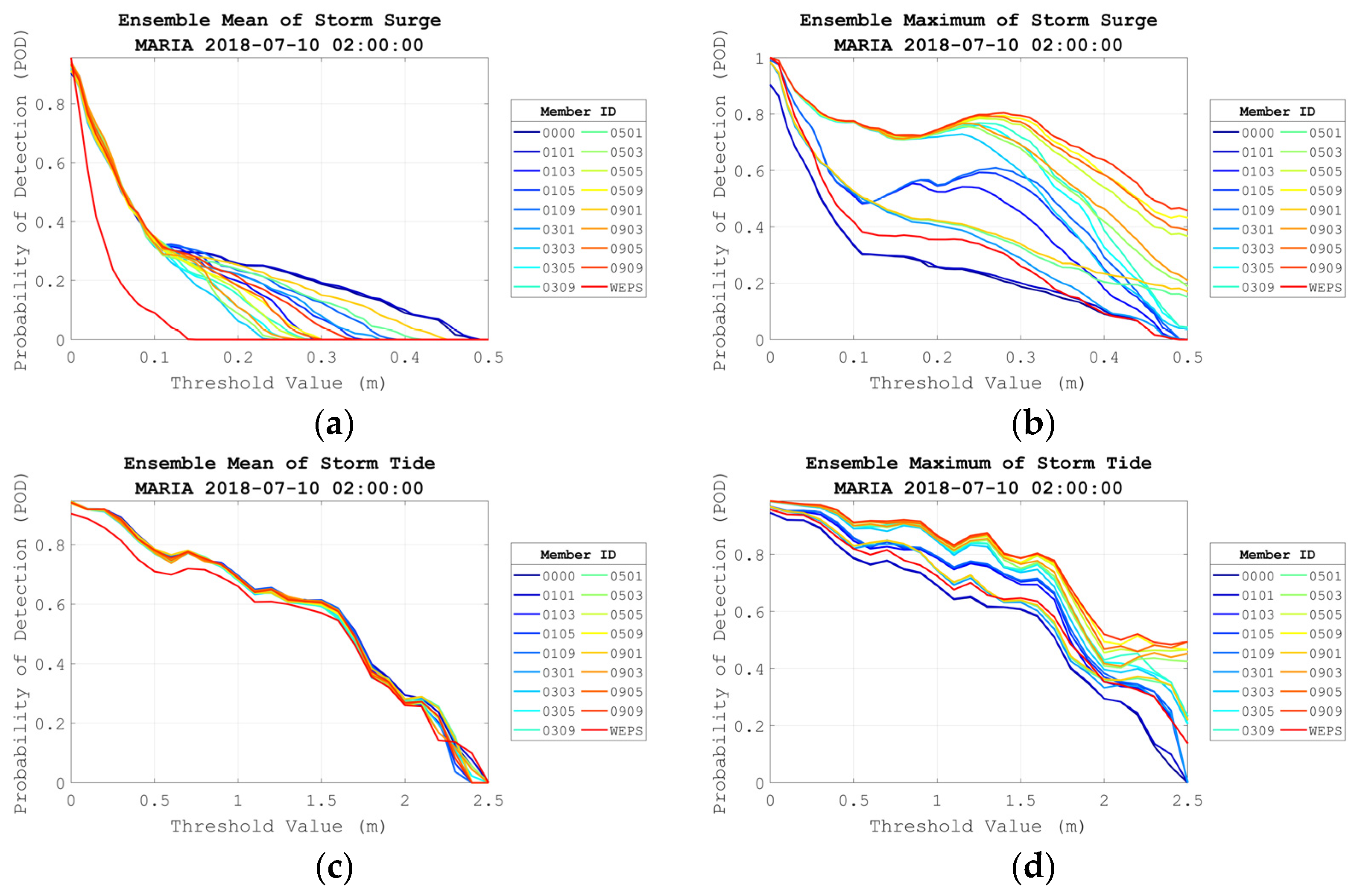
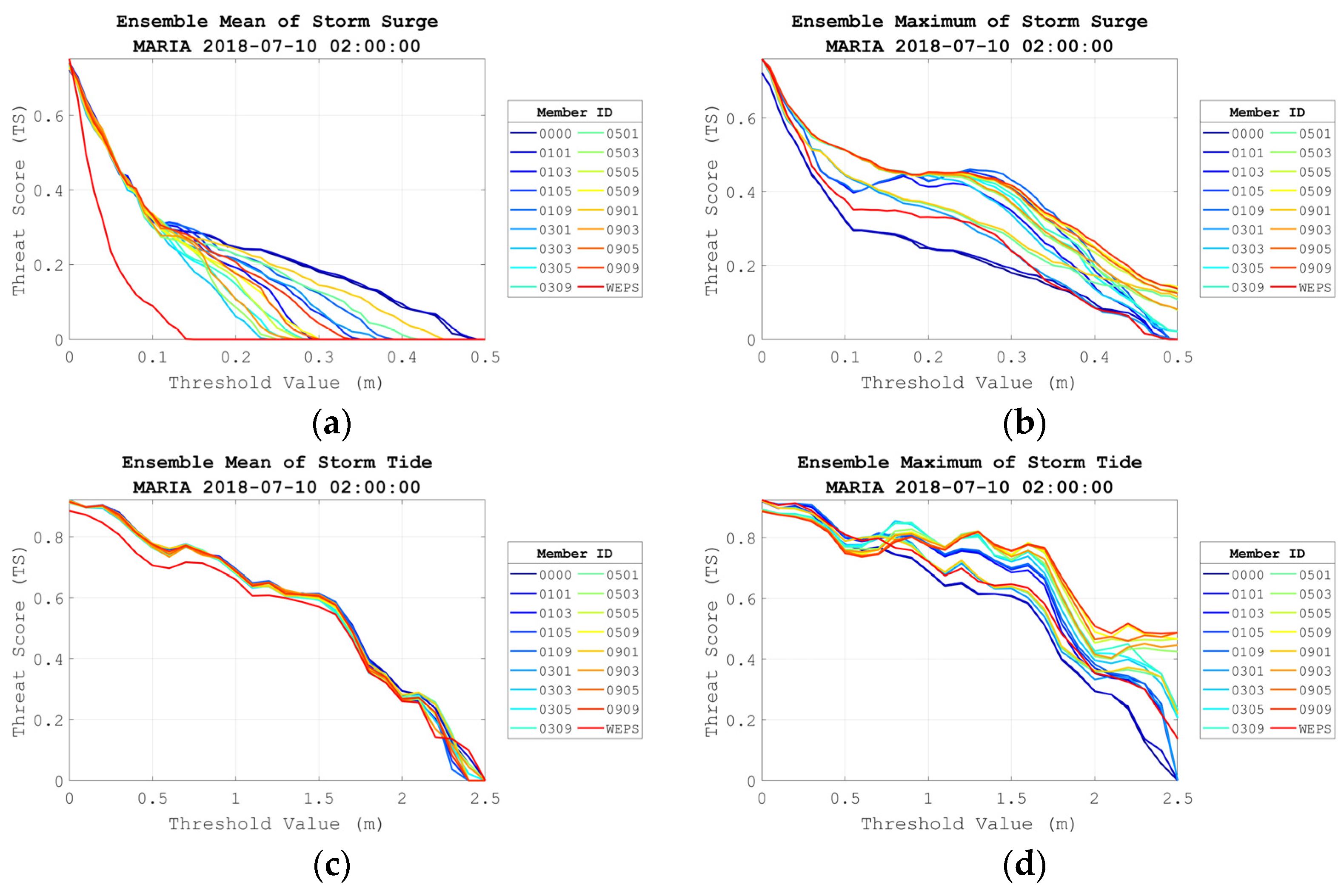
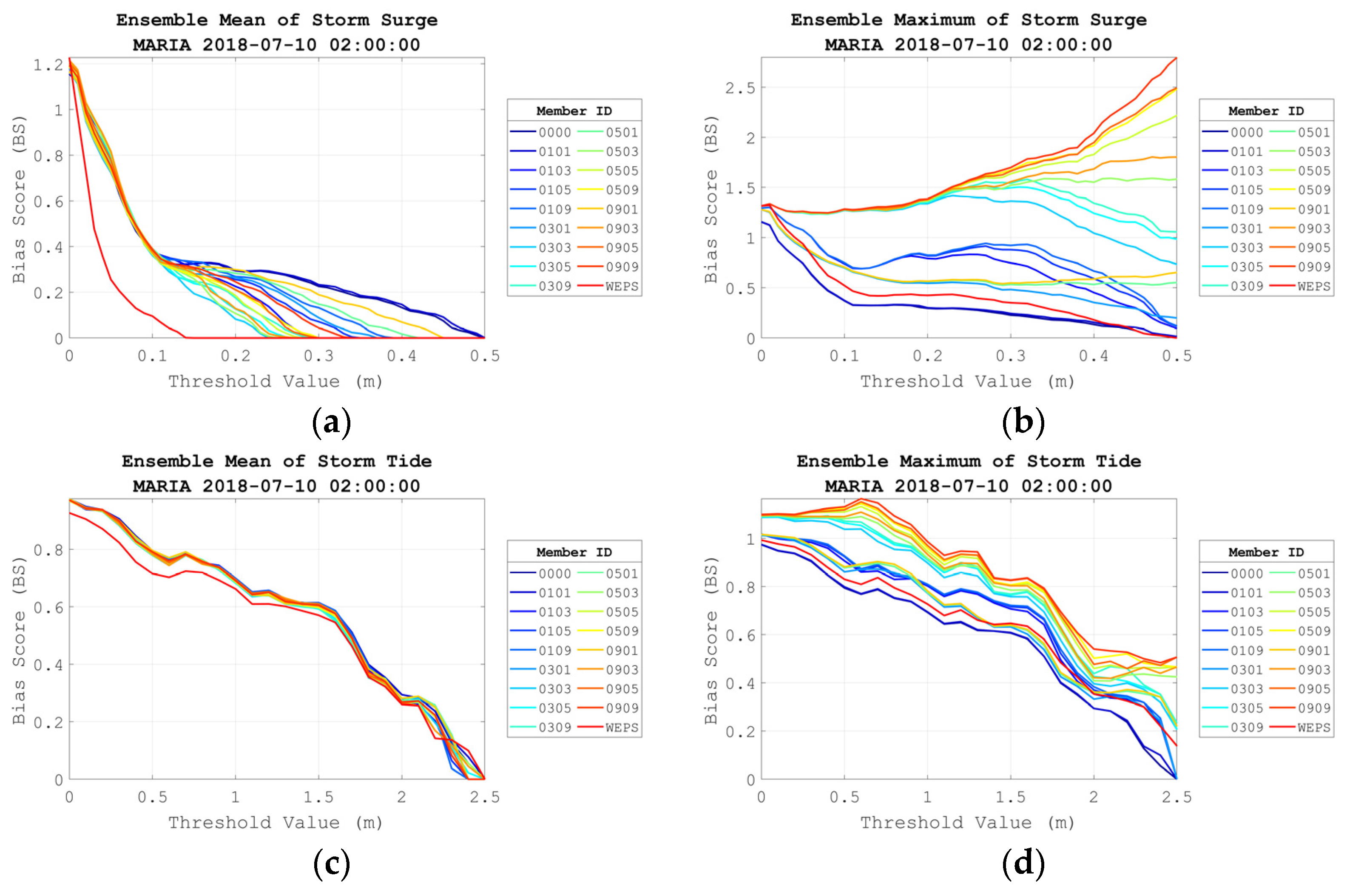
3.4. Statistic Evaluation
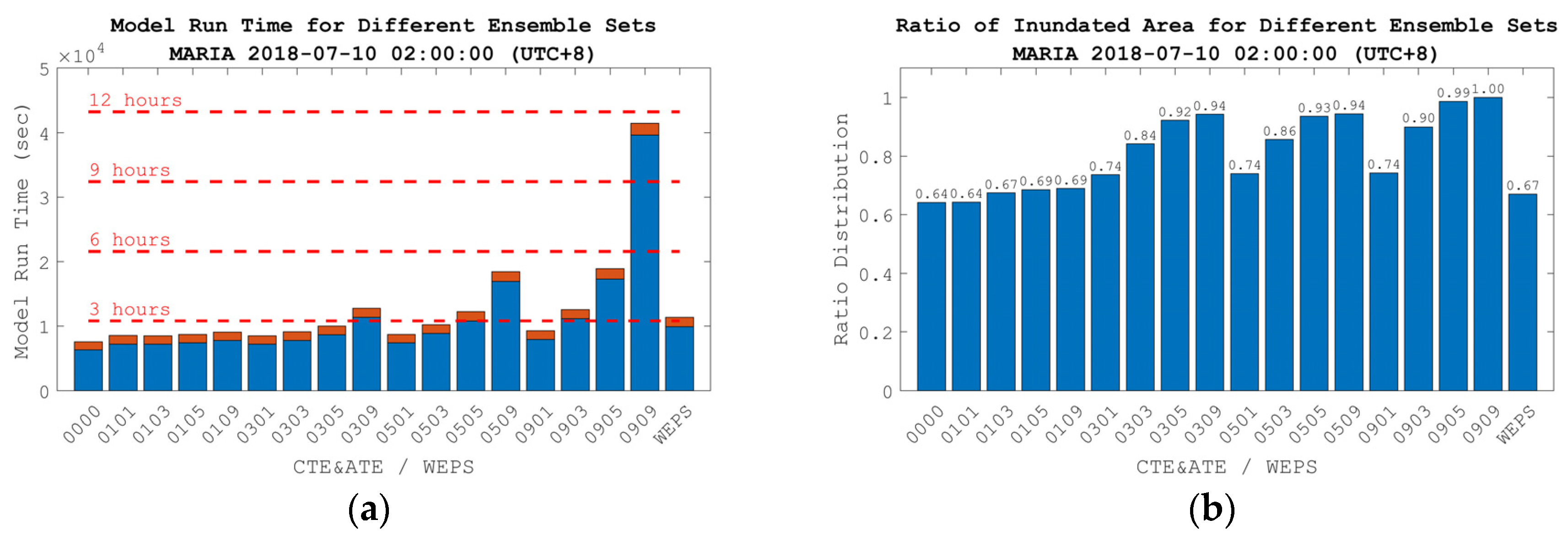
3.5. Computational Efficiency
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Observed | ||||
|---|---|---|---|---|
| Yes | No | Total | ||
| Forecast | Yes | Hits | False alarms | Forecast yes |
| No | Misses | Correct negatives | Forecast no | |
| Total | Observed yes | Observed no | Total | |
- Probability of Detection (POD)
- 2
- Probability of false detection (POFD)
- 3
- Threat Score (T.S.)
- 4
- Bias Score (B.S.)
References
- Kohno, N.; Dube, S.K.; Entel, M.; Fakhruddin, S.H.M.; Greenslade, D.; Leroux, M.D.; Rhome, J.; Thuy, N.B. Recent Progress in Storm Surge Forecasting. Trop. Cyclone Res. Rev. 2018, 7, 128–139. [Google Scholar] [CrossRef]
- Huang, W.-K.; Wang, J.-J. Typhoon damage assessment model and analysis in Taiwan. Nat. Hazards 2015, 79, 497–510. [Google Scholar] [CrossRef]
- Yu, Y.-C.; Chen, H.; Shih, H.-J.; Chang, C.-H.; Hsiao, S.-C.; Chen, W.-B.; Chen, Y.-M.; Su, W.-R.; Lin, L.-Y. Assessing the Potential Highest Storm Tide Hazard in Taiwan Based on 40-Year Historical Typhoon Surge Hindcasting. Atmosphere 2019, 10, 346. [Google Scholar] [CrossRef]
- Hsiao, L.-F.; Chen, D.S.; Hong, J.S.; Yeh, T.C.; Fong, C.T. Improvement of the Numerical Tropical Cyclone Prediction System at the Central Weather Bureau of Taiwan: TWRF (Typhoon WRF). Atmosphere 2020, 11, 657. [Google Scholar] [CrossRef]
- Molteni, F.; Buizza, R.; Palmer, T.N.; Petroliagis, T. The Ecmwf Ensemble Prediction System: Methodology and Validation. Q. J. R. Meteorol. Soc. 1996, 122, 73–119. [Google Scholar] [CrossRef]
- Mel, R.; Lionello, P. Storm Surge Ensemble Prediction for the City of Venice. Weather Forecast. 2014, 29, 1044–1057. [Google Scholar] [CrossRef]
- Kristensen, N.M.; Røed, L.P.; Sætra, Ø. A forecasting and warning system of storm surge events along the Norwegian coast. Environ. Fluid Mech. 2022, 23, 307–329. [Google Scholar] [CrossRef]
- Flowerdew, J.; Horsburgh, K.; Wilson, C.; Mylne, K. Development and Evaluation of an Ensemble Forecasting System for Coastal Storm Surges. Q. J. R. Meteorol. Soc. 2010, 136, 1444–1456. [Google Scholar] [CrossRef]
- Bernier, N.B.; Thompson, K.R. Deterministic and Ensemble Storm Surge Prediction for Atlantic Canada with Lead Times of Hours to Ten Days. Ocean Model. 2015, 86, 114–127. [Google Scholar] [CrossRef]
- Cavaleri, L.; Sclavo, M. The calibration of wind and wave model data in the Mediterranean Sea. Coast. Eng. 2006, 53, 613–627. [Google Scholar] [CrossRef]
- Signell, R.P.; Carniel, S.; Cavaleri, L.; Chiggiato, J.; Doyle, J.D.; Pullen, J.; Sclavo, M. Assessment of wind quality for oceanographic modelling in semi-enclosed basins. J. Mar. Syst. 2005, 53, 217–233. [Google Scholar] [CrossRef]
- Taylor, A.A.; Glahn, B. Probabilistic Guidance for Hurricane Storm Surge. In Proceedings of the 19th Conference on Probability and Statistics, New Orleans, LA, USA, 21 January 2008; Volume 74. [Google Scholar]
- Pan, Y.; Chen, Y.P.; Li, J.X.; Ding, X.L. Improvement of wind field hindcasts for tropical cyclones. Water Sci. Eng. 2016, 9, 58–66. [Google Scholar] [CrossRef]
- Hasegawa, H.; Kohno, N.; Higaki, M.; Itoh, M. Upgrade of JMA’s storm surge prediction for the WMO Storm Surge Watch Scheme (SSWS). Tech. Rev. 2017, 19, 1–9. [Google Scholar]
- Bode, L.; Hardy, T.A. Progress and Recent Developments in Storm Surge Modeling. J. Hydraul. Eng. 1997, 123, 315–331. [Google Scholar] [CrossRef]
- Wang, X. User Manual for Comcot Version 1.7 (First Draft); Cornel University: Ithaca, NY, USA, 2009; Volume 65. [Google Scholar]
- Wu, T.R.; Tsai, Y.L.; Terng, C.T. The recent development of storm surge modeling in Taiwan. Procedia IUTAM 2017, 25, 70–73. [Google Scholar] [CrossRef]
- Wu, T.R.; Huang, H.C. Modeling Tsunami Hazards from Manila Trench to Taiwan. J. Asian Earth Sci. 2009, 36, 21–28. [Google Scholar] [CrossRef]
- Holland, G.J. An Analytic Model of the Wind and Pressure Profiles in Hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Harper, B.; Holland, G. An Updated Parametric Model of the Tropical Cyclone. In Proceedings of the 23rd Conference on Hurricanes and Tropical Meteorology, Dallas, TX, USA, 10–15 January 1999. [Google Scholar]
- Arakawa, A.; Lamb, V.R. Computational Design of the Basic Dynamical Processes of the UCLA General Circulation Model. Gen. Circ. Model. Atmos. 1977, 17, 173–265. [Google Scholar]
- Egbert, G.D.; Erofeeva, S.Y. Efficient Inverse Modeling of Barotropic Ocean Tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Li, C.H.; Hong, J. The Study of Regional Ensemble Forecast: Evaluation for the Performance of Perturbed Methods. Atmos. Sci. 2014, 42, 153–179, (In Chinese with English Abstract). [Google Scholar]
- Li, C.H.; Berner, J.; Hong, J.S.; Fong, C.T.; Kuo, Y.H. The Taiwan WRF Ensemble Prediction System: Scientific Description, Model-Error Representation, and Performance Results. Asia-Pac. J. Atmos. Sci. 2020, 56, 1–15. [Google Scholar] [CrossRef]
- Regulation on the Centralized Issuance of Weather Forecasts and Warnings. Available online: https://law.moj.gov.tw/ENG/LawClass/LawAll.aspx?pcode=K0100002 (accessed on 14 March 2023).
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Powers, J.G.; Huang, X.Y.; Wang, W. A Description of the Advanced Research WRF Version 3; NCAR Tech. Note NCAR/TN-475+ STR; University Corporation for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Anderson, J.L. An Ensemble Adjustment Kalman Filter for Data Assimilation. Mon. Weather Rev. 2001, 129, 2884–2903. [Google Scholar] [CrossRef]
- Tsai, Y.L.; Wu, T.R.; Terng, C.T.; Chu, C.H. The Development of Storm Surge Ensemble Forecasting System Combing with Meso-Scale Wrf Model. In Proceedings of the 20th EGU General Assembly, EGU2018, Vienna, Austria, 4–13 April 2018; p. 6594. [Google Scholar]
- Leroux, M.-D.; Wood, K.; Elsberry, R.L.; Cayanan, E.O.; Hendricks, E.; Kucas, M.; Otto, P.; Rogers, R.; Sampson, B.; Yu, Z. Recent Advances in Research and Forecasting of Tropical Cyclone Track, Intensity, and Structure at Landfall. Trop. Cyclone Res. Rev. 2018, 7, 85–105. [Google Scholar]
- Chen, D.-S.; Hsiao, L.-F.; Xie, J.-H.; Hong, J.-S.; Fong, C.-T.; Yeh, T.-C. Improve Tropical Cyclone Prediction of TWRF with the Application of Advanced Observation Data. In Proceedings of the 22nd EGU General Assembly Conference Abstracts, Online, 4–8 May 2020; p. 4327. [Google Scholar]
- Normal Distribution. Available online: https://www.mathworks.com/help/stats/prob.normaldistribution.html (accessed on 14 March 2023).
- Location-Scale Distribution. Available online: https://www.mathworks.com/help/stats/t-location-scale-distribution.html (accessed on 14 March 2023).
- Logistic Distribution. Available online: https://www.mathworks.com/help/stats/prob.logisticdistribution.html (accessed on 14 March 2023).
- Jian, G.-J.; Teng, J.-H.; Wang, S.-T.; Cheng, M.-D.; Cheng, C.-P.; Chen, J.-H.; Chu, Y.-J. An Overview of the Tropical Cyclone Database at the Central Weather Bureau of Taiwan. Terr. Atmos. Ocean. Sci. 2022, 33, 26. [Google Scholar] [CrossRef]
- WWRP/WGNE Joint Working Group on Forecast Verification Research. Forecast Verification—Issues, Methods and FAQ. Available online: https://www.cawcr.gov.au/projects/verification/verif_web_page.html (accessed on 14 March 2023).
- Davis, C.; Wang, W.; Chen, S.S.; Chen, Y.; Corbosiero, K.; DeMaria, M.; Dudhia, J.; Holland, G.; Klemp, J.; Michalakes, J. Prediction of Landfalling Hurricanes with the Advanced Hurricane Wrf Model. Mon. Weather Rev. 2008, 136, 1990–2005. [Google Scholar] [CrossRef]
- Liu, P.L.-F.; Cho, Y.S.; Yoon, S.; Seo, S. Numerical Simulations of the 1960 Chilean Tsunami Propagation and Inundation at Hilo, Hawaii. In Tsunami: Progress in Prediction, Disaster Prevention and Warning; Springer: Berlin/Heidelberg, Germany, 1995; pp. 99–115. [Google Scholar]
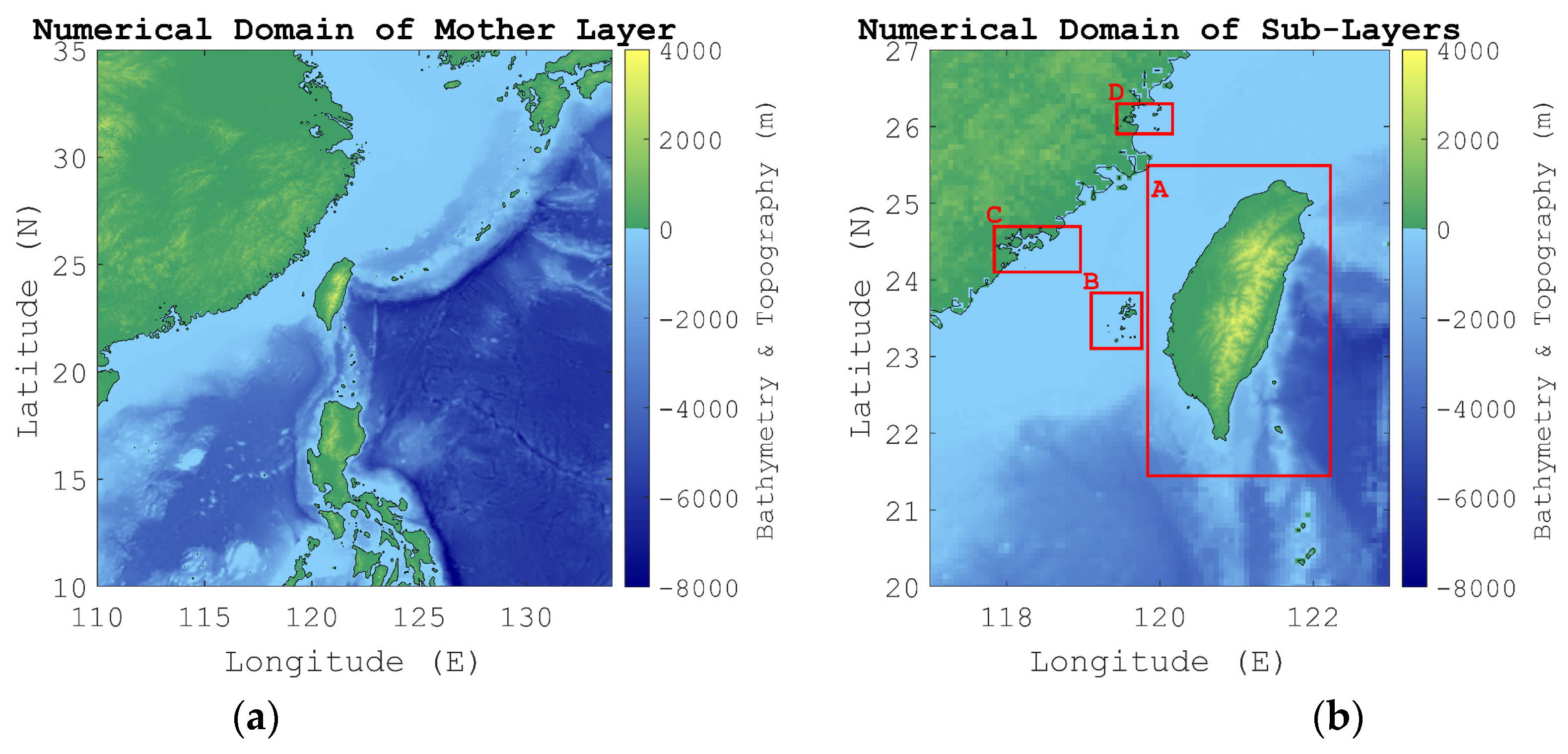
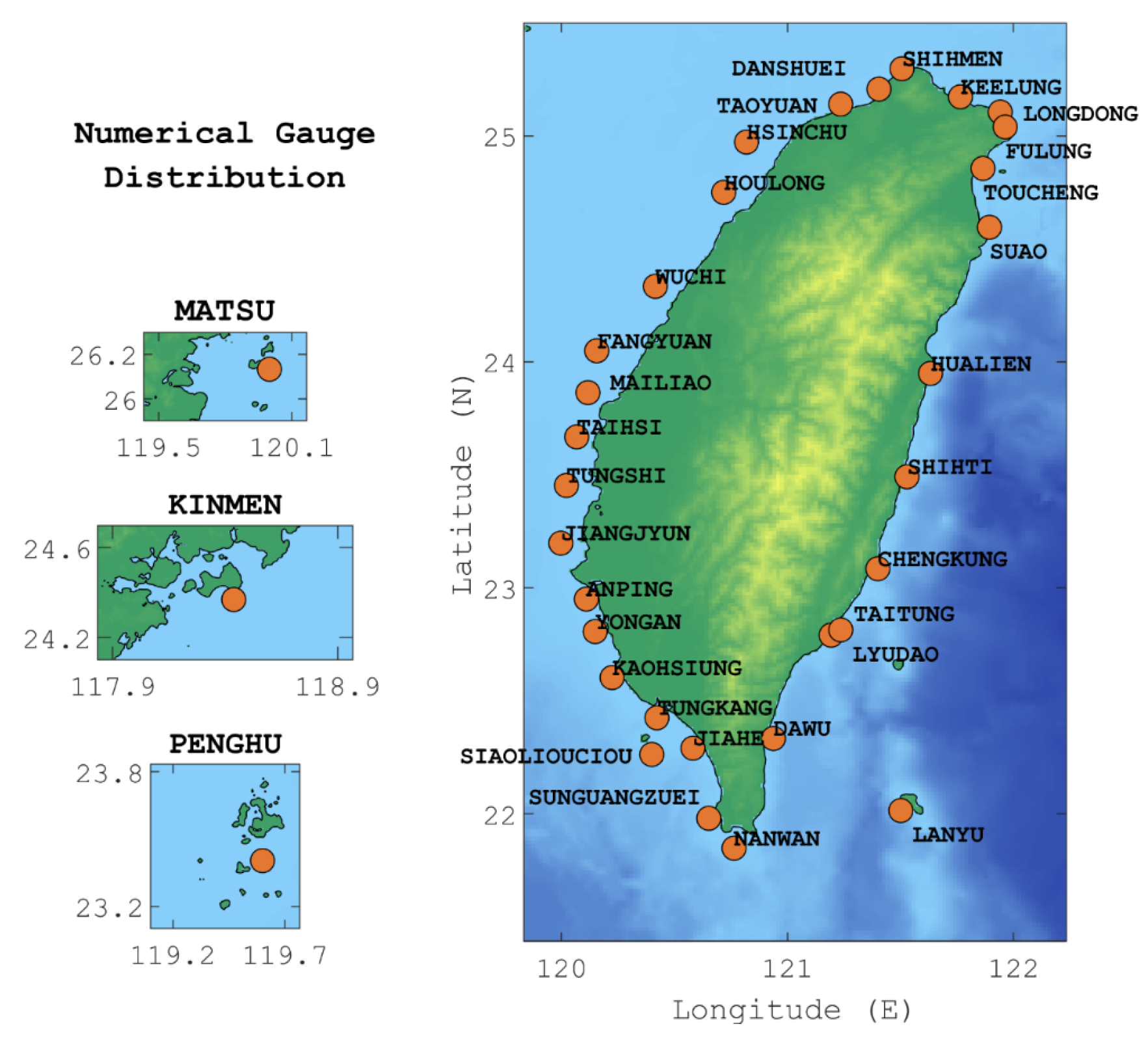

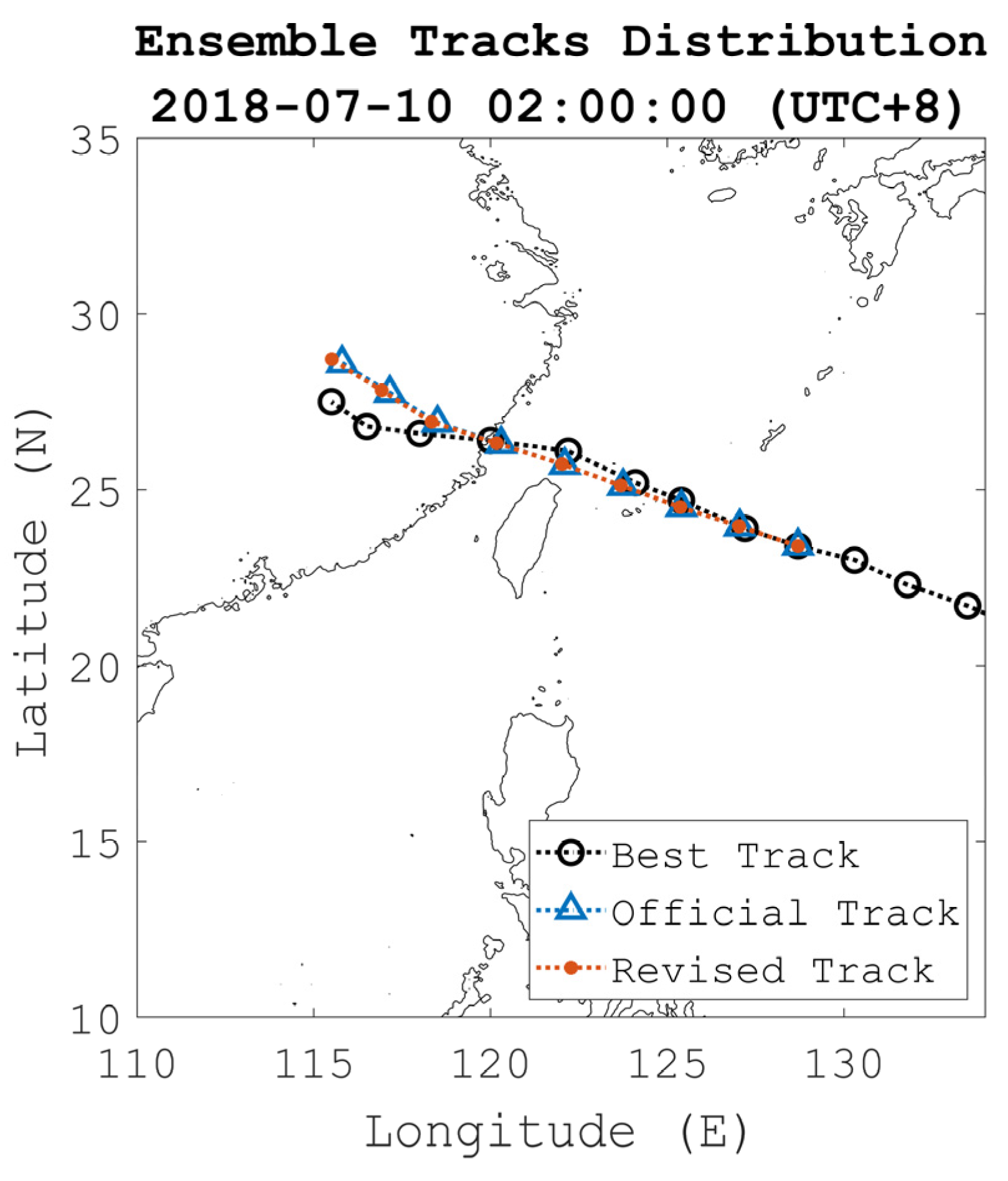
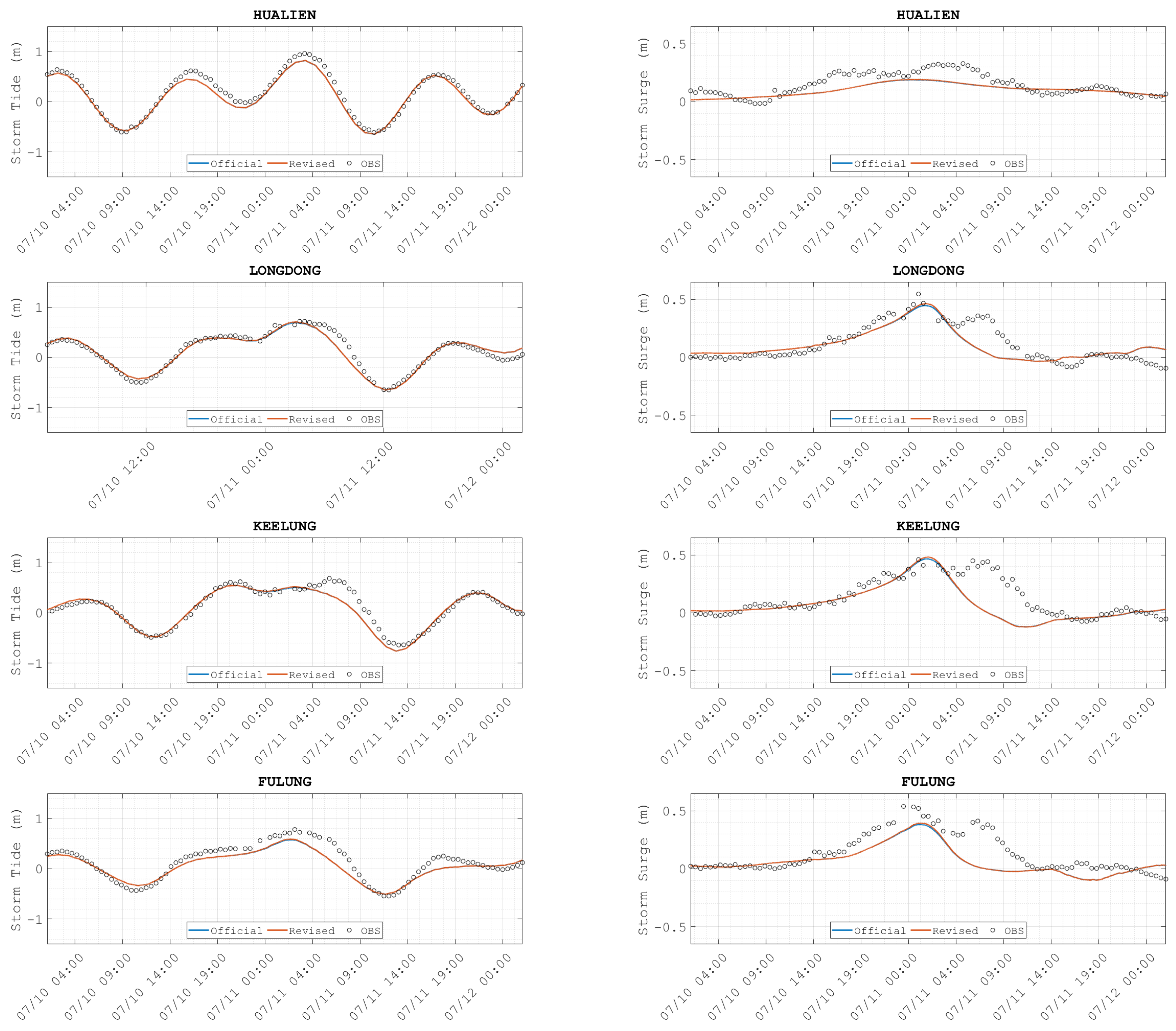
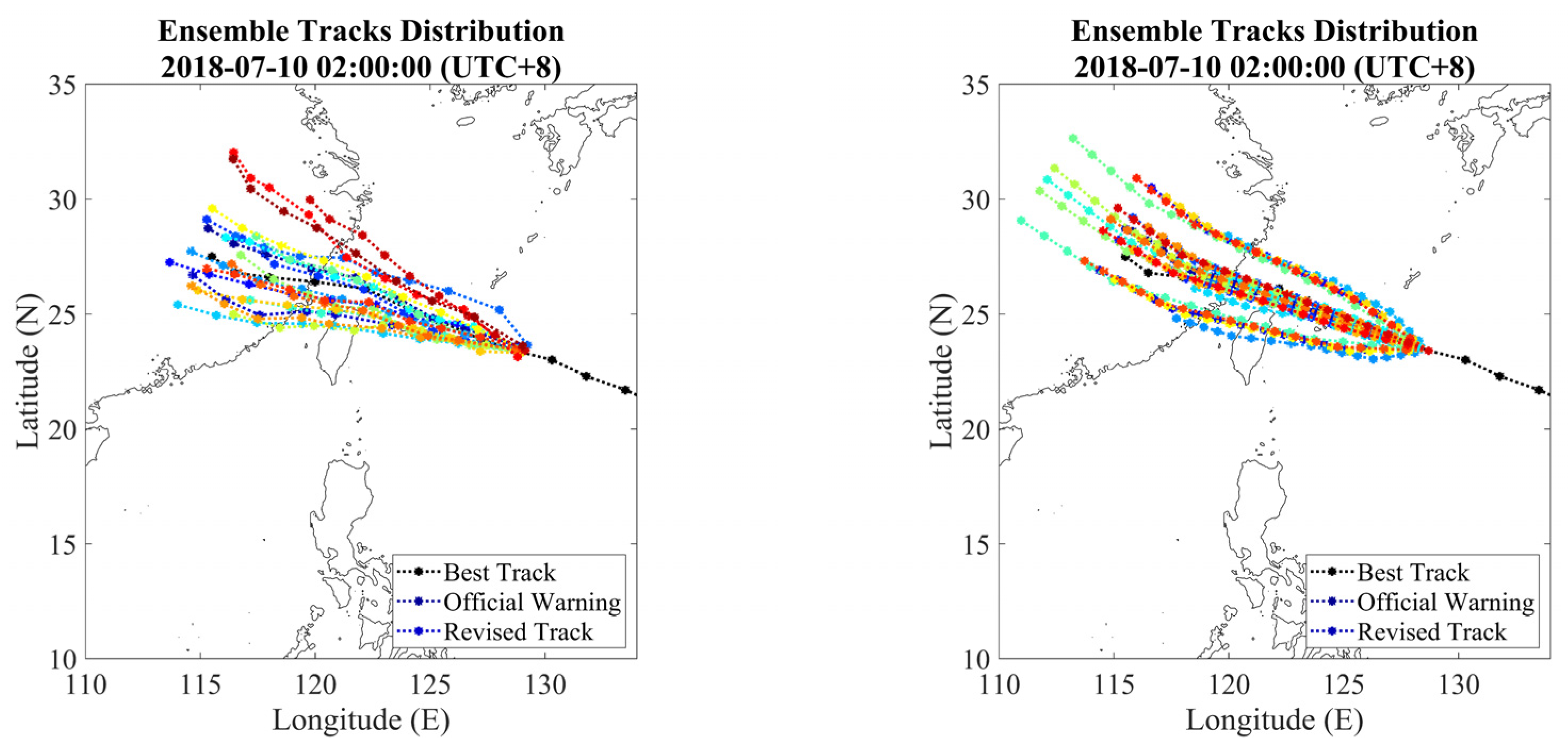
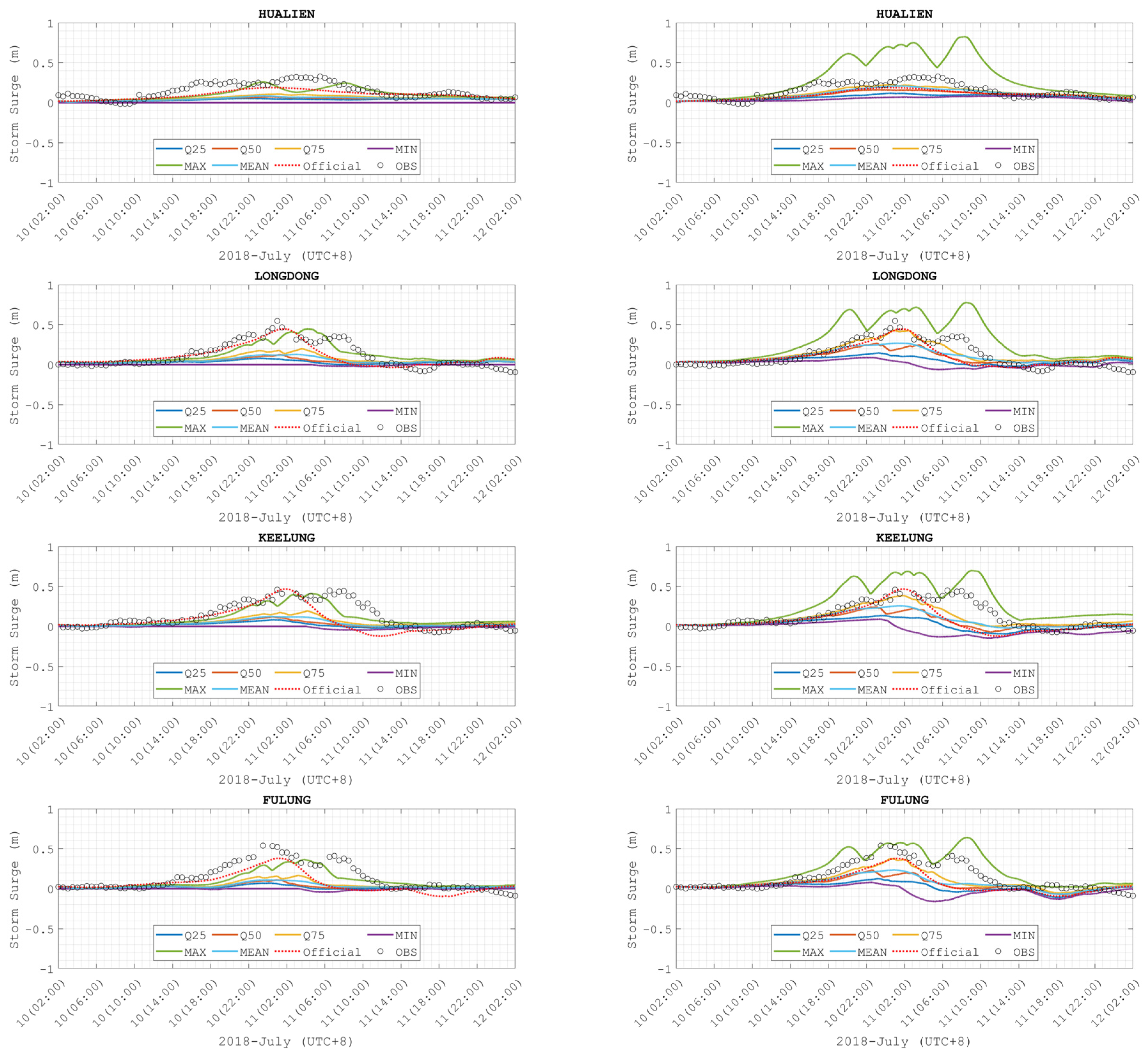

| Layer ID | Region | Resolution | Source |
|---|---|---|---|
| 01 | 110.00 E–134.00 E 10.00 N–35.00 N | 4 arc minute (8 km) | ETOPO1 |
| 02-A | 119.80 E–122.25 E 21.40 N–25.50 N | 0.5 arc minute (1 km) | GEBCO 2021 |
| 02-B | 119.09 E–119.80 E 23.05 N–23.89 N | 15 arc second (0.5 km) | GEBCO 2021 |
| 02-C | 117.80 E–118.99 E 24.09 N–24.70 N | 15 arc second (0.5 km) | GEBCO 2021 |
| 02-D | 119.39 E–120.19 E 25.84 N–26.35 N | 15 arc second (0.5 km) | GEBCO 2021 |
| Type | Forecast Hour | Normal Distribution | Logistic Distribution | T Location-Scale Distribution | ||||
|---|---|---|---|---|---|---|---|---|
| parameter | ||||||||
| CTE | 12 | 2.461 | 44.978 | 1.440 | 23.782 | 1.094 | 33.849 | 4.473 |
| 24 | −0.998 | 61.019 | −2.623 | 32.543 | −3.050 | 47.108 | 4.804 | |
| 36 | −1.654 | 76.908 | −4.215 | 42.352 | −3.877 | 66.239 | 7.583 | |
| 48 | 2.964 | 99.601 | −0.658 | 54.746 | −0.571 | 84.932 | 7.200 | |
| ATE | 12 | −0.463 | 48.625 | −2.643 | 26.388 | −2.988 | 39.572 | 5.772 |
| 24 | −2.666 | 75.400 | −3.811 | 40.407 | −4.109 | 58.929 | 4.984 | |
| 36 | −6.588 | 97.913 | −4.555 | 53.688 | −4.369 | 82.476 | 6.703 | |
| 48 | −8.483 | 143.738 | −1.692 | 77.997 | −0.682 | 117.505 | 5.997 | |
| Type | Forecast Hour | Number of Areas | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 6 | ||||||||
| CTE (km) | 12 | 1.1 | −118.6 | 120.8 | −23.7 | 25.9 | −35.6 | −14.5 | 16.7 | 37.8 |
| 24 | −3 | −164.3 | 158.2 | −37.4 | 31.3 | −53.7 | −24.6 | 18.5 | 47.6 | |
| 36 | −3.9 | −198.3 | 190.5 | −50.8 | 43 | −72.3 | −33.6 | 25.8 | 64.6 | |
| 48 | −5.2 | −253.2 | 252.1 | −60.9 | 59.7 | −88.6 | −38.7 | 37.6 | 87.5 | |
| ATE (km) | 12 | 3 | −129 | 123 | −31.5 | 25.5 | −44.8 | −20.9 | 15 | 38.8 |
| 24 | 4.1 | −202.6 | 194.5 | −46.9 | 38.7 | −67.2 | −31.1 | 22.8 | 59 | |
| 36 | 4.4 | −254.7 | 246 | −63.2 | 54.4 | −90.3 | −41.5 | 32.8 | 81.6 | |
| 48 | 6.8 | −369.3 | 369.3 | −85 | 83.7 | −124.3 | −53.9 | 52.5 | 123 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-W.; Wu, T.-R.; Tsai, Y.-L.; Chuang, S.-C.; Chu, C.-H.; Terng, C.-T. Member Formation Methods Evaluation for a Storm Surge Ensemble Forecast System in Taiwan. Water 2023, 15, 1826. https://doi.org/10.3390/w15101826
Lin C-W, Wu T-R, Tsai Y-L, Chuang S-C, Chu C-H, Terng C-T. Member Formation Methods Evaluation for a Storm Surge Ensemble Forecast System in Taiwan. Water. 2023; 15(10):1826. https://doi.org/10.3390/w15101826
Chicago/Turabian StyleLin, Chun-Wei, Tso-Ren Wu, Yu-Lin Tsai, Shu-Chun Chuang, Chi-Hao Chu, and Chuen-Teyr Terng. 2023. "Member Formation Methods Evaluation for a Storm Surge Ensemble Forecast System in Taiwan" Water 15, no. 10: 1826. https://doi.org/10.3390/w15101826
APA StyleLin, C.-W., Wu, T.-R., Tsai, Y.-L., Chuang, S.-C., Chu, C.-H., & Terng, C.-T. (2023). Member Formation Methods Evaluation for a Storm Surge Ensemble Forecast System in Taiwan. Water, 15(10), 1826. https://doi.org/10.3390/w15101826











