Research on Improvement of Slope Protection Concrete Precast Block Joints Based on Physical Model Experiment
Abstract
:1. Introduction
2. Experiment Design
2.1. Materials
2.2. Mix Proportions and Preparation of Samples
2.2.1. Mix Proportions and Preparation of Prefabricated Blocks
2.2.2. Mix Proportions and Preparation of Joint Mortar
2.3. Width Model of Paving Seam
2.3.1. Observation and Monitoring Equipment
2.3.2. General Layout of Model
2.3.3. Laying the Precast Block and Setting the Paving Seam
2.4. Test Program Design
2.4.1. Paving seam Width
2.4.2. Paving Seam Materials
3. Analysis of Model Test Results
3.1. Statistics of Paving Seam Width
3.2. Variation Law of Pore Water Pressure
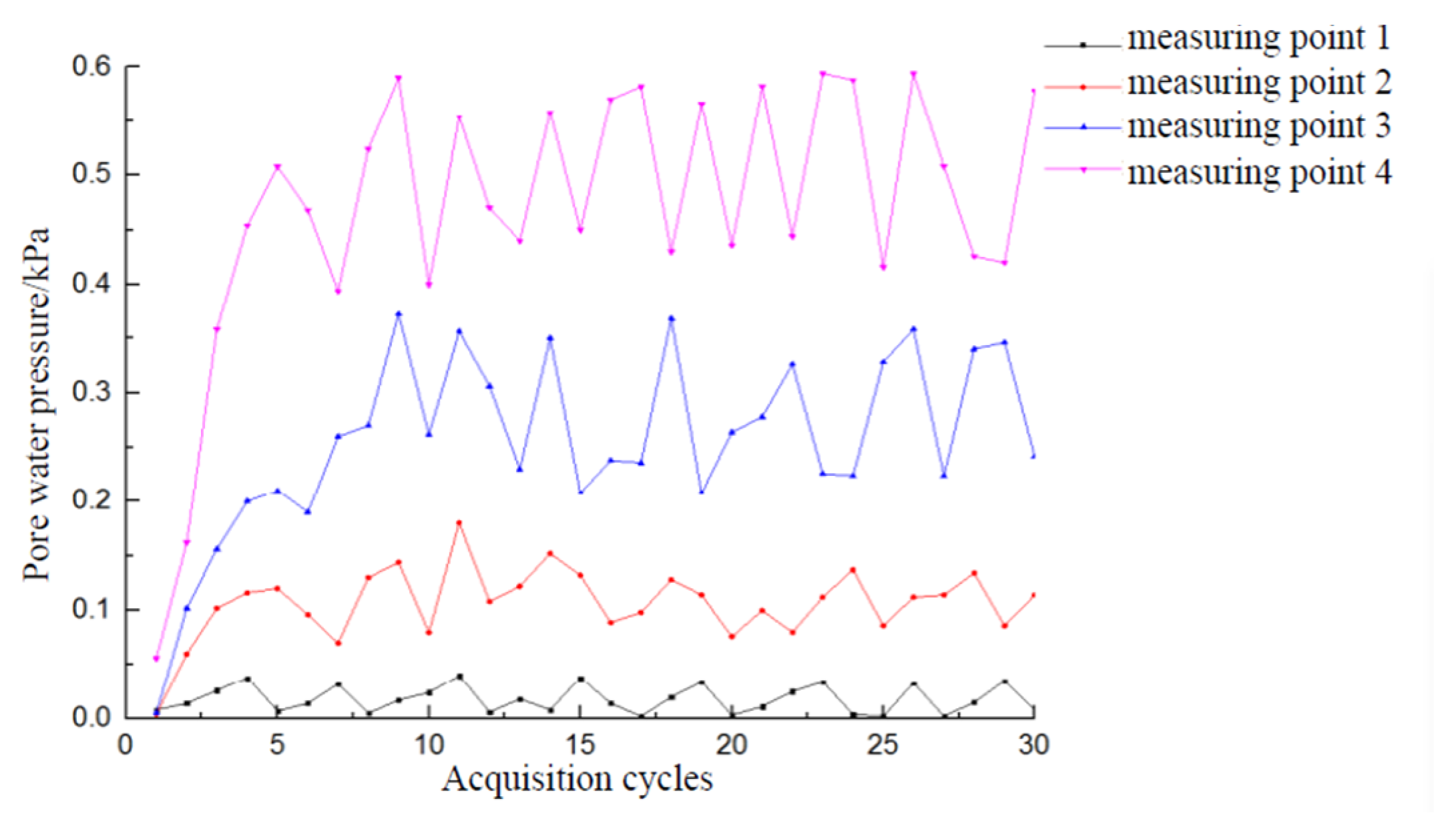
3.2.1. Variation Law of Pore Water Pressure at Different Positions
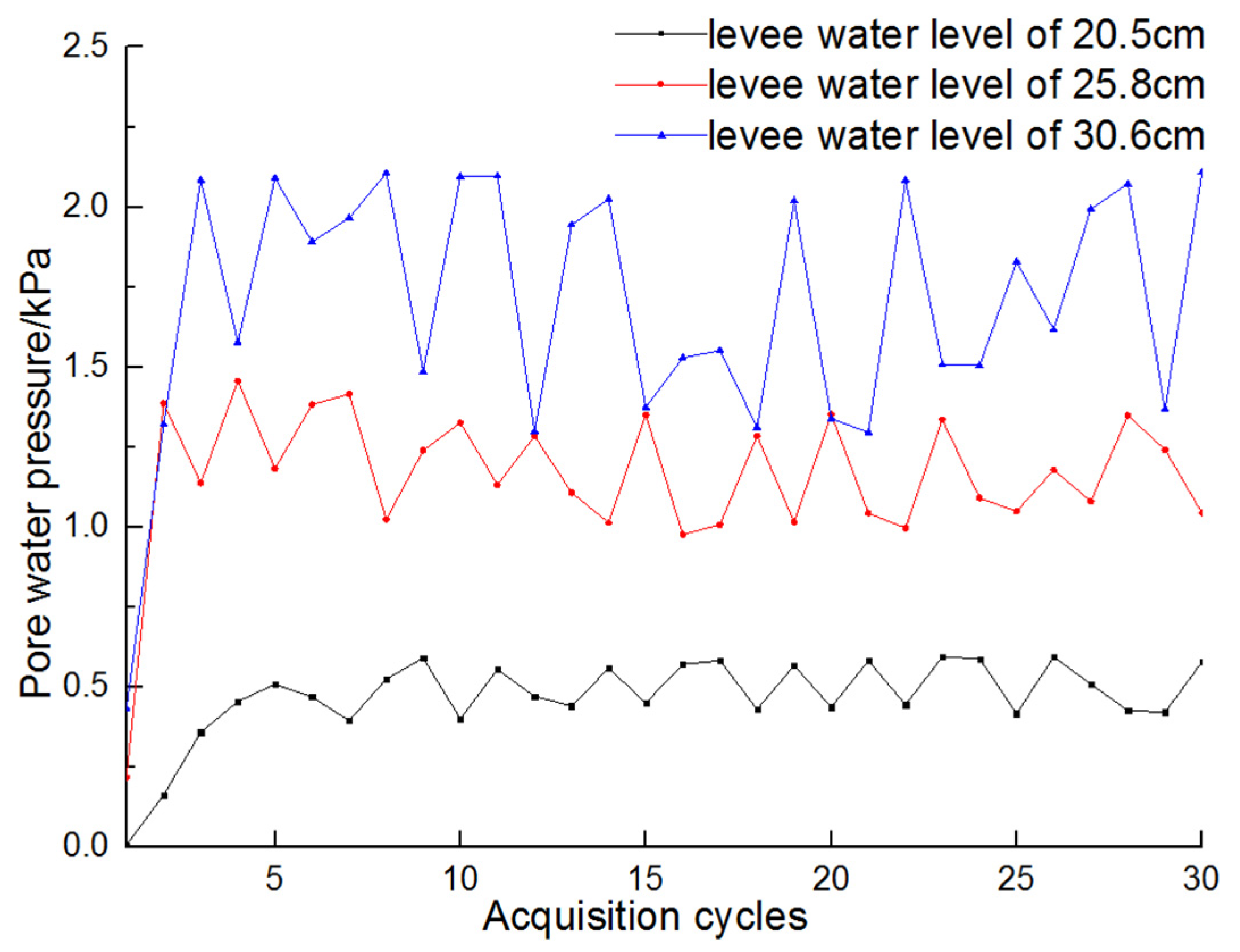
3.2.2. Variation Law of Pore Water Pressure at Different Levee Water Levels
3.2.3. Variation Law of Pore Water Pressure at Different Paving Seam Widths
3.3. Compressive/Shear Strength of Paving Seam Materials
3.4. Microstructure Analysis of Paving Seam Materials
4. Conclusions
- (1)
- Pore water pressure is significantly affected by the position of the slope cushion, the water level in front of the embankment, and the width of the paving seam;
- (2)
- Control of the paving seam width to less than 1 cm is an effective measure for preventing cushion loss considering the influence of construction and other factors.
- (3)
- Paving seam plumpness and mortar strength are both crucial factors that affect the shear strength of the cemented surface of paving seam materials, and they have a mutual influence on each other;
- (4)
- Properly adding an expansion agent can improve the properties of mortar paving seam materials and significantly enhance the bond property between mortar and slope protection concrete.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- SL634-2012; Standard for Acceptance and Evaluation of Construction Quality of Embankment Projects. CWP (China Water Power Press): Beijing, China, 2012.
- Kang, J. Deformation analysis and treatment suggestions of precast concrete block slope protection. Hebei Prov. Water Conserv. 2018, 10, 38. [Google Scholar]
- Li, B. Key points of construction technology of precast concrete slope protection for Henan Keji Dam. Heilongjiang Sci. Technol. Inf. 2016, 6, 196. [Google Scholar]
- Zhou, A. Damage reason, harm and prevention of slope protection of earth-rock dam. Henan Sci. Technol. 2014, 19, 176–177. [Google Scholar]
- Mikhnevich, E.I. Methodology for calculation of of rigidity in earth dam slope protection under conditions of wave impact. Sci. Tech. 2018, 12, 100–105. [Google Scholar] [CrossRef]
- Zhao, N.; Lu, H.; Zhang, R. The Coupling Effect of Pore Water Pressure and Pore Water Gravity in Unsaturated Soils under Rainfall Condition and Its Influence on Slope Stability. Geofluids 2022, 2022, 9492514. [Google Scholar] [CrossRef]
- Wang, X.; Xia, X.; Zhang, X.; Gu, X.; Zhang, Q. Probabilistic Risk Assessment of Soil Slope Stability Subjected to Water Drawdown by Finite Element Limit Analysis. Appl. Sci. 2022, 12, 10282. [Google Scholar] [CrossRef]
- Zheng, Z. Application of concrete block slope protection in hydraulic engineering. China’s Water Transp. 2011, 11, 140–141. [Google Scholar]
- Zheng, J.; Zhang, C.; Liu, C. Discussion on quality acceptance of laying joint width in precast concrete block slope protection project. China Water Transp. 2015, 15, 305–306. [Google Scholar]
- Liu, Y.; Zhang, W.; Zhang, L.; Zhu, Z.; Hu, J.; Wei, H. Probabilistic stability analyses of undrained slopes by 3D random fields and finite element methods. Geosci. Front. 2018, 9, 1657–1664. [Google Scholar] [CrossRef]
- Niu, D.; Han, S.; Li, X.; Li, B.; Ren, W. Mechanical property of asphalt with additive. J. Traffic Transp. Eng. 2016, 16, 8–16. [Google Scholar]
- Liu, D.; Chen, J.; Yue, W.; Zhang, Y. Stability Analysis of Reservoir Bank and Study on Landslide Control Measures—Taking Baiheqiao Reservoir in Kaixian County, Chongqing as an example. In Proceedings of the 8th International Symposium on Project Management, Beijing, China, 4–5 July 2020; pp. 223–236. [Google Scholar] [CrossRef]
- Seifan, M.; Mendoza, S.; Aydin, B. Effect of nano and micro iron oxide particles on the workability, strength and absorption rate of cement mortar containing fly ash. Eur. J. Environ. Civ. Eng. 2022, 26, 3898–3912. [Google Scholar] [CrossRef]
- Chen, H.; Wang, F.; Xu, G.; Guo, L. Laboratory Model Test of Eco-Concrete Slab Slope Protection. In Proceedings of the 8th International Conference on Civil Engineering, Nanchang, China, 4–5 December 2021; pp. 372–381. [Google Scholar] [CrossRef]
- Dan, L.; Zheng, C.; Qin, Y.; Bi, H.; Li, K.; Huang, J. Analysing the effects of the mesoscopic characteristics of mineral powder fillers on the cohesive strength of asphalt mortars at low temperatures. Constr. Build. Mater. 2014, 65, 330–337. [Google Scholar] [CrossRef]
- John, S.K.; Nadir, Y.; Girija, K. Effect of source materials, additives on the mechanical properties and durability of fly ash and fly ash-slag geopolymer mortar: A review. Constr. Build. Mater. 2021, 280, 122443. [Google Scholar] [CrossRef]
- Rocha, J.H.A.; Galarza, F.P. Mechanical Properties Evaluation of Render Mortars with Different Waterproof Additive Compositions. Key Eng. Mater. 2021, 6202, 161–167. [Google Scholar] [CrossRef]
- Savchenko, S.; Antoniuk, N. Assessment of the impact of modifier and filler on the physical and mechanical and operational properties of plastering mortars. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1164, 012004. [Google Scholar] [CrossRef]
- Corinaldesi, V.; Nardinocchi, A.; Donnini, J. The influence of expansive agent on the performance of fibre reinforced cement-based composites. Constr. Build. Mater. 2015, 91, 171–179. [Google Scholar] [CrossRef]
- Feng, Y.; Yang, Q.; Chen, Q.; Kero, J.; Andersson, A.; Ahmed, H.; Engström, F.; Samuelsson, C. Characterization and evaluation of the pozzolanic activity of granulated copper slag modified with CaO. J. Cleaner Prod. 2019, 232, 1112–1120. [Google Scholar] [CrossRef]
- Polat, R.; Demirbog, R.; Khushefati, W.H. Effects of nano and micro size of CaO and MgO, nano-clay and expanded perlite aggregate on the autogenous shrinkage of mortar. Constr. Build. Mater. 2015, 81, 268–275. [Google Scholar] [CrossRef]
- Jia, Z.; Yang, Y.; Yang, L.; Zhang, Y.; Sun, Z. Hydration products, internal relative humidity and drying shrinkage of alkali activated slag mortar with expansion agents. Constr. Build. Mater. 2018, 158, 198–207. [Google Scholar] [CrossRef]
- GB175-2007; Common Portland Cement. CNSMC (China National Standardization Management Committee): Beijing, China, 2007.
- DL/T 5144-2015; Specifications for Hydraulic Concrete Construction. CNEA (China National Energy Administration): Beijing, China, 2015.
- CWP. Hydraulic Design Manual, 2nd ed.; China Water Power Press: Beijing, China, 2014. [Google Scholar]
- Guo, W.; Zhu, J.; Wen, Y. Unified description for four grading scale methods for coarse aggregate. Chin. J. Geotech. Eng. 2016, 38, 1473–1480. [Google Scholar]
- Wei, M. System Parameters Calculation and Software Design for Port Engineering Model Text. Ph.D. Thesis, Tianjin University of Technology, Tianjin, China, 2012. [Google Scholar]
- Brue, F.; Davy, C.A.; Skoczylas, F.; Burlion, N.; Bourbon, X. Effect of temperature on the water retention properties of two high performance concretes. Cem. Concr. Res. 2012, 42, 384–396. [Google Scholar] [CrossRef]
- Stovall, T.; de Larrard, F.; Buil, M. Linear packing density model of grain mixtures. Powder Technol. 1986, 48, 1–12. [Google Scholar] [CrossRef]











| Specific Surface Area (m2/kg) | Initial Setting Time (min) | Final Setting Time (min) | Flexural Strength (MPa) | Compressive Strength (MPa) | |||
|---|---|---|---|---|---|---|---|
| 3 d | 28 d | 3 d | 28 d | ||||
| P.O 42.5 | 340 | 168 | 279 | 4.8 | 7.7 | 27.6 | 46.4 |
| Density (g/cm3) | Specific Surface Area (m2/kg) | Initial Setting Time (min) | Final Setting Time (min) | Compressive Strength (MPa) | Restrained Expansion Rate (%) | |||
|---|---|---|---|---|---|---|---|---|
| 7 d | 28 d | 7 d | 28 d | |||||
| HME | 2.90 | 390 | 170 | 220 | 22.9 | 41.8 | 0.15 | 0.10 |
| SiO3 | CaO | MgO | Fe2O3 | Al2O3 | K2O | Na2O | SO3 | |
|---|---|---|---|---|---|---|---|---|
| HME | 1.03 | 52.70 | 1.81 | 0.66 | 13.61 | 0.40 | 0.14 | 28.33 |
| Aperture Size (mm) | 5.0 | 2.5 | 1.25 | 0.63 | 0.315 | 0.16 | <0.16 | Fineness Module |
|---|---|---|---|---|---|---|---|---|
| Cumulative Residue Amount (wt.%) | 1.5 | 5.2 | 11.9 | 39.2 | 90.5 | 98.0 | 100.0 | 2.9 |
| Aperture Size (mm) | 40 | 30 | 20 | 10 | 5 | <5.0 |
|---|---|---|---|---|---|---|
| Cumulative Residue Amount (wt.%) | 0 | 6.7 | 43.5 | 73.2 | 99.2 | 100.0 |
| Cement | Sand | Water | Compressive Strength of 28 d/MPa | |
|---|---|---|---|---|
| C15 | 260 | 764 | 173 | 17.8 |
| Cement | Water | Sand | Expanding Agent | W/b | |
|---|---|---|---|---|---|
| M15 | 400 | 350 | 1350 | / | 0.875 |
| M20 | 300 | 210 | 1350 | / | 0.70 |
| M20+ | 300 | 210 | 1350 | 24 | 0.70 |
| Sensor Number | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Vertical distance from the axis of the embankment top/mm | 360 | 510 | 660 | 810 |
| Vertical distance from the embankment bottom/mm | 330 | 270 | 210 | 150 |
| Working Condition | The Width of Paving Seam/mm | Water Depth in Front of the Dam/cm | Actual Simulation of Wave Height/m | Wave Period/s |
|---|---|---|---|---|
| 1 | 0.5 | 27.6 | 0.15 | 1.875 |
| 2 | 1.0 | 27.6 | 0.15 | 1.875 |
| 3 | 1.5 | 27.6 | 0.15 | 1.875 |
| 4 | 1.5 | 22.5 | 0.12 | 1.875 |
| 5 | 1.5 | 30.6 | 0.17 | 1.875 |
| No. | The Width of Paving Seam/mm | No. | The Width of Paving Seam/mm | ||||
|---|---|---|---|---|---|---|---|
| Level Direction | Vertical Direction | Oblique Direction | level Direction | Vertical Direction | Oblique Direction | ||
| 1 | 7.5 | 6.7 | 11.2 | 11 | 8.3 | 7.6 | 13.5 |
| 2 | 5.8 | 6.9 | 13.2 | 12 | 10.2 | 6.7 | 10.3 |
| 3 | 8.4 | 9.3 | 10.7 | 13 | 9.6 | 6.9 | 11.3 |
| 4 | 9.6 | 8.2 | 15.8 | 14 | 7.9 | 7.9 | 15.2 |
| 5 | 7.6 | 10.5 | 5.2 | 15 | 11.3 | 8.2 | 9.5 |
| 6 | 7.7 | 9.5 | 5.5 | 16 | 8.7 | 9.3 | 9.6 |
| 7 | 5.5 | 8.6 | 10.6 | 17 | 6.8 | 10.1 | 9.8 |
| 8 | 6.9 | 6.9 | 5.9 | 18 | 10.6 | 10.6 | 5.7 |
| 9 | 10.9 | 8.3 | 11.3 | 19 | 5.9 | 8.8 | 7.6 |
| 10 | 7.3 | 7.8 | 12.5 | 20 | 6.9 | 7.6 | 9.8 |
| Acquisition Cycles | Pore Water Pressure of Measuring Point/kPa | Acquisition Cycles | Pore Water Pressure of Measuring Point/kPa | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | ||
| 1 | 0.008 | 0.004 | 0.005 | 0.056 | 16 | 0.014 | 0.089 | 0.238 | 0.570 |
| 2 | 0.014 | 0.060 | 0.102 | 0.162 | 17 | 0.002 | 0.098 | 0.236 | 0.582 |
| 3 | 0.026 | 0.102 | 0.156 | 0.358 | 18 | 0.020 | 0.128 | 0.368 | 0.430 |
| 4 | 0.038 | 0.116 | 0.200 | 0.454 | 19 | 0.034 | 0.114 | 0.208 | 0.566 |
| 5 | 0.007 | 0.120 | 0.210 | 0.508 | 20 | 0.003 | 0.076 | 0.264 | 0.436 |
| 6 | 0.014 | 0.096 | 0.190 | 0.468 | 21 | 0.011 | 0.100 | 0.278 | 0.582 |
| 7 | 0.032 | 0.070 | 0.260 | 0.394 | 22 | 0.025 | 0.080 | 0.326 | 0.444 |
| 8 | 0.005 | 0.130 | 0.270 | 0.524 | 23 | 0.034 | 0.112 | 0.226 | 0.594 |
| 9 | 0.017 | 0.144 | 0.372 | 0.590 | 24 | 0.004 | 0.137 | 0.224 | 0.588 |
| 10 | 0.024 | 0.080 | 0.262 | 0.400 | 25 | 0.002 | 0.086 | 0.328 | 0.416 |
| 11 | 0.040 | 0.180 | 0.356 | 0.554 | 26 | 0.033 | 0.112 | 0.358 | 0.594 |
| 12 | 0.006 | 0.108 | 0.306 | 0.470 | 27 | 0.002 | 0.114 | 0.224 | 0.508 |
| 13 | 0.018 | 0.122 | 0.230 | 0.440 | 28 | 0.015 | 0.134 | 0.340 | 0.426 |
| 14 | 0.008 | 0.152 | 0.350 | 0.558 | 29 | 0.035 | 0.086 | 0.346 | 0.420 |
| 15 | 0.038 | 0.132 | 0.208 | 0.450 | 30 | 0.008 | 0.114 | 0.242 | 0.578 |
| Acquisition Cycles | Pore Water Pressure of Different Levee Levels/kPa | Acquisition Cycles | Pore Water Pressure of Different Levee Levels/kPa | ||||
|---|---|---|---|---|---|---|---|
| 20.5 cm | 25.8 cm | 30.6 cm | 20.5 cm | 25.8 cm | 30.6 cm | ||
| 1 | 0.006 | 0.216 | 0.432 | 16 | 0.570 | 0.976 | 1.529 |
| 2 | 0.162 | 1.386 | 1.320 | 17 | 0.582 | 1.007 | 1.551 |
| 3 | 0.358 | 1.137 | 2.084 | 18 | 0.430 | 1.284 | 1.310 |
| 4 | 0.454 | 1.456 | 1.576 | 19 | 0.566 | 1.015 | 2.019 |
| 5 | 0.508 | 1.182 | 2.090 | 20 | 0.436 | 1.352 | 1.338 |
| 6 | 0.468 | 1.382 | 1.891 | 21 | 0.582 | 1.043 | 1.295 |
| 7 | 0.394 | 1.415 | 1.966 | 22 | 0.444 | 0.996 | 2.084 |
| 8 | 0.524 | 1.023 | 2.106 | 23 | 0.594 | 1.335 | 1.507 |
| 9 | 0.590 | 1.239 | 1.485 | 24 | 0.588 | 1.090 | 1.504 |
| 10 | 0.400 | 1.325 | 2.094 | 25 | 0.416 | 1.049 | 1.828 |
| 11 | 0.554 | 1.131 | 2.097 | 26 | 0.594 | 1.178 | 1.616 |
| 12 | 0.470 | 1.284 | 1.298 | 27 | 0.508 | 1.080 | 1.994 |
| 13 | 0.440 | 1.107 | 1.944 | 28 | 0.426 | 1.348 | 2.072 |
| 14 | 0.558 | 1.013 | 2.025 | 29 | 0.420 | 1.241 | 1.367 |
| 15 | 0.450 | 1.350 | 1.373 | 30 | 0.578 | 1.043 | 2.109 |
| Grade | Serial Number | Mortar Strength/MPa | Measured Value of Mortar Strength/MPa | Average Shear Strength/MPa |
|---|---|---|---|---|
| M15 | 1 | 17.2 | 0.86 | 0.82 |
| 2 | 0.79 | |||
| 3 | 0.82 | |||
| M20 | 4 | 22.5 | 1.25 | 1.23 |
| 5 | 1.24 | |||
| 6 | 1.21 | |||
| M20+ | 7 | 23.0 | 1.46 | 1.49 |
| 8 | 1.48 | |||
| 9 | 1.52 |
| Classes of Mortar | Materials of Paving Seam | Pore Size Distribution/% | ||
|---|---|---|---|---|
| Less Damaged Holes 20–50 μm | Harmful Holes/50–200 μm | Very Harmful Holes/over 200 μm | ||
| M20 |  | 12.70% | 27.90% | 57.40% |
| M20+ |  | 30.50% | 25.90% | 41.60% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, F.; Hu, S.; Fang, Q.; Ju, L.; Liu, D.; Huang, Z. Research on Improvement of Slope Protection Concrete Precast Block Joints Based on Physical Model Experiment. Water 2023, 15, 1874. https://doi.org/10.3390/w15101874
Chen F, Hu S, Fang Q, Ju L, Liu D, Huang Z. Research on Improvement of Slope Protection Concrete Precast Block Joints Based on Physical Model Experiment. Water. 2023; 15(10):1874. https://doi.org/10.3390/w15101874
Chicago/Turabian StyleChen, Fang, Songtao Hu, Qinghe Fang, Liehong Ju, Da Liu, and Zhe Huang. 2023. "Research on Improvement of Slope Protection Concrete Precast Block Joints Based on Physical Model Experiment" Water 15, no. 10: 1874. https://doi.org/10.3390/w15101874
APA StyleChen, F., Hu, S., Fang, Q., Ju, L., Liu, D., & Huang, Z. (2023). Research on Improvement of Slope Protection Concrete Precast Block Joints Based on Physical Model Experiment. Water, 15(10), 1874. https://doi.org/10.3390/w15101874






