Size Effects of Rough Fracture Seepage in Rocks of Different Scales
Abstract
:1. Introduction
2. Seepage Experiments with Different Fracture Lengths and Fracture Inclinations
2.1. Experimental Equipment
- (1)
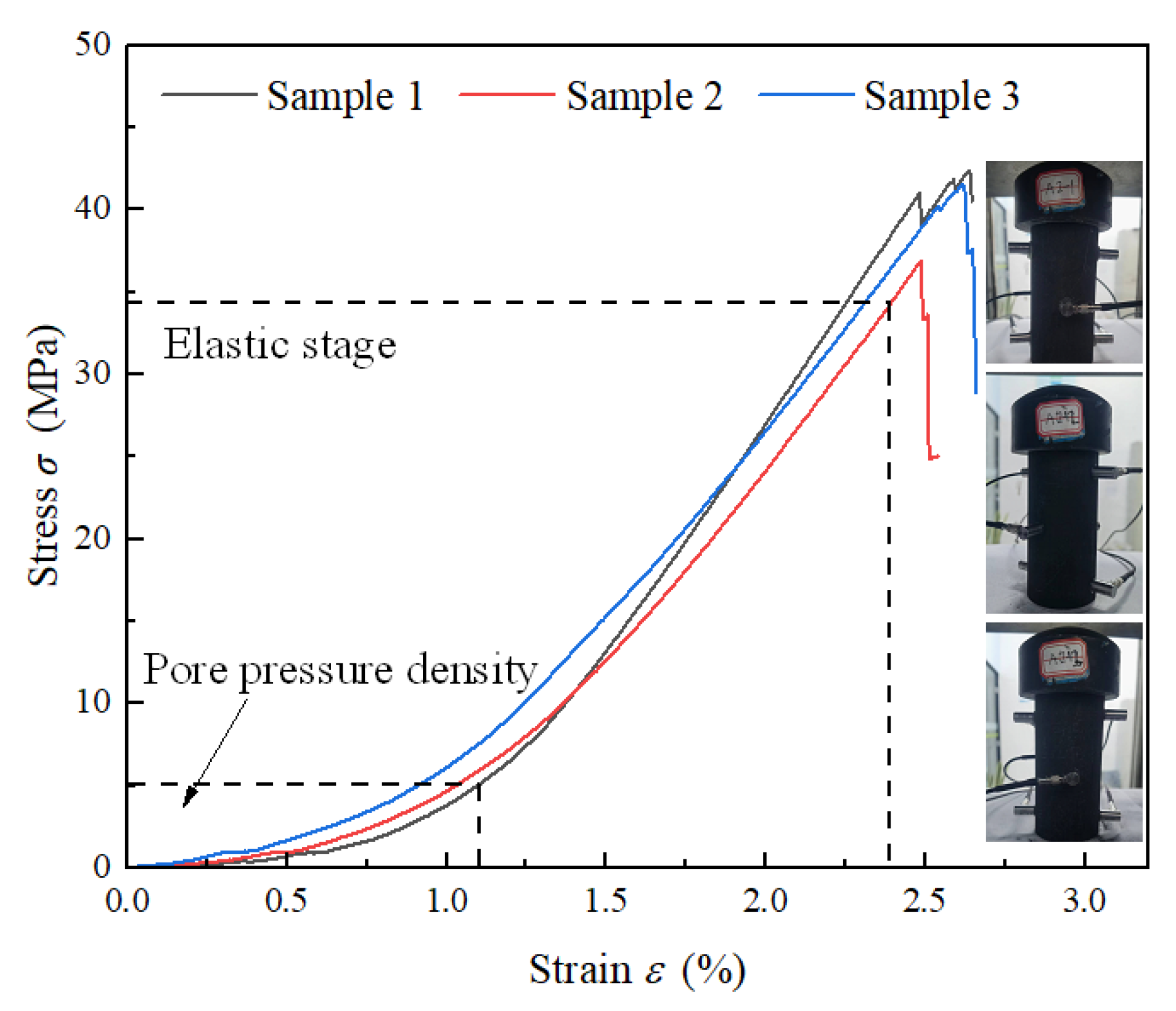
- Coal-sample compressive strength experiments. To ensure that the coal sample is subjected to a variety of stresses in the seepage experiment, and to reduce the interference of the anisotropy of the coal sample in the experiment, the seepage loading scheme should be set to ensure that the maximum loading stress is within the elastic range of the coal sample as far as possible. To prevent the coal sample from being damaged during the loading process and changing its seepage path, a compressive strength experiment on the cylindrical coal sample should be conducted first.
- (2)
- Seepage experiments with different fracture lengths. Because of the need to investigate the effect of fracture length and the relationship between fracture length and other factors when coupled with each other, in this part of the experiment, the different lengths of fractures that exist within the coal or rock in a realistic environment were simulated by processing multiple sets of prefabricated fractures of different lengths.
- (3)
- Seepage experiments with different fracture inclination angles. To consider the influence of multiple factors, the fracture geometry, surrounding pressure, axial pressure, and fracture inclination were coupled; therefore, seepage experiments with different fracture inclination angles were required.
2.2. Sample Preparation
2.3. Experimental Programme
2.4. Compressive Strength Test of Coal
2.5. Seepage Law of Coal Fracture under Size Effect
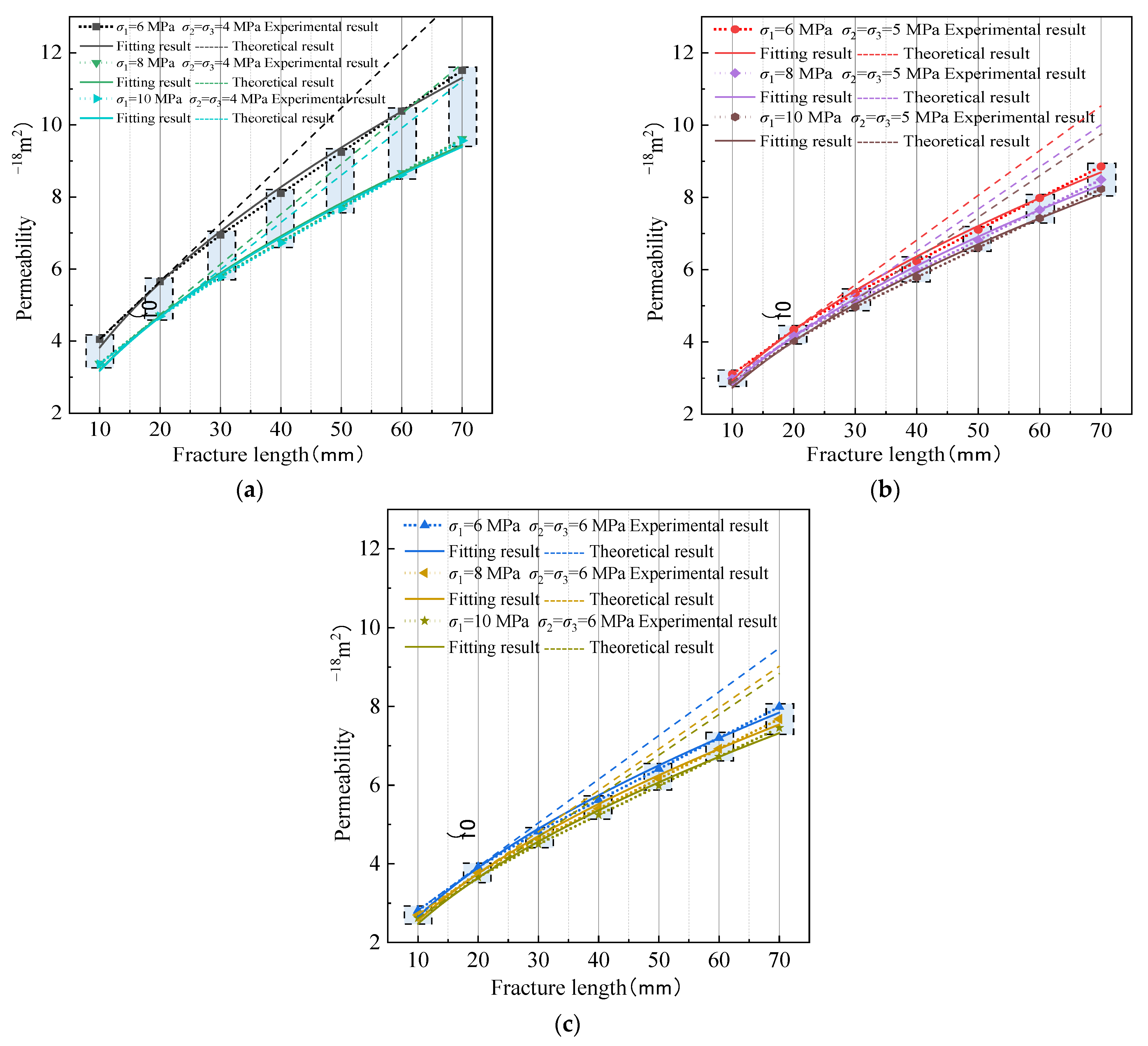
2.5.1. Seepage of Coal Samples with Multiple Fracture Lengths under Different Axial Pressures
2.5.2. Seepage of Coal Samples with Multiple Fracture Lengths under Different Confining Pressures
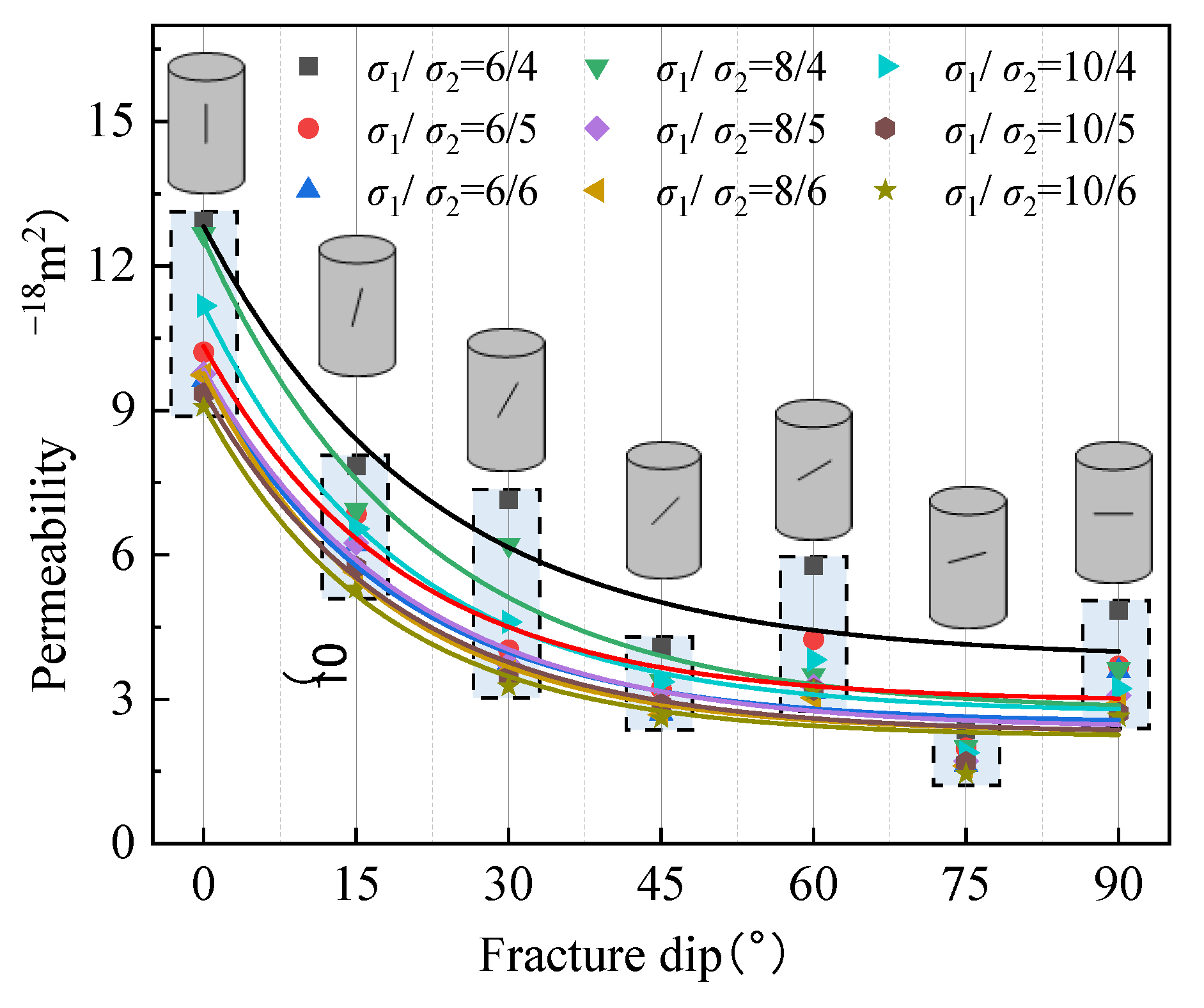
2.6. Fracture Seepage Patterns in Coal at Different Fracture Dips
3. Numerical Simulation Study of the Fracture Seepage Field under Size Effects
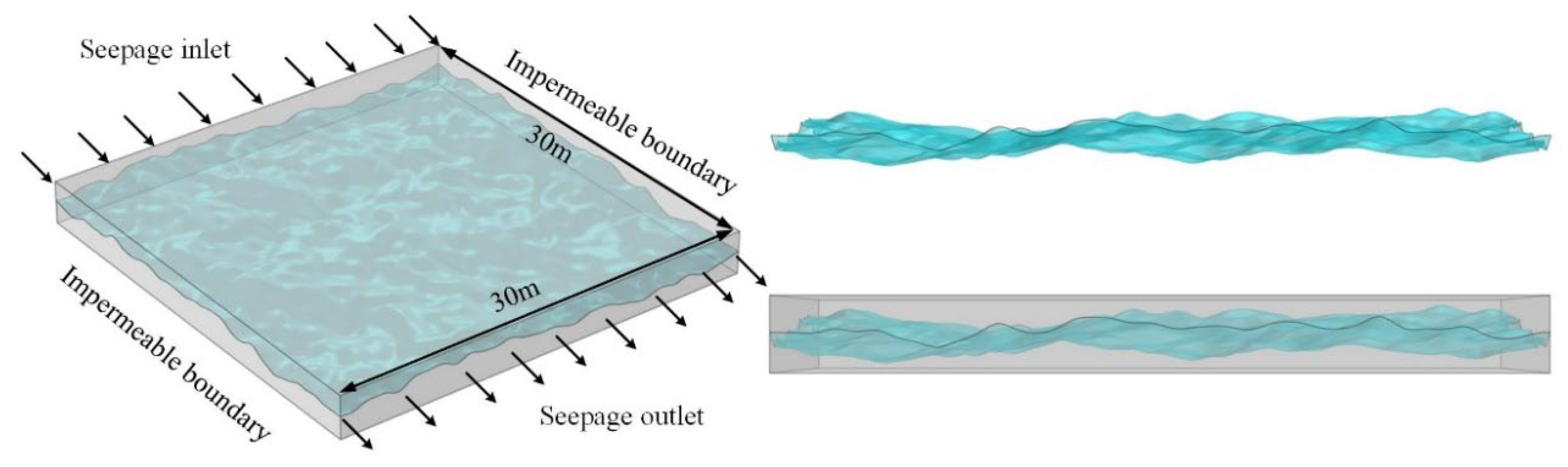
3.1. Fracture Seepage Simulation
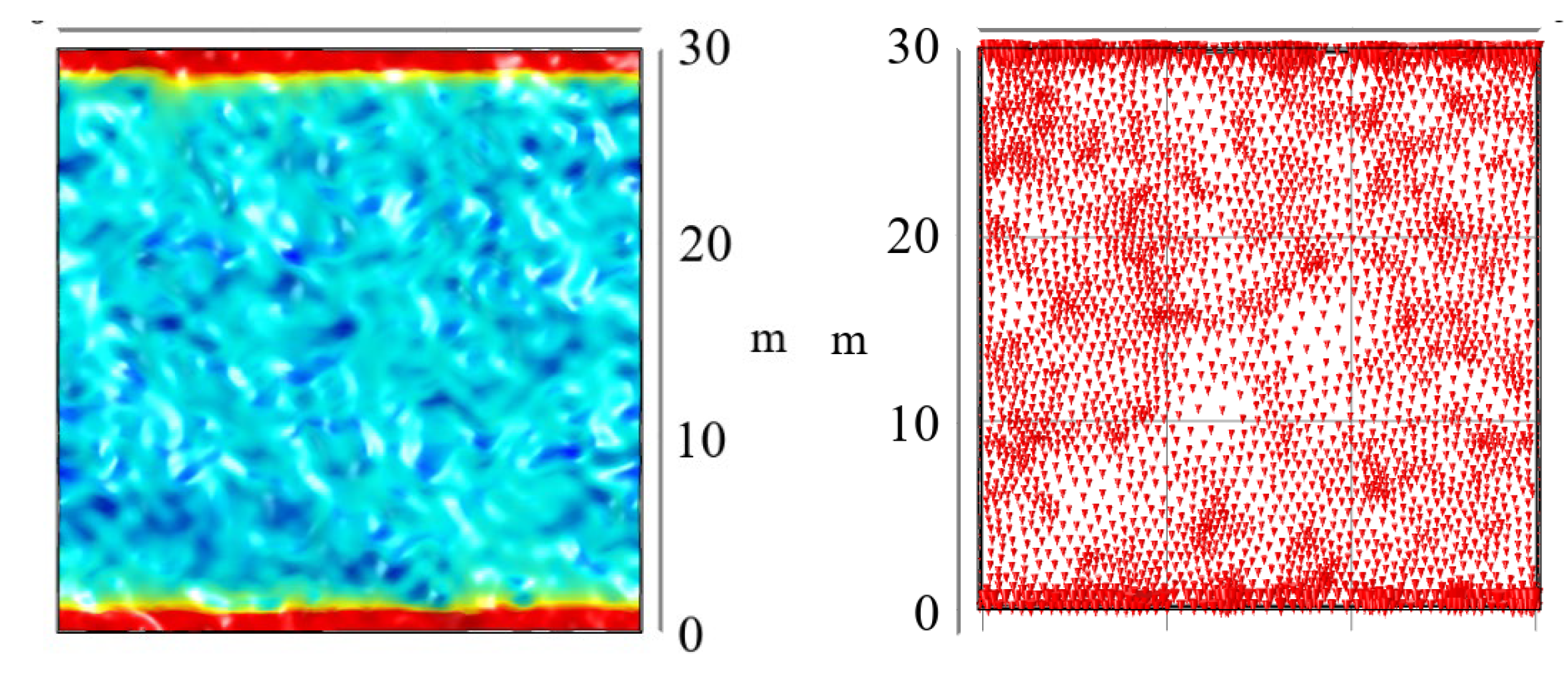
3.1.1. Seepage Phenomena under Size Effects
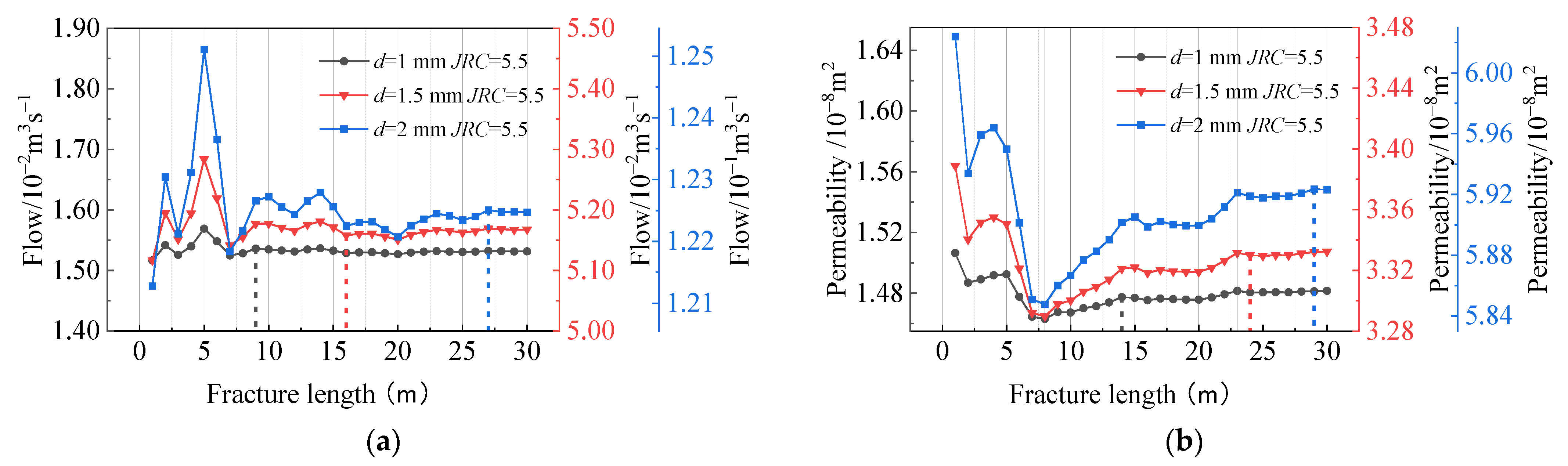
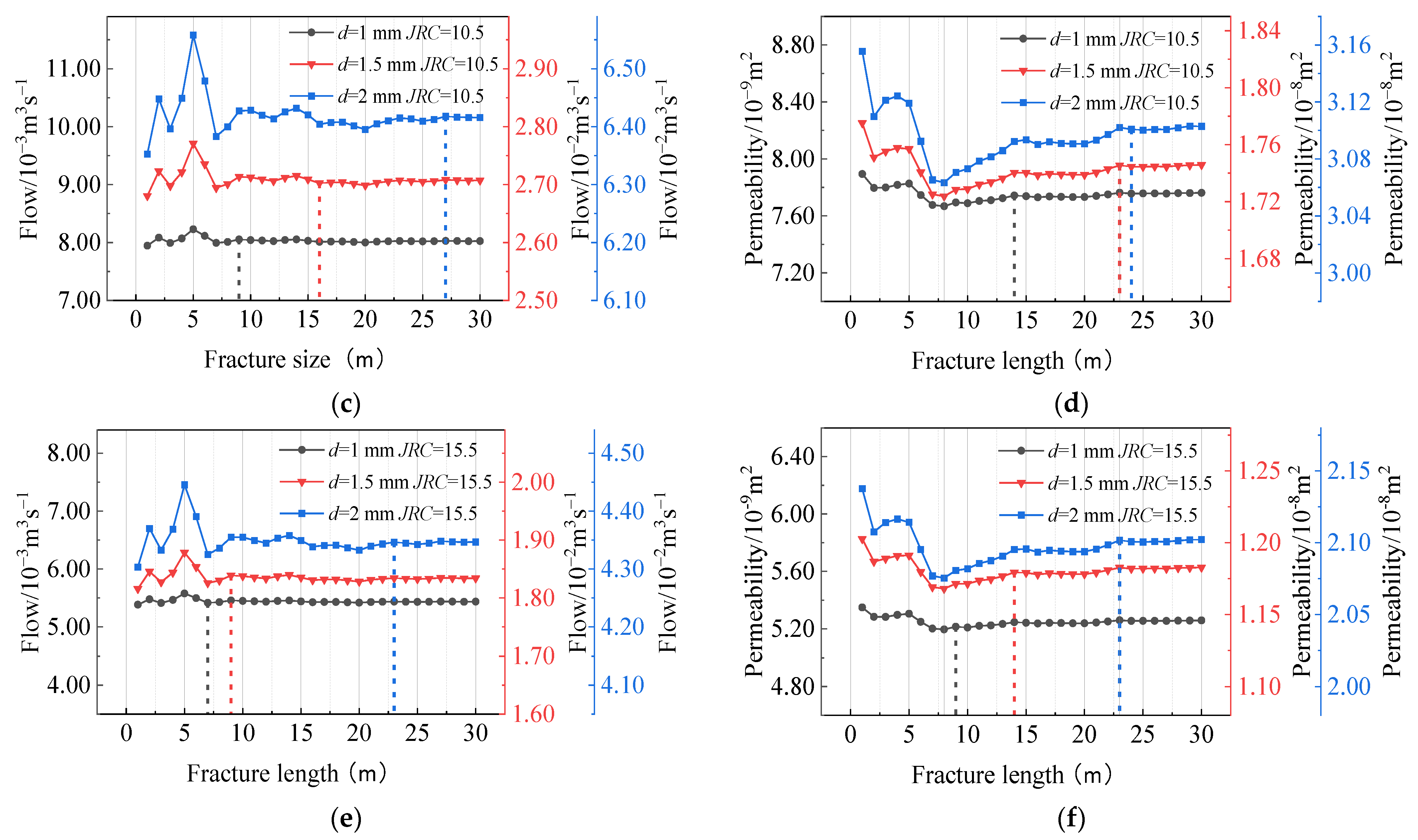
3.1.2. Seepage Patterns for Different Fracture Widths under Size Effects
3.1.3. Fracture Seepage for Different Fracture Roughness Values with Size Effect
4. Fracture Geometry Stress Multifactor Analysis
4.1. Analysis Method
4.2. Results of the Multi-Factor Coupling Analysis
5. Main Conclusions and Recommendations
- (1)
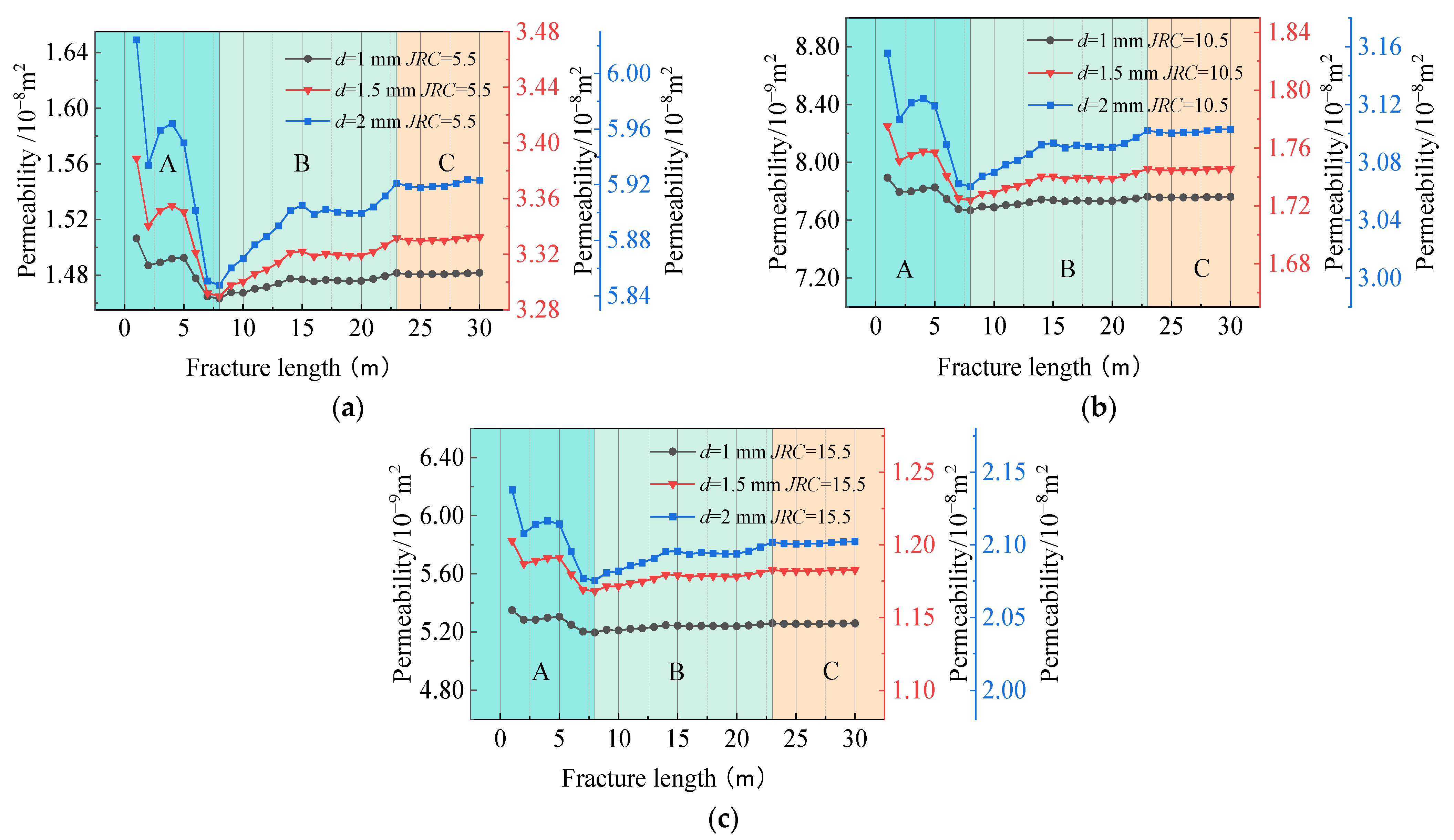
- There was a significant size effect on coal seepage. In small-size fracture seepage from 10 to 70 mm, permeability increases with increasing fracture length, with an overall increase of approximately 1.8 times, with a trend of positive correlation and non-linear variation, which gradually stabilizes. In large fracture seepage from 1 to 30 m, permeability decreases and then increases with increasing fracture length, with an overall variation of approximately 0.03 times, which is non-linear and gradually stabilizes. With the above conclusions, it can be found that there is a significant size effect in the fracture seepage of coal or rock.
- (2)
- The overall change in permeability for different fracture lengths in large-size fracture seepage from 1 to 30 m is divided into three stages: the significant change stage, stabilization stage, and stability stage. These stages were within the ranges of 0–8 m, 8–23 m, and 23–30 m, respectively. There is a certain critical size value, and, when reaching this size, the permeability reaches a steady state. All other things being equal, the critical size of the seepage increases when fracture width increases and decreases when fracture roughness increases.
- (3)
- Permeability decreases with increasing stress under the action of perimeter and axial pressures. When the amount of change in circumferential and axial pressure is the same, the change in permeability due to circumferential pressure is approximately 3.5 times greater than that due to the axial pressure. For fractures, stresses perpendicular to the fracture direction have a greater effect on fracture permeability.
- (4)
- Regression analysis was carried out for some of the influencing factors of seepage from small-sized fractures and some of the influencing factors of seepage from large-sized fractures, respectively. The following conclusions were obtained. The sensitivity ratio of fracture seepage to fracture length, surrounding pressure and fracture dip was 0.93:0.89:1 for the small-size fractures. The influences of these factors were similar. In large-size fractures, the sensitivity factor ratio of fracture seepage to fracture length, fracture roughness, and fracture width is 0.0014:0.83:1. Fracture length has less influence on fracture seepage in large sizes.
- (5)
- There are still a number of unresolved issues regarding the study of fracture seepage in coal [34,35]. The next step is to consider research in terms of structural changes and stress changes in the coal and explore the dynamic changes in permeability at various stages of the seepage process under the influence of anisotropy and other factors. The effect of cyclic loading and unloading on seepage in different fracture geometries can also be investigated in subsequent studies to further explore the fracture seepage characteristics.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yao, Q.L.; Hao, Q.; Chen, X.Y.; Zhou, B.; Fang, J. Design of coal pillar dam widths for underground reservoirs in coal mines. J. China Coal Soc. 2019, 44, 891–899. [Google Scholar] [CrossRef]
- Xu, J.L.; Zhu, W.B.; Wang, X.Z. A method for predicting the height of hydraulic fracture zones based on the location of key layers. J. China Coal Soc. 2012, 37, 762–769. [Google Scholar]
- Yao, Q.L.; Tang, C.J.; Liu, Z.C. Analysis of coal-water co-mining in ecologically fragile mining areas in western China. Coal Sci. Technol. 2021, 49, 225–232. [Google Scholar] [CrossRef]
- Gu, D.Z. Theoretical framework and technical system of underground water reservoirs in coal mines. J. China Coal Soc. 2015, 40, 239–246. [Google Scholar]
- Xie, H.P.; Xu, W.L.; Liu, C. Strategic Concept and Key Technology Perspectives for Underground Hydraulic Engineering. Chin. J. Rock Mech. Eng. 2018, 37, 781–791. [Google Scholar]
- Yao, Q.L.; Zhu, L.; Huang, Q.X.; Yang, P.; Xu, Z. Experimental study on the effect of water content on creep characteristics of fine-grained feldspathic clastic sandstone. J. Min. Saf. Eng. 2019, 36, 1034–1042+1051. [Google Scholar]
- Yao, Q.L.; Tang, C.J.; Xu, Q. A technical framework for the development and utilization of water resources in coal mining. China Sci. Pap. 2020, 15, 973–979. [Google Scholar]
- Zhao, Z.H.; Yan, L.; Gao, X.C.; Li, X.; Yao, Q.; Zheng, C. Study on hydraulic fracture extension and seepage morphology in naturally fractured reservoirs. J. Min. Saf. Eng. 2020, 37, 1263–1273. [Google Scholar]
- Fang, J.; Yao, Q.L.; Wang, W.N. Study on the effect of water content on strength damage and acoustic emission characteristics of muddy siltstone. J. China Coal Soc. 2018, 43, 412–419. [Google Scholar] [CrossRef]
- Wang, F.T.; Liang, N.N.; Li, G. Damage and Failure Evolution Mechanism for Coal Pillar Dams Affected by Water Immersion in Underground Reservoirs. Geofluids 2019, 2019, 2985691. [Google Scholar] [CrossRef]
- Sun, Y.J.; Xu, D.D.; Fan, D.; Wu, T. Study of factors influencing permeability of fractured rock masses. Explor. Eng. (Rock Soil Drill. Tunn.) 2011, 38, 76–80. [Google Scholar]
- Wang, G.; Han, D.; Qin, X.; Liu, Z.; Liu, J. A comprehensive method for studying pore structure and seepage characteristics of coal mass based on 3D CT reconstruction and NMR. Fuel 2020, 281, 118735. [Google Scholar] [CrossRef]
- Shi, X.; Zhou, W.; Cai, Q.; Lu, X. Experimental Study on Nonlinear Seepage Characteristics and Particle Size Gradation Effect of Fractured Sandstones. Adv. Civ. Eng. 2018, 2018, 8640535. [Google Scholar] [CrossRef]
- Chen, J.; Fang, Y.; Gu, R.; Lu, X. Study on pore size effect of low permeability clay seepage. Arab. J. Geosci. 2019, 12, 238. [Google Scholar] [CrossRef]
- Rong, G.; Zhou, C.B.; Wang, E.Z. Preliminary study on the calculation of permeability tensor and its characterization unit volume in fractured rock masses. Chin. J. Rock Mech. Eng. 2007, 4, 740–746. [Google Scholar]
- Shang, L.M.; Li, T.C.; Chen, W.; Li, Y.; Gao, F. Study on the size effect of three-dimensional built-in fractures in rocks. J. Wuhan Univ. Technol. 2015, 37, 72–77. [Google Scholar]
- Jing, D.J.; Meng, X.X.; Ge, S.C.; Zhang, T.; Ma, M.; Tong, L. Reconstruction and seepage simulation of a coal pore-fracture network based on CT technology. PLoS ONE 2021, 16, e0252277. [Google Scholar] [CrossRef]
- Di, S.T.; Jia, C.; Qiao, W.G.; Yu, W.; Li, K. Theoretical and Experimental Investigation of Characteristics of Single Fracture Stress-Seepage Coupling considering Microroughness. Math. Probl. Eng. 2017, 2017, 6431690. [Google Scholar] [CrossRef]
- Hudson, J.A.; Cornet, F.H.; Christiansson, R. ISRM suggested methods for rock stress estimation—Part 1: Strategy for rock stress estimation. Int. J. Rock Mech. Min. Sci. 2003, 40, 991–998. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Q.; Song, Z.; Zhang, Y.; Liu, X. Mechanical properties and damage constitutive model for uniaxial compression of salt rock at different loading rates. Int. J. Damage Mech. 2021, 30, 739–763. [Google Scholar] [CrossRef]
- Kou, M.M.; Liu, X.R.; Wang, Z.Q.; Tang, S.-D. Laboratory investigations on failure, energy and permeability evolution of fissured rock-like materials under seepage pressures. Eng. Fract. Mech. 2021, 247, 107694. [Google Scholar] [CrossRef]
- Liu, J.S.; Chen, Z.W.; Elsworth, D.; Miao, X.; Mao, X. Linking gas-sorption induced changes in coal permeability to directional strains through a modulus reduction ratio. Int. J. Coal Geol. 2010, 83, 21–30. [Google Scholar] [CrossRef]
- Duan, L.L.; Deng, H.F.; Xiong, Y.; Zhi, Y.; Pan, D.; Qi, Y. Study on the influence of fracture face morphological characteristics on the seepage characteristics of rock bodies. J. Disaster Prev. Mitig. Eng. 2021, 41, 110–117. [Google Scholar] [CrossRef]
- Guo, Z.H. Permeability prediction of rock masses based on fracture geometry features. Coal Eng. 2021, 53, 156–161. [Google Scholar]
- Du, S.G.; Chen, Y.; Fan, L.B. Mathematical expression of the JRC modified straight-edge method. J. Eng. Geol. 1996, 2, 36–43. [Google Scholar]
- Rasouli, V.; Hosseinian, A. Correlations Developed for Estimation of Hydraulic Parameters of Rough Fractures Through the Simulation of JRC Flow Channels. Rock Mech. Rock Eng. 2011, 44, 447–461. [Google Scholar] [CrossRef]
- Chen, J.; Ye, J.; Du, S. Scale Effect and Anisotropy Analyzed for Neutrosophic Numbers of Rock Joint Roughness Coefficient Based on Neutrosophic Statistics. Symmetry 2017, 9, 208. [Google Scholar] [CrossRef]
- Le, H.K.; Huang, W.; Liao, M.; Weng, M.C. Spatial characteristics of rock joint profile roughness and mechanical behavior of a randomly generated rock joint. Eng. Geol. 2018, 245, 97–105. [Google Scholar] [CrossRef]
- Tanner-Smith, E.E.; Tipton, E. Robust variance estimation with dependent effect sizes: Practical considerations including a software tutorial in Stata and SPSS. Res. Synth. Methods 2014, 5, 13–30. [Google Scholar] [CrossRef]
- Yin, Y. Model-free tests for series correlation in multivariate linear regression. J. Stat. Plan. Inference 2020, 206, 179–195. [Google Scholar] [CrossRef]
- Preinerstorfer, D.; Poetscher, B.M. On the power of invariant tests for hypotheses on a covariance matrix. Econom. Theory 2017, 33, 1–68. [Google Scholar] [CrossRef]
- Chen, Y. Spatial Autocorrelation Approaches to Testing Residuals from Least Squares Regression. PLoS ONE 2016, 11, e0146865. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H. Multicollinearity and misleading statistical results. Korean J. Anesthesiol. 2019, 72, 558–569. [Google Scholar] [CrossRef] [PubMed]
- Menezes, F.F. Anisotropy of volume change and permeability evolution of hard sandstones under triaxial stress conditions. J. Pet. Sci. Eng. 2019, 174, 921–939. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, B.; Liu, T.; Li, Q.; Kong, J. Gas flow field evolution around hydraulic slotted borehole in anisotropic coal. J. Nat. Gas Sci. Eng. 2018, 58, 189–200. [Google Scholar] [CrossRef]












| No. | Group | Length of Fracture (mm) | No. | Group | Fracture Dip (°) |
|---|---|---|---|---|---|
| 1 | l-10 | 10 | 8 | a-0 | 0 |
| 2 | l-20 | 20 | 9 | a-15 | 15 |
| 3 | l-30 | 30 | 10 | a-30 | 30 |
| 4 | l-40 | 40 | 11 | a-45 | 45 |
| 5 | l-50 | 50 | 12 | a-60 | 60 |
| 6 | l-60 | 60 | 13 | a-75 | 75 |
| 7 | l-70 | 70 | 14 | a-90 | 90 |
| No. | Axial Stress σ1 (MPa) | Surrounding Stress σ2, σ3 (MPa) | Seepage Pressure pw (MPa) |
|---|---|---|---|
| 1 | 6 | 4 | 3 |
| 2 | 6 | 5 | 3 |
| 3 | 6 | 6 | 3 |
| 4 | 8 | 4 | 3 |
| 5 | 8 | 5 | 3 |
| 6 | 8 | 6 | 3 |
| 7 | 10 | 4 | 3 |
| 8 | 10 | 5 | 3 |
| 9 | 10 | 6 | 3 |
| Parameters | Values (in Units) | Parameters | Values (in Units) |
|---|---|---|---|
| Simulated object | Fracture seepage | Young’s modulus of the substrate | 4 GPa |
| Size | 1 × 1~30 × 30 m | Initial porosity of the substrate | 0.25 |
| Roughness factor JRC | 5.5, 10.5, 15.5 | Substrate density | 1250 kg/m3 |
| Fracture width | 1, 1.5, 2 mm | Poisson’s ratio | 0.35 |
| Normal stress | 5~20 MPa | Fluid dynamic viscosity | 0.001 Pa·s |
| Category | R | R2 | Adjusted R2 | Error in Standard Estimation | Durbin–Watson |
|---|---|---|---|---|---|
| Experiment a | 0.809 | 0.655 | 0.628 | 1.683 × 10−18 | 1.931 |
| Numerical simulation b | 0.932 | 0.869 | 0.868 | 5.751 × 10−9 | 1.198 |
| Models | Unstandardised Factor | Standardisation Factor | t | Significance | Covariance Statistics | ||
|---|---|---|---|---|---|---|---|
| B | Standard Error | Beta | Tolerance | ||||
| Experiment | (Constant) | 1.084 × 10−17 | 1.74 × 10−18 | 6.229 | 2.76 × 10−7 | ||
| Fracture length | 7.088 × 10−17 | 1.726 × 10−17 | 0.416 | 4.108 | 2.05 × 10−4 | 0.884 | |
| Surrounding pressure | −1.326 × 10−18 | 3.18 × 10−19 | −0.397 | −4.170 | 1.7 × 10−4 | 1.000 | |
| Fracture dip | −3.918 × 10−20 | 8.932 × 10−21 | −0.445 | −4.386 | 8.8 × 10−5 | 0.884 | |
| Numerical simulation | (Constant) | 4.956 × 10−9 | 1.726 × 10−9 | 2.871 | 0.004 | ||
| Fracture length | −1.817 × 10−12 | 4.043 × 10−11 | −0.001 | −0.045 | 0.964 | 1.000 | |
| Fracture roughness | −2.304 × 10−9 | 8.572 × 10−11 | −0.596 | −26.878 | 8.705 × 10−78 | 1.000 | |
| Fracture width | 2.776 × 10−8 | 8.572 × 10−10 | 0.717 | 32.378 | 2.880 × 10−94 | 1.000 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Z.; Yao, Q.; Wang, W.; Su, F.; Li, X.; Zhu, L.; Wu, C. Size Effects of Rough Fracture Seepage in Rocks of Different Scales. Water 2023, 15, 1912. https://doi.org/10.3390/w15101912
Shi Z, Yao Q, Wang W, Su F, Li X, Zhu L, Wu C. Size Effects of Rough Fracture Seepage in Rocks of Different Scales. Water. 2023; 15(10):1912. https://doi.org/10.3390/w15101912
Chicago/Turabian StyleShi, Zhuolin, Qiangling Yao, Weinan Wang, Fengsheng Su, Xuehua Li, Liu Zhu, and Chengle Wu. 2023. "Size Effects of Rough Fracture Seepage in Rocks of Different Scales" Water 15, no. 10: 1912. https://doi.org/10.3390/w15101912
APA StyleShi, Z., Yao, Q., Wang, W., Su, F., Li, X., Zhu, L., & Wu, C. (2023). Size Effects of Rough Fracture Seepage in Rocks of Different Scales. Water, 15(10), 1912. https://doi.org/10.3390/w15101912






