Analysis of Water Infiltration Characteristics and Hydraulic Parameters of Sierozem Soil under Humic Acid Addition
Abstract
:1. Introduction
2. Materials and Methods
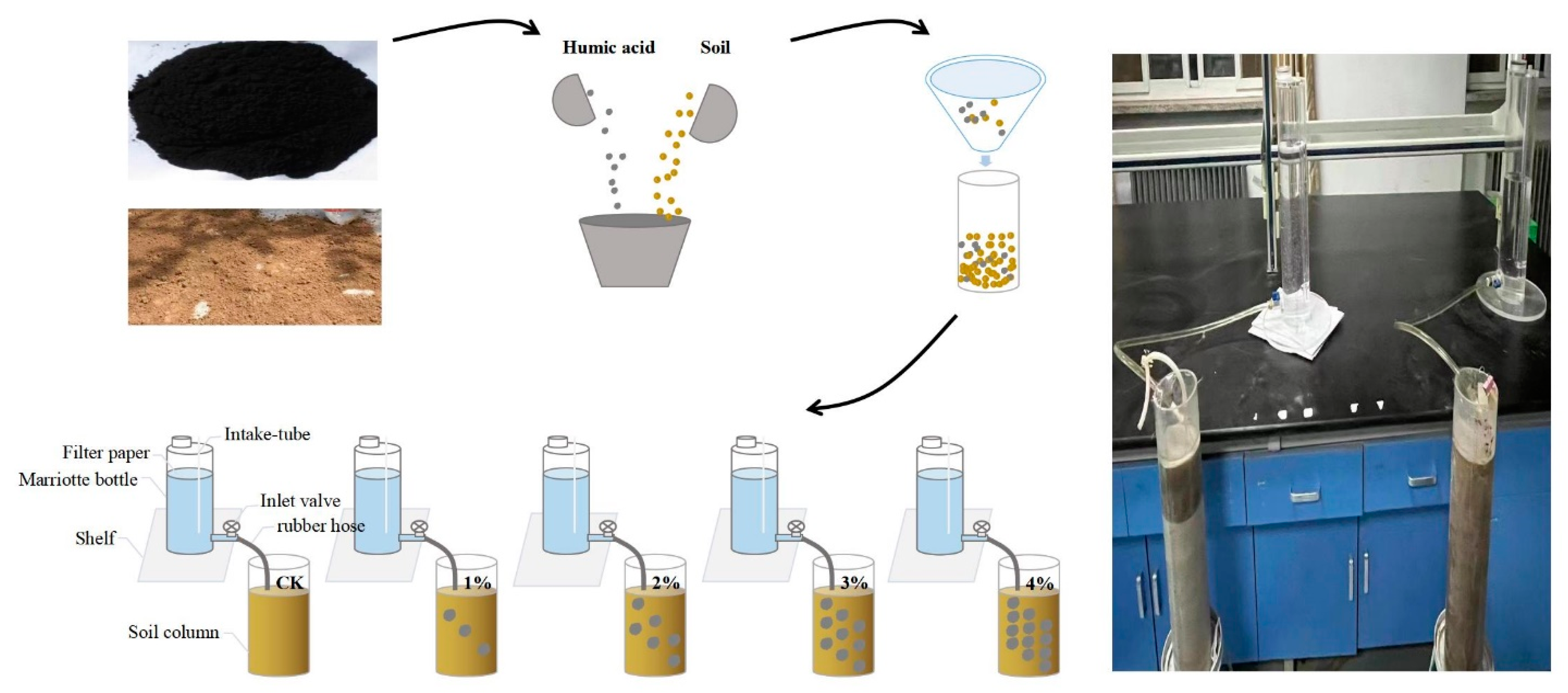
2.1. Materials
2.2. Methods
2.3. Comparison of Infiltration Model Analysis
- (1)
- The Philip model equation [12] is as follows:
- (2)
- The Horton model equation [13] is as follows:
- (3)
- The Kostiakov model equation [14] is as follows:.
- (4)
- Wetting front fitting.
2.4. Hydrus-1D Basic Equation
2.5. Model Evaluation
3. Results and Analysis
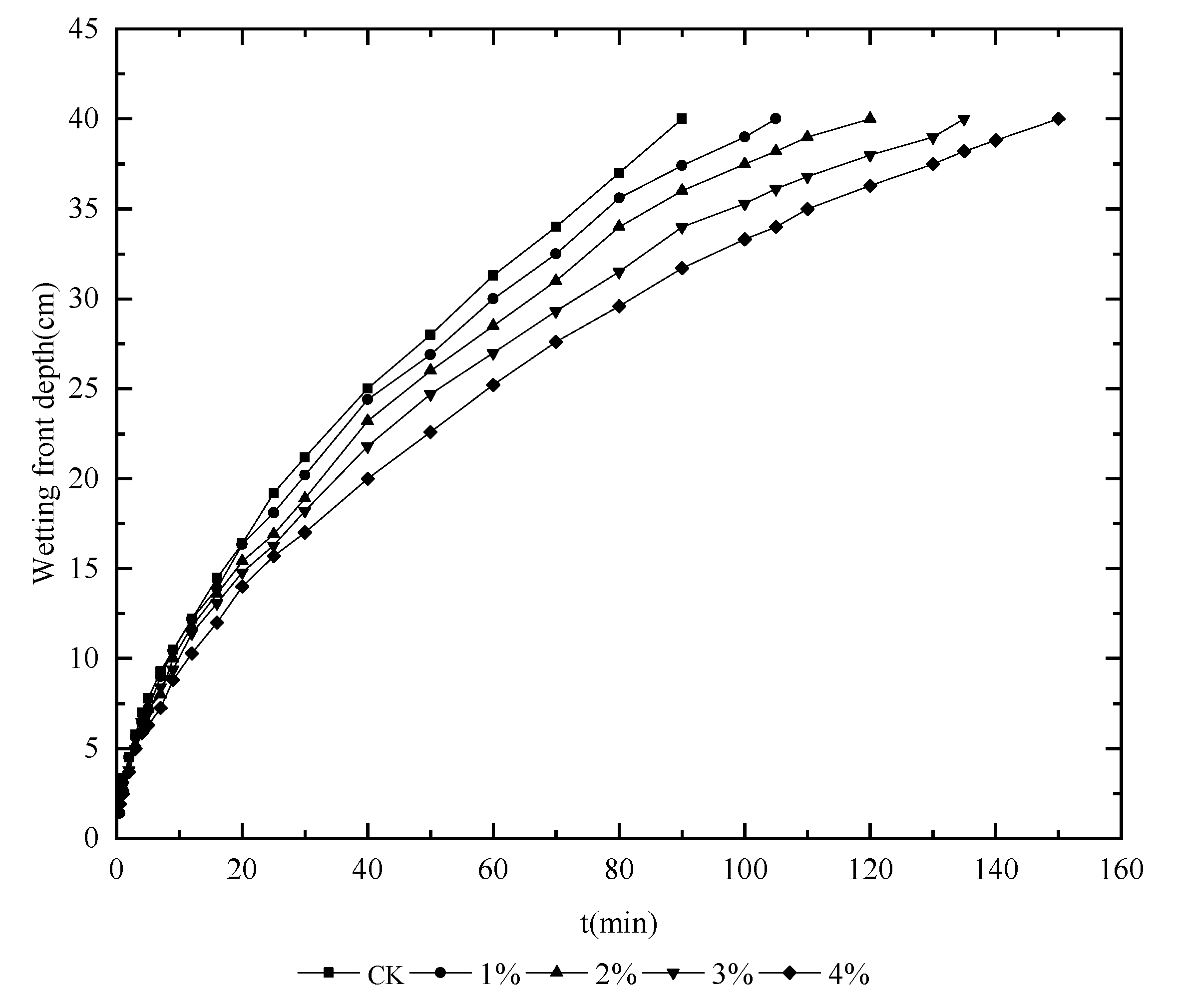
3.1. Effects of Humic Acid Concentration on the Wetting Front
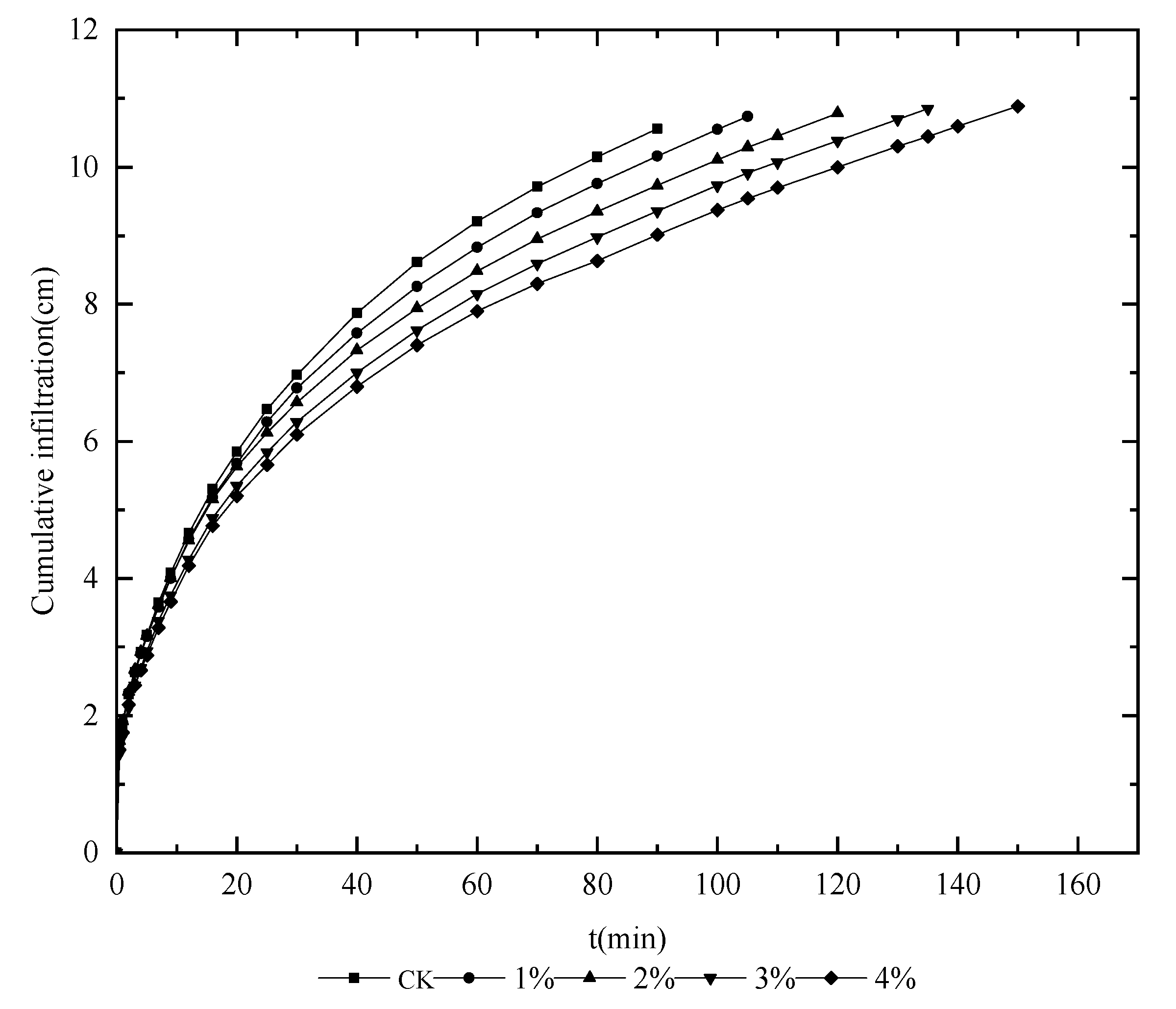
3.2. Effects of Humic Acid Concentration on the Cumulative Infiltration Amount
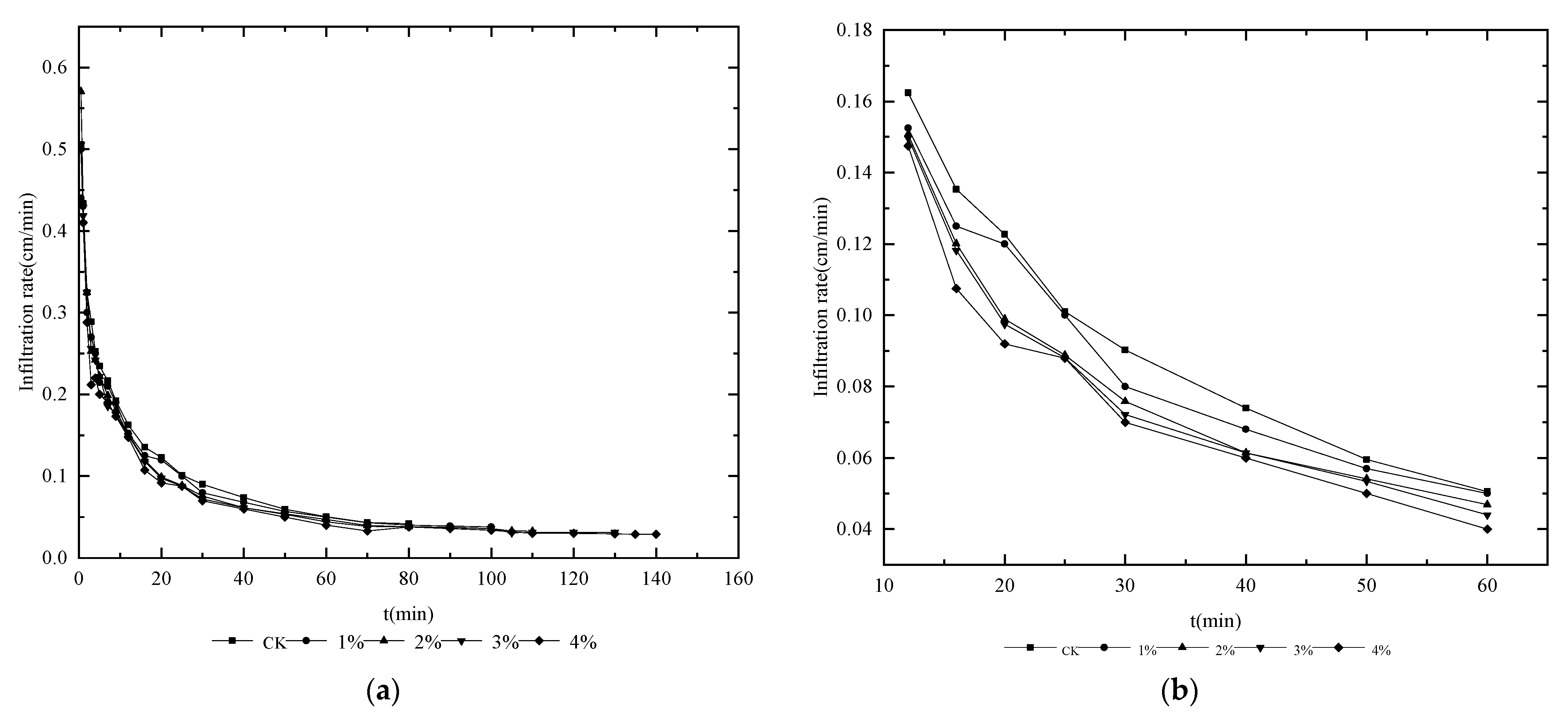
3.3. Effect of Humic Acid Concentration on Infiltration Rate
3.4. Model Fitting of Soil Water Infiltration Process
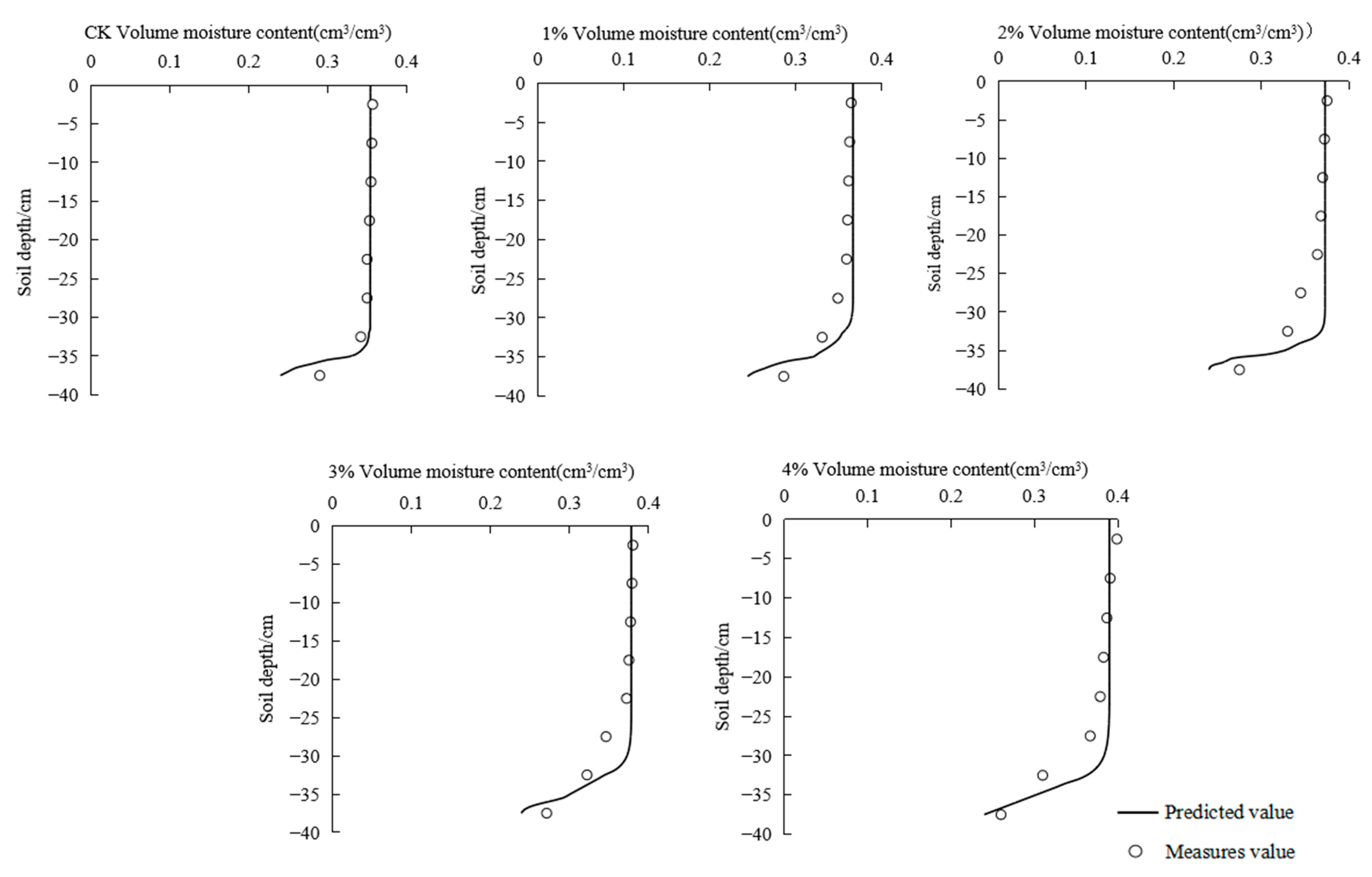
3.5. Verification of Parameters and Effect of Humic Acid Concentration on Soil Hydraulics Parameters
4. Discussion
4.1. Effects of Humic Acid Concentration on the Wetting Front, the Cumulative Infiltration Amount and Infiltration Rate
4.2. Effect of Humic Acid Concentration on Soil Hydraulics Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sepahvand, A.; Golkarian, A.; Billa, L.; Wang, K.; Rezaie, F.; Panahi, S.; Samadianfard, S.; Khosravi, K. Evaluation of deep machine learning-based models of soil cumulative infiltration. Earth Sci. Inform. 2022, 15, 1861–1877. [Google Scholar] [CrossRef]
- Lozano Olivério, G.; dos Santos Batista Bonini, C.; Fernanda Dias Souza, J.; Luís Sanchez Perusso, R.; Meirelles, G.C.; Andrighetto, C.; Carlos Lupatini, G.; Pavan Mateus, G.; Lapaz, A.D.M.; Heinrichs, R.; et al. Water Infiltration, Resistance to Penetration and Soil Moisture in Integrated Agricultural Yield Systems over Time. Commun. Soil Sci. Plant Anal. 2022, 53, 327–336. [Google Scholar] [CrossRef]
- Geris, J.; Verrot, L.; Gao, L.; Peng, X.; Oyesiku-Blakemore, J.; Smith, J.U.; Hodson, M.E.; McKenzie, B.M.; Zhang, G.; Hallett, P.D. Importance of short-term temporal variability in soil physical properties for soil water modelling under different tillage practices. Soil Till. Res. 2021, 213, 105132. [Google Scholar] [CrossRef]
- Savarese, C.; Drosos, M.; Spaccini, R.; Cozzolino, V.; Piccolo, A. Molecular characterization of soil organic matter and its extractable humic fraction from long-term field experiments under different cropping systems. Geoderma 2021, 383, 114700. [Google Scholar] [CrossRef]
- Martin, D.P.; Seiter, J.M.; Lafferty, B.J.; Bednar, A.J. Exploring the ability of cations to facilitate binding between inorganic oxyanions and humic acid. Chemosphere 2017, 166, 192–196. [Google Scholar] [CrossRef]
- Wu, X.; Xia, Y.; Yuan, L.; Xia, K.; Jiang, Y.; Li, N.; He, X. Molecular Dynamics Simulation of the Interaction between Common Metal Ions and Humic Acids. Water 2020, 12, 3200. [Google Scholar] [CrossRef]
- Liu, M.; Wang, C.; Liu, X.; Lu, Y.; Wang, Y. Saline-alkali soil applied with vermicompost and humic acid fertilizer improved macroaggregate microstructure to enhance salt leaching and inhibit nitrogen losses. Appl. Soil Ecol. 2020, 156, 103705. [Google Scholar] [CrossRef]
- Mamedov, A.I.; Bar-Yosef, B.; Levkovich, I.; Rosenberg, R.; Silber, A.; Fine, P.; Levy, G.J. Amending Soil with Sludge, Manure, Humic Acid, Orthophosphate and Phytic Acid: Effects on Infiltration, Runoff and Sediment Loss. Land Degrad. Dev. 2016, 27, 1629–1639. [Google Scholar] [CrossRef]
- Magdalena, B.S.; Bozena, D.; Erika, T. Properties of humic acids depending on the land use in different parts of Slovakia. Environ. Sci. Pollut. Res. Int. 2021, 28, 58068. [Google Scholar]
- Jing, H. Study on The Effect of Humic Acid on The Migration Distance of Wetting Front during Water Infiltration. IOP Conf. Ser. Earth Environ. Sci. 2021, 30, 8329–8335. [Google Scholar] [CrossRef]
- Mendoza, K.V.; Horn, R. Changes in Water Infiltration after Simulated Wetting and Drying Periods in two Biochar Amendments. Soil Syst. 2019, 3, 63. [Google Scholar] [CrossRef]
- Philip, R.J. The theory of infiltration: 1. The infiltration equation and its solution. Soil Sci. 1957, 83, 345–358. [Google Scholar] [CrossRef]
- Horton, R.E. An Approach Toward a Physical Interpretation of Infiltration-Capacity. Soil Sci. Soc. Am. J. 1941, 63, 399–417. [Google Scholar] [CrossRef]
- Hartley, D.M. Interpretation of Kostiakov Infiltration Parameters for Borders. J. Irrigat. Drainage Eng. 1992, 118, 156–165. [Google Scholar] [CrossRef]
- Li, X.J.; Shan, Y.Y.; Wang, Q.J.; Ma, C.G.; Yu, L. Effect of humic acid on characteristics of salt and water transport in coastal saline alkali soil. J. Soil Water Conserv. 2020, 34, 288–293. [Google Scholar]
- Wu, J.H.; Li, Y.C.; Shao, F.F.; Wang, Z.X. Effects of biochemical fulvic acid on physical properties and water movement characteristics. J. Soil Water Conserv. 2021, 35, 159–164+171. [Google Scholar]
- Wang, H.; Yang, Q.; Ma, H.; Liang, J. Chemical compositions evolution of groundwater and its pollution characterization due to agricultural activities in Yinchuan Plain, northwest China. Environ. Res. 2021, 200, 111449. [Google Scholar] [CrossRef] [PubMed]
- Zou, Y.; Zhang, S.; Shi, Z.; Zhou, H.; Zheng, H.; Hu, J.; Mei, J.; Bai, L.; Jia, J. Effects of mixed-based biochar on water infiltration and evaporation in aeolian sand soil. J. Arid Land 2022, 14, 374–389. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Bai, Y.R.; Zhan, X.L. Spatial Variability of Soil Nutrients at Different Sampling Scales in Farmland in the Yellow River Irrigated Area in Ningxia. Res. Arid Areas 2014, 31, 209–215. [Google Scholar]
- Zheng, F.L.; Wang, X.N.; Ge, M.; Li, C.Y.; Tan, J.L. Characteristics of Vertical Water Infiltration in a Sierozem Soil under Gravel-Sand Mulching Condition. Chin. J. Soil Sci. 2021, 52, 314–321. [Google Scholar]
- Zhou, X.B.; Luan, Y.X.; Lin, Q.; Xu, S.H. Numerical Inversion-based Simulation of Hydraulic Properties of Stratic Soil. Acta Pedol. Sin. 2021, 58, 1214–1223. [Google Scholar]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, Y.; Chen, J.; Zhang, Z.; Li, Y.; Du, Y. The applicability of HYDRUS-1D to infiltration of water repellent soil at different depths. Eur. J. Soil Sci. 2021, 72, 2020–2032. [Google Scholar] [CrossRef]
- Liu, Y.F.; Zhang, Z.; Liu, Y.; Cui, Z.; Leite, P.A.; Shi, J.; Wang, Y.; Wu, G.L. Shrub encroachment enhances the infiltration capacity of alpine meadows by changing the community composition and soil conditions. Catena 2022, 213, 106222. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, Y.; Long, L.; Lei, S. Soil Water Behavior of Sandy Soils under Semiarid Conditions in the Shendong Mining Area (China). Water 2022, 14, 2159. [Google Scholar] [CrossRef]
- Zhang, J.H.; Wang, Q.J.; Mu, W.Y.; Wei, K.; Guo, Y.; Sun, Y. Experimental Investigation of the Different Polyacrylamide Dosages on Soil Water Movement under Brackish Water Infiltration. Polymers 2022, 14, 2495. [Google Scholar] [CrossRef]
- Mamedov, A.I.; Levy, G.J.; Shainberg, I.; Letey, J. Wetting rate, sodicity, and soil texture effects on infiltration rate and runoff. Soil Res. 2001, 39, 1293–1305. [Google Scholar] [CrossRef]
- Cleophas, F.; Isidore, F.; Musta, B.; Ali, B.M.; Mahali, M.; Zahari, N.Z.; Bidin, K. Effect of soil physical properties on soil infiltration rates. J. Phys. Conf. Ser. 2022, 10, 727–736. [Google Scholar] [CrossRef]
- Vand, A.S.; Sihag, P.; Singh, B.; Zand, M. Comparative Evaluation of Infiltration Models. KSCE J. Civil. Eng. 2018, 22, 4173–4184. [Google Scholar] [CrossRef]
- Gopi, C.V.; Sambaiah, A.; Rajesh, B.R.A.; Balakrishna, V.; Geetha, B. Effect of Soil, Water Quality and Tillage Dynamics on Infiltration Rate in Different Soil. Int. J. Agric. Sci. 2018, 10, 7428–7431. [Google Scholar]
- Zhao, W.J.; Hu, J.Z.; Cui, Z.; Dou, P.X.; Fan, Y.W. Effects of superabsorbent polymers on the vertical infiltration of soil water with sand mulching. Environ. Earth Sci. 2019, 78, 1–6. [Google Scholar] [CrossRef]
- Li, Y.B.; Liu, Y.; Nie, W.B.; Ma, X.Y. Inverse Modeling of Soil Hydraulic Parameters Based on a Hybrid of Vector-Evaluated Genetic Algorithm and Particle Swarm Optimization. Water 2018, 10, 84. [Google Scholar] [CrossRef]
- Ma, M.M.; Lin, Q.; Xu, S.H. Water Infiltration Characteristics of Layered Soil under Influences of Different Factors and Estimation of Hydraulic Parameters. Acta Pedol. Sin. 2020, 57, 347–358. [Google Scholar]
- Wang, X.F.; Li, Y.; Si, B.C.; Ren, X.; Chen, J.Y. Simulation of Water Movement in Layered Water-Repellent Soils using HYDRUS-1D. Soil Sci. Soc. Am. J. 2018, 82, 1101–1112. [Google Scholar] [CrossRef]
- Zheng, C.; Lu, Y.; Guo, X.; Li, H.; Sai, J.; Liu, X. Application of HYDRUS-1D model for research on irrigation infiltration characteristics in arid oasis of northwest China. Environ. Earth Sci. 2017, 76, 785. [Google Scholar] [CrossRef]
- Homolák, M.; Pichler, V.; Gömöryová, E.; Bebej, J. Effect of surface humus on water infiltration and redistribution in beech forest stands with different density. Central Eur. For. J. 2017, 63, 73–78. [Google Scholar] [CrossRef]
- Paul, P.L.C.; Bell, R.W.; Barrett-Lennard, E.G.; Kabir, E. Straw mulch and irrigation affect solute potential and sunflower yield in a heavy textured soil in the Ganges Delta. Agric. Water Manag. 2020, 239, 106211. [Google Scholar] [CrossRef]
- Ndzelu, B.S.; Dou, S.; Zhang, X.; Zhang, Y.; Ma, R.; Liu, X. Tillage effects on humus composition and humic acid structural characteristics in soil aggregate-size fractions. Soil Till. Res. 2021, 213, 105090. [Google Scholar] [CrossRef]
- Gu, X.; Ren, C.M.; Zhang, H.Y.; Wang, L.N.; Yang, L.; Li, N.; Han, M. Study on water holding capacity of soda saline-alkali soil under application of lignite containing humic acid. China Rural Water Hydropower 2022. Available online: https://kns.cnki.net/kcms/detail/42.1419.TV.20220913.1127.034.html (accessed on 7 March 2023).
- Kargas, G.; Soulis, K.X.; Kerkides, P. Implications of Hysteresis on the Horizontal Soil Water Redistribution after Infiltration. Water 2021, 13, 2773. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, Y.; Liu, H.; Xiao, W.; Chen, S. Evaluating the Water Holding Capacity of Multilayer Soil Profiles Using Hydrus-1D and Multi-Criteria Decision Analysis. Water 2020, 12, 773. [Google Scholar] [CrossRef]
- Shan, Y.Y.; Ma, C.G.; Wang, Q.J.; Li, X.J.; Tao, W.H.; Zhang, J.H.; Su, L.J.; Cao, L. The effect of sodium carboxymethyl cellulose on water movement and soil hydraulic parameters of loamy sand. Acta Pedol. Sin. 2022, 7, 1–12. [Google Scholar]
- Ahmad, I.; Ali, S.; Khan, K.S.; Hassan, F.; Bashir, K. Use of Coal Derived Humic Acid as Soil Conditioner to Improve Soil Physical Properties and Wheat Yield. Int. J. Plant Soil Sci. 2015, 5, 268–275. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, B.K.; Mitra, S.; Datta, M. Identification of Water Deficit and Surplus Periods and Prediction of Profile Water Content from Surface Soil Water Status in Upland of Tripura. J. Indian Soc. Soil Sci. 1997, 45, 698–701. [Google Scholar]
| Soil Bulk Density BD/(g/cm3) | Saturated Moisture Content θs/(cm3/cm3) | Initial Moisture Content θr/(cm3/cm3) | Saturated Water Conductivity Ks/(mm/h) | Cation Exchange Capacity CEC/(cmol/kg) | |
|---|---|---|---|---|---|
| Sierozem soil | 1.650 | 0.353 | 0.005 | 1.624 | 8.456 |
| Treatments | Fitting Parameters | ||
|---|---|---|---|
| a | b | R2 | |
| CK | 3.022 | 0.572 | 0.999 |
| 1% | 3.051 | 0.556 | 0.999 |
| 2% | 2.954 | 0.551 | 0.999 |
| 3% | 3.062 | 0.528 | 0.999 |
| 4% | 2.763 | 0.537 | 0.999 |
| Philip Model | Horton Model | Kostiakov Model | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S/(cm/min0.5) | ic/(cm/min) | R2 | ic/(cm/min) | i1/(cm/min) | k | R2 | c/(cm/min) | d | R2 | |
| CK | 0.761 | 0.034 | 0.948 | 0.074 | 0.483 | 0.164 | 0.952 | 0.412 | 0.400 | 0.970 |
| T1 | 0.707 | 0.031 | 0.920 | 0.059 | 0.430 | 0.133 | 0.955 | 0.382 | 0.392 | 0.948 |
| T2 | 0.854 | 0.005 | 0.983 | 0.060 | 0.538 | 0.209 | 0.938 | 0.429 | 0.465 | 0.986 |
| T3 | 0.795 | 0.009 | 0.966 | 0.051 | 0.478 | 0.165 | 0.957 | 0.401 | 0.445 | 0.975 |
| T4 | 0.767 | 0.005 | 0.974 | 0.048 | 0.463 | 0.179 | 0.930 | 0.385 | 0.460 | 0.979 |
| Humic Acid Application Rate /(g/kg) | Retained Water Content /(θr (cm3/cm3)) | Saturated Soil Water Content (θs/(cm3/cm3)) | Reciprocal of Air-Entry /(α (1/cm)) | Shape Factor/(n) | Saturated Hydraulic Conductivity /(Ks (cm/min)) |
|---|---|---|---|---|---|
| CK | 0.051 ± 0.0020 b | 0.362 ± 0.0053 b | 0.140 ± 0.0056 a | 1.510 ± 0.1127 d | 0.040 ± 0.0045 a |
| 1% | 0.052 ± 0.0018 b | 0.366 ± 0.0199 b | 0.116 ± 0.0213 ab | 1.800 ± 0.1044 bc | 0.033 ± 0.0036 b |
| 2% | 0.048 ± 0.0008 c | 0.373 ± 0.0061 bc | 0.116 ± 0.0062 ab | 1.700 ± 0.0624 cd | 0.031 ± 0.0034 b |
| 3% | 0.052 ± 0.0009 b | 0.378 ± 0.0061 bc | 0.103 ± 0.0161 bc | 2.000 ± 0.1734 ab | 0.028 ± 0.0019 bc |
| 4% | 0.059 ± 0.0007 a | 0.390 ± 0.0105 a | 0.090 ± 0.0058 c | 2.100 ± 0.2000 a | 0.025 ± 0.0005 c |
| Evaluation Indicators | Processing | ||||
|---|---|---|---|---|---|
| CK | 1% | 2% | 3% | 4% | |
| MAE (%) | 0.009 | 0.013 | 0.014 | 0.012 | 0.015 |
| RMSE (%) | 0.018 | 0.018 | 0.021 | 0.017 | 0.022 |
| D | 0.979 | 0.970 | 0.972 | 0.980 | 0.973 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Bai, Y.; Liu, X.; Wang, Y. Analysis of Water Infiltration Characteristics and Hydraulic Parameters of Sierozem Soil under Humic Acid Addition. Water 2023, 15, 1915. https://doi.org/10.3390/w15101915
Ma X, Bai Y, Liu X, Wang Y. Analysis of Water Infiltration Characteristics and Hydraulic Parameters of Sierozem Soil under Humic Acid Addition. Water. 2023; 15(10):1915. https://doi.org/10.3390/w15101915
Chicago/Turabian StyleMa, Xian, Yiru Bai, Xu Liu, and Youqi Wang. 2023. "Analysis of Water Infiltration Characteristics and Hydraulic Parameters of Sierozem Soil under Humic Acid Addition" Water 15, no. 10: 1915. https://doi.org/10.3390/w15101915
APA StyleMa, X., Bai, Y., Liu, X., & Wang, Y. (2023). Analysis of Water Infiltration Characteristics and Hydraulic Parameters of Sierozem Soil under Humic Acid Addition. Water, 15(10), 1915. https://doi.org/10.3390/w15101915





