Modelling and Numerical Simulation Approaches to the Stage–Discharge Relationships of the Lansheng Bridge
Abstract
:1. Introduction
2. Study Area
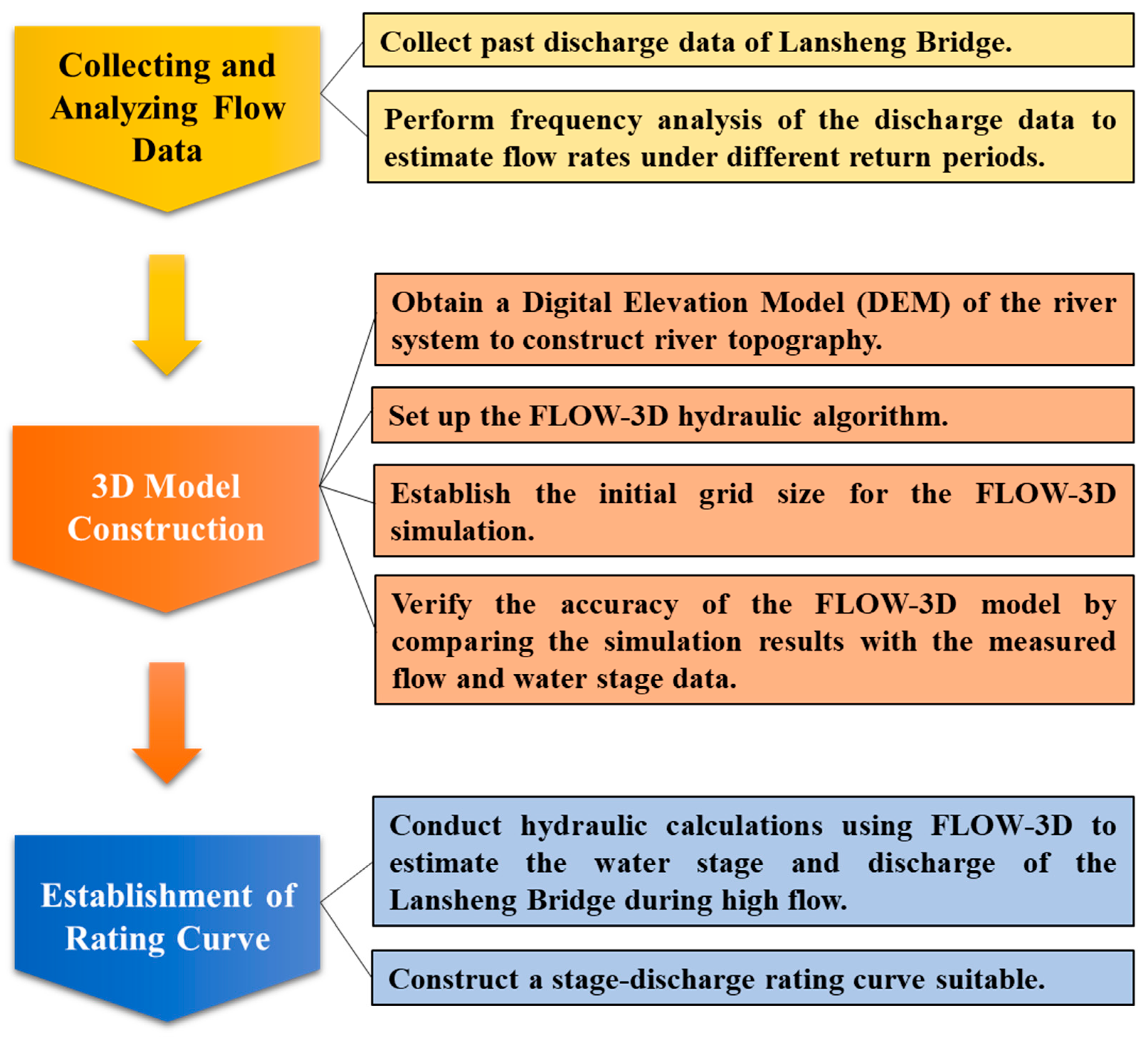
3. Three-Dimensional Hydraulic Calculation
3.1. FLOW-3D
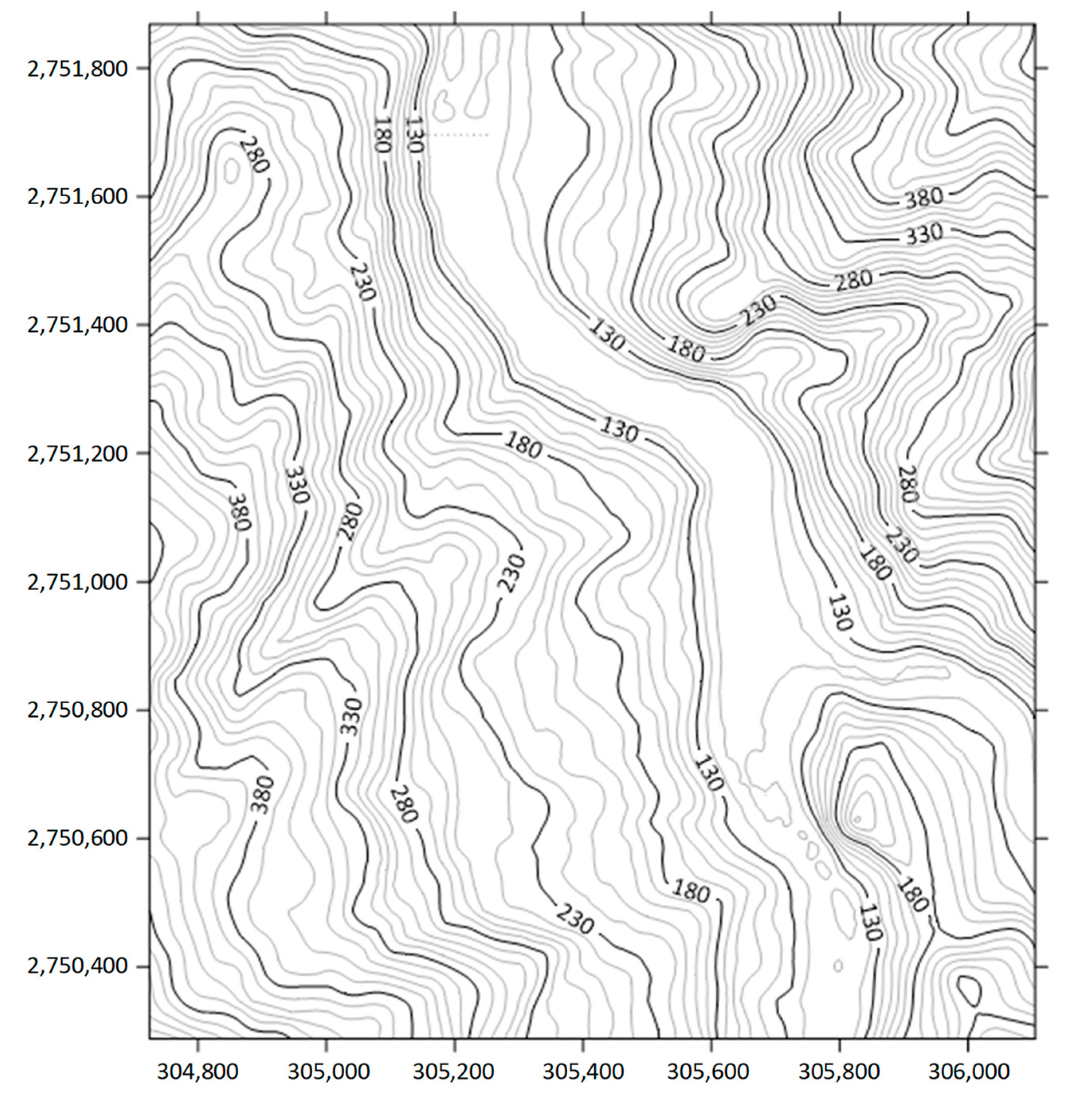
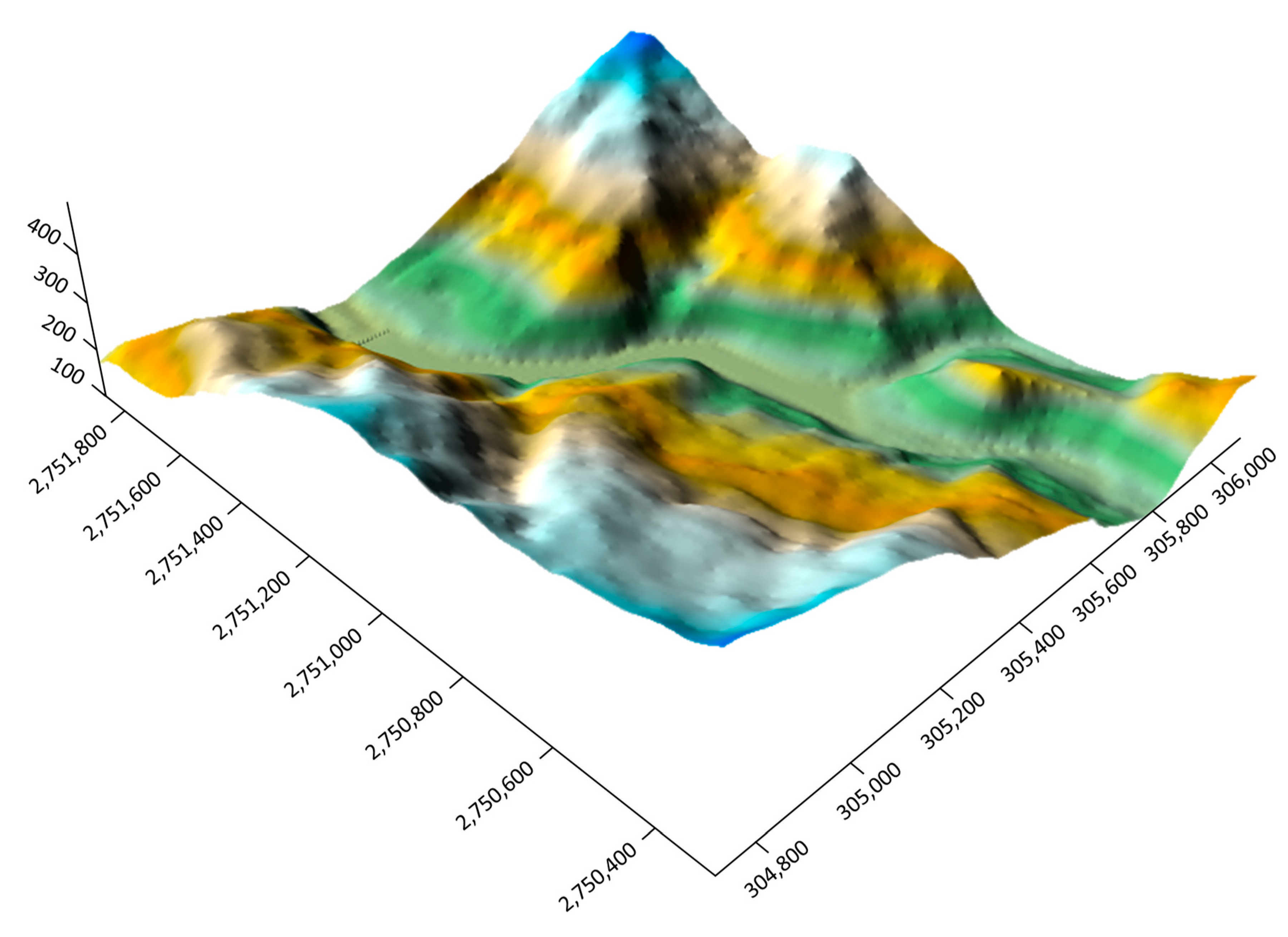
3.2. River Topography Data
3.3. Frequency Analysis for Determining the Discharges
3.4. Establishment of 3D Model
4. Simulation Results
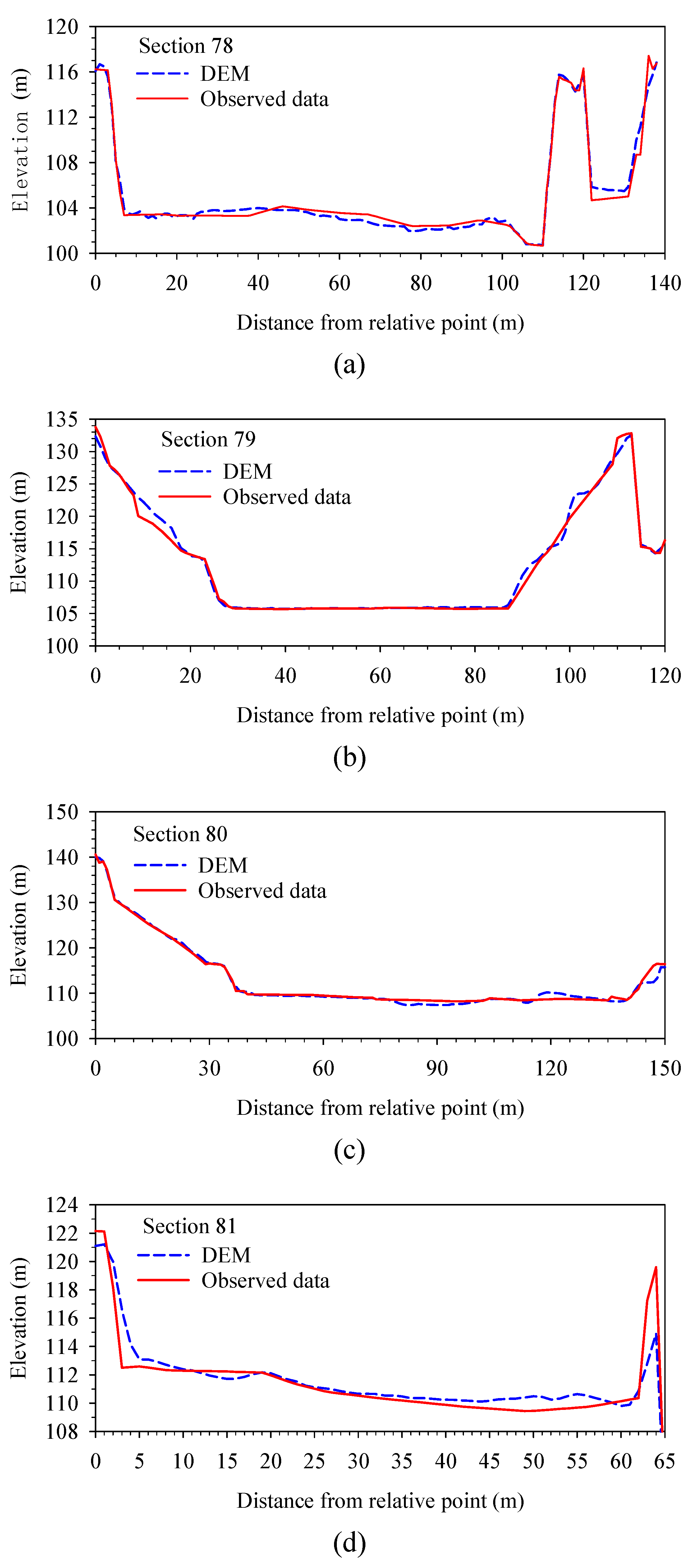
4.1. Creation of River Topography
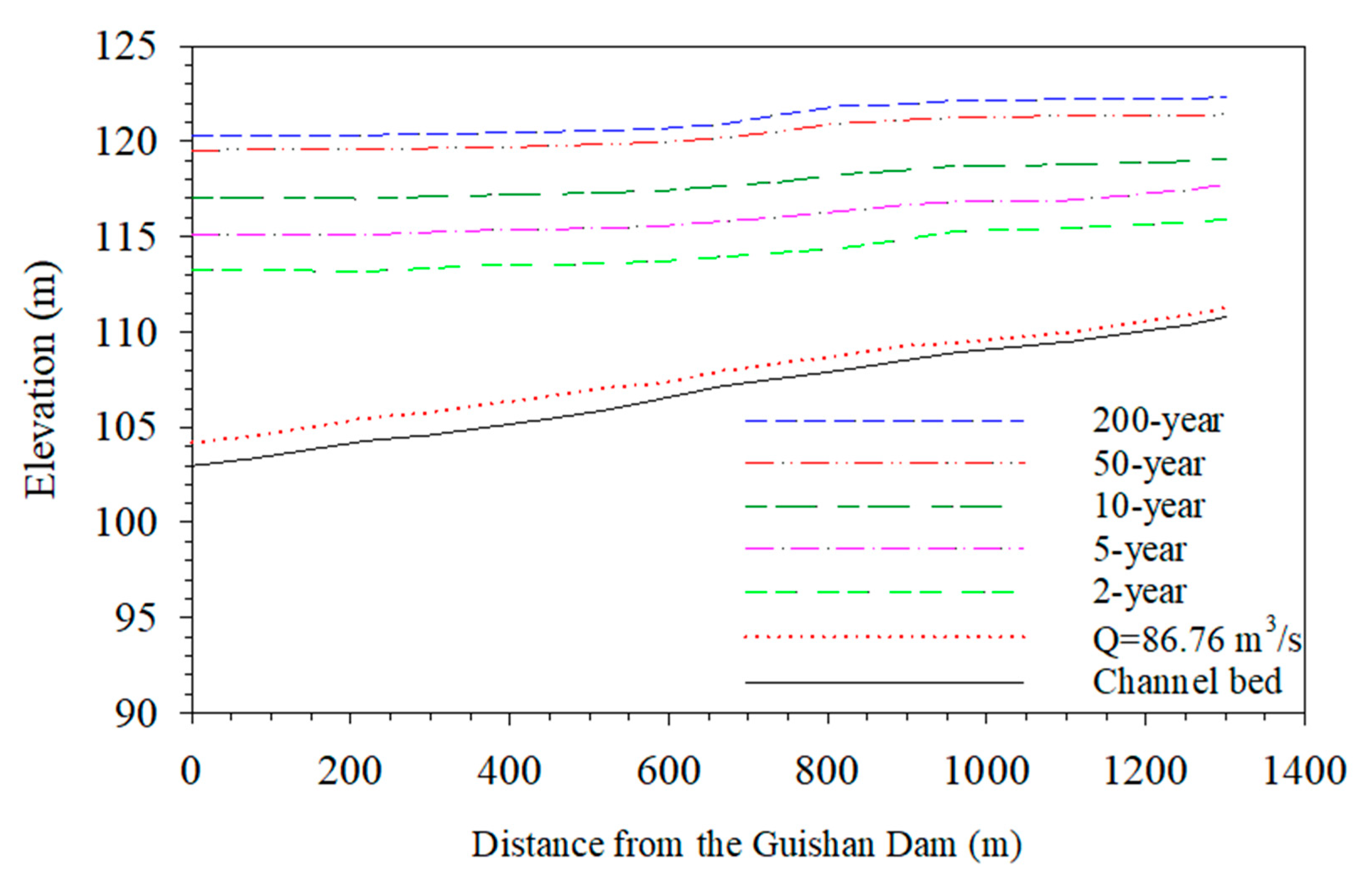
4.2. Estimation of Discharges in Different Return Periods
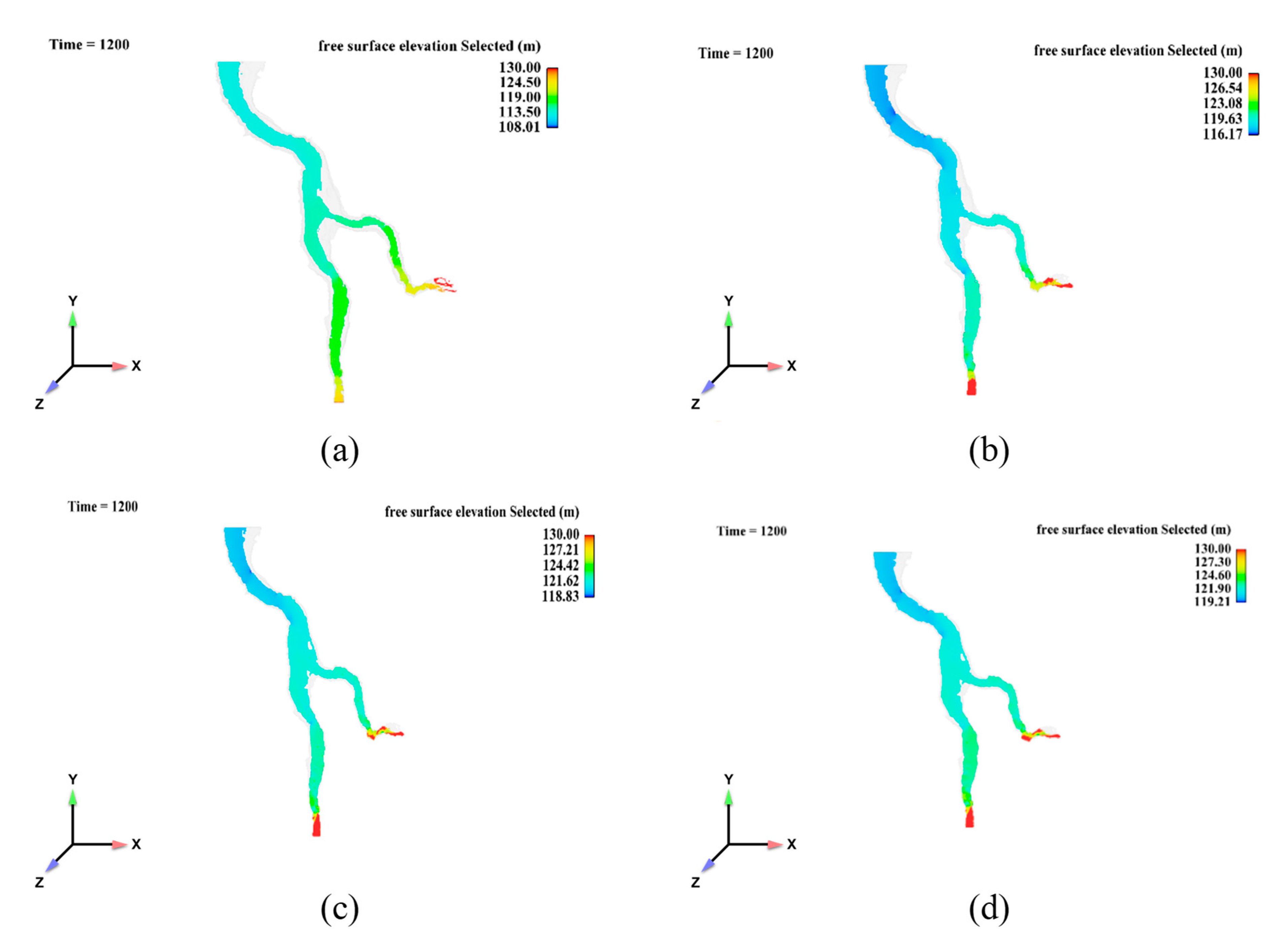
4.3. Estimate Water Level with FLOW-3D
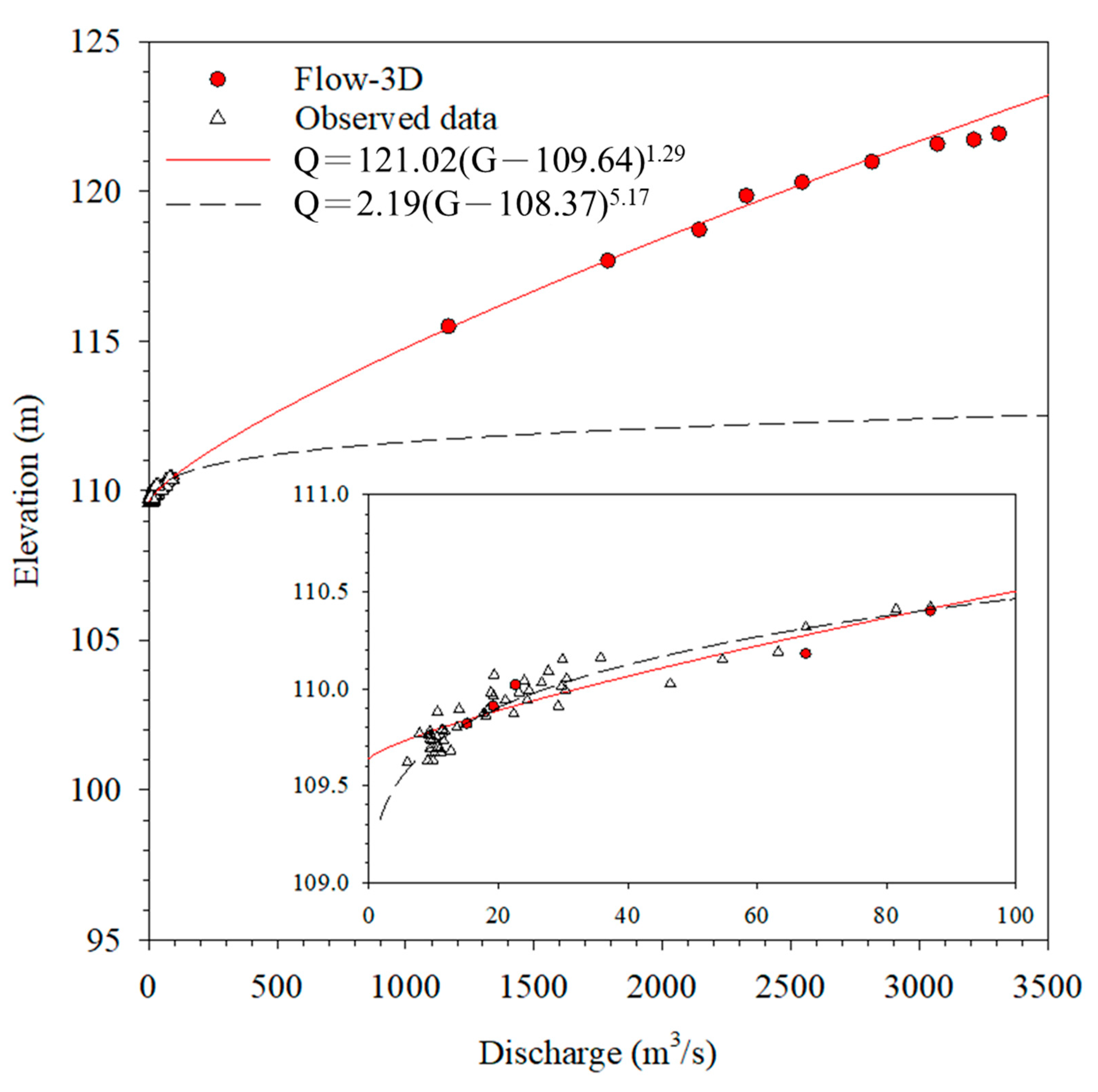
4.4. Rating Curve Establishment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Y.C. Flood discharge measurement of a mountain river–Nanshih River in Taiwan. Hydrol. Earth Syst. Sci. 2013, 17, 1951–1962. [Google Scholar] [CrossRef] [Green Version]
- Taipei Water Management Office. Hydrological System Measurement of the Area Protected by the Taipei Water Management Office (2022–2023); Taipei Water Management Office: New Taipei City, Taiwan, 2022. [Google Scholar]
- Herschy, R.W. Streamflow Measurement; Routledge: New York, NY, USA, 2009. [CrossRef]
- Bijankhan, M.; Ferro, V. Dimensional analysis and stage-discharge relationship for weirs: A review. J. Agric. Eng. 2017, 48, 1–11. [Google Scholar] [CrossRef]
- Huţanu, E.; Mihu-Pintilie, A.; Urzica, A.; Paveluc, L.E.; Stoleriu, C.C.; Grozavu, A. Using 1D HEC-RAS modeling and LiDAR data to improve flood hazard maps accuracy: A case study from Jijia Floodplain (NE Romania). Water 2020, 12, 1624. [Google Scholar] [CrossRef]
- Patel, D.P.; Ramirez, J.A.; Srivastava, P.K.; Bray, M.; Han, D. Assessment of flood inundation mapping of Surat city by coupled 1D/2D hydrodynamic modeling: A case application of the new HEC-RAS 5. Nat. Hazards 2017, 89, 93–130. [Google Scholar] [CrossRef] [Green Version]
- Quirogaa, V.M.; Kurea, S.; Udoa, K.; Manoa, A. Application of 2D numerical simulation for the analysis of the February 2014 Bolivian Amazonia flood: Application of the new HEC-RAS version 5. Ribagua 2016, 3, 25–33. [Google Scholar] [CrossRef] [Green Version]
- Erena, S.H.; Worku, H.; De Paola, F. Flood hazard mapping using FLO-2D and local management strategies of Dire Dawa city, Ethiopia. J. Hydrol. Reg. Stud. 2018, 19, 224–239. [Google Scholar] [CrossRef]
- Bayon, A.; Valero, D.; García-Bartual, R.; López-Jiménez, P.A. Performance assessment of OpenFOAM and FLOW-3D in the numerical modeling of a low Reynolds number hydraulic jump. Environ. Model. Softw. 2016, 80, 322–335. [Google Scholar] [CrossRef]
- Soudi, M.; Ahmadi, H.; Yasi, M.; Sibilla, S.; Fenocchi, A.; Hamidi, S.A. Investigation over the capability of MIKE 3 flow model FM to simulate the hydrodynamics and salinity distribution of hypersaline lakes: Lake Urmia (Iran) as case study. Coast. Eng. J. 2019, 61, 486–501. [Google Scholar] [CrossRef]
- Cheng, Y.; Chen, K.; Sun, H.; Zhang, Y.; Tao, F. Data and knowledge mining with big data towards smart production. J. Ind. Inf. Integr. 2018, 9, 1–13. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, G.; Wang, H.; Li, T. Evaluation of geothermal development in fractured hot dry rock based on three dimensional unified pipe-network method. Appl. Therm. Eng. 2018, 136, 219–228. [Google Scholar] [CrossRef]
- Grivalszki, P.; Fleit, G.; Baranya, S.; Józsa, J. Assessment of cfd model performance for flows around a hydraulic structure of complex geometry. Period. Polytech. Civ. Eng. 2021, 65, 109–119. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, J.; Li, T. Dam-break flows: Comparison between flow-3D, MIKE 3 FM, and analytical solutions with experimental data. Appl. Sci. 2018, 8, 2456. [Google Scholar] [CrossRef] [Green Version]
- Duguay, J.M.; Lacey, R.W.J.; Gaucher, J. A case study of a pool and weir fishway modeled with OpenFOAM and FLOW-3D. Ecol. Eng. 2017, 103, 31–42. [Google Scholar] [CrossRef]
- Mostafazadeh-Fard, S.; Samani, Z. Dissipating Culvert End Design for Erosion Control Using CFD Platform FLOW-3D Numerical Simulation Modeling. J. Pipeline Syst. Eng. Pract. 2023, 14, 04022064. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Shipkowski, S.P.; Perez-Raya, I. Precise and analytical calculation of interface surface area in sharp interfaces and multiphase modeling. Int. J. Heat Mass Transf. 2023, 202, 123683. [Google Scholar] [CrossRef]
- Lee, J.R.; Aziz MS, A.; Ishak, M.H.H.; Khor, C.Y. A review on numerical approach of reflow soldering process for copper pillar technology. Int. J. Adv. Manuf. Technol. 2022, 121, 4325–4353. [Google Scholar] [CrossRef]
- Liu, P. Computational Fluid Dynamics. In A General Theory of Fluid Mechanics; Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Sharma, M.; Garg, R.D.; Badenko, V.; Fedotov, A.; Min, L.; Yao, A. Potential of airborne LiDAR data for terrain parameters extraction. Quat. Int. 2021, 575, 317–327. [Google Scholar] [CrossRef]
- Yen, B.C. Hydraulic resistance in open channels. In Channel Flow Resistance-Centennial of Manning’s Formula; Water Resources Publications: Littleton, CO, USA, 1992; pp. 1–135. [Google Scholar]
- The 10th River Management Office. Review on the Regulation Planning of Xindian River (Lan-Sheng Bridge to Bi-Tan Weir); The 10th River Management Office: New Taipei City, Taiwan, 2017.
- Li, Q.; Peng, Y.; Wang, G.; Wang, H.; Xue, B.; Hu, X. A combined method for estimating continuous runoff by parameter transfer and drainage area ratio method in ungauged catchments. Water 2019, 11, 1104. [Google Scholar] [CrossRef] [Green Version]
- Musyoka, F.K.; Strauss, P.; Zhao, G.; Srinivasan, R.; Klik, A. Multi-step calibration approach for SWAT model using soil moisture and crop yields in a small agricultural catchment. Water 2021, 13, 2238. [Google Scholar] [CrossRef]
- Mosley, M.P.; McKerchar, A.I. Streamflow. In Handbook of Hydrology; McGraw Hill: New York, NY, USA, 1993; Volume 8, pp. 1–8. [Google Scholar]
- Braca, G. Stage-Discharge Relationships in Open Channels: Practices and Problems; Università degli Studi di Trento: Trento, Italy, 2008. [Google Scholar]
- Kisi, Ö.; Çobaner, M. Modeling River Stage-Discharge Relationships Using Different Neural Network Computing Techniques. CLEAN–Soil Air Water 2009, 37, 160–169. [Google Scholar] [CrossRef]
- Guven, A.; Aytek, A. New approach for stage–discharge relationship: Gene-expression programming. J. Hydrol. Eng.-ASCE 2009, 14, 773–893. [Google Scholar] [CrossRef]




| X | Y | Z | ||
|---|---|---|---|---|
| Block 1 | Min | 305,122 | 2,751,400 | 90 |
| Max | 305,382 | 2,751,694 | 130 | |
| Block 2 | Min | 305,482 | 2,750,620 | 90 |
| Max | 305,792 | 2,750,770 | 130 | |
| Block 3 | Min | 305,782 | 2,750,760 | 90 |
| Max | 305,972 | 2,751,200 | 130 | |
| Block 4 | Min | 305,482 | 2,750,760 | 90 |
| Max | 305,792 | 2,751,210 | 130 | |
| Block 5 | Min | 305,122 | 2,751,200 | 90 |
| Max | 305,382 | 2,751,410 | 130 | |
| Block 6 | Min | 305,372 | 2,751,200 | 90 |
| Max | 305,492 | 2,751,410 | 130 | |
| Block 7 | Min | 305,482 | 2,751,200 | 90 |
| Max | 305,792 | 2,751,410 | 130 | |
| Block 8 | Min | 305,482 | 2,750,590 | 90 |
| Max | 305,882 | 2,750,750 | 130 | |
| Block 9 | Min | 305,962 | 2,750,430 | 90 |
| Max | 306,182 | 2,750,960 | 130 | |
| Block 10 | Min | 306,172 | 2,750,430 | 90 |
| Max | 306,332 | 2,750,600 | 130 |
| Year | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Discharge (m3/s) | 2094 | 1712 | 1867 | 1169 | 617 | 624 | 375 | 1559 | 601 | 503 | 2255 |
| Return Period (Year) | 2 | 5 | 10 | 15 | 25 | 50 | 100 | 150 | 200 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Discharge (m3/s) | Nanshih River | 1166 | 1788 | 2143 | 2327 | 2544 | 2816 | 3070 | 3212 | 3310 |
| Tonghou River | 437 | 671 | 804 | 873 | 954 | 1056 | 1151 | 1205 | 1241 |
| Date | Observed Discharge (m3/s) | Observed Elevation (m) | Estimated Elevation (m) | Error (m) |
|---|---|---|---|---|
| 6 January 2022 | 15.11 | 109.82 | 109.78 | −0.04 |
| 10 February 2022 | 19.22 | 109.91 | 109.85 | −0.06 |
| 9 June 2022 | 22.65 | 110.02 | 110.15 | +0.13 |
| 5 August 2021 | 86.76 | 110.40 | 110.36 | −0.04 |
| 18 August 2021 | 67.49 | 110.18 | 110.21 | +0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-C.; Yang, H.-C.; Liao, Y.-J.; Chen, Y.-T. Modelling and Numerical Simulation Approaches to the Stage–Discharge Relationships of the Lansheng Bridge. Water 2023, 15, 2179. https://doi.org/10.3390/w15122179
Chen Y-C, Yang H-C, Liao Y-J, Chen Y-T. Modelling and Numerical Simulation Approaches to the Stage–Discharge Relationships of the Lansheng Bridge. Water. 2023; 15(12):2179. https://doi.org/10.3390/w15122179
Chicago/Turabian StyleChen, Yen-Chang, Han-Chung Yang, Yi-Jiun Liao, and Yen-Tzu Chen. 2023. "Modelling and Numerical Simulation Approaches to the Stage–Discharge Relationships of the Lansheng Bridge" Water 15, no. 12: 2179. https://doi.org/10.3390/w15122179
APA StyleChen, Y.-C., Yang, H.-C., Liao, Y.-J., & Chen, Y.-T. (2023). Modelling and Numerical Simulation Approaches to the Stage–Discharge Relationships of the Lansheng Bridge. Water, 15(12), 2179. https://doi.org/10.3390/w15122179







