Novel Techniques to Study the Effect of Parapet Wall Geometry on the Performance of Piano Key Weirs
Abstract
1. Introduction
2. Techniques and Materials
2.1. Dimensionless Analysis
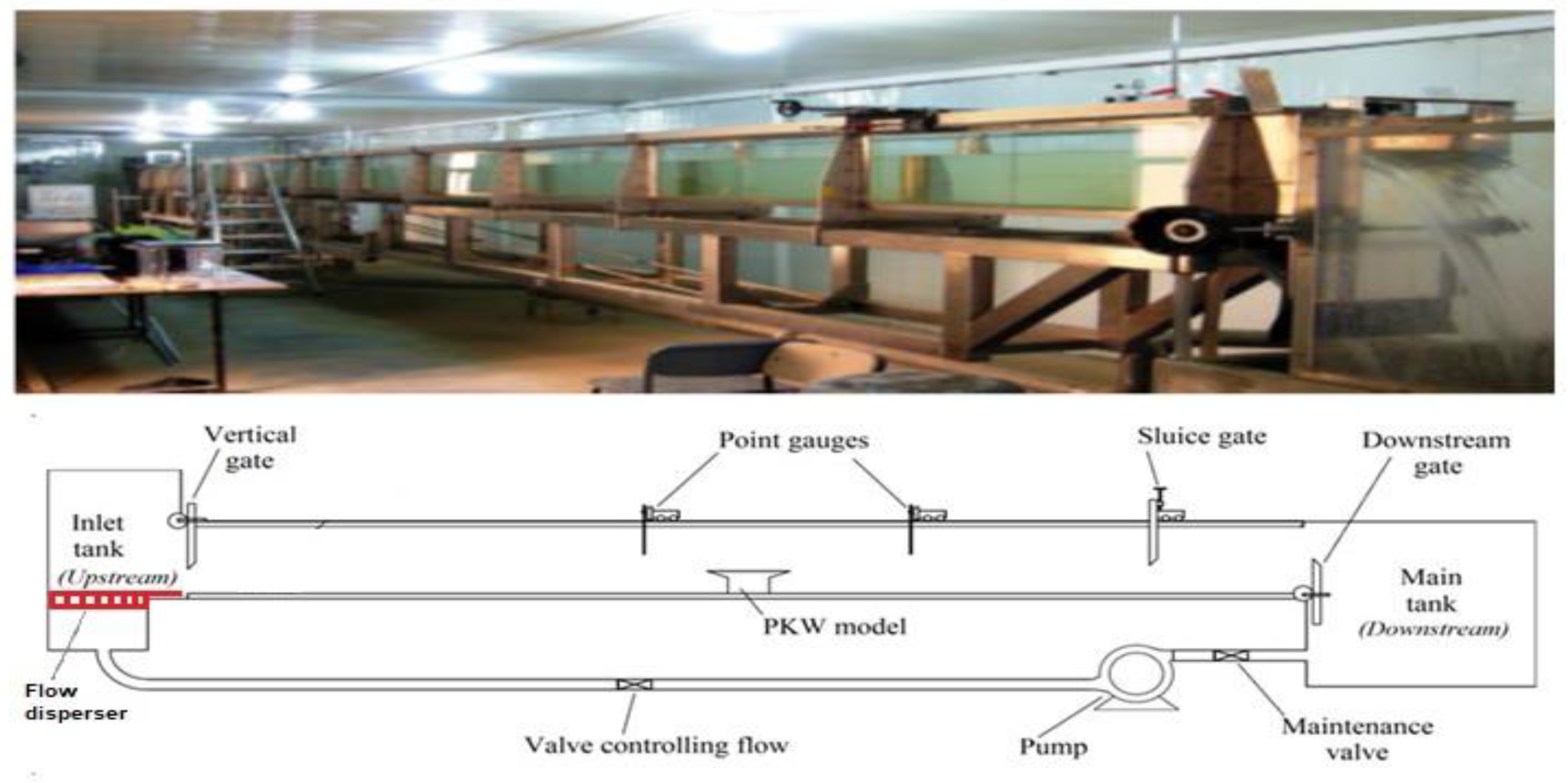
2.2. Material and Method
2.3. Experimental Process
3. Results and Discussion
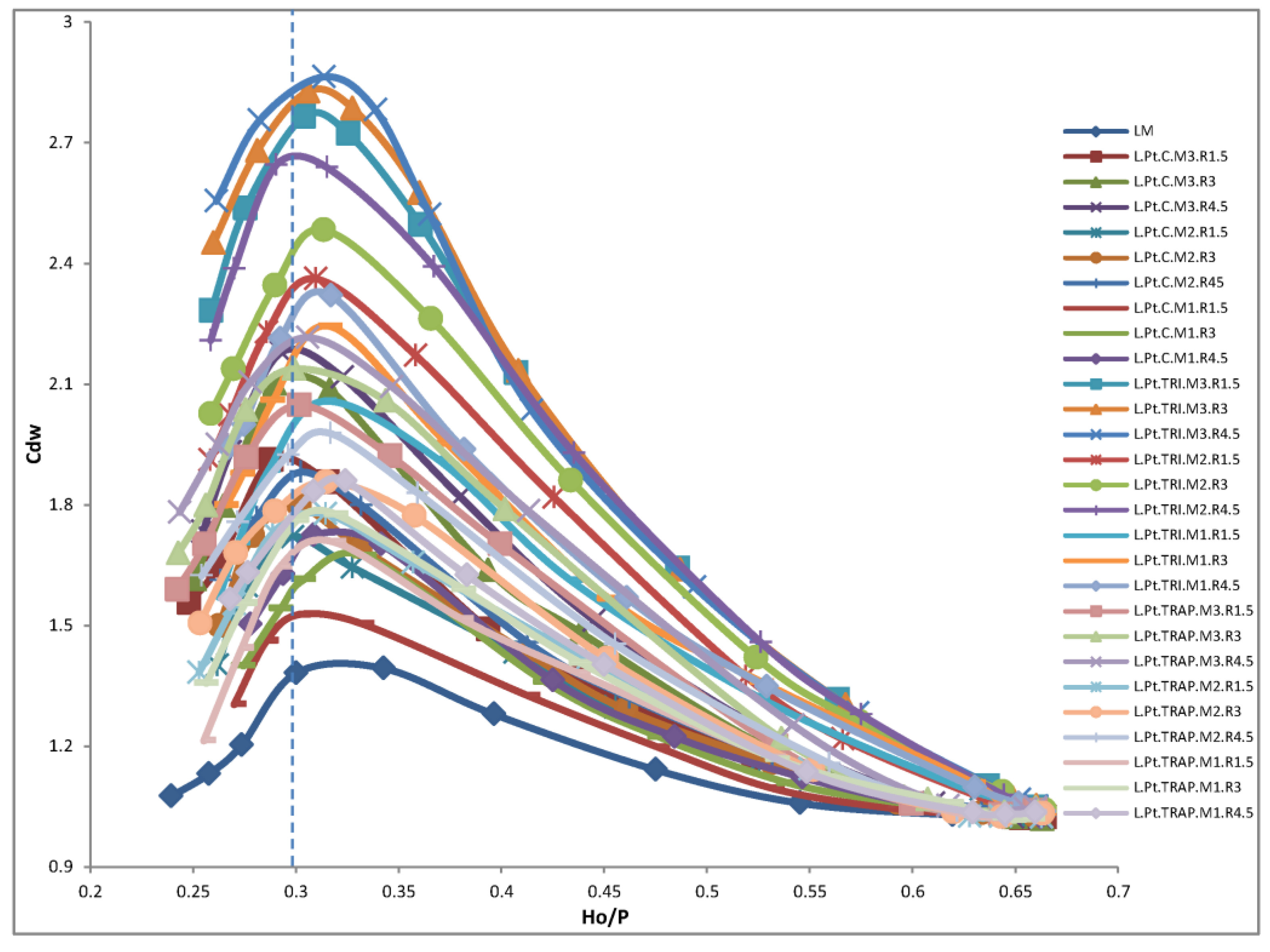
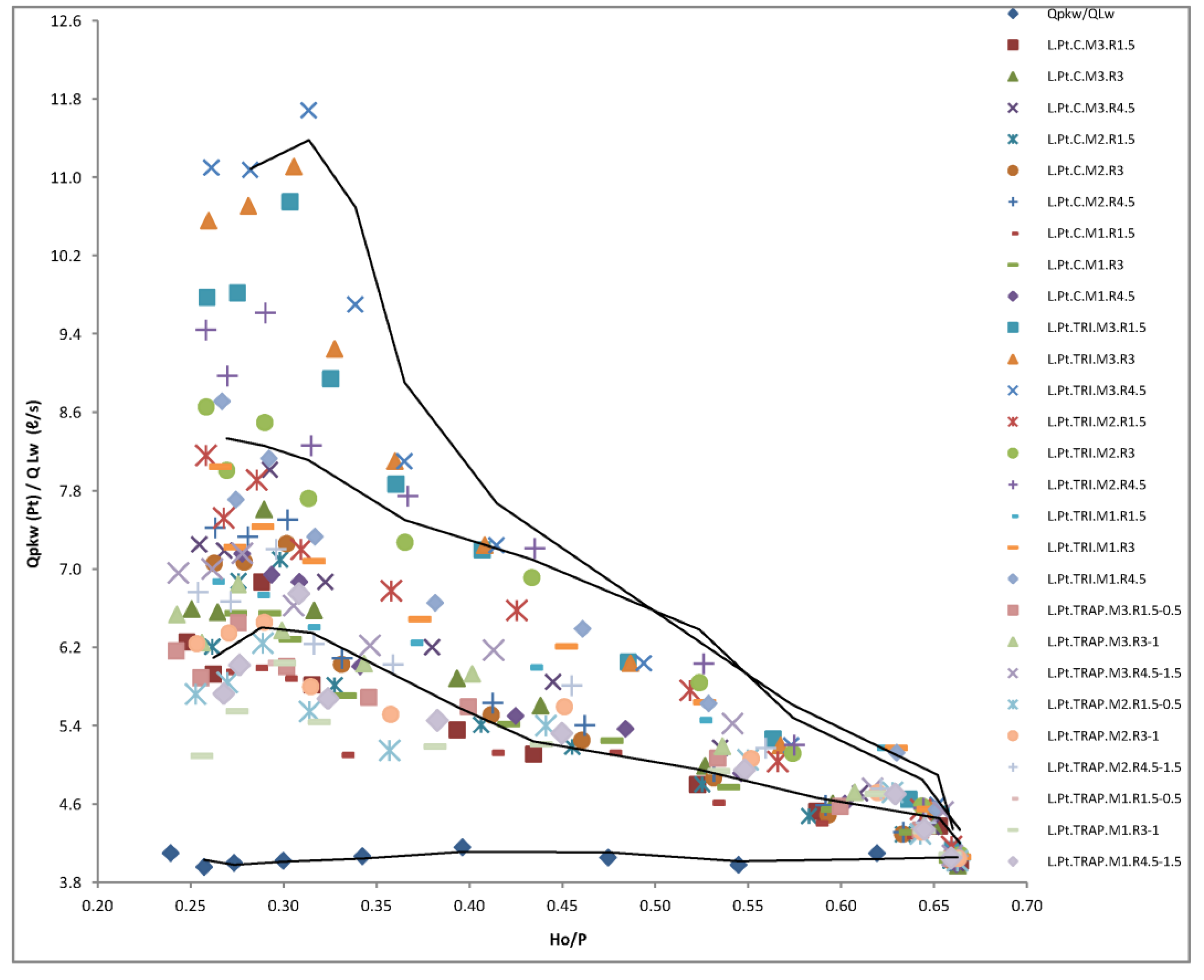
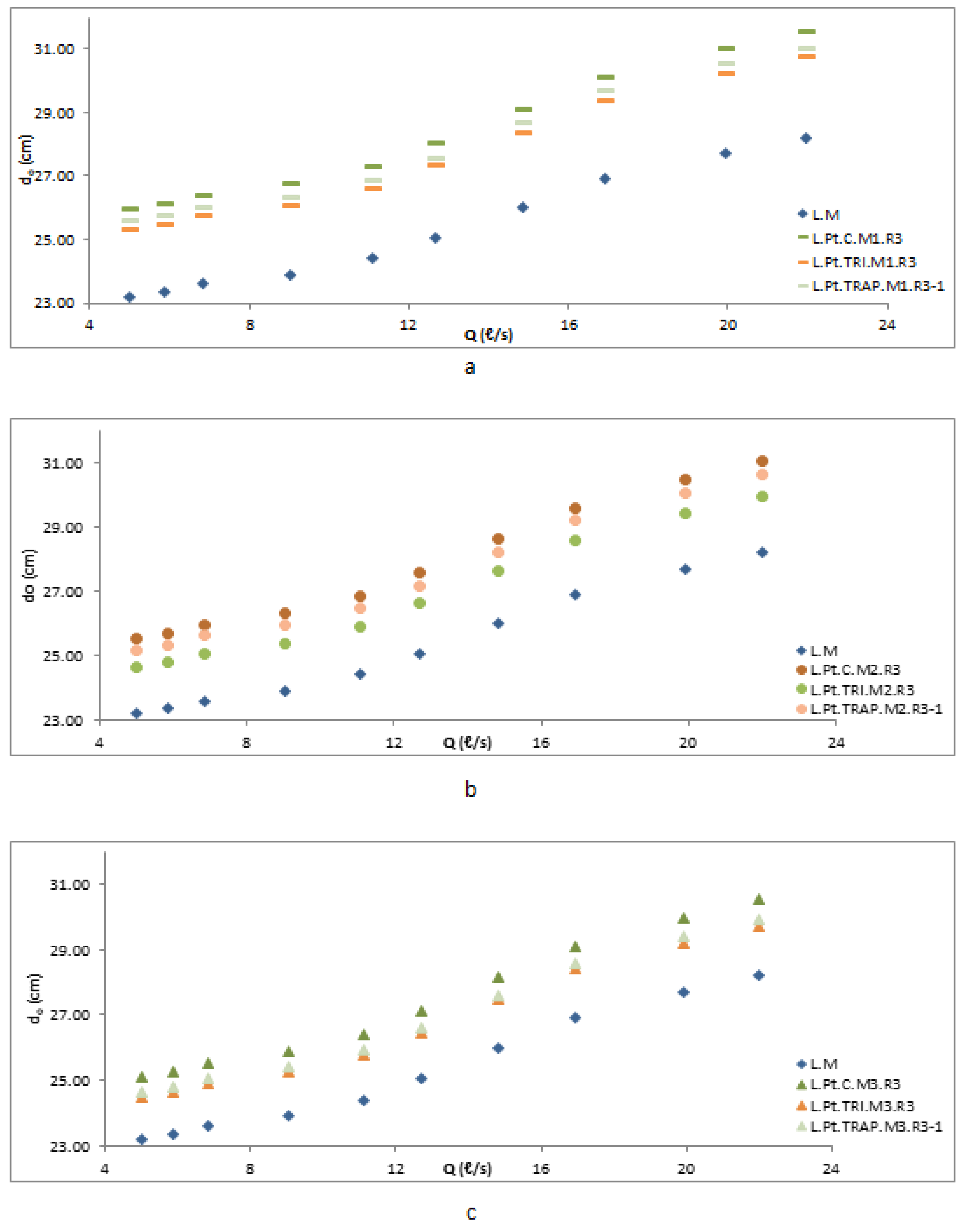
3.1. Effect of Parapet Walls on Discharge Coefficient and Performance Efficiency
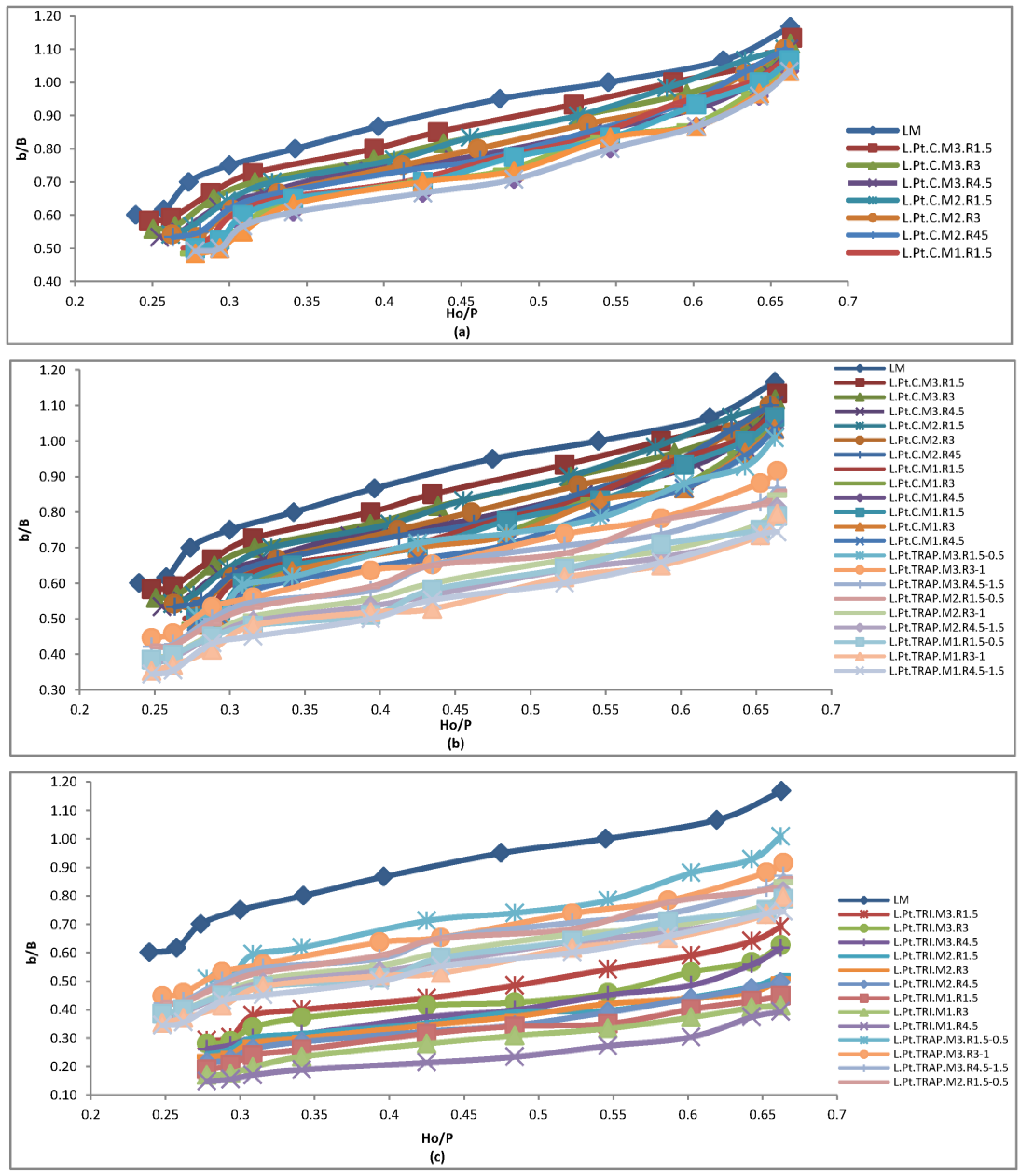
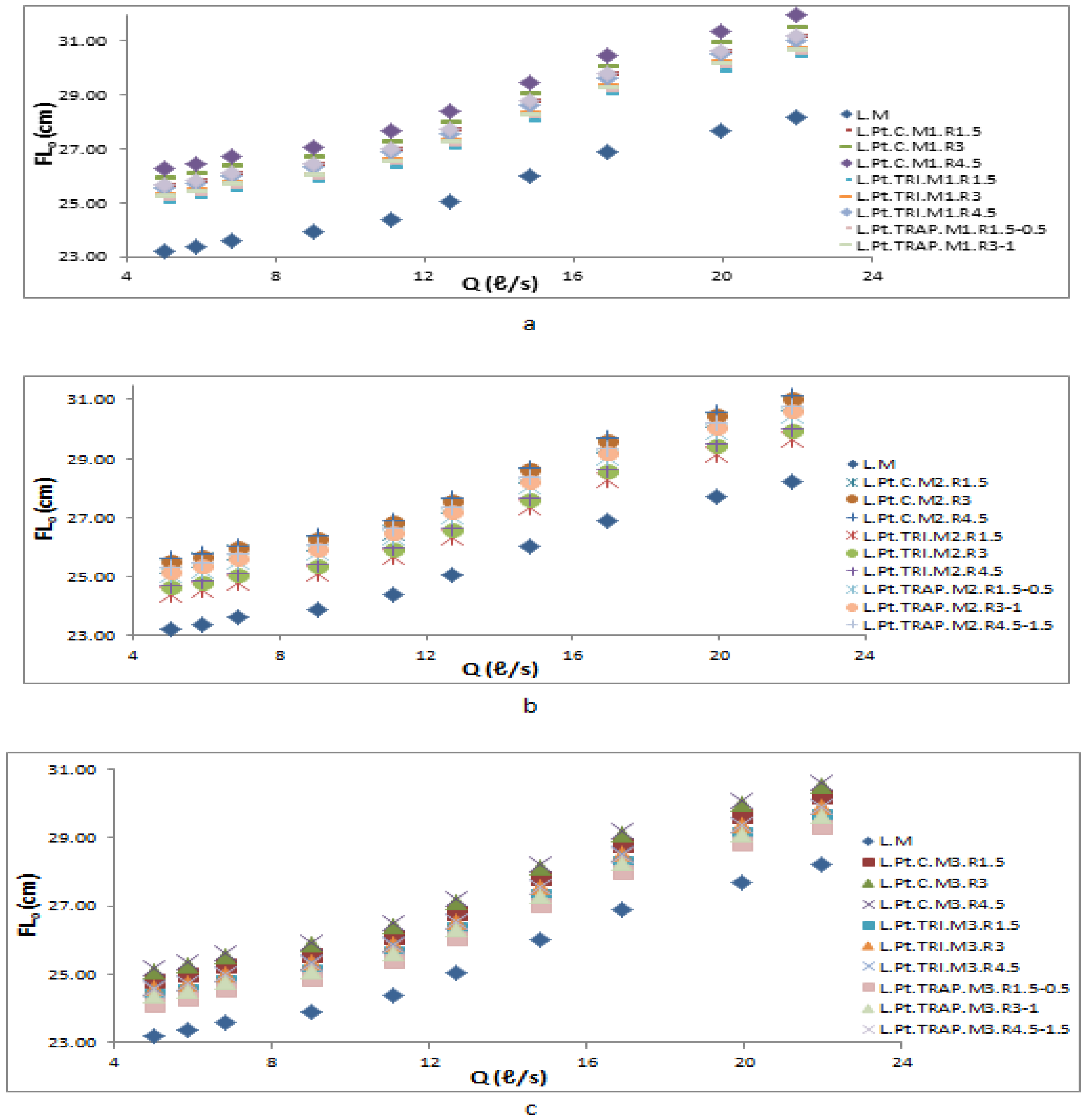
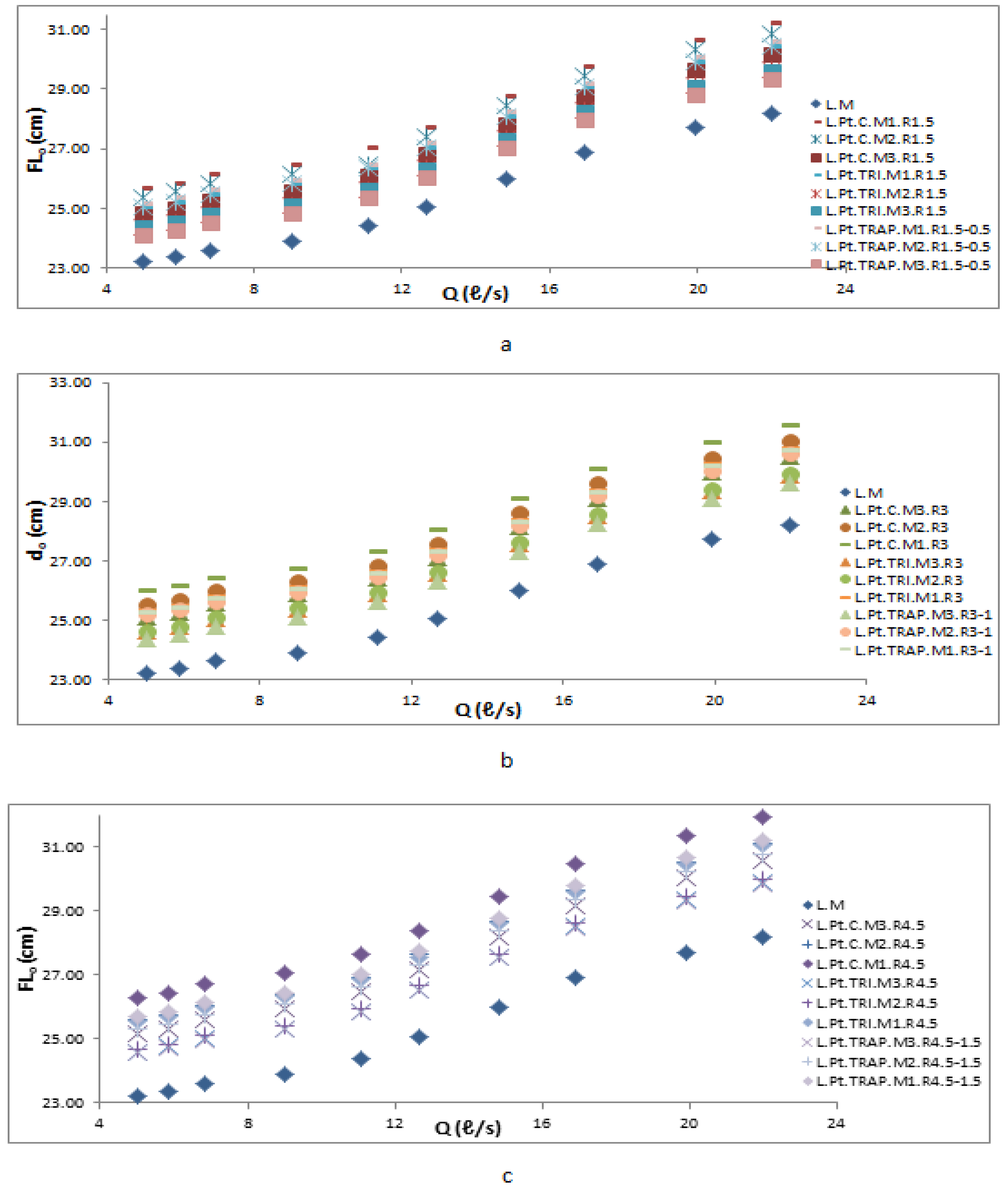
3.2. Parapet Walls Affect the Water Level and Upstream Head
3.3. Effects of Parapet Walls Height and Profile Shape (The Linearity)
3.4. Effect of the Instalment Mode and Profile Shape, Specifically the Linearity, on the Parapet Walls
3.5. Effect of the Profile Form of a Parapet Wall
4. Conclusions
- At an R/P ratio of 0.36, the transfer of mode from M1 to M3 results in a reduction of parapet wall effect on the rising total head by 32%, 28% and 33% for parapet walls with rectangular, triangular and trapezoidal profile shapes, respectively.
- When comparing the constant linearity (rectangular) profile of parapet walls with R/P = 0.36 to RPKW without parapet walls, the discharge coefficient of the weir in the M3 mode exhibited a 26–15% increase compared with the M1 and M2 situations, respectively. In the context of parapet wall variation linearity, specifically triangular and trapezoidal profiles with an R/P ratio of 0.36, the discharge coefficient of the weir in M3 mode exhibits a notable increase of 23–10% and 20–13% compared with M1 and M2 modes, respectively.
- In situations where parapet walls possess a constant linearity (rectangular) profile with R/P = 0.36, a comparison with an RPKW lacking parapet walls reveals that the weir’s discharge capacity in M3 mode is 15.6% greater than that of M1 and M2 positions. The variance of linearity between triangular and trapezoidal profile shapes is 20% and 15.6%, respectively.
- The geometric configuration of the parapet walls situated along the width of the inlet and outlet keys exerts a considerable influence on alterations in water level and discharge coefficient.
- The linearity of parapet walls is effective in the improvement of the RPKW function.
- When variations in the performance, upstream water level, and discharge coefficient (Cdw) of RPKWs are to be studied, the effects of the free flow condition must be considered.
- The novel parapet wall designs investigated in this study, along with their demonstrated impact on water level variations and discharge capacity, can contribute to enhancing the efficiency of Piano Key Weirs (PKWs). By implementing these advanced configurations, we can achieve significant improvements in water control and discharge capacity, which are critical aspects for effective water management and maximizing storage capacity.
- The value of Ho/P = 0.30 can be the typical threshold for the aerated state of the analysed PKWs. However, the aeration states may vary based on the specific weir geometry (sensitive to weir scale and profile shape of parapet wall). The present investigation, along with previous research [28], indicates that a PKW exhibits superior aeration characteristics when compared with a labyrinth weir.
- The utilisation of 3D printing technology, specifically for models with intricate geometries, may provide a more suitable and expeditious approach to creating models for hydraulic experimental modelling.
- The optimized parapet wall configurations identified in our study can contribute to the design and operation of weirs and dams by improving their discharge capacity and overall performance efficiency.
- By reducing flow interference and enhancing weir efficiency, these findings can help mitigate the risk of collapses resulting from inadequate discharge capacities.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lantz, W.; Crookston, B.M.; Palermo, M. Apron and cutoff wall scour protection for piano key weirs. Water 2021, 13, 2332. [Google Scholar] [CrossRef]
- Anderson, R.M.; Tullis, B.P. Piano Key Weir Hydraulics and Labyrinth Weir Comparison. J. Irrig. Drain. Eng. 2013, 139, 246–253. [Google Scholar] [CrossRef]
- Bekheet, A.A.; AboulAtta, N.M.; Saad, N.Y.; El-Molla, D.A. Effect of the shape and type of piano key weirs on the flow efficiency. Ain Shams Eng. J. 2022, 13, 101620. [Google Scholar] [CrossRef]
- Safarzadeh, A.; Noroozi, B. 3D Hydrodynamics of Trapezoidal Piano Key Spillways. Int. J. Civ. Eng. 2017, 15, 89–101. [Google Scholar] [CrossRef]
- Bhukya, R.K.; Pandey, M.; Valyrakis, M.; Michalis, P. Discharge Estimation over Piano Key Weirs: A Review of Recent Developments. Water 2022, 14, 3029. [Google Scholar] [CrossRef]
- Oertel, M.; Shen, X. 3D Printing Technique for Experimental Modeling of Hydraulic Structures: Exemplary Scaled Weir Models. Water 2022, 14, 2153. [Google Scholar] [CrossRef]
- Belzner, F.; Merkel, J.; Gebhardt, M.; Thorenz, C. Piano Key and Labyrinth Weirs at German waterways: Recent and future research of the BAW. In Labyrinth Piano Key Weirs III—PKW 2017; CRC Press: Boca Raton, FL, USA, 2017; pp. 167–174. [Google Scholar]
- Ouamane, A.; Lempérière, F. Design of a new economic shape of weir. In International Symposium on Dams in the Societies of the 21st Century; CRC Press: Boca Raton, FL, USA, 2006; Volume 1, pp. 463–470. [Google Scholar]
- Machiels, O. Experimental study of the hydraulic behaviour of Piano Key Weirs. Ph.D. Thesis, University of Liege, Liège, Belgium, 2012. [Google Scholar]
- Anderson, R.; Tullis, B. Influence of Piano KeyWeir geometry on discharge. In Labyrinth and Piano Key Weirs; CRC Press: Boca Raton, FL, USA, 2011; pp. 75–80. [Google Scholar]
- Anderson, R.M.; Tullis, B.P. Comparison of Piano Key and Rectangular Labyrinth Weir Hydraulics. J. Hydraul. Eng. 2012, 138, 358–361. [Google Scholar] [CrossRef]
- Kabiri-Samani, A.; Javaheri, A. Discharge coefficients for free and submerged flow over Piano Key weirs. J. Hydraul. Res. 2012, 50, 114–120. [Google Scholar] [CrossRef]
- Leite Ribeiro, M.; Bieri, M.; Boillat, J.-L. Hydraulic capacity improvement of existing spillways—Design of a piano key weirs. In Proceedings of the Proceedings (on CD) of the 23rd Congress of the Int. Commission on Large Dams CIGB-ICOLD, Brasilia, Brazil, 25–29 May 2009; pp. 100–118. [Google Scholar]
- Machiels, O.; Erpicum, S.; Archambeau, P.; Dewals, B.; Pirotton, M. Parapet Wall Effect on Piano Key Weir Efficiency. J. Irrig. Drain. Eng. 2013, 139, 506–511. [Google Scholar] [CrossRef]
- Erpicum, S.; Archambeau, P.; Dewals, B.; Pirotton, M. Overview of design and construction of 11 Piano Key Weirs spillways developed in France by EDF from 2003 to 2016. In Labyrinth and Piano Key Weirs III; CRC Press: Boca Raton, FL, USA, 2017; pp. 27–36. [Google Scholar]
- Hu, H.; Qian, Z.; Yang, W.; Hou, D.; Du, L. Numerical study of characteristics and discharge capacity of piano key weirs. Flow Meas. Instrum. 2018, 62, 27–32. [Google Scholar] [CrossRef]
- Bilhan, O.; Aydin, M.C.; Emiroglu, M.E.; Miller, C.J. Experimental and CFD Analysis of Circular Labyrinth Weirs. J. Irrig. Drain. Eng. 2018, 144, 04018007. [Google Scholar] [CrossRef]
- Leite Ribeiro, M.; Bieri, M.; Boillat, J.L.; Schleiss, A.J.; Singhal, G.; Sharma, N. Discharge Capacity of Piano Key Weirs. J. Hydraul. Eng. 2012, 138, 199–203. [Google Scholar] [CrossRef]
- Haghnazar, H.; Saneie, M. Impacts of pit distance and location on river sand mining management. Model. Earth Syst. Environ. 2019, 5, 1463–1472. [Google Scholar] [CrossRef]
- Ettema, R.; Arndt, R.; Roberts, P.; Wahl, T. Hydraulic Modeling; Amer Society of Civil Engineers: Reston, VA, USA, 2013; ISBN 0-7844-0415-1. [Google Scholar]
- Monjezi, R.; Heidarnejad, M.; Masjedi, A.; Purmohammadi, M.H.; Kamanbedast, A. Laboratory investigation of the Discharge Coefficient of flow in arced labyrinth weirs with triangular plans. Flow Meas. Instrum. 2018, 64, 64–70. [Google Scholar] [CrossRef]
- Pfister, M.; Capobianco, D.; Tullis, B.; Schleiss, A.J. Debris-Blocking Sensitivity of Piano Key Weirs under Reservoir-Type Approach Flow. J. Hydraul. Eng. 2013, 139, 1134–1141. [Google Scholar] [CrossRef]
- Erpicum, S.; Tullis, B.P.; Lodomez, M.; Archambeau, P.; Dewals, B.J.; Pirotton, M. Scale effects in physical piano key weirs models. J. Hydraul. Res. 2016, 54, 692–698. [Google Scholar] [CrossRef]
- Novak, P.; Moffat, A.I.B.; Nalluri, C.; Narayanan, R.A. Hydraulic Structures, 4th ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Kheir-Abadi, M.A.; Moghadam, M.K.; Sabzevari, T.; Ghadampour, Z. An experimental study of the effects of the parapet walls geometry on the discharge coefficient of trapezoidal piano key weirs. Flow Meas. Instrum. 2020, 73, 101742. [Google Scholar] [CrossRef]
- Denys, F.J.M.; Basson, G.R. Unsteady Hydrodynamic Behavior at Piano Key Weirs. J. Hydraul. Eng. 2020, 146, 04020028. [Google Scholar] [CrossRef]
- Laiadi, A.; Athmani, B.; Belaabed, F.; Ouamane, A. The effect of the geometric shape of the alveoli on the performance of Piano Key Weirs. In Labyrinth and Piano Key Weirs III—PKW 2017; CRC Press: Boca Raton, FL, USA, 2017; pp. 93–100. [Google Scholar]
- Crookston, B.M.; Tullis, B.P. Hydraulic Design and Analysis of Labyrinth Weirs. I: Discharge Relationships. J. Irrig. Drain. Eng. 2013, 139, 363–370. [Google Scholar] [CrossRef]
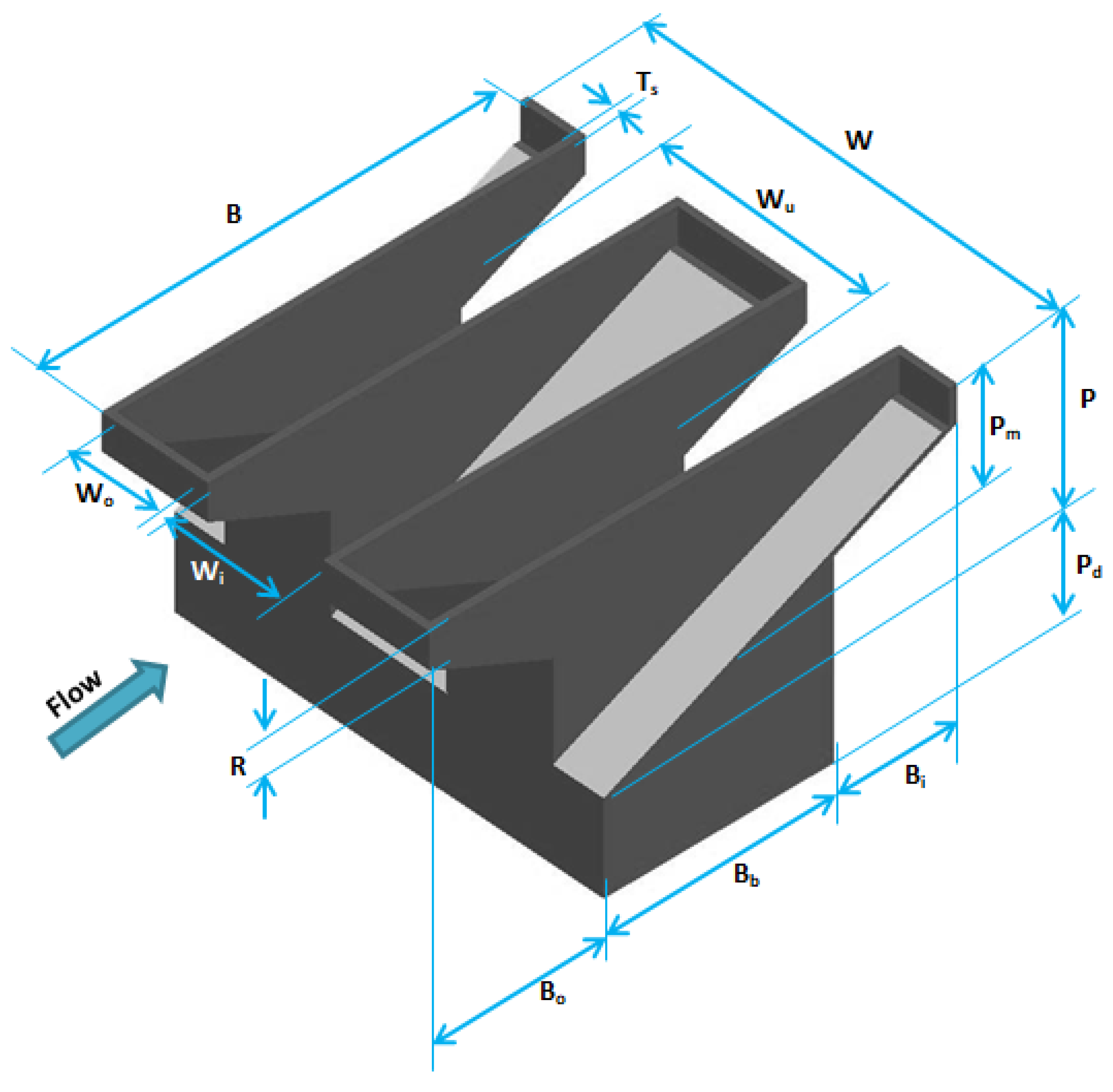
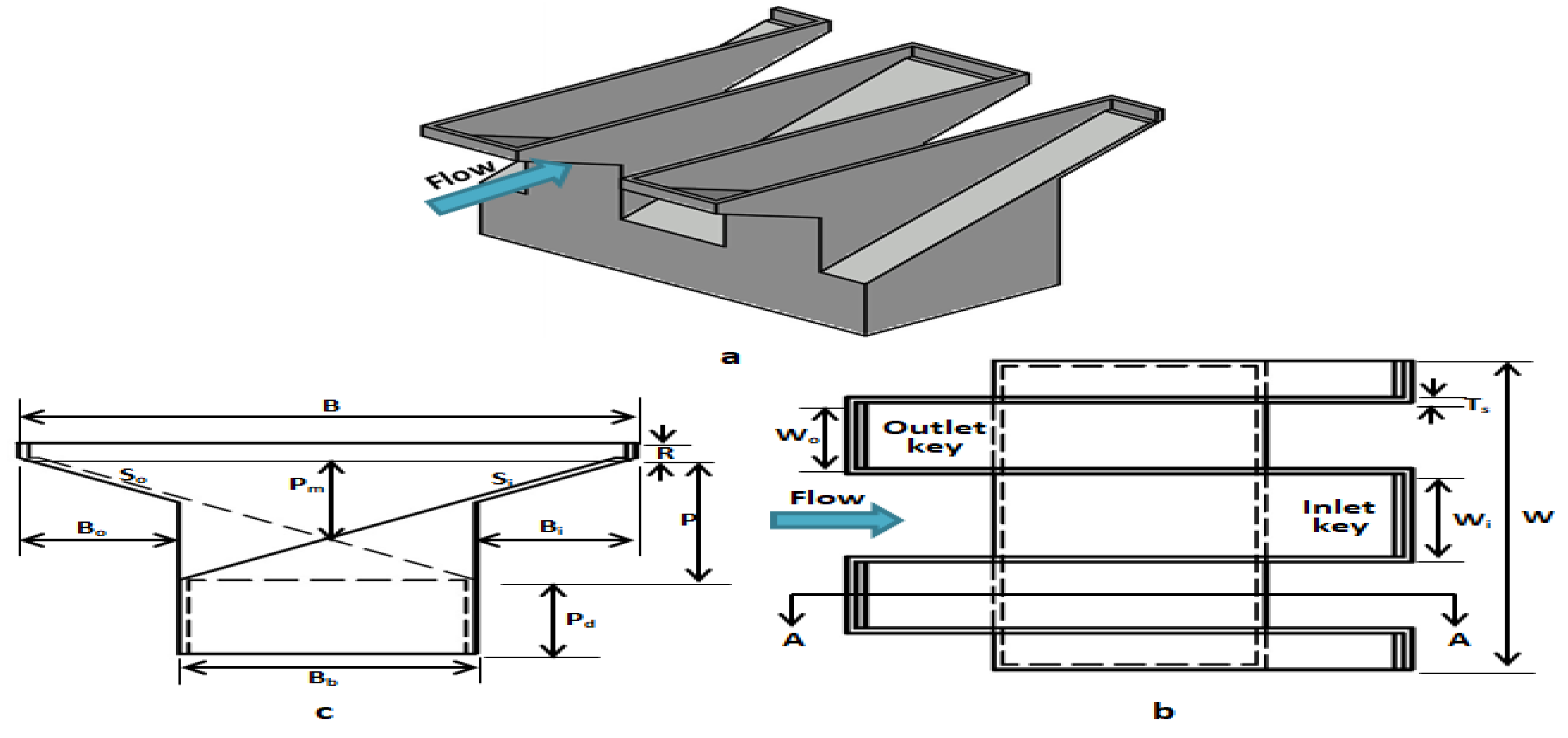






| Parameter | Explanation |
|---|---|
| Wi, Wo | Key widths for inlets and outlets (m) |
| W | Total PKW width (m) |
| Wu | Width of Cycle (m) |
| Wp | ‘Parapet wall’ lengths for key inlets and outlets (m) |
| B | Upstream–downstream length of a weir (m) |
| Bb | Length of weir foot (m) |
| Bi, Bo | Upstream/downstream overhang lengths (m) |
| Bp | Length of parapet wall from upstream to downstream (m) |
| L | Developed crown length in its entirety (m) |
| P | Weir height (m) |
| Pd | Dam height (m) |
| Ts | Weir wall thickness (distance of its peak between either side) (m) |
| R | Height of a parapet wall (m) |
| N | Number of PKW units (cycles) (constant) |
| Ho | Total head at upstream (m) |
| ho | Upstream head at free flow (m) |
| h1 | Water depth over the upstream peak of the PKW (m) |
| Q | Discharge (m3/s) |
| V | PKW upstream flow velocity (m/s) |
| g | Gravity acceleration (m/s2) |
| So, Si | Inlet and outlet apron key slopes (m/m) |
| σ | Surface tension (N/ m) |
| μ | Water viscosity (kg/ms) |
| ρ | Density of water (kg/m3) |
| Cdw | Coefficient of discharge |
| Re | Reynolds number |
| We | Weber number |
| R/P | Height ratio of the parapet wall and PKW |
| R/Bp | (Sp) Parapet wall height-to-upstream–downstream length ratio |
| Ho/P | Total upstream head/PKW height ratio |
| b/B | Flow interference length to upstream–downstream length ratio |
| Ho/R | Ratio of the total upstream head to the parapet wall’s height |
| P (cm) | Wi (cm) | Wo (cm) | B (cm) | L (cm) | Mode | R (cm) | Parapet Wall Shape Profile |
|---|---|---|---|---|---|---|---|
| 7.6 | 6.44 | 8.06 | 30.3 | 152.2 | M1, M2, M3 | 1.5, 3, 4.5 | Rectangular, Triangular, Trapezoidal |
| Weir and Parapet Walls | Abbreviation |
|---|---|
| Lemperer model | L.M. |
| Lemperer model with parapet wall type rectangular (nonconstant/slope linearity) | L.Ppt.C. |
| Lemperer model with rectangular parapet wall (constant/nonslope linearity) | L.Ppt.TRI. |
| Lemperer model with trapezoidal parapet wall (nonconstant/slope linearity) | L.Ppt.TRAP. |
| Parapet walls put over the PKW’s crest | M1 |
| Parapet walls above PKW sides and input keys | M2 |
| PKWs have side parapet walls only | M3 |
| Height of parapet walls = 1.5 cm (R1) | R1.5 |
| Height of parapet walls = 3 cm (R2) | R3 |
| Height of parapet walls = 4.5 cm (R3) | R4.5 |
| Parapet Profile Shape | Ratio of Height (R/P) | Installation Mode % | ||
|---|---|---|---|---|
| M1 | M2 | M3 | ||
| Rectangular | 0.12 | (10) 44 | (6.6) 29 | (5.5) 24 |
| 0.24 | (14.3) 63 | (11.8) 52 | (9.5) 42 | |
| 0.36 | (21) 91 | (17) 75 | (13.6) 60 | |
| Triangular | 0.12 | (4.5) 20 | (3.4) 15 | (3)13 |
| 0.24 | (7.7) 34 | (6.1) 27 | (5) 22 | |
| 0.36 | (11) 48 | (8.9) 39 | (7.3) 32 | |
| Trapezoidal | 0.12 | (5.7) 25 | (5) 22 | (3.6) 16 |
| 0.24 | (9.8) 49 | (8.5) 37 | (6.1) 27 | |
| 0.36 | (14.1) 62 | (11.8) 52 | (9.1) 40 | |
| Profile | Rectangular | Triangular | Trapezoidal | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mode | R1 | R2 | R3 | R1 | R2 | R3 | R1 | R2 | R3 | |
| % | % | % | ||||||||
| M1 | 40 | 69 | 111 | 35 | 61 | 86 | 40 | 69 | 100 | |
| M2 | 51 | 61 | 89 | 29 | 49 | 70 | 33 | 61 | 89 | |
| M3 | 38 | 70 | 79 | 25 | 41 | 58 | 24 | 45 | 67 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaker, M.; Yusuf, B.; Khassaf, S.; Mohamed, B.; Alias, N.A. Novel Techniques to Study the Effect of Parapet Wall Geometry on the Performance of Piano Key Weirs. Water 2023, 15, 2307. https://doi.org/10.3390/w15132307
Shaker M, Yusuf B, Khassaf S, Mohamed B, Alias NA. Novel Techniques to Study the Effect of Parapet Wall Geometry on the Performance of Piano Key Weirs. Water. 2023; 15(13):2307. https://doi.org/10.3390/w15132307
Chicago/Turabian StyleShaker, Majed, Badronnisa Yusuf, Saleh Khassaf, Balqis Mohamed, and Nor Azlina Alias. 2023. "Novel Techniques to Study the Effect of Parapet Wall Geometry on the Performance of Piano Key Weirs" Water 15, no. 13: 2307. https://doi.org/10.3390/w15132307
APA StyleShaker, M., Yusuf, B., Khassaf, S., Mohamed, B., & Alias, N. A. (2023). Novel Techniques to Study the Effect of Parapet Wall Geometry on the Performance of Piano Key Weirs. Water, 15(13), 2307. https://doi.org/10.3390/w15132307






