A New Model for Solving Hydrological Connectivity Inside Soils by Fast Field Cycling NMR Relaxometry
Abstract
:1. Introduction
2. Applying FFC NMR Relaxometry
3. Defining Hydrological Connectivity Inside A Soil (HCS)
4. Materials and Methods
4.1. Soils
4.2. Samples for the FFC NMR Analyses
4.3. FFC NMR Relaxometry and Data Analysis
5. Results
5.1. Plotting the Integral Curve of the Relaxogram in Gumbel’s Diagram
5.2. Characteristic Values of T1A, T1B, F(T1A), and F(T1B)
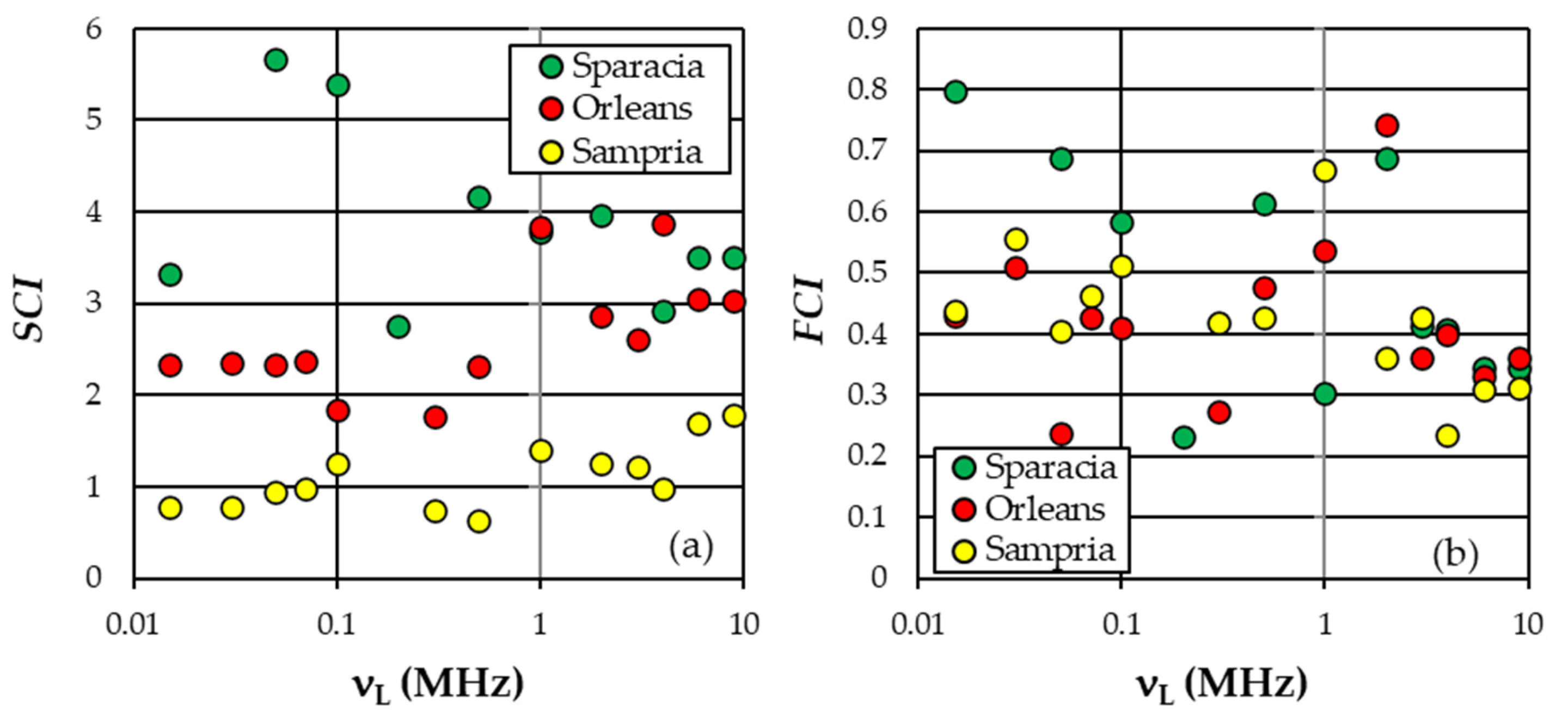
5.3. Definition of the Structural and Functional Connectivity Indices
6. Discussion
6.1. Plotting the Integral Curve of the Relaxogram in Gumbel’s Diagram
6.2. Characteristic Values of T1A, T1B, F(T1A), and F(T1B)
6.3. Definition of the Structural and Functional Connectivity Indices
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marchamalo, M.; Hooke, J.M.; Sandercock, P.J. Flow and Sediment Connectivity in Semi-arid Landscapes in SE Spain: Patterns and Controls. Land Degrad. Dev. 2016, 27, 1032–1044. [Google Scholar] [CrossRef]
- Keesstra, S.D.; Bagarello, V.; Ferro, V.; Finger, D.; Parsons, A.J. Connectivity in hydrology and sediment dynamics. Land Degrad. Dev. 2020, 31, 2525–2528. [Google Scholar] [CrossRef]
- Pringle, C. What is hydrologic connectivity and why is it ecologically important? Hydrol. Process. 2003, 17, 2685–2689. [Google Scholar] [CrossRef]
- Bracken, L.J.; Wainwright, J.; Ali, G.A.; Tetzlaff, D.; Smith, M.W.; Reaney, S.M.; Roy, A.G. Concepts of hydrological connectivity: Research approaches, Pathways and future agendas. Earth Sci. Rev. 2013, 119, 17–34. [Google Scholar] [CrossRef] [Green Version]
- Reaney, S.M.; Bracken, L.J.; Kirkby, M.J. The importance of surface controls on overland flow connectivity in semi-arid environments: Results from a numerical experimental approach. Hydrol. Process. 2014, 28, 2116–2128. [Google Scholar] [CrossRef] [Green Version]
- López-Vicente, M.; Nadal-Romero, E.; Cammeraat, E.L.H. Hydrological Connectivity Does Change Over 70 Years of Abandonment and Afforestation in the Spanish Pyrenees. Land Degrad. Dev. 2017, 28, 1298–1310. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Zhang, Y.; Dai, L.; Xie, L.; Zhao, S.; Liu, Y.; Zhang, Z. Hydrological connectivity improves soil nutrients and root architecture at the soil profile scale in a wetland ecosystem. Sci. Total. Environ. 2021, 762, 143162. [Google Scholar] [CrossRef]
- Wainwright, J.; Turnbull, L.; Ibrahim, T.G.; Lexartza-Artza, I.; Thornton, S.F.; Brazier, R.E. Linking environmental régimes, space and time: Interpretations of structural and functional connectivity. Geomorphology 2011, 126, 387–404. [Google Scholar] [CrossRef]
- Belisle, M. Measuring landscape connectivity: The challenge of behavioural landscape ecology. Ecology 2005, 86, 1988–1995. [Google Scholar] [CrossRef] [Green Version]
- Turnbull, L.; Wainwright, J.; Brazier, R.E. A conceptual framework for understanding semi-arid land degradation: Ecohydrological interactions across multiple-space and time scales. Ecohydrology 2008, 1, 23–34. [Google Scholar] [CrossRef] [Green Version]
- Uezu, A.; Metzger, J.P.; Vielliard, J.M.E. Effects of structural and functional connectivity and patch size on the abundance of seven Atlantic forest bird species. Biol. Conserv. 2005, 123, 507–519. [Google Scholar] [CrossRef]
- Bracken, J.; Croke, J. The concept of hydrological connectivity and its contribution to understanding runoff-dominated geomorphic systems. Hydrol. Process 2007, 21, 1749–1763. [Google Scholar] [CrossRef]
- Baartman, J.E.M.; Masselink, R.; Keesstra, S.D.; Temme, A.J.A.M. Linking landscape morphological complexity and sediment connectivity. Earth Surf. Process. Landf. 2013, 38, 1457–1471. [Google Scholar] [CrossRef]
- Conte, P.; Di Stefano, C.; Ferro, V.; Laudicina, V.A.; Palazzolo, E. Assessing hydrological connectivity inside a soil by fast-field-cycling nuclear magnetic resonance relaxometry and its link to sediment delivery processes. Environ. Earth Sci. 2017, 76, 526. [Google Scholar] [CrossRef]
- Conte, P.; Ferro, V. Measuring hydrological connectivity inside a soil by low field nuclear magnetic resonance relaxometry. Hydrol. Process. 2018, 32, 93–101. [Google Scholar] [CrossRef]
- Conte, P.; Ferro, V. Standardizing the use of fast-field cycling NMR relaxometry for measuring hydrological connectivity inside the soil. Magn. Reson. Chem. 2020, 58, 41–50. [Google Scholar] [CrossRef]
- Conte, P.; Ferro, V. Measuring hydrological connectivity inside soils with different texture by fast field cycling nuclear magnetic resonance relaxometry. Catena 2022, 209, 105848. [Google Scholar] [CrossRef]
- Conte, P. Environmental Applications of Fast Field-cycling NMR Relaxometry. In Field-Cycling NMR Relaxometry: Instrumentation, Model Theories and Applications; Kimmich, R., Ed.; The Royal Society of Chemistry: Croydon, UK, 2019; pp. 229–254. [Google Scholar]
- Conte, P.; Lo Meo, P. Nuclear Magnetic Resonance with Fast Field-Cycling Setup: A Valid Tool for Soil Quality Investigation. Agronomy 2020, 10, 1040. [Google Scholar] [CrossRef]
- Jaeger, F.; Bowe, S.; Schaumann, G.E. Evaluation of 1H NMR relaxometry for the assessment of pore size distribution in soil samples. Eur. J. Soil Sci. 2009, 60, 1052–1064. [Google Scholar] [CrossRef]
- Meyer, M.; Buchmann, C.; Schaumann, G.E. Determination of quantitative pore-size distribution of soils with 1H NMR relaxometry. Eur. J. Soil Sci. 2018, 69, 393–406. [Google Scholar] [CrossRef]
- Novotny, E.H.; deAzevedo, E.R.; de Godoy, G.; Consalter, D.M.; Cooper, M. Determination of soil pore size distribution and water retention curve by internal magnetic field modulation at low field 1H NMR. Geoderma 2023, 431, 116363. [Google Scholar] [CrossRef]
- Pohlmeier, A.; Haber-Pohlmeier, S.; Stapf, S. A Fast Field Cycling Nuclear Magnetic Resonance Relaxometry Study of Natural Soils. Vadose Zone J. 2009, 8, 735–742. [Google Scholar] [CrossRef]
- Pagliai, M.; Vignozzi, N. The soil pore system as an indicator of soil quality. In Sustainable Land Management-Environmental Protection. A Soil Physical Approach; Pagliai, M., Jones, R., Eds.; Advances in GeoEcology, Catena Verlag; IUSS: Reiskirchen, Germany, 2002; pp. 71–82. [Google Scholar]
- Bagarello, V.; Ferro, V. Plot-scale measurement of soil erosion at the experimental area of Sparacia (southern Italy). Hydrol. Process 2004, 18, 141–157. [Google Scholar] [CrossRef]
- Bagarello, V.; Di Piazza, G.V.; Ferro, V.; Giordano, G. Predicting unit plot soil loss in Sicily, south Italy. Hydrol. Process. 2008, 22, 586–595. [Google Scholar] [CrossRef]
- Hillel, D. Environmental Soil Physics; Academic Press: New York, NY, USA, 1998. [Google Scholar]
- Carollo, F.G.; Di Stefano, C.; Nicosia, A.; Palmeri, V.; Pampalone, V.; Ferro, V. Flow resistance in mobile bed rills shaped in soils with different texture. Eur. J. Soil Sci. 2021, 72, 2062–2075. [Google Scholar] [CrossRef]
- Di Stefano, C.; Nicosia, A.; Palmeri, V.; Pampalone, V.; Ferro, V. Rill flow resistance law under sediment transport. J. Soils Sediments 2022, 22, 334–347. [Google Scholar] [CrossRef]
- Caraballo-Arias, N.A.; Conoscenti, C.; Di Stefano, C.; Ferro, V. Testing GIS-morphometric analysis of some Sicilian badlands. Catena 2014, 113, 370–376. [Google Scholar] [CrossRef]
- Phillips, C.P. The badlands of Italy: A vanishing landscape? Appl. Geogr. 1998, 18, 243–257. [Google Scholar] [CrossRef]
- Caraballo-Arias, N.A.; Di Stefano, C.; Ferro, V. Morphological characterization of calanchi (badland) hillslope connectivity. Land Degrad. Dev. 2017, 29, 1190–1197. [Google Scholar] [CrossRef]
- Haber-Pohlmeier, S.; Stapf, S.; Pohlmeier, A. NMR Fast Field Cycling Relaxometry of Unsaturated Soils. Appl. Magn. Reson. 2014, 45, 1099–1115. [Google Scholar] [CrossRef]
- Haber-Pohlmeier, S.; Stapf, S.; Van Dusschoten, D.; Pohlmeier, A. Relaxation in a Natural Soil: Comparison of Relaxometric Imaging, T 1-T 2 Correlation and Fast-Field Cycling NMR. Open Magn. Reson. J. 2010, 3, 57–62. [Google Scholar] [CrossRef]
- Gumbel, E.J. Statistics of Extremes; Columbia University Press: New York, NY, USA, 1958. [Google Scholar]
- Santner, J.F. An Introduction to Gumbel or Extreme Value Probability Paper; EPA-430/1-73-016; US Environmental Protection Agency, Water Programs Operations: Cincinnati, OH, USA, 1973. [Google Scholar]

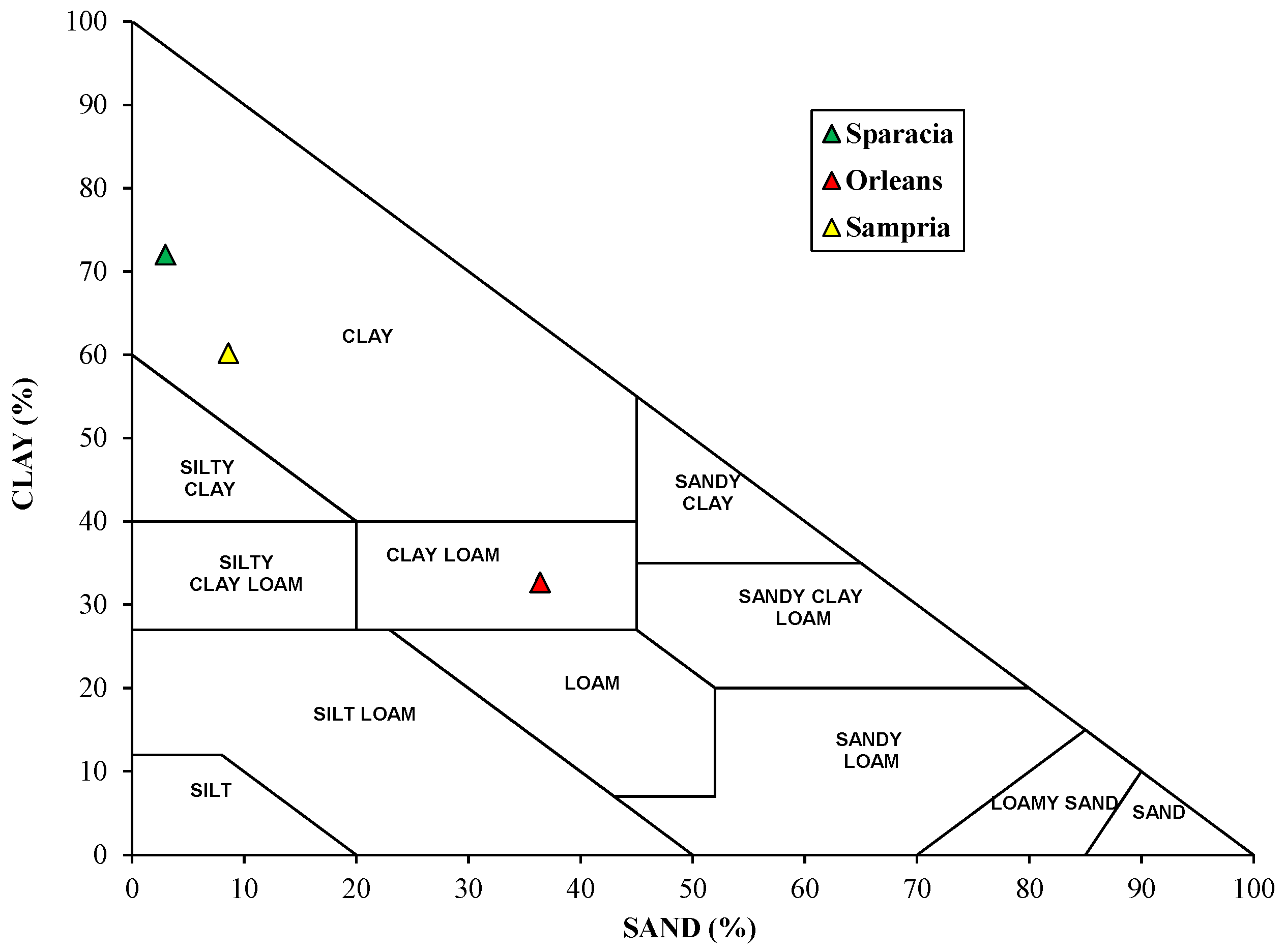


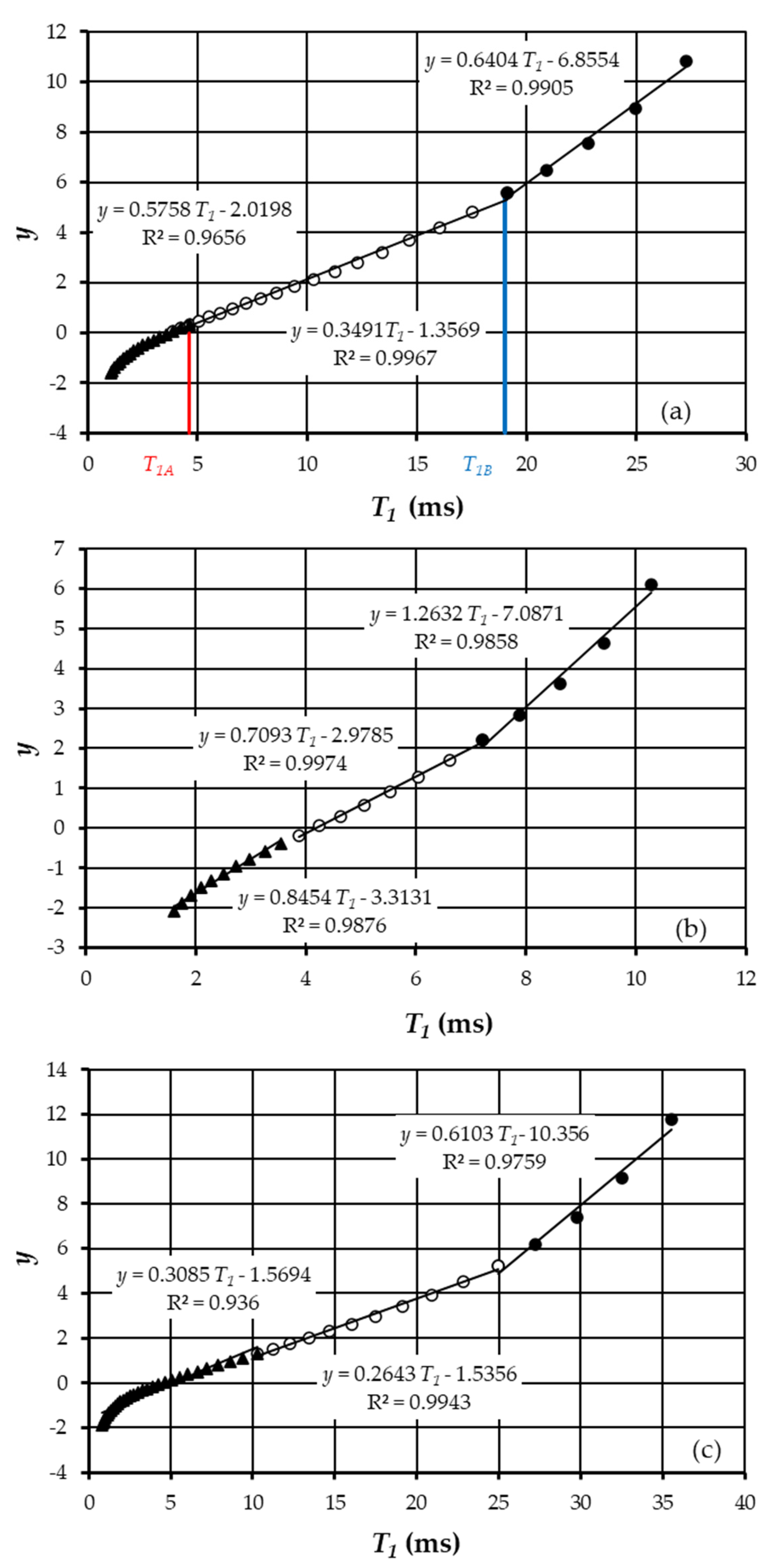
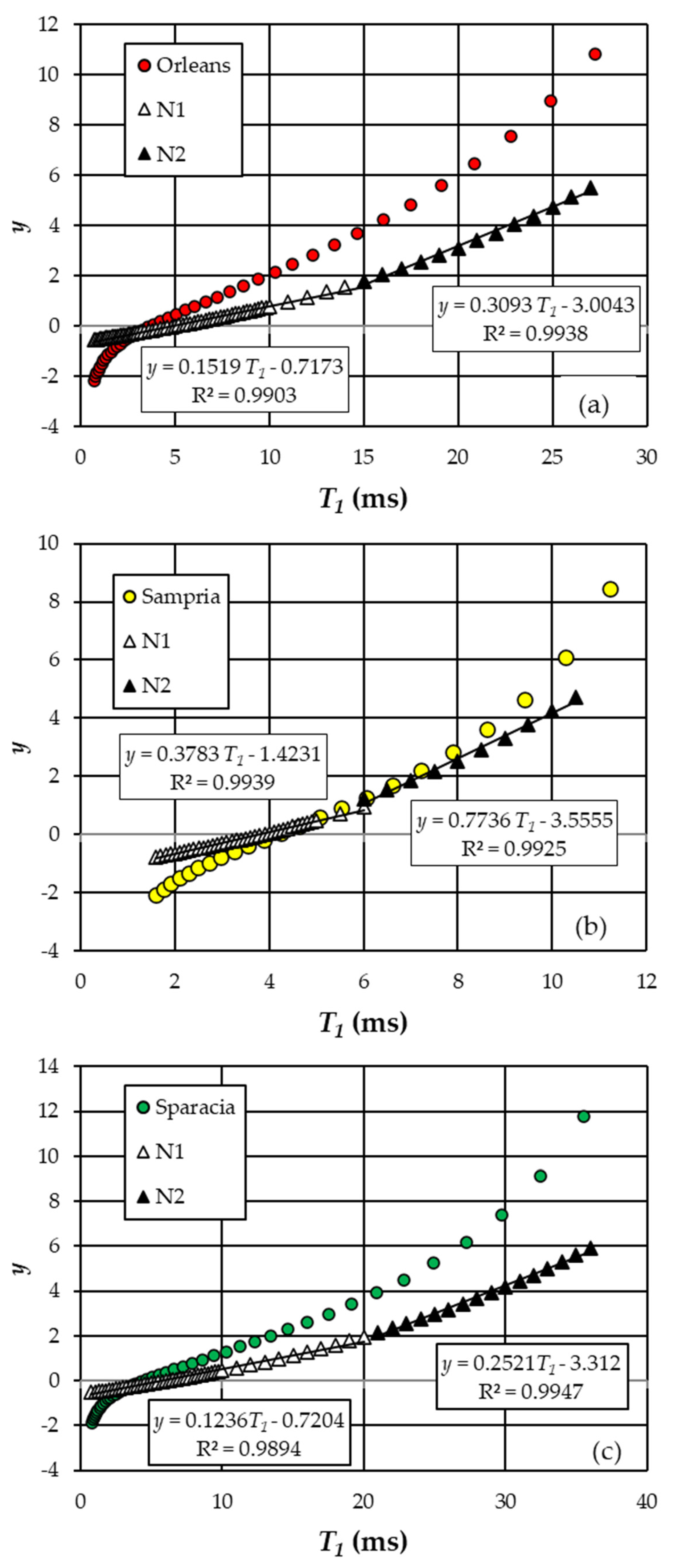
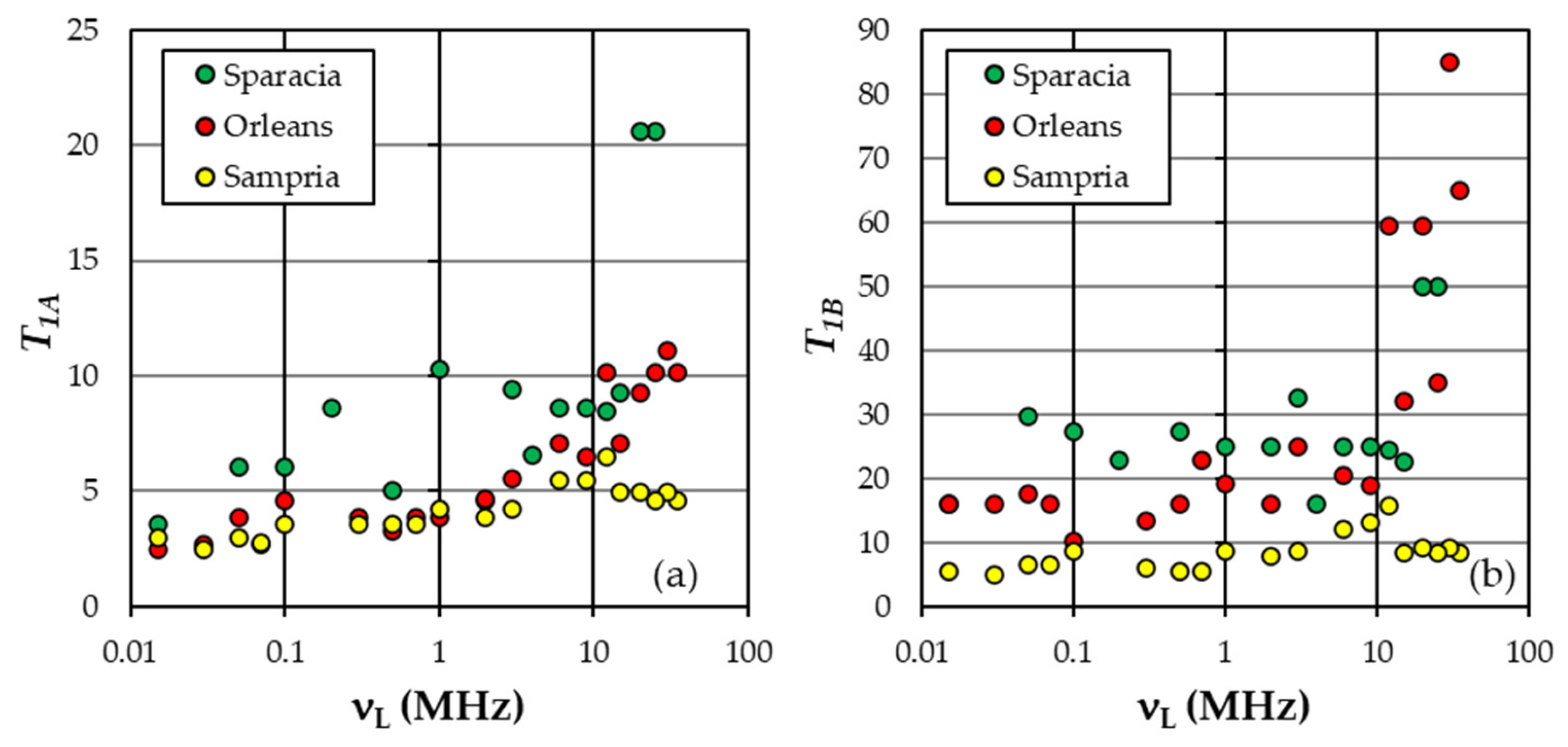
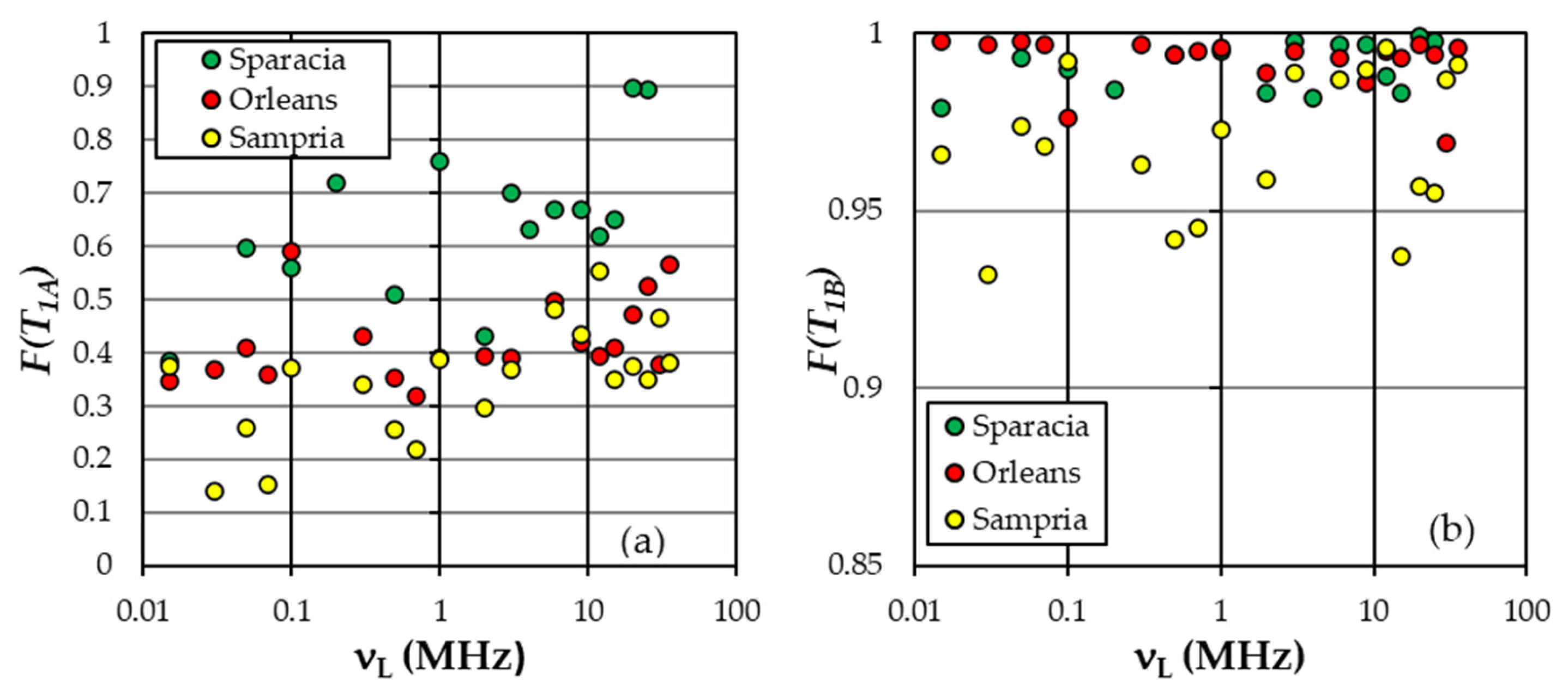

| Soil | νL (MHz) | m(T1) (ms) | s(T1) (ms) | G(T1) | T1A (ms) | T1B (ms) | F(T1A) | F(T1B) |
|---|---|---|---|---|---|---|---|---|
| Orleans | 0.1 | 4.4 | 4.3 | 1.23 | 4.6 | 10.3 | 0.59 | 0.976 |
| 1 | 7.5 | 7.4 | 1.23 | 4.6 | 19.1 | 0.39 | 0.996 | |
| 3 | 8.8 | 9.5 | 1.35 | 5.5 | 24.9 | 0.39 | 0.995 | |
| Sparacia | 0.1 | 10.3 | 11.3 | 1.37 | 10.3 | 24.9 | 0.77 | 0.983 |
| 1 | 9.3 | 9.6 | 1.28 | 10.3 | 24.9 | 0.76 | 0.995 | |
| 3 | 10.9 | 11.4 | 1.30 | 9.4 | 32.5 | 0.70 | 0.998 | |
| Sampria | 0.1 | 4.6 | 2.7 | 0.73 | 3.5 | 8.61 | 0.37 | 0.992 |
| 1 | 4.7 | 2.6 | 0.70 | 3.9 | 7.20 | 0.38 | 0.973 | |
| 3 | 4.8 | 2.4 | 0.61 | 4.2 | 8.61 | 0.37 | 0.989 |
| Soil | m(T1A) | s(T1A) | m(T1B) | s(T1B) | MFT1A | SFT1A | MFT1B | SFT1B | PMI (%) | PME (%) | PMA (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Orleans | 4.24 | 1.39 | 17.50 | 3.98 | 0.405 | 0.072 | 0.993 | 0.006 | 40.5 | 58.8 | 0.7 |
| Sparacia | 7.04 | 2.18 | 24.64 | 5.03 | 0.603 | 0.121 | 0.990 | 0.007 | 60.3 | 38.7 | 1.0 |
| Sampria | 3.74 | 0.92 | 7.69 | 2.55 | 0.313 | 0.104 | 0.968 | 0.019 | 31.3 | 65.5 | 3.2 |
| Soil | νL (MHz) | S1 | S3 | SCI | FCI | PMI (%) | PME (%) | PMA (%) |
|---|---|---|---|---|---|---|---|---|
| Orleans | 0.1 | 0.5741 | 1.0906 | 1.84 | 0.41 | 59 | 38.6 | 2.4 |
| 1 | 0.3847 | 0.6404 | 3.84 | 0.54 | 39 | 60.6 | 0.4 | |
| 3 | 0.2811 | 0.6640 | 2.61 | 0.36 | 39 | 60.5 | 0.5 | |
| Sparacia | 0.1 | 0.3347 | 0.3617 | 5.39 | 0.58 | 77 | 21.3 | 1.7 |
| 1 | 0.3085 | 0.6103 | 3.78 | 0.30 | 76 | 23.5 | 0.5 | |
| 3 | 0.3240 | 0.6042 | 4.54 | 0.41 | 70 | 28.8 | 1.2 | |
| Sampria | 0.1 | 0.9485 | 1.4911 | 1.26 | 0.51 | 37 | 62.2 | 0.8 |
| 1 | 0.8454 | 1.2632 | 0.86 | 0.21 | 38 | 59.3 | 2.7 | |
| 3 | 0.9270 | 1.6645 | 1.21 | 0.43 | 37 | 61.9 | 1.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Conte, P.; Nicosia, A.; Ferro, V. A New Model for Solving Hydrological Connectivity Inside Soils by Fast Field Cycling NMR Relaxometry. Water 2023, 15, 2397. https://doi.org/10.3390/w15132397
Conte P, Nicosia A, Ferro V. A New Model for Solving Hydrological Connectivity Inside Soils by Fast Field Cycling NMR Relaxometry. Water. 2023; 15(13):2397. https://doi.org/10.3390/w15132397
Chicago/Turabian StyleConte, Pellegrino, Alessio Nicosia, and Vito Ferro. 2023. "A New Model for Solving Hydrological Connectivity Inside Soils by Fast Field Cycling NMR Relaxometry" Water 15, no. 13: 2397. https://doi.org/10.3390/w15132397






