Energy Transfer and Reverse Flow Characteristics in the Interaction Process between Non-Breaking Solitary Wave and a Steep Seawall: A Case Study
Abstract
:1. Introduction
2. Numerical Method and Verification
2.1. Numerical Method
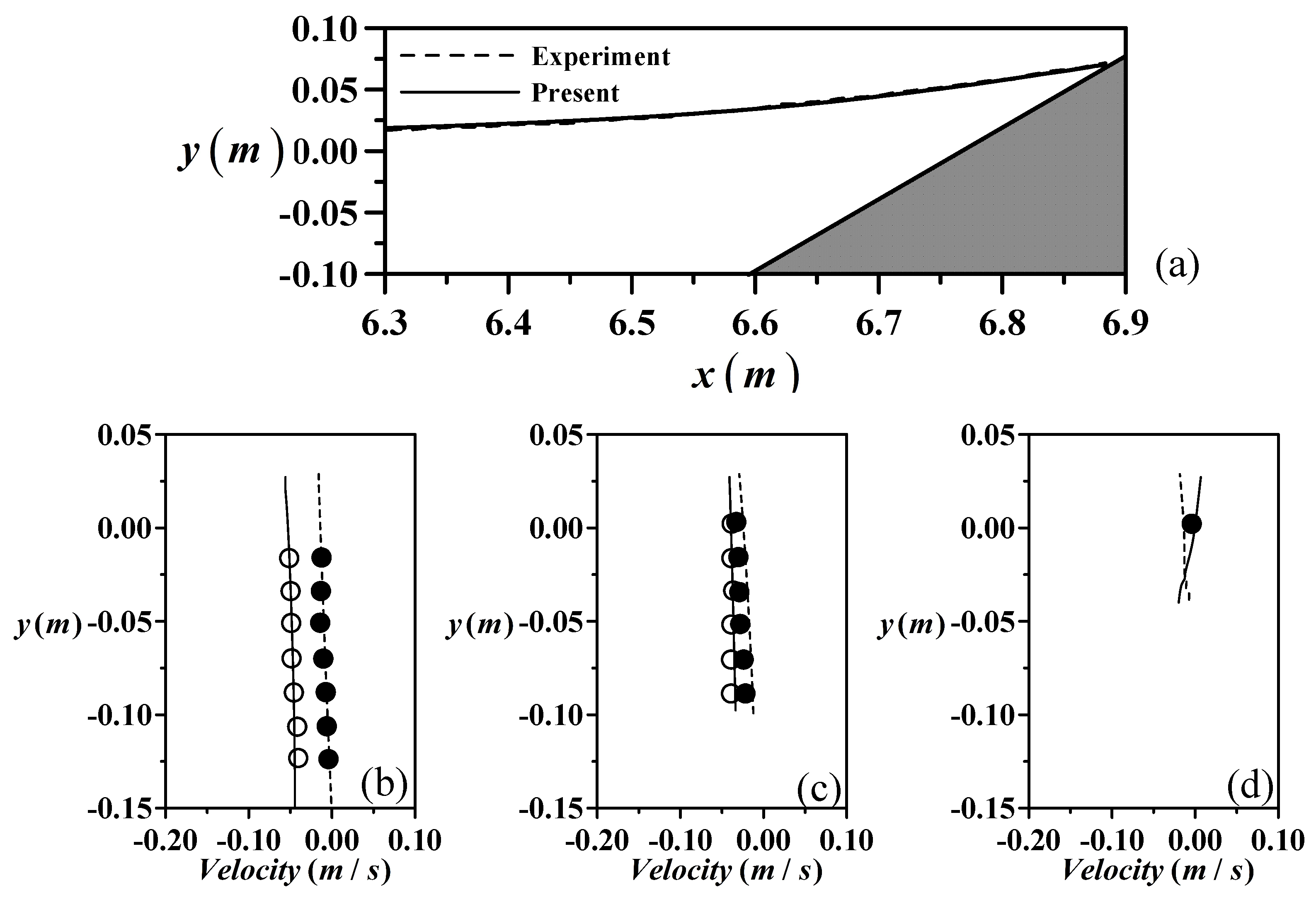
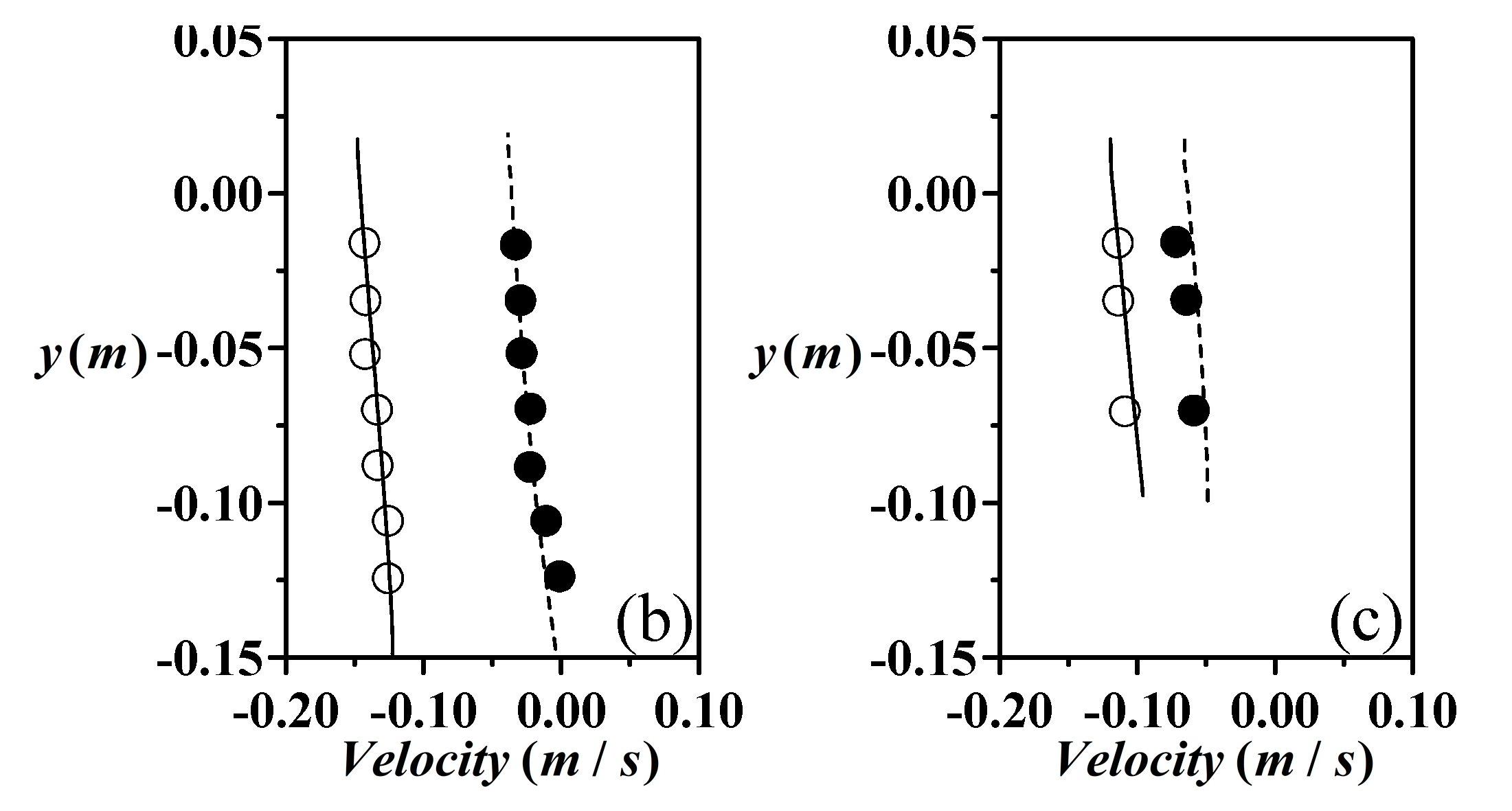
2.2. Verification
3. Results and Discussion
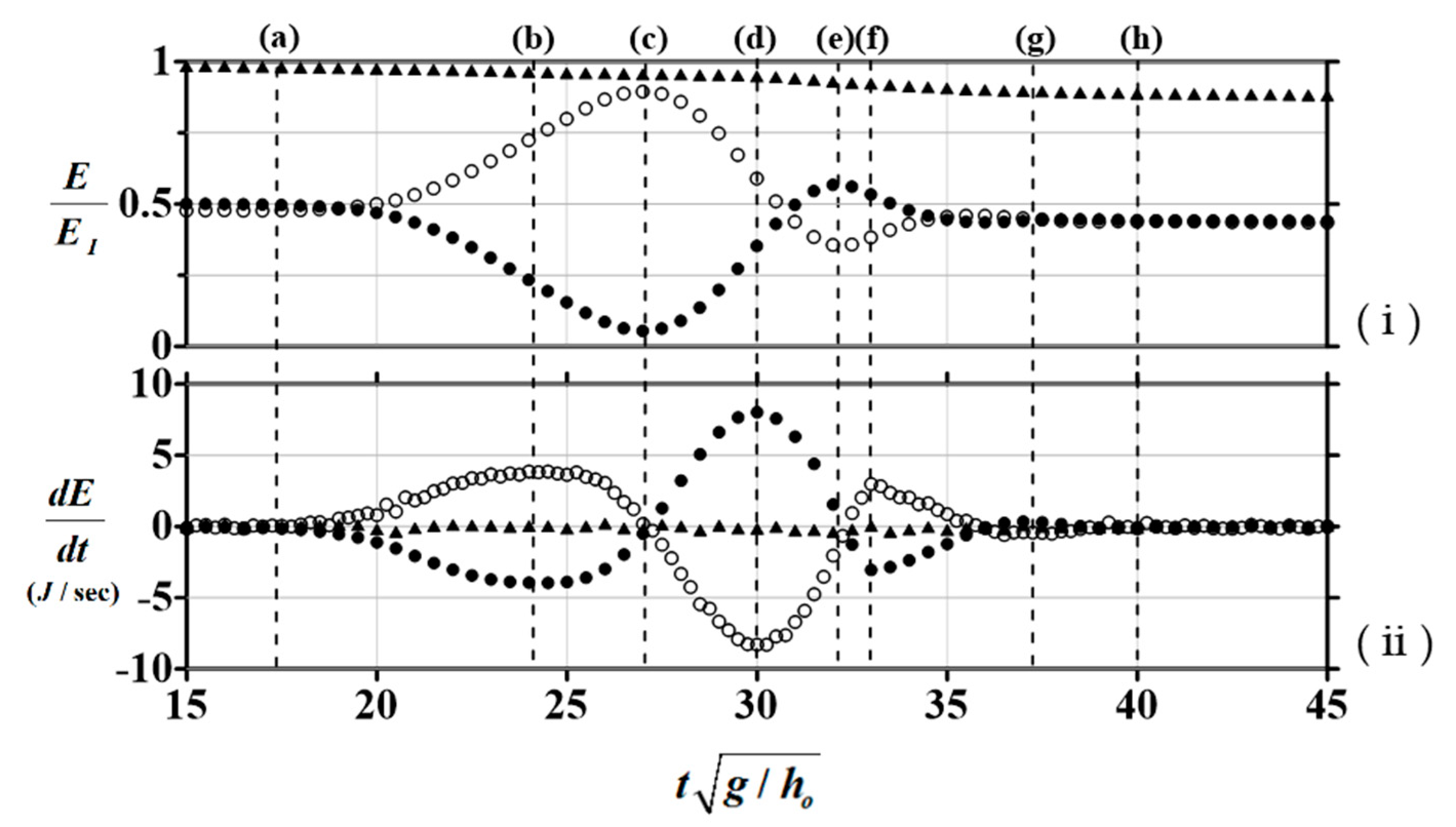
3.1. Relationship between Run-Up Height and Energy Evolution
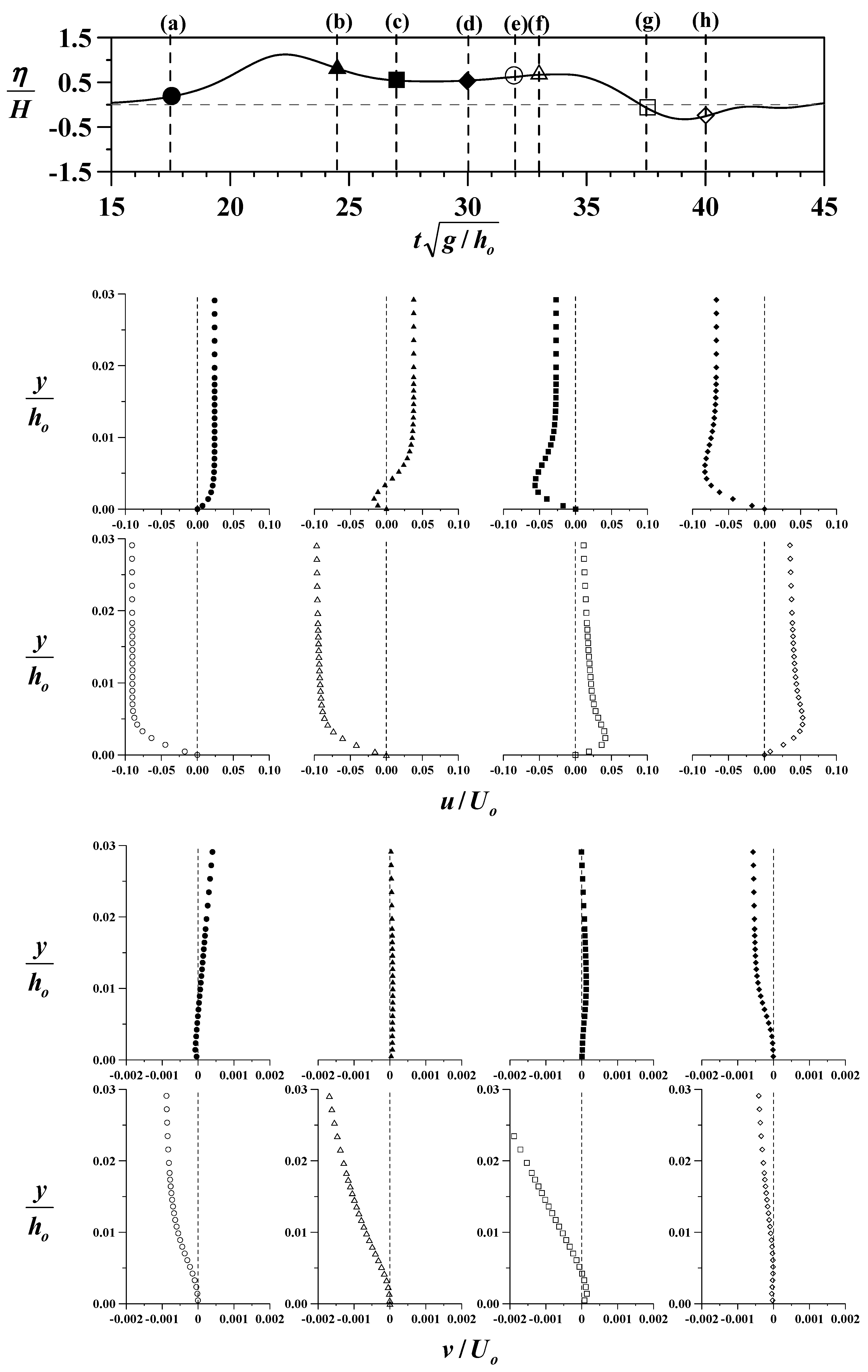
3.2. Relationship between Flow Field and Energy Evolution
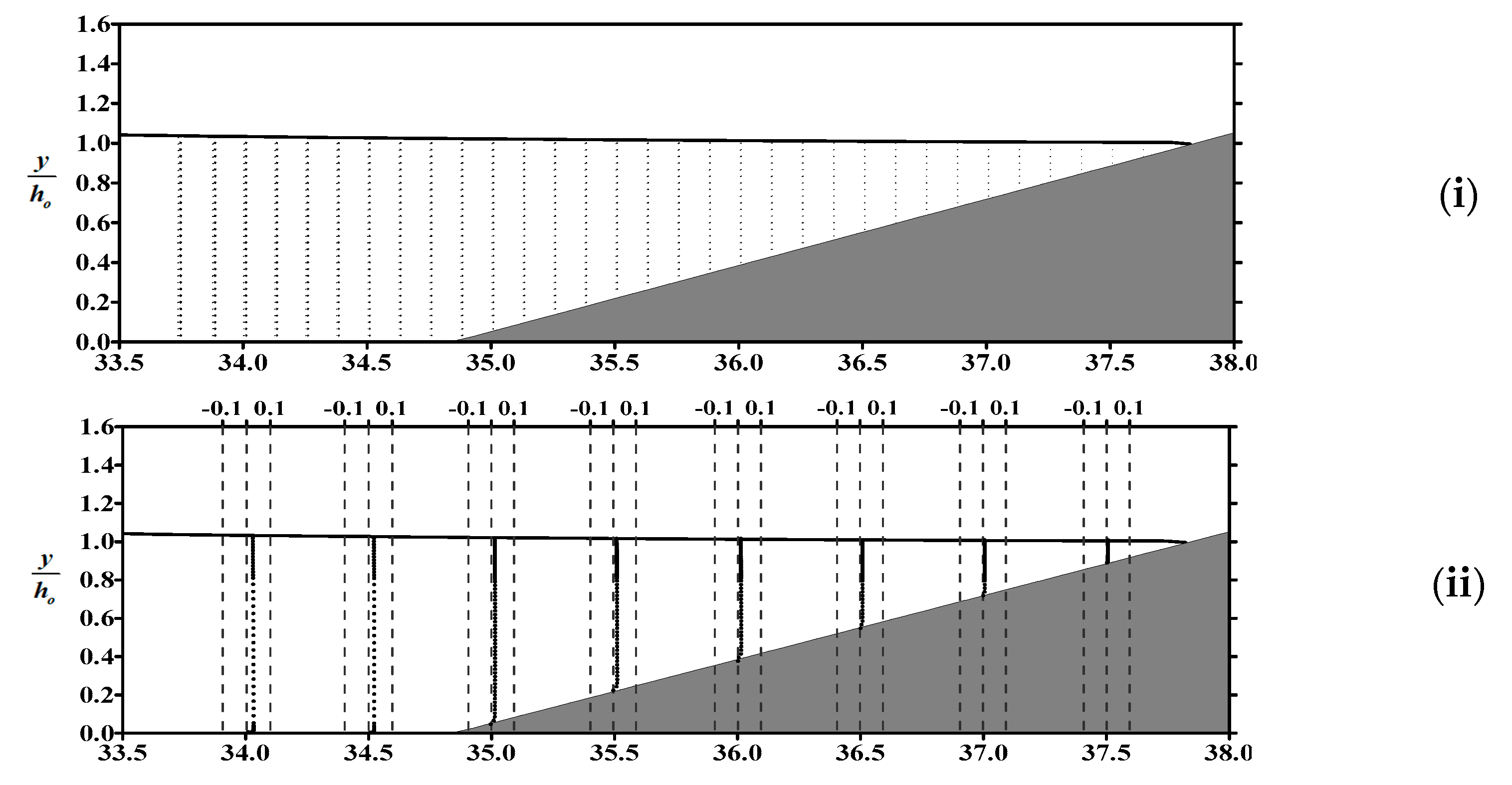
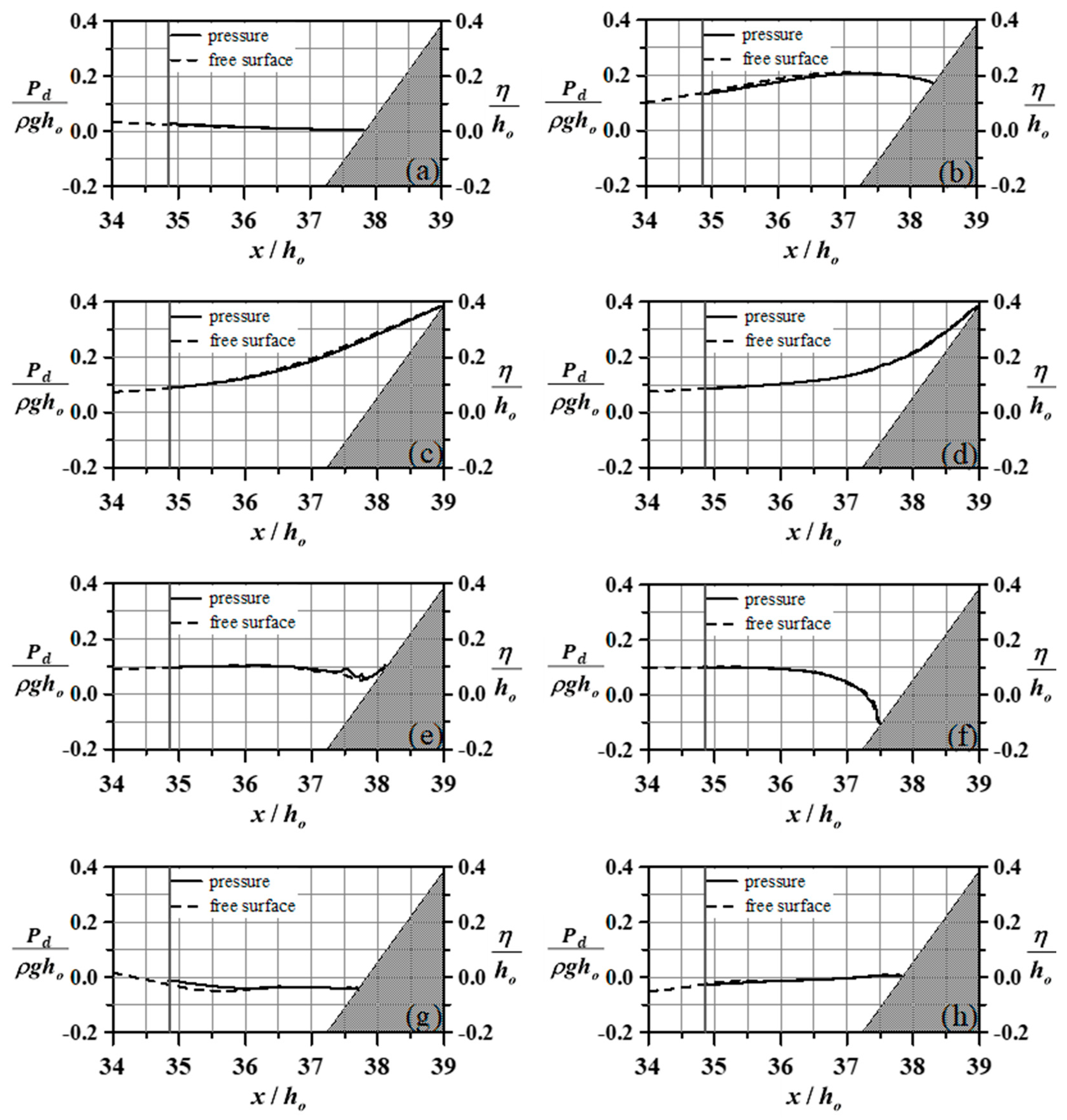
3.3. Reverse Flow and Dynamic Pressure
4. Conclusions
- Compared with the laboratory experimental data of free surface elevations and velocity profiles, it is demonstrated that the numerical model successfully reproduces the various stages of the solitary wave run-up and run-down on a steep seawall.
- The free surface variations during the process of a non-breaking solitary wave entering and leaving a slope at various stages are shown, as well as energy and rate of energy change over time. It can be observed that the maximum run-up height occurs when the potential energy reaches its maximum, and then reaches minimum run-up height when the second-highest rate of change in potential energy occurs.
- After the arrival of the wave crest on the slope, the potential energy gradually increases and the rate of change reaches its peak. The higher velocities are concentrated at the front of the water body during the wave run-up process.
- When the leading edge of the solitary wave approaches the maximum run-up height, most of the kinetic energy in the wave has been converted into potential energy required for run-up, and most velocities approach zero, resulting in minimum kinetic energy.
- During the run-down process, the potential energy of the solitary wave is converted into kinetic energy, redirecting the velocity of the water front in the seaward direction. The maximum flow velocity was approximately 0.304 , occurring at 37.5 as = 32. The flow field indicates that the highest velocity on the slope was not near the free surface but close to the sloping bed. When the water body returns to its static position, the kinetic energy and potential energy of the solitary wave tend to equalize, with approximately 10–20% of the total energy being dissipated.
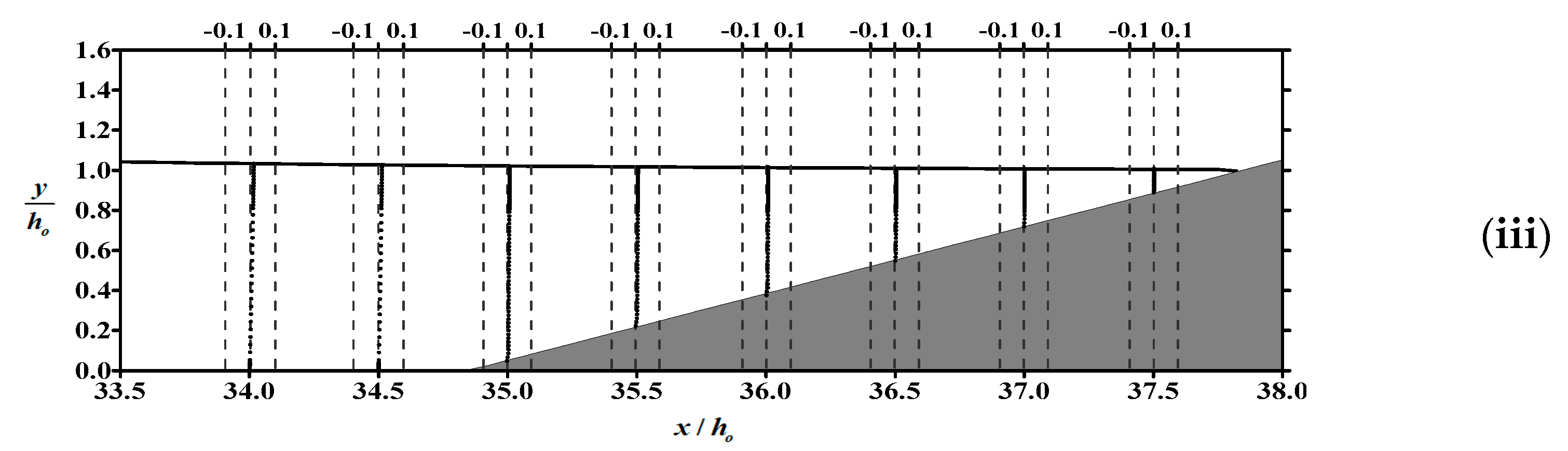
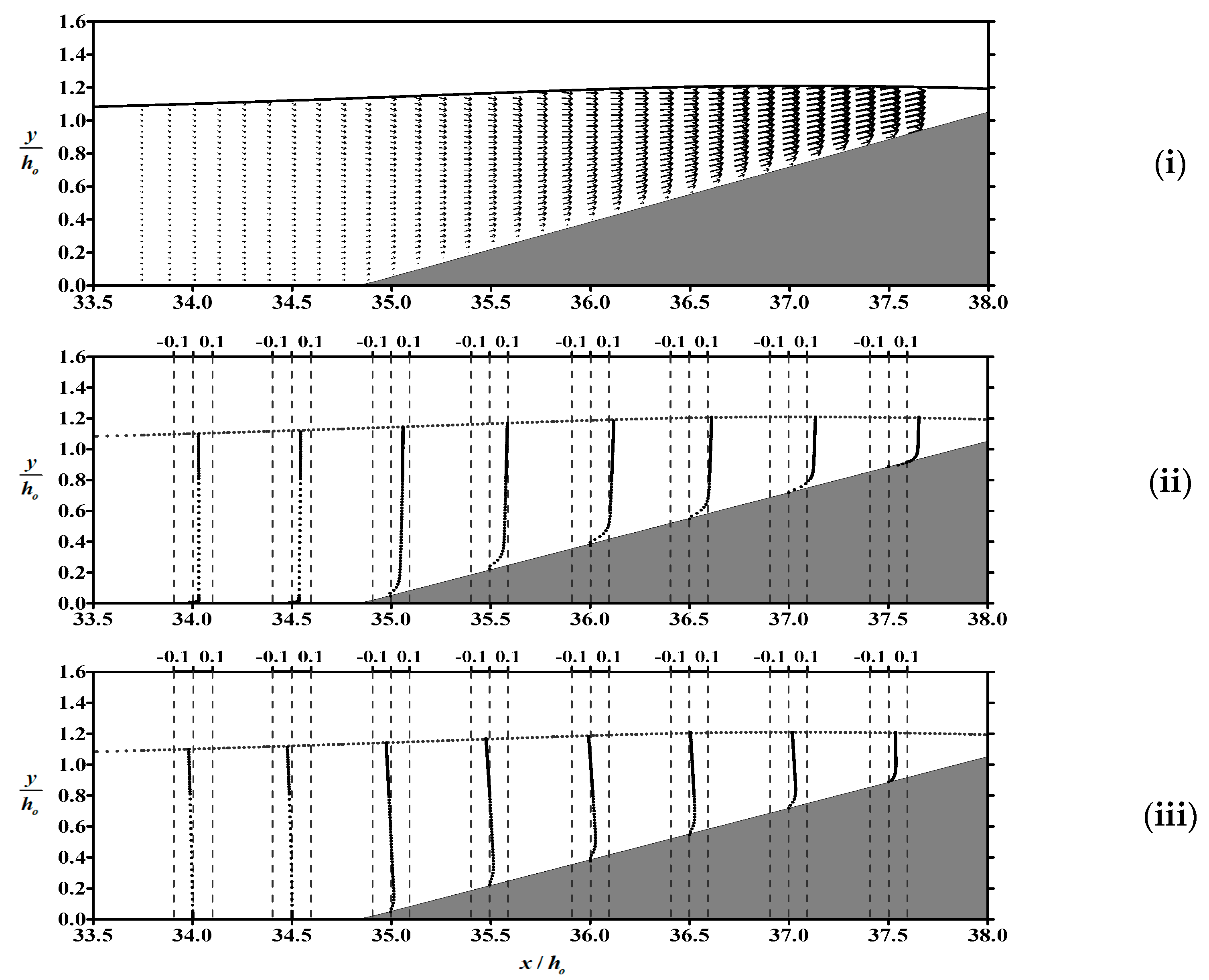
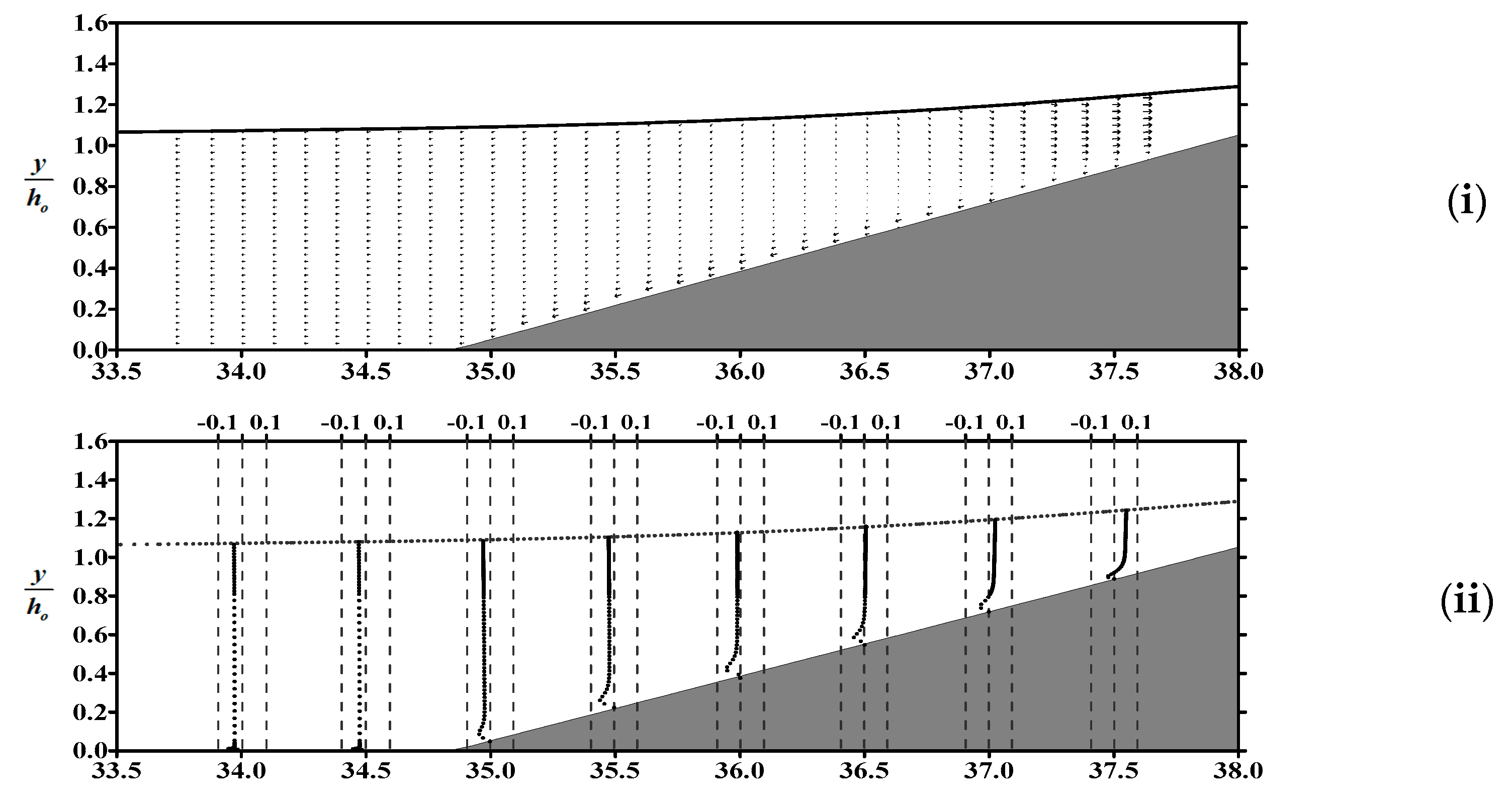
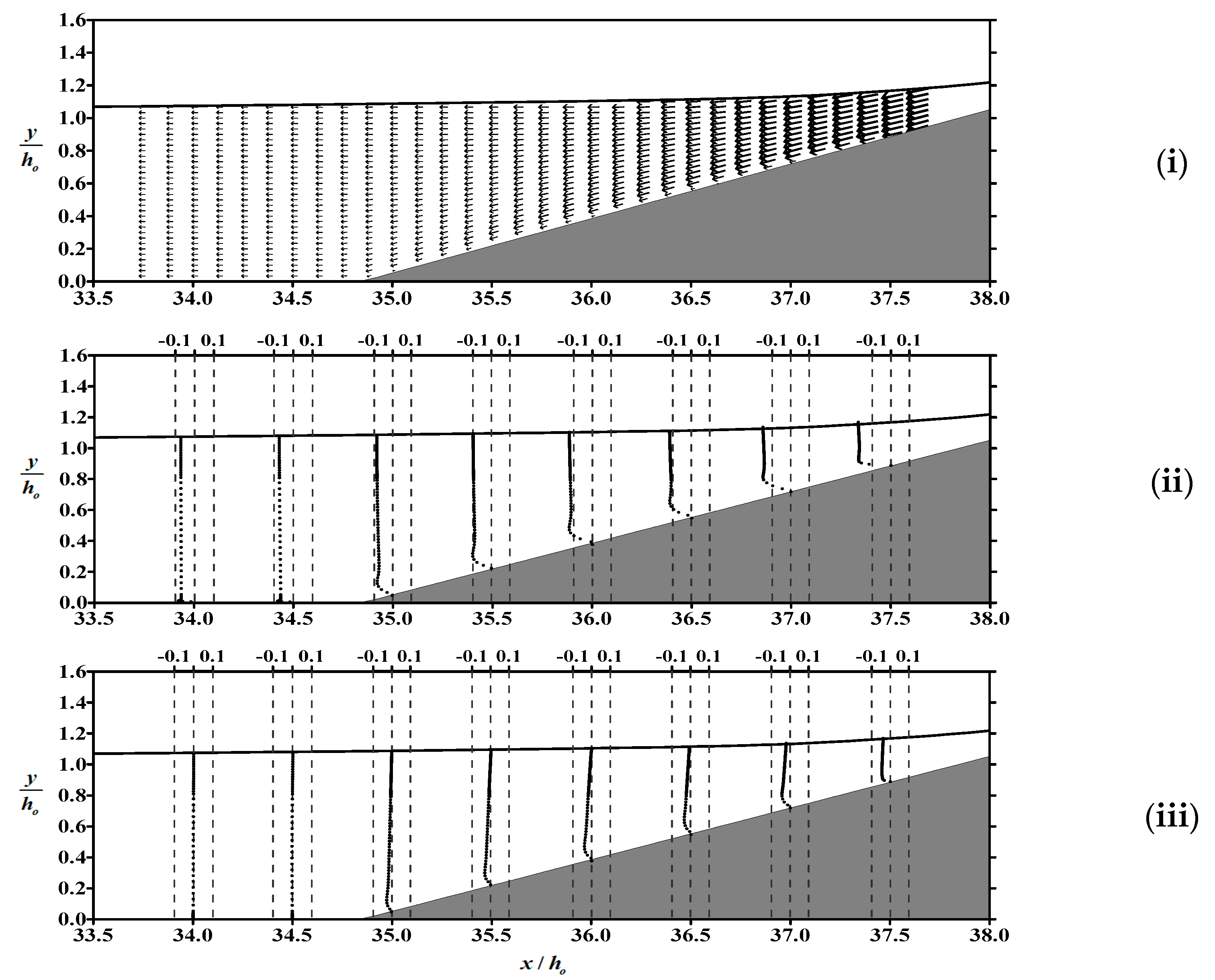
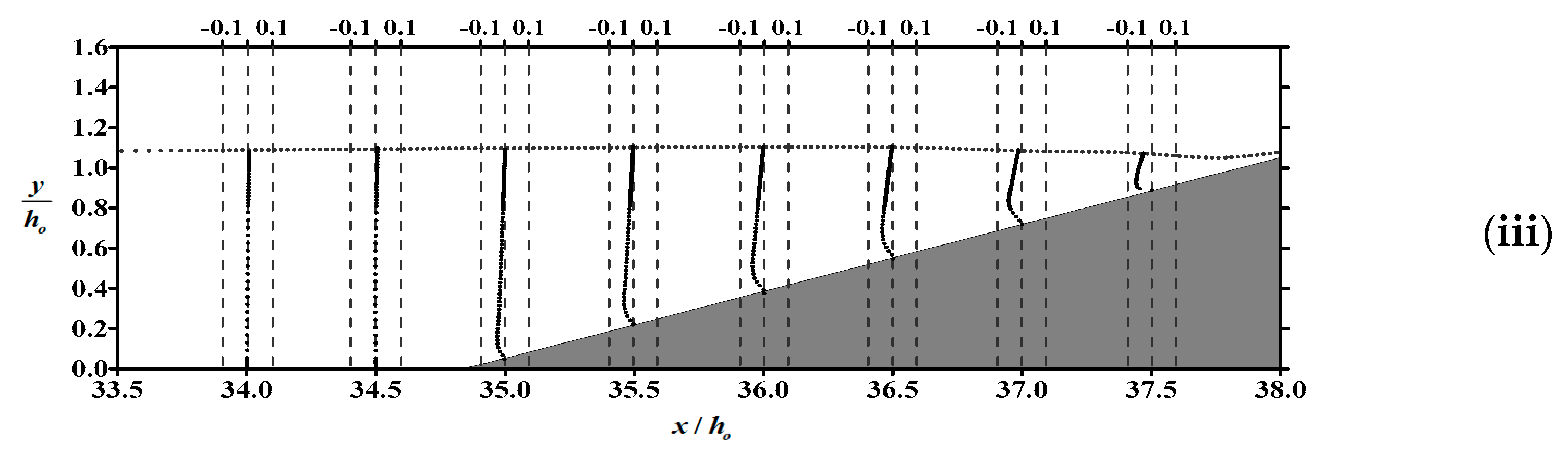
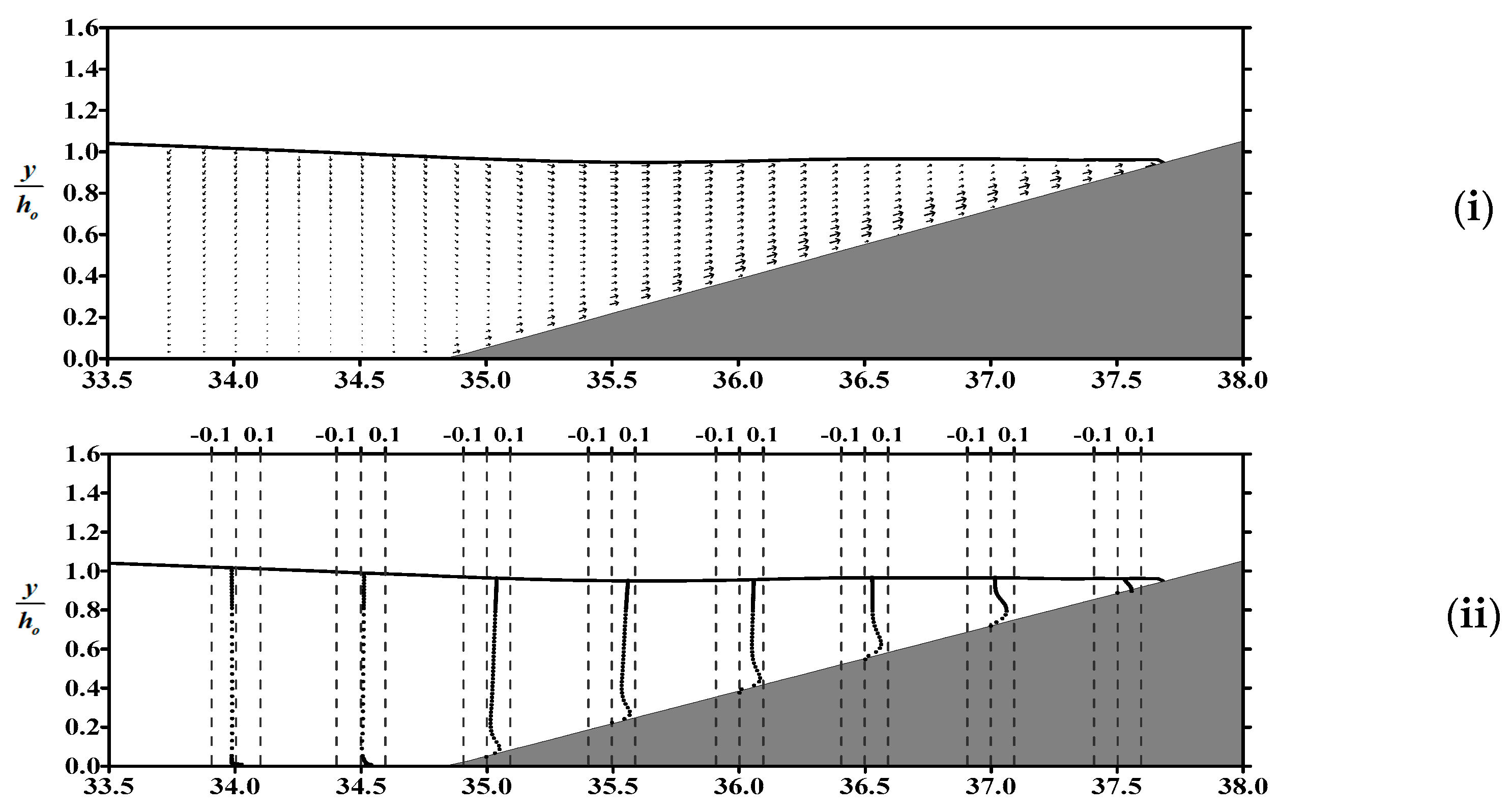
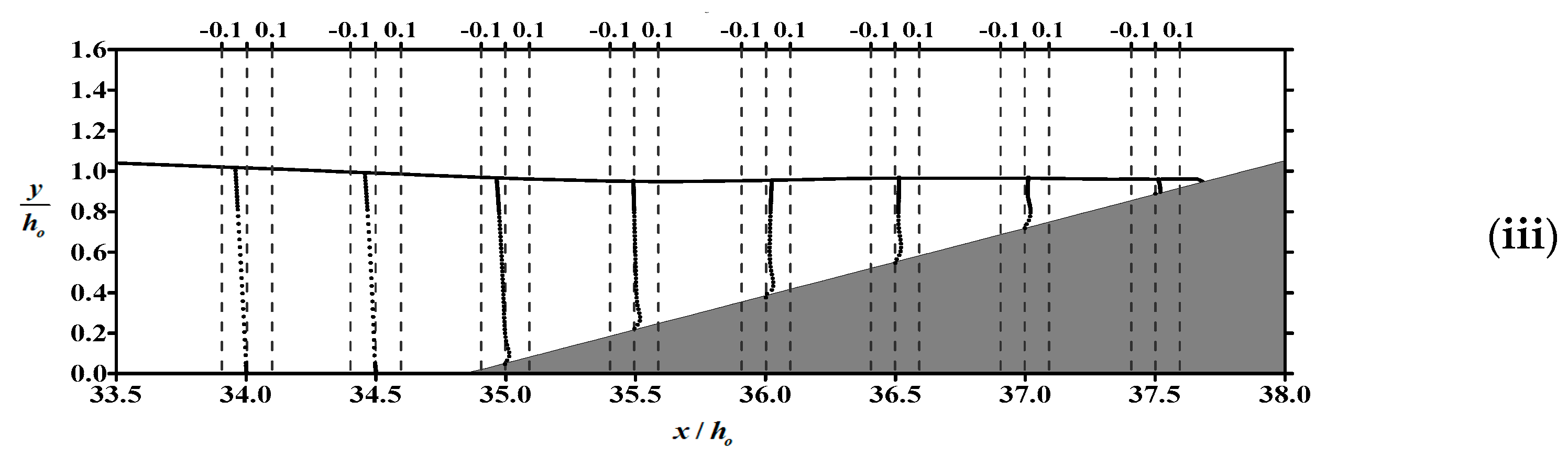
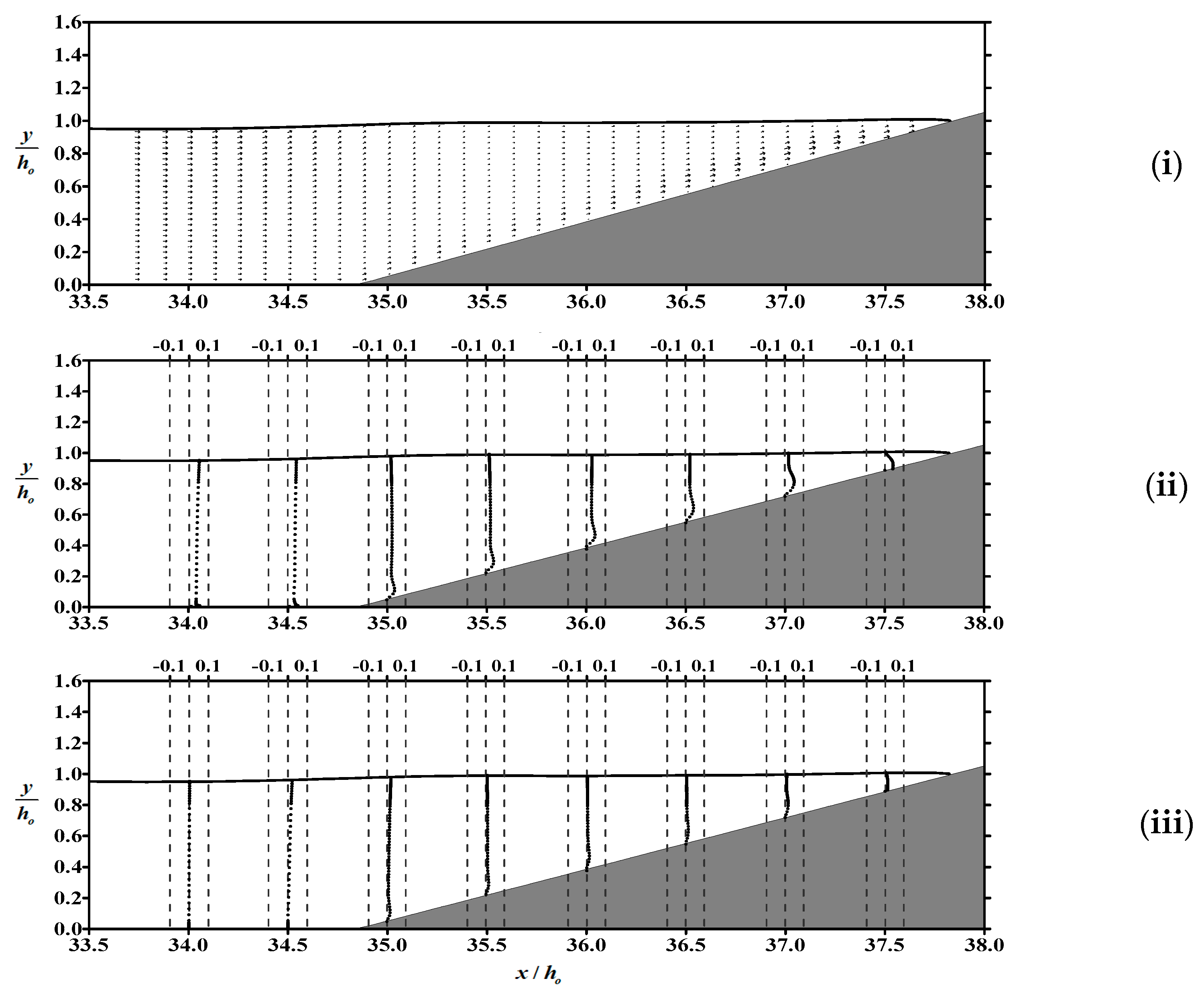
- Within the boundary layer of the flat bottom in front of the slope, the boundary layer flow is dominated by horizontal velocity. The phenomenon of reverse flow occurs in the flow field, as well as on the slope, and the gradient of velocity profile in the boundary layer near the flat bottom is significantly greater than that over the slope.
- The dynamic pressure on the sloping bed is proportional to the free surface elevation. Due to the dominant influence of the dynamic pressure gradient on the flow field in the vicinity of the bed, we can indirectly ascertain the occurrence time of undertow by examining the spatial variations in water level.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Carrier, G.F.; Greenspan, H.P. Water waves of finite amplitude on a sloping beach. J. Fluid Mech. 1958, 4, 97–109. [Google Scholar] [CrossRef]
- Johnson, R.S.; King, R.A. Nonlinear Waves in Fluids: Finite-Amplitude Waves, Instability and Turbulence; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Wazwaz, A.M. Partial Differential Equations and Solitary Waves Theory; Higher Education Press and Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Hall, J.; Watts, J. Laboratory Investigation of the Vertical Rise of Solitary Waves on Impermeable Slopes; Beach Erosion Board, US Army Corps of Engineer, Tech. Memo: Washington, DC, USA, 1953; Volume 33, p. 14. [Google Scholar]
- Zelt, J. The run-up of nonbreaking and breaking solitary waves. Coast. Eng. 1991, 15, 205–246. [Google Scholar] [CrossRef]
- Li, Y.; Raichlen, F. Solitary Wave Runup on Plane Slopes. J. Waterw. Port Coast. Ocean Eng. 2001, 127, 33–44. [Google Scholar] [CrossRef]
- Shuto, N. Standing Waves in Front of a Sloping Dike. Coast. Eng. Jpn. 1972, 15, 13–23. [Google Scholar] [CrossRef]
- Goto, C.; Shuto, N. Numerical simulation of tsunami run-up. Coast. Eng. Jpn. 1978, 21, 13–20. [Google Scholar]
- Goto, C.; Shuto, N. Run-up of tsunamis by linear and nonlinear theories. In Proceedings of the 17th International Conference on Coastal Engineering, JSCE, Sydney, Australia, 23–28 March 1980; pp. 56–60. [Google Scholar]
- Kim, S.K.; Liu, P.L.-F.; Liggett, J.A. Boundary integral equation solutions for solitary wave generation, propagation and run-up. Coast. Eng. 1983, 7, 299–317. [Google Scholar] [CrossRef]
- Pelinovsky, E.; Mazova, R.K. Exact analytical solutions of nonlinear problems of tsunami wave run-up on slopes with different profiles. Nat. Hazards 1992, 6, 227–249. [Google Scholar] [CrossRef]
- Carrier, G.F.; Wu, T.T.; Yeh, H. Tsunami run-up and draw-down on a plane beach. J. Fluid Mech. 2003, 475, 79–99. [Google Scholar] [CrossRef]
- Synolakis, C.E. The runup of solitary waves. J. Fluid Mech. Digit. Arch. 1987, 185, 523–545. [Google Scholar] [CrossRef]
- Tadepalli, S.; Synolakis, C.E. The run-up of N-waves on sloping beaches. Proc. R. Soc. A Math. Phys. Eng. Sci. 1994, 445, 99–112. [Google Scholar]
- Kânoğlu, U.; Synolakis, C.E. Long wave runup on piecewise linear topographies. J. Fluid Mech. 1998, 374, 1–28. [Google Scholar] [CrossRef]
- Kânoğlu, U. Nonlinear evolution and runup–rundown of long waves over a sloping beach. J. Fluid Mech. 2004, 513, 363–372. [Google Scholar] [CrossRef]
- Matteo, A.; Brocchini, M. Maximum run-up, breaking conditions and dynamical forces in the swash zone: A boundary value approach. Coast. Eng. 2008, 55, 732–740. [Google Scholar] [CrossRef]
- Synolakis, C.E. The Runup of Long Waves. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1986. [Google Scholar]
- Li, Y.; Raichlen, F. Energy Balance Model for Breaking Solitary Wave Runup. J. Waterw. Port Coast. Ocean Eng. 2003, 129, 47–59. [Google Scholar] [CrossRef]
- Lin, P.; Chang, K.-A.; Liu, P.L.-F. Runup and Rundown of Solitary Waves on Sloping Beaches. J. Waterw. Port Coast. Ocean Eng. 1999, 125, 247–255. [Google Scholar] [CrossRef]
- Jensen, A.; Pedersen, G.K.; Wood, D.J. An experimental study of wave run-up at a steep beach. J. Fluid Mech. 2003, 486, 161–188. [Google Scholar] [CrossRef] [Green Version]
- Yeh, H.H. Tsunami bore runup. Nat. Hazards 1991, 4, 209–220. [Google Scholar] [CrossRef]
- Lin, C.; Wong, W.-Y.; Raikar, R.V.; Hwung, H.-H.; Tsai, C.-P. Characteristics of Accelerations and Pressure Gradient during Run-Down of Solitary Wave over Very Steep Beach: A Case Study. Water 2019, 11, 523. [Google Scholar] [CrossRef] [Green Version]
- Hibberd, S.; Peregrine, D.H. Surf and run-up on a beach: A uniform bore. J. Fluid Mech. 1979, 95, 323–345. [Google Scholar] [CrossRef]
- Kobayashi, N.; Karjadi, E.A. Surf-similarity parameter for breaking solitary-wave runup. J. Waterw. Port Coast. Ocean. Eng. 1994, 120, 645–650. [Google Scholar] [CrossRef]
- Titov, V.V.; Synolakis, C.E. Modeling of Breaking and Nonbreaking Long-Wave Evolution and Runup Using VTCS-2. J. Waterw. Port Coast. Ocean Eng. 1995, 121, 308–316. [Google Scholar] [CrossRef]
- Titov, V.V.; Synolakis, C.E. Numerical Modeling of Tidal Wave Runup. J. Waterw. Port Coast. Ocean Eng. 1998, 124, 157–171. [Google Scholar] [CrossRef]
- Li, Y.; Raichlen, F. Non-breaking and breaking solitary wave run-up. J. Fluid Mech. 2002, 456, 295–318. [Google Scholar] [CrossRef] [Green Version]
- Hubbard, M.E.; Dodd, N. A 2D numerical model of wave run-up and overtopping. Coast. Eng. 2002, 47, 1–26. [Google Scholar] [CrossRef]
- Peregrine, D.H. Long waves on a beach. J. Fluid Mech. 1967, 27, 815–827. [Google Scholar] [CrossRef]
- Nwogu, O. Alternative Form of Boussinesq Equations for Nearshore Wave Propagation. J. Waterw. Port Coast. Ocean Eng. 1993, 119, 618–638. [Google Scholar] [CrossRef] [Green Version]
- Lynett, P.J.; Wu, T.-R.; Liu, P.L.-F. Modeling wave runup with depth-integrated equations. Coast. Eng. 2002, 46, 89–107. [Google Scholar] [CrossRef]
- Avgeris, I.; Karambas, T.; Prinos, P. Boussinesq modeling of wave run-up and overtopping. In Proceedings of the 7th International Conference on HydroScience and Engineering, Philadelphia, PA, USA, 10–13 September 2006. [Google Scholar]
- Korycansky, D.G.; Lynett, P.J. Run-up from impact tsunami. Geophys. J. Int. 2007, 170, 1076–1088. [Google Scholar] [CrossRef] [Green Version]
- Fuhrman, D.R.; Madsen, P.A. Tsunami generation, propagation, and run-up with a high-order Boussinesq model. Coast. Eng. 2009, 56, 747–758. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P.L.-F. A numerical study of breaking waves in the surf zone. J. Fluid Mech. 1998, 359, 239–264. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P. Turbulence transport, vorticity dynamics, and solute mixing under plunging breaking waves in surf zone. J. Geophys. Res. Oceans 1998, 103, 15677–15694. [Google Scholar] [CrossRef]
- Wood, D.J.; Pedersen, G.K.; Jensen, A. Modelling of run up of steep non-breaking waves. Ocean Eng. 2003, 30, 625–644. [Google Scholar] [CrossRef]
- Hieu, P.D.; Tanimoto, K. Verification of a VOF-based two-phase flow model for wave breaking and wave–structure interactions. Ocean Eng. 2006, 33, 1565–1588. [Google Scholar] [CrossRef]
- Dong, Z.; Zhan, J.-M. Numerical Modeling of Wave Evolution and Runup in Shallow Water. J. Hydrodyn. 2009, 21, 731–738. [Google Scholar] [CrossRef]
- Huang, C.-J.; Lin, Y.-T.; Lin, C.-Y. Viscous Flow Fields Induced by a Breaking Solitary Wave over a Shelf. J. Mar. Sci. Technol. 2015, 23, 855–863. [Google Scholar]
- Lin, C.-Y.; Huang, C.-J.; Hsu, T.-W. Viscous Flow Fields Induced by the Run-Up of Periodic Waves on Vertical and Sloping Seawalls. J. Mar. Sci. Eng. 2022, 10, 1512. [Google Scholar] [CrossRef]
- Chen, C.-J.; Chen, H.-C. Finite analytic numerical method for unsteady two-dimensional Navier-Stokes equations. J. Comput. Phys. 1984, 53, 209–226. [Google Scholar] [CrossRef]
- Grimshaw, R. The solitary wave in water of variable depth. J. Fluid Mech. 1970, 42, 639–656. [Google Scholar] [CrossRef]
- Bagherizadeh, E.; Zhang, Z.; Farhadzadeh, A.; Angelidis, D.; Ghazian Arabi, M.; Moghimi, S.; Khosronejad, A. Numerical modelling of solitary wave and structure interactions using level-set and immersed boundary methods by adopting adequate inlet boundary conditions. J. Hydraul. Res. 2021, 59, 559–585. [Google Scholar] [CrossRef]
- Enright, D.; Fedkiw, R.; Ferziger, J.; Mitchell, I. A Hybrid Particle Level Set Method for Improved Interface Capturing. J. Comput. Phys. 2002, 183, 83–116. [Google Scholar] [CrossRef] [Green Version]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef] [Green Version]
- Jiang, G.-S.; Shu, C.-W. Efficient Implementation of Weighted ENO Schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef] [Green Version]
- Peng, D.; Merriman, B.; Osher, S.; Zhao, H.; Kang, M. A PDE-Based fast local level set method. J. Comput. Phys. 1999, 155, 410–438. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.-J.; Lin, C.-Y.; Chen, C.-H. Numerical simulations of fluid-structure interaction based on Cartesian grids with two boundary velocities. Int. J. Numer. Methods Fluids 2015, 79, 138–161. [Google Scholar] [CrossRef]
- Goring, D.G. Tsunami: The Propagation of Long Waves onto a Shelf; Technical Report No. KH-R-38; W. M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology: Pasadena, CA, USA, 1978. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-Y.; Huang, C.-J.; Hsu, T.-W.; Chen, C.-H. Energy Transfer and Reverse Flow Characteristics in the Interaction Process between Non-Breaking Solitary Wave and a Steep Seawall: A Case Study. Water 2023, 15, 2412. https://doi.org/10.3390/w15132412
Lin C-Y, Huang C-J, Hsu T-W, Chen C-H. Energy Transfer and Reverse Flow Characteristics in the Interaction Process between Non-Breaking Solitary Wave and a Steep Seawall: A Case Study. Water. 2023; 15(13):2412. https://doi.org/10.3390/w15132412
Chicago/Turabian StyleLin, Chun-Yuan, Ching-Jer Huang, Tai-Wen Hsu, and Chih-Hsin Chen. 2023. "Energy Transfer and Reverse Flow Characteristics in the Interaction Process between Non-Breaking Solitary Wave and a Steep Seawall: A Case Study" Water 15, no. 13: 2412. https://doi.org/10.3390/w15132412
APA StyleLin, C.-Y., Huang, C.-J., Hsu, T.-W., & Chen, C.-H. (2023). Energy Transfer and Reverse Flow Characteristics in the Interaction Process between Non-Breaking Solitary Wave and a Steep Seawall: A Case Study. Water, 15(13), 2412. https://doi.org/10.3390/w15132412






