Numerical Simulation of the Lower and Middle Reaches of the Yarkant River (China) Using MIKE SHE
Abstract
:1. Introduction
2. Materials and Methods
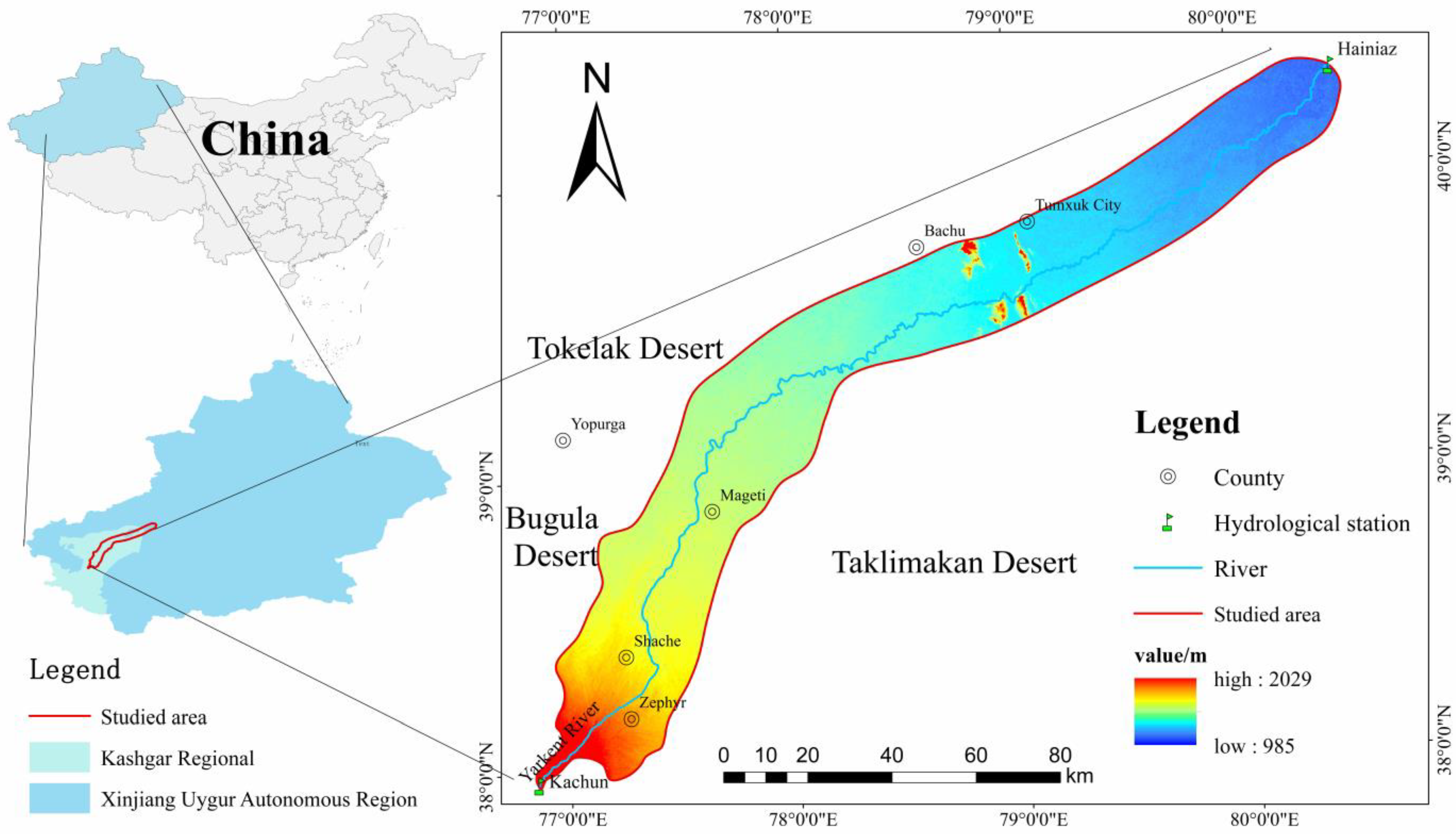
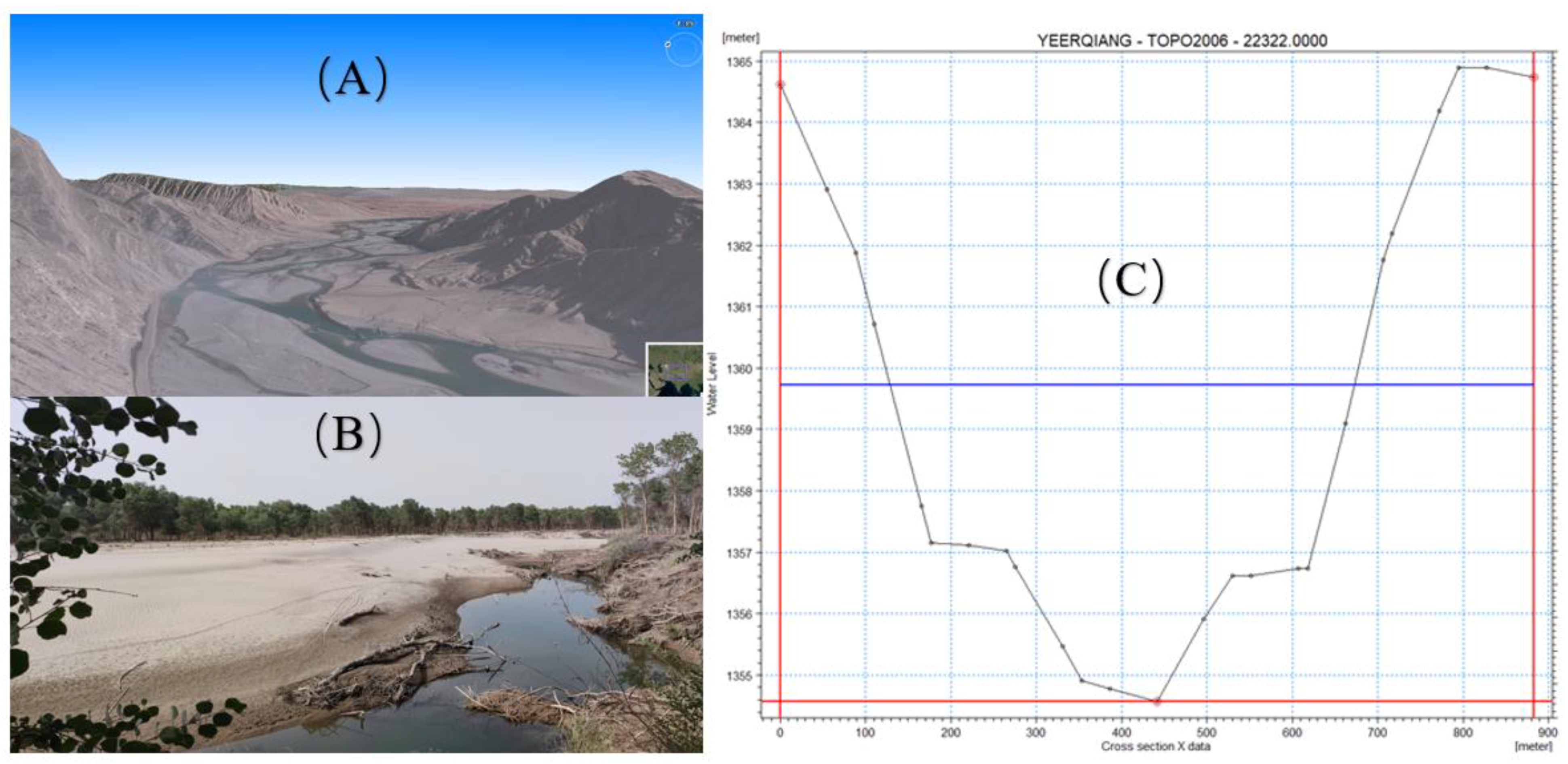
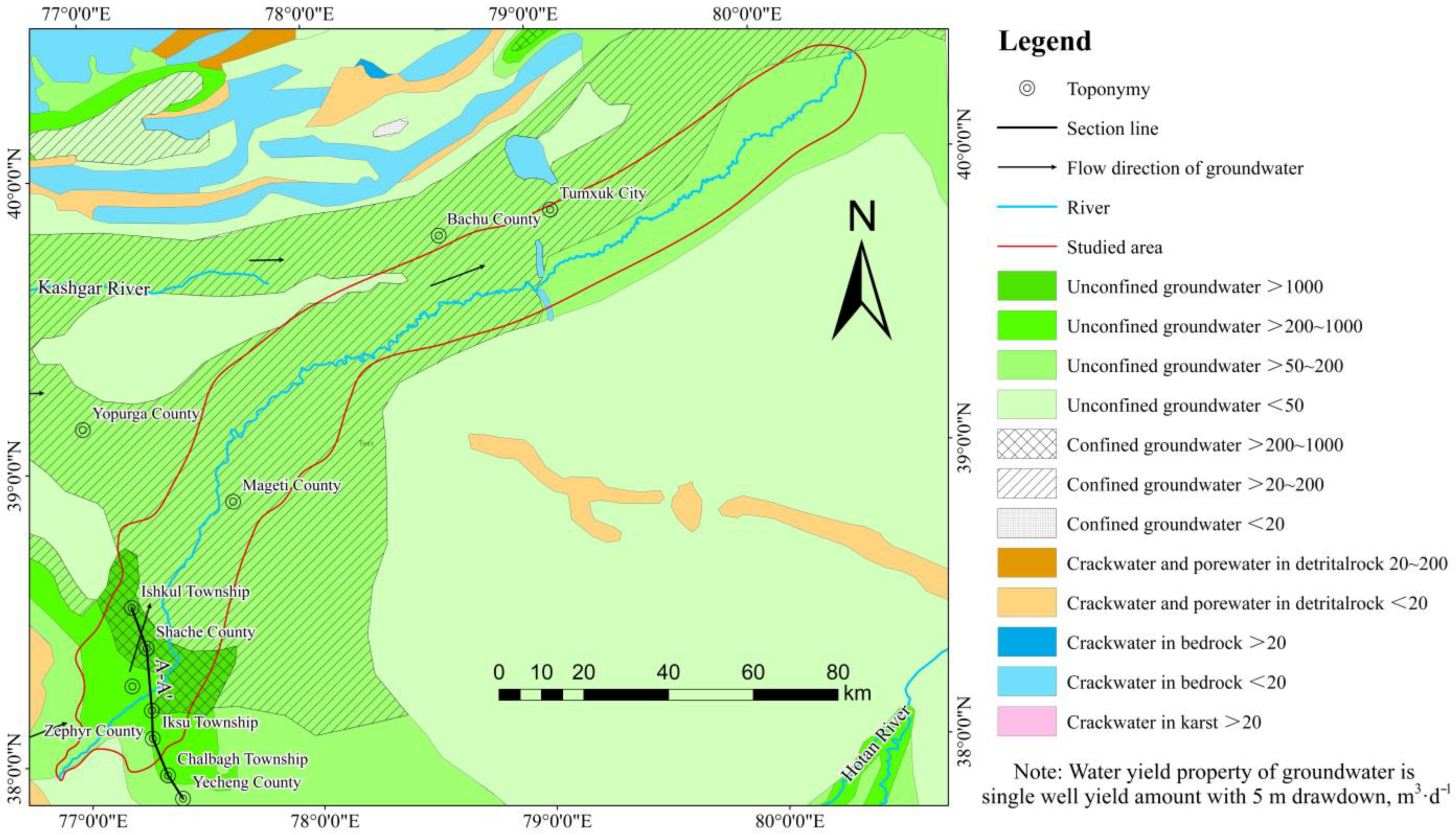
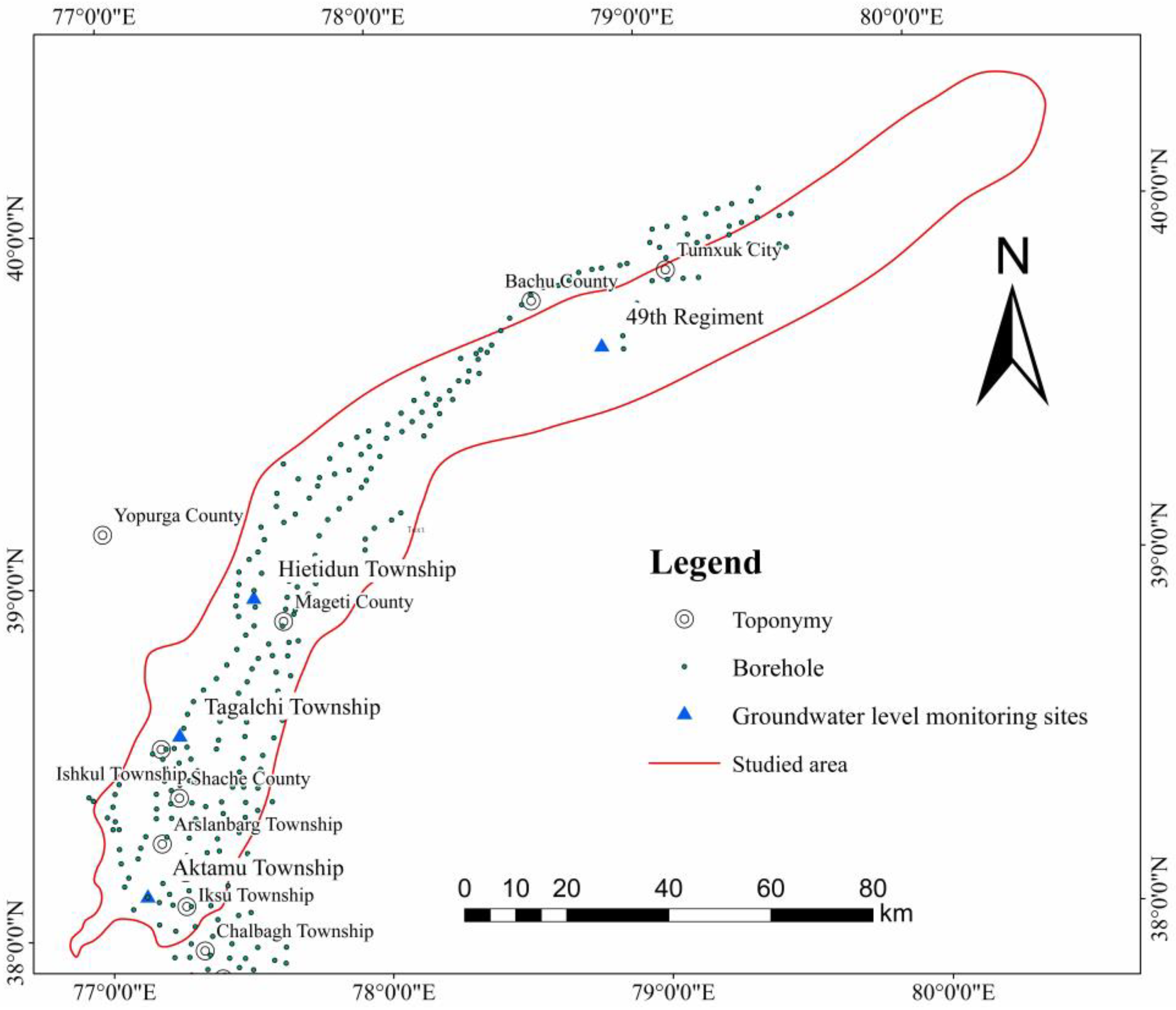
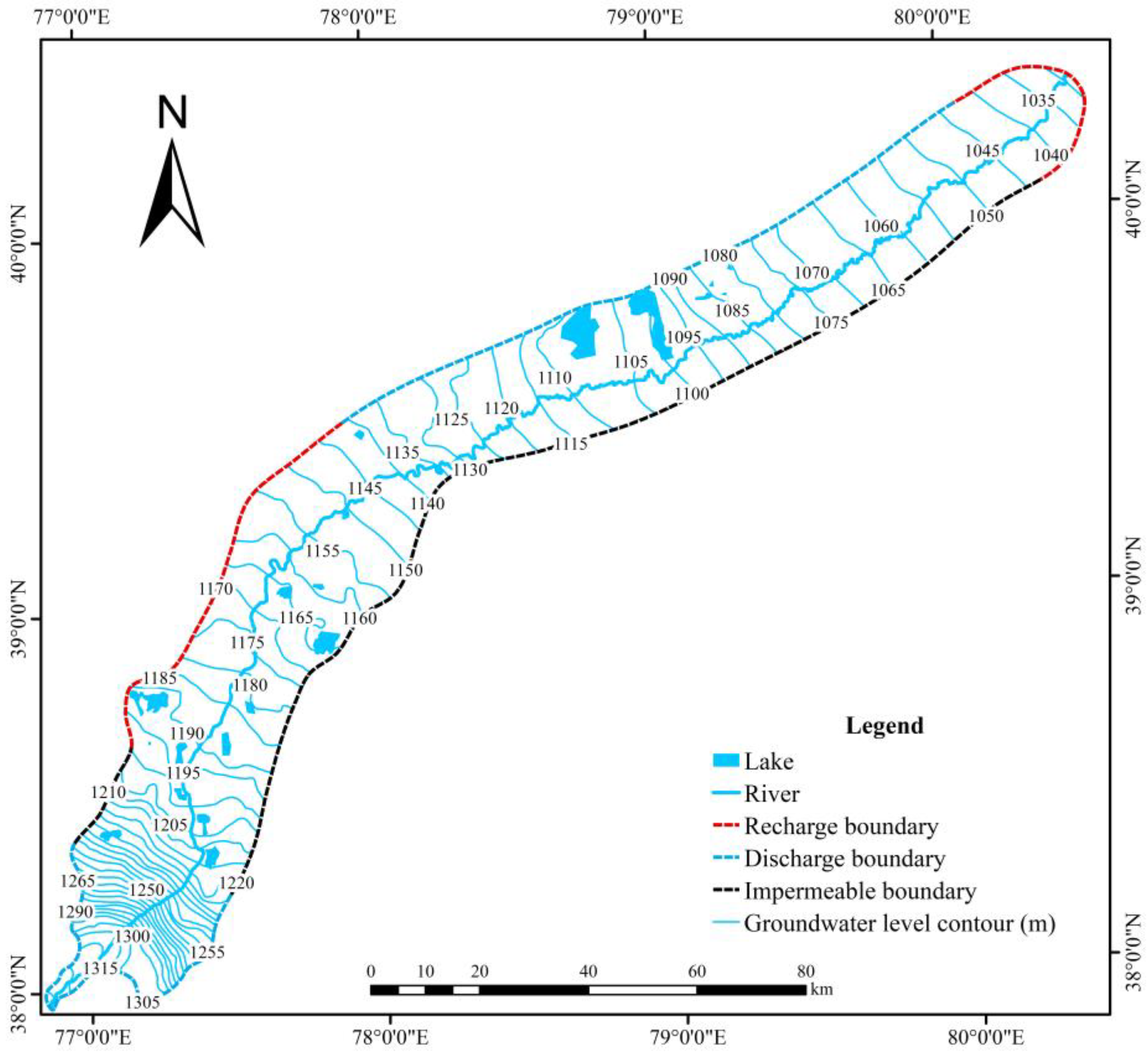
2.1. Study Area Overview
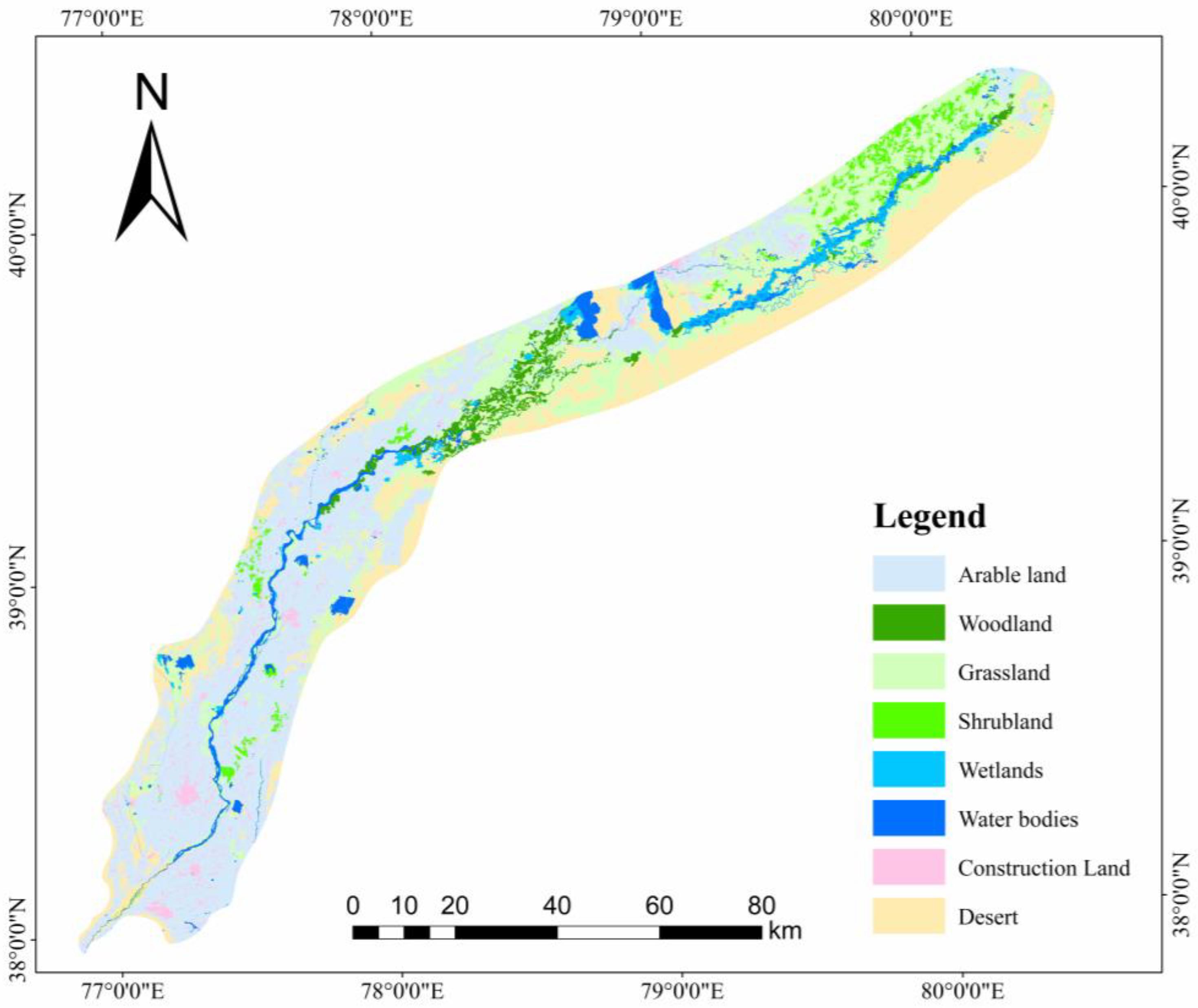
2.2. Data Sources
2.3. MIKE SHE Model
2.4. Model Building
2.4.1. Discretization
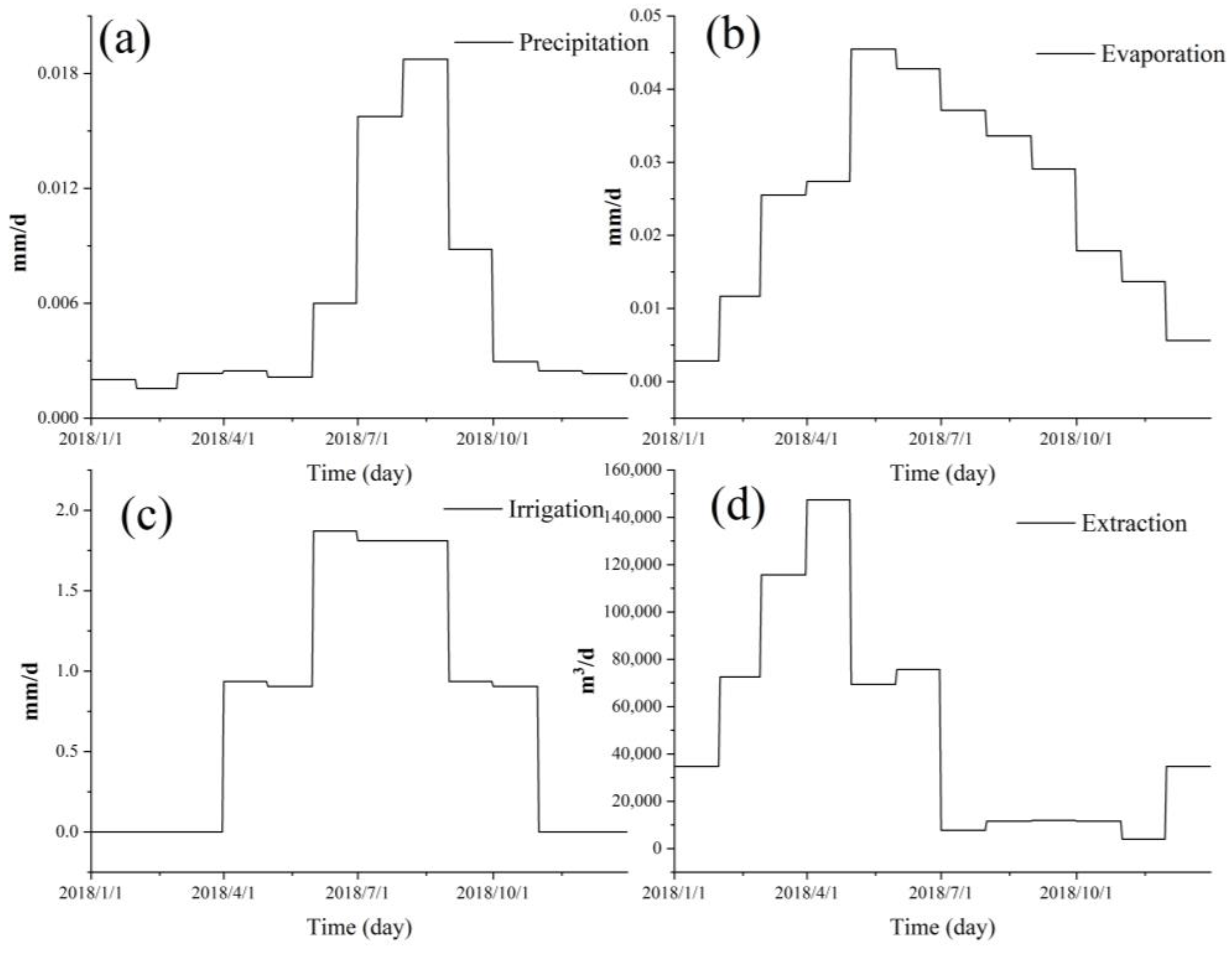
2.4.2. Data Input
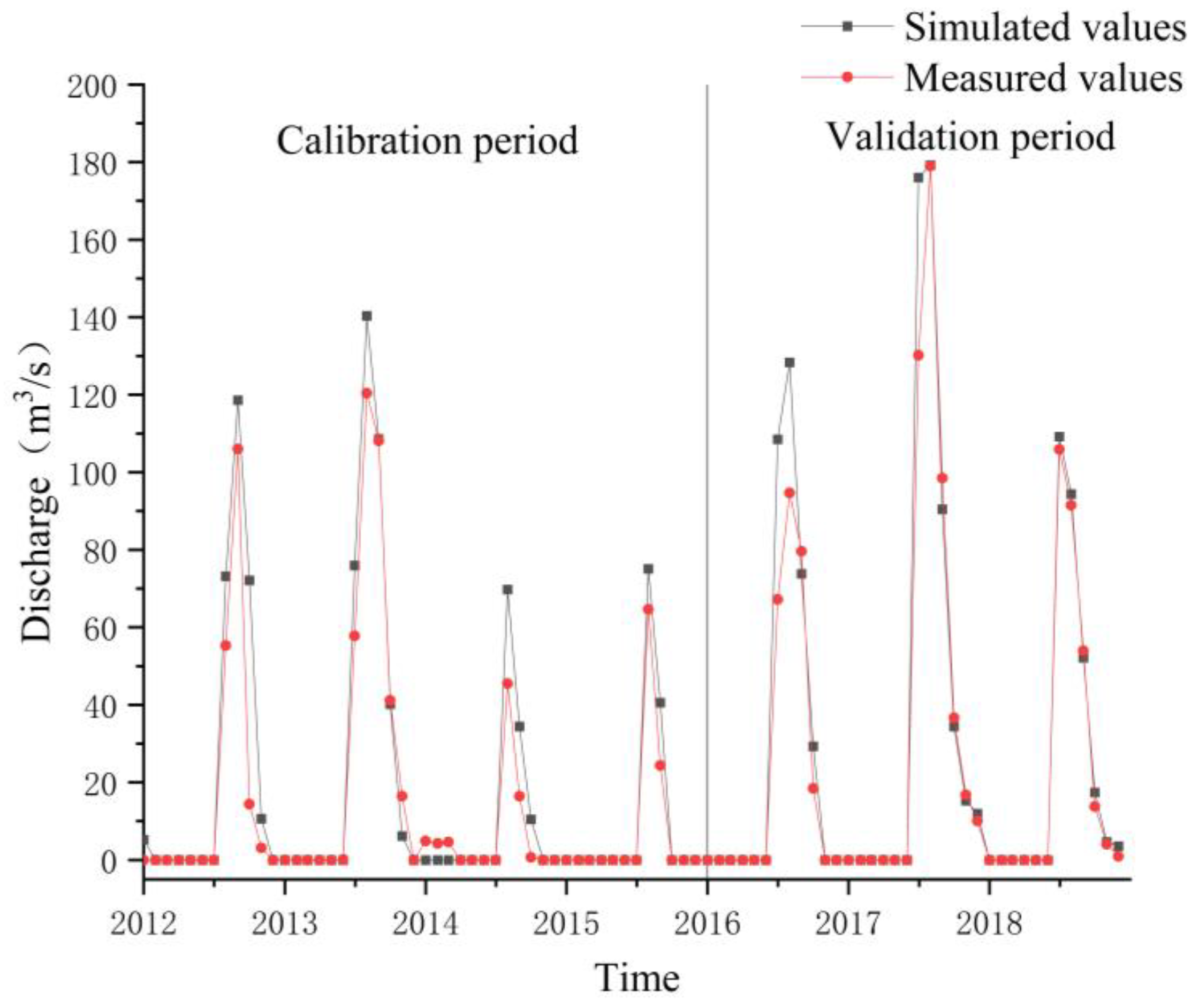
2.4.3. Model Validation and Calibration
3. Results and Discussion
3.1. Parameter Values after Calibration
3.2. Results from the Surface Runoff Calibration and Validation
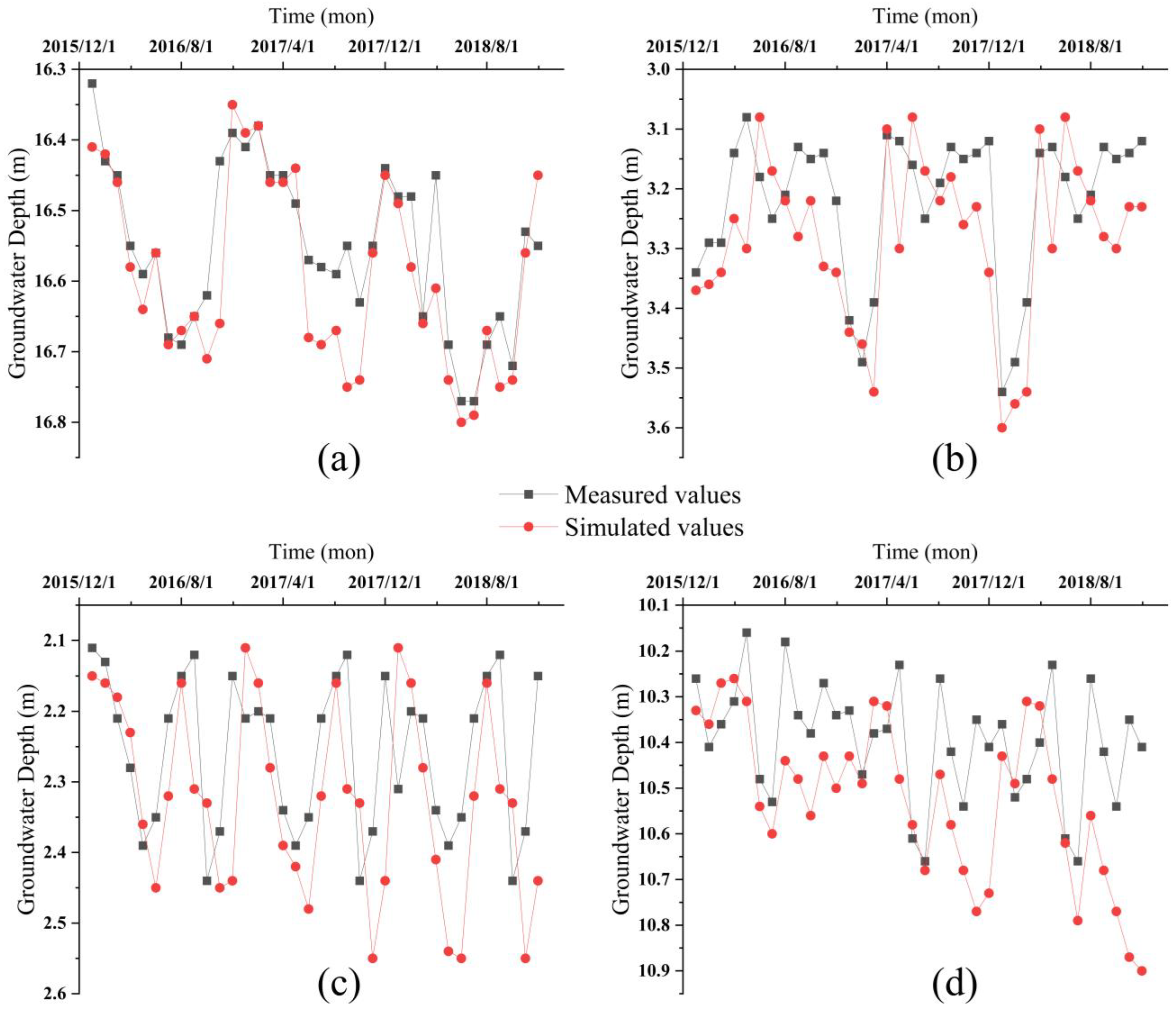
3.3. Groundwater Simulation Validation
3.4. Sensitivity Analysis
3.5. Sensitivity Analysis for the Water Content at Saturation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, R.J.; Fan, Z.L.; Wang, Y.Q. Groundwater resources and their characteristics in the arid zone of northwest China. J. Nat. Res. 2002, 3, 321–326. [Google Scholar]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydrological System — System Hydrologique Europeen, “SHE”, 1: History and philosophy of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Arnone, E.; Noto, L.V.; Lepore, C.; Bras, R.L. Physically-based and distributed approach to analyze rainfall-triggered landslides at watershed scale. Geomorphology. 2011, 133, 121–131. [Google Scholar] [CrossRef] [Green Version]
- Xiao, S.Y.; Yang, G.; He, X.L. Hydrological modeling of MIKE SHE in the Manas River basin. J. Mt. Sci. 2021, 39, 1–9. [Google Scholar] [CrossRef]
- Liang, M.; He, C.G.; Bian, H.F. MIKE SHE modeling of ecohydrological processes: Merits, applications, and challenges. Ecol. Eng. 2016, 96, 137–149. [Google Scholar] [CrossRef]
- Liu, S.W.; Liu, H.L.; Wang, L. Research on the development and application of the MIKE SHE model. Hydrology 2018, 38, 23–28. [Google Scholar]
- Patrick, K.; Markus, D.; Ümüt, H. Effects of Land Use and Climate Change on Groundwater and Ecosystems at the Middle Reaches of the Tarim River Using the MIKE SHE Integrated Hydrological Model. Water 2015, 7, 3040–3056. [Google Scholar] [CrossRef] [Green Version]
- Paparrizos, S.; Maris, F. Hydrological simulation of the Sperchios River basin in Central Greece using the MIKE SHE model and geographic information systems. Appl. Water Sci. 2017, 7, 591–599. [Google Scholar] [CrossRef] [Green Version]
- Jiang, L.F.; Xue, L.Q.; Liu, Y.H. Research on the effect of water-saving irrigation on groundwater levels in arid areas based on the MIKE SHE model. J. Irrig. Drain Eng. 2016, 35, 59–65. [Google Scholar] [CrossRef]
- Lai, D.R.; Qin, H.H.; Wan, W. Analysis of water resources utilization scenarios in North China Plain based on the MIKE SHE model. J. Water Resour. Water Eng. 2018, 29, 60–67. [Google Scholar]
- Guo, Y.; Wu, X.M.; Qie, Z.H. Parameter rate determination of MIKE SHE model based on BP neural network. J. Yangtze River Sci. Res. Inst. 2019, 36, 26–30. [Google Scholar]
- Liu, J.; Liu, T.; Huang, Y. Simulation and analysis of hydrological processes in the Yarkant River basin based on remote sensing data. Adv. Geophys. 2017, 36, 753–761. [Google Scholar]
- Brohan, P.; Kennedy, J.J.; Harris, I.; Tett, S.F.B.; Jones, P.D. Uncertainty estimates in regional and global observed temperature changes: A new data set from 1850. J. Geophys. Res. 2006, 111, D12106. [Google Scholar] [CrossRef] [Green Version]
- Ren, J.G. Study the Transformation of Three Glasses of Water in Xinjiang’s Plain Area of the Yarkant River Basin. Master’s Thesis, Chengdu University of Technology, Chengdu, China, 2004. [Google Scholar]
- Chen, Y.N.; Yang, Q.; Luo, Y. Reflections on Water Resources in the Northwest Arid Zone. AZG 2012, 35, 1–9. [Google Scholar]
- Zhai, J.Q.; Liu, K.; Zhao, Y. Research progress of groundwater level regulation methods and models in oases in arid areas. J. Hydrol. 2021, 41, 1–7. [Google Scholar] [CrossRef]
- Huang, C.J.; Li, C.G.; Jing He, F.X. Impact of land use and precipitation changes on groundwater level in the area around the Yellow River in the Zhongning section of Ningxia based on the MIKE SHE model. Hydropower Energy Sci. 2022, 40, 14–17. [Google Scholar]
- Park, G.T.; An, S.H.; Jang, D.W. Runoff Estimation in Ungauged Watershed and Sensitivity Analysis According to the Soi Characteristics: Case Study of the Saint Blaise Vallon in France. Sustainability 2022, 14, 9848. [Google Scholar] [CrossRef]
- Lu, R.K. Soil Agricultural Chemical Analysis Method; Chinese Agricultural Science and Technology Press: Beijing, China, 1999. (In Chinese) [Google Scholar]
- Zhang, J. Study on the Evolution of Groundwater Quality and Its Formation Mechanism in the Plain Area of the Yarkant River Basin. Ph.D. Thesis, Xinjiang Agricultural University, Urumqi, China, 2021. [Google Scholar]
- Rouhani, S.; Myers, D.E. Problems in space-time kriging of geohydrological data. Math. Geol. 1990, 22, 611–623. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, J.L.; Nai, Y.H. Spatial distribution and causes of shallow groundwater salinization in the plain area of Yarkant River basin, Xinjiang. J. Agric. Engitaly 2019, 35, 126–134. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I-a discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Ma, Q. Research on Drought Assessment and Forecasting Model of Huangshui Basin Based on MIKE SHE Model. Master’s Thesis, Northwest Agriculture and Forestry University of Science and Technology, Xi’an, China, 2014. [Google Scholar]
- Wang, Z.G.; Xia, J.; Liu, C.M.; Ou, C.P.; Zhang, Y.Y. Exploration of parameter rate determination and sensitivity analysis of distributed hydrological model. J. Nat. Resour. 2007, 4, 649–655. [Google Scholar]
- Ma, Q. Deterministic Hydrological Modelling for Real Time Decision Support System: Application to the Var Catchment. Ph.D. Thesis, Université Côte d’Azur, Nice, France, 2018. [Google Scholar]
- Mariotti, A.; Blard, P.H.; Charreau, J.; Petit, C.; Molliex, S.; Bourles, D.L. Denudation systematics inferred from in situ cosmogenic10Be concentrations in fine (50–100 µm) and medium (100–250 µm) sediments of the Var River basin, southern French Alps. Earth Surf. Dynam. 2019, 7, 1059–1074. [Google Scholar] [CrossRef] [Green Version]




| Data Types | Description of the Data | Data Sources |
|---|---|---|
| DEM data | Resolution 30 × 30 m | http://www.gscloud.cn (accessed on 14 June 2022) |
| Meteorological data | Monthly data of five weather stations from 2012 to 2018 | Kashgar Regional Meteorological Bureau |
| Land use data | Land use data at a 30 m spatial resolution | http://www.globallandcover.com (accessed on 29 June 2022) |
| Hydrological data | Monthly runoff data of Kachun and Hainiaz hydrological station from 2012 to 2018 | Xinjiang Institute of Water Resources and Hydropower Survey and Design |
| Soil data | Resolution 1 km | National Scientific Data Center for Glacial Permafrost Desert (http://www.ncdc.ac.cn) (accessed on 29 June 2022). |
| Soil particle data | 9 sampling sites | Xinjiang Geotechnical Testing Centre |
| Borehole data | 261 boreholes, including parametric and groundwater level data | Xinjiang Corps Survey and Design Institute |
| Groundwater balance data | Groundwater recharge and discharge in the study area | Xinjiang Corps Survey and Design Institute |
| Code | Land Use Types | LAI | Root Depth (mm) |
|---|---|---|---|
| 10 | cropland | 1.5–5.0 | 200–1000 |
| 20 | woodland | 6.0 | 800 |
| 30 | grassland | 1.1–4.0 | 300 |
| 40 | shrubland | 6.0 | 800 |
| 50 | wetland | 0.8 | 100 |
| 60 | water body | 0 | 0 |
| 80 | building land | 0.8 | 100 |
| 90 | bare land | 0 | 0 |
| Parameter | Value | Unit |
|---|---|---|
| Rivers and lakes | ||
| Resistance value Yarkant riverbed (Manning M) | 45 | m1/3·s−1 |
| Leakage coefficient | 0.00001 | — |
| Overland Flow | ||
| Resistance value (Manning M) | 35 | m1/3·s−1 |
| Detention storage | 0.01 | mm |
| Initial water depth | 0 | m |
| Saturated & Unsaturated zones | ||
| Sand: Qs; Qr; Sy; Ks | 0.38; 0.08; 0.33; 1.0 × 10−3 | —; —; —; m/s |
| Loamy sand: Qs; Qr; Sy; Ks | 0.07; 0.31; 2.3 × 10−4 | —; —; —; m/s |
| Sandy loam: Qs; Qr; Sy; Ks | 0.02; 0.30; 1.2 × 10−4 | —; —; —; m/s |
| Loam: Qs; Qr; Sy; Ks | 0.02; 0.15; 5.2 × 10−5 | —; —; —; m/s |
| Silty loam: Qs; Qr; Sy; Ks | 0.08; 0.18; 4.7 × 10−5 | —; —; —; m/s |
| Silt: Qs; Qr; Sy; Ks | 0.28; 0.11; 0.14; 5.0 × 10−5 | —;—;—;m/s |
| Silty clay: Qs; Qr; Sy; Ks | 0.27; 0.09; 0.11; 2.6 × 10−6 | —;—;—;m/s |
| Clay: Qs; Qr; Sy; Ks | 0.56; 0.22; 0.05; 3.0 × 10−6 | —;—;—;m/s |
| Stage | Monthly Runoff | ||
|---|---|---|---|
| Efficiency Coefficient | Water Balance Coefficient | Correlation Coefficient | |
| Calibration period | 0.85 | 0.61 | 0.96 |
| Validation period | 0.93 | 0.83 | 0.97 |
| Location of the Observation Wells | Hietidun Township | Aktamu Township | 49th Regiment | Tagalchi Township |
|---|---|---|---|---|
| Relative Error | 3.45% | 1.59% | 2.52% | 0.35% |
| Water Content at Saturation | Water Content at Wilting Point | Saturated Hydraulic Conductivity (m/s) | |
|---|---|---|---|
| Sand | 0.38 | 0.08 | 1.0 × 10−3 |
| Loamy sand | 0.39 | 0.07 | 2.3 × 10−4 |
| Sandy loam | 0.33 | 0.10 | 1.2 × 10−4 |
| Loam | 0.39 | 0.12 | 5.2 × 10−5 |
| Silty loam | 0.29 | 0.08 | 4.7 × 10−5 |
| Silt | 0.28 | 0.11 | 5.0 × 10−5 |
| Silty clay | 0.37 | 0.19 | 2.6 × 10−6 |
| Clay | 0.56 | 0.22 | 3.0 × 10−6 |
| Peak Discharge: 39.72 m3/s |
| Water Content at Saturation | Water Content at Wilting Point | Saturated Hydraulic Conductivity (m/s) | |
|---|---|---|---|
| Sand | 0.494 | 0.08 | 1.0 × 10−3 |
| Loamy sand | 0.507 | 0.07 | 2.3 × 10−4 |
| Sandy loam | 0.429 | 0.10 | 1.2 × 10−4 |
| Loam | 0.507 | 0.12 | 5.2 × 10−5 |
| Silty loam | 0.377 | 0.08 | 4.7 × 10−5 |
| Silt | 0.364 | 0.11 | 5.0 × 10−5 |
| Silty clay | 0.481 | 0.19 | 2.6 × 10−6 |
| Clay | 0.728 | 0.22 | 3.0 × 10−6 |
| Peak Discharge: 9.42 m3/s |
| Clay | Clay Loam | Loam | Sand | Sandy Clay Loam | Sandy Loam | Silty Clay | Silty Loam | |
|---|---|---|---|---|---|---|---|---|
| Arable land | 0.5% | 13.7% | 47.9% | 11.2% | 2.1% | 0% | 16.2% | 8.4% |
| Range | −30% | −20% | −10% | Standard | +10% | +20% | +30% |
|---|---|---|---|---|---|---|---|
| Loam | 0.273 | 0.312 | 0.351 | 0.390 | 0.429 | 0.468 | 0.507 |
| Peak Discharge (m3/s) | 47.26 | 46.5 | 43.58 | 39.72 | 36.52 | 35.34 | 34.87 |
| Range | −30% | −20% | −10% | Standard | +10% | +20% | +30% |
|---|---|---|---|---|---|---|---|
| Loam | 0.273 | 0.312 | 0.351 | 0.390 | 0.429 | 0.468 | 0.507 |
| Hietidun Township (m) | 2.40 | 2.38 | 2.35 | 2.34 | 2.31 | 2.30 | 2.29 |
| Aktamu Township (m) | 10.61 | 10.61 | 10.60 | 10.60 | 10.59 | 10.57 | 10.57 |
| 49th Regiment (m) | 3.35 | 3.34 | 3.32 | 3.32 | 3.33 | 3.34 | 3.36 |
| Tagalchi Township (m) | 16.65 | 16.65 | 16.65 | 16.65 | 16.65 | 16.65 | 16.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Li, S.; Ge, Y. Numerical Simulation of the Lower and Middle Reaches of the Yarkant River (China) Using MIKE SHE. Water 2023, 15, 2492. https://doi.org/10.3390/w15132492
Wang B, Li S, Ge Y. Numerical Simulation of the Lower and Middle Reaches of the Yarkant River (China) Using MIKE SHE. Water. 2023; 15(13):2492. https://doi.org/10.3390/w15132492
Chicago/Turabian StyleWang, Bohui, Sheng Li, and Yanyan Ge. 2023. "Numerical Simulation of the Lower and Middle Reaches of the Yarkant River (China) Using MIKE SHE" Water 15, no. 13: 2492. https://doi.org/10.3390/w15132492
APA StyleWang, B., Li, S., & Ge, Y. (2023). Numerical Simulation of the Lower and Middle Reaches of the Yarkant River (China) Using MIKE SHE. Water, 15(13), 2492. https://doi.org/10.3390/w15132492




