Incorporating Wetland Delineation and Impacts in Watershed-Scale Hydrologic Modeling
Abstract
1. Introduction
2. Materials and Methods
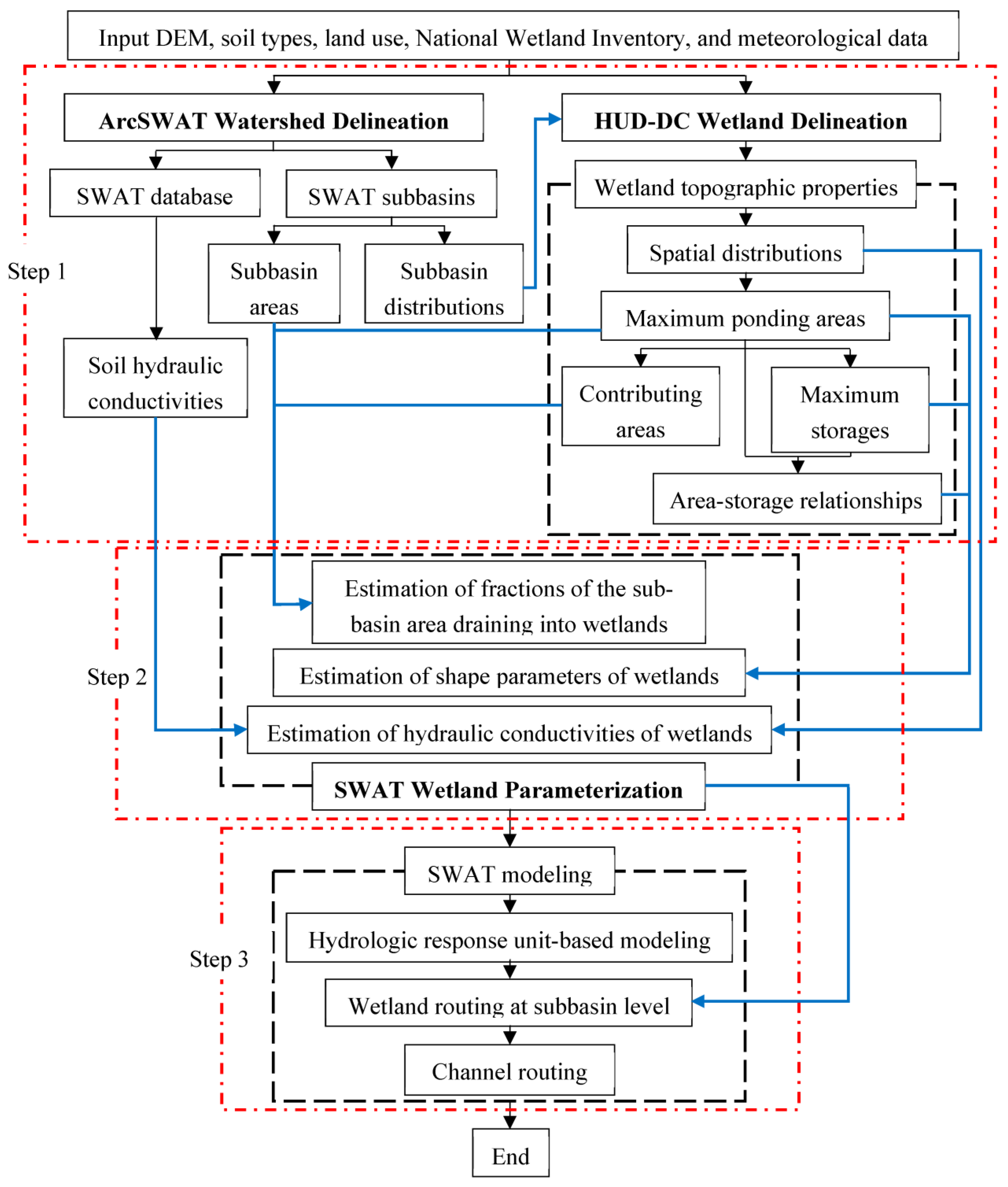
2.1. Overall Modeling Framework
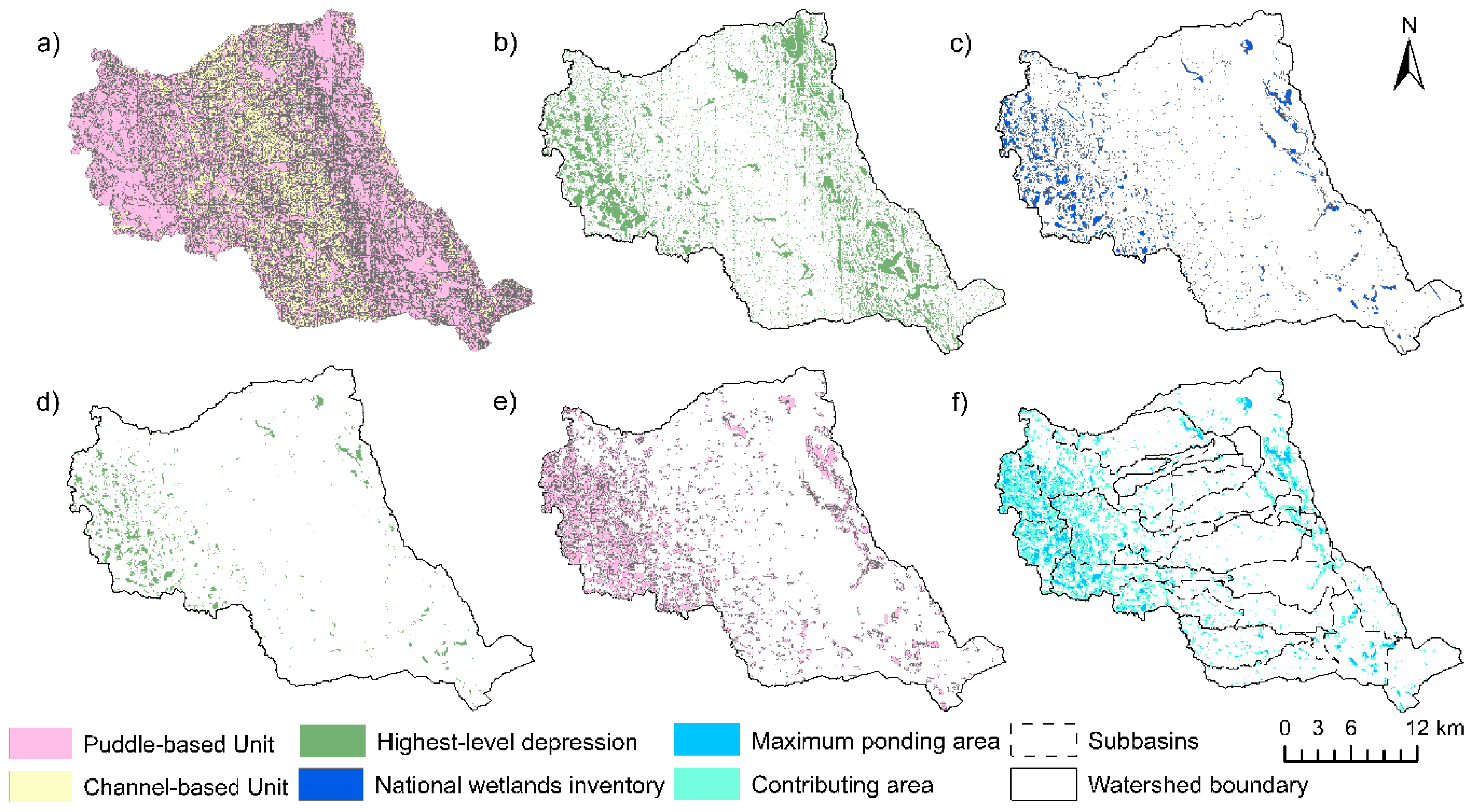
2.2. HUD-DC Wetland Delineation
2.3. Introduction to SWAT Modeling
2.4. Wetland Parameterization
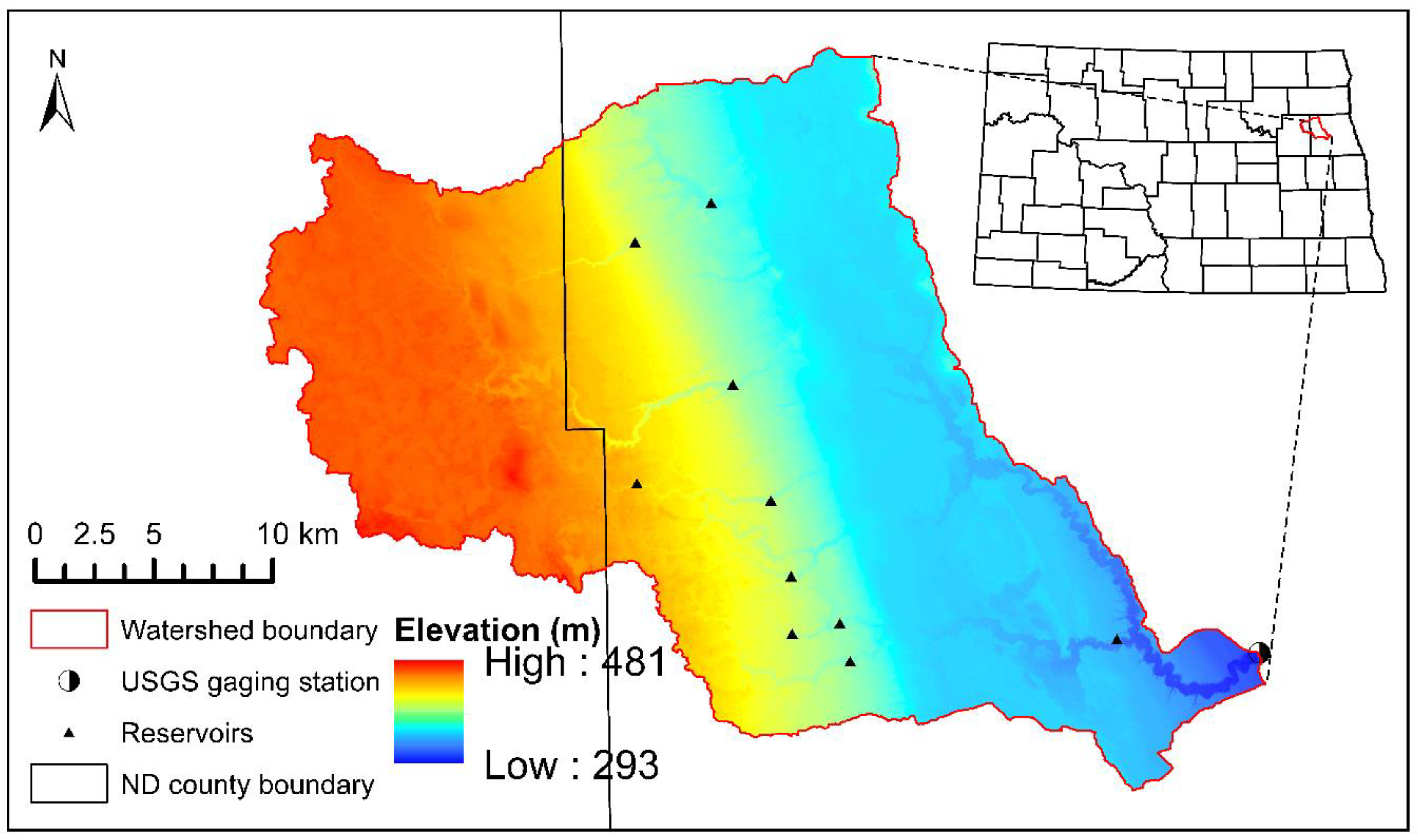
2.5. Study Area and Model Setup
3. Results and Discussion
3.1. Delineation of Wetlands
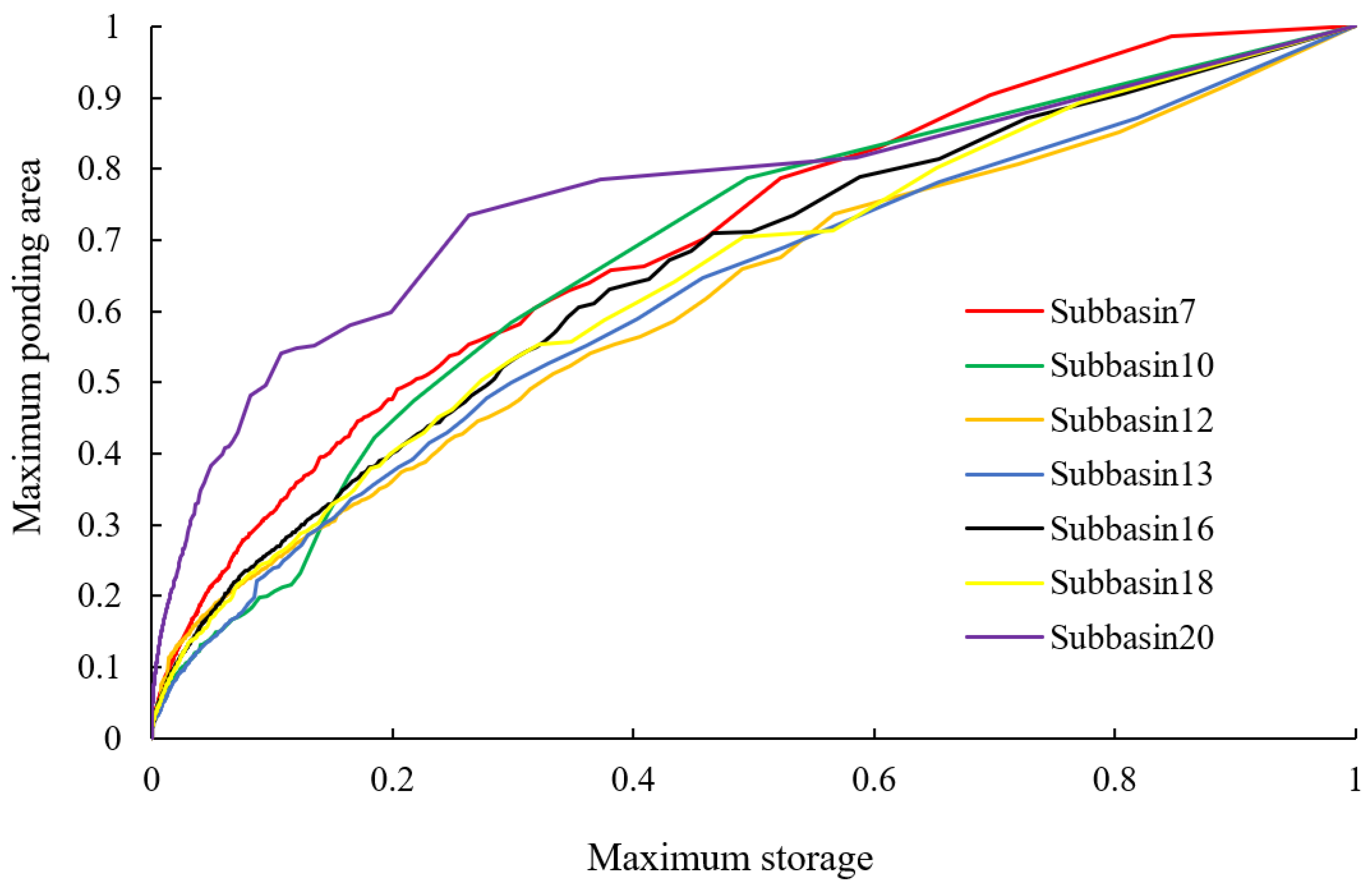
3.2. Wetland-Related Parameters
3.3. Joint Model Performance for Wetland-Influenced Areas
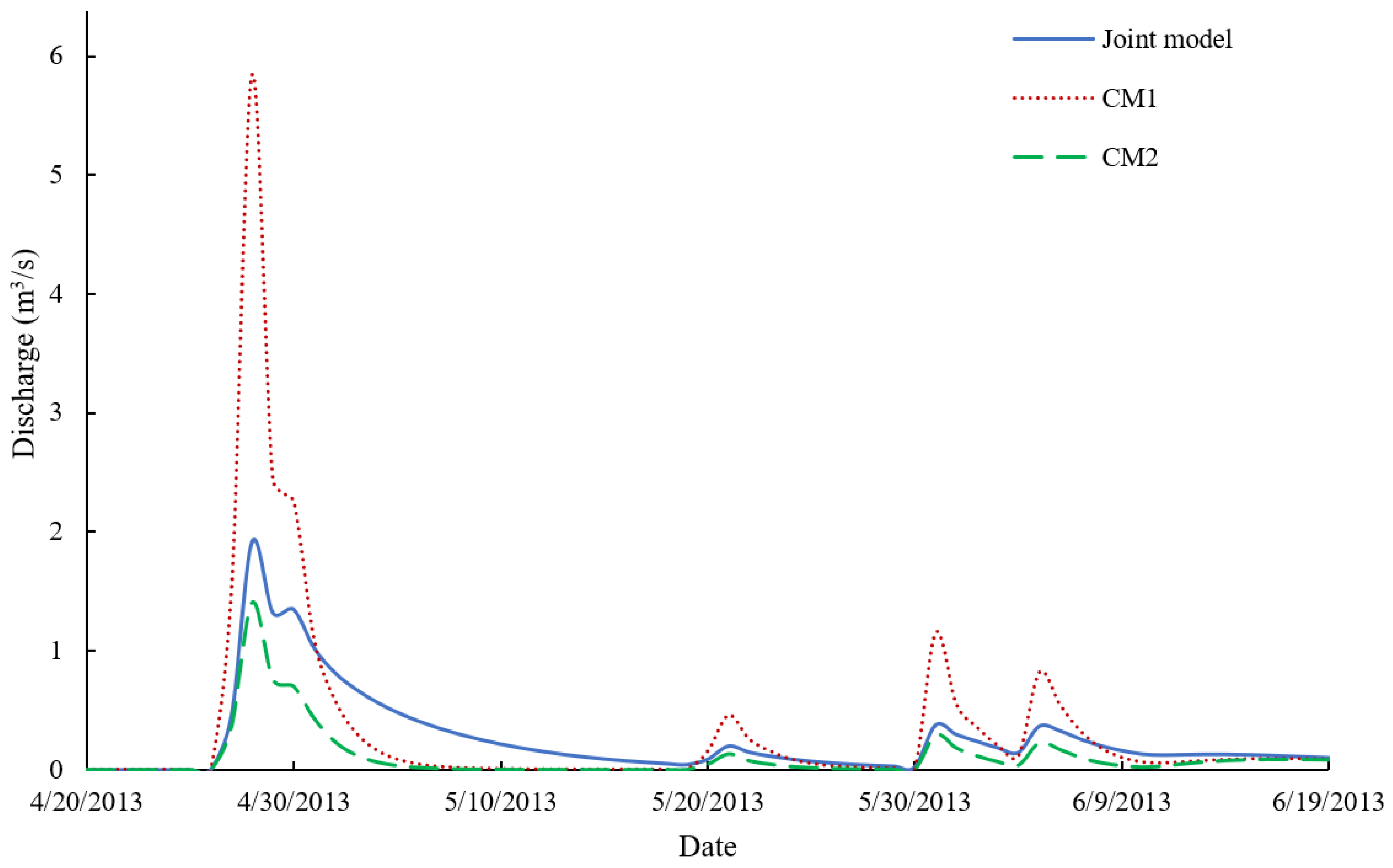
3.4. Joint Model vs. Two Other SWAT Models
3.5. Impacts of Vnor and SAnor
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jalowska, A.M.; Yuan, Y. Evaluation of SWAT impoundment modeling methods in water and sediment simulations. J. Am. Water Resour. Assoc. 2019, 55, 209–227. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Yang, W.; Wang, X. Development of a SWAT extension module to simulate riparian wetland hydrologic processes at a watershed scale. Hydrol. Process. 2008, 22, 2901–2915. [Google Scholar] [CrossRef]
- Wu, K.; Johnston, C.A. Hydrologic comparison between a forested and a wetland/lake dominated watershed using SWAT. Hydrol. Process. 2008, 22, 1431–1442. [Google Scholar] [CrossRef]
- Blanchette, M.; Rousseau, A.N.; Savary, S.; Foulon, É. Are spatial distribution and aggregation of wetlands reliable indicators of stream flow mitigation? J. Hydrol. 2022, 608, 127646. [Google Scholar] [CrossRef]
- Evenson, G.R.; Golden, H.E.; Lane, C.R.; D’Amico, E. Geographically isolated wetlands and watershed hydrology: A modified model analysis. J. Hydrol. 2015, 529, 240–256. [Google Scholar] [CrossRef]
- Evenson, G.R.; Jones, C.N.; McLaughlin, D.L.; Golden, H.E.; Lane, C.R.; DeVries, B.; Alexander, L.C.; Lang, M.W.; McCarty, G.W.; Sharifi, A. A watershed-scale model for depressional wetland-rich landscapes. J. Hydrol. X 2018, 1, 100002. [Google Scholar] [CrossRef]
- Golden, H.E.; Sander, H.A.; Lane, C.R.; Zhao, C.; Price, K.; D’Amico, E.; Christensen, J.R. Relative effects of geographically isolated wetlands on streamflow: A watershed-scale analysis. Ecohydrology 2016, 9, 21–38. [Google Scholar] [CrossRef]
- Haque, A.; Ali, G.; Badiou, P. Event-based analysis of wetland hydrologic response in the Prairie Pothole Region. J. Hydrol. 2022, 604, 127237. [Google Scholar] [CrossRef]
- Lee, S.; Yeo, I.Y.; Lang, M.W.; Sadeghi, A.M.; McCarty, G.W.; Moglen, G.E.; Evenson, G.R. Assessing the cumulative impacts of geographically isolated wetlands on watershed hydrology using the SWAT model coupled with improved wetland modules. J. Environ. Manag. 2018, 223, 37–48. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Martinez, E.; Nejadhashemi, A.P.; Woznicki, S.A.; Love, B.J. Modeling the hydrological significance of wetland restoration scenarios. J. Environ. Manag. 2014, 133, 121–134. [Google Scholar] [CrossRef]
- Perez-Valdivia, C.; Cade-Menun, B.; McMartin, D.W. Hydrological modeling of the pipestone creek watershed using the Soil Water Assessment Tool (SWAT): Assessing impacts of wetland drainage on hydrology. J. Hydrol. Reg. Stud. 2017, 14, 109–129. [Google Scholar] [CrossRef]
- Smith, A.; Tetzlaff, D.; Gelbrecht, J.; Kleine, L.; Soulsby, C. Riparian wetland rehabilitation and beaver re-colonization impacts on hydrological processes and water quality in a lowland agricultural catchment. Sci. Total Environ. 2020, 699, 134302. [Google Scholar] [CrossRef] [PubMed]
- Fluet-Chouinard, E.; Stocker, B.D.; Zhang, Z.; Malhotra, A.; Melton, J.R.; Poulter, B.; Kaplan, J.O.; Goldewijk, K.K.; Siebert, S.; Minayeva, T.; et al. Extensive global wetland loss over the past three centuries. Nature 2023, 614, 281–286. [Google Scholar] [CrossRef]
- Otte, M.L.; Fang, W.T.; Jiang, M. A framework for identifying reference wetland conditions in highly altered landscapes. Wetlands 2021, 41, 40. [Google Scholar] [CrossRef]
- Chu, X.; Rediske, R. Modeling metal and sediment transport in a stream-wetland system. J. Environ. Eng. 2012, 138, 152–163. [Google Scholar] [CrossRef]
- Frei, S.; Lischeid, G.; Fleckenstein, J.H. Effects of micro-topography on surface–subsurface exchange and runoff generation in a virtual riparian wetland—A modeling study. Adv. Water Resour. 2010, 33, 1388–1401. [Google Scholar] [CrossRef]
- Hughes, D.A.; Tshimanga, R.M.; Tirivarombo, S.; Tanner, J. Simulating wetland impacts on stream flow in southern Africa using a monthly hydrological model. Hydrol. Process. 2014, 28, 1775–1786. [Google Scholar] [CrossRef]
- Ju, X.; Du, C.; Feng, F.; Zhou, D.; Deng, X. An eco-hydrological model for modelling hydrological processes in a riparian wetland with the unclosed boundary. Ecohydrol. Hydrobiol. 2022. [Google Scholar] [CrossRef]
- Rezaeianzadeh, M. Wetland Hydrologic Modeling through Physically-Based and Data-Driven Approaches. Ph.D. Thesis, Auburn University, Auburn, AL, USA, 28 July 2017. [Google Scholar]
- Shook, K.; Pomeroy, J.W.; Spence, C.; Boychuk, L. Storage dynamics simulations in prairie wetland hydrology models: Evaluation and parameterization. Hydrol. Process. 2013, 27, 1875–1889. [Google Scholar] [CrossRef]
- Wen, L.; Macdonald, R.; Morrison, T.; Hameed, T.; Saintilan, N.; Ling, J. From hydrodynamic to hydrological modelling: Investigating long-term hydrological regimes of key wetlands in the Macquarie Marshes, a semi-arid lowland floodplain in Australia. J. Hydrol. 2013, 500, 45–61. [Google Scholar] [CrossRef]
- Weng, P.; Sánchez-Pérez, J.M.; Sauvage, S.; Vervier, P.; Giraud, F. Assessment of the quantitative and qualitative buffer function of an alluvial wetland: Hydrological modelling of a large floodplain (Garonne River, France). Hydrol. Process. 2003, 17, 2375–2392. [Google Scholar] [CrossRef]
- Zhang, L.; Mitsch, W.J. Modelling hydrological processes in created freshwater wetlands: An integrated system approach. Environ. Model. Softw. 2005, 20, 935–946. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M.; Morgan, D.S. Hydrologic model for design and constructed wetlands. Wetlands 2001, 21, 167–178. [Google Scholar] [CrossRef]
- Evenson, G.R.; Golden, H.E.; Lane, C.R.; D’Amico, E. An improved representation of geographically isolated wetlands in a watershed-scale hydrologic model. Hydrol. Process. 2016, 30, 4168–4184. [Google Scholar] [CrossRef]
- Ikenberry, C.D.; Crumpton, W.G.; Arnold, J.G.; Soupir, M.L.; Gassman, P.W. Evaluation of existing and modified wetland equations in the SWAT model. J. Am. Water Resour. Assoc. 2017, 53, 1267–1280. [Google Scholar] [CrossRef]
- Qi, J.; Zhang, X.; Lee, S.; Moglen, G.E.; Sadeghi, A.M.; McCarty, G.W. A coupled surface water storage and subsurface water dynamics model in SWAT for characterizing hydroperiod of geographically isolated wetlands. Adv. Water Resour. 2019, 131, 103380. [Google Scholar] [CrossRef]
- Rahman, M.M.; Thompson, J.R.; Flower, R.J. An enhanced SWAT wetland module to quantify hydraulic interactions between riparian depressional wetlands, rivers and aquifers. Environ. Model. Softw. 2016, 84, 263–289. [Google Scholar] [CrossRef]
- Wang, X.; Yang, W.; Melesse, A.M. Using hydrologic equivalent wetland concept within SWAT to estimate streamflow in watersheds with numerous wetlands. Trans. ASABE 2008, 51, 55–72. [Google Scholar] [CrossRef]
- Zeng, L.; Shao, J.; Chu, X. Improved hydrologic modeling for depression-dominated areas. J. Hydrol. 2020, 590, 125269. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, W.; Leon, L.; Wong, I.; McCrimmon, C.; Dove, A.; Fong, P. Hydrologic modeling and evaluation of Best Management Practice scenarios for the Grand River watershed in Southern Ontario. J. Great Lakes Res. 2016, 42, 1289–1301. [Google Scholar] [CrossRef]
- Yang, W.; Liu, Y.; Ou, C.; Gabor, S. Examining water quality effects of riparian wetland loss and restoration scenarios in a southern Ontario watershed. J. Environ. Manag. 2016, 174, 26–34. [Google Scholar] [CrossRef]
- Wang, N.; Chu, X. A new algorithm for delineation of surface depressions and channels. Water 2020, 12, 7. [Google Scholar] [CrossRef]
- Winchell, M.; Srinivasan, R.; Di Luzio, M.; Arnold, J. ArcSWAT Interface for SWAT 2005 User’s Guide; Blackland Research Center & Grassland, Soil and Water Research Laboratory: Temple, TX, USA, 2007. [Google Scholar]
- USGS. National Map Viewer. Available online: https://www.usgs.gov/tools/national-map-viewer (accessed on 7 June 2022).
- U.S. Fish & Wildlife Service. National Wetlands Inventory. Available online: https://data.nal.usda.gov/dataset/national-wetlands-inventory (accessed on 15 July 2022).
- Chu, X.; Zhang, J.; Chi, Y.; Yang, J. An improved method for watershed delineation and computation of surface depression storage. In Watershed Management 2010: Innovations in Watershed Management Under Land Use and Climate Change, Proceedings of the 2010 Watershed Management Conference, Madison, WI, USA, 23–27 August 2010; Potter, K.W., Frevert, D.K., Eds.; American Society of Civil Engineers: New York, NY, USA, 2012; pp. 1113–1122. [Google Scholar]
- Chu, X.; Yang, J.; Chi, Y.; Zhang, J. Dynamic puddle delineation and modeling of puddle-to-puddle filling-spilling-merging-splitting overland flow processes. Water Resour. Res. 2013, 49, 3825–3829. [Google Scholar] [CrossRef]
- Chu, X. Delineation of pothole-dominated wetlands and modeling of their threshold behaviors. J. Hydrol. Eng. 2017, 22, D5015003. [Google Scholar] [CrossRef]
- Wang, N.; Chu, X.; Zhang, X. Functionalities of surface depressions in runoff routing and hydrologic connectivity modeling. J. Hydrol. 2021, 593, 125870. [Google Scholar] [CrossRef]
- Zeng, L.; Shen, H.; Cui, Y.; Chu, X.; Shao, J. Incorporating the Filling–Spilling Feature of Depressions into Hydrologic Modeling. Water 2022, 14, 652. [Google Scholar] [CrossRef]
- Zeng, L.; Chu, X. A new probability-embodied model for simulating variable contributing areas and hydrologic processes dominated by surface depressions. J. Hydrol. 2021, 602, 126762. [Google Scholar] [CrossRef]
- Zeng, L.; Chu, X. Integrating depression storages and their spatial distribution in watershed-scale hydrologic modeling. Adv. Water Resour. 2021, 151, 103911. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- USDA. Web Soil Survey. Available online: http://websoilsurvey.nrcs.usda.gov/ (accessed on 7 June 2022).
- Dewitz, J. National Land Cover Database (NLCD) 2019 Products; U.S. Geological Survey data release; Version 2.0; U.S. Geological Survey: Reston, VA, USA, 2021. [Google Scholar] [CrossRef]
- PRISM Climate Group. PRISM Climate Data. Available online: https://prism.oregonstate.edu (accessed on 6 June 2022).
- NASA. NASA Prediction of Worldwide Energy Resources (POWER). Available online: https://power.larc.nasa.gov/ (accessed on 6 June 2022).
- Shabani, A.; Zhang, X.; Chu, X.; Dodd, T.P.; Zheng, H. Mitigating Impact of Devils Lake Flooding on the Sheyenne River Sulfate Concentration. J. Am. Water Resour. Assoc. 2020, 56, 297–309. [Google Scholar] [CrossRef]
- USGS. National Water Information System. Available online: http://waterdata.usgs.gov/nwis/ (accessed on 26 July 2022).
- Abbaspour, K.C. SWAT-CUP: SWAT Calibration and Uncertainty Program—A User Manual; Eawag—Swiss Federal Institute of Aquatic Science and Technology: Dübendorf, Switzerland, 2015. [Google Scholar]
- Rouholahnejad, E.; Abbaspour, K.C.; Vejdani, M.; Srinivasan, R.; Schulin, R.; Lehmann, A. A parallelization framework for calibration of hydrological models. Environ. Model. Softw. 2012, 31, 28–36. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Tahmasebi Nasab, M.; Grimm, K.; Bazrkar, M.H.; Zeng, L.; Shabani, A.; Zhang, X.; Chu, X. SWAT modeling of non-point source pollution in depression-dominated basins under varying hydroclimatic conditions. Int. J. Environ. Res. Public Health 2018, 15, 2492. [Google Scholar] [CrossRef] [PubMed]
- Qiu, L.J.; Zheng, F.L.; Yin, R.S. SWAT-based runoff and sediment simulation in a small watershed, the loessial hilly-gullied region of China: Capabilities and challenges. Int. J. Sediment Res. 2012, 27, 226–234. [Google Scholar] [CrossRef]
- Grimaldi, S.; Volpi, E.; Langousis, A.; Papalexiou, S.M.; De Luca, D.L.; Piscopia, R.; Nerantzaki, S.D.; Papacharalampous, G.; Petroselli, A. Continuous hydrologic modelling for small and ungauged basins: A comparison of eight rainfall models for sub-daily runoff simulations. J. Hydrol. 2022, 610, 127866. [Google Scholar] [CrossRef]

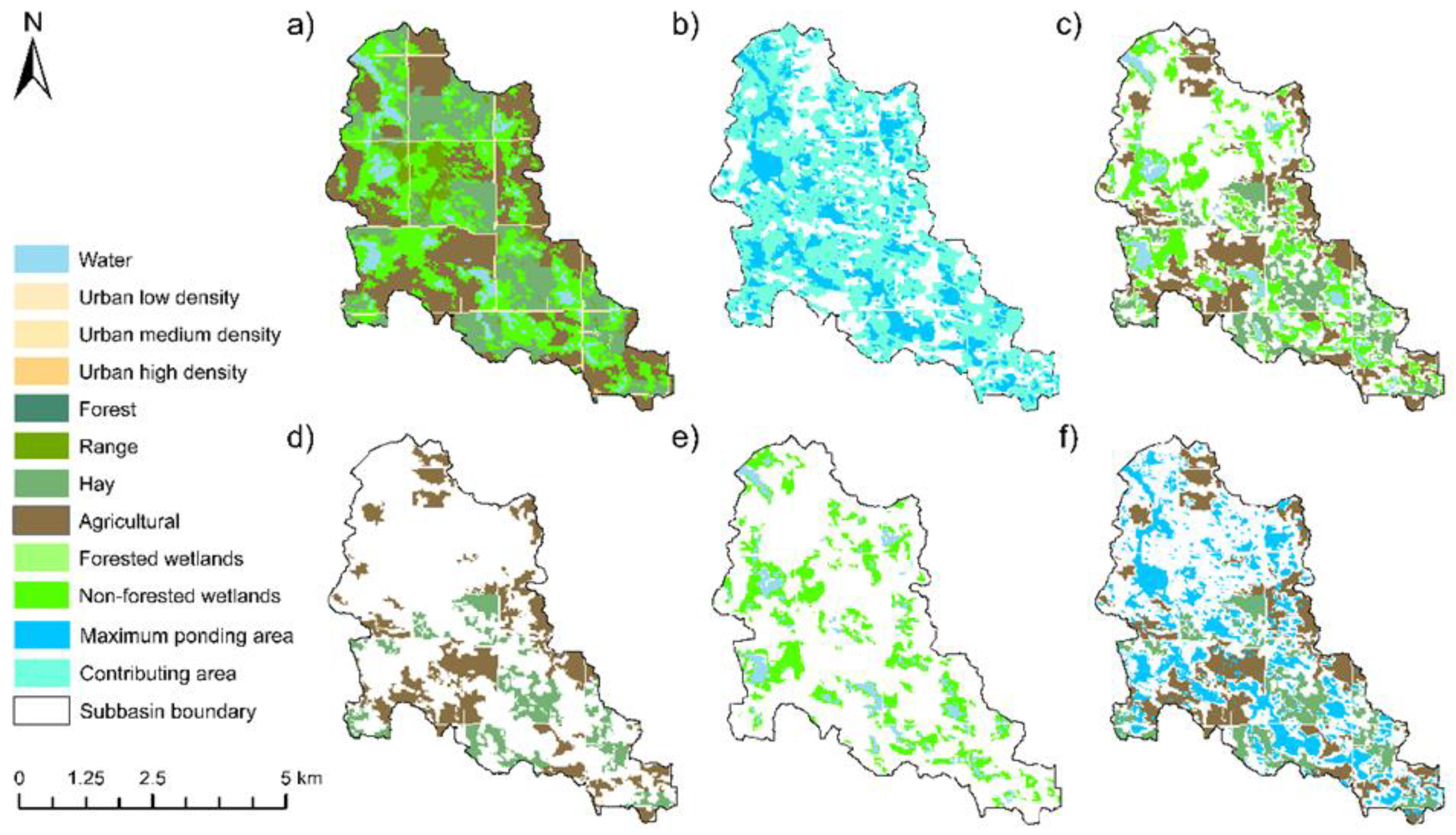
| Data | Sources |
|---|---|
| Digital Elevation Model (DEM) | 3D Elevation Program [35] |
| Soils | Soil Survey Geographic (SSURGO) Database [45] |
| Land Use and Land Cover (LULC) | National Land Cover Database (NLCD) [46] |
| Daily Precipitation, Max and Min Temperatures | Parameter-elevation Regressions on Independent Slopes Model (PRISM) [47] |
| Daily Solar Radiation, Wind Speed, and Relative Humidity | Prediction Of Worldwide Energy Resources (POWER) Data Access Viewer [48] |
| Reservoirs | North Dakota Department of Water Resources (NDDWR) (Unpublished) |
| Wetlands | National Wetlands Inventory [36] |
| Subbasin | Area (km2) | Number of Wetlands | Maximum Ponding Area | Contributing Area | Maximum Storage (104 m3) | ||
|---|---|---|---|---|---|---|---|
| Area (km2) | Percentage | Area (km2) | Percentage | ||||
| 1 | 40.792 | 200 | 0.855 | 2.10 | 3.312 | 8.12 | 202.607 |
| 2 | 12.050 | 38 | 0.076 | 0.63 | 0.487 | 4.04 | 3.266 |
| 3 | 18.123 | 93 | 0.160 | 0.88 | 1.175 | 6.48 | 5.271 |
| 4 | 3.796 | 7 | 0.013 | 0.34 | 0.185 | 4.87 | 1.271 |
| 5 | 21.153 | 91 | 0.080 | 0.38 | 0.898 | 4.25 | 2.305 |
| 6 | 7.599 | 4 | 0.008 | 0.11 | 0.017 | 0.22 | 0.409 |
| 7 | 43.748 | 628 | 3.029 | 6.92 | 10.180 | 23.27 | 268.418 |
| 8 | 25.589 | 200 | 0.181 | 0.71 | 1.448 | 5.66 | 3.412 |
| 9 | 4.356 | 123 | 0.118 | 2.71 | 0.542 | 12.44 | 1.591 |
| 10 | 68.716 | 354 | 2.943 | 4.28 | 6.506 | 9.47 | 199.461 |
| 11 | 3.719 | 1 | 0.001 | 0.03 | 0.010 | 0.27 | 0.014 |
| 12 | 22.630 | 707 | 4.774 | 21.10 | 11.345 | 50.13 | 249.907 |
| 13 | 19.789 | 351 | 4.178 | 21.11 | 8.044 | 40.65 | 397.397 |
| 14 | 4.073 | 121 | 0.157 | 3.85 | 0.976 | 23.96 | 2.513 |
| 15 | 45.900 | 166 | 0.215 | 0.47 | 1.568 | 3.42 | 9.454 |
| 16 | 47.839 | 811 | 3.939 | 8.23 | 13.947 | 29.15 | 338.077 |
| 17 | 8.557 | 78 | 0.245 | 2.86 | 1.233 | 14.41 | 37.719 |
| 18 | 31.656 | 465 | 4.064 | 12.84 | 9.811 | 30.99 | 547.857 |
| 19 | 33.766 | 156 | 0.161 | 0.48 | 1.225 | 3.63 | 3.656 |
| 20 | 26.144 | 425 | 1.344 | 5.14 | 5.670 | 21.69 | 250.435 |
| 21 | 32.292 | 111 | 0.272 | 0.84 | 1.451 | 4.49 | 24.786 |
| 22 | 23.335 | 145 | 0.208 | 0.89 | 1.335 | 5.72 | 7.389 |
| 23 | 31.652 | 180 | 0.519 | 1.64 | 2.852 | 9.01 | 97.408 |
| 24 | 3.732 | 25 | 0.054 | 1.45 | 0.267 | 7.15 | 2.090 |
| 25 | 24.389 | 101 | 0.131 | 0.54 | 0.903 | 3.70 | 4.875 |
| 26 | 31.804 | 130 | 1.391 | 4.37 | 2.838 | 8.92 | 373.399 |
| 27 | 27.040 | 75 | 0.222 | 0.82 | 1.064 | 3.93 | 7.925 |
| Subbasin | Fr (-) | SAnor (ha) | Vnor (m3) | SAmx (ha) | Vmx (104 m3) | Kwet (mm/h) |
|---|---|---|---|---|---|---|
| 1 | 0.102 | 1.1 | 104.2 | 85.5 | 202.607 | 28.6 |
| 2 | 0.047 | 0.5 | 278.8 | 7.6 | 3.266 | 32.4 |
| 3 | 0.074 | 0.3 | 41.4 | 16.0 | 5.271 | 28.9 |
| 4 | 0.052 | 0.2 | 18.0 | 1.3 | 1.271 | 32.4 |
| 5 | 0.046 | 0.3 | 38.1 | 8.0 | 2.305 | 32.4 |
| 6 | 0.003 | 0.1 | 185.9 | 0.8 | 0.409 | 13.2 |
| 7 | 0.302 | 1.2 | 118.9 | 302.9 | 268.418 | 28.2 |
| 8 | 0.064 | 0.8 | 21.2 | 18.1 | 3.412 | 21.2 |
| 9 | 0.152 | 0.2 | 4.0 | 11.8 | 1.591 | 19.1 |
| 10 | 0.138 | 0.4 | 7.0 | 294.3 | 199.461 | 24.8 |
| 11 | 0.003 | 0.1 | 140.1 | 0.1 | 0.014 | 32.4 |
| 12 | 0.712 | 2.1 | 201.0 | 477.4 | 249.907 | 28.9 |
| 13 | 0.618 | 0.5 | 37.3 | 417.8 | 397.397 | 27.8 |
| 14 | 0.278 | 0.4 | 17.0 | 15.7 | 2.513 | 23.7 |
| 15 | 0.039 | 0.1 | 1.3 | 21.5 | 9.454 | 25.2 |
| 16 | 0.374 | 1.4 | 156.0 | 393.9 | 338.077 | 27.5 |
| 17 | 0.173 | 0.2 | 157.9 | 24.5 | 37.719 | 24.0 |
| 18 | 0.438 | 1.1 | 121.0 | 406.4 | 547.857 | 22.9 |
| 19 | 0.041 | 0.5 | 14.9 | 16.1 | 3.656 | 25.7 |
| 20 | 0.268 | 1.4 | 115.4 | 134.4 | 250.435 | 17.8 |
| 21 | 0.053 | 0.2 | 13.4 | 27.2 | 24.786 | 31.7 |
| 22 | 0.066 | 0.5 | 26.9 | 20.8 | 7.389 | 53.2 |
| 23 | 0.107 | 0.1 | 3.0 | 51.9 | 97.408 | 33.5 |
| 24 | 0.086 | 0.3 | 177.0 | 5.4 | 2.090 | 25.6 |
| 25 | 0.042 | 0.2 | 3.6 | 13.1 | 4.875 | 32.4 |
| 26 | 0.133 | 0.4 | 32.3 | 139.1 | 373.399 | 56.9 |
| 27 | 0.048 | 0.5 | 74.1 | 22.2 | 7.925 | 43.2 |
| Parameters | Description | Acceptable Range | Calibrated Values/Ranges |
|---|---|---|---|
| SMTMP | Threshold temperature for snowmelt (°C) | −5 to 5 | 2.11 |
| SFTMP | Snowfall temperature (°C) | −5 to 5 | 1.68 |
| TIMP | Snowpack temperature lag factor | 0 to 1 | 0.56 |
| SURLAG | Surface runoff lag coefficient | 0 to 24 | 10.25 |
| CN2 | Curve number | ±25% of initial values | 4.7% of initial values |
| ALPHA_BF | Baseflow recession constant | 0 to 1 | 0.67 |
| GW_DELAY | Groundwater delay (days) | 0 to 500 | 78.90 |
| REVAPMN | Threshold depth of water in the shallow aquifer for “revap” to occur (mm) | 0 to 1000 | 327.50 |
| ESCO | Soil evaporation compensation coefficient | 0 to 1 | 0.76 |
| SLSUBBSN | Average slope length (m) | ±25% of initial values | 13.7% of initial values |
| HRU_SLP | Average slope steepness (m/m) | ±25% of initial values | 19.5% of initial values |
| SOL_AWC | Available water capacity of the soil layer | ±25% of initial values | −15.3% of initial values |
| SOL_BD | Soil bulk density (mg/m3) | ±25% of initial values | 8.1% of initial values |
| CH_K1 | Effective hydraulic conductivity in tributary channel alluvium (mm/h) | 0 to 300 | 40.08 |
| CH_K2 | Effective hydraulic conductivity in main channel alluvium (mm/h) | 0 to 500 | 24.88 |
| CH_N2 | Manning’s “n” value for the main channel | 0 to 0.3 | 0.29 |
| Kwet | Effective saturated hydraulic conductivity of the wetland bottom (mm/h) | ±25% of initial values | −15.0% of initial values |
| Statistical Metrics | Calibration Period | Validation Period | ||
|---|---|---|---|---|
| Metrics Value | Model Performance | Metrics Value | Model Performance | |
| NSE | 0.82 | Very good | 0.61 | Satisfactory |
| PBIAS (%) | 5.01 | Very good | 6.23 | Very good |
| Land Use and Land Cover Types | Area (km2) | Percent (%) |
|---|---|---|
| Wetlands in the original reclassified LULC | 7.40 | 32.71 |
| Used wetlands for HRU definition | 3.87 | 17.11 |
| Defined wetland HRUs in CM1, CM2, and joint model | 7.73 | 34.16 |
| Water in the original reclassified LULC | 1.56 | 6.88 |
| Used water for HRU definition | 1.23 | 5.45 |
| Defined water HRUs in CM1, CM2, and joint model | 2.46 | 10.89 |
| Maximum ponding area in CM2 and joint model | 4.77 | 21.08 |
| Maximum ponding area and its contributing area in CM2 and joint model | 16.12 | 71.23 |
| HRUs | Joint Model (%) | CM2 (%) |
|---|---|---|
| Hay | −21.91 | −71.16 |
| Agricultural land | −19.24 | −71.12 |
| Wetlands | −29.46 | −71.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, T.; Khanaum, M.M.; Boutin, K.; Otte, M.L.; Lin, Z.; Chu, X. Incorporating Wetland Delineation and Impacts in Watershed-Scale Hydrologic Modeling. Water 2023, 15, 2518. https://doi.org/10.3390/w15142518
Qi T, Khanaum MM, Boutin K, Otte ML, Lin Z, Chu X. Incorporating Wetland Delineation and Impacts in Watershed-Scale Hydrologic Modeling. Water. 2023; 15(14):2518. https://doi.org/10.3390/w15142518
Chicago/Turabian StyleQi, Tiansong, Mosammat Mustari Khanaum, Kyle Boutin, Marinus L. Otte, Zhulu Lin, and Xuefeng Chu. 2023. "Incorporating Wetland Delineation and Impacts in Watershed-Scale Hydrologic Modeling" Water 15, no. 14: 2518. https://doi.org/10.3390/w15142518
APA StyleQi, T., Khanaum, M. M., Boutin, K., Otte, M. L., Lin, Z., & Chu, X. (2023). Incorporating Wetland Delineation and Impacts in Watershed-Scale Hydrologic Modeling. Water, 15(14), 2518. https://doi.org/10.3390/w15142518









