Analysis of Structure Stability of Underwater Shield Tunnel under Different Temperatures Based on Finite Element Method
Abstract
:1. Introduction
2. Model Working Conditions
3. Analysis of Results
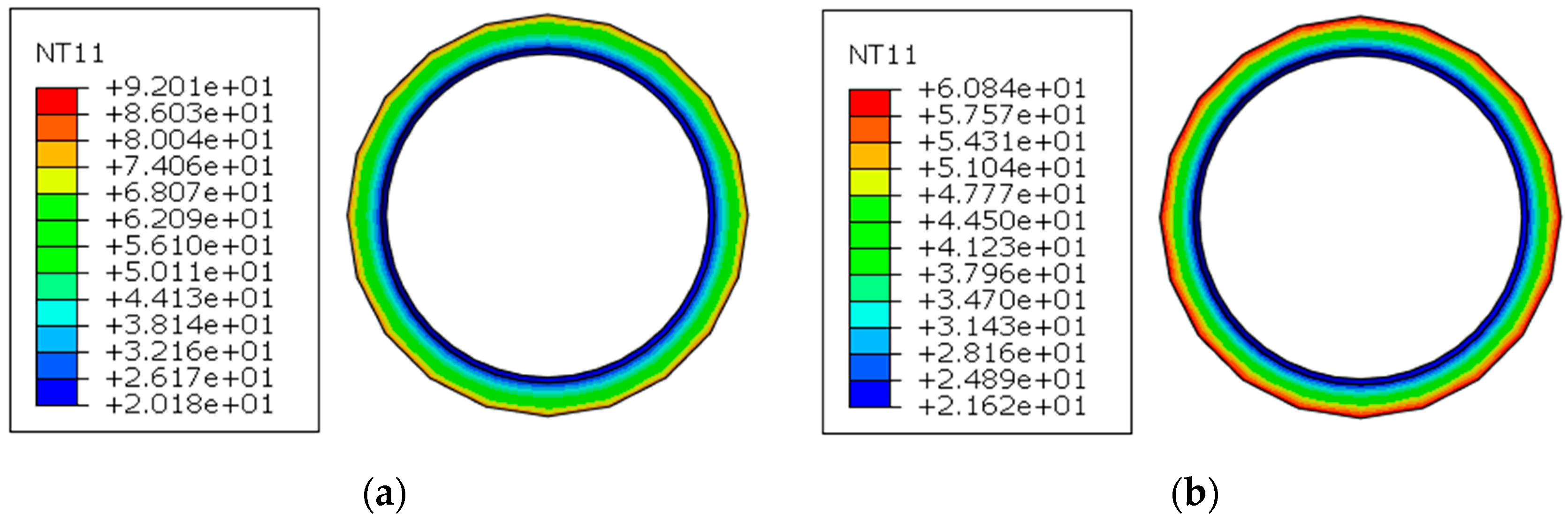
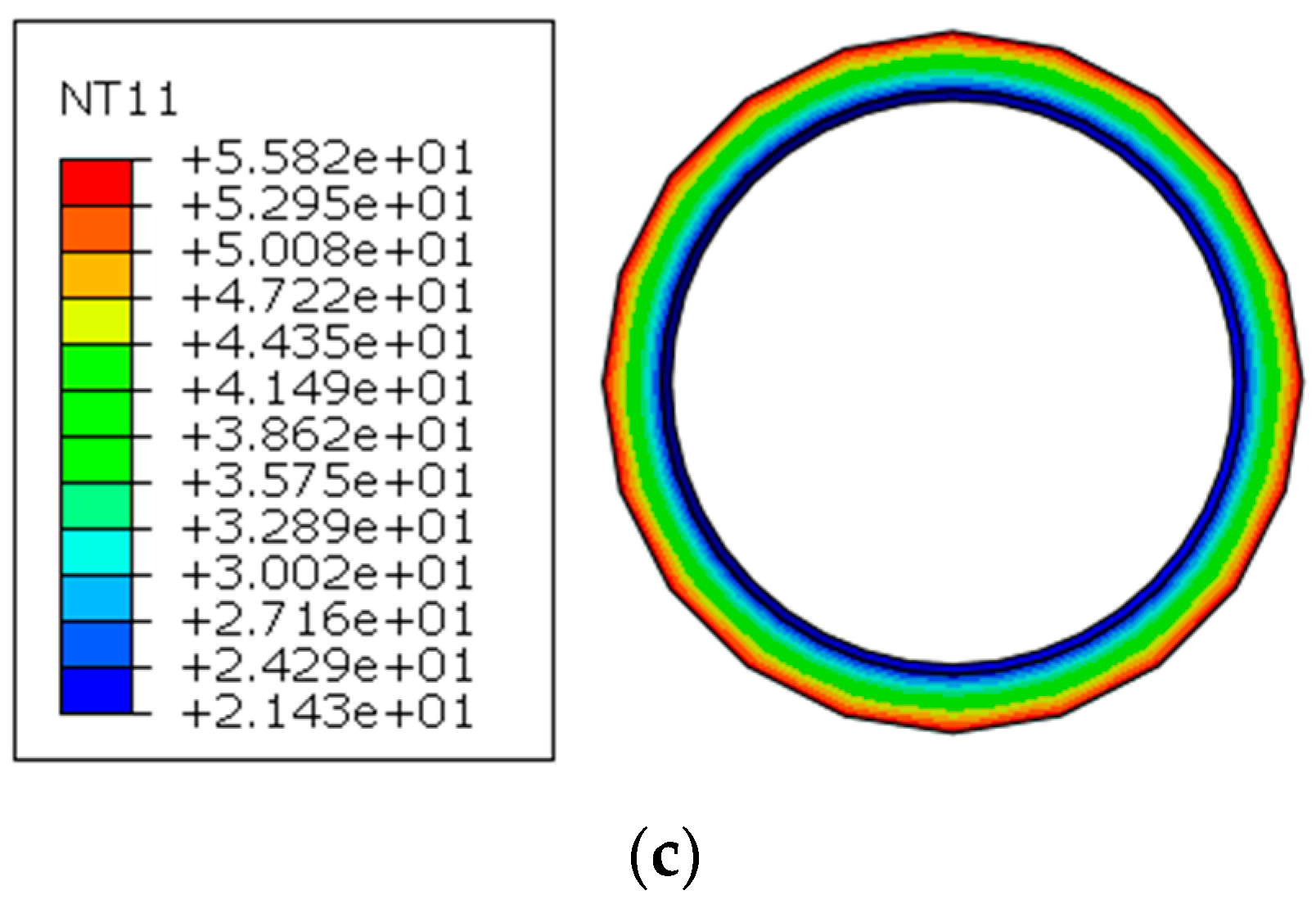
3.1. Analysis of the Temperature Field in Underwater Shield Tunnels
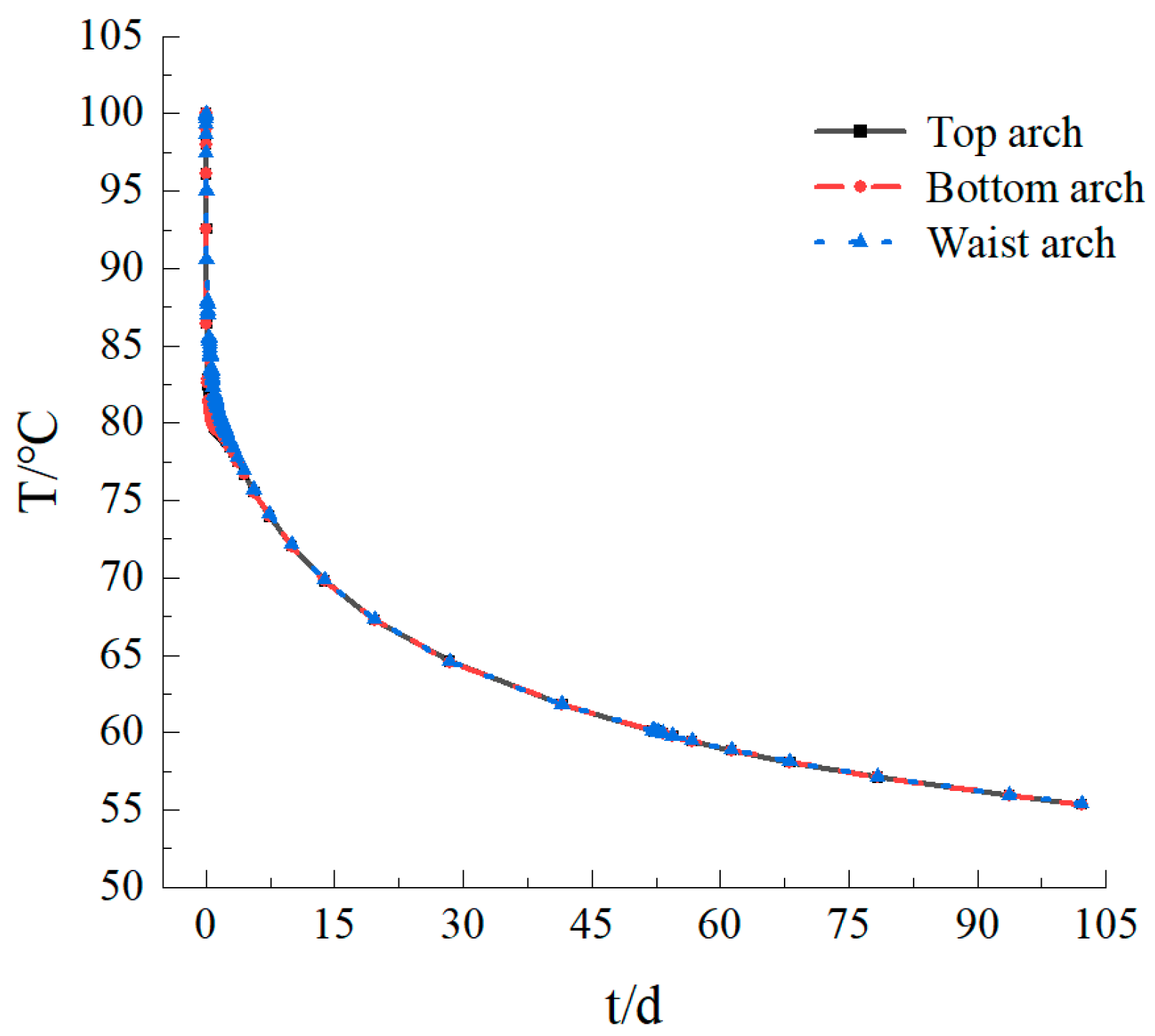
3.2. Analysis of Temperature Transfer between Envelope and Lining
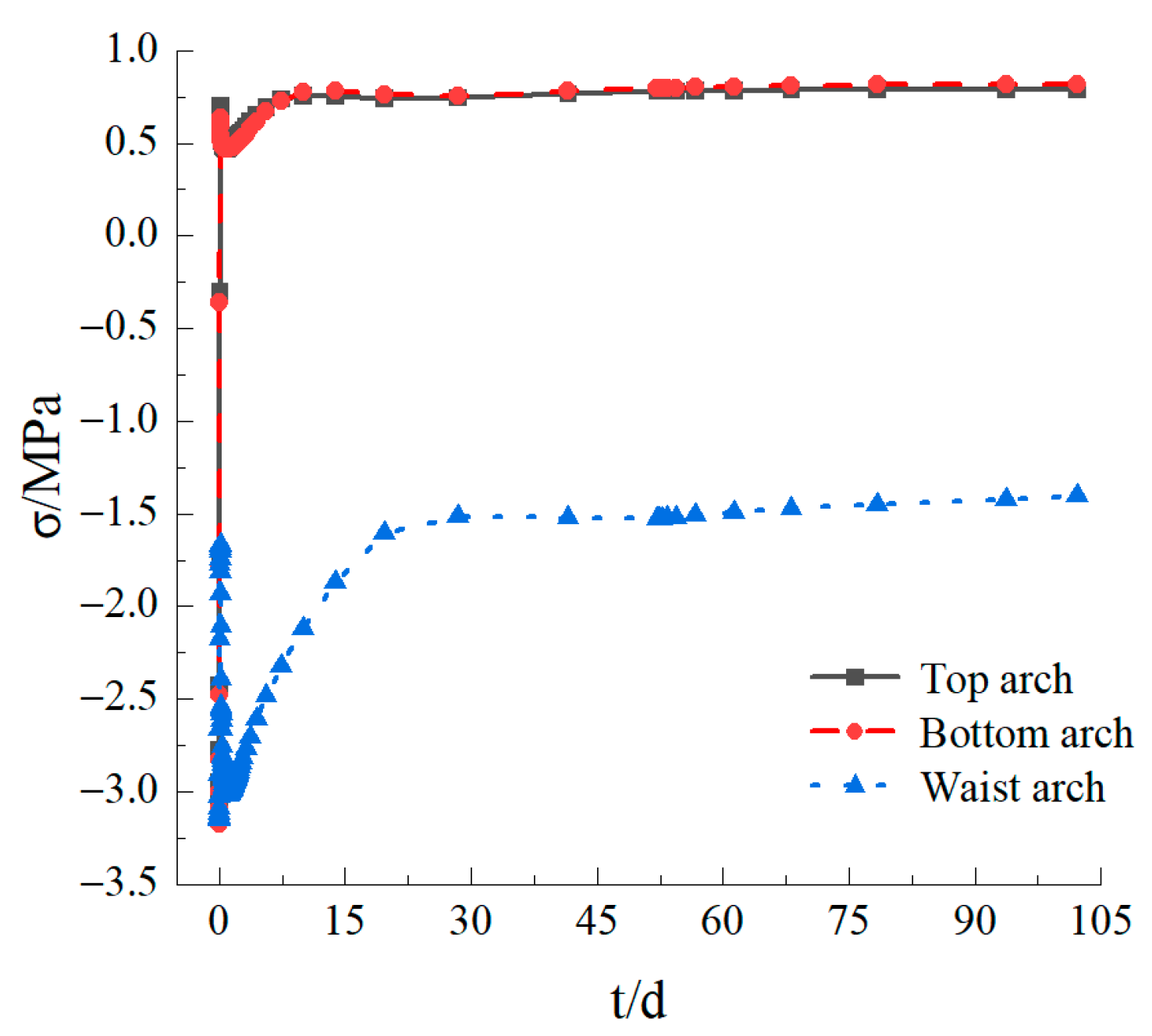
3.3. Analysis of the Maximum Principal Stress between the Soil and the Lining
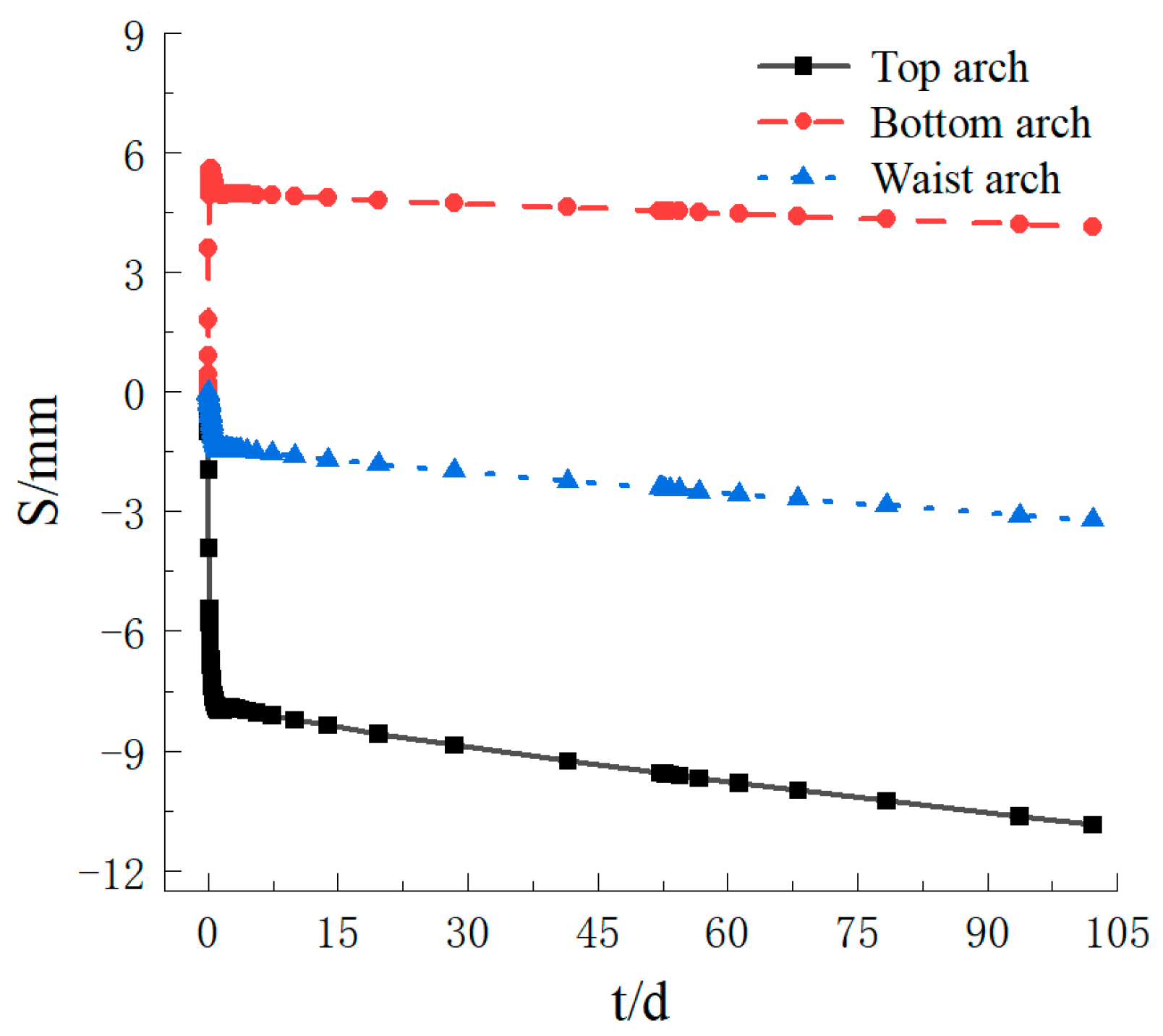
3.4. Settlement Analysis between Enclosure and Lining
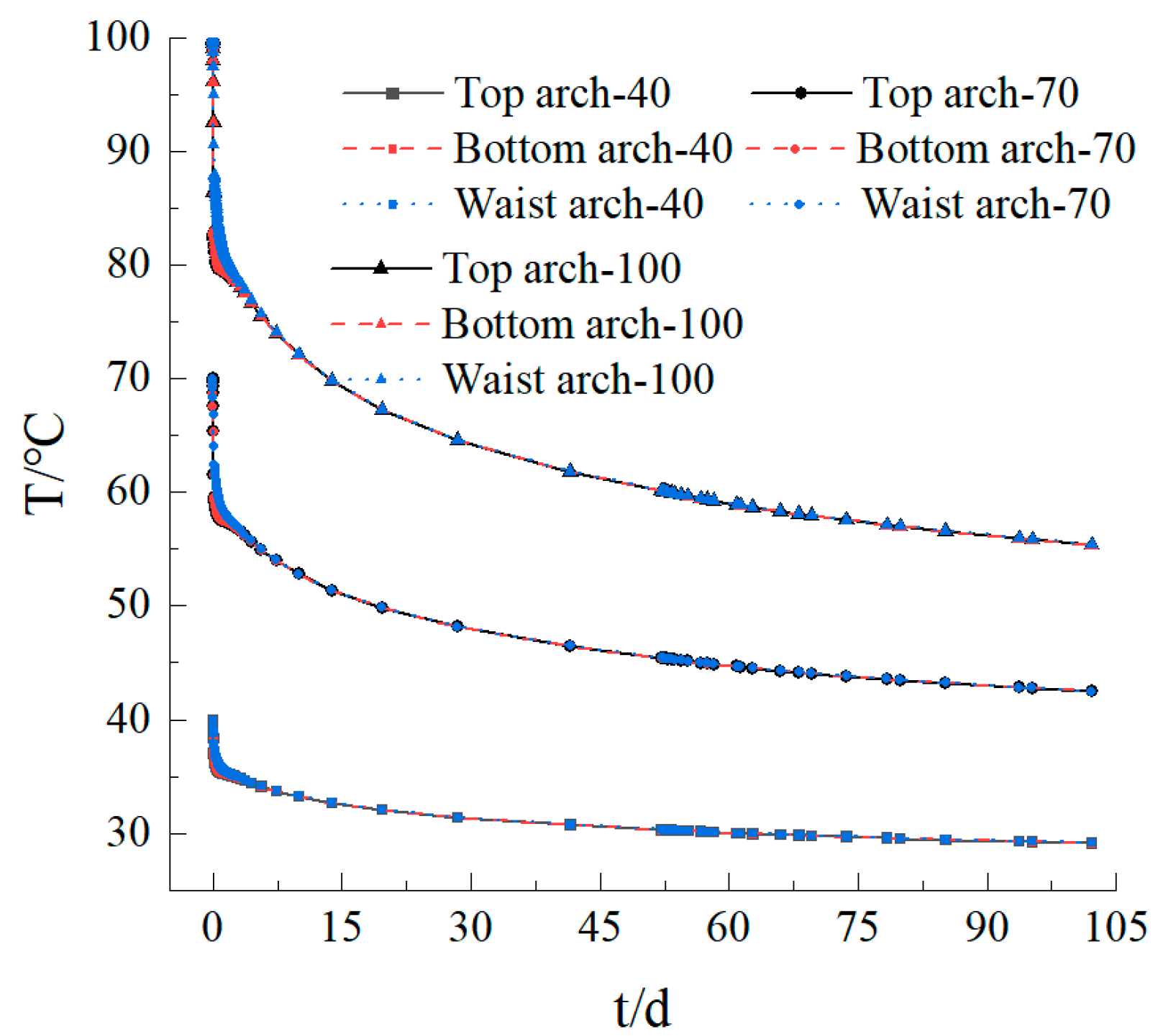
3.5. Temperature Transfer between Soil and Lining at Different High Structure Temperatures
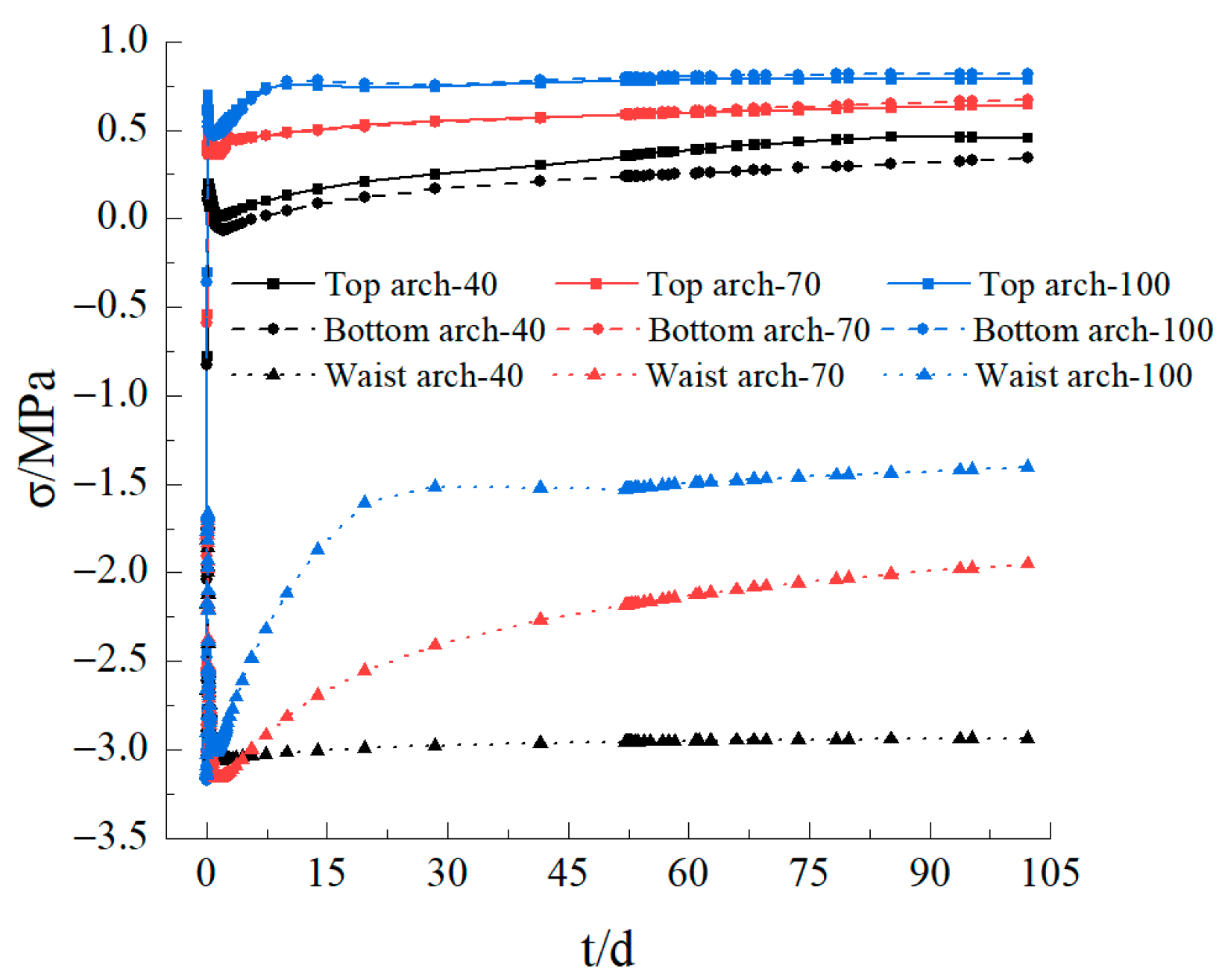
3.6. Analysis of the Maximum Principal Stress between the Soil and the Lining at Different High Temperatures
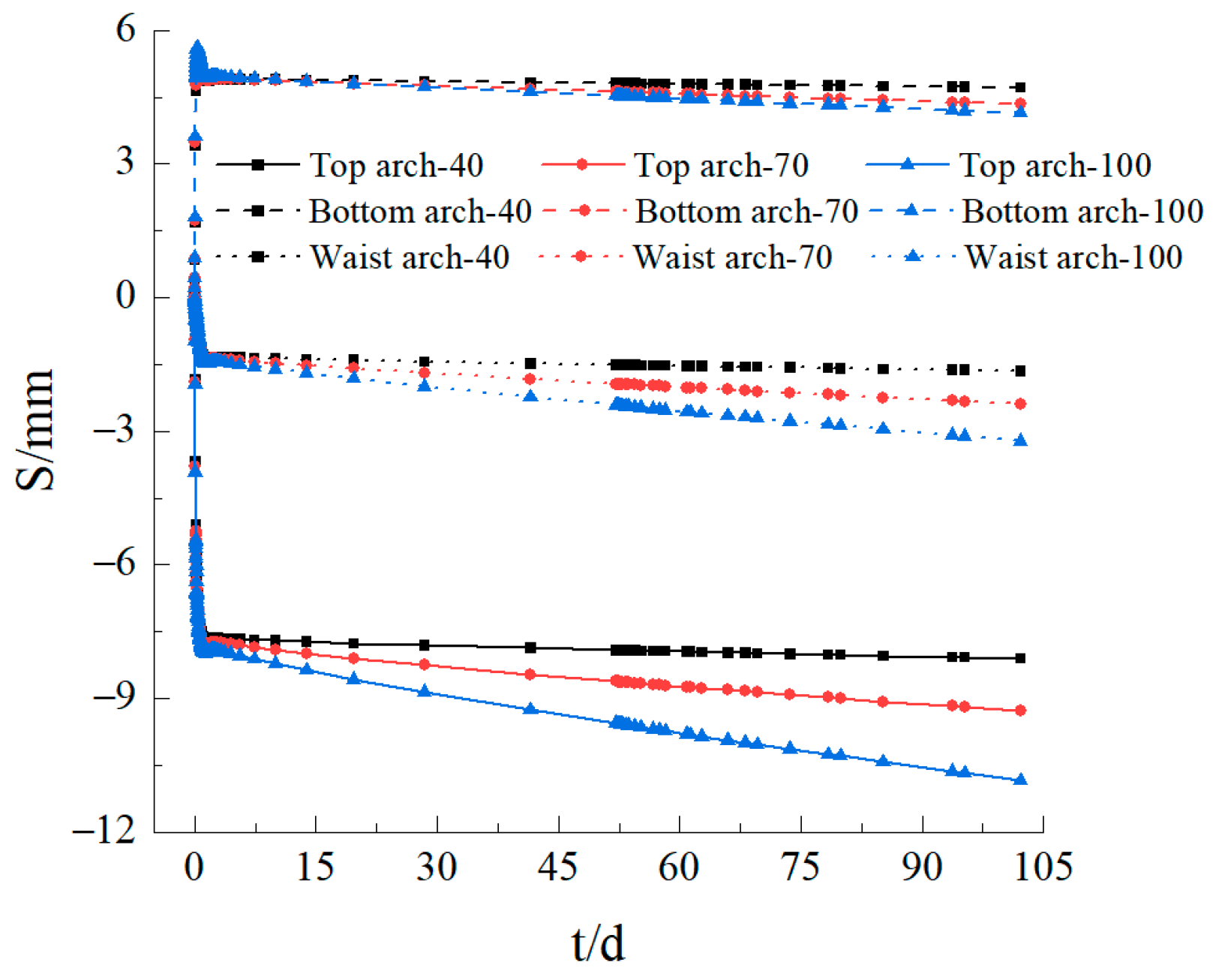
3.7. Settlement Analysis between Different High Structure Temperature Enclosures and Liners
4. Conclusions
- (1)
- The early excavation time of the underwater shield tunnel was short, and the temperature circle was small. The temperature circle expanded rapidly after 50 days of operation. The spread increased by 256.7%. The temperature change curves of the top, bottom, and waist arches decreased with time. The higher the temperature of the soil around the underwater shield tunnel, the greater the temperature drop.
- (2)
- The process of the change in the maximum principal stress in the top, bottom, and waist arches could be divided into three phases: the period of sudden stress change, the period of stress fluctuation, and the period of stress stabilization. The higher the temperature in the soil, the more complex the temperature transfer between the soil and the lining was while generating greater temperature stresses and reducing the safety of the tunnel. When in high-temperature conditions, the temperature between the tunnel and the soil should be controlled to avoid creating additional temperature stresses that could affect the stability of the tunnel.
- (3)
- Settlement changes could be divided into three phases: the abrupt settlement period and the settlement fluctuation period and settlement creep period. After the excavation, with a decrease in the temperature, the strength of the soil and lining increased. The settlement of the top arch, bottom arch, and waist arch increased slowly with time, and the growth rate decreased gradually. The higher the temperature of the tunnel structure, the greater the settlement and the more detrimental this was to the stability of the tunnel.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, M.; Zhou, P.; Jiang, Y.; Zhou, F.; Lin, J.; Wang, Z. Numerical investigation on comprehensive control system of cooling and heat insulation for high geothermal tunnel: A case study on the highway tunnel with the highest temperature in China. Int. J. Therm. Sci. 2022, 173, 107385. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, M.; Wang, Q.; Liu, D.; Tong, J. Field test of thermal environment and thermal adaptation of workers in high geothermal tunnel. Build. Environ. 2019, 160, 106174. [Google Scholar] [CrossRef]
- Zhang, G.; Cao, Z.; Wang, W.; Mei, X.; Zhao, X.; Shen, S.; Na, T. Field test and numerical investigation on thermal environment of tunnel with air layer structure. Build. Environ. 2021, 203, 108105. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, X.; Zhong, Z.; Liang, N.; Wang, Y.; Zhang, X. Study on temperature field and influencing factors of the high geothermal tunnel with extra-long one-end construction ventilation. Int. J. Therm. Sci. 2023, 191, 108322. [Google Scholar] [CrossRef]
- Duan, L.; Zhang, Y.; Lai, J. Influence of Ground Temperature on Shotcrete-to-Rock Adhesion in Tunnels. Adv. Mater. Sci. Eng. 2019, 2019, 8709087. [Google Scholar] [CrossRef] [Green Version]
- Luo, K.; Li, Y.; Zheng, C.; Gao, X.; Fan, J. Numerical simulation of temperature effect on particles behavior via electrostatic precipitators. Appl. Therm. Eng. 2015, 88, 127–139. [Google Scholar] [CrossRef]
- Uejio, C.K.; Morano, L.H.; Jung, J.; Kintziger, K.; Jagger, M.; Chalmers, J.; Holmes, T. Occupational heat exposure among municipal workers. Int. Arch. Occup. Environ. Health 2018, 91, 705–715. [Google Scholar] [CrossRef] [PubMed]
- Srinavin, K.; Mohamed, S. Thermal environment and construction workers’ productivity: Some evidence from Thailand. Build. Environ. 2003, 38, 339–345. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, J.; Li, L.; Hu, T.; Zhao, Y. Analytical solution for the temperature field of an elliptical tunnel in cold regions. Cold Reg. Sci. Technol. 2023, 208, 103793. [Google Scholar] [CrossRef]
- Zhou, P.; Feng, Y.; Zhou, F.; Wei, Z.; Gou, S.; Xu, H.; Wang, Z. Evaluation system of worker comfort for high geothermal tunnel during construction: A case study on the highway tunnel with the highest temperature in China. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2023, 135, 105028. [Google Scholar] [CrossRef]
- John, H.; Kamelia, A. Fire-induced damage in tunnels: Thermo-mechanical modeling incorporating support system and geological conditions. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2023, 135, 105027. [Google Scholar]
- Zhang, D.; Zhao, B.; Zhu, K. Mechanical characteristics analysis of horizontal lifting of subsea pipeline with different burial depths. Front. Earth Sci. 2022, 10, 1011291. [Google Scholar]
- Wang, M.; Hu, Y.; Liu, D.; Jiang, C.; Wang, Q.; Wang, Y. A Study on the Heat Transfer of Surrounding Rock-Supporting Structures in High-Geothermal Tunnels. Appl. Sci. 2020, 10, 2307. [Google Scholar] [CrossRef] [Green Version]
- Wei, Y.; Sun, K.; Zhong, X.; Jia, J.; Huang, Q.; Qin, J.; Xiong, Z. Study on effects of the train-induced airflow on the temperature field of high-speed railway tunnels in cold regions. Therm. Sci. Eng. Prog. 2023, 41, 101837. [Google Scholar] [CrossRef]
- Kang, F.; Li, Y.; Tang, C. Numerical study on airflow temperature field in a high-temperature tunnel with insulation layer. Appl. Therm. Eng. 2020, 179, 115654. [Google Scholar] [CrossRef]
- Zhou, X.; Zeng, Y.; Fan, L. Temperature field analysis of a cold-region railway tunnel considering mechanical and train-induced ventilation effects. Appl. Therm. Eng. 2016, 100, 114–124. [Google Scholar] [CrossRef]
- Sun, B.; Xu, Z.D.; Zhou, H. A multiple back propagation neural network fusion algorithm for ceiling temperature prediction in tunnel fires. Eng. Struct. 2023, 280, 115601. [Google Scholar] [CrossRef]
- Wan, H.; Xiao, Y.; Wei, S.; Zhang, Y.; Oka, Y. Experimental study on multiple fire hazards in a naturally ventilated tunnel: Assessment of the flame interaction and extension of two unequal fires. Int. J. Therm. Sci. 2023, 187, 108209. [Google Scholar] [CrossRef]
- He, K.; Shi, L.; Zhang, S.; Cong, W.; Yang, H.; Cheng, X. Experimental study on temperature attenuation of smoke flow driven by dual fire sources in a tunnel. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2023, 134, 105004. [Google Scholar] [CrossRef]
- Sun, S.; Yan, S.; Cao, X.; Zhang, W. Distribution Law of the Initial Temperature Field in a Railway Tunnel with High Rock Temperature: A Model Test and Numerical Analysis. Appl. Sci. 2023, 13, 1638. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z.; Li, G.; Xu, Y. Heat Hazard Control in High-Temperature Tunnels: Experimental Study of Coupled Cooling with Ventilation and Partial Insulation for Synergistic Geothermal Extraction. Int. J. Environ. Res. Public Health 2023, 20, 1941. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Zhang, B.; Zubin, A.I.; Bu, X.; Pan, H.; Chen, S. Spatial-temporal evolution principle of temperature field in a high-temperature geothermal highway tunnel. Ain Shams Eng. J. 2023, 14, 101965. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, C.; Xie, D. Study on creep deformation law of surrounding rock of slate tunnel considering temperature effect. J. Hebei Univ. Sci. Technol. 2022, 43, 90–98. [Google Scholar]


| Elastic Modulus (GPa) | Poisson’s Ratio | Angle of Internal Friction (°) | Cohesion (MPa) | Thermal Conductivity (W/m·°C) | Coefficient of Linear Expansion (°C−5) | Specific Heat Capacity (J/Kg·°C) | Temperature (°C) |
|---|---|---|---|---|---|---|---|
| 6.5 | 0.25 | 42 | 1.1 | 7.6 | 8.3 | 1285 | 100 |
| 6.7 | 0.25 | 42 | 1.1 | 8.0 | 7.6 | 1240 | 80 |
| 6.8 | 0.25 | 42 | 1.1 | 8.4 | 6.9 | 1195 | 65 |
| 6.9 | 0.25 | 42 | 1.1 | 8.9 | 6.2 | 1150 | 50 |
| 7.0 | 0.25 | 42 | 1.1 | 9.4 | 5.6 | 1105 | 35 |
| 7.1 | 0.25 | 42 | 1.1 | 10 | 5.0 | 1060 | 20 |
| Elastic Modulus (GPa) | Poisson’s Ratio | Angle of Internal Friction (°) | Cohesion (MPa) | Thermal Conductivity (W/m·°C) | Coefficient of Linear Expansion (°C−5) | Specific Heat Capacity (J/Kg·°C) | Temperature (°C) |
|---|---|---|---|---|---|---|---|
| 30.0 | 0.17 | 54 | 2.42 | 1.69 | 1.00 | 913 | 20 |
| 29.6 | 0.17 | 54 | 2.42 | 1.68 | 1.01 | 916 | 35 |
| 29.1 | 0.17 | 54 | 2.42 | 1.67 | 1.02 | 919 | 50 |
| 28.9 | 0.17 | 54 | 2.42 | 1.66 | 1.03 | 923 | 65 |
| 28.7 | 0.17 | 54 | 2.42 | 1.65 | 1.04 | 926 | 80 |
| 28.4 | 0.17 | 54 | 2.42 | 1.64 | 1.05 | 929 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, L.; Wu, Q.; Jiang, Y.; Li, Z.; Wang, Y. Analysis of Structure Stability of Underwater Shield Tunnel under Different Temperatures Based on Finite Element Method. Water 2023, 15, 2577. https://doi.org/10.3390/w15142577
Zhu L, Wu Q, Jiang Y, Li Z, Wang Y. Analysis of Structure Stability of Underwater Shield Tunnel under Different Temperatures Based on Finite Element Method. Water. 2023; 15(14):2577. https://doi.org/10.3390/w15142577
Chicago/Turabian StyleZhu, Lei, Qianwen Wu, Yuke Jiang, Zhenyu Li, and Yuke Wang. 2023. "Analysis of Structure Stability of Underwater Shield Tunnel under Different Temperatures Based on Finite Element Method" Water 15, no. 14: 2577. https://doi.org/10.3390/w15142577
APA StyleZhu, L., Wu, Q., Jiang, Y., Li, Z., & Wang, Y. (2023). Analysis of Structure Stability of Underwater Shield Tunnel under Different Temperatures Based on Finite Element Method. Water, 15(14), 2577. https://doi.org/10.3390/w15142577








