The Improved Reservoir Module of SWAT Model with a Dispatch Function and Its Application on Assessing the Impact of Climate Change and Human Activities on Runoff Change
Abstract
:1. Introduction
2. Study Area and Data
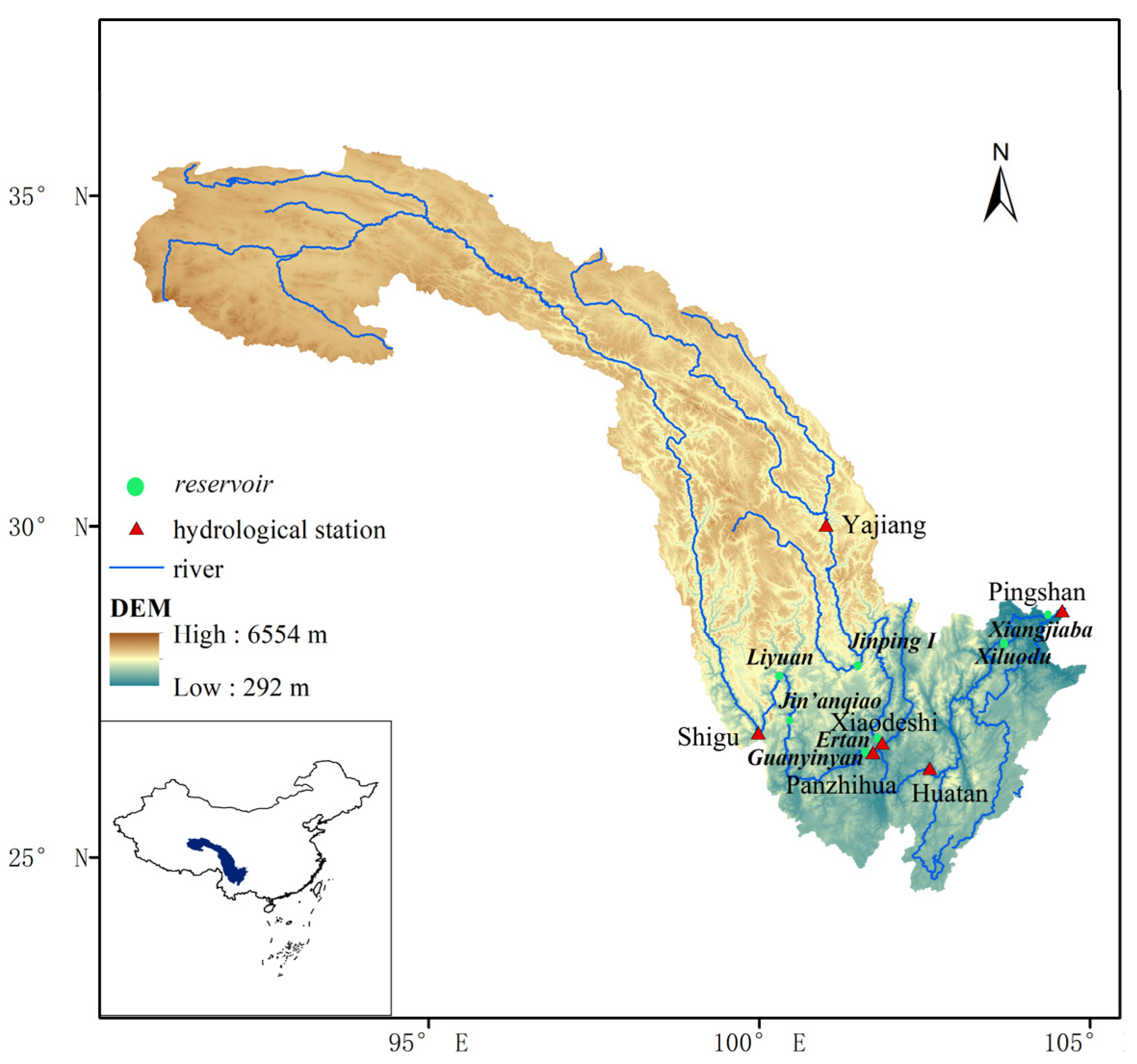
2.1. Study Area
2.2. Data
3. Methods
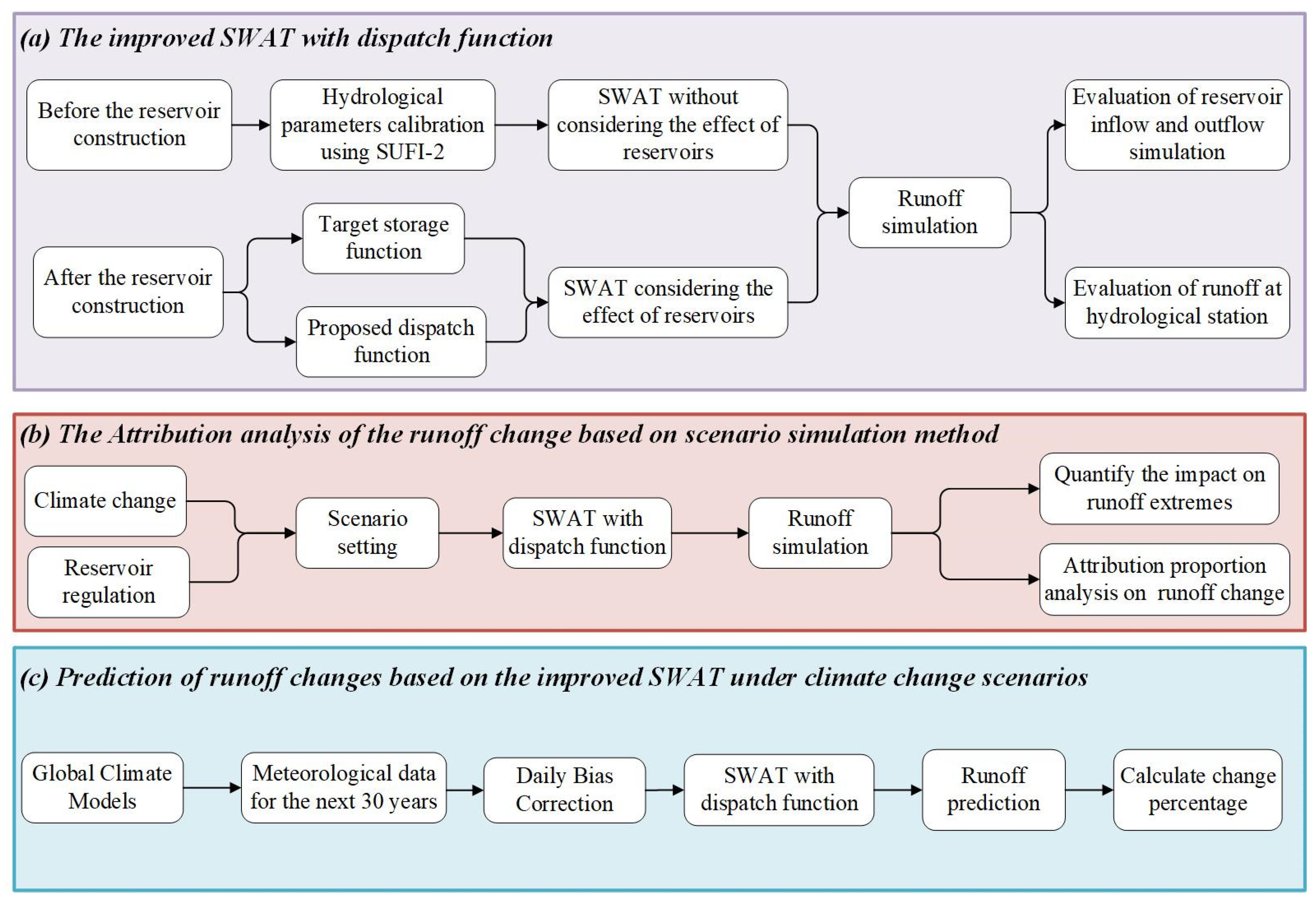
3.1. The Improved SWAT Model with the Dispatch Function
3.1.1. SWAT Model
3.1.2. The Dispatch Function
3.1.3. Evaluation Indicators
3.2. Attribution Analysis of the Impact of Reservoir Regulation and Climate Change on Runoff
3.2.1. Mann–Kendall Trend Test
3.2.2. Scenario Setting and Simulation Method
3.2.3. Quantitative Assessment of the Impact on Runoff
3.3. Runoff Change Prediction under Climate Change in the Next 30 Years
3.3.1. Selection of Typical GCMs
3.3.2. Runoff Prediction under Climate Change
4. Results
4.1. The Improved SWAT Model with a Dispatch Function
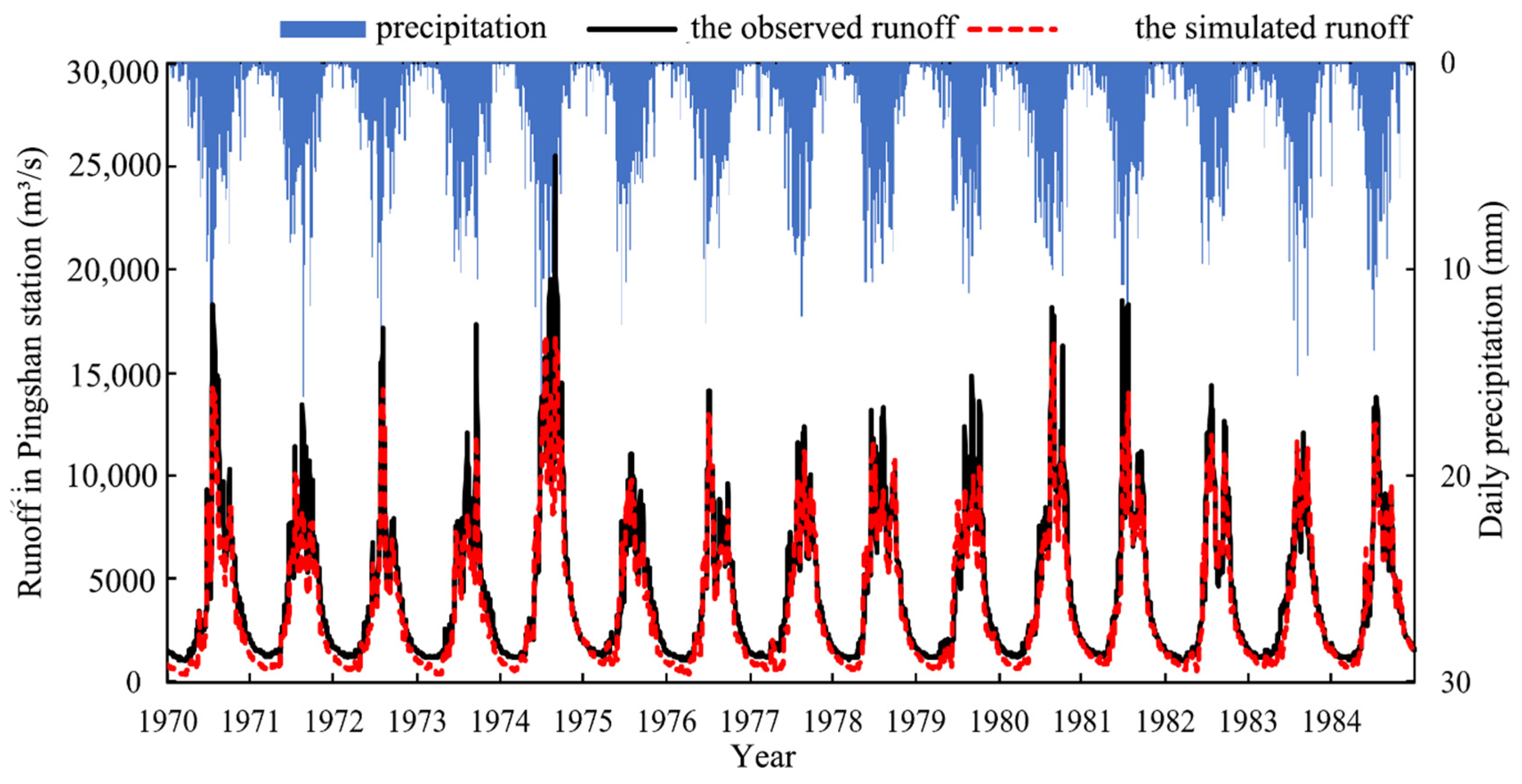
4.1.1. Hydrological Parameter Calibration before the Reservoir Impact Period
4.1.2. The Dispatch Function of Reservoirs
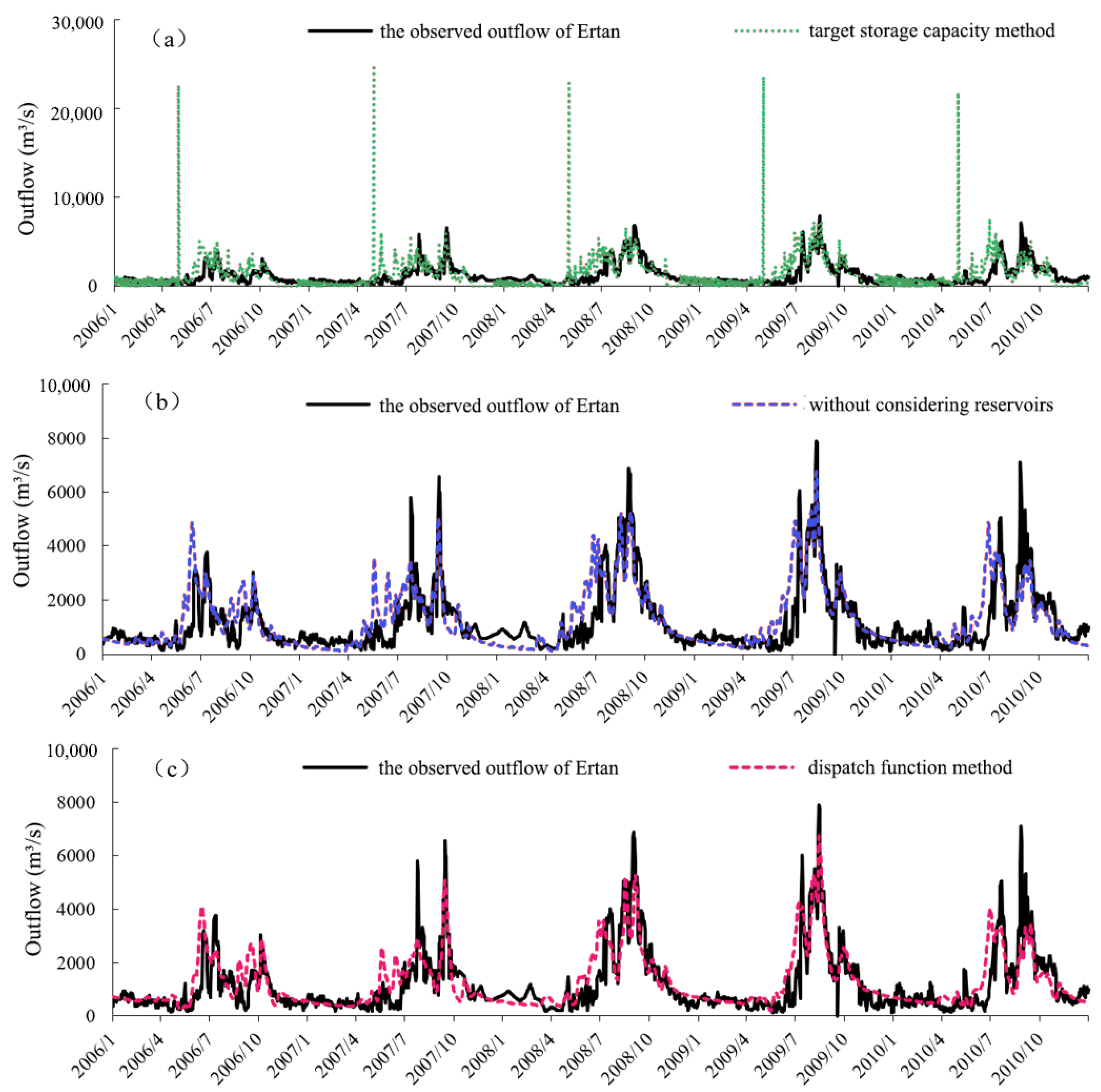
4.1.3. Evaluation of the Improved SWAT Based on Reservoir Inflow and Outflow Simulation
4.1.4. Evaluation of the Improved SWAT Based on Runoff Simulation at Hydrological Stations
4.2. Attribution Analysis on Runoff Changes
4.2.1. Trend Analysis of Runoff
4.2.2. Quantitative Assessment of the Impacts of Climate Change and Human Activities on Extreme Runoff
4.2.3. Quantitative Assessment of the Impacts of Climate Change and Human Activities on Mean Runoff
4.3. Prediction of Runoff Changes in Future under Climate Change Scenarios
4.3.1. Changes of Meteorological and Hydrological Elements in Future
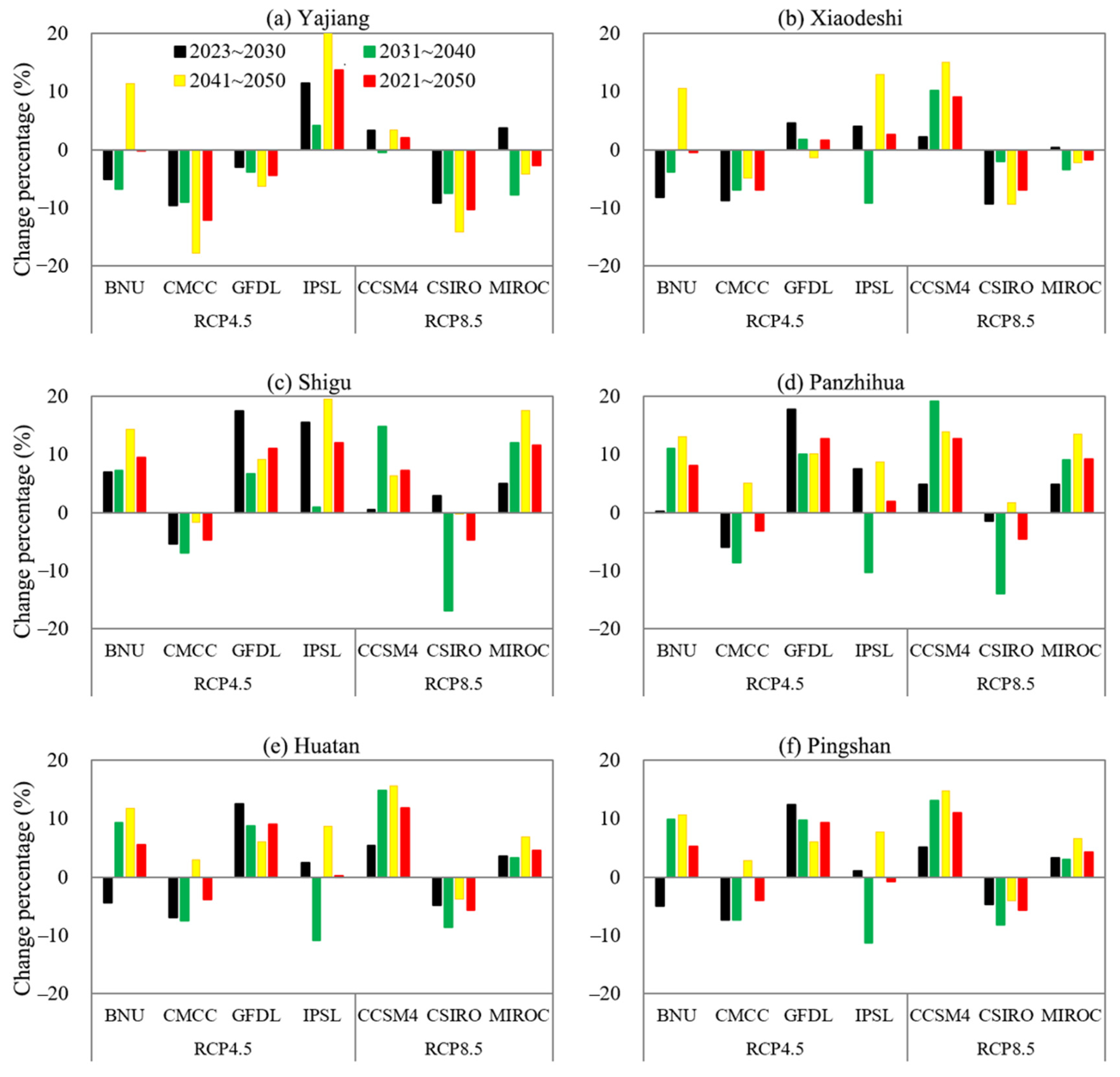
4.3.2. Change Percentages of Simulated Runoff under Different Decades
5. Discussion
6. Conclusions
- (1)
- The dispatch function method exhibits superior performance in simulating reservoir outflow and runoff at hydrological stations compared to the original reservoir module in the SWAT model. The advantages of the dispatch function method are more pronounced when applied to reservoirs with greater regulation capacity.
- (2)
- The attribution analyses demonstrate that the operation of reservoirs leads to a certain reduction in the basin’s runoff volume. However, the positive impact of climate change on runoff is more pronounced and has a dominant effect on river runoff.
- (3)
- Over the next 30 years, both precipitation and temperature will increase compared to the base period (1970–2005), with a larger increase in precipitation. However, the changes in runoff do not follow a consistent pattern and exhibit a higher level of uncertainty. An increase in precipitation does not necessarily result in a proportional change in runoff.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | Full Name |
| BNU | Beijing Normal University Earth System Model |
| CCSM4 | Community Climate System Model version 4 |
| CMCC | Cambiamenti Climatici Climate Model |
| CMIP5 | Coupled Model Intercomparison Project Phase 5 |
| CSIRO | Commonwealth Scientific and Industrial Research Organisation |
| DEM | Digital Elevation Model |
| DHSVM | Distributed Hydrology Soil Vegetation Model |
| GCM | Global Climate Model |
| GFDL | Geophysical Fluid Dynamics Laboratory |
| HEC-HMS | Hydrologic Engineering Center-Hydrologic Modeling System |
| HIMS | Hydroinformatic Modeling System |
| IPCC | Intergovernmental Panel on Climate Change |
| IPSL | Institute Pierre Simon Laplace |
| LARSIM | Large Area Runoff Simulation Model |
| LULC | Land Use/Land Cover |
| MIROC | Model for Interdisciplinary Research on Climate |
| Pref | Reference period |
| Ptest | Test period |
| RCP | Representative Concentration Pathway |
| SUFI-2 | Uncertainty in Sequential Uncertainty Fitting |
| SWAT | Soil and Water Assessment Tool |
| SWIM | Soil and Water Integrated Model |
References
- Dey, P.; Mishra, A. Separating the impacts of climate change and human activities on streamflow: A review of methodologies and critical assumptions. J. Hydrol. 2017, 548, 278–290. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, S.; Bai, X.; Shu, D.; Tian, Y. Runoff response to climate change and human activities in a typical karst watershed, SW China. PLoS ONE 2018, 13, e0193073. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, M.; Chen, J.; Zhong, P.-A.; Wu, X.; Wu, S. Multiscale attribution analysis for assessing effects of changing environment on runoff: Case study of the Upstream Yangtze River in China. J. Water Clim. Chang. 2020, 12, 627–646. [Google Scholar] [CrossRef]
- Di Cicco, M.E.; Ferrante, G.; Amato, D.; Capizzi, A.; De Pieri, C.; Ferraro, V.A.; Furno, M.; Tranchino, V.; La Grutta, S. Climate Change and Childhood Respiratory Health: A Call to Action for Paediatricians. Int. J. Environ. Res. Public Health 2020, 17, 5344. [Google Scholar] [CrossRef] [PubMed]
- Zeng, F.; Ma, M.-G.; Di, D.-R.; Shi, W.-Y. Separating the Impacts of Climate Change and Human Activities on Runoff: A Review of Method and Application. Water 2020, 12, 2201. [Google Scholar] [CrossRef]
- McCrystall, M.R.; Stroeve, J.; Serreze, M.; Forbes, B.C.; Screen, J.A. New climate models reveal faster and larger increases in Arctic precipitation than previously projected. Nat. Commun. 2021, 12, 6765. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Xue, L.; Zhou, L.; Wei, L.; Hu, S.; Wu, H.; Zhang, H.; Xiang, C.; Li, X. Cumulative ecosystem response to Hydraulic Engineering Infrastructure Projects in an arid basin. Sci. Total Environ. 2023, 856, 159110. [Google Scholar] [CrossRef]
- Ai, P.; Xiong, C.; Li, K.; Song, Y.; Gong, S.; Yue, Z. Effect of Data Characteristics Inconsistency on Medium and Long-Term Runoff Forecasting by Machine Learning. IEEE Access 2023, 11, 11601–11612. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, X.; Hao, F.; Wu, Y.; Li, C.; Xu, Y. Evaluating the contributions of climate change and human activities to runoff in typical semi-arid area, China. J. Hydrol. 2020, 590, 125555. [Google Scholar] [CrossRef]
- Omer, A.; Wang, W.; Basheer, A.K.; Yong, B. Integrated assessment of the impacts of climate variability and anthropogenic activities on river runoff: A case study in the Hutuo River Basin, China. Hydrol. Res. 2016, 48, 416–430. [Google Scholar] [CrossRef] [Green Version]
- Tien Bui, D.; Talebpour Asl, D.; Ghanavati, E.; Al-Ansari, N.; Khezri, S.; Chapi, K.; Amini, A.; Thai Pham, B. Effects of Inter-Basin Water Transfer on Water Flow Condition of Destination Basin. Sustainability 2020, 12, 338. [Google Scholar] [CrossRef] [Green Version]
- Cheng, G.; Liu, Y.; Chen, Y.; Gao, W. Spatiotemporal variation and hotspots of climate change in the Yangtze River Watershed during 1958–2017. J. Geogr. Sci. 2022, 32, 141–155. [Google Scholar] [CrossRef]
- de Larminat, P. Earth climate identification vs. anthropic global warming attribution. Annu. Rev. Control 2016, 42, 114–125. [Google Scholar] [CrossRef] [Green Version]
- Van Loon, A.F.; Rangecroft, S.; Coxon, G.; Breña Naranjo, J.A.; Van Ogtrop, F.; Van Lanen, H.A.J. Using paired catchments to quantify the human influence on hydrological droughts. Hydrol. Earth Syst. Sci. 2019, 23, 1725–1739. [Google Scholar] [CrossRef] [Green Version]
- Shahid, M.; Cong, Z.; Zhang, D. Understanding the impacts of climate change and human activities on streamflow: A case study of the Soan River basin, Pakistan. Theor. Appl. Climatol. 2018, 134, 205–219. [Google Scholar] [CrossRef]
- Zhang, A.; Zhang, C.; Fu, G.; Wang, B.; Bao, Z.; Zheng, H. Assessments of Impacts of Climate Change and Human Activities on Runoff with SWAT for the Huifa River Basin, Northeast China. Water Resour. Manag. 2012, 26, 2199–2217. [Google Scholar] [CrossRef]
- Zhan, C.S.; Jiang, S.S.; Sun, F.B.; Jia, Y.W.; Niu, C.W.; Yue, W.F. Quantitative contribution of climate change and human activities to runoff changes in the Wei River basin, China. Hydrol. Earth Syst. Sci. 2014, 18, 3069–3077. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Huang, S.; Liu, D.; Leng, G.; Zhou, S.; Huang, Q. Assessing the effects of climate change and human activities on runoff variations from a seasonal perspective. Stoch. Environ. Res. Risk Assess. 2020, 34, 575–592. [Google Scholar] [CrossRef]
- Zhao, G.; Gao, H.; Naz, B.S.; Kao, S.-C.; Voisin, N. Integrating a reservoir regulation scheme into a spatially distributed hydrological model. Adv. Water Resour. 2016, 98, 16–31. [Google Scholar] [CrossRef] [Green Version]
- Koch, H.; Liersch, S.; de Azevedo, J.R.G.; Silva, A.L.C.; Hattermann, F.F. Assessment of observed and simulated low flow indices for a highly managed river basin. Hydrol. Res. 2018, 49, 1831–1846. [Google Scholar] [CrossRef]
- Men, B.; Liu, H.; Tian, W.; Wu, Z.; Hui, J. The Impact of Reservoirs on Runoff Under Climate Change: A Case of Nierji Reservoir in China. Water 2019, 11, 1005. [Google Scholar] [CrossRef] [Green Version]
- Dash, S.S.; Sahoo, B.; Raghuwanshi, N.S. How reliable are the evapotranspiration estimates by Soil and Water Assessment Tool (SWAT) and Variable Infiltration Capacity (VIC) models for catchment-scale drought assessment and irrigation planning? J. Hydrol. 2021, 592, 125838. [Google Scholar] [CrossRef]
- Naqash, T.B.; Ahanger, M.A.; Maity, R. Multi-site hydrometeorological simulation of streamflow for upper Jhelum basin in northwest Himalayas using HEC–HMS soil moisture accounting algorithm. Model. Earth Syst. Environ. 2023, 9, 431–455. [Google Scholar] [CrossRef]
- Ishikawa, M.; Haag, I.; Krumm, J.; Teltscher, K.; Lorke, A. The effect of stream shading on the inflow characteristics in a downstream reservoir. River Res. Appl. 2021, 37, 943–954. [Google Scholar] [CrossRef]
- Koch, H.; Liersch, S.; Hattermann, F.F. Integrating water resources management in eco-hydrological modelling. Water Sci. Technol. 2013, 67, 1525–1533. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, H.; Zhang, J.; Hou, Y.; Shen, M.; Chen, J.; Xu, C. Impacts of climate change and LULC change on runoff in the Jinsha River Basin. J. Geogr. Sci. 2020, 30, 85–102. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Zhang, J.; Yang, M.; Lei, X.; Guo, B.; Yang, L.; Zeng, Z.; Qu, J. Application of SWAT Model with CMADS Data to Estimate Hydrological Elements and Parameter Uncertainty Based on SUFI-2 Algorithm in the Lijiang River Basin, China. Water 2018, 10, 742. [Google Scholar] [CrossRef] [Green Version]
- Yuan, S.; Quiring, S.M.; Kalcic, M.M.; Apostel, A.M.; Evenson, G.R.; Kujawa, H.A. Optimizing climate model selection for hydrological modeling: A case study in the Maumee River basin using the SWAT. J. Hydrol. 2020, 588, 125064. [Google Scholar] [CrossRef]
- Neitsch, S.; Arnold, J.; Kiniry, J.; Williams, J. Soil and Water Assessment Tool Theoretical Documentation, Version 2009, Texas Water Resources Institute Technical Report No.406; Texas Water Resources Institute: Texas, TX, USA, 2011. [Google Scholar]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol.-Amst. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Johnson, C.A.; Genuchten, M. Estimating Uncertain Flow and Transport Parameters Using a Sequential Uncertainty Fitting Procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Pukelsheim, F. The Three Sigma Rule. Am. Stat. 1994, 48, 88–91. [Google Scholar] [CrossRef] [Green Version]
- Xiao, H.; Zhang, Y.; Liu, X.; Yin, H.; Liu, P.; Liu, D.C. A Rapid Ultrasound Vascular Disease Screening Method using PauTa Criterion. J. Phys. Conf. Ser. 2021, 1769, 012009. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison With Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: Oxford, UK, 1948. [Google Scholar]
- Gumus, V.; Avsaroglu, Y.; Simsek, O. Streamflow trends in the Tigris river basin using Mann−Kendall and innovative trend analysis methods. J. Earth Syst. Sci. 2022, 131, 34. [Google Scholar] [CrossRef]
- Lian, Y.; Sun, M.; Wang, J.; Luan, Q.; Jiao, M.; Zhao, X.; Gao, X. Quantitative impacts of climate change and human activities on the runoff evolution process in the Yanhe River Basin. Phys. Chem. Earth Parts A/B/C 2021, 122, 102998. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Pellicciotti, F.; Bierkens, M. Rising river flows throughout the twenty-first century in two Himalayan glacierized watersheds. Nat. Geosci. 2013, 6, 742–745. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Chaumont, D.; Braun, M. Performance and uncertainty evaluation of empirical downscaling methods in quantifying the climate change impacts on hydrology over two North American river basins. J. Hydrol. 2013, 479, 200–214. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, H.; Wang, J.; Zhao, Y.; Chen, J.; Xu, C. Impacts of Climate Change and Land-Use Change on Hydrological Extremes in the Jinsha River Basin. Water 2019, 11, 1398. [Google Scholar] [CrossRef] [Green Version]
- Cui, H.; Jiang, S.; Gao, B.; Ren, L.; Xiao, W.; Wang, M.; Ren, M.; Xu, C.-Y. On method of regional non-stationary flood frequency analysis under the influence of large reservoir group and climate change. J. Hydrol. 2023, 618, 129255. [Google Scholar] [CrossRef]
- Liu, X.; Yang, M.; Meng, X.; Wen, F.; Sun, G. Assessing the Impact of Reservoir Parameters on Runoff in the Yalong River Basin using the SWAT Model. Water 2019, 11, 643. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Yuan, X.; Lu, Y.; Guo, Z.; Wang, J.; Luo, H. Quantifying the Impact of Cascade Reservoirs on Streamflow, Drought, and Flood in the Jinsha River Basin. Sustainability 2023, 15, 4989. [Google Scholar] [CrossRef]
- Yun, X.; Tang, Q.; Wang, J.; Liu, X.; Zhang, Y.; Lu, H.; Wang, Y.; Zhang, L.; Chen, D. Impacts of climate change and reservoir operation on streamflow and flood characteristics in the Lancang-Mekong River Basin. J. Hydrol. 2020, 590, 125472. [Google Scholar] [CrossRef]
- Zhang, P.; Cai, Y.; Xie, Y.; Yi, Y.; Yang, W.; Li, Z. Effects of a cascade reservoir system on runoff and sediment yields in a River Basin of southwestern China. Ecol. Eng. 2022, 179, 106616. [Google Scholar] [CrossRef]
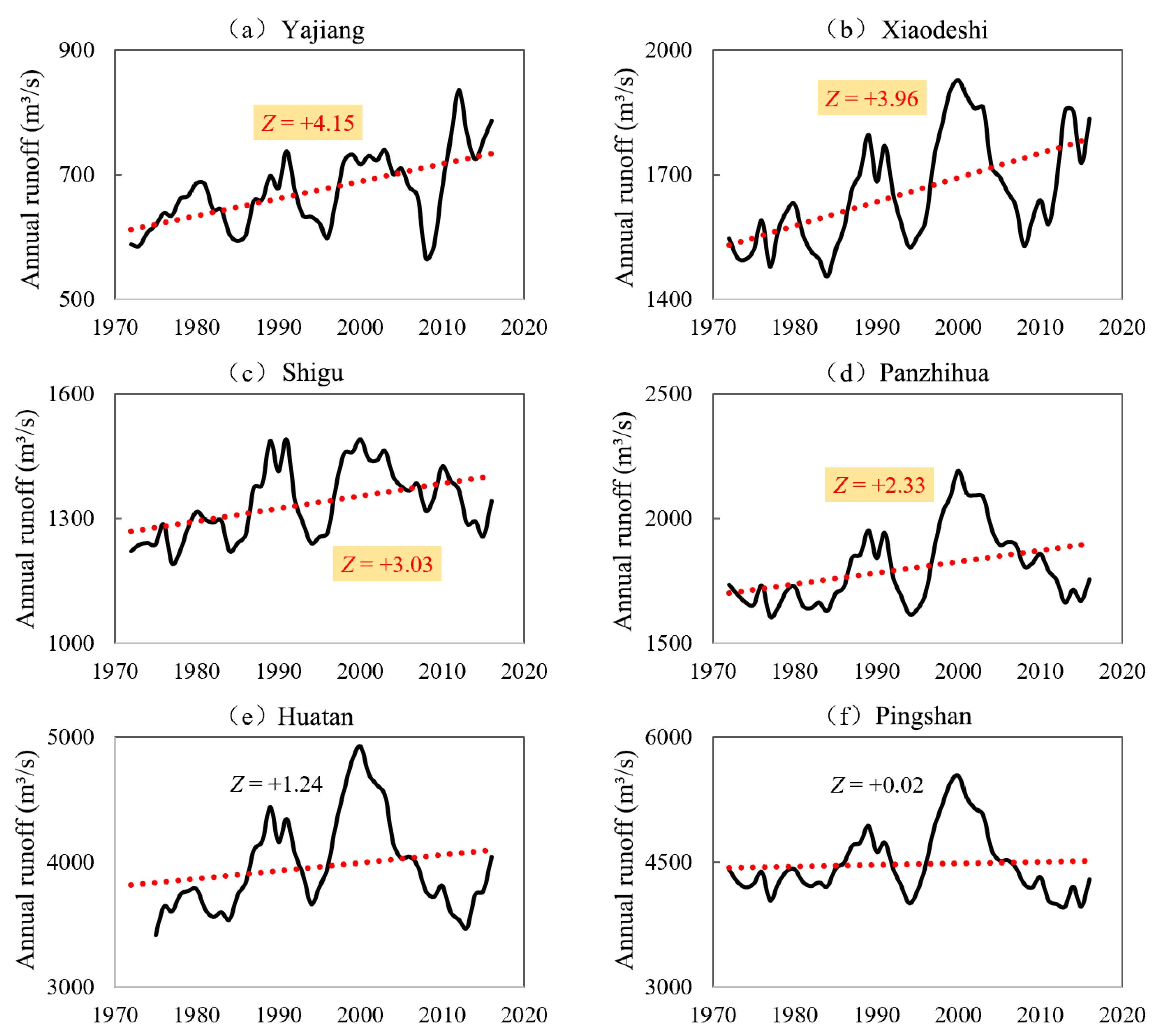
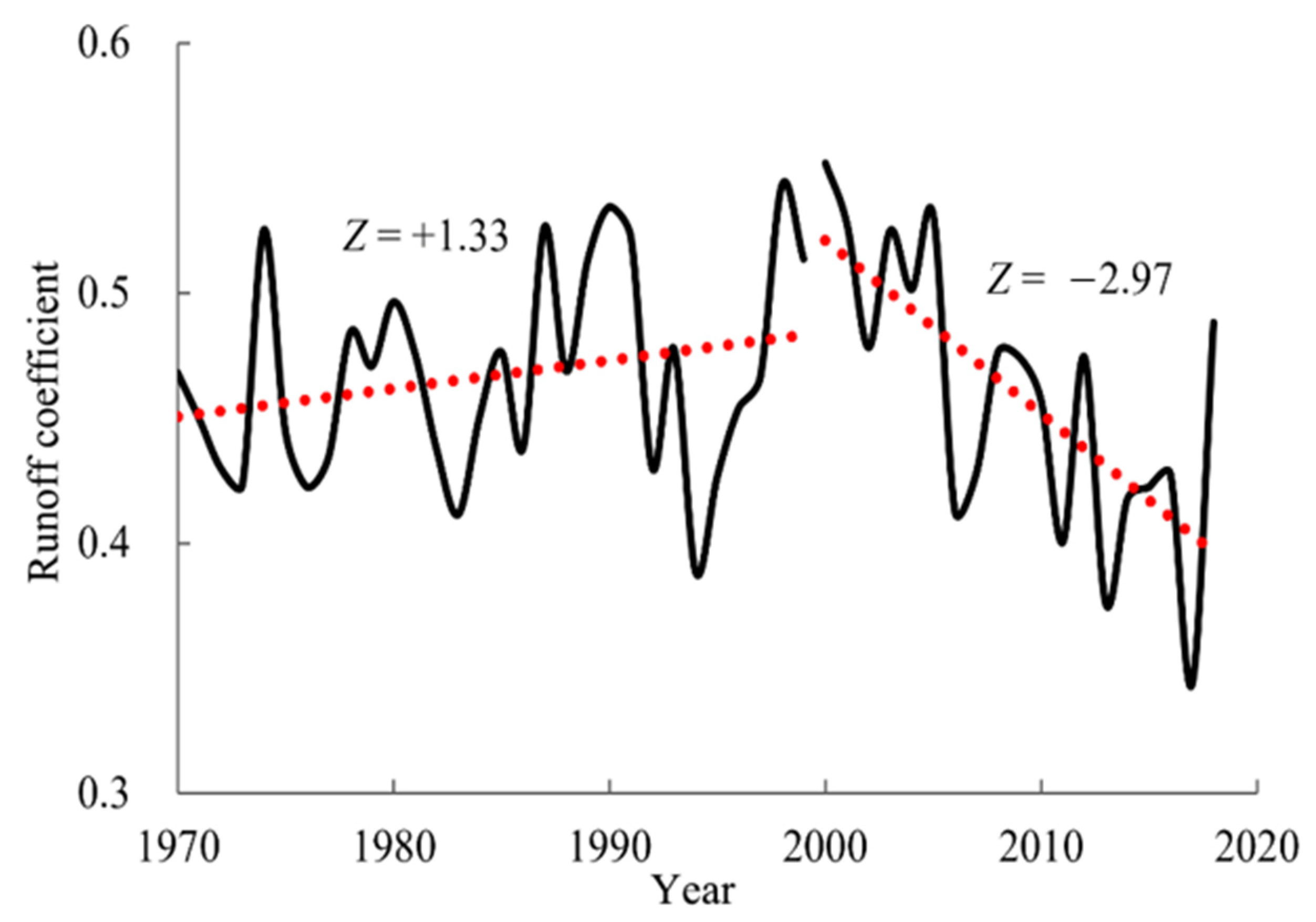
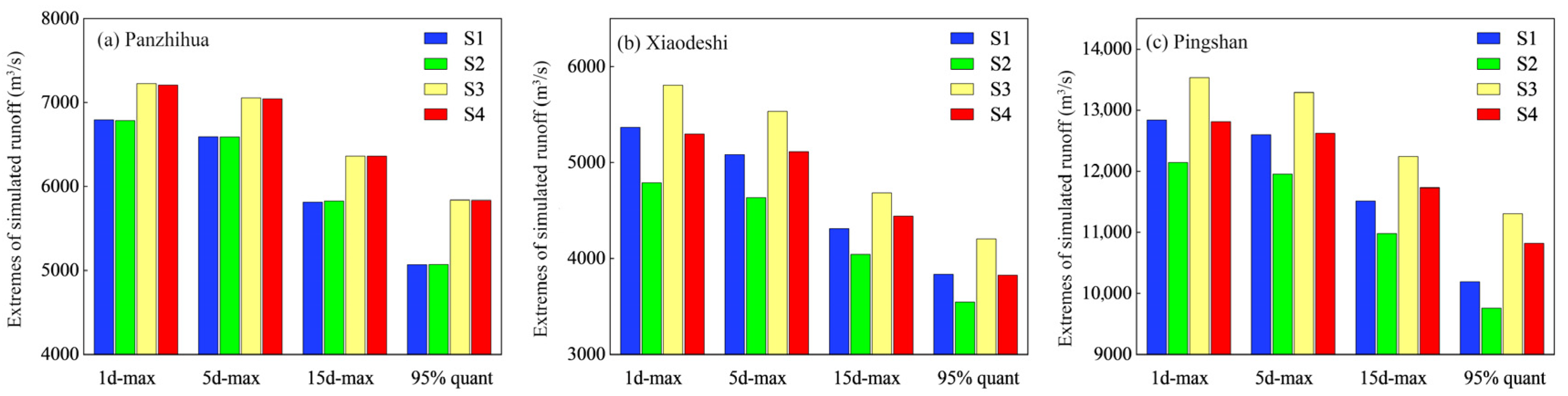
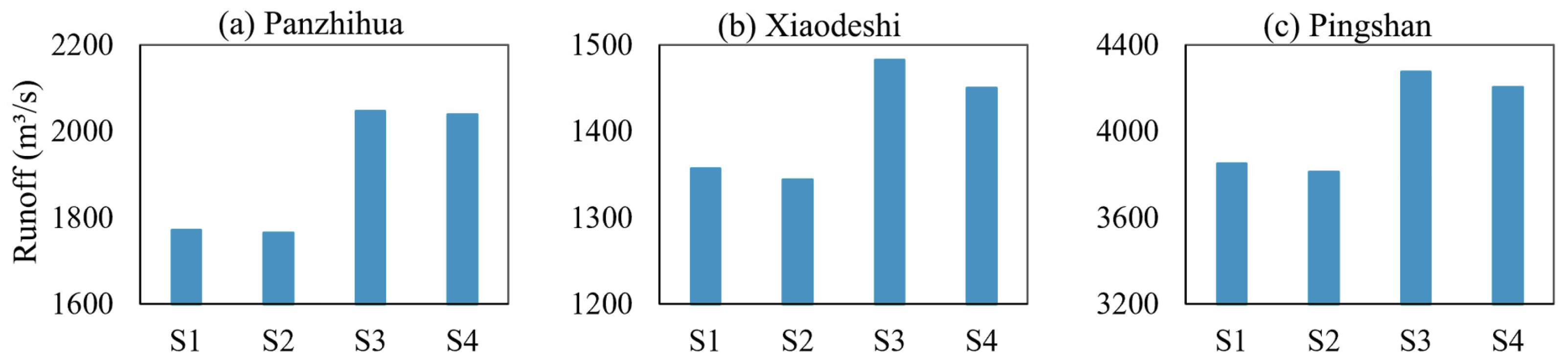

| River System | Reservoir | Initial Water Storage Time | Normal Storage Water Level (m) | Regulation Performance | Total Reservoir Capacity (108 m3) |
|---|---|---|---|---|---|
| Middle reaches of the Jinsha River | Liyuan | 2014.11 | 1618 | weekly | 8.05 |
| Jin’anqiao | 2010.11 | 1418 | weekly | 9.13 | |
| Guanyinyan | 2014.10 | 1134 | weekly | 20.72 | |
| Lower reaches of the Jinsha River | Xiluodu | 2013.5 | 600 | incomplete annual | 126.7 |
| Xiangjiaba | 2012.10 | 380 | seasonal | 51.63 | |
| Lower reaches of the Yalong River | Jinping I | 2012.11 | 1880 | annual | 77.6 |
| Ertan | 1998.5 | 1200 | seasonal | 58 |
| Datatype | Data Description | Source |
|---|---|---|
| DEM | The resolution of 200 m | Geospatial Data Cloud (http://www.gscloud.cn, accessed on 1 May 2020) |
| Soil data | Harmonized World Soil Database (v1.1), with a resolution of 1000 m | Cold and Arid Regions Sciences Data Center at Lanzhou (http://westdc.westgis.ac.cn, accessed on 1 June 2020) |
| Land-use data | Land-use dates of 1980, 1990, 2000, 2015, with the resolution of 1000 m | Resources and Environment Data Cloud Platform (http://www.resdc.cn, accessed on 1 June 2020) |
| Meteorological data | Daily precipitation, min/max/average temperature, relative humidity, solar radiation, and wind speed from 30 weather stations in 1970–2018 | China Meteorological Science Data Center (http://data.cma.cn, accessed on 1 July 2020) |
| Runoff data | Daily runoff data in 6 hydrological stations in 1970–2018 | Bureau of Hydrology, Changjiang Water Resources Commission |
| Reservoir operation data | The storage capacity, daily inflow, outflow, and water level of 7 reservoirs | |
| GCMs in CMIP5 | Daily precipitation, min/max/ The average temperature in 1970–2050 | Lawrence Livermore National Laboratory (https://esgf-node.llnl.gov, accessed on 1 July 2020) |
| Scenarios | Reservoir Regulation | Climate Data | Mean Annual Simulated Runoff Depth (mm) |
|---|---|---|---|
| S1 | Pref | Pref | R1 (benchmark) |
| S2 | Ptest | Pref | R2 (only influenced by reservoirs) |
| S3 | Pref | Ptest | R3 (only influenced by climate) |
| S4 | Ptest | Ptest | R4 (jointly influence) |
| Stations | Water System | Calibration Period (1985–1997) | Validation Period (1970–1984) | ||||
|---|---|---|---|---|---|---|---|
| R2 | NSE | PBIAS (%) | R2 | NSE | PBIAS (%) | ||
| Yajiang | Yalong River | 0.82 | 0.80 | –3.4 | 0.80 | 0.79 | 3.7 |
| Xiaodeshi | Yalong River | 0.88 | 0.86 | 13.1 | 0.86 | 0.83 | 14.8 |
| Shigu | Upper Jinsha River | 0.82 | 0.77 | 10.2 | 0.83 | 0.78 | 12.3 |
| Panzhihua | Middle reaches of Jinsha River | 0.89 | 0.84 | –3.5 | 0.90 | 0.86 | 0.7 |
| Huatan | Lower reaches of Jinsha River | 0.93 | 0.92 | 6.4 | 0.93 | 0.92 | 2.1 |
| Pingshan | Lower reaches of Jinsha River | 0.94 | 0.92 | 11.0 | 0.93 | 0.91 | 13.3 |
| Absolute average | 0.88 | 0.85 | 5.63 | 0.88 | 0.85 | 7.82 | |
| Reservoirs | Flood Season | Non-Flood Season | ||
|---|---|---|---|---|
| Dispatch Function | CC | Dispatch Function | CC | |
| Ertan | 0.94 | 0.88 | ||
| Jinping I | 0.93 | 0.97 | ||
| Liyuan | 0.99 | 0.91 | ||
| Jin’anqiao | 0.98 | 0.87 | ||
| Guanyinyan | 0.96 | 0.91 | ||
| Xiluodu | 0.94 | 0.90 | ||
| Xiangjiaba | 0.97 | 0.95 | ||
| Station | Yajiang | Shigu | Xiaodeshi | Panzhihua | Huatan | Pingshan | |
|---|---|---|---|---|---|---|---|
| Evaluation Period | 1998–2008 | 2011–2018 | 1999–2018 | 2011–2018 | 2011–2018 | 2011–2018 | |
| Target storage capacity method | NSE | 0.84 | 0.77 | −0.78 | 0.69 | 0.57 | 0.37 |
| R2 | 0.84 | 0.86 | 0.24 | 0.84 | 0.73 | 0.66 | |
| PBIAS (%) | 2.6 | −10 | −3.2 | −17.9 | −4.2 | 0.9 | |
| Without considering the reservoir influence | NSE | 0.84 | 0.77 | 0.52 | 0.71 | 0.75 | 0.73 |
| R2 | 0.84 | 0.86 | 0.58 | 0.86 | 0.83 | 0.82 | |
| PBIAS (%) | 2.6 | −10 | −5.4 | −18.4 | −5.3 | −1.2 | |
| Dispatch function method | NSE | 0.84 | 0.77 | 0.67 | 0.72 | 0.84 | 0.78 |
| R2 | 0.84 | 0.86 | 0.68 | 0.85 | 0.87 | 0.80 | |
| PBIAS (%) | 2.6 | −10 | −3.1 | −17.8 | −4.0 | 1.4 | |
| Influence Rate (%) | Hydraulic Engineering | Climate Change | Joint Effect | |
|---|---|---|---|---|
| Panzhihua | 1d-max | −0.1 | 6.3 | 6.1 |
| 5d-max | −0.1 | 7.0 | 6.9 | |
| 15d-max | 0.2 | 9.4 | 9.4 | |
| 95% quant | 0.0 | 15.1 | 15.1 | |
| Xiaodeshi | 1d-max | −10.7 | 8.2 | −1.2 |
| 5d-max | −8.9 | 8.8 | 0.5 | |
| 15d-max | −6.2 | 8.7 | 3.1 | |
| 95% quant | −7.6 | 9.6 | −0.2 | |
| Pingshan | 1d-max | −5.4 | 5.4 | −0.2 |
| 5d-max | −5.1 | 5.5 | 0.2 | |
| 15d-max | −4.7 | 6.3 | 1.9 | |
| 95% quant | −4.2 | 11.0 | 6.2 | |
| Attribution Proportions (%) | Panzhihua | Xiaodeshi | Pingshan |
|---|---|---|---|
| Reservoir regulation | −2.0 | −11.3 | −10.6 |
| Climate change | +102.0 | +111.3 | +110.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, S.; Chen, Q.; Li, J.; Chen, H. The Improved Reservoir Module of SWAT Model with a Dispatch Function and Its Application on Assessing the Impact of Climate Change and Human Activities on Runoff Change. Water 2023, 15, 2620. https://doi.org/10.3390/w15142620
Sheng S, Chen Q, Li J, Chen H. The Improved Reservoir Module of SWAT Model with a Dispatch Function and Its Application on Assessing the Impact of Climate Change and Human Activities on Runoff Change. Water. 2023; 15(14):2620. https://doi.org/10.3390/w15142620
Chicago/Turabian StyleSheng, Sheng, Qihui Chen, Jingjing Li, and Hua Chen. 2023. "The Improved Reservoir Module of SWAT Model with a Dispatch Function and Its Application on Assessing the Impact of Climate Change and Human Activities on Runoff Change" Water 15, no. 14: 2620. https://doi.org/10.3390/w15142620
APA StyleSheng, S., Chen, Q., Li, J., & Chen, H. (2023). The Improved Reservoir Module of SWAT Model with a Dispatch Function and Its Application on Assessing the Impact of Climate Change and Human Activities on Runoff Change. Water, 15(14), 2620. https://doi.org/10.3390/w15142620








