Copula-Based Severity–Duration–Frequency (SDF) Analysis of Streamflow Drought in the Source Area of the Yellow River, China

Abstract

In classical severity–duration–frequency (SDF) analysis, the dependence between drought characteristics is not effectively considered. The present study aims to propose the SDF relationships of streamflow drought in the source area of the Yellow River (SAYR) using a copula-based approach. Comparison of multiple time-varying threshold levels and the integration and elimination of drought events were considered. Selection of marginal probability distribution and copula-based joint probability distribution was properly conducted with multiple means. Copula-based joint and conditional probabilities were computed. The findings support carrying out integration and elimination processing on the preliminarily identified streamflow droughts through a run analysis with a time-varying threshold level of the 80% quantile of daily streamflow. The Gaussian copula was selected as the optimal model for constructing bivariate joint probability distribution, with generalized extreme value and log-normal as the suitable marginal probability distributions of streamflow drought duration and severity. The proposed copula-based SDF relationships of streamflow drought events can provide more critical information in addition to univariate frequency analysis, benefitting from the joint and conditional probabilities. The multivariate probabilistic analyses can effectively consider the connection and interaction between drought characteristics, while conditional probability distribution allows analyzing the impact of one drought characteristic on another. The results also indicate a relatively high risk of streamflow drought with short duration and low severity in the region, requiring effective drought-mitigation strategies and measures.

1. Introduction

Drought is a kind of natural phenomenon with complicated causes, mainly manifested as abnormal water supply conditions. From different research perspectives, droughts are usually divided into meteorological, agricultural, hydrological, socio-economic, ecological, and groundwater categories [1,2]. Among them, hydrological drought refers to the reduction of surface water due to lack of precipitation, such as river flow and lake/reservoir storage, which may cause serious consequences [3]. Streamflow drought is the focus of hydrological drought research, and it is usually possible to identify streamflow drought events based on the theory of runs [4]. In run analysis, the truncation threshold can be either fixed or time-varying. However, considering the significant difference in river flow between wet and dry seasons, it is unreasonable to use a fixed threshold to identify streamflow drought during a long period [5]. At the same time, in identifying drought events, there are often cases where the time interval between adjacent drought events is very short as well as cases where many drought events have rather a short duration or low severity, which may affect the objectivity in the statistical analysis of drought characteristics. Therefore, it is necessary to select the most suitable threshold to identify streamflow drought events and facilitate additional integration and elimination of drought events [6].

In general, drought events have multivariate characteristics such as duration, inter-arrival time, severity, severity peak, etc. The severity–duration–frequency (SDF) curve, which is analogous to the well-known intensity–duration–frequency (IDF) curve used for rainfall, is a foundation for risk assessment and a planning tool for drought analysis. It effectively identifies multivariate hydrological drought using severity, duration, and frequency [7]. As IDF analyses of rainfall are crucial for the design of hydraulic infrastructure, SDF analyses of drought can help to quantify and reduce the risk of failure in water supply and mitigate drought impact from an agricultural perspective [5,8,9]. Ref. [10] constructed regional SDF curves for two Colombian catchments and confirmed their potential as useful tools for the prioritization of drought-vulnerable zones. Ref. [11] derived SDF curves of streamflow droughts using fixed and variable thresholds based on thirty-year daily discharge data. Ref. [12] developed SDF curves for identifying drought proneness in semi-arid regions using ground-based rainfall and temperature data and suggested that SDF curves serve as a convenient tool for risk assessment, preparedness, and mitigation against agricultural droughts. Ref. [13] also carried out risk assessment to determine the spatiotemporal characteristics of meteorological drought through SDF contour maps using satellite-based precipitation products.

Traditionally, drought properties (e.g., duration and severity) are assumed to be independent of each other and investigated using univariate frequency analysis [14,15,16]. Accordingly, it mainly aims to calculate the design severities for given exceedance probabilities over a range of durations in traditional SDF analysis of droughts [5]. In other words, the dependence between drought duration and severity is not well considered, which may lead to an under or over estimation of drought risks. On the other hand, multivariate drought characterization has significantly improved with advancement in data aggregation techniques such as copulas [17]. While some studies jointly model drought duration and severity using bivariate distributions [18,19], a copula-based approach tackles the dependence between drought duration and severity [20] and allows their marginal distributions that belong to different families [21]. A series of studies extended univariate frequency analysis of droughts to bivariate and trivariate cases using copulas [22,23,24,25,26,27,28]. The copula-based joint probability distribution makes it possible to develop the SDF curves of drought considering the dependent relationship between drought characteristics (i.e., duration and severity) [29]. Based on a bivariate copula, ref. [30,31] successfully derived SDF relationships of drought and assessed the spatial variability of drought risks.

The source area of the Yellow River (SAYR) plays a key role in the water supply, ecological security, and socio-economic sustainability of the entire Yellow River Basin [32]. However, the SDF relationships of streamflow drought in the SAYR have not yet been well established, which is essential for risk assessment and mitigation of streamflow droughts. Therefore, the primary objective of the present study is to propose the SDF relationships of streamflow drought in the SAYR using a copula-based approach. Comparison of multiple time-varying threshold levels and integration and elimination of drought events are considered to identify streamflow drought characteristics correctly. The selection of marginal probability distribution and copula-based joint probability distribution is also properly conducted with multiple means, including graphical inspections as well as goodness-of-fit tests and criteria. The remainder of the paper is organized as follows. Section 2 describes the materials and methods used, while Section 3 presents the results as given by illustrations and tables. Afterwards, relevant discussion and conclusions are provided in Section 4.

2. Materials and Methods

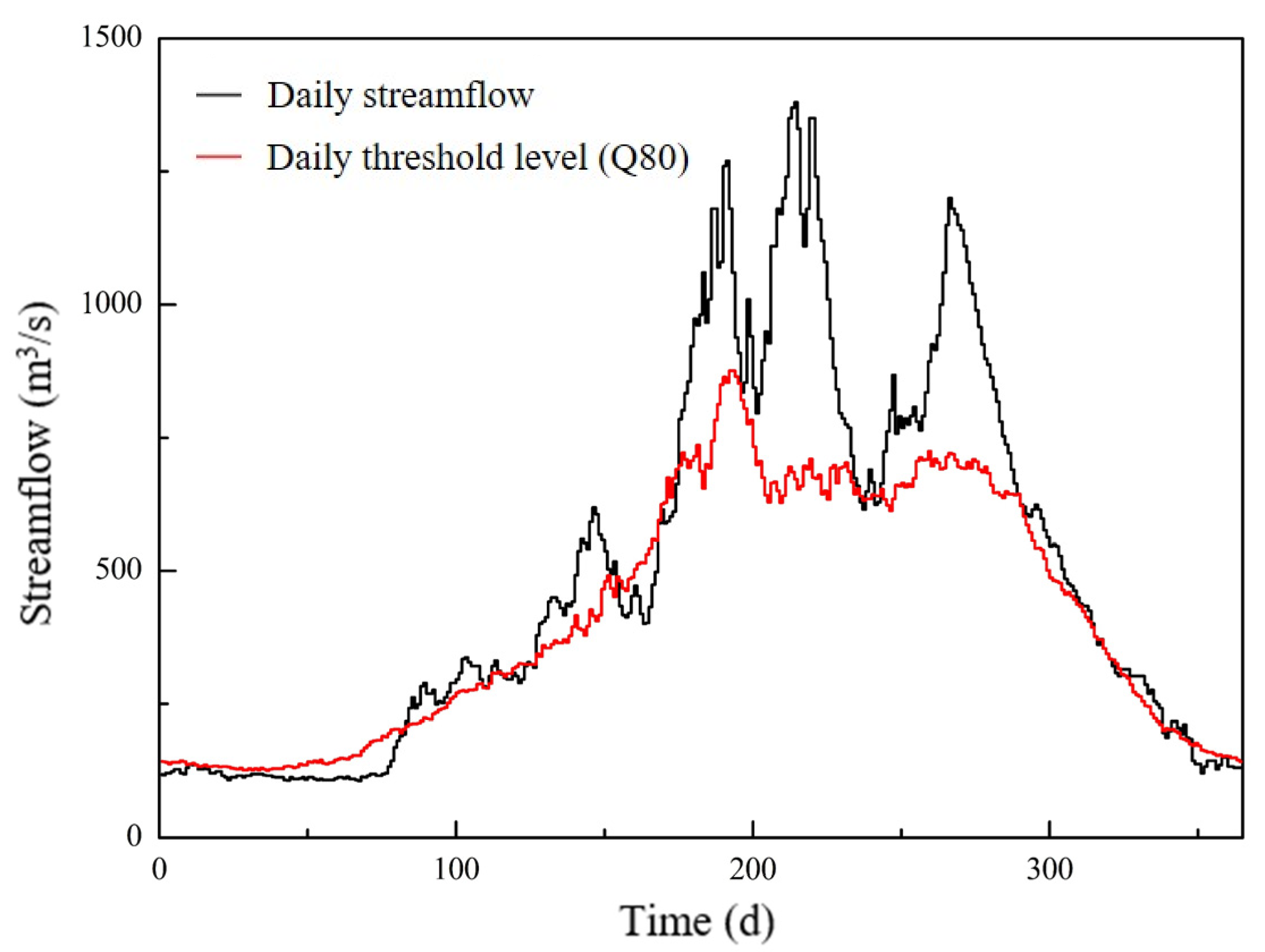
2.1. Study Area and Data

The source area of the Yellow River (SAYR) is located in the northeast of the Qinghai-Tibet Plateau. As the gateway of the SAYR, the Tangnaihai gauge (100°09′ E, 35°30′ N) is situated on the main stream of the Yellow River at Tangnaihai Township, Xinghai County, Qinghai Province, China, providing important basic data about variations of hydrological processes and water resources as well as changes in the water–sediment relationship in the upper reaches of the Yellow River. The geographical features of the SAYR and relevant catchment area drained at the Tangnaihai gauge are shown in Figure 1. In this study, the observational datasets of daily averaged streamflow at the Tangnaihai gauge from 1956 to 2018 were used to analyze the historical streamflow drought characteristics (e.g., duration, severity, and severity peak) and their joint probabilistic relationships from a multivariate perspective in the SAYR.

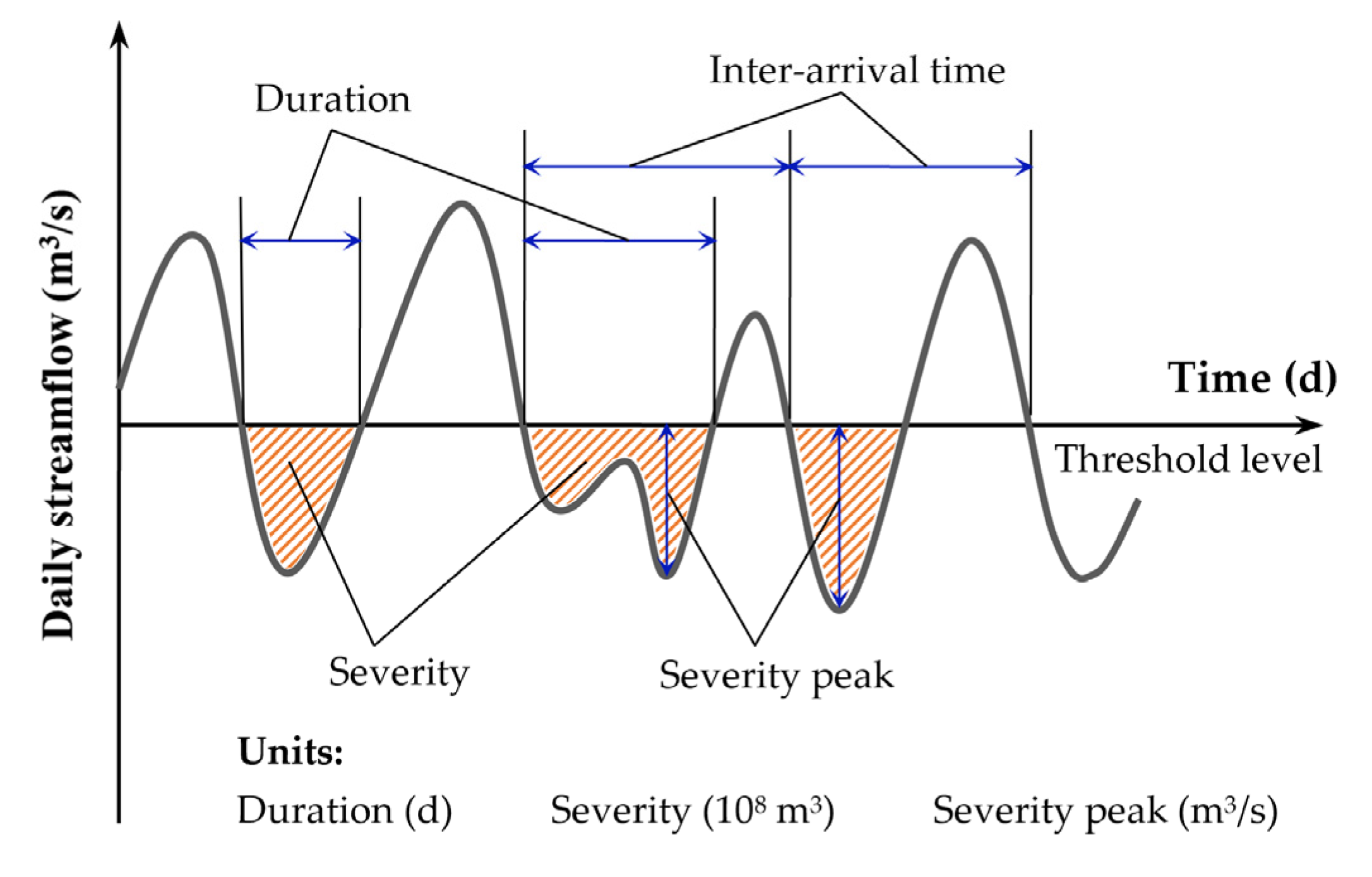
2.2. Streamflow Drought Identification

To start with, a series of abnormally low streamflow episodes can be identified based on the run theory and using a given flow rate as a threshold level. As a useful tool, the run analysis is commonly used to examine the internal coherence of a time-dependent sequence based on the arrangement of sample markers (i.e., adjacently identical or different). Through run analyses, a negative run process is defined as a streamflow drought when daily streamflow is consistently lower than the threshold level during a continuous period. As illustrated in Figure 2, a streamflow drought is generally characterized by duration ($D$, d), severity ($S$, 10⁸ m³), severity peak ($P$, m³/s), and inter-arrival time (d). Specifically, duration refers to the length of time from the beginning to the end of a streamflow drought, severity records the accumulative water shortage (in the form of volume) relevant to drought duration, severity peak reflects the maximum negative anomaly of streamflow during an identified drought episode, and inter-arrival time indicates the time span between two neighboring streamflow droughts. According to previous studies (e.g., [5]), the 70% to 95% quantiles of daily streamflow (i.e., Q70 to Q95) are usually used as candidates of threshold levels for run analyses in streamflow drought identification. In this way, the daily threshold becomes time-varying and is composed of 365 or 366 threshold values per year, which could be derived from daily streamflow datasets of a relatively long record through frequency calculation. Figure 3 shows the illustration of streamflow drought identification using a time-varying threshold level of the 80% quantile of daily streamflow (Q80). It is seen that the daily streamflow fluctuates below and above the threshold level from time to time during a calendar year, while a series of streamflow droughts and relevant characteristics (e.g., duration, severity, and severity peak) can be extracted regarding a daily streamflow lower than Q80. Meanwhile, more and relatively longer streamflow droughts are generally identified during low-flow season.

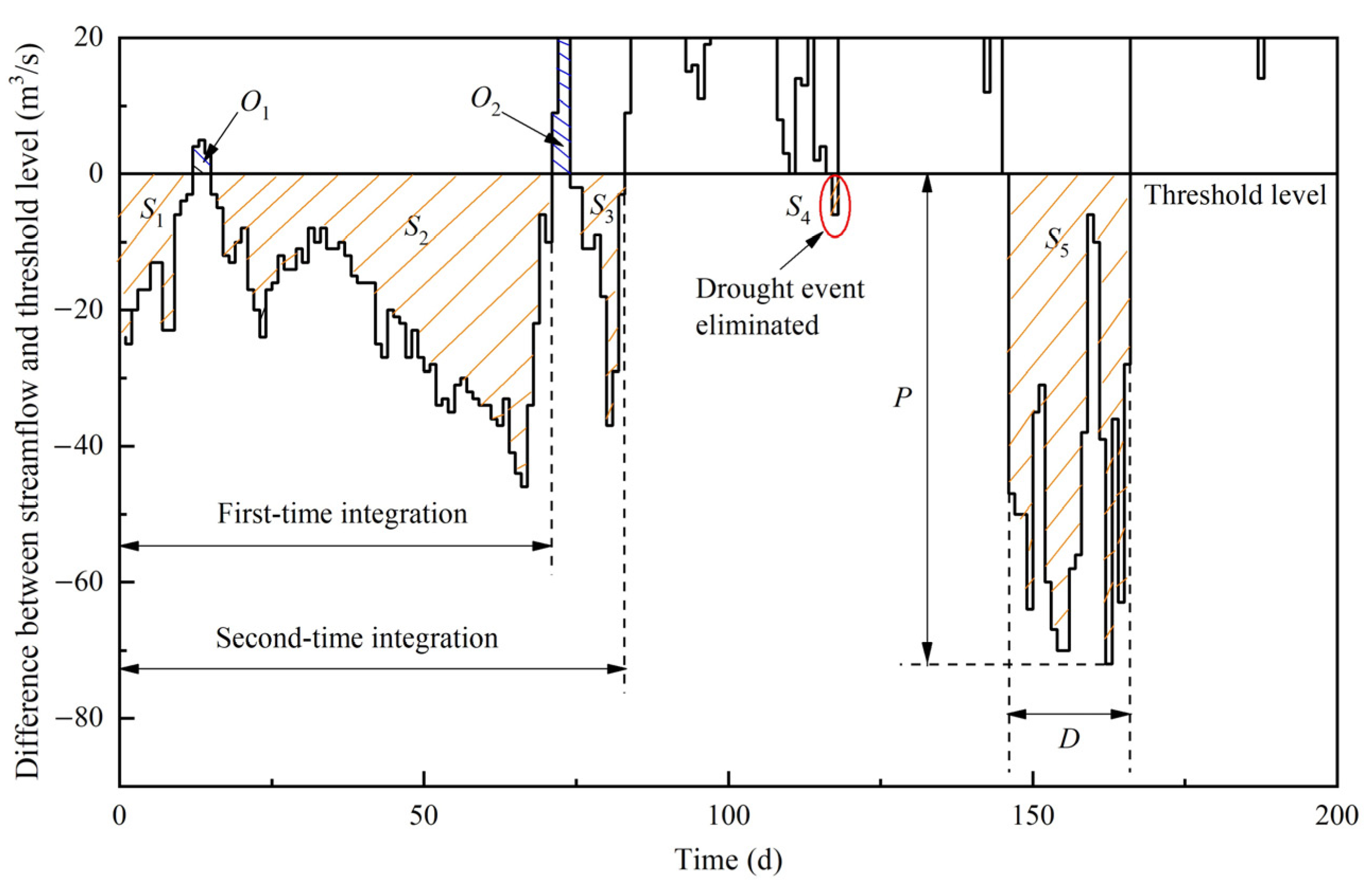
2.3. Integration and Elimination of Drought Events

For daily streamflow series, there are often cases where the streamflow temporarily exceeds the threshold level (theoretically non-drought) between two identified adjacent streamflow droughts with relatively long duration and high severity. In this situation, it is usually considered that there might be a connection between these two artificially fragmented droughts, and they should be integrated into one drought event of a longer duration and higher magnitude (see Figure 4). Ref. [33] introduced a method for integrating drought events according to the interval and over-threshold flow rate between two adjacent droughts. Assume that there are two adjacent streamflow droughts, denoted by $R_i$ and $R_{i+1}$, whose duration, severity, and severity peak are ${(D}_i$, $S_i$, $P_i)$ and ${(D}_{i+1}$, $S_{i+1}$, $P_{i+1})$, respectively, and they should be integrated if the following conditions are met:

$$\left\{\begin{array}{c}{T}_i\le T_c\\ \frac{O_i}{S_i}={\rho }_i<{\rho }_c\end{array}\right.$$

(1)

where $T_i$ is the time interval between two adjacent droughts; $T_c$ is the critical value of $T_i$, assumed to be 5 days in this study; $O_i$ is the sum of over-threshold flow; $S_i$ is the severity of streamflow drought $R_i$; ${\rho }_c$ is the critical value of ${\rho }_i$ (ratio of $O_i$ and $S_i$), generally taking a value of 0.1.

Supposing an integrated streamflow drought, $R_U$, the drought integration is specifically conducted as follows:

$$\left\{\begin{array}{c}{D}_U=D_i+D_{i+1}+T_i\\ S_U=S_i+S_{i+1}-O_i\\ P_U=max\left(P_i,P_{i+1}\right)\end{array}\right.$$

(2)

where $D_U$, $S_U$, and $P_U$ are the duration, severity, and severity peak of the integrated streamflow drought $R_U$, respectively.

For integrated and following streamflow droughts, the criteria described in Equation (1) are examined as well. To be specific, if the interval and over-threshold flow rate have not reached given critical values, the integration of these two adjacent droughts are further carried out using the above procedure given by Equation (2). In other words, the integration of streamflow droughts would iterate until the requirements of the interval and over-threshold flow rate are no longer met. For example, the three streamflow droughts in the left part of Figure 4 (with severities of $S_1$, $S_2$, and $S_3$, and sums of the over-threshold flow of $O_1$ and $O_2$) are integrated into only one drought event with a two-round integration, of which the duration, severity, and severity peak can be derived according to Equation (2).

After the integration of drought events, there might still be many drought events of short duration or low severity. These minor drought events are of little statistical significance for drought analysis and are suggested to be eliminated, such as the fourth drought event with the severity of $S_4$ in Figure 4. Assuming the mathematical expectations of duration and severity of all drought events are $E\left\{\left.D\right\}\right.$ and $E\left\{\left.S\right\}\right.$, respectively, a streamflow drought event should be eliminated if its duration is shorter than $r_{d}E\left\{\left.D\right\}\right.$, or its severity is smaller than $r_{s}E\left\{\left.S\right\}\right.$, where $r_d=r_s=0.3$ are predetermined coefficients [33].

2.4. Marginal Probability Distribution

The characteristics (duration, severity, and severity peak) of streamflow drought events after integration and elimination treatments, as random variables, are separately fitted to appropriate probability distributions that can produce good agreements between their empirical and theoretical frequencies. To this end, the L-moment ratio diagrams are used to select the most suitable distributions out of quite a few two- and three-parameter candidate ones. As a useful visual inspection tool, the L-moment ratio diagrams can provide comparative information on shape features (i.e., L-moments that specify a unique distribution, especially the L-skewness ${\tau }_3$ and L-kurtosis ${\tau }_4$) of empirical and theoretical distributions [34,35]. The marginal probability distributions selected for streamflow drought duration, severity, and severity peak are given, respectively, as follows.

(1)

The generalized extreme value (GEV) distribution with a probability density function:

$$f\left(x\right)=\frac{1}{\kappa }{\left[1+\kappa \left(\frac{x-\mu }{\sigma }\right)\right]}^{-\frac{1}{\kappa -1}}exp\left\{-{\left[1+\kappa \left(\frac{x-\mu }{\sigma }\right)\right]}^{-\frac{1}{\kappa }}\right\}$$

(3)

(2)

The log-normal distribution with a probability density function:

$$f\left(x\right)=\frac{1}{x\sqrt{2\pi }\sigma }\exp \left[-\frac{1}{2{\sigma }^2}{\left(\ln x-\mu \right)}^2\right]$$

(4)

(3)

The generalized Pareto distribution with a probability density function:

$$f\left(x\right)=\frac{1}{\kappa }{\left(1-\frac{\kappa x}{\sigma }\right)}^{\kappa }$$

(5)

where $x$ stands for the drought variable (duration, severity, or severity peak); $\mu$, $\sigma$, and $\kappa$ are location, scale, and shape parameters of relevant probability distributions, respectively, which can be estimated through the maximum likelihood approach.

The goodness-of-fit of streamflow drought characteristics (duration, severity, and severity peak) fitted with selected theoretical distributions are also examined by root mean square error (RMSE) and Kolmogorov–Smirnov (K-S) test. The RMSE is an effective bias statistic based on mean square error (MSE):

$$\mathrm{MSE}=\frac{1}{n-m}{\displaystyle \sum }_{i=1}^n{\left(p_{ei}-p_i\right)}^2$$

(6)

$$\mathrm{RMSE}=\sqrt{\mathrm{MSE}}$$

(7)

where $n$ is the sample size, and $m$ is the number of parameters in the considered probability distribution or statistical model; $p_e$ and $p$ are the probabilities calculated through the empirical plotting-position formula and derived from the selected theoretical model, respectively. In general, a small RMSE value indicates little fitting bias and good fitness between empirical points and theoretical model.

As a nonparametric statistical method, the sample statistic $K_n$ of K-S test can be calculated as given:

$$K_n=\underset{1\le i\le n}{\max }\left[\frac{i}{n}-p_{\left(i\right)}, p_{\left(i\right)}-\frac{i-1}{n}\right]$$

(8)

where $n$ is the sample size, and $p_{(\bullet )}$ stands for the theoretical probabilities based on an ascendingly sorted sample: $x_1<x_2<\cdots <x_i<\cdots <x_n$. Given a statistically significant level (e.g., $\alpha =0.05$), the critical statistic $K_0$ of the K-S test is obtained through Monte Carlo stochastic simulation, with a bootstrap repetition of 5000 times. If the sample statistic $K_n$ is less than the critical statistic $K_0$, the null hypothesis of the K-S test is accepted. In other words, the goodness-of-fit of the observed sample fitted with the checked theoretical model is supported by the K-S test.

2.5. Joint Probability Distribution

Copulas are sophisticated tools connecting marginal probability distributions of dependent variables to produce multivariate joint probability distribution. The dependence structure of correlated variables is implicitly considered by appropriate copula functions. Thus, correlationship analysis is needed to preclude independent cases. Both linear (Pearson’s ${\gamma }_n$) and nonlinear rank-based (Spearman’s ${\rho }_n$ and Kendall’s ${\tau }_n$) correlation coefficients are used to measure the paired dependence of streamflow drought characteristics (i.e., duration–severity, duration–peak, and severity–peak). A larger correlation coefficient suggests a relatively higher dependent relationship between analyzed variables. At the same time, the paired dependence of streamflow drought characteristics (e.g., duration and severity) is also inspected using graphic analysis tools of Chi-plot and K-plot. The Chi-plot and K-plot are both based on the rank of sample points and can diagnose potential relationships through comparing the distribution of sample points against the theoretical dependent area [36,37].

Two meta-elliptical (Gaussian and Student’s t) and three Archimedean (Frank, Gumbel, and Clayton) copulas are used to construct a bivariate joint probability distribution of significantly dependent streamflow drought characteristics (e.g., duration and severity). Among them, the expression of Gaussian copula is given below, while readers are referred to other literature (e.g., [38,39]) for more details on other copula functions. Specifically, the cumulative distribution function of a two-dimensional Gaussian copula is as follows:

$$C\left(u_1,u_2;\mathit{\Sigma }\right)={\mathsf{\Phi }}_{\Sigma }\left[{\mathsf{\Phi }}^{-1}\left(u_1\right),{\mathsf{\Phi }}^{-1}\left(u_2\right)\right]={{\displaystyle \int }}_{-\infty }^{{\Phi }^{-1}\left(u_1\right)}{{\displaystyle \int }}_{-\infty }^{{\Phi }^{-1}\left(u_2\right)}\frac{1}{2\pi \sqrt{\left|\mathit{\Sigma }\right|}}exp\left(-\frac{1}{2}{\mathbf{w}}^T{\mathit{\Sigma }}^{-1}\mathbf{w}\right)d\mathbf{w}$$

(9)

where $C\left(\bullet \right)$ stands for the cumulative probability of bivariate joint distribution; $u_1=F_D\left(d\right)$ and $u_2=F_S\left(s\right)$ are the marginal probability distributions of streamflow drought duration ($D$) and severity ($S$), respectively; ${\mathsf{\Phi }}^{-1}\left(\bullet \right)$ is the inverse of the standard normal distribution $\mathbf{\Phi }\left(\bullet \right)$; ${\mathsf{\Phi }}_{\mathsf{\Sigma }}\left[{\mathsf{\Phi }}^{-1}\left(u_1\right),{\mathsf{\Phi }}^{-1}\left(u_2\right)\right]$ denotes the bivariate standard normal distribution; $\mathit{\Sigma }=\left[\begin{array}{cc}1& {\rho }_{12}\\ {\rho }_{21}& 1\end{array}\right]$ is the symmetrical covariance matrix, and ${\rho }_{12}={\rho }_{21}=\rho$ is the parameter of two-dimensional Gaussian copula to be estimated through the maximum likelihood approach; $\mathit{w}={\left[w_1,w_2\right]}^T$ represents the vector of integral variables.

In addition to the RMSE, the Akaike information criterion (AIC) and Bayesian information criterion (BIC) are also adopted to assess the goodness-of-fit of constructed bivariate joint distribution using different copula functions. The AIC and BIC, taking into account both model-fitting bias and the number of parameters, are, respectively, formulated as follows:

$$\mathrm{AIC}=n\ln \left(\mathrm{MSE}\right)+2m$$

(10)

$$\mathrm{BIC}=n\ln \left(\mathrm{MSE}\right)+m\ln \left(n\right)$$

(11)

where $n$ is the sample size; $m$ is the number of model parameters; $2m$ and $m\ln \left(n\right)$ are the penalty terms; $\mathrm{M}\mathrm{S}\mathrm{E}$ is as defined in Equation (6). The minimum value of AIC and/or BIC values indicates the best fitness between sample points and the theoretical model. Moreover, the K-S test with a modified bootstrap procedure based on Rosenblatt’s transformation is also conducted to validate the goodness-of-fit of the selected copula function. Analogous to the K-S test of marginal probability distribution, the theoretical and empirical probabilities in Equation (8) are, respectively, derived from bivariate copula and plotting-position formula for joint probability distribution, whose difference provides a critical basis for calculating the statistics of K-S test. For a detailed methodology and procedure, one may refer to [28].

2.6. Copula-Based Joint and Conditional Probabilities

Since the joint distribution of streamflow drought characteristics (e.g., duration and severity) is finally described with selected copula function, the bivariate joint non-exceedance probability can be derived as given:

$$P\left(D\le d,S\le s\right)=F_{D,S}\left(d,s\right)=C\left(F_D\left(d\right),F_S\left(s\right)\right)=C\left(u_1,u_2\right)$$

(12)

where $F_{D,S}\left(d,s\right)$ is the joint probability distribution of drought duration and severity, with $F_D\left(d\right)$ and $F_S\left(s\right)$ being the marginal probability distribution functions; $C\left(u_1,u_2\right)$ denotes the cumulative distribution function of the two-dimensional copula, while $u_1=F_D\left(d\right)$ and $u_2=F_S\left(s\right)$.

Accordingly, the bivariate joint exceedance probability is then obtained:

$$P\left(D>d,S>s\right)=1-F_D\left(d\right)-F_S\left(s\right)+C\left(F_D\left(d\right),F_S\left(s\right)\right)=1-u_1-u_2+C\left(u_1,u_2\right)$$

(13)

Based on the bivariate joint probability distribution, the conditional non-exceedance probability of the streamflow drought duration (severity) given severity (duration) exceeding a certain magnitude can also be estimated:

$$P\left(D\le d|S>s\right)=\frac{F_D\left(d\right)-C\left(F_D\left(d\right),F_S\left(s\right)\right)}{1-F_S\left(s\right)}=\frac{u_1-C\left(u_1,u_2\right)}{1-u_2}$$

(14)

$$P\left(S\le s|D>d\right)=\frac{F_S\left(s\right)-C\left(F_D\left(d\right),F_S\left(s\right)\right)}{1-F_D\left(d\right)}=\frac{u_2-C\left(u_1,u_2\right)}{1-u_1}$$

(15)

3. Results

3.1. Drought Identification

In order to ascertain the impact of different threshold levels on identified streamflow droughts and determine the most appropriate threshold for the Tangnaihai gauge, six comparable thresholds were considered, namely Q70, Q75, Q80, Q85, Q90, and Q95 of daily streamflow, to extract the drought events together with corresponding duration ($D$), severity ($S$), and severity peak ($P$), whose statistics are compared in

Table 1. Statistics of streamflow drought events with different daily threshold levels.

Daily Threshold Levels	Drought Events (No.)	Short-Duration Drought Events * (No.)	Percentages of Short-Duration Drought Events (%)	Averages of Drought Duration (d)	Averages of Drought Severity (108 m3)
Q70	569	359	63.1	11.6	0.88
Q75	527	342	64.9	10.5	0.71
Q80	429	267	62.2	10.3	0.61
Q85	370	239	64.6	8.9	0.43
Q90	303	211	69.6	7.3	0.29
Q95	208	149	71.6	8.3	0.55

Note: * The short-duration drought events refer to those no longer than five days.

. It was found that with the gradual reduction of daily thresholds from Q70 to Q95, the number of droughts (including short-duration droughts) and the averages of drought duration and severity generally show a downward trend. However, if the threshold is too small (e.g., Q95), although the proportion of short-duration droughts is relatively higher, the averages of drought duration and severity are larger than those of the daily threshold of Q90. It implies that a very small threshold level would lead to a few drought events with considerably long duration and huge severity, thereby failing to reflect the essential statistics of streamflow drought characteristics. Meanwhile, although the number of short-duration droughts declines with decreasing threshold levels, its proportion overall increases. In other words, the use of too-small threshold levels would result in a high fraction of short-duration droughts having little significance but causing interference with statistical analysis of streamflow droughts. Therefore, too-small threshold levels should be avoided for streamflow drought identification. It was also seen that the daily threshold level of Q80 yields the smallest proportion of short-duration droughts. Thus, the following parts mainly focus on analyses of streamflow droughts at the Tangnaihai gauge using Q80 of daily streamflow as a selected time-varying threshold level.

Drought integration and elimination were further conducted on preliminarily identified streamflow drought events with a selected daily threshold level of Q80. The statistics of streamflow drought events with different treatments (untreated, only integration, and integration and elimination) are displayed in

Table 2. Statistics of streamflow drought events with different treatments and selected daily threshold level (Q80).

Different Treatments	Drought Events (No.)	Averages of Drought Duration (d)	Averages of Drought Severity (108 m3)
Untreated	429	10.3	0.61
Only integration	290	16.0	0.90
Integration and elimination	93	41.2	2.72

. It can be seen that with no treatment, up to 429 drought events were identified at the Tangnaihai gauge from 1956 to 2018, i.e., the occurrence of a drought event every 1.76 months on average. After integration and elimination, a total of 93 drought events were concentrated instead, i.e., a drought event occurring about every 8.13 months. Accordingly, the average of drought duration increases from 10.3 to 41.2 days. It is considered that the statistics of duration and severity with drought integration and elimination can better reflect the properties of streamflow drought occurrence and persistence. Therefore, it is of great significance to integrate and eliminate identified streamflow drought events before fitting the drought characteristics (e.g., duration, severity, and severity peak) to suitable probability distributions and analyzing their joint probabilistic relationships.

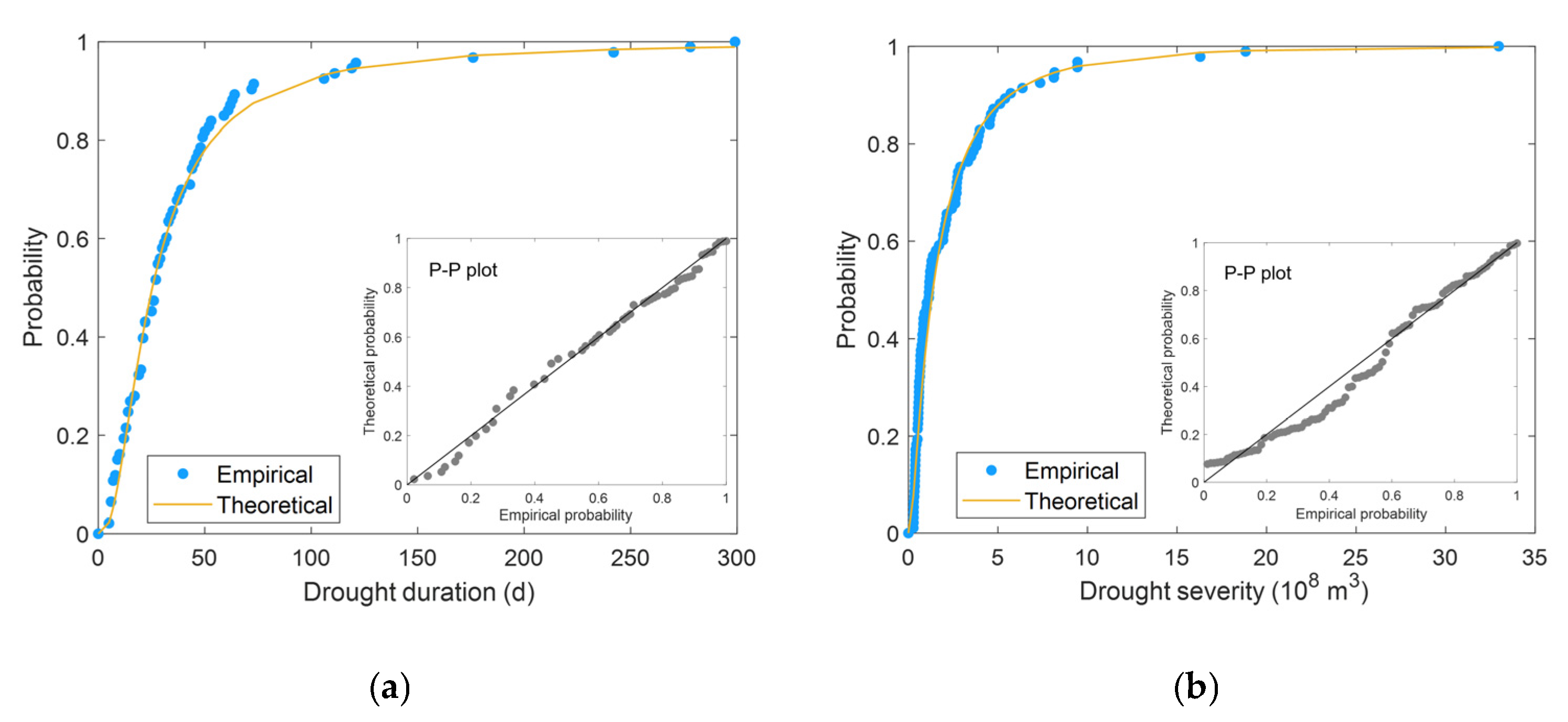
3.2. Selection of Marginal Probability Distributions

It is convenient and visible to select appropriate probability distributions for streamflow drought duration, severity, and severity peak using the L-moment ratio diagram (see Figure 5). To be specific, the ratio of given L-moments (i.e., L-skewness ${\tau }_3$ and L-kurtosis ${\tau }_4$) of normal, exponential, and Gumbel distributions as points with fixed positions and generalized Pareto, log-logistic, GEV, Pearson type III, and log-normal distributions as a cluster of curves were drawn as reference. Then, the sample L-moments (L-skewness ${\tau }_3$ and L-kurtosis ${\tau }_4$) of drought duration, severity, and severity peak were calculated and displayed against the theoretical L-moments of the above candidate probability distributions. As shown in Figure 5, the ratio of L-skewness ${\tau }_3$ and L-kurtosis ${\tau }_4$ of drought duration ($D$) is close to the theoretical curve of GEV or log-logistic distribution, while log-normal and generalized Pareto distributions stand out in generating the sample L-moments of drought severity ($S$) and severity peak ($P$), respectively. By contrast, the theoretical L-moments of other probability distributions are far away from the sample L-moments of drought duration ($D$) and severity ($S$), such as normal, exponential, and Gumbel distributions.

The cumulative probabilities of streamflow drought duration and severity based on GEV and log-normal distributions are demonstrated in Figure 6. As can be seen, the theoretical probabilistic plots of GEV and log-normal distributions generally produce an acceptable fitness to the empirical frequency of drought duration and severity, respectively. Moreover, the theoretical and empirical probabilities are also compared using the P-P plots, which generally show an agreement with most data points near the 45-degree line (especially the upper tail, with a larger duration or severity that is of greater significance for drought analysis).

For streamflow drought characteristics fitted by different probability distributions (i.e., GEV for duration, log-normal for severity, and generalized Pareto for severity peak), the distribution parameters are estimated using the maximum likelihood approach and given in

Table 3. Probability distribution parameters and goodness-of-fit of streamflow drought characteristics.

Drought Characteristics	Probability Distributions	Distribution Parameters			RMSE	Kolmogorov–Smirnov (K-S) Test
		Location $\mathit{\mu }$	Scale $\mathit{\sigma }$	Shape $\mathit{\kappa }$		$\mathbf{Test} \mathbf{Statistics} \left({\mathit{T}}_0\right)$	$\mathbf{Critical} \mathbf{Statistics} ({\mathit{T}}_{\mathit{k}}, \mathit{\alpha }=0.05)$
Duration (D)	Generalized extreme value	19.3352	14.9743	0.5256	0.0258	0.0800	0.1378
Severity (S)	Log-normal	0.3125	1.1120		0.0494	0.1058	0.1392
Severity peak (P)	Generalized Pareto		226.2524	−0.4392	0.0519	0.1166	0.1376

. By doing so, the probabilistic properties of drought duration, severity, and severity peak are largely characterized by selected probability distributions with estimated location, scale, and shape parameters. Meanwhile, the RMSE values, showing relative biases between theoretical and empirical probabilities, are very small and suggest a good fitness of drought characteristics to corresponding probability distributions. Furthermore, the selection of marginal probability distributions for drought duration, severity, and severity peak is also supported by the Kolmogorov–Smirnov (K-S) goodness-of-fit tests since all sample statistics are smaller than relevant critical values at the significant level of 0.05 (see the last two columns of Table 3).

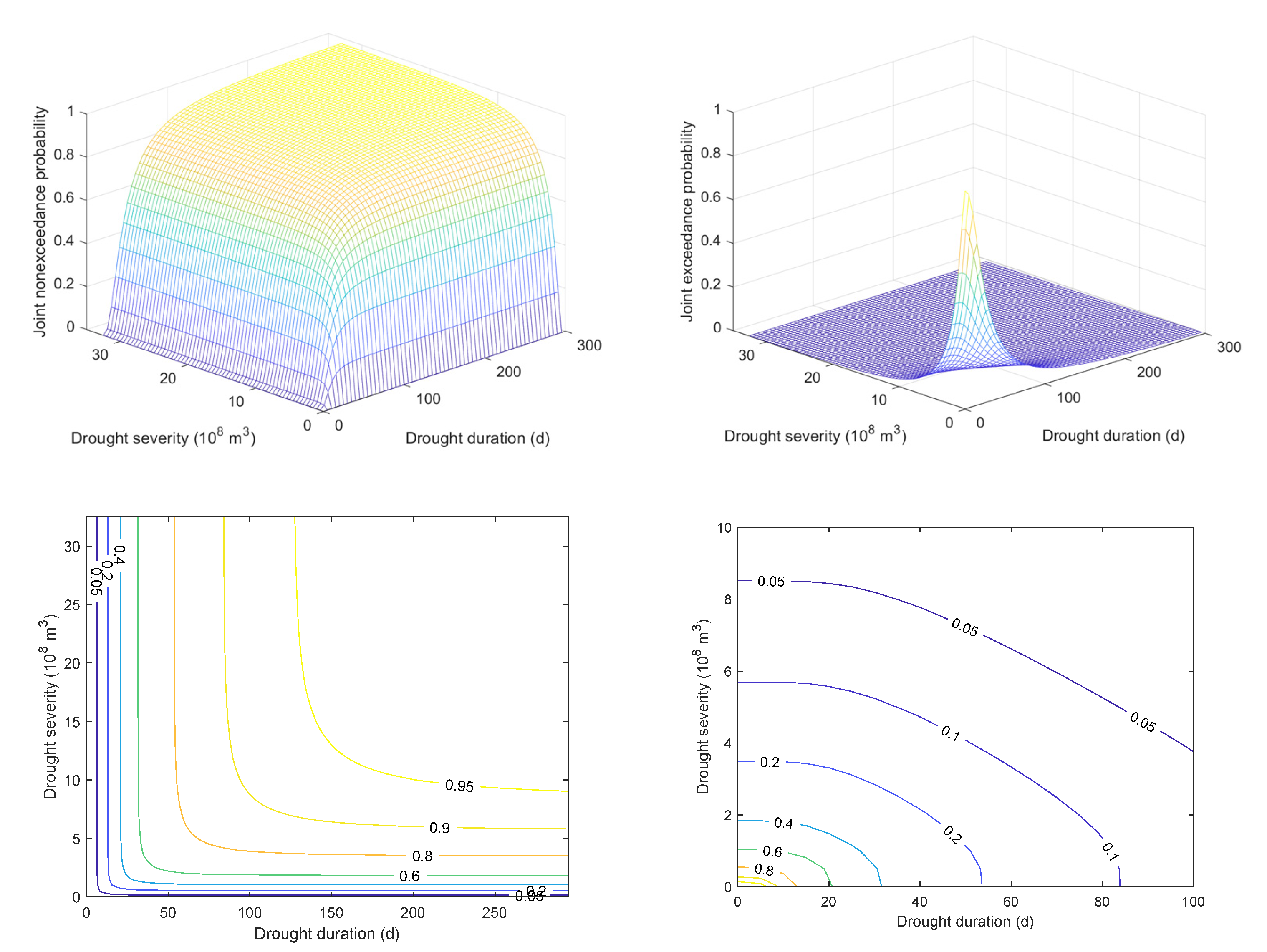
3.3. Construction of Bivariate Joint Probability Distribution

Cross-correlation analysis between variables is required before using the copula function to construct the joint probability distribution of drought characteristics. The results of multiple correlation coefficients, including Pearson’s ${\gamma }_n$, Spearman’s ${\rho }_n$, and Kendall’s ${\tau }_n$, were computed and are presented in

Table 4. Paired correlation coefficients of streamflow drought characteristics.

Correlation Coefficients	Duration and Severity	Duration and Peak	Severity and Peak
Pearson (${\gamma }_n$)	0.8451	0.2834	0.6234
Spearman (${\rho }_n$)	0.6259	0.1487	0.8064
Kendall (${\tau }_n$)	0.4819	0.1078	0.6036

. It is indicated that drought duration ($D$) and severity ($S$) are highly correlated, with Pearson’s linear correlation coefficient ${\gamma }_n$ being up to 0.85. However, drought severity ($S$) and severity peak ($P$) seem to have a relatively higher correlation from a nonlinear perspective, with larger correlation coefficients of Spearman’s ${\rho }_n$. On the other hand, drought duration ($D$) and severity peak ($P$) show a relatively low correlation in terms of both linear and nonlinear correlation coefficients.

In addition, the significant correlationship between drought duration ($D$) and severity ($S$) is also visible in the rank-based Chi-plot and K-plot (see Figure 7). In the Chi-plot, the area between two dotted horizontal lines of $\pm 0.18$ is defined as the confidence band, with a significant level of 0.05, which means an independent relationship. Since most of the data points fall outside the confidence band in Chi-plot, it can be generally concluded that apparent dependence exists between drought duration ($D$) and severity ($S$). Meanwhile, the dotted vertical zero line and the distribution of data points also imply a positive asymmetric correlation structure between the two drought characteristics. On the contrary, the range enclosed by the dotted curve and diagonal line in the K-plot indicates a dependent relationship. Further, the closer the data points to the curve, the higher the suggested dependence. It is seen that almost all the data points fall inside the dependent area and closer to the indicative curve for the upper tail. Overall, the correlation and dependence between drought duration ($D$) and severity ($S$) are validated, and thereby, it is possible to construct their joint probability distribution using appropriate copula functions.

For the construction of bivariate joint distribution of drought duration and severity, the maximum likelihood estimates of parameters of five two-dimensional copulas (i.e., Gaussian, Student’s t, Frank, Gumbel, and Clayton) are provided in

Table 5. Comparison of two-dimensional copulas for constructing joint probability distribution of streamflow drought duration and severity.

Copulas	Parameters	Parameter Estimates	Goodness-of-Fit
			AIC	BIC	RMSE
Gaussian	$\rho$	0.6868	−626.0448	−620.9796	0.0338
Student’s t *	$\rho$	0.6868	−622.4832	−614.8854	0.0341
Frank	$\theta$	4.7964	−611.7692	−609.2366	0.0369
Gumbel	$\theta$	1.8102	−603.9915	−601.4589	0.0385
Clayton	$\theta$	1.2453	−602.5924	−600.0598	0.0388

Note: * The degree of freedom for Student’s t copula is $\upsilon =6$

. Using these estimated parameters, the theoretical bivariate joint probabilities can be derived from the cumulative distribution functions of different copulas (e.g., Gaussian). Comparing to bivariate empirical probabilities based on the plotting-position formula, the fitting biases in terms of RMSE were calculated. Moreover, AIC and BIC were further computed to compare the goodness-of-fit of different copulas as a joint probability distribution of drought duration and severity. As shown in Table 5, Gaussian copula generally has the best performance, resulting in the smallest RMSE, AIC, and BIC values. The P-P plot of the joint probability distribution of streamflow drought duration and severity using a Gaussian copula is illustrated in Figure 8, where horizontal and vertical axes show the empirical and theoretical probabilities derived from the plotting-position formula and bivariate copula (using estimated parameters presented in Table 5), respectively. It is seen that the data points are all along the 45-degree line, suggesting a good agreement between the bivariate empirical and theoretical probabilities. Moreover, the competence of Gaussian copula is still supported by the K-S goodness-of-fit test. Specifically, the sample statistic (0.0684) is less than the relevant critical value (0.1497), with a significant level of 0.05.

3.4. Gaussian Copula-Based SDF Relationships of Streamflow Drought

The severity–duration–frequency (SDF) relationships of streamflow drought in the SAYR were finally developed based on the two-dimensional Gaussian copula. For this purpose, the bivariate joint non-exceedance and exceedance probability as well as relevant conditional non-exceedance probability were computed on the basis of Equations (12)–(15). The probabilistic relationship among streamflow drought duration, severity, and frequency (in terms of bivariate joint probability) is illustrated by a three-dimensional surface and corresponding contours (see Figure 9). Accordingly, it is possible to obtain the joint probability with different combinations of drought characteristics. For instance, a combination of 100-day duration and 8 × 10⁸ m³ severity corresponds to a non-exceedance probability of about 0.9, while many other combinations of different duration and severity values would also produce the same non-exceedance probability for streamflow drought analysis. It is very different from drought frequency analysis, which considers only one variable (e.g., duration or severity) and fails to consider the connection and interaction between multiple drought characteristics well. Specifically, the univariate-based design value is just equivalent to the intersection of concerned probability contour and horizontal/vertical axis. For example, the design severity corresponding to a non-exceedance probability of 0.9 turns out to be about 6 × 10⁸ m³ using marginal probability distribution of duration in traditional SDF analysis of droughts. Likewise, the design duration of the same non-exceedance probability is about 80 days according to marginal probability distribution of severity. In other words, with an identical probability level, the traditional SDF curves would significantly underestimate the design values of drought characteristics (e.g., duration and severity) relative to the copula-based SDF analysis that is based on joint rather than marginal probability distribution. Similarly, the concurrent drought risk of both duration and severity exceeding specific values can also be estimated by the Gaussian copula-based bivariate exceedance probability and its contours, as shown in Figure 9. For example, the exceedance probability of drought duration and severity simultaneously exceeding 60 days and 3.5 × 10⁸ m³, respectively, is about 0.1. In general, the bivariate exceedance probability when drought duration and severity reach certain levels (e.g., 100-day duration and 8.5 × 10⁸ m³ severity, respectively) becomes relatively small, such as less than 0.05. The bivariate joint exceedance probability focuses on the concurrent risk of both drought duration and severity exceeding critical alert levels, which might trigger a failure in water supply and/or destruction of infrastructure. On the other hand, the joint non-exceedance probability indicates the possibility of both drought duration and severity within tolerable limits, which provides an implication about the conditions of safety. A combined interpretation of them can help to achieve a more comprehensive evaluation of exposed risks to drought.

In addition, Figure 10 provides the conditional non-exceedance probability of the drought duration (severity) given severity (duration) exceeding a series of relevant levels. As shown, the conditional non-exceedance probability of drought duration and severity decreases with the increase in the corresponding conditional factor. It is also valuable and interesting to compare the marginal, joint, and conditional non-exceedance probabilities of bivariate streamflow drought characteristics. For example, Figure 11 details the case of drought duration and severity being 30 days and 2 × 10⁸ m³, respectively. It is seen that a non-exceedance probability of about 0.6 is recognized through univariate frequency analysis with the given drought duration and severity. However, the conditional non-exceedance probability of either of them with the other one exceeding the given value reduces dramatically to about 0.3, whereas the bivariate joint non-exceedance probability of at least one of them not exceeding the given value(s) turns out to be around 0.45. The above-derived bivariate joint and conditional probabilities of drought characteristics can provide useful information for water resources planning and management, which would help to comprehensively evaluate the risk of malfunction for a specific streamflow drought event and further estimate the return period of a specific situation in which a water supply system fails to meet the requirement of water demand.

4. Discussion and Conclusions

For classical severity–duration–frequency (SDF) curves, the correlation between drought duration and severity is not effectively considered, which only provides, in essence, the severity–frequency relationship with given discrete values of duration or the duration–frequency relationship with given discrete values of severity. By contrast, the proposed copula-based SDF relationships take into account the dependence (e.g., degree and structure) between drought characteristics, providing superior severity–duration–frequency relationships that are more comprehensive and conform to reality. Using higher-dimensional (e.g., three-dimensional) copula functions, more complicated multivariate relationships and curves of drought characteristics, such as four-dimensional duration–severity–peak–frequency relationships of streamflow drought events, could further be considered and constructed according to the framework and procedure adopted by the present study.

Using daily streamflow observations at the Tangnaihai gauge in the SAYR from 1956 to 2018, this study first obtained the time series of drought duration (D), severity (S), and severity peak (P) based on run analysis with a time-varying daily threshold and integration and elimination of drought events. Then, the bivariate joint probability distribution of drought duration and severity was constructed using two-dimensional copula functions with selected marginal probability distributions. Finally, the severity–duration–frequency (SDF) relationships based on Gaussian copula were developed and analyzed, mainly in terms of bivariate joint and conditional non-exceedance/exceedance probabilities. The main findings and conclusions are summarized as follows.

(1)

The proportion of short-duration droughts generally increases as the threshold decreases, which suggests avoiding too-small thresholds, and the time-varying daily threshold level of Q80 is recommended for streamflow drought identification in the SAYR. After integration and elimination, the streamflow drought events are more consistent with the drought occurrence and persistence feature, highlighting the necessity to carry out integration and elimination processing on preliminarily identified streamflow droughts through run analysis;

(2)

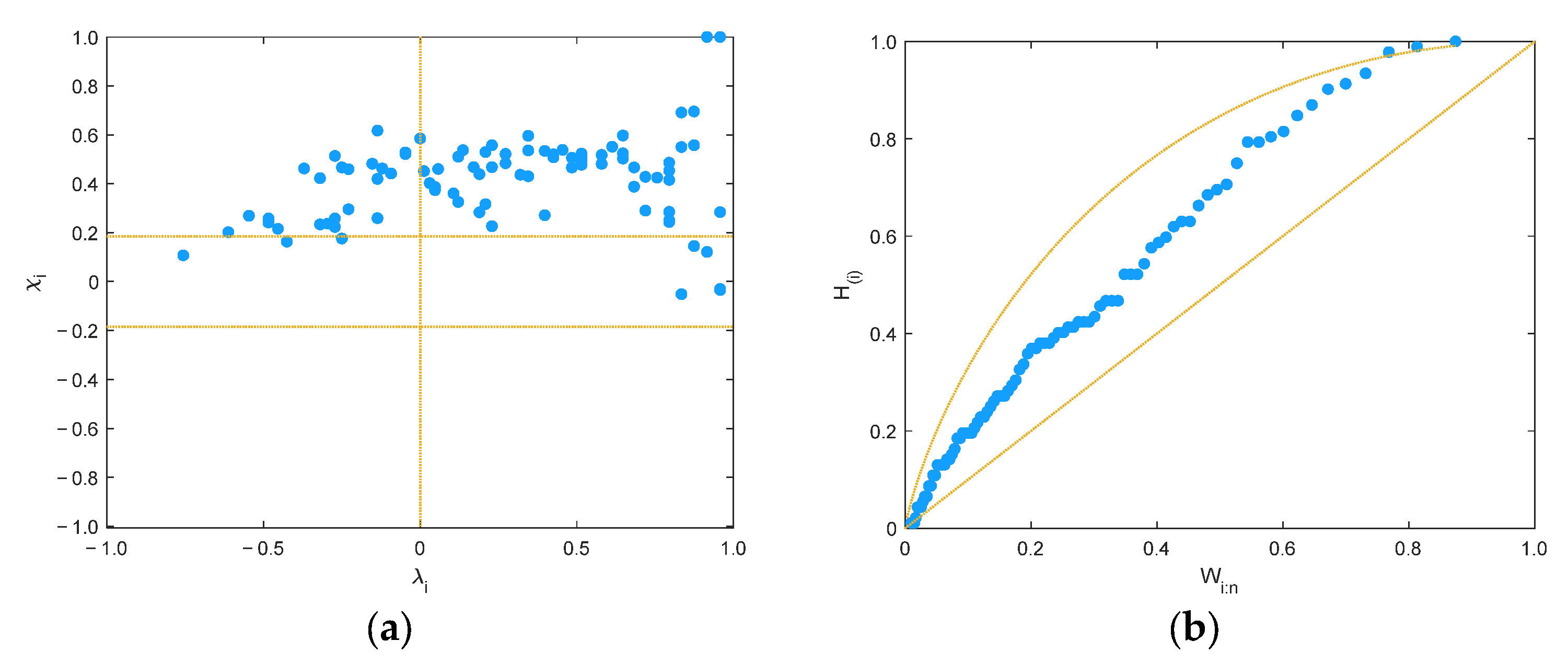
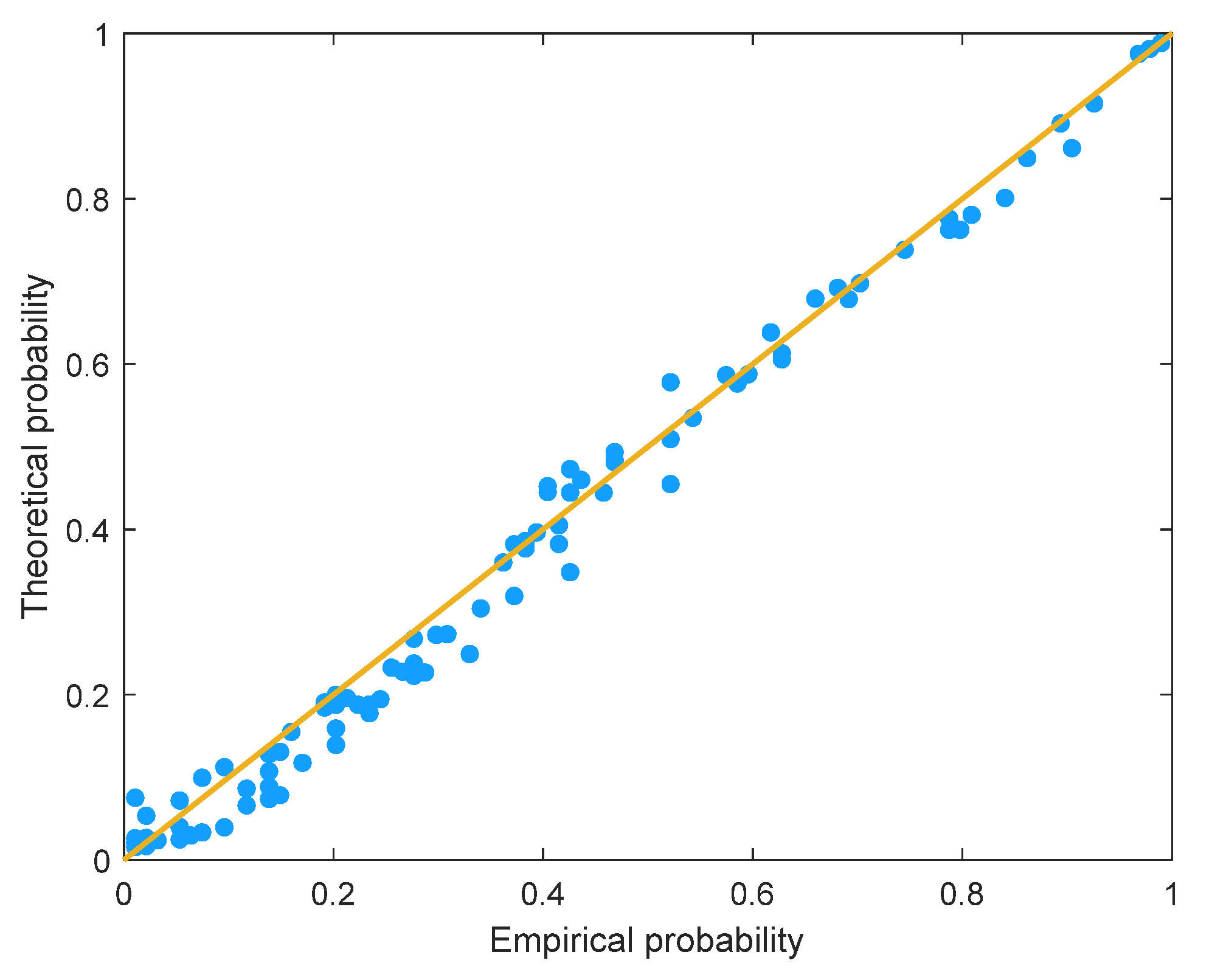
According to the L-moment ratio diagram, P-P plot, and RMSE, the generalized extreme value, log-normal, and generalized Pareto are, respectively, suitable as marginal probability distributions of streamflow drought duration, severity, and severity peak at the Tangnaihai gauge. The correlation coefficient and rank-based correlation diagram suggested a significant asymmetric, positive correlation between drought duration and severity. Then, supported by the RMSE, AIC, and BIC, the Gaussian copula was selected as the optimal model for constructing bivariate joint probability distribution of streamflow drought duration and severity. In addition, the marginal and joint probability distributions of drought characteristics passed the K-S goodness-of-fit tests at the significant level of 0.05;

(3)

Compared to traditional SDF analysis, the proposed copula-based SDF relationships of streamflow drought events can provide more critical information. Specifically, with given non-exceedance/exceedance probabilities, it can consider the different combinations of multiple drought characteristics, making up for the defect of ignoring their connection and interaction in univariate frequency analysis. Thus, the corresponding multivariate probabilistic analyses are more comprehensive and more consistent with the essential attributes of drought events. Moreover, the conditional probability distribution effectively reflects the trend of gradually decreasing non-exceedance probabilities of drought duration (severity) with increasing severity (duration), which has practical significance for analyzing the probabilistic impact of one drought characteristic on another. From a multivariate perspective, the probability of one or two drought characteristics exceeding specific values would increase with decreasing non-exceedance but increasing exceedance probabilities. That is, the expected inter-arrival time of the designed drought event would be shorter as well. The results also indicate that the overall risk of streamflow drought with short duration and low severity is relatively high in the SAYR, and more attention is needed regarding effective drought-mitigation strategies and measures.