Low-Flow (7-Day, 10-Year) Classical Statistical and Improved Machine Learning Estimation Methodologies

Abstract

Water resource managers require accurate estimates of the 7-day, 10-year low flow (7Q10) of streams for many reasons, including protecting aquatic species, designing wastewater treatment plants, and calculating municipal water availability. StreamStats, a publicly available web application developed by the United States Geologic Survey that is commonly used by resource managers for estimating the 7Q10 in states where it is available, utilizes state-by-state, locally calibrated regression equations for estimation. This paper expands StreamStats’ methodology and improves 7Q10 estimation by developing a more regionally applicable and generalized methodology for 7Q10 estimation. In addition to classical methodologies, namely multiple linear regression (MLR) and multiple linear regression in log space (LTLR), three promising machine learning algorithms, random forest (RF) decision trees, neural networks (NN), and generalized additive models (GAM), are tested to determine if more advanced statistical methods offer improved estimation. For illustrative purposes, this methodology is applied to and verified for the full range of unimpaired, gaged basins in both the northeast and mid-Atlantic hydrologic regions of the United States (with basin sizes ranging from 2–1419 mi²) using leave-one-out cross-validation (LOOCV). Pearson’s correlation coefficient (R²), root mean square error (RMSE), Kling–Gupta Efficiency (KGE), and Nash–Sutcliffe Efficiency (NSE) are used to evaluate the performance of each method. Results suggest that each method provides varying results based on basin size, with RF displaying the smallest average RMSE (5.85) across all ranges of basin sizes.

1. Introduction

Estimates of the magnitude and reoccurrence intervals of low-flow events on rivers and streams are a necessary input for many natural resources planning activities, including municipal, industrial, and agricultural planning [1]. Resource managers in the northeast and mid-Atlantic United States are specifically interested in 7-day, 10-year low-flow (7Q10) estimation for protecting aquatic species that may be impacted by water withdrawal, hydropower production, or discharge of wastewater. In addition, 7Q10 estimation is used in a variety of other design facets, including water quality management, water supply planning, cooling plant design, hydropower regulation, irrigation, recreation, and more [2]. Classical 7Q10 estimation in ungaged basins commonly relies on simple statistical models that are calculated at similar, gaged sites [3]. For example, the USGS’s widely used statistical estimation program StreamStats uses multiple linear regression equations derived in log space, calibrated on gaged sites, to estimate flow statistics at ungaged sites [4]. These regression equations make use of the concept of “stationarity”, i.e., the assumption that the statistical properties of streams do not change over time. Relatively recent studies have suggested that the climate and associated hydrologic processes no longer satisfy that assumption, exposing a weakness in the stationary modelling approach [5,6,7,8]. For instance, it is estimated that the southwestern United States is currently experiencing its driest 22 yr period since 800 CE and approximately 20% of it can be attributed to recent anthropogenic changes [9]. In contrast, studies in the northeast have found both average baseflows and 7-day summer baseflows are increasing with statistical significance [10,11]. In the mid-Atlantic, Blum et al. (2019) found increasing 7Q10s in the northern part of the mid-Atlantic (New York, Pennsylvania) and decreasing 7Q10s in lower mid-Atlantic (Virginia, Maryland), concluding that because of these trends, “using the most recent 30 years of record when a trend is detected reduces error and bias in 7Q10 estimators compared to use of the full record” [2]. Outside of trend detection, few statistical alternatives exist in practice to account for changing climatic conditions in statistical 7Q10 estimation in ungaged basins.

In addition to assuming stationarity, StreamStats’ 7Q10 estimation suffers from a variety of other drawbacks, including (1) lack of development in some states, (2) being applicable to only relatively small basins, and (3) minimal statistically significant input variables that vary greatly by state. Because the 7Q10 is an extremely common planning metric, many states rely on 7Q10 estimation for permits related to stream withdrawals and wastewater treatment. In 2019, the Connecticut Department of Energy and Environmental Protection was forced to change their permitting laws from using the 7Q10 to using a similar drought metric, the Q99 flow, because StreamStats 7Q10 estimation has not been developed for Connecticut: https://portal.ct.gov/DEEP/Water/Water-Quality/Triennial-Review-of-the-Connecticut-Water-Quality-Standards (accessed on 6 April 2021). The use of state boundaries to dictate homogenous hydrologic areas also limits the amount of unimpaired data that is available to develop the regression equations. Developing these regression equations requires ample unimpaired training data in a homogenous area of interest, which can sometimes be impossible to achieve in practice [12], as exemplified by the case of Rhode Island. Due to a lack of sufficient unimpaired, gaged basins in Rhode Island, some gages from Massachusetts and Connecticut (which itself does not have 7Q10 estimation developed) were used to develop the 7Q10 regression equations for Rhode Island [13]. This suggests that we may be able to expand these regression equations to cover larger geographic footprints that are not dictated by state lines, as we are already using data from other states to develop these equations. Classical 7Q10 estimation techniques also rely on regression equations that were only developed for relatively small basin sizes (i.e., <100 mi²), either state by state or localized to larger watersheds [4]. This helps maintain the homogeneity of the applicable area, which maintains the accuracy of estimates but does not allow for larger basin estimation and limits the ability to compare estimates between states, regions, and watersheds since different equations and input variables are used to make estimates in nearby states. In the extreme case, ungaged locations a few feet apart on the same stream but across a state border can utilize differing regression equations, which can result in different estimates. These equations rely heavily on the watershed area as the most significant variable, but the other variables vary significantly depending on the state. In some cases, watershed size is the only significant variable used to make 7Q10 estimates [14]. Many other studies in this area have attempted to apply landcover, climate, and topographical variables with varying levels of success [15,16,17,18]. One set of statistically significant input variables for the entire northeast and mid-Atlantic would allow (1) data augmentation where 7Q10 estimation has not been developed, (2) comparisons of 7Q10 estimates between states, and (3) better understanding of the input variables themselves, including potential sensitivity analyses that involve changing climate and/or landcover inputs.

Regression equations typically rely on multiple linear regression in log space (LTLR) rather than standard multiple linear regression (MLR) because Tasker and Stedinger (1989) [19] demonstrated that (log-transformed) GLS analysis is theoretically most appropriate and generally provides the best results when used for hydrologic regressions, which was then used in standard regression analysis of peak- and low-flow frequency statistics, such as the 100-year peak flow and the 7-day, 10-year low flow [20]. Applying a more advanced statistical method may allow for improved estimation, requiring less input data, detecting the subtle importance of additional variables, and maintaining accuracy over larger spatial footprints. Though machine learning has been used in hydrology for several decades, the application of this technique has accelerated with increased access to data and computational power [21]. Many recent studies have benefitted from machine learning to improve streamflow estimation, including using artificial neural networks (ANN), support vector machines (SVM), and random forests (RF) [22,23,24,25,26]. Studies have even demonstrated that machine-learning-based models, which are calibrated based on historical streamflow records in gaged basins, can produce more accurate streamflow predictions in ungaged basins than traditional process-based models [27]. Specifically for low-flow prediction, machine learning algorithms have been used to estimate low-flow indices [28], for direct low-flow prediction using random forest [29], and for evaluation of statistical methods in low-flow prediction [30]. Due to these successes, Nearing et al. (2021) state, “it is entirely possible that successful water resources and water hazard predictions might not require anything that looks even like a simple hydrology model in the future” [27].

To address the issues noted previously, this paper suggests three strategies to improve estimations of 7Q10 flow for the northeast and mid-Atlantic United States:

• Develop a single, generalized methodology for 7Q10 estimation that is applicable to larger geographical regions (such as the northeast and mid-Atlantic regions of the United States). This methodology will make use of publicly available data as inputs, allowing resource managers to create accurate 7Q10 estimates in states where StreamStats 7Q10 estimation has not been developed or as an alternative to StreamStats where 7Q10 estimation has been developed;
• Expand the range of applicable basin sizes to account for every gaged basin in the northeast and mid-Atlantic that has been determined to be unimpaired. StreamStats’ state-by-state 7Q10 estimation relies on regression equations that were only developed for small basins (i.e., <100 mi²) in most states, but unimpaired gaged basins in the study area range from 2 to 1400 mi². Our methodology is trained on every location, ensuring sufficient locations for model training and allowing the application of the method to a larger range of basin sizes than classical methods;
• Include multiple landcover, climate, and topographical variables as inputs for estimation. The additional input variables will increase the accuracy of 7Q10 estimates over the large area of study, and the inclusion of landcover and climate variables will facilitate future sensitivity analyses related to changing landcover and climate variables in conjunction with physical hydrology models.

Additionally, we test three machine learning algorithms, random forest (RF) decision trees, neural networks (NN), and generalized additive models (GAM), against classical statistical methods for 7Q10 estimation (MLR and LTLR) which have been found to perform similarly in practice [31]. These machine learning methods are applied for three reasons: (1) They do not make assumptions about the underlying distribution of the data. (2) Even though complex and essentially non-parametric, they are accurate and widely applied. And (3) they are relatively easy to implement, making them appealing for resource managers to use as alternatives to classical methods.

2. Data and Study Area

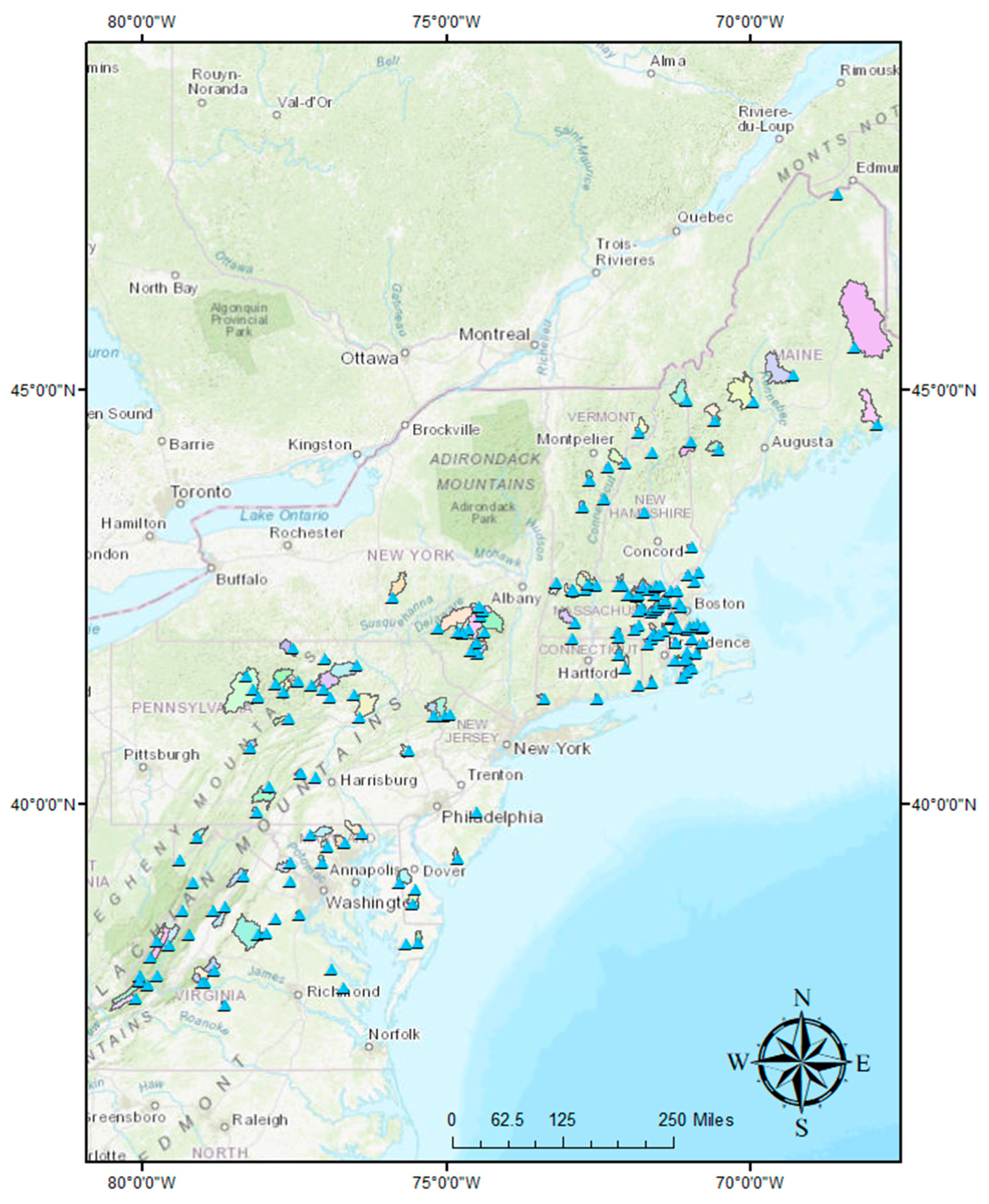
2.1. Study Area and Gages

The study area for this research is the northeast and mid-Atlantic United States, defined here as the states of Maine, New Hampshire, Vermont, Massachusetts, Rhode Island, Connecticut, New York, Pennsylvania, New Jersey, Delaware, Maryland, Virginia, and West Virginia. The USGS’s Hydro-Climatic Data Network, HCDN-2009 [32] was used to identify unimpaired streams in gaged watersheds of varying sizes and physical attributes in the study area (ranging from 2.1 mi² to 1419 mi², Figure 1). Data for these 106 stations from the HCDN were downloaded from the USGS Current Water Data for the Nation: https://waterdata.usgs.gov/nwis/rt (accessed on 18 December 2020). After reviewing the watershed size distribution of the HCDN sites, we determined it lacked a sufficient number of gages in extremely small watersheds (<30 mi²) for training data. In addition to the HCDN sites, 59 small sites in Massachusetts, determined to be sufficient for 7Q10 training data [20], were added to the training data for a total of 165 sites throughout the area of study. Appendix A includes a table of all sites used, and Figure 1 displays the corresponding watersheds.

2.2. Input Variables/Data

Daily precipitation and temperature data were extracted at each gage from the Livneh et al. (2015) [33] hydrometeorological dataset [34]. This dataset contains air temperature and precipitation data from approximately 20,000 weather stations monitored by GHCN-daily (U.S.), Environment Canada, and Servicio Meteorológico Nacional (Mexico) [33]. A minimum of 20 years of data was required for CONUS and Canadian stations, but due to the relative paucity of station data in Mexico, the authors followed the procedure recommended by Zhu and Lettenmaier (2007) [35], which requires a minimum of 50 valid days of data in any given year for a station to be included. From this station data, the data was interpolated using the SYMAP algorithm [36], which employs statistical methods such as clustering analysis, regression analysis, and correlation analysis to identify patterns and relationships within spatial data. After interpolation, the authors followed procedures for quality control by computing a monthly coefficient of variation based on the standard deviation of the daily values compared to their monthly mean and removed months with a ratio of less than 0.18, determined empirically using 25 stations from 7 states with at least 15 years of data [33]. This dataset is publicly available, with gridded climate variables at 1/16° horizontal resolution (~6 km) from 1950–2013 [34]. Static land data, including mean basin elevation, mean basin slope, forest and wetland percentages of the basin, and watershed area, were collected from USGS StreamStats Data-Collection Station reports: https://streamstatsags.cr.usgs.gov/gagePages/html/ (accessed on 19 July 2021).

2.3. 7Q10 Comparison Data

To compare 7Q10 estimates from this experiment to current statistical methodologies, we use the USGS’s statistical estimation program StreamStats because of its wide usage in the states for which it has been developed in the northeast and mid-Atlantic. This program uses logarithmic-transformed linear regression (LTLR) equations to estimate flow statistics [4]. Where applied, different regression equations and variables are calculated for each state. Furthermore, states in the mid-Atlantic region use different equations (and in some cases, different variables) based on hydrologic regions within each state.

Table 1. StreamStats 7Q10 estimation by state.

State	Variables Used for 7Q10 Estimation
Massachusetts [20]	Drainage area Area of stratified-drift deposits per unit of stream length plus 0.1 Mean basin slope Indicator variable, 0 in the eastern region, 1 in the western region
Rhode Island [13]	Drainage area Stream density
New Hampshire [16]	Drainage area Mean annual temperature Jun to Oct average gage precipitation
Maine [15]	Drainage area Fraction of sand and gravel aquifers
Pennsylvania [17] Region 1 (Southeast) 1 Region 2 (Central-east) 2 Region 3 (Northwest) 3 Region 4 (Southwest) 4 Region 5 (Northeast) 5	Drainage area 1,2,3,4,5 Basin slope1 Mean elevation 3,4 Mean annual precipitation 2,3 Stream density 2 Soil thickness 1,2 Percent glaciation 5 Percent carbonate bedrock 2 Percent forested area 5 Percent urban area 1
Virginia [14] Coastal Plain 1 Piedmont 2 Blue Ridge 3 Valley and Ridge 4 Appalachian Plateaus 5 Mesozoic Basins 6	Drainage area 1,2,3,4,5,6
West Virginia [18] North 1 South Central 2 Eastern Panhandle 3	Drainage area 1,2,3 Longitude of basin centroid 1
Connecticut, Delaware, Maryland, New Jersey, New York, Vermont	Unavailable

lists the candidate states and the corresponding variables used for 7Q10 estimation. Connecticut, Delaware, Maryland, New Jersey, New York, and Vermont are included last, as StreamStats 7Q10 estimates have not been developed for these states. Out of the 165 gaged sites used for training, raw 7Q10 estimates from StreamStats were available for 128 sites.

3. Materials and Methods

In this section, the materials and methods used in this research are described. This includes the calculation of the historical 7Q10 at each site (Section 3.1) based on the historical data, each statistical method being compared (Section 3.2), the input variables included (Section 3.3), a cross-validation procedure for testing (Section 3.4), and the various efficiency/error metrics used to evaluate the performance of each method (Section 3.5).

3.1. 7Q10 Values at Each Site

The historical 7Q10 values based on historical data for each site were extracted from the USGS’s StreamStats Data-Collection Station Reports described in Section 2.2. In addition, if at least 30 years of continuous, daily streamflow data is available for a site, the “fasstr” software package: https://cran.r-project.org/web/packages/fasstr/index.html (accessed on 19 July 2021) is used to calculate the 7Q10 directly from the daily streamflow data. This package fits a quantile distribution to daily streamflow data that allows for the efficient calculation of low-flow frequency analysis metrics, including the 7Q10. As expected, these 7Q10 values were virtually identical to the 7Q10 values calculated by the USGS at each site. These values, noted as the “true 7Q10” values for each site, can also be found in Appendix A.

3.2. Statistical Methods

In this analysis, five statistical methods are applied. Two classical statistical methods, namely multiple linear regression (Section 3.2.1) and logarithmic-transformed linear regression (Section 3.2.2), are tested alongside three machine learning algorithms, namely random forest decision trees (Section 3.2.3), neural networks (Section 3.2.4), and generalized additive models (Section 3.2.5). For the machine learning algorithms, feature scaling is applied to the input variables before method application using min-max normalization:

$$x=\frac{x-x_{min}}{x_{max}-x_{min}}$$

(1)

3.2.1. Multiple Linear Regression

Multiple linear regression (MLR) is a simple, common methodology that takes the general form of

$$Y_i=b_0+b_1{X}_1+b_2{X}_2+\dots +b_n{X}_n+{\epsilon }_i$$

(2)

where $Y_i$ is the estimate of the dependent variable for site i, $X_1$ to $X_n$ are the n independent variables, $b_0$ to $b_n$ are the n + 1 regression model coefficients, and ${\epsilon }_i$ is the residual error for site i. Assumptions for use of MLR are (1) the relationship displays linearity, (2) the mean of ${\epsilon }_i$ is zero, (3) the variance of the ${\epsilon }_i$ is constant and independent of $X_n$, (4) the ${\epsilon }_i$ are normally distributed, and (5) the ${\epsilon }_i$ are independent [37]. For this study, we force the intercept $b_0$ to be 0 since a basin with 0 area should have 0 flow.

3.2.2. Logarithmic-Transformed Linear Regression

Logarithmic-transformed linear regression (LTLR) is the most used method for 7Q10 estimation because it can correct for spatial correlation and differences in streamflow record lengths [19]. In addition, streamflow and basin characteristics used in hydrologic regression have been found to be log-normally distributed, with residuals (calculated by subtracting the estimated values from the observed values) that were not randomly distributed when multiple linear regression was applied, suggesting that the variables should be transformed to log space [20]. This results in a model of the form

$$\log Y_i=b_0+b_1\log X_1+b_2\log X_2+\dots +b_n\log X_n+{\epsilon }_i$$

Using base 10, the equation takes the general form of

$$Y_i={10}^{b_0}\left(X_1^{b_1}\right)\left(X_2^{b_2}\right)\dots \left(X_n^{b_n}\right){10}^{{\epsilon }_i}$$

(3)

Though theory suggests that LTLR is the preferred method for 7Q10 estimation, in practice, both MLR and LTLR have been found to perform similarly [31].

3.2.3. Random Forest

The random forest (RF) algorithm applied here is a non-parametric, tree-based regression model [38]. RFs use bootstrap aggregation, where bootstrap samples are randomly chosen with substitution seeking a lower test error by variance reduction. RFs consist of numerous decision trees (Figure 2).

The RF model is optimized by tuning or calibrating its three major hyperparameters: (1) “m_try”, the number of predictors that will be randomly sampled at each split when creating the tree models; (2) “n_trees”, the number of decision trees contained in the ensemble; and (3) the minimum size of terminal nodes, “n_t”. All parameters were manually tuned to create a stable model using the package “randomForest”: https://cran.r-project.org/web/packages/randomForest/index.html (accessed on 20 July 2021) in R.

3.2.4. Neural Networks

Neural networks (NN) are a class of machine learning algorithms inspired by the structure and function of the human brain [39]. The three primary types of layers are the input layer, one or more hidden layers, and the output layer. Each neuron takes inputs, performs a weighted sum of these inputs, applies an activation function to produce an output, and then passes this output to neurons in the next layer. The connections between neurons have associated weights, which the network learns from data during the training process. The network adjusts its weights iteratively using optimization algorithms to minimize the difference between its predictions and the actual targets. A simple neural network structure is highlighted in Figure 3.

Neural networks are optimized by tuning major parameters, including the number of hidden layers, the limiting threshold for the partial derivatives of the error function as stopping criteria, and the maximum allowable steps for training. Additionally, the number of neurons per hidden layer, initial weights, activation functions, and learning rate can be customized for different scenarios. All parameters were manually tuned to create a stable model that converges using the “neuralnet” package: https://www.rdocumentation.org/packages/neuralnet/versions/1.44.2/topics/neuralnet (accessed on 21 July 2021) in R.

3.2.5. Generalized Additive Models

Generalized additive models (GAM) [40] represent a flexible extension of traditional linear models. GAMs capture non-linear dependencies of data through the application of smoothing functions which allows for finding complex relationships between variables. By employing smoothing functions such as cubic regression splines, GAMs accommodate non-linear patterns and mitigate issues of model misspecification. This property of GAMs makes it well-suited for scenarios where linear models may fall short in capturing intricate patterns. Furthermore, GAM does not impose assumptions on the underlying distribution of the response variable, enabling it to incorporate various response distributions appropriately. An example of a standard linear model and a GAM applied to the same data is provided in Figure 4.

GAMs are optimized by tuning several parameters, including “gamma” to increase smoothing, “family” to specify the distribution to be used, and “weights” to designate prior weights on the contribution of the data to the log-likelihood. All parameters were manually tuned to create a stable model using the GAM function from the “mgcv” package: https://www.rdocumentation.org/packages/mgcv/versions/1.9-0/topics/gam (accessed on 17 August 2021) in R.

3.3. Input Variables

Statical land data, including mean basin elevation, percent mean basin slope, percent landcover considered wetland and forest, and basin area, were collected from the USGS’s StreamStats Data-Collection Station Reports. These data are direct inputs into the statistical models. In addition, timeseries of daily precipitation and maximum temperature were extracted at each of the gages from Livneh et al., 2015. A running cumulative 30-day precipitation value was calculated, as well as the corresponding average 30-day maximum daily temperature. Attempting to isolate when a 7Q10 flow would occur, we extracted the lowest 30-day cumulative precipitation limited to only 30-day periods of high temperatures (>90th percentile). The 30-day cumulative precipitation and corresponding high average temperature were recorded. A list of all input variables is included in

Table 2. Input variables for estimating 7Q10.

Variable	Description
Area (mi2)	Watershed area
Mean Elevation (ft)	Average elevation of the watershed
Slope (%)	Average basin slope
Percent Wetland (%)	Wetland percentage of the watershed
Percent Forest (%)	Forest percentage of the watershed
Min 30-day Cumulative Precipitation (mm)	Lowest 30-day cumulative precipitation, limited to abnormally hot periods (X > 90th percentile temperatures)
Average 30-day High Temperatures (C)	Average 30-day temperature during the corresponding period of low cumulative precipitation

.

3.4. Leave-One-Out Cross-Validation (LOOCV)

The leave-one-out cross-validation (LOOCV) method is an extreme version of K-fold cross-validation where K = N [41]. It is an iterative process that is executed the same number of times as the number of data points. Only one value is used as the test set, while all other values are used as the training set. This iterative process is run for every value so that there is a test set value for every value in the dataset, which allows for a new test set to be created with all of the individual test set values (Figure 5). The new test set can then be evaluated using traditional error metrics and analysis. LOOCV can be computationally intensive, but for relatively small datasets, it can provide better performance than K-fold cross-validation due to the largest possible training set being used to estimate each test set value [41].

3.5. Error Metrics

R² and RMSE are used to directly evaluate the random and systematic error of each method. In addition, the Nash–Sutcliffe Efficiency (NSE) and the Kling–Gupta Efficiency (KGE) are also included because of their frequent usage for evaluating streamflow models.

The widely known coefficient of determination, R² [42], will be one of the metrics for evaluating model performance. Values range from 0 (no correlation) to 1 (perfect correlation). This value is calculated using the following equation:

$$R^2=1-\frac{\sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}{\sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}$$

(4)

Here, $y_i$ is the observed 7Q10, $\widehat{y}$ is the model predicted 7Q10, and n is the number of samples used in the calculation.

RMSE is used to evaluate error because it is among the most used indicators for evaluation of model performance [43]. Similar studies have also chosen RMSE over MAE for its sensitivity to outliers [44]. The general equation is given by

$$RMSE=\sqrt{\frac{1}{n}\ast \sum _1^n{\left(y_i-{\widehat{y}}_i\right)}^2}$$

(5)

Hydrologists commonly use the Nash–Sutcliffe Efficiency [45] and Kling–Gupta Efficiency [46] for streamflow modelling evaluation. The Nash–Sutcliffe Efficiency (NSE) signals a model’s ability to predict variables different from the mean. NSE is calculated given

$$NSE=1-\frac{\sum _{i=1}^n{\left(O_i-P_i\right)}^2}{\sum _{i=1}^n{\left(O_i-\overline{O}\right)}^2}$$

(6)

NSE values range from negative infinity (indicating a poor model) and 1 (indicating a perfect fit between observed and predicted values). Negative values indicate that the mean is a better predictor of the observed values than the model.

Furthermore, the Kling–Gupta Efficiency (KGE) [46] is widely used for hydrologic applications [47,48]. KGE provides three components, the general correlation (r term), the bias (beta term), and the relative variability (alpha term), between the modelled and observed values. KGE is calculated using the following formula:

$$KGE=1-\sqrt{{\left(r-1\right)}^2+{\left(\alpha -1\right)}^2+{\left(\beta -1\right)}^2}$$

(7)

$$\alpha =\frac{{\sigma }_m}{{\sigma }_o}$$

$$\beta =\frac{{\mu }_m}{{\mu }_o}$$

where ${\sigma }_m$ is the standard deviation of model, ${\sigma }_o$ is the standard deviation of reference, ${\mu }_m$ is the mean of model, and ${\mu }_o$ is the mean of reference. Like NSE, KGE values range from negative infinity (poor performance) to 1 (best performance). Here, r is Pearson’s correlation coefficient, α represents the variability error, and β indicates the bias error.

The methodology of this paper is summarized in Figure 6. This figure includes all datasets, variables, and methods utilized.

4. Results and Discussion

In this section, the development (Section 4.1, Section 4.2, Section 4.3, Section 4.4 and Section 4.5) and general performance (Section 4.6 and Section 4.7) of each statistical model are evaluated. For all methods excluding neural networks where it is not applicable, we present the significance of variables using the standard p-value, with four thresholds given by minorly significant (0.1 > X > 0.05), moderately significant (0.05 > X > 0.01), largely significant (0.01 > X > 0.001), and extremely significant (X < 0.001).

4.1. Multiple Linear Regression

Applying multiple linear regression to the input variables, with the constraint that the intercept $b_0$ is set to 0, gives the following results (

Table 3. Multiple linear regression variables and significance.

Variable	Estimate	p-Value	Significance
Area (mi2)	0.0579833	2 × 10−16	<0.001
Mean Elevation (ft)	0.0014461	0.05343	<0.1
Slope (%)	−0.2804801	0.00197	<0.01
Percent Wetland (%)	−0.0618991	0.27690	No significance
Percent Forest (%)	0.0048811	0.86061	No significance
Min 30-day Cumulative Precipitation (mm)	0.3421899	0.00246	<0.01
Average 30-day High Temperatures (C)	−0.0466718	0.58980	No significance

).

As expected, the area was found to be extremely significant at the 0.001 level. In addition, slope and precipitation were found to be largely significant at the 0.01 level. Elevation was found to be minimally significant at the 0.1 level but did show significance and improved results. Neither landcover variable, the percentage of basin considered to be forest or wetland, showed significance. The resulting equation, only including statistically significant variables, results in the following:

$$7Q10=0.0579833\ast \left(\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}\right)+0.0014461\ast \left(\mathrm{E}\mathrm{l}\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\right)-0.2804801\ast \left(\mathrm{S}\mathrm{l}\mathrm{o}\mathrm{p}\mathrm{e}\right)+0.3421899\ast \left(\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{p}\right)$$

(R Square = 0.7481, Residual Standard Error = 7.693, p-Value = 2 × 10⁻¹⁶).

The sign of each variable aligns intuitively with the expected relationship between that variable and the 7Q10. Increasing area and precipitation allows for additional water during low flows, leading to positive coefficients. Elevation and slope relate directly to baseflows, and as baseflows play a large role in low flows, the relationship between baseflow and 7Q10s should be similar. High elevations are typically associated with higher baseflows [49], leading to an increasing relationship between 7Q10s and elevation. The relationship between slope and 7Q10 was expected to be positive, but as noted by Rumsey et al. (2015), “positive correlations between slope and baseflow are expected to be related to effects of elevation, but slope steepness is known to affect rates of groundwater transmission and determines whether groundwater will reach a channel network or be retained in the soil” [49], making it reasonable that increasing slope may not increase 7Q10s.

Figure 7 presents the MLR 7Q10 estimates and the actual and historical 7Q10s. The line represents a perfect fit, and the points closest to the line indicate lower bias.

A known weakness of applying MLR for extremely low flow estimation is that the residuals are not randomly distributed, as noted in most StreamStats low flow reports cited earlier. Plotting the residuals, from the smallest to largest observed 7Q10, confirms this (Figure 8).

Though the MLR fit is statistically significant, the plot of residuals suggests that MLR may not be the appropriate method for this case. Because of this, the next method, logarithmic-transformed linear regression (LTLR), is the traditional method for estimating 7Q10s in small basins. This method is traditionally used by StreamStats, though StreamStats reports refer to it as generalized least squares regression with a logarithmic transformation. This methodology accounts for the drawbacks of simple MLR, including the non-random residuals, spatially distributed correlation, and differences in record lengths.

4.2. Logarithmic-Transformed Linear Regression

Similarly, applying LTLR to the same input data leads to the following results, given in

Table 4. Logarithmic-transformed linear regression variables and significance.

Variable	Estimate	p-Value	Significance
Intercept	4.27157	0.1590	No significance
Area (mi2)	1.31308	2 × 10−16	<0.001
Mean Elevation (ft)	−0.11573	0.2908	No significance
Slope (%)	−0.19413	0.0303	<0.05
Percent Wetland (%)	−0.02036	0.7542	No significance
Percent Forest (%)	0.22437	0.0489	<0.05
Min 30-day Cumulative Precipitation (mm)	0.31049	0.0160	<0.05
Average 30-day High Temperatures (C)	−4.37462	0.0309	<0.05

.

In log space, only area was found to be extremely significant at the 0.001 level, while slope, precipitation, and temperature are moderately significant at the 0.05 level. Additionally, the percentage of the basin considered to be forest was found to be moderately significant at the 0.05 level in log space when it was not found to be significant using basic MLR. Once again, the percentage of the basin considered to be wetland was not found to be significant, but surprisingly, elevation was not found to be significant in log space, while it was just above the threshold for moderate importance (p-value~0.05) using MLR. Only including the significant variables leads to the following equation:

$$\begin{gathered} \log \left(7Q10\right)=1.31308\ast \mathrm{l}\mathrm{o}\mathrm{g}\left(\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}\right)-0.19413\ast \mathrm{l}\mathrm{o}\mathrm{g}\left(\mathrm{S}\mathrm{l}\mathrm{o}\mathrm{p}\mathrm{e}\right)+0.22437\ast \log \left(\mathrm{F}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{t}\right)+ \\ 0.31049\ast \mathrm{l}\mathrm{o}\mathrm{g}\left(\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{p}\right)-4.37462\ast \mathrm{l}\mathrm{o}\mathrm{g}\left(\mathrm{T}\mathrm{e}\mathrm{m}\mathrm{p}\right) \end{gathered}$$

R Square = 0.67, Residual Standard Error = 0.6139, p-Value = 2 × 10⁻¹⁶.

Once again, plotting the estimated values vs. the actual historical 7Q10s (but this time, in log space) is displayed in Figure 9.

This fit is noticeably more linear but moves away from linearity for extremely small 7Q10 values (Actual 7Q10s < 10⁻¹ cfs). These extremely small points can be ignored due to significant figures, as these very small numbers suggest that the stream’s 7Q10 is essentially 0 flow (ephemeral streams). More importantly, a goal of this experiment is to include much larger basin areas (and their corresponding 7Q10s) than are traditionally accounted for in regression equations. The largest 7Q10s, which correspond with the largest basins in the analysis, are found in the top right of Figure 9 and seem to continue to fit the general trend of linearity in log space. However, it should be noted that even though those points are similar distances from the line in log space, the difference is much larger than Figure 6 suggests. The three points correspond to actual 7Q10s of 79.67, 59.16, and 90.51 cfs, with their corresponding estimates to be 151.21, 170.09, and 167.49 cfs, respectively. To further examine this, Figure 10 displays the residuals in log space, once again arranged from smallest to largest 7Q10.

Besides the three points in the bottom right corner of Figure 10, which were discussed previously, the residuals in Figure 10 appear to be more consistently distributed than the residuals in Figure 8, suggesting that using LTLR is the preferred method over general MLR for 7Q10 estimation.

The final equation, translated back into standard space, is given below.

$$7Q10={Area}^{1.31308}{Slope}^{-0.19413}{Forest}^{0.22437}{Precip}^{0.31049}{Temp}^{-4.37462}$$

4.3. Random Forest

Applying the random forest (RF) machine learning algorithm to the input data yields the following results in

Table 5. Random forest variables and significance.

Variable	% Included MSE	p-Value	Significance
Area (mi2)	57.580982	0.0099	<0.01
Mean Elevation (ft)	6.911398	0.03465	<0.05
Slope (%)	2.257348	0.07228	<0.1
Percent Wetland (%)	−2.099959	0.9901	No significance
Percent Forest (%)	3.335443	0.08911	<0.1
Min 30-day Cumulative Precipitation (mm)	7.726635	0.04275	<0.05
Average 30-day High Temperatures (C)	1.265636	0.6634	No significance

.

Area was found to be significant at the 0.01 level, with elevation and precipitation significant at the 0.05 level, and both slope and percent forest significant at the 0.1 level. Temperature was not found to be significant using the random forest model or the multiple linear regression model, making it only significant in log space. In all three cases so far (MLR, LTLR, and RF), the percentage of the basin considered wetland was not found to be significant. Figure 11 displays the estimated out-of-bag error as a function of the number of decision trees.

Figure 11 displays that the model stabilized around 100 trees. Though the RF method does not make assumptions about normality, a plot of the residuals given in Figure 12, once again arranged from the smallest to largest 7Q10, shows that they are not randomly distributed.

Plotting the 7Q10 values estimated using the random forest method vs. the actual historical 7Q10s is given in Figure 13.

For relatively smaller 7Q10s, RF estimates are similar to the other methods. However, RF underestimates actual historical 7Q10s that are over 20 cfs. For this range, there are only 3 points above the line (overestimation) and 11 points under the line (underestimation). This range is specifically difficult to estimate because there are very few unimpaired watersheds in the study area that are large enough to have 7Q10s in this range, limiting the available training data.

4.4. Neural Network

Neural networks were applied to the input data using a variety of tuning parameters. The addition of multiple hidden layers increased computation time, caused failure to converge in some cases, and did not improve model performance, so the final neural network described only included one hidden layer, an associated convergence threshold of 0.01, and a maximum step of 1 × 10⁵. In this section, no table of variable importance and significance is included, as calculating p-values for neural networks is not common practice. Neural networks are highly complex models with multiple weights and parameters. When calculating p-values for each weight or parameter, it is effectively conducting multiple hypothesis tests for each. This introduces the risk of the multiple comparisons problem [50], where the probability of obtaining false positives (significant p-values) increases, which can lead to misleading results. Instead, we display the general results in Figure 14.

Figure 14 displays that the NN model overestimates smaller 7Q10s (especially in the 0–20 cfs range) and overestimates 7Q10s larger than 20 cfs (7 points below the line, as opposed to 2 above). This should be corroborated by the residuals, which are displayed in Figure 15, once again organized from smallest actual 7Q10 to largest.

Figure 15 suggests that the neural network consistently overestimates the smaller 7Q10 values and underestimates the larger 7Q10 values. Even if this model proves to have the smallest error metrics in Section 4.6 and Section 4.7, this is a significant drawback.

4.5. Generalized Additive Model

GAM was applied to the input data with a variety of tuning parameters. No initial weights or scale parameters were given, and the optimal model was found using the Gaussian distribution with generalized cross-validation (GCV). The optimal GAM model yields the following results in

Table 6. Generalized additive model variables and significance.

Variable	Estimated Degrees of Freedom	p-Value	Significance
Area (mi2)	8.407	0.000000	<0.001
Mean Elevation (ft)	8.143	0.000608	<0.001
Slope (%)	1.000	0.230267	No significance
Percent Wetland (%)	1.315	0.160834	No significance
Percent Forest (%)	3.548	0.484701	No significance
Min 30-day Cumulative Precipitation (mm)	1.661	0.017755	<0.05
Average 30-day High Temperatures (C)	1.466	0.007338	<0.01

.

Area and elevation were both found to be extremely significant, while precipitation and temperature were found to be moderately and largely significant. The only other methodology where temperature was found to be significant was LTLR (linear regression in log space), suggesting that there may be a subtle importance of this variable that was not detected in standard space by MLR or RF. In addition to slope, neither of the landcover variables were found to be significant using GAM. The estimated 7Q10 values vs. the actual historical values are presented in Figure 16.

Figure 16 does not suggest an obvious pattern in residuals. To further analyze the model fit, we plot the residuals in Figure 17, once again organized from smallest actual 7Q10 to largest.

The residuals for the larger basins seem to deviate from the perfect fit line, but the residuals in Figure 17 seem to be much more randomly distributed than the neural network model that displayed a clear pattern in Figure 15.

In the following sections, we will evaluate how each method performs in comparison to StreamStats (Section 4.6) and in relation to each other (Section 4.7). Additionally, all methods seem to perform worst for large 7Q10s, so Section 4.7 will highlight under what range of basin sizes each method performs best, using RMSE as the main metric compared to StreamStats estimates.

4.6. Comparisons to StreamStats Estimates

Current 7Q10 estimates were derived using the USGS’s StreamStats program, discussed in Section 2.3. Estimates are only available for some states in the domain, leaving 128 data points for comparison out of the 165 total used for training. In addition, no test set was used in the StreamStats derivations, so comparing exact estimates from each method without using a validation procedure is given in

Table 7. Multiple method comparisons to current estimates.

Method	R2	KGE	NSE	RMSE
StreamStats Estimates	0.66	0.66	0.65	9.88
Log-Transformed Linear Regression	0.67	0.54	0.62	13.50
Multiple Linear Regression	0.70	0.80	0.63	7.14
Random Forest	0.63	0.76	0.53	7.97
Neural Network	0.73	0.82	0.67	6.79
Generalized Additive Model	0.84	0.91	0.83	5.19

.

Most methods perform similarly, but GAM displays the best R², KGE, NSE, and RMSE by far out of all the methods. Because of the high flexibility of GAMs, they are prone to overfitting, and this success will be further tested in Section 4.7 with LOOCV. The NN model also displays a high R² and KGE, but that is with the drawback that it overestimates small 7Q10s and underestimates large 7Q10s, as highlighted in Figure 15. MLR and RF outperform current estimates by an average of 12% in terms of KGE, as well as 25% in terms of RMSE, which is arguably the most important metric as it directly measures error. RF’s success could also be due to overfitting, which is tested in the next section. MLR, however, is a classical method for 7Q10 estimation and is not prone to overfitting. Given its success compared to StreamStats for the exact same locations that were derived using state-by-state equations, results suggest that a single, generalized methodology is appropriate.

4.7. General Performance

Comparing each method using leave-one-out cross-validation results in the following metrics, given in

Table 8. Comparisons between statistical methods using leave-one-out cross-validation.

Method	R2	KGE	NSE	RMSE
Log-Transformed Linear Regression	0.72	0.50	0.62	15.24
Multiple Linear Regression	0.60	0.73	0.47	8.53
Random Forest	0.61	0.69	0.41	8.39
Neural Network	0.53	0.69	0.36	9.41
Generalized Additive Model	0.53	0.65	0.52	12.15

.

Table 8 confirms that the success displayed by both NN and GAM in the previous section was due to overfitting. They display the two worst R²s and have RMSEs larger than both RF and MLR. With the addition of a test set, the RF method performance only declined 3.17% for R² (0.61, down from 0.63), 9.21% for KGE (0.69, down from 0.76), 22.64% for NSE (0.41, down from 0.53), and increased 5.27% for RMSE (8.39, up from 7.97). The average decline for MLR and LTLR was similar, at 3.41% for R², 8.08% for KGE, 12.70% for NSE, and an increase of 16.18% for RMSE. This suggests that RF’s previous success was not due to overfitting, as it displayed similar declines to LTLR and MLR, which utilize straight lines for fitting.

Each method performs differently based on the evaluation metric used. One explanation for this is the wide range of basin sizes included in this analysis. This is highlighted in the plots of residuals earlier, which demonstrated that many models perform poorer for larger 7Q10s. Splitting the data into three distinct subsets based on basin size will allow us to further examine why some methods display high R² but poor RMSE. For this analysis, small basins are defined as basins under 15 mi², while medium basins are basins between 15 and 70 mi², and large basins are basins larger than 70 mi². These thresholds do not have any physical meaning and are simply selected to divide the full dataset into three equally sized subsets for further analysis. In

Table 9. RMSE comparisons between methods for specified size ranges.

	RMSE for Each Methodology
Subset	MLR	LTLR	RF	NN	GAM
Small Basins (<15 mi2)	2.11	0.34	0.44	2.77	2.97
Medium Basins (15–70 mi2)	3.96	2.83	3.09	3.87	4.66
Large Basins (>70 mi2)	14.02	26.23	14.01	15.60	20.32
Average	6.70	9.80	5.85	7.41	9.31

, we provide the RMSE for each method applied to each basin size range. Especially for these subsets, RMSE is the best metric to base success on, as it measures the error of estimates vs. the actual values, which is the most important metric for resource managers who need accurate 7Q10 estimates.

Table 9 demonstrates that LTLR and RF perform similarly well for 7Q10 estimation in both small- and medium-sized basins, greatly outperforming MLR, NN, and GAM. However, for large basins, LTLR performs poorly because of the extreme overestimation discussed earlier, while MLR, RF, and NN perform similarly well (RMSE = 14.02, 14.01, and 15.60, respectively). Based on this experiment, RF performs the best across all ranges of basin sizes (Avg. RMSE = 5.85), while LTLR performs similarly well in small- and medium-sized basins where it is traditionally used, and MLR performs similarly well in large basins. Based on RF’s success for all ranges of basin sizes, we include Figure 18 to compare raw 7Q10 estimates for the RF method to both classical methods, MLR and LTLR. Figure 18a–c displays the actual 7Q10, as well as the LTLR, MLR, and RF estimates, arranged from the smallest historical 7Q10 to the largest.

The results in Figure 18a–c corroborate the results from Table 9. Logarithmic-transformed linear regression performs best overall in terms of R² and NSE but performs poorly in KGE and RMSE due to its poor estimates in large basins, reflected in Figure 18c. LTLR estimates the largest historical 7Q10, which is 90 cfs, to be 181 cfs, more than double the actual value. Similarly, LTLR estimates the next two largest 7Q10s, which are 59.2 cfs and 79.7 cfs, to be 186 cfs and 160 cfs, respectively. Though the LTLR vs. actual 7Q10 graph (Figure 9) previously suggested that LTLR may be able to be expanded for large basins because the largest 7Q10s seemed to maintain a constant distance from the perfect fit line, Figure 9 is in log space, and differences in log space are amplified for larger numbers when returning to standard space. Conversely, multiple linear regression performs well in large basins but poorly in small basins, as it attempts to minimize the overall error and gives more weight to larger 7Q10s. Lastly, the random forest method performs well overall, especially in larger basins, suggesting that this flexible machine learning algorithm may be able to account for the drawbacks of both LTLR and MLR.

5. Conclusions

This research improves upon current methodologies for statistically estimating the 7Q10 by analyzing multiple statistical methods, testing various topographical, landcover, and climate variables for significance, and widening the geographical and watershed size ranges of current methodologies. Results support that a single, generalized methodology can be used for 7Q10 estimation throughout the entire northeast and mid-Atlantic, with similar R², RMSE, NSE, and KGE compared to current state-by-state StreamStats’ estimates while only requiring one equation/model. Estimates from StreamStats display an R², KGE, NSE, and RMSE of 0.66, 0.66, 0.65, and 9.88, respectively, for the unimpaired gages where it is available in the study area, while the random forest method displays an R², KGE, NSE, and RMSE of 0.61, 0.69, 0.41, and 8.39, respectively, for the full range of gages even after cross-validation was applied. Two other machine learning algorithms (neural networks and generalized additive models) were tested as well but displayed significantly worse R²s, KGEs, NSEs, and RMSEs (0.53, 0.69, 0.36, and 9.41 and 0.53, 0.65, 0.52, and 12.15, respectively) with the addition of the cross-validation test set.

Future work could involve testing other advanced statistical methods and/or machine learning algorithms for better low-flow estimation. Because we were able to successfully apply this methodology to such a large geographical footprint, other future work may include determining the boundaries at which assuming hydrologic homogeneity is no longer satisfied. Additional future work directly related to this study may involve landcover and climate-altered futures. The inclusion of climate and landcover input variables, which were both found to be statistically significant, can be used prescriptively in conjunction with physical hydrology models to test how changing landcover and climate conditions affect 7Q10 estimates. Because of additional stakeholder input, future work may also involve only using 7Q10 data derived from the last 30 years of streamflow data at each site for use as the actual historical 7Q10. Blum et al. (2019) found that using the most recent 30 years of streamflow record to derive the “true” 7Q10 when a trend is detected reduces error and bias in 7Q10 estimators compared to using the full record of streamflow [2]. This may account for recent climatic and hydrologic conditions that will be more representative of future 7Q10 conditions at a particular site, but additional studies must be completed to confirm this relationship.