A Study on the Characteristics of Beach Profile Evolution According to the Particle Size Variation of Beach Nourishment
Abstract
:1. Introduction
2. Methods
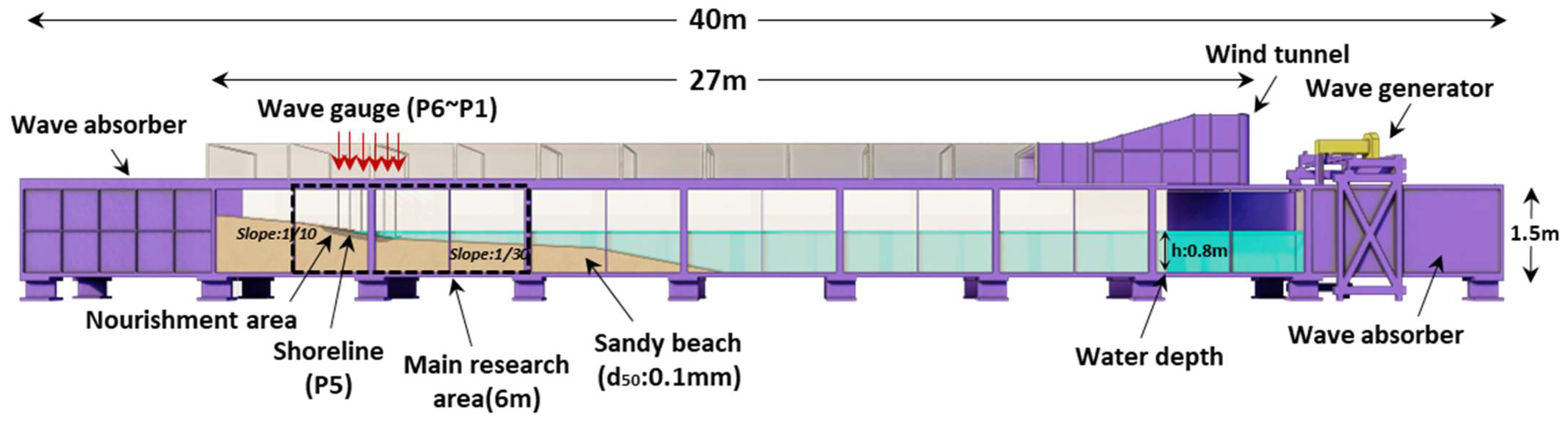
2.1. Setup for Test Profile
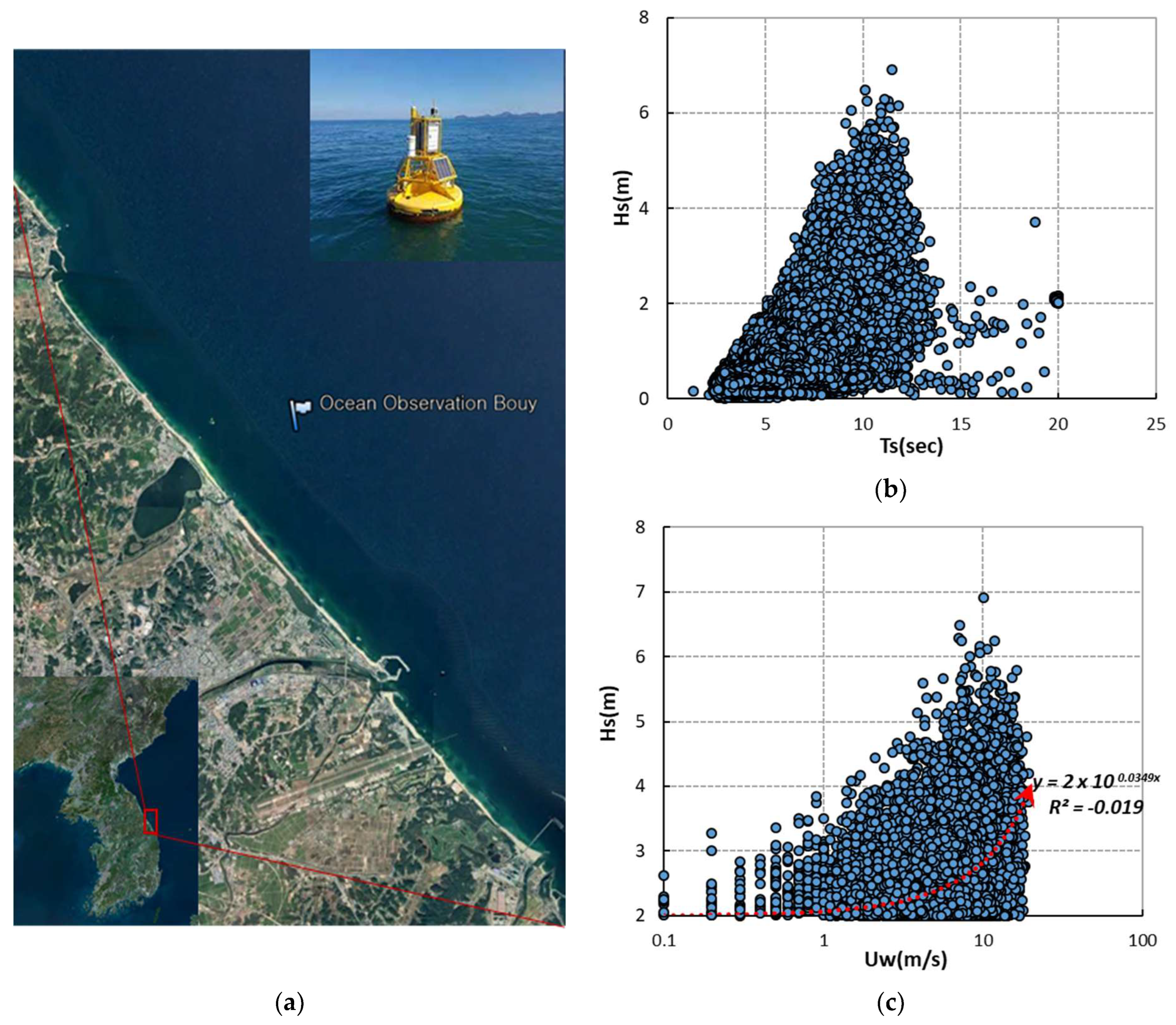
2.2. External Force Condition
2.3. Method of Measurement and Analysis
3. Results
3.1. Sediment Transport Variation According to Cross-Sectional Profile Changes
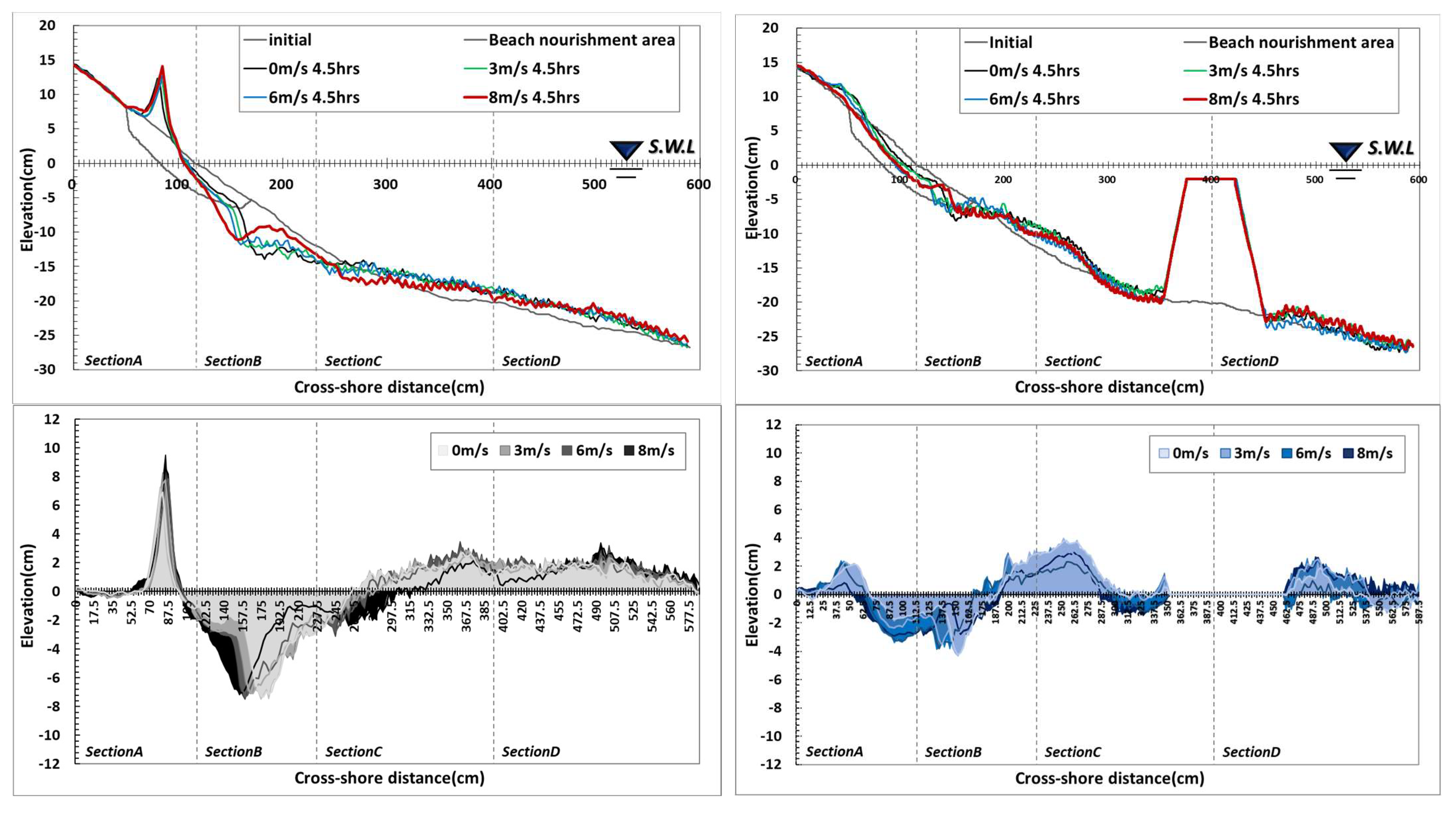
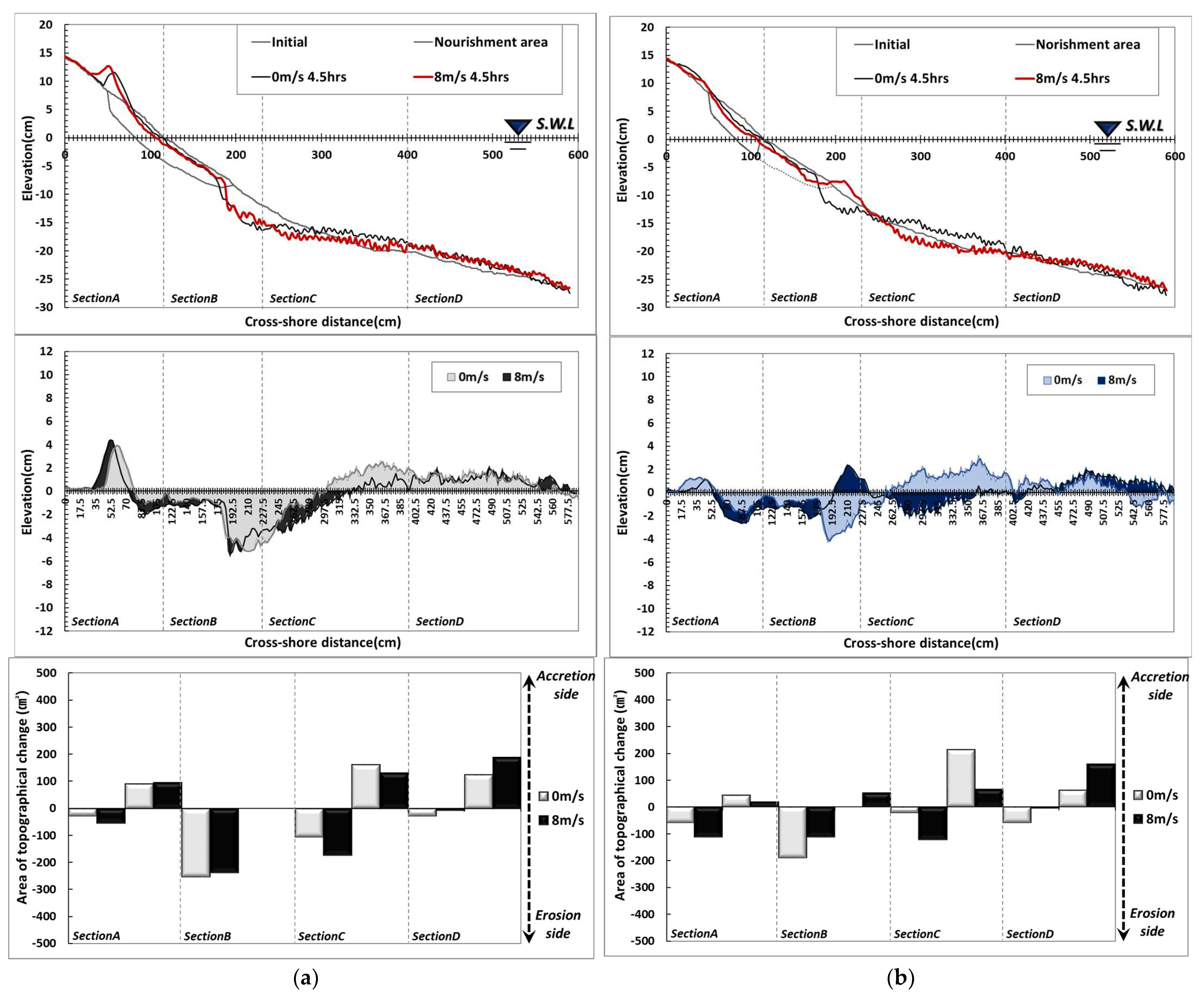
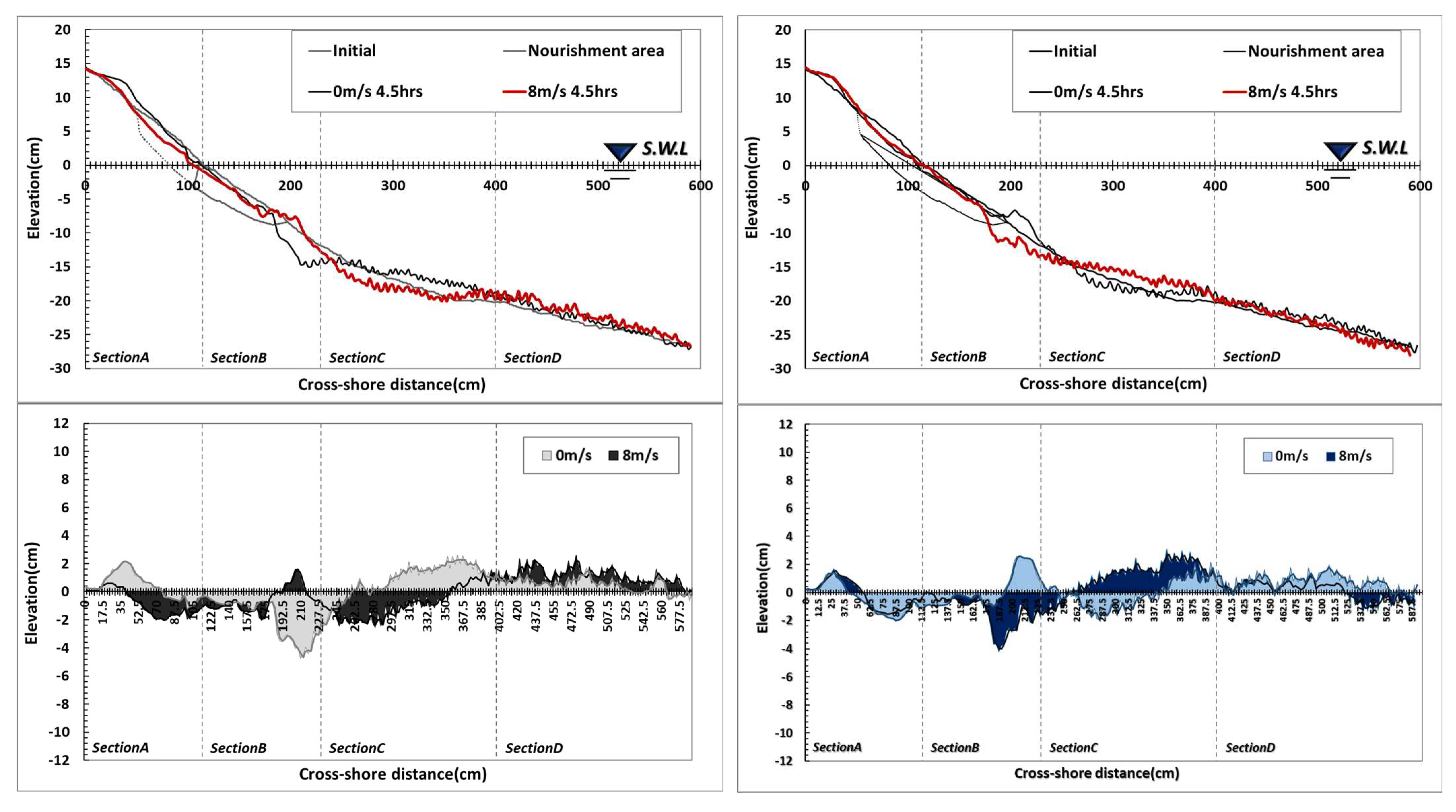
3.1.1. Topography Change
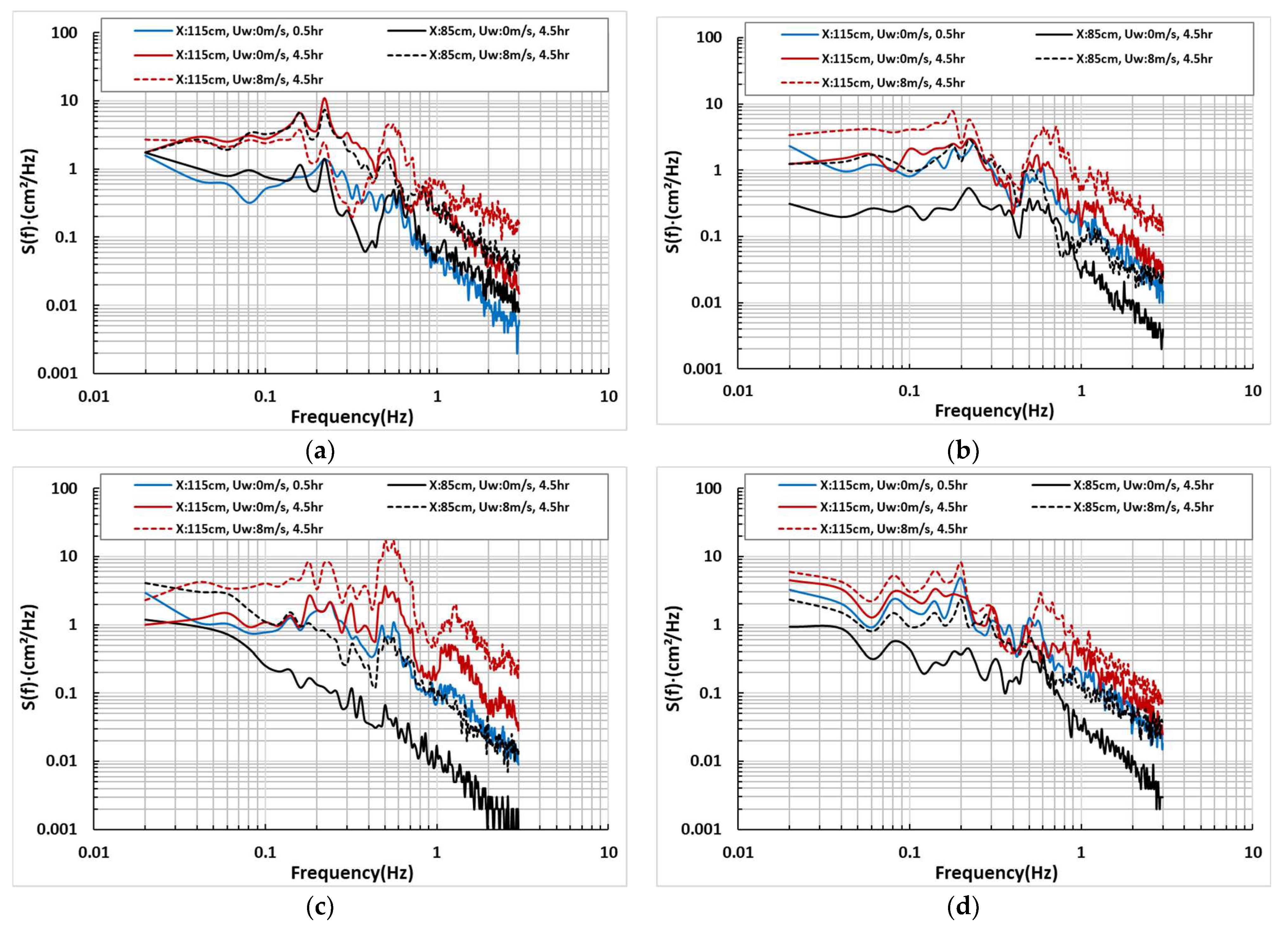
3.1.2. Spectrum Analysis
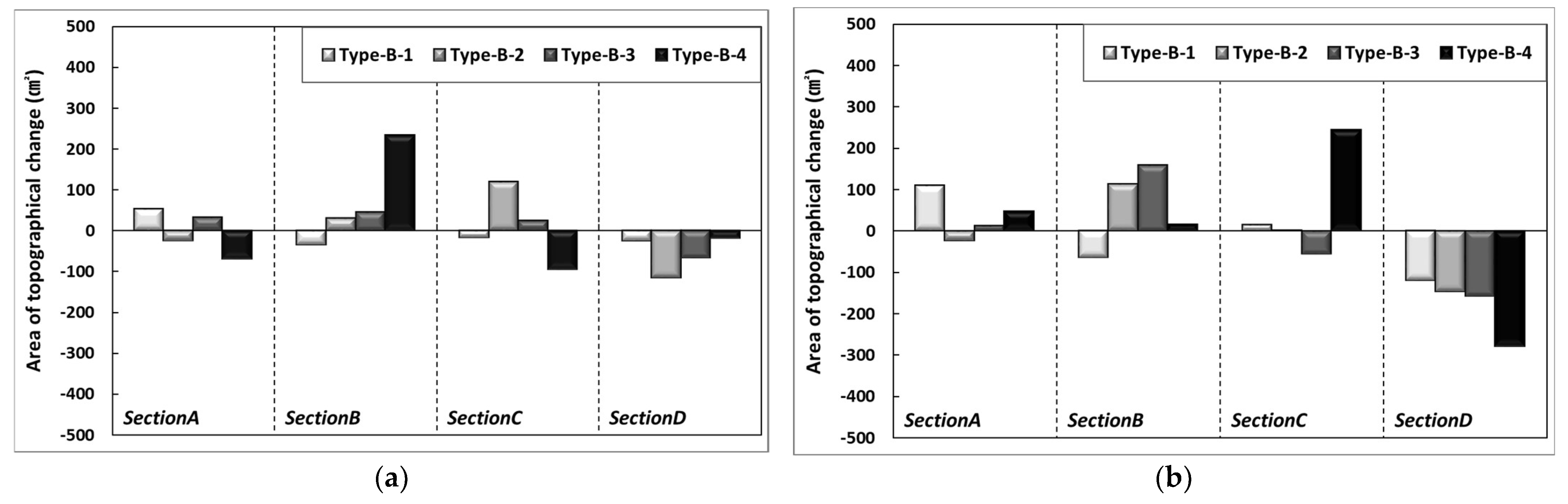
3.2. Sediment Transport according to Changes in Nourishment Area
3.2.1. Topography Change
3.2.2. Spectrum Analysis
4. Discussion
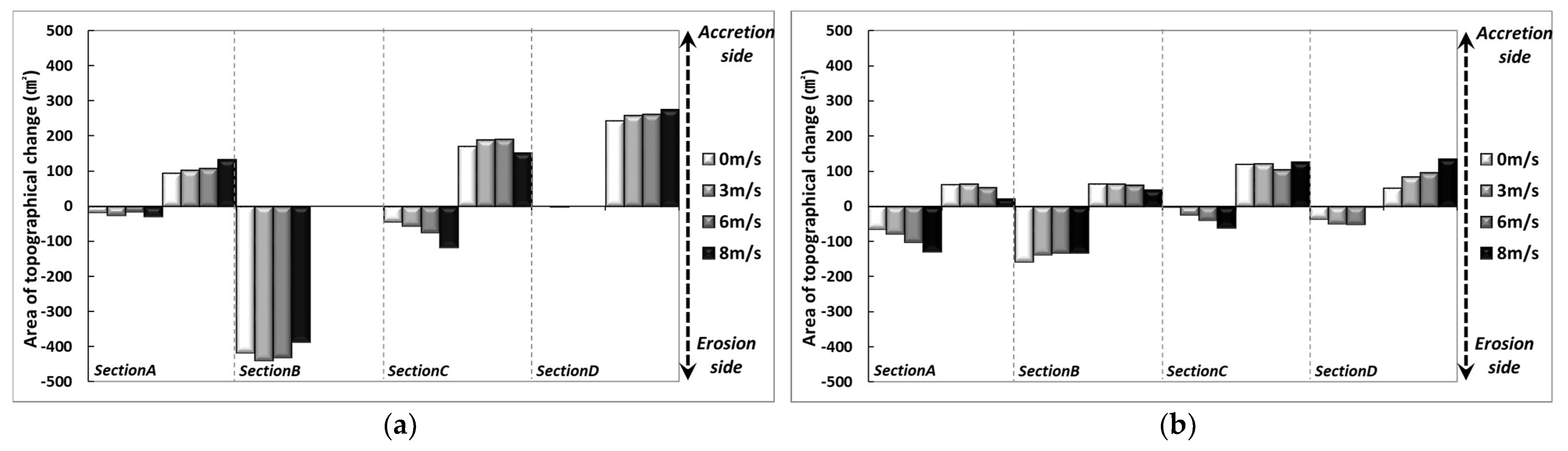
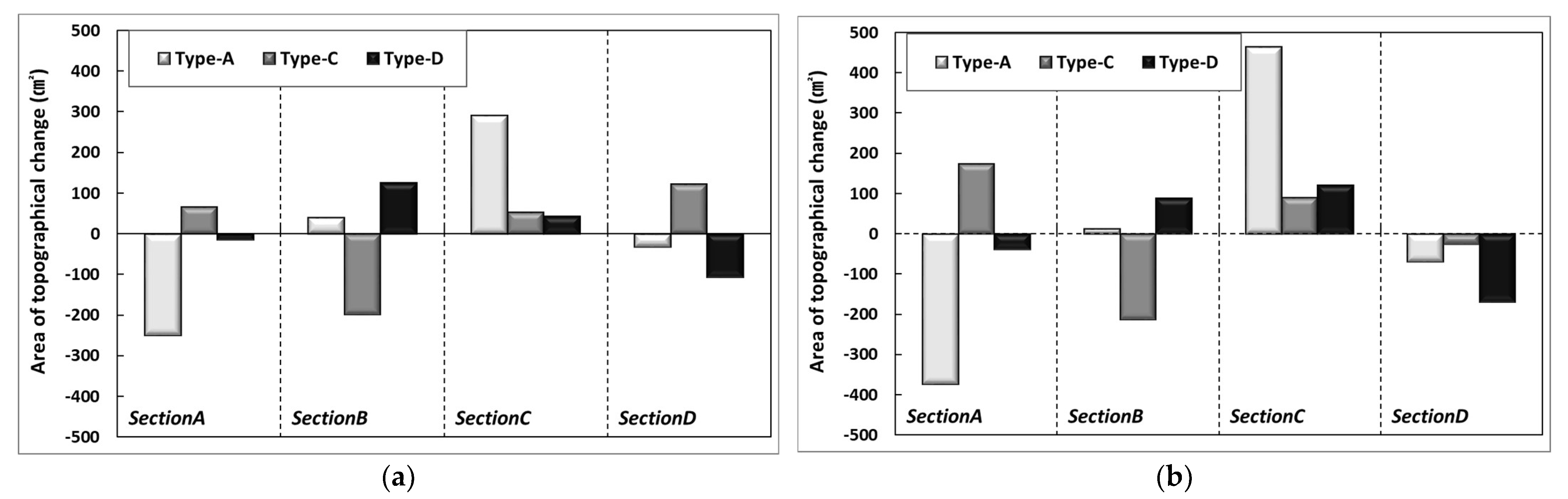
4.1. Comparison of Topographical Evolution According to Cross-Sectional Changes
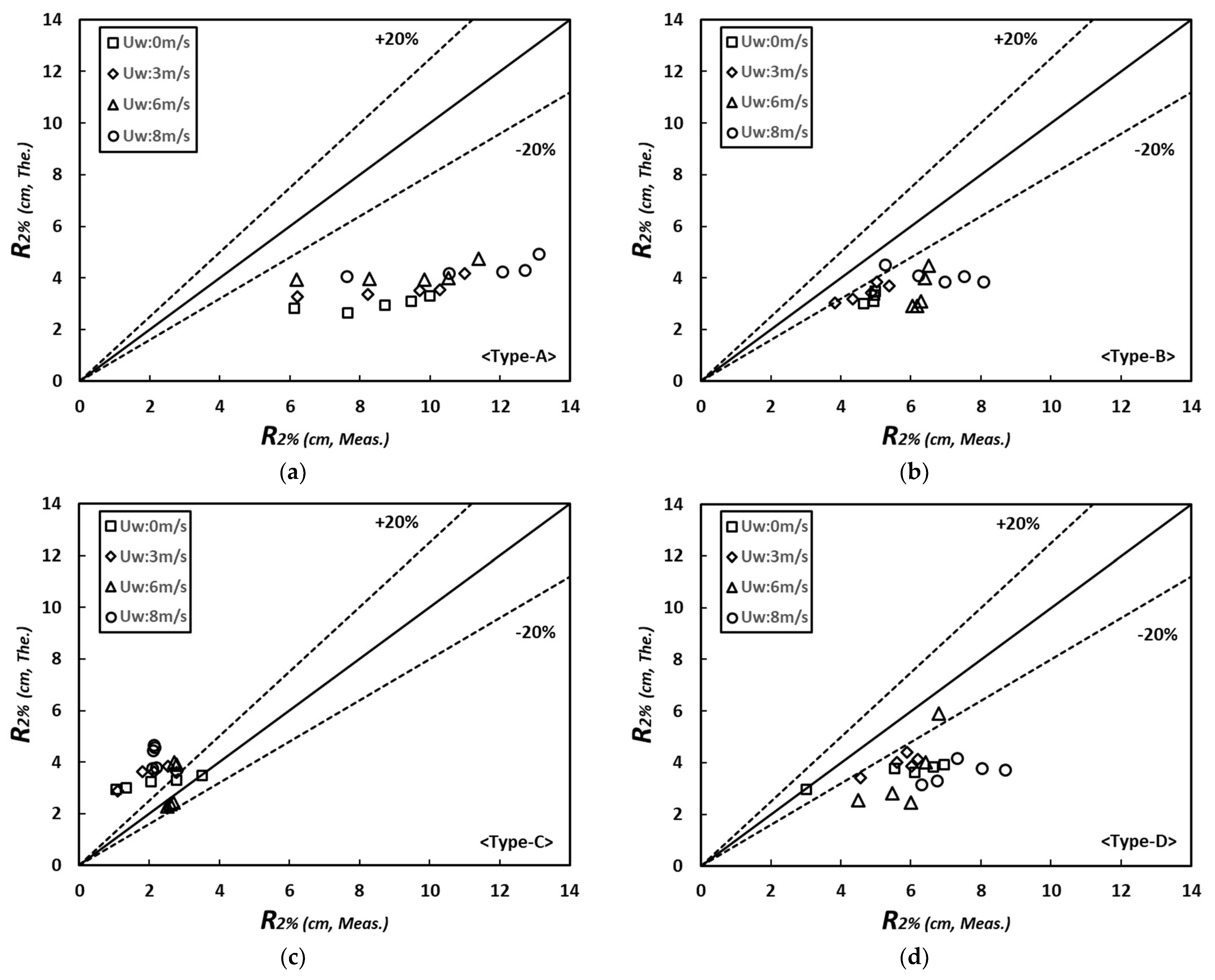
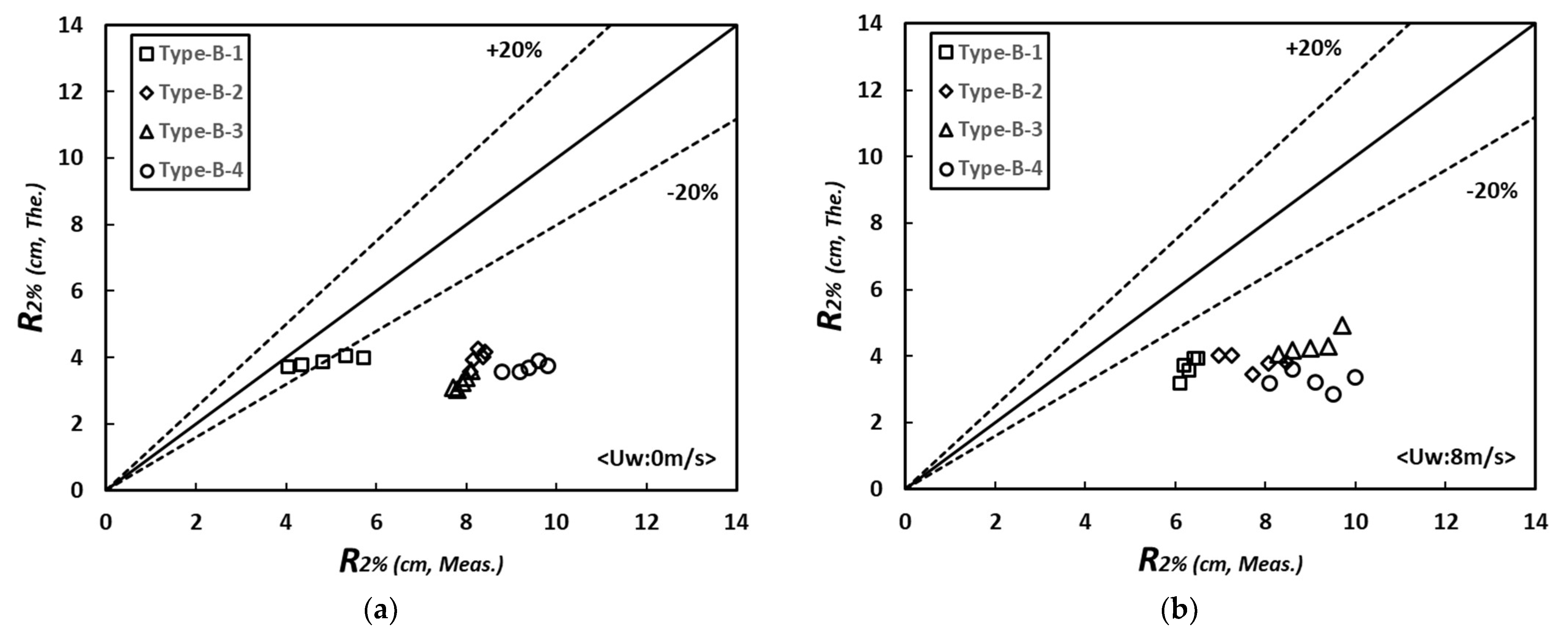
4.2. Analysis of Wave Run-Up Characteristic
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Masselink, G.; McCall, R.; Poate, T.; van Geer, P. Modelling storm response on gravel beaches using XBeach-G. Proc. Inst. Civ. Eng. Marit. Eng. 2014, 167, 173–191. [Google Scholar] [CrossRef]
- Brown, S.I.; Dickson, M.E.; Kench, P.S.; Bergillos, R.J. Modelling gravel barrier response to storms and sudden relative sea-level change using XBeach-G. Mar. Geol. 2019, 410, 164–175. [Google Scholar] [CrossRef]
- Stokes, K.; Poate, T.; Masselink, G.; King, E.; Saulter, A.; Ely, N. Forecasting coastal overtopping at engineered and naturally defended coastlines. Coast. Eng. 2021, 164, 103827. [Google Scholar] [CrossRef]
- Pollard, J.A.; Christie, E.K.; Brooks, S.M.; Spencer, T. Impact of Management Regime and Regime Change on Gravel Barrier Response to a Major Storm Surge. J. Mar. Sci. Eng. 2021, 9, 147. [Google Scholar] [CrossRef]
- Pranzini, E.; Anfuso, G.; Cinelli, I.; Piccardi, M.; Vitale, G. Shore Protection Structures Increase and Evolution on the Northern Tuscany Coast (Italy): Influence of Tourism Industry. Water 2018, 10, 1647. [Google Scholar] [CrossRef]
- Masria, A.; Iskander, M.; Negm, A. Coastal protection measures, case study (Mediterranean zone, Egypt). J. Coast. Conserv. 2015, 19, 281–294. [Google Scholar] [CrossRef]
- Mimura, N.; Nunn, P. Trends of Beach Erosion and Shoreline Protection in Rural Fiji. J. Coast. Res. 1998, 14, 37–46. [Google Scholar]
- Liew, M.; Xiao, M.; Jones, B.M.; Farquharson, L.M.; Romanovsky, V.E. Prevention and control measures for coastal erosion in northern high-latitude communities: A systematic review based on Alaskan case studies. Environ. Res. Lett. 2020, 15, 093002. [Google Scholar] [CrossRef]
- Andreadi, O.; Chatzipavlis, A.; Hasiotis, T.; Monioudi, I.; Manoutsoglou, E.; Velegrakis, A. Assessment of and Adaptation to Beach Erosion in Islands: An Integrated Approach. J. Mar. Sci. Eng. 2021, 9, 859. [Google Scholar] [CrossRef]
- Mendes, D.; Pais-Barbosa, J.; Baptista, P.; Silva, P.A.; Bernardes, C.; Pinto, C. Beach Response to a Shoreface Nourishment (Aveiro, Portugal). J. Mar. Sci. Eng. 2021, 9, 1112. [Google Scholar] [CrossRef]
- Pinto, C.A.; Taborda, R.; Andrade, C.; Baptista, P.; Silva, P.A.; Mendes, D.; Pais-Barbosa, J. Morphological Development and Behaviour of a Shoreface Nourishment in the Portuguese Western Coast. J. Mar. Sci. Eng. 2022, 10, 146. [Google Scholar] [CrossRef]
- Shim, K.-T.; Kim, K.-H.; Kim, H.-D.; Kwak, K.-S. Analysis on Sediment Transport System in the East Coast of Korea. J. Coast. Res. 2020, 95, 643–648. [Google Scholar] [CrossRef]
- Frandsen, J.B.; Xharde, R.; Berube, F.; Tremblay, O.G. Large Scale Experimental Storm Impact on Nourished Beach using Cobble-Gravel-Sand Mix. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshre and Arctic Engineering, Newfoundland, Canada, 31 May 2015; pp. 1–10. [Google Scholar]
- McCall, R.T.; Masselink, G.; Poate, T.G.; Roelvink, J.A.; Almeida, L.P.; Davidson, M.; Russe, P.E. Modelling Strom Hydrody-namics on Gravel Beaches with XBeach-G. Coast. Eng. 2014, 91, 231–250. [Google Scholar] [CrossRef]
- Frades, J.L.; Negro, V.; Barba, J.G.; Martín-Antón, M.; López-Gutiérrez, J.S.; Esteban, M.D.; Blasco, L.J.M. Preliminary Design for Wave Run-Up in Offshore Wind Farms: Comparison between Theoretical Models and Physical Model Tests. Energies 2019, 12, 492. [Google Scholar] [CrossRef]
- Myrhaug, D.; Sunde, T. Wave runup and wave rundown estimation based on long-term variation of wind statistics. Proc. Inst. Civ. Eng. Marit. Eng. 2018, 171, 40–46. [Google Scholar] [CrossRef]
- Demirbilek, Z.; Nwogu, O.G.; Ward, D.L. Laboratory Study of Wind Effect on Runup over Fringing Reefs, Data Report, Coastal and Hydraulics Laboratory Techical Report ERDC/CHL-TR-07-4 2007; U.S. Army Engineering Research and Development Center: Washington, DC, USA, 2007. [Google Scholar]
- Medvedev, A.V.; Ratovsky, K.G.; Tolstikov, M.V.; Vasilyev, R.V.; Artamonov, M.F. Method for Determining Neutral Wind Velocity Vectors Using Measurements of Internal Gravity Wave Group and Phase Velocities. Atmosphere 2019, 10, 546. [Google Scholar] [CrossRef]
- Shemer, L. On Evolution of Young Wind Waves in Time and Space. Atmosphere 2019, 10, 562. [Google Scholar] [CrossRef]
- Sherman, D.J.; Orford, J.D.; Carter, R.W.G. Development of cusp-related, gravel size and shape facies at Malin Head, Ireland. Sedimentology 1993, 40, 1139–1152. [Google Scholar] [CrossRef]
- Buscombe, D.; Masselink, G. Concepts in gravel beach dynamics. Earth-Sci. Rev. 2006, 79, 33–52. [Google Scholar] [CrossRef]
- Roberts, T.M.; Wang, P.; Puleo, J.A. Storm-driven cyclic beach morphodynamics of a mixed sand and gravel beach along the Mid-Atlantic Coast, USA. Mar. Geol. 2013, 346, 403–421. [Google Scholar] [CrossRef]
- Ions, K.; Karunarathna, H.; Reeve, D.E.; Pender, D. Gravel Barrier Beach Morphodynamic Response to Extreme Conditions. J. Mar. Sci. Eng. 2021, 9, 135. [Google Scholar] [CrossRef]
- Shim, K.-T.; Kim, K.-H.; Park, J.-H. The Effectiveness of Adaptive Beach Protection Methods under Wind Application. J. Mar. Sci. Eng. 2019, 7, 385. [Google Scholar] [CrossRef]
- Shim, K.-T.; Kim, K.-H. A Study of Hydraulic Characteristics in Front of the Seawall under the Coexistence of Wave and Wind. J. Korean Soc. Coast. Ocean Eng. 2020, 32, 575–586. [Google Scholar] [CrossRef]
- Sunamura, T.; Horikawa, K. Two-dimensional Beach Transformation due to Waves. In Proceedings of the 14th Conference on Coastal Engineering, Copenhagen, Denmark, 24–28 June 1974; pp. 920–938. [Google Scholar]
- Dean, R.G. Heuristic Models of Sand Transport in the Surf Zone. In Proceedings of the Conference on Engineering Dynamics in the Surf Zone; Institution of Engineers: Sydney, Australia, 1973; pp. 208–214. [Google Scholar]
- Rubey, W.W. Settling velocity of gravel, sand, and silt particles. Am. J. Sci. 1933, 148, 325–338. [Google Scholar] [CrossRef]
- Bennett, S.J.; Bridge, J.S.; Best, J.L. Fluid and sediment dynamics of upper stage plane beds. J. Geophys. Res. Oceans 1998, 103, 1239–1274. [Google Scholar] [CrossRef]
- Lamb, M.P.; Venditti, J.G. The grain size gap and abrupt gravel-sand transitions in rivers due to suspension fallout. Geophys. Res. Lett. 2016, 43, 3777–3785. [Google Scholar] [CrossRef]
- Hunt, I.A. Design of seawalls and breakwaters. J. Waterw. Harb. Div. 1959, 85, 123–152. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.; Stewart, R. Radiation stresses in water waves; a physical discussion, with applications. Deep. Sea Res. Oceanogr. Abstr. 1964, 11, 529–562. [Google Scholar] [CrossRef]
- Fitzgerald, C.J.; Taylor, P.H.; Orszaghova, J.; Borthwick, A.G.; Whittaker, C.; Raby, A.C. Irregular wave runup statistics on plane beaches: Application of a Boussinesq-type model incorporating a generating–absorbing sponge layer and second-order wave generation. Coast. Eng. 2016, 114, 309–324. [Google Scholar] [CrossRef]
- Kim, L.N.; Brodie, K.L.; Cohn, N.T.; Giddings, S.N.; Merrifield, M. Observations of beach change and runup, and the performance of empirical runup parameterizations during large storm events. Coast. Eng. 2023, 184, 104357. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Holman, R.A.; Howd, P.A.; Sallenger, A.H., Jr. Empirical parameterization of setup, swash, and runup. Coast. Eng. 2006, 53, 573–588. [Google Scholar] [CrossRef]





| Beach Profile | Nourishment Material | Nourishment Section | Time Interval (h) | Beach Slope | Measurement Items | ||
|---|---|---|---|---|---|---|---|
| 0.8 0.1 1.4 | 0 3 6 8 | Type A Type B Type C Type D | 0.1 1.0 5.0 0.1 + Submerged BW | All | 0.5 | 1/10 | Topographical |
| 1.5 | (foreshore) | Change | |||||
| 2.5 | Wind speed | ||||||
| 3.5 | 1/30 | Wave | |||||
| 4.5 | (offshore) | variation |
| Beach Profile | Nourishment Material (d50, mm) | Nourishment Section | Time Interval (h) | Beach Slope | Measurement Items | ||
|---|---|---|---|---|---|---|---|
| 0.8 0.1 1.4 | 0 8 | Type B-1 Type B-2 Type B-3 Type B-4 | 1.0 | Expansion of Type B Half of Type B-1 (left side) Half of Type B-1 (right side) Half of Type B-1 (bottom side) | 0.5 1.5 2.5 3.5 4.5 | 1/10 (foreshore) 1/30 (offshore) | Topographical change Wind speed Wave variation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shim, K.-T.; Kim, K.-H. A Study on the Characteristics of Beach Profile Evolution According to the Particle Size Variation of Beach Nourishment. Water 2023, 15, 2956. https://doi.org/10.3390/w15162956
Shim K-T, Kim K-H. A Study on the Characteristics of Beach Profile Evolution According to the Particle Size Variation of Beach Nourishment. Water. 2023; 15(16):2956. https://doi.org/10.3390/w15162956
Chicago/Turabian StyleShim, Kyu-Tae, and Kyu-Han Kim. 2023. "A Study on the Characteristics of Beach Profile Evolution According to the Particle Size Variation of Beach Nourishment" Water 15, no. 16: 2956. https://doi.org/10.3390/w15162956
APA StyleShim, K.-T., & Kim, K.-H. (2023). A Study on the Characteristics of Beach Profile Evolution According to the Particle Size Variation of Beach Nourishment. Water, 15(16), 2956. https://doi.org/10.3390/w15162956







