Investigation of Structural Strength and Fatigue Life of Rotor System of a Vertical Axial-Flow Pump under Full Operating Conditions
Abstract
:1. Introduction
2. Methodology
2.1. Fluid Governing Equations
2.2. Structural Governing Equations
3. Numerical Settings
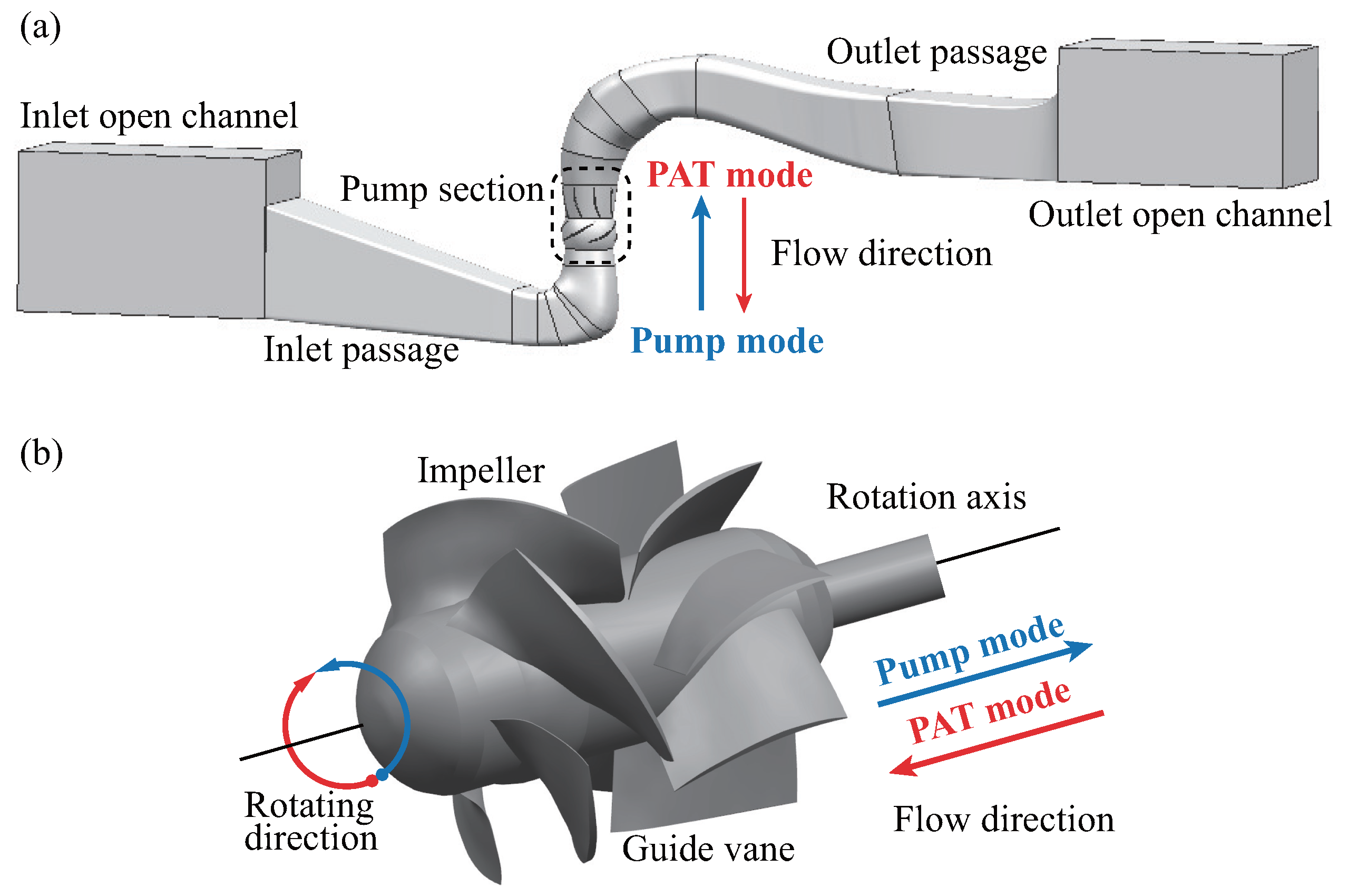
3.1. Geometry of Pump Device
3.2. Fluid Field
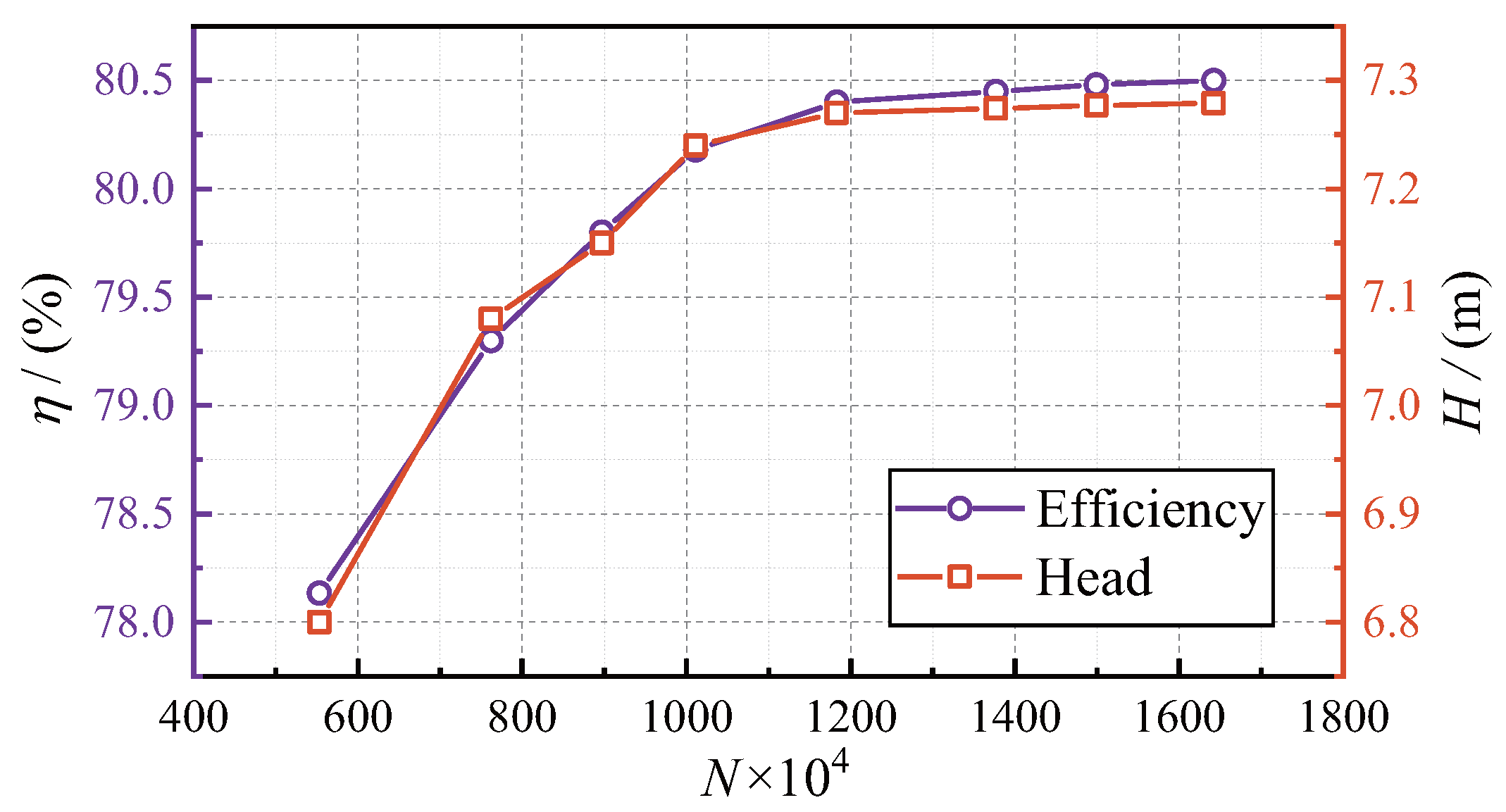
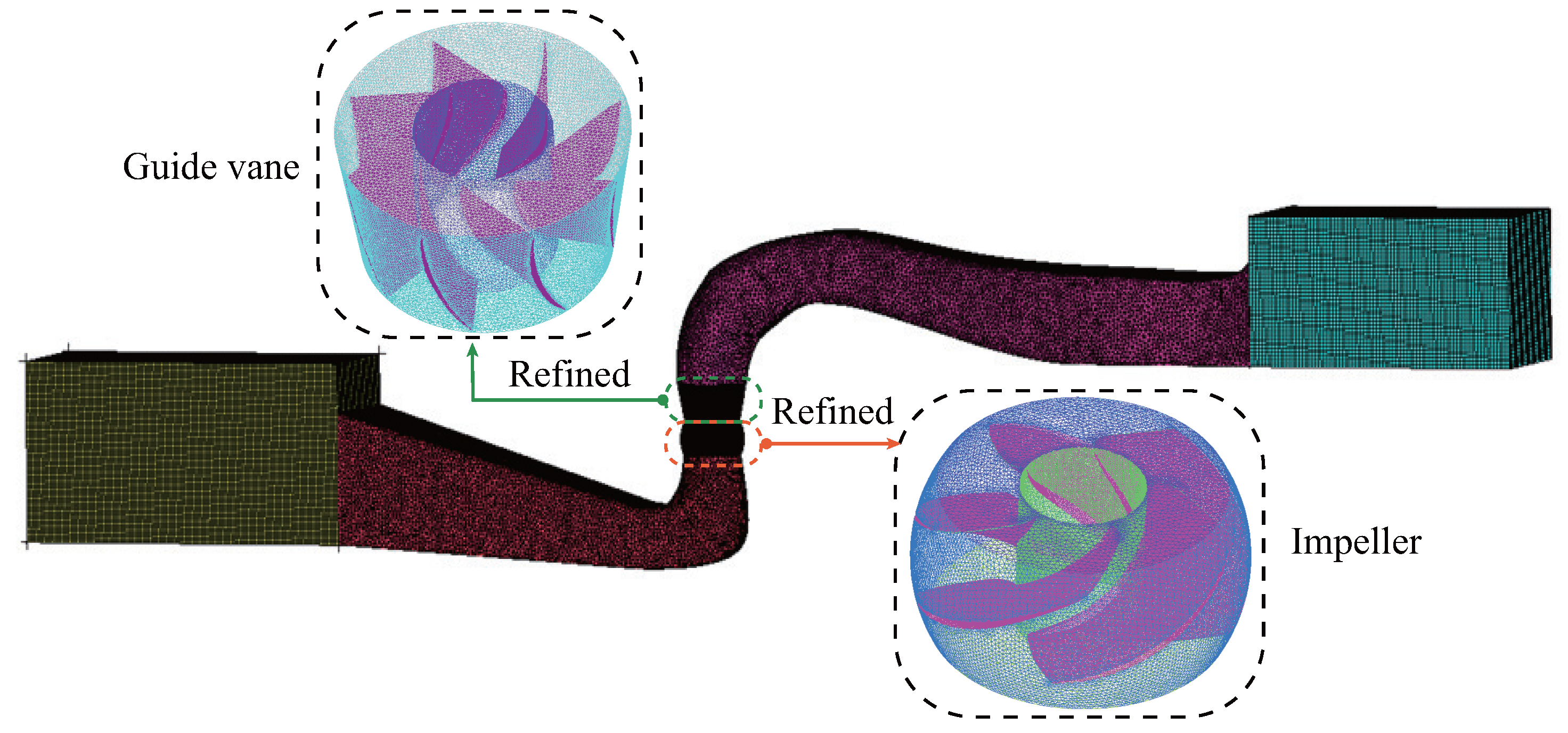
3.2.1. Spatial Discretization
3.2.2. Solution Method and Boundary Conditions
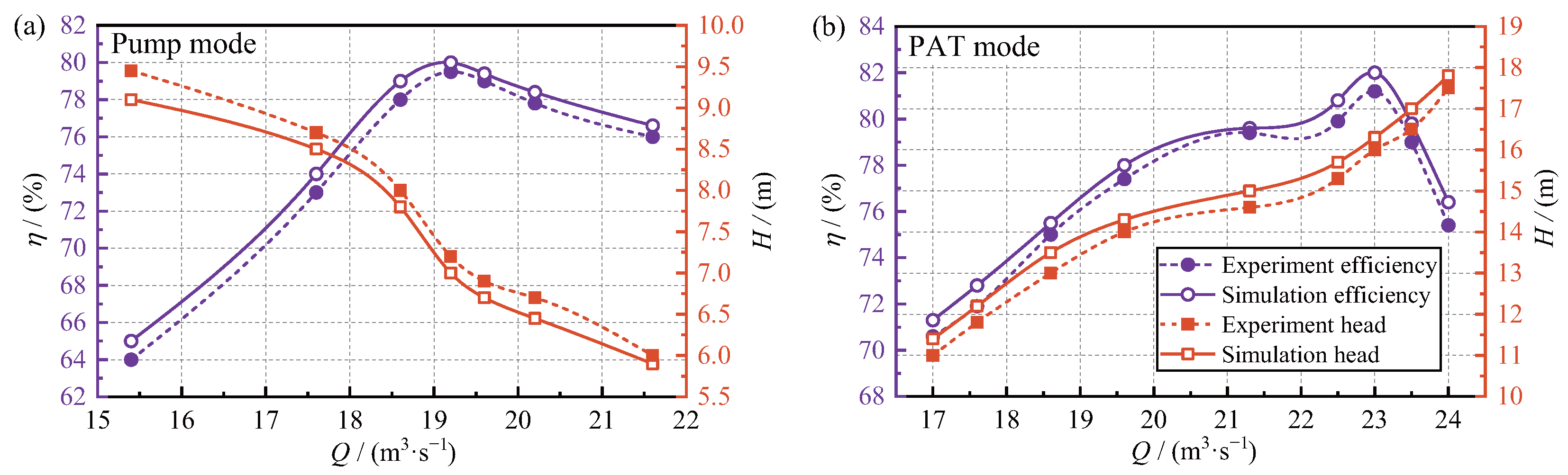
3.2.3. Validation of External Characteristics
3.3. Structural Field
4. Results and Discussion
4.1. Analysis of Deformation and Stress of Blades
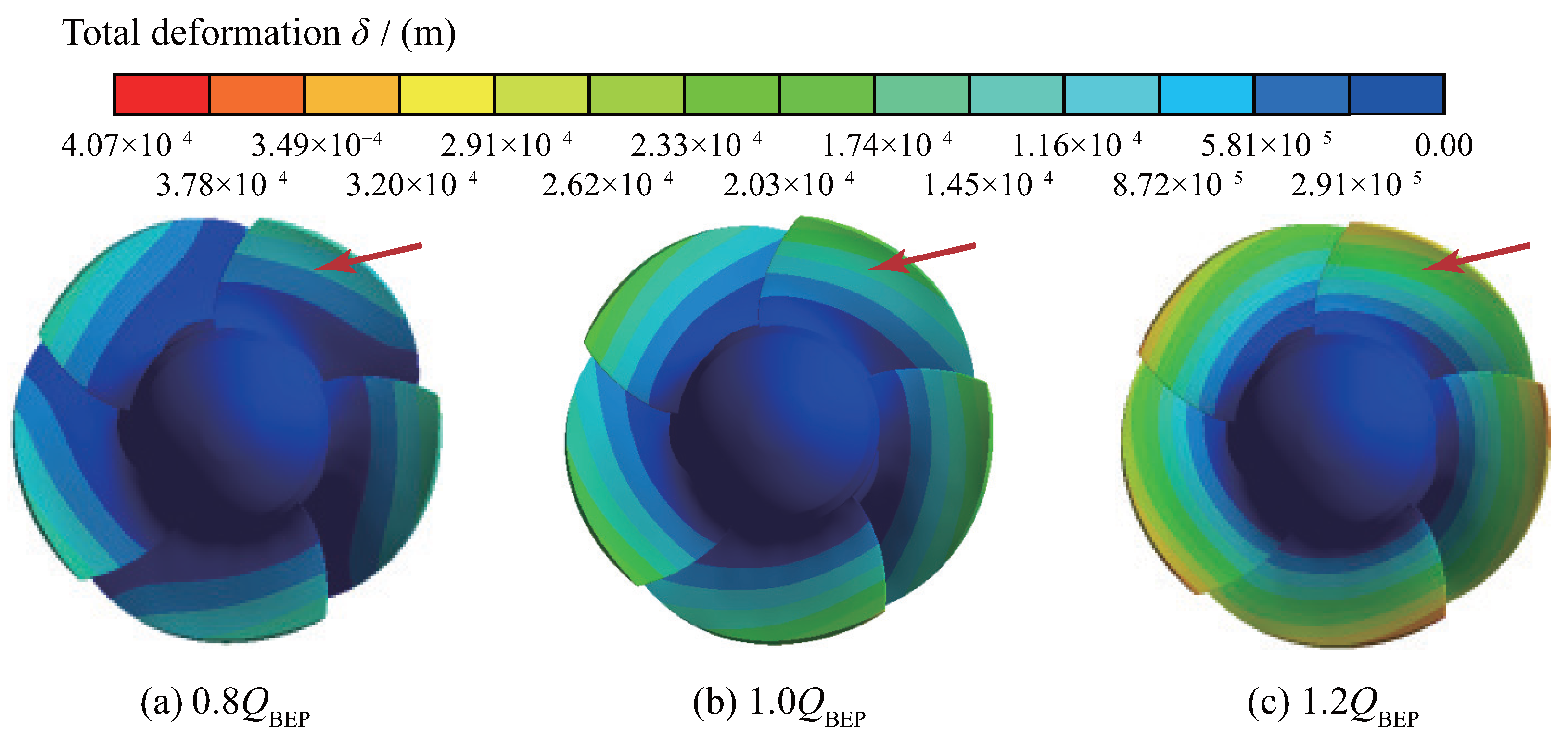
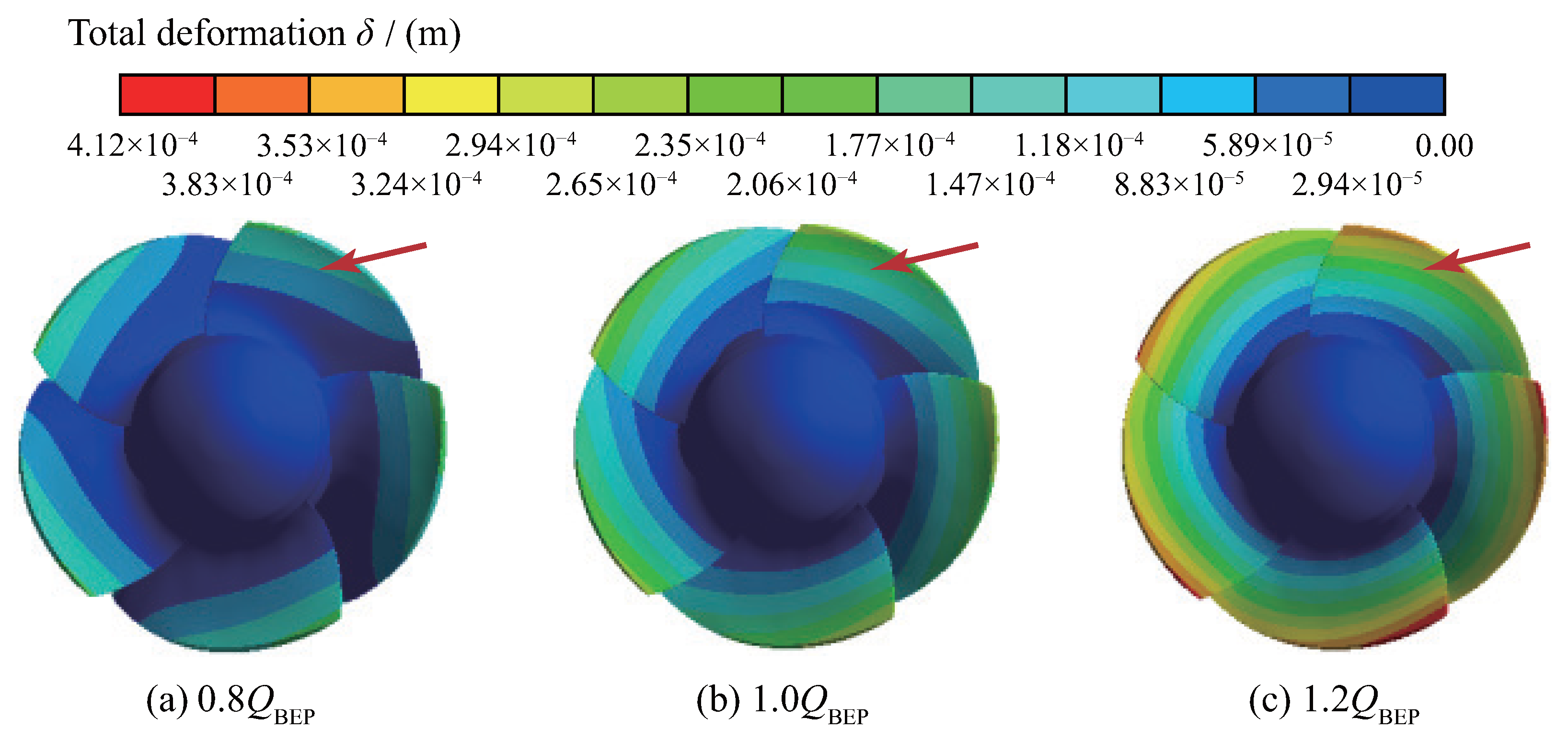
4.1.1. Total Deformation of Blades
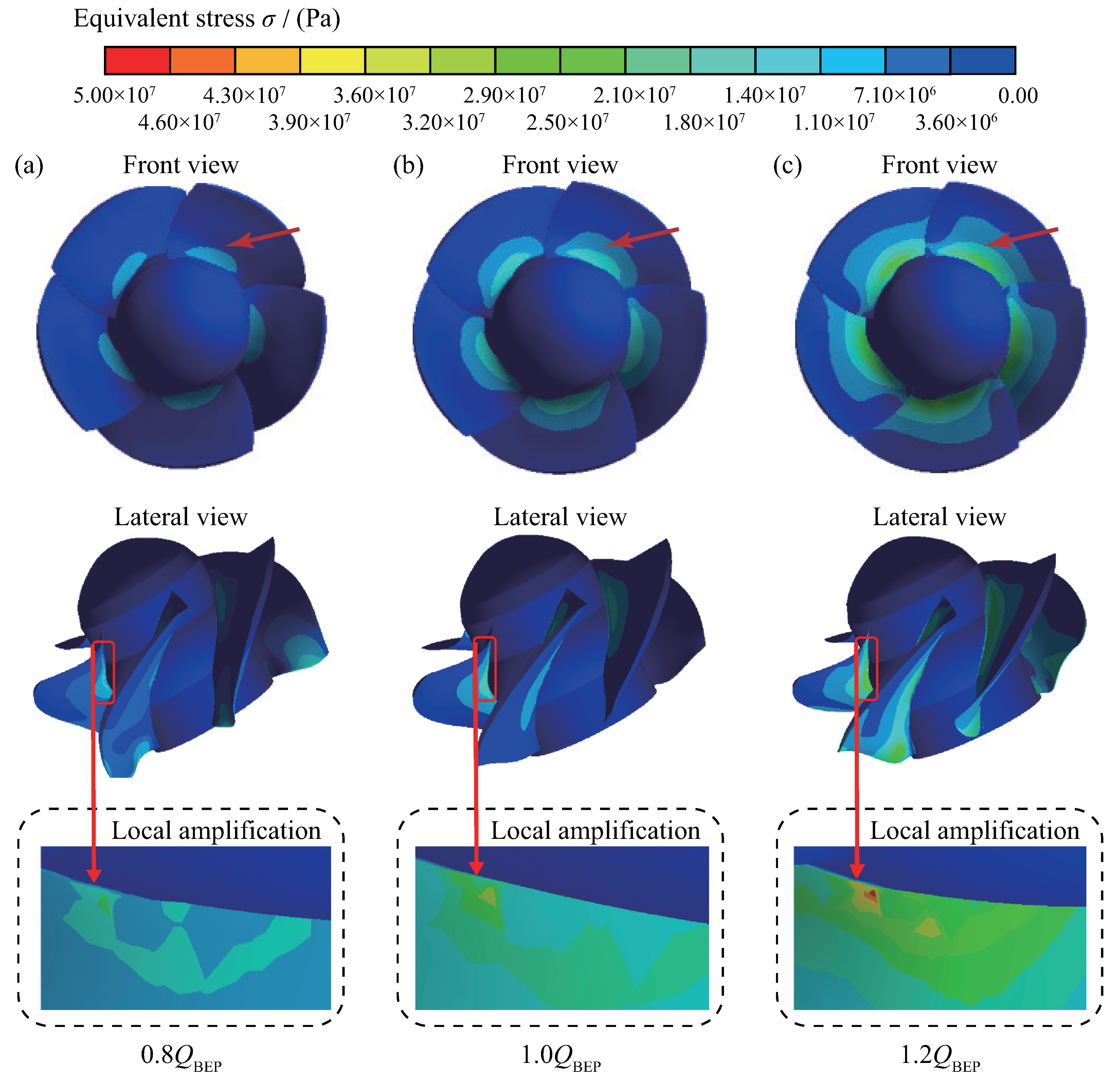
4.1.2. Equivalent Stress of Blades
4.2. Analysis of Fatigue Life of Impeller
4.2.1. Number of Stress Cycles
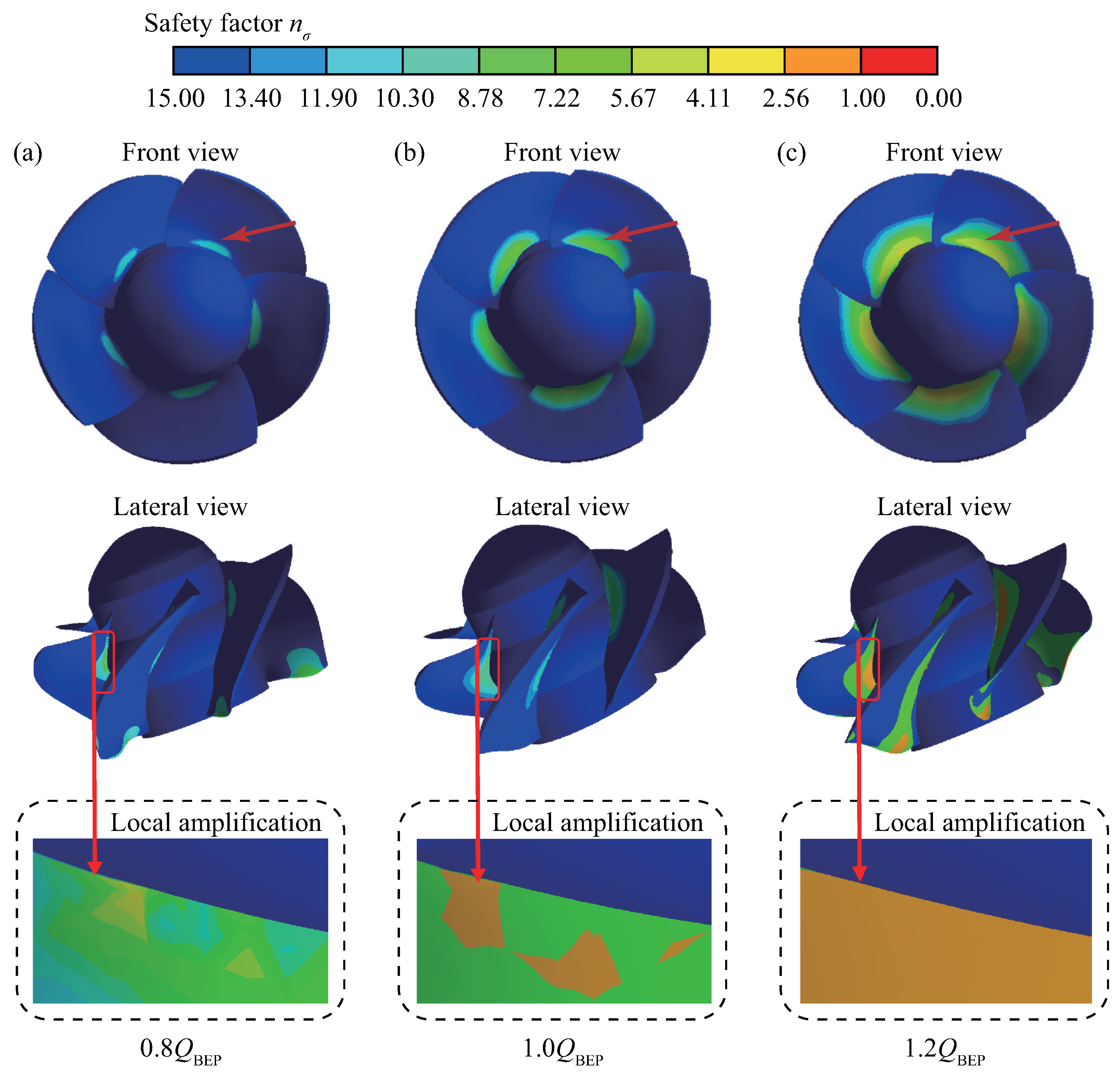
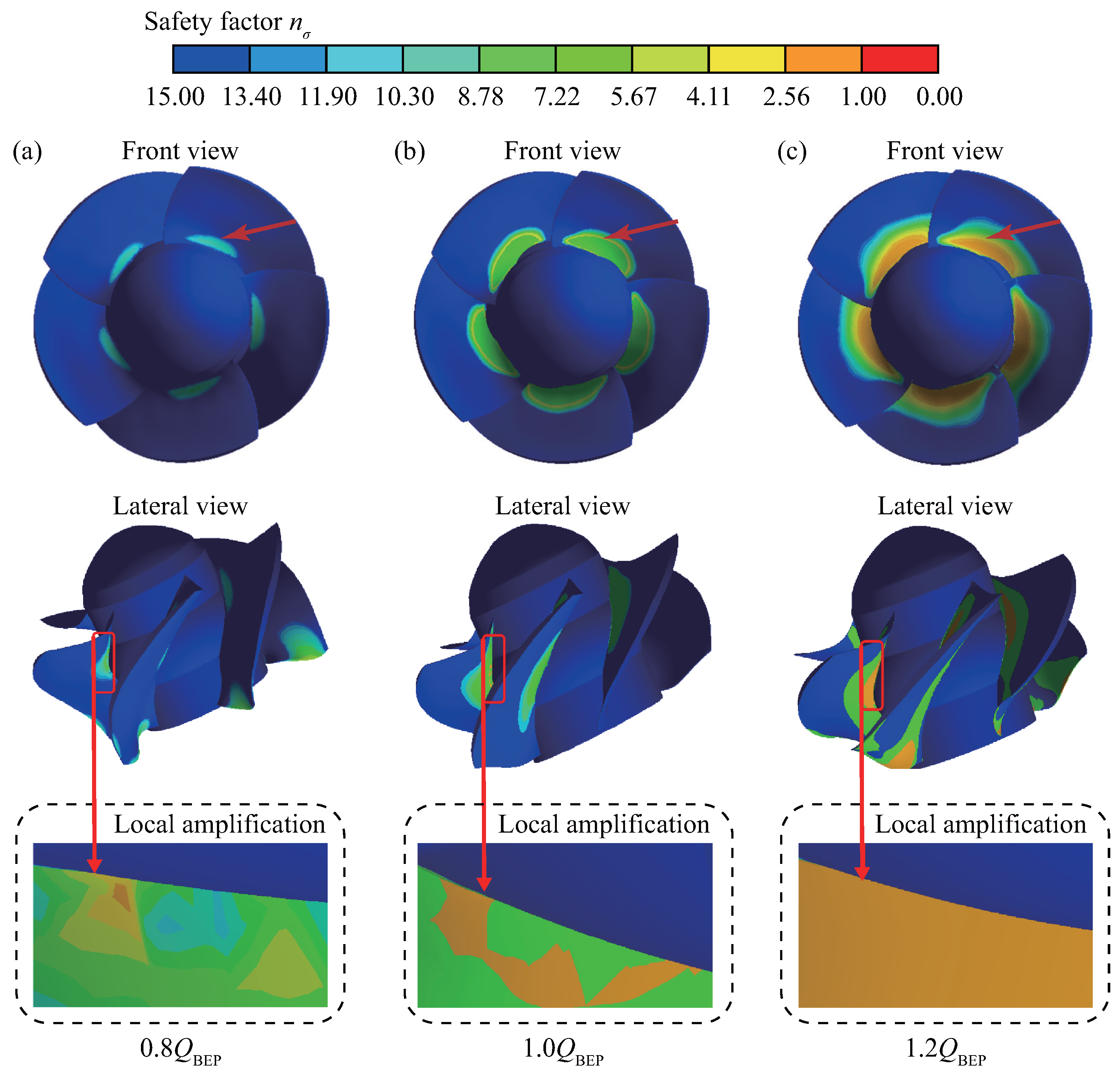
4.2.2. Blade Safety Factor
5. Conclusions
- (1)
- When the axial-flow pump device operates in both pump mode and PAT mode, the maximum blade deformation increases with the increasing flow rate. The deformation at the blade root can be neglected and the radial deflection gradient is small, while the deflection gradient increases gradually near the top of the blade. In comparison, the maximum deformation in the PAT mode is generally higher than that in the pump mode at all flow rates.
- (2)
- Under all operating conditions, the stress concentration phenomenon mainly occurs at the blade root, with the maximum equivalent stress at the impeller root occurring at the blade suction surface, and the stress gradually decreasing from the blade root to the blade edge. Comparing different flow rate conditions, the maximum equivalent stress of both modes occurs at a flow rate of . Under the same flow rate conditions, the equivalent stress in the PAT mode is relatively higher than in the pump mode.
- (3)
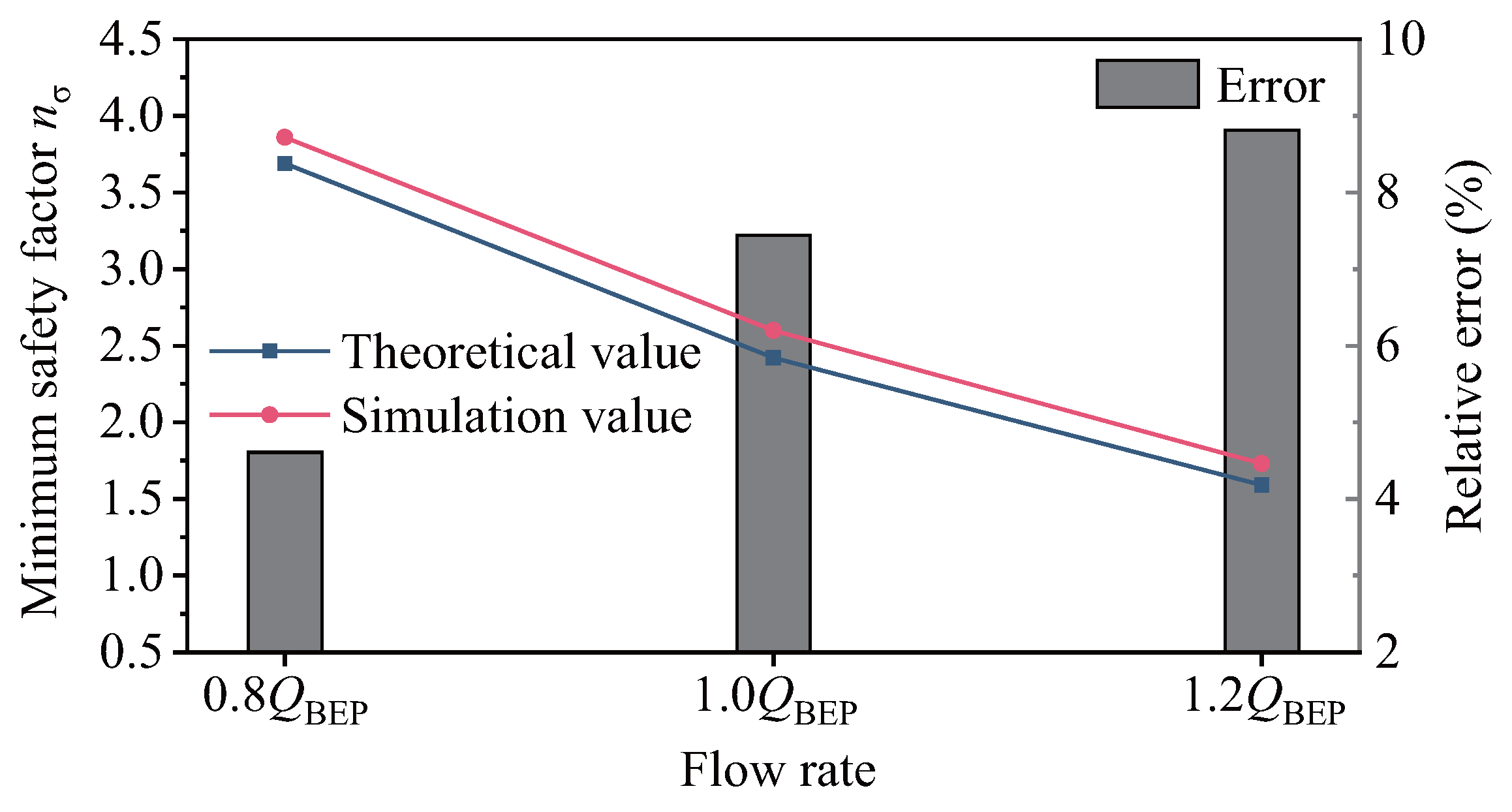
- The number of cycles of the impeller exceeds under all operating conditions, indicating that the load carrying capacity of the impeller is within the safe allowable range when the axial-flow pump device operates in both modes. The simulated impeller safety factor in the pump mode and the pump-turbine mode is slightly higher than the theoretical calculation value, which is reasonable. The minimum safety factor appears at the blade root, and the safety factor is smaller when operating in the PAT mode. Therefore, the blade root of the blade needs to be strengthened during processing to ensure the safe and stable operation of the pump device.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational fluid dynamics |
| FEM | Finite element method |
| FSI | Fluid–structure interaction |
| FFT | Fast Fourier transform |
| PAT | Pump as turbine |
| RNG | Re-normalization group |
| RANS | Reynolds-averaged Navier–Stokes |
| BEP | Best efficiency point |
| PS | Pressure surface |
| SS | Suction surface |
| LE | Leading edge |
| TE | Trailing edge |
| and | Velocity components in x, y and z direction |
| i and j | Directional indices for x, y and z |
| t | Physical time |
| Fluid density | |
| Fluid dynamic viscosity | |
| External force | |
| k | Turbulence kinetic energy |
| Turbulence dissipation rate | |
| , , and | Constants of the RNG model |
| Matrix of structure mass | |
| Matrix of structural damping | |
| Matrix of structural rigidity | |
| Nodal acceleration vector | |
| Nodal velocity vector | |
| Nodal displacement vector | |
| Fluid load vector | |
| Efficiency | |
| H | Head |
| D | Impeller diameter |
| Q | Flow rate |
| Rated flow rate | |
| n | Rotation speed |
| Rated rotation speed | |
| Deformation | |
| Equivalent stress | |
| , and | Principle stresses |
| Safety factor | |
| Fatigue limit | |
| Fatigue reduction coefficient | |
| Stress amplitude | |
| Safety allowance coefficient |
References
- Feng, J.; Luo, X.; Guo, P.; Wu, G. Influence of tip clearance on pressure fluctuations in an axial flow pump. J. Mech. Sci. Technol. 2016, 30, 1603–1610. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, W.; Jiao, H.; Tang, F.; Wang, L.; Sun, D.; Shi, W. Numerical simulation and experimental study on the comparison of the hydraulic characteristics of an axial-flow pump and a full tubular pump. Renew. Energy 2020, 153, 1455–1464. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, F.; Chen, Y.; Huang, C.; Chen, Y.; Wang, L.; Shi, L. Experimental study on the internal pressure pulsation characteristics of a bidirectional axial flow pump operating in forward and reverse directions. Machines 2022, 10, 167. [Google Scholar] [CrossRef]
- Abera, F.F.; Asfaw, D.H.; Engida, A.N.; Melesse, A.M. Optimal Operation of Hydropower Reservoirs under Climate Change: The Case of Tekeze Reservoir, Eastern Nile. Water 2018, 10, 273. [Google Scholar] [CrossRef]
- Xi, S.; Desheng, Z.; Bin, X.; Weidong, S.; van Esch, B.B. Experimental and numerical investigation on the effect of tip leakage vortex induced cavitating flow on pressure fluctuation in an axial flow pump. Renew. Energy 2021, 163, 1195–1209. [Google Scholar] [CrossRef]
- Kan, K.; Yang, Z.; Lyu, P.; Zheng, Y.; Shen, L. Numerical study of turbulent flow past a rotating axial-flow pump based on a level-set immersed boundary method. Renew. Energy 2021, 168, 960–971. [Google Scholar] [CrossRef]
- Shen, S.; Qian, Z.; Ji, B.; Agarwal, R.K. Numerical investigation of tip flow dynamics and main flow characteristics with varying tip clearance widths for an axial-flow pump. Proc. Inst. Mech. Eng. Part A J. Power Energy 2019, 233, 476–488. [Google Scholar] [CrossRef]
- Wang, C.; Wang, F.; Tang, Y.; Zi, D.; Xie, L.; He, C.; Zhu, Q.; Huang, C. Investigation into the phenomenon of flow deviation in the S-shaped discharge passage of a slanted axial-flow pumping system. J. Fluids Eng. 2020, 142, 041205. [Google Scholar] [CrossRef]
- Zhang, D.S.; Shi, W.D.; Bin, C.; Guan, X.F. Unsteady flow analysis and experimental investigation of axial-flow pump. J. Hydrodyn. Ser. B 2010, 22, 35–43. [Google Scholar] [CrossRef]
- Zhang, D.; Shi, W.; Van Esch, B.B.; Shi, L.; Dubuisson, M. Numerical and experimental investigation of tip leakage vortex trajectory and dynamics in an axial flow pump. Comput. Fluids 2015, 112, 61–71. [Google Scholar] [CrossRef]
- Keck, H.; Sick, M. Thirty years of numerical flow simulation in hydraulic turbomachines. Acta Mech. 2008, 201, 211–229. [Google Scholar] [CrossRef]
- Hübner, B.; Weber, W.; Seidel, U. The role of fluid-structure interaction for safety and life time prediction in hydraulic machinery. In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2016; Volume 49, p. 072007. [Google Scholar]
- Trivedi, C.; Cervantes, M.J. Fluid-structure interactions in Francis turbines: A perspective review. Renew. Sustain. Energy Rev. 2017, 68, 87–101. [Google Scholar] [CrossRef]
- Pei, J.; Meng, F.; Li, Y.; Yuan, S.; Chen, J. Fluid–structure coupling analysis of deformation and stress in impeller of an axial-flow pump with two-way passage. Adv. Mech. Eng. 2016, 8, 1687814016646266. [Google Scholar] [CrossRef]
- Liu, X.; Xu, F.; Cheng, L.; Pan, W.; Jiao, W. Stress Characteristics Analysis of Vertical Bi-Directional Flow Channel Axial Pump Blades Based on Fluid–Structure Coupling. Machines 2022, 10, 368. [Google Scholar] [CrossRef]
- Shi, L.; Zhu, J.; Wang, L.; Chu, S.; Tang, F.; Jin, Y. Comparative Analysis of Strength and Modal Characteristics of a Full Tubular Pump and an Axial Flow Pump Impellers Based on Fluid-Structure Interaction. Energies 2021, 14, 6395. [Google Scholar] [CrossRef]
- Zhang, D.; Pan, D.; Xu, Y.; Shao, P.; Wang, G. Numerical investigation of blade dynamic characteristics in an axial flow pump. Therm. Sci. 2013, 17, 1511–1514. [Google Scholar] [CrossRef]
- Gao, J.; Hou, Y.; Xi, S.; Cai, Z.; Yao, P.; Shi, H. Prediction of flow-induced dynamic stress in an axial pump impeller using FEM. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2013; Volume 52, p. 022041. [Google Scholar]
- Zhang, L.; Wang, S.; Yin, G.; Guan, C. Fluid–structure interaction analysis of fluid pressure pulsation and structural vibration features in a vertical axial pump. Adv. Mech. Eng. 2019, 11, 1687814019828585. [Google Scholar] [CrossRef]
- Kan, K.; Xu, Z.; Chen, H.; Xu, H.; Zheng, Y.; Zhou, D.; Muhirwa, A.; Maxime, B. Energy loss mechanisms of transition from pump mode to turbine mode of an axial-flow pump under bidirectional conditions. Energy 2022, 257, 124630. [Google Scholar] [CrossRef]
- Kan, K.; Zhang, Q.; Xu, Z.; Zheng, Y.; Gao, Q.; Shen, L. Energy loss mechanism due to tip leakage flow of axial flow pump as turbine under various operating conditions. Energy 2022, 255, 124532. [Google Scholar] [CrossRef]
- Singh, V.K.; Nath, T. Energy generation by small hydro power plant under different operating condition. Int. J. Hydromechatron. 2021, 4, 331–349. [Google Scholar] [CrossRef]
- Asomani, S.N.; Yuan, J.; Wang, L.; Appiah, D.; Zhang, F. Geometrical effects on performance and inner flow characteristics of a pump-as-turbine: A review. Adv. Mech. Eng. 2020, 12, 1687814020912149. [Google Scholar] [CrossRef]
- Kan, K.; Binama, M.; Chen, H.; Zheng, Y.; Zhou, D.; Su, W.; Muhirwa, A. Pump as turbine cavitation performance for both conventional and reverse operating modes: A review. Renew. Sustain. Energy Rev. 2022, 168, 112786. [Google Scholar] [CrossRef]
- Nautiyal, H.; Kumar, A. Reverse running pumps analytical, experimental and computational study: A review. Renew. Sustain. Energy Rev. 2010, 14, 2059–2067. [Google Scholar] [CrossRef]
- Meng, F.; Yuan, S.; Li, Y. Fluid–structure coupling analysis of impeller in unstable region for a reversible axial-flow pump device. Adv. Mech. Eng. 2018, 10, 1687814017751762. [Google Scholar] [CrossRef]
- Bai, Y.; Wu, D. Study on Fatigue Characteristics of Axial-Flow Pump Based on Two-Way Fluid–Structure Coupling. Energies 2022, 15, 8965. [Google Scholar] [CrossRef]
- Kan, K.; Chen, H.; Zheng, Y.; Zhou, D.; Binama, M.; Dai, J. Transient characteristics during power-off process in a shaft extension tubular pump by using a suitable numerical model. Renew. Energy 2021, 164, 109–121. [Google Scholar] [CrossRef]
- Li, Y.; Wang, F. Numerical investigation of performance of an axial-flow pump with inducer. J. Hydrodyn. 2007, 19, 705–711. [Google Scholar] [CrossRef]
- Shi, W.; Zhang, D.; Guan, X.; Leng, H. Numerical and experimental investigation of high-efficiency axial-flow pump. Chin. J. Mech. Eng. 2010, 23, 38–44. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, H. Numerical analysis of cavitation within slanted axial-flow pump. J. Hydrodyn. 2013, 25, 663–672. [Google Scholar] [CrossRef]
- Shi, L.; Yuan, Y.; Jiao, H.; Tang, F.; Cheng, L.; Yang, F.; Jin, Y.; Zhu, J. Numerical investigation and experiment on pressure pulsation characteristics in a full tubular pump. Renew. Energy 2021, 163, 987–1000. [Google Scholar] [CrossRef]
- Birajdar, R.; Keste, A. Prediction of flow-induced vibrations due to impeller hydraulic unbalance in vertical turbine pumps using one-way fluid- structure interaction. J. Vib. Eng. Technol. 2020, 8, 417–430. [Google Scholar] [CrossRef]
- Pei, J.; Yuan, S.; Yuan, J. Fluid-structure coupling effects on periodically transient flow of a single-blade sewage centrifugal pump. J. Mech. Sci. Technol. 2013, 27, 2015–2023. [Google Scholar] [CrossRef]
- Chen, X.; Zheng, Y.; Xu, J.; Zhang, Y.; Fernandez-Rodriguez, E.; Li, C.; Zhou, Y.; Jiang, T. Fatigue life study of francis pump under reverse generation condition based on fluid solid coupling. Water 2020, 12, 1162. [Google Scholar] [CrossRef]
- Balakrishna, A.; Mishra, P. Modelling and analysis of static and modal responses of leaf spring used in automobiles. Int. J. Hydromechatron. 2021, 4, 350–367. [Google Scholar] [CrossRef]





| Impeller Diameter D/(mm) | Rated Rotational Speed /(r/min) | Rated Flow Rate /(m/s) | Number of Impeller Blades | Number of Guide Vanes |
|---|---|---|---|---|
| 2350 | 166.7 | 16.67 | 5 | 8 |
| Scheme | Grid Size at Blade/(mm) | Number of Units | Number of Nodes | Ultimate Stress/(Mpa) | Maximum Offset/(mm) |
|---|---|---|---|---|---|
| I | 45 | 45,557 | 83,243 | 38.87 | 0.398 |
| II | 35 | 74,511 | 133,740 | 43.86 | 0.412 |
| III | 25 | 145,001 | 255,622 | 47.92 | 0.413 |
| IV | 15 | 322,237 | 557,320 | 49.93 | 0.408 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Cai, Z.; Zheng, Y.; Feng, J.; Xu, H.; Chen, H.; Binama, M.; Kan, K. Investigation of Structural Strength and Fatigue Life of Rotor System of a Vertical Axial-Flow Pump under Full Operating Conditions. Water 2023, 15, 3041. https://doi.org/10.3390/w15173041
Li H, Cai Z, Zheng Y, Feng J, Xu H, Chen H, Binama M, Kan K. Investigation of Structural Strength and Fatigue Life of Rotor System of a Vertical Axial-Flow Pump under Full Operating Conditions. Water. 2023; 15(17):3041. https://doi.org/10.3390/w15173041
Chicago/Turabian StyleLi, Haoyu, Zhizhou Cai, Yuan Zheng, Jiangang Feng, Hui Xu, Huixiang Chen, Maxime Binama, and Kan Kan. 2023. "Investigation of Structural Strength and Fatigue Life of Rotor System of a Vertical Axial-Flow Pump under Full Operating Conditions" Water 15, no. 17: 3041. https://doi.org/10.3390/w15173041
APA StyleLi, H., Cai, Z., Zheng, Y., Feng, J., Xu, H., Chen, H., Binama, M., & Kan, K. (2023). Investigation of Structural Strength and Fatigue Life of Rotor System of a Vertical Axial-Flow Pump under Full Operating Conditions. Water, 15(17), 3041. https://doi.org/10.3390/w15173041










