Assessment of Empirical Methods for Estimating Reference Evapotranspiration in Different Climatic Zones of Bosnia and Herzegovina
Abstract
:1. Introduction
- -
- The FAO (Food and Agriculture Organization), the FAO Expert Group on the Revision of Methods for Calculating Plant Water Requirements, which issued a publication called “FAO Irrigation and Drainage paper 56” and adopted grass as a reference crop.
- -
- The ASCE-EWRI (American Association of Civil Engineers—Institute for Water Resources and the Environment), the Committee for Standardization of Reference Evapotranspiration, which issued a report on standardized ETo and adopted alfalfa as a reference crop.
2. Materials and Methods
2.1. Weather Data Acquisition and Description
2.2. Data Quality Analysis, Elaboration, and Adjustment
2.2.1. Data Quality Analysis
2.2.2. Missing Data
2.2.3. Solar Radiation Data Analysis and Correction
2.3. Methods Used to Estimate Reference Evapotranspiration (ETo)
2.3.1. FAO Penman–Monteith Method (FAO-PM)
2.3.2. Hargreaves–Samani Method (HS)
2.3.3. Modified Hargreaves–Samani Method
2.3.4. Calibrated Hargreaves–Samani Method (HC)
2.3.5. Priestley–Taylor Method (PT)
2.3.6. Makkink Method (MAK)
2.3.7. Copais Method (COP)
2.3.8. Penman–Monteith Method with Limited Data Availability—Based on Air Temperature Data (PMT)
Penman–Monteith Method Based on Air Temperature and Overall Average Windspeed (PMT2)
Penman–Monteith Method Based on Air Temperature and Regional Average Windspeed (PMT1.3)
Penman–Monteith Method Based on Air Temperature and Site-Specific Windspeed (PMTlok)
2.4. Statistical Evaluation of the Methods’ Performance
2.4.1. TOPSIS Ranking Method
- 1.
- Constructing the normalized decision matrix to convert various attribute dimensions to nondimensional ones. Elements of the normalized decision matrix are calculated as follows:
- 2.
- Constructing a weighted normalized decision matrix. A weighted normalized decision matrix is obtained by multiplying the values in the columns of the normalized matrix by the corresponding criterion’s weight.
- 3.
- The identification of the best (“ideal solution”, A*) and the worst (“negative—ideal solution”, A−) values in each column.
- 4.
- Computing the separation measure.
- 5.
- Calculating relative closeness to ideal solution.
- 6.
- Ranking alternatives. The best-ranked alternative has the value of Qi* closest to 1.
2.4.2. Mann–Kendall Test (MK)
2.4.3. Sen’s Slope Evaluation
3. Results
3.1. Correction of Solar Radiation Data
3.2. Calibrated Hargreaves–Samani Method (HC)
3.3. The Performance of Empirical Methods for ETo Estimation
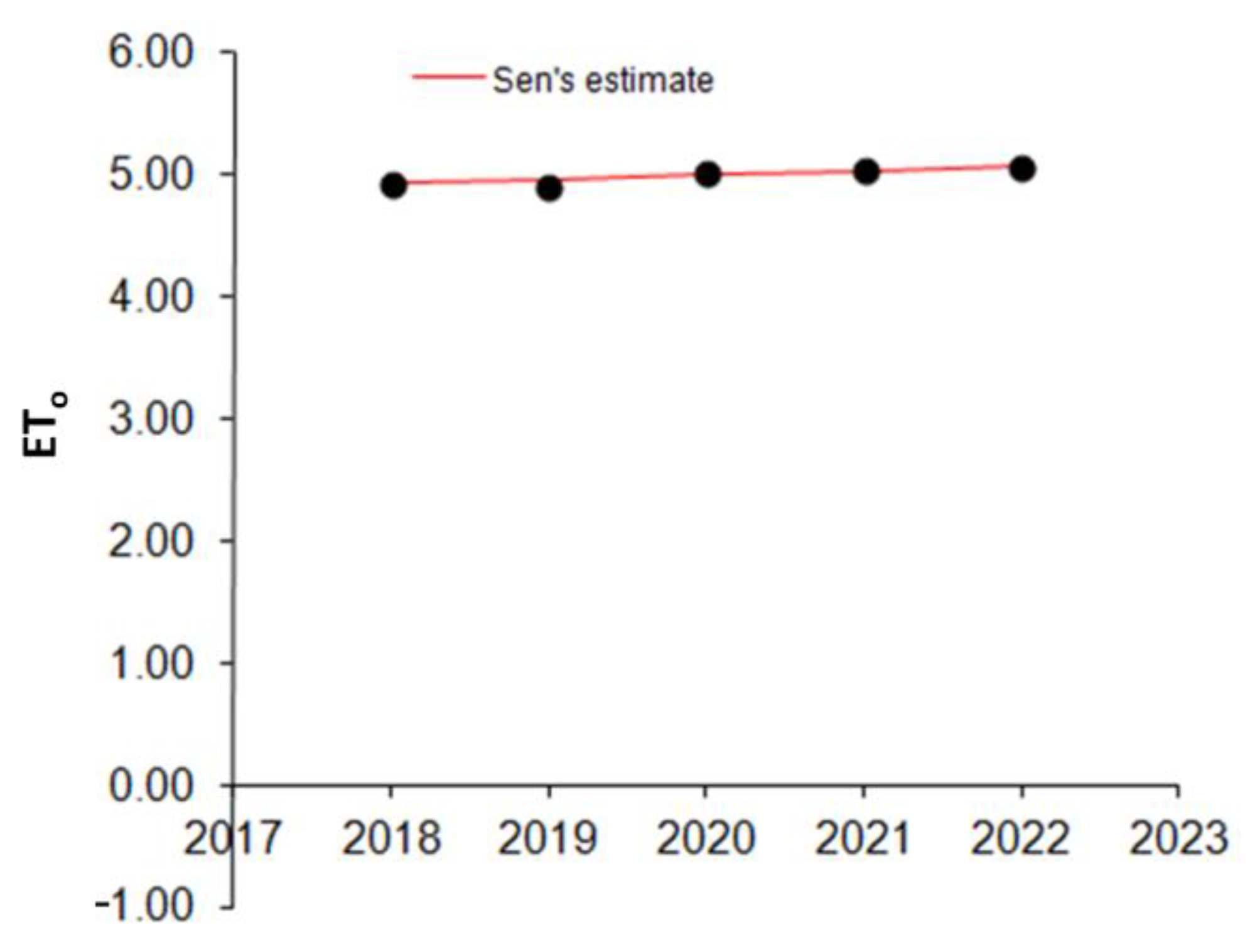
3.4. Mann–Kendall Test Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Method/Station | Bijeljina | Višegrad | Grančarevo | Trebinje | Mostar | Sum of Ranks | Ranking Based on the Sum of Ranks |
|---|---|---|---|---|---|---|---|
| HS | 9 | 5 | 3 | 1 | 1 | 19 | 3 |
| HM | 1 | 8 | 7 | 8 | 8 | 32 | 7 |
| HC | 4 | 3 | 1 | 2 | 2 | 12 | 1 |
| PT | 7 | 7 | 6 | 4 | 4 | 28 | 6 |
| MAK | 5 | 9 | 8 | 6 | 6 | 34 | 8 |
| COP | 8 | 4 | 9 | 9 | 9 | 39 | 9 |
| PMT2 | 6 | 2 | 2 | 3 | 3 | 16 | 2 |
| PMT1.3 | 3 | 6 | 5 | 5 | 5 | 24 | 5 |
| PMTlok | 2 | 1 | 4 | 7 | 7 | 21 | 4 |
Appendix B
| Method/Station | DO | BI | TU | JA | BL | PR | NG | SM | SO | GA | ZE | BU | SA | LO | SB | Sum of Ranks | Ranking Based on the Sum of Ranks |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HS | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 8 | 9 | 9 | 7 | 9 | 9 | 132 | 9 |
| HM | 1 | 3 | 3 | 3 | 5 | 1 | 2 | 2 | 7 | 5 | 3 | 2 | 3 | 3 | 2 | 45 | 2 |
| HC | 2 | 4 | 2 | 4 | 8 | 2 | 1 | 1 | 4 | 6 | 2 | 3 | 5 | 4 | 3 | 51 | 3 |
| PT | 6 | 2 | 4 | 1 | 1 | 6 | 6 | 5 | 2 | 1 | 1 | 1 | 1 | 6 | 1 | 44 | 1 |
| MAK | 3 | 1 | 1 | 5 | 6 | 4 | 3 | 6 | 1 | 4 | 6 | 4 | 8 | 1 | 6 | 59 | 4 |
| COP | 8 | 8 | 7 | 2 | 2 | 8 | 7 | 4 | 3 | 2 | 5 | 5 | 6 | 7 | 7 | 81 | 7 |
| PMT2 | 7 | 7 | 8 | 8 | 7 | 7 | 8 | 8 | 8 | 7 | 8 | 7 | 2 | 6 | 8 | 106 | 8 |
| PMT1.3 | 5 | 5 | 6 | 6 | 3 | 5 | 4 | 3 | 6 | 3 | 4 | 6 | 9 | 5 | 5 | 75 | 5 |
| PMTlok | 4 | 6 | 5 | 7 | 4 | 3 | 5 | 7 | 5 | 9 | 7 | 7 | 4 | 2 | 4 | 79 | 6 |
Appendix C
| Method/Zone | DSH Zone Method Ranking | MSH Zone Method Ranking |
|---|---|---|
| HS | 3 | 9 |
| HM | 7 | 2 |
| HC | 1 | 3 |
| PT | 6 | 1 |
| MAK | 8 | 4 |
| COP | 9 | 7 |
| PMT2 | 2 | 8 |
| PMT1.3 | 5 | 5 |
| PMTlok | 4 | 6 |
Appendix D
| Method/Station | Bijeljina | Višegrad | Trebinje | Mostar | Sum of Ranks | Ranking Based on the Sum of Ranks |
|---|---|---|---|---|---|---|
| HS | 9 | 3 | 2 | 5 | 19 | 5 |
| HM | 3 | 8 | 9 | 9 | 29 | 9 |
| HC | 4 | 2 | 1 | 4 | 11 | 1 |
| PT | 6 | 9 | 3 | 1 | 19 | 4 |
| MAK | 1 | 7 | 6 | 8 | 22 | 7 |
| COP | 7 | 4 | 4 | 3 | 18 | 3 |
| PMT2 | 8 | 1 | 5 | 6 | 20 | 6 |
| PMT1.3 | 5 | 6 | 7 | 7 | 25 | 8 |
| PMTlok | 2 | 5 | 8 | 2 | 17 | 2 |
Appendix E
| Method/Station | Banja Luka | Gacko | Sum of Ranks | Ranking Based on the Sum of Ranks |
|---|---|---|---|---|
| HS | 9 | 5 | 14 | 7 |
| HM | 5 | 8 | 13 | 6 |
| HC | 3 | 1 | 4 | 1 |
| PT | 4 | 4 | 8 | 4 |
| MAK | 8 | 7 | 15 | 8–9 |
| COP | 6 | 9 | 15 | 8–9 |
| PMT2 | 7 | 2 | 9 | 5 |
| PMT1.3 | 2 | 3 | 5 | 2 |
| PMTlok | 1 | 6 | 7 | 3 |
Appendix F
| Method/Station | DO | BI | TU | PR | NG | SM | SO | ZE | BU | SA | Sum of Ranks | Ranking Based on the Sum of Ranks |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HS | 9 | 9 | 9 | 8 | 9 | 9 | 9 | 9 | 9 | 6 | 86 | 9 |
| HM | 5 | 6 | 4 | 4 | 4 | 1 | 6 | 3 | 4 | 4 | 41 | 5 |
| HC | 2 | 3 | 2 | 3 | 3 | 2 | 3 | 2 | 2 | 3 | 25 | 1 |
| PT | 6 | 1 | 6 | 6 | 6 | 5 | 1 | 1 | 1 | 1 | 34 | 3 |
| MAK | 4 | 5 | 1 | 1 | 1 | 4 | 2 | 5 | 3 | 7 | 33 | 2 |
| COP | 8 | 8 | 8 | 9 | 8 | 7 | 8 | 7 | 8 | 8 | 79 | 8 |
| PMT2 | 7 | 7 | 7 | 7 | 7 | 8 | 7 | 8 | 7 | 5 | 70 | 7 |
| PMT1.3 | 3 | 2 | 5 | 5 | 5 | 3 | 5 | 4 | 5 | 9 | 46 | 6 |
| PMTlok | 1 | 4 | 3 | 2 | 2 | 6 | 4 | 6 | 6 | 2 | 36 | 4 |
Appendix G
| Method/Zone | SA Zone Method Ranking | DSH Zone Method Ranking | MSH Zone Method Ranking |
|---|---|---|---|
| HS | 4 | 7 | 9 |
| HM | 9 | 6 | 5 |
| HC | 1 | 1 | 1 |
| PT | 4 | 4 | 3 |
| MAK | 7 | 8–9 | 2 |
| COP | 3 | 8–9 | 8 |
| PMT2 | 6 | 5 | 7 |
| PMT1.3 | 8 | 2 | 6 |
| PMTlok | 2 | 3 | 4 |
References
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and drainage paper 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; Volume 56, p. 300. [Google Scholar]
- Baldocchi, D. ‘Breathing’ of the terrestrial biosphere: Lessons learned from a global network of carbon dioxide flux measurement systems. Aust. J. Bot. 2008, 56, 1–26. [Google Scholar] [CrossRef]
- Hill, T.; Chocholek, M.; Clement, R. The case for increasing the statistical power of eddy covariance ecosystem studies: Why, where and how? Glob. Chang. Biol. 2017, 23, 2154–2165. [Google Scholar] [CrossRef] [PubMed]
- Cunliffe, A.M.; Boschetti, F.; Clement, R.; Sitch, S.; Anderson, K.; Duman, T.; Zhu, S.; Schlumpf, M.; Litvak, M.E.; Brazier, R.E.; et al. Strong correspondence in evapotranspiration and carbon dioxide fluxes between different eddy covariance systems enables quantification of landscape heterogeneity in dryland fluxes. J. Geophys. Res. Biogeosci. 2022, 127, e2021JG006240. [Google Scholar] [CrossRef]
- Schrader, F.; Durner, W.; Fank, J.; Gebler, S.; Pütz, T.; Hannes, M.; Wollschläger, U. Estimating Precipitation and Actual Evapotranspiration from Precision Lysimeter Measurements. J. Procedia Environ. Sci. 2013, 19, 543–552. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; Hunsaker, D.J.; López-Urrea, R.; Mohammadi Shad, Z. Standard Single and Basal Crop Coefficients for Field Crops. Updates and Advances to the FAO56 Crop Water Requirements Method. Agric. Water Manag. 2021, 243, 106466. [Google Scholar] [CrossRef]
- Rallo, G.; Paço, T.A.; Paredes, P.; Puig-Sirera, À.; Massai, R.; Provenzano, G.; Pereira, L.S. Updated single and dual crop coefficients for tree and vine fruit crops. Agric. Water Manag. 2021, 250, 106645. [Google Scholar] [CrossRef]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, N.S.; Singh, R. Evaluation of Variable-Infiltration Capacity Model and MODIS-Terra Satellite-Derived Grid-Scale Evapotranspiration Estimates in a River Basin with Tropical Monsoon-Type Climatology. J. Irrig. Drain. Eng. 2017, 143, 04017028. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Kumari, N.; Dharpure, J.K.; Mokhtar, A.; Alsafadi, K.; Kumar, M.; Mehdinejadiani, B.; Etedali, H.R.; Brouziyne, Y.; Towfiqul Islam, A.R.M.; et al. Prediction of Combined Terrestrial Evapotranspiration Index (CTEI) over Large River Basin Based on Machine Learning Approaches. Water 2021, 13, 547. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; López-Urrea, D.; Jovanovic, N. Updates and advances to the FAO56 crop water requirements method. Agric. Water Manag. 2021, 248, 106697. [Google Scholar] [CrossRef]
- Allen, R.; Dhungel, R.; Dhungana, B.; Huntington, J.; Kilic, A.; Morton, C. Conditioning point and gridded weather data under aridity conditions for calculation of reference evapotranspiration. Agric. Water Manag. 2020, 245, 106531. [Google Scholar] [CrossRef]
- Blankenau, P.A.; Kilic, A.; Allen, R. An evaluation of gridded weather data sets for the purpose of estimating reference evapotranspiration in the United States. Agric. Water Manag. 2020, 242, 106376. [Google Scholar] [CrossRef]
- Paredes, P.; Pereira, L.S.; Almorox, J.; Darouich, H. Reference grass evapotranspiration with reduced data sets: Parameterization of the FAO Penman-Monteith temperature approach and the Hargeaves-Samani equation using local climatic variables. Agric. Water Manag. 2020, 240, 106210. [Google Scholar] [CrossRef]
- Paredes, P.; Trigo, I.; de Bruin, H.; Simões, N.; Pereira, L.S. Daily grass reference evapotranspiration with Meteosat Second Generation shortwave radiation and reference ET products. Agric. Water Manag. 2021, 248, 106543. [Google Scholar] [CrossRef]
- Čadro, S.; Uzunovic, M.; Cherni-Čadro, S.; Žurovec, J. Changes in the Water Balance of Bosnia and Herzegovina as a Result of Climate Change. Agric. For. 2019, 65, 19–32. [Google Scholar] [CrossRef]
- Tegos, A.; Stefanidis, S.; Cody, J.; Koutsoyiannis, D. On the Sensitivity of Standardized-Precipitation-Evapotranspiration and Aridity Indexes Using Alternative Potential Evapotranspiration Models. Hydrology 2023, 10, 64. [Google Scholar] [CrossRef]
- Wang, W.; Guo, B.; Zhang, Y.; Zhang, L.; Ji, M.; Xu, Y.; Zhang, X.; Zhang, Y. The sensitivity of the SPEI to potential evapotranspiration and precipitation at multiple timescales on the Huang-Huai-Hai Plain, China. Theor. Appl. Climatol. 2021, 143, 87–99. [Google Scholar] [CrossRef]
- Ortiz-Gómez, R.; Flowers-Cano, R.S.; Medina-García, G. Sensitivity of the RDI and SPEI Drought Indices to Different Models for Estimating Evapotranspiration Potential in Semiarid Regions. Water Resour. Manag. 2022, 36, 2471–2492. [Google Scholar] [CrossRef]
- Čadro, S.; Uzunović, M.; Žurovec, J.; Žurovec, O. Validation and calibration of various reference evapotranspiration alternative methods under the climate conditions of Bosnia and Herzegovina. Int. Soil Water Conserv. Res. 2017, 5, 309–324. [Google Scholar] [CrossRef]
- Pandey, P.K.; Nyori, T.; Pandey, V. Estimation of reference evapotranspiration using data driven techniques under limited data conditions. Model. Earth Syst. Environ. 2017, 3, 1449–1461. [Google Scholar] [CrossRef]
- Jayashree, T.R.; Subba Reddy, N.V.; Dinesh Acharya, U. Modeling Daily Reference Evapotranspiration from Climate Variables: Assessment of Bagging and Boosting Regression Approaches. Water Resour. Manag. 2023, 37, 1013–1032. [Google Scholar] [CrossRef]
- Idrizović, D.F.; Matović, S.G.; Gregorić, N.E.; Stričević, J.R. Analysis of seven indirect methods for evaluation of reference evapotranspiration under climate conditions of Serbia. J. Agric. Sci. 2018, 63, 67–81. [Google Scholar] [CrossRef]
- Droogers, P.; Allen, R.G. Estimating reference evapotranspiration under inaccurate data conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Awal, R.; Rahman, A.; Habibi, H.; Fares, A.; Habibi, H. Calibration and Evaluation of Empirical Methods to Estimate Reference Crop Evapotranspiration in West Texas. Water 2022, 14, 3032. [Google Scholar] [CrossRef]
- Dimitriadou, S.; Nikolakopoulos, K.G. Multiple Linear Regression Models with Limited Data for the Prediction of Reference Evapotranspiration of the Peloponnese, Greece. Hydrology 2022, 9, 124. [Google Scholar] [CrossRef]
- Todorovic, M. Single-layer evapotranspiration model with variable canopy resistance. J. Irrig. Drain. Eng. 1999, 125, 235–245. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.-L.; Sun, X.; Bi, Y. Temporal upscaling of instantaneous evapotranspiration on clear-sky days using the constant reference evaporative fraction method with fixed or variable surface resistances at two cropland sites. J. Geophys. Res. Atmos. 2017, 122, 784–801. [Google Scholar] [CrossRef]
- Zhu, B.; Feng, Y.; Gong, D.; Jiang, S.; Zhao, L.; Cui, N. Hybrid particle swarm optimization with extreme learning machine for daily reference evapotranspiration prediction from limited climatic data. Comput. Electron. Agric. 2020, 173, 105430. [Google Scholar] [CrossRef]
- Gocić, M.; Amiri, M.A. Reference evapotranspiration prediction using neural networks and optimum time lags. Water Resour. Manag. 2021, 35, 1913–1926. [Google Scholar] [CrossRef]
- Fan, J.; Yue, W.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Xiang, Y. Evaluation of SVM, ELM and four tree-based ensemble models for predicting daily reference evapotranspiration using limited meteorological data in different climates of China. Agric. For. Meteorol. 2018, 263, 225–241. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Nagy, A.; Mohammed, S.; Pande, C.B.; Kumar, M.; Bhat, S.A.; Zsembeli, J.; Huzsvai, L.; Tamás, J.; Kovács, E.; et al. Combination of Limited Meteorological Data for Predicting Reference Crop Evapotranspiration Using Artificial Neural Network Method. Agronomy 2022, 12, 516. [Google Scholar] [CrossRef]
- Chakraborty, S. TOPSIS and Modified TOPSIS: A comparative analysis. Decis. Anal. J. 2022, 2, 100021. [Google Scholar] [CrossRef]
- Meshram, S.G.; Alvandi, E.; Meshram, C.; Kahya, E.; Al-Quraishi, F.; Ayad, M. Application of SAW and TOPSIS in Prioritizing Watersheds. Water Resour. Manag. 2020, 34, 715–732. [Google Scholar] [CrossRef]
- Shadmani, M.; Marofi, S.; Roknian, M. Trend Analysis in Reference Evapotranspiration Using Mann-Kendall and Spearman’s Rho Tests in Arid Regions of Iran. Water Resour. Manag. 2012, 26, 211–224. [Google Scholar] [CrossRef]
- Agency for Statistics of Bosnia and Herzegovina (BHAS). Bosnia and Herzegovina in Figures—Statistical Bulletin; Agency for Statistics of Bosnia and Herzegovina (BHAS): Sarajevo, Bosnia and Herzegovina, 2013. [Google Scholar]
- European Union. European Union, Copernicus Land Monitoring Service 2018, European Environment Agency (EEA). Available online: https://land.copernicus.eu/faq/ (accessed on 5 February 2023).
- European Environment Agency. Land Cover 2012, Bosnia and Herzegovina. 2017. Available online: https://www.eea.europa.eu/themes/landuse/land-cover-country-fact-sheets/land-cover-country-fact-sheets-2012/ba-bosnia-and-herzegovina-landcover-2012.pdf (accessed on 25 April 2023).
- Todorovic, M.; Karic, B.; Pereira, L.S. Reference evapotranspiration estimate with limited weather data across a range of Mediterranean climates. J. Hydrol. 2013, 481, 166–176. [Google Scholar] [CrossRef]
- Zomer, R.J.; Xu, J.; Trabucco, A. Version 3 of the Global Aridity Index and Potential Evapo-transpiration Database. Sci. Data 2022, 9, 409. [Google Scholar] [CrossRef]
- Nastos, P.T.; Politi, N.; Kapsomenakis, J. Spatial and temporal variability of the aridity index in Greece. Atmos. Res. 2013, 119, 140–152. [Google Scholar] [CrossRef]
- Allen, R.G. Assessing integrity of weather data for use in reference evapotranspiration of estimation. J. Irrig. Drain. Eng. 1996, 122, 97–106. [Google Scholar] [CrossRef]
- Trajkovic, S. Hargreaves versus Penman-Monteith under humid conditions. J. Irrig. Drain. Eng. 2007, 133, 38–42. [Google Scholar] [CrossRef]
- Trajković, S. A simple empirical formula for the calculation of reference evapotranspiration. Vodoprivreda 2007, 39, 397–400. [Google Scholar]
- Makkink, G.F. Testing the penman formula by means of lysimeters. J. Inst. Water Eng. 1957, 11, 277–288. [Google Scholar]
- Alexandris, S.; Kerkides, P.; Liakatas, A. Daily reference evapotranspiration estimates by the “Copais” approach. Agric. Water Manag. 2006, 82, 371–386. [Google Scholar] [CrossRef]
- Celestin, S.; Qi, F.; Li, R.; Yu, T.; Cheng, W. Evaluation of 32 Simple Equations against the Penman–Monteith Method to Estimate the Reference Evapotranspiration in the Hexi Corridor, Northwest China. Water 2020, 12, 2772. [Google Scholar] [CrossRef]
- Ndiaye, P.M.; Bodian, A.; Diop, L.; Deme, A.; Dezetter, A.; Djaman, K. Evaluation and Calibration of Alternative Methods for Estimating Reference Evapotranspiration in the Senegal River Basin. Hydrology 2020, 7, 24. [Google Scholar] [CrossRef]
- Zakwan, M.; Niazkar, M. Chapter 33—Innovative triangular trend analysis of monthly precipitation at Shiraz Station, Iran. In Current Directions in Water Scarcity Research; Elsevier: Amsterdam, The Netherlands, 2022; Volume 7, pp. 589–598. [Google Scholar] [CrossRef]
- Salmi, T.; Määttä, A.; Anttila, P.; Ruoho-Airola, T.; Amnell, T. Detecting trends of annual values of atmospheric pollutants by the Mann-Kendall test and Sen’s slope estimates – the excel template application MAKESENS; Finish Meteorological Institute: Helsinki, Finland, 2002; p. 35. ISBN 951 – 697 – 563 – 1.
- World Meteorological Organization. Guide to Climatological Practices, 2nd ed.; WMO: Geneva, Switzerland, 2018. [Google Scholar]
- Aditya, F.; Gusmayanti, E.; Sudrajat, J. Rainfall trend analysis using Mann-Kendall and Sen’s slope estimator test in West Kalimantan. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 893, p. 012006. [Google Scholar] [CrossRef]
- Koudahe, K.; Djaman, K.; Adewumi, J.K. Evaluation of the Penman–Monteith reference evapotranspiration under limited data and its sensitivity to key climatic variables under humid and semiarid conditions. Model. Earth Syst. Environ. 2018, 4, 1239–1257. [Google Scholar] [CrossRef]
- Martel, M.; Glenn, A.; Wilson, H.; Krobel, R. Simulation of actual evapotranspiration from agricultural landscapes in the Canadian Prairies. J. Hydrol. Reg. Stud. 2018, 15, 105–118. [Google Scholar] [CrossRef]
- Ndulue, E.; Onyekwelu, I.; Ogbu, K.N.; Ogwo, V. Performance evaluation of solar radiation equations for estimating reference evapotranspiration (ETo) in a humid tropical environment. J. Water Land Dev. 2019, 42, 124–135. Available online: https://api.semanticscholar.org/CorpusID:198963774 (accessed on 20 February 2023). [CrossRef]
- Awal, R.; Habibi, H.; Fares, A.; Deb, S. Estimating reference crop evapotranspiration under limited climate data in West Texas. J. Hydrol. Reg. Stud. 2020, 28, 100677. [Google Scholar] [CrossRef]
- Valero, J.F.M.; Álvarez, V.M.; Real, M.M.G. Regionalization of the Hargreaves coefficient to estimate long-term reference evapotranspiration series in SE Spain. Span. J. Agric. Res. 2013, 11, 1137–1152. [Google Scholar] [CrossRef]
- Rodrigues, G.C.; Braga, R.P. Estimation of Reference Evapotranspiration during the Irrigation Season Using Nine Temperature-Based Methods in a Hot-Summer Mediterranean Climate. Agriculture 2021, 11, 124. [Google Scholar] [CrossRef]
- Trajkovic, S. Temperature-based approaches for estimating reference evapotranspiration. J. Irrig. Drain. Eng. 2005, 131, 316–323. [Google Scholar] [CrossRef]
- Trajković, S.; Živković, S. Effect of actual vapor pressure on estimating evapotranspiration at Serbia. Facta Univ. Ser. Archit. Civ. Eng. 2009, 7, 7171–7178. [Google Scholar] [CrossRef]
- Lobit, P.; López Pérez, L.; Lhomme, J.P. Retrieving air humidity, global solar radiation, and reference evapotranspiration from daily temperatures: Development and validation of new methods for Mexico. Part II: Radiation. Theor. Appl. Climatol. 2018, 133, 799–810. [Google Scholar] [CrossRef]
- Burn, D.H.; Hesch, N.M. Trends in evaporation for the Canadian Prairies. J. Hydrol. 2007, 336, 61–73. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Bhadra, A.; Raghuwanshi, N.S.; Singh, R. Temporal trends in estimates of reference evapotranspiration over India. J. Hydrol. Eng. 2009, 14, 508–515. [Google Scholar] [CrossRef]
- Alexandris, S.; Stricevic, R.; Petkovic, S. Comparative analysis of reference evapotranspiration from the surface of rainfed grass in central Serbia, calculated by six empirical methods against the Penman-Monteith formula. Eur. Water 2008, 21, 17–28. [Google Scholar]
- Trajkovic, S.; Kolakovic, S. Evaluation of reference evapotranspiration equation under humid conditions. Water Resour. Manag. 2009, 23, 3057–3067. [Google Scholar] [CrossRef]
- Tabari, H. Evaluation of reference crop evapotranspiration equations in various climates. Water Resour. Manag. 2010, 24, 2311–2337. [Google Scholar] [CrossRef]
- Berti, A.; Tardivo, G.; Chiaudani, A.; Rech, F.; Borin, M. Assessing reference evapotranspiration by the Hargreaves method in north-eastern Italy. Agric. Water Manag. 2014, 140, 20–25. [Google Scholar] [CrossRef]
- Itenfisu, D.; Elliot, R.L.; Allen, R.G.; Walter, I.A. Comparison of reference evapotranspiration calculation as part of ASCE standardization effort. J. Irrig. Drain. Eng. 2003, 129, 440–448. [Google Scholar] [CrossRef]
- Vanderlinden, K.; Giráldez, J.V.; Meirvenne, M.V. Assessing reference evapotranspiration by the Hargreaves method in Southern Spain. J. Irrig. Drain. Eng. 2004, 130, 184–191. [Google Scholar] [CrossRef]
- Allen, R.G. Evaluation of a Temperature Difference Method for Computing Grass Reference Evapotranspiration; UN-FAO Water Resources Development and Management Service, Land and Water Dev: Rome, Italy, 1993; p. 50. [Google Scholar]
- Trajkovic, S. Estimating Reference Evapotranspiration at French Humid Locations by Modified Hargeaves Method; International Conference BALWOIS, Topic 2; Hydrological Regimes and Water Balances: Ohrid, Republic of Macedonia, 2004. [Google Scholar]
- Trajkovic, S.; Gocic, M.; Pongracz, R. Assessment of Reference Evapotranspiration by Regionally Calibrated Temperature-Based Equations. KSCE J. Civ. Eng. 2020, 24, 1020–1027. [Google Scholar] [CrossRef]
- Irmak, S.; Allen, R.G.; Whitty, E.B. Daily grass and alfalfa reference evapotranspiration estimates and alfalfa to grass evapotranspiration ratios in Florida. J. Irrig. Drain. Eng. 2003, 129, 360–370. [Google Scholar] [CrossRef]
- Schneider, K.; Ketzer, B.; Breuer, L.; Vache, K.B.; Bernhofer, C.; Frede, H.G. Evaluation of evapotranspiration methods for model validation in a semi-arid watershed in northern China. Adv. Geosci. 2007, 11, 37–42. [Google Scholar] [CrossRef]
- Trajkovic, S.; Gocic, M. Comparison of some empirical equations for estimating daily reference evapotranspiration. Facta Univ. Ser. Arch. Civ. Eng. 2010, 8, 163–168. [Google Scholar] [CrossRef]
- Gavilan, P.; Estevez, J.; Berengena, J. Comparison of Standardized Reference Evapotranspiration Equations in Southern Spain. J. Irrig. Drain. Eng. 2008, 134, 1–12. [Google Scholar] [CrossRef]
- Song, X.; Lu, F.; Xiao, W.; Zhu, K.; Zhou, Y.; Xie, Z. Performance of 12 reference evapotranspiration estimation methods compared with the Penman-Monteith method and the potential influences in northeast China. Meteorol. Appl. 2019, 26, 83–96. [Google Scholar] [CrossRef]
- Varga-Haszonits, Z.; Szalka, É.; Szakál, T. Determination of Reference Evapotranspiration Using Penman-Monteith Method in Case of Missing Wind Speed Data under Subhumid Climatic Condition in Hungary. Atmos. Clim. Sci. 2022, 12, 235–245. Available online: https://www.scirp.org/journal/acs (accessed on 10 May 2023). [CrossRef]
- Popova, Z.; Kercheva, M.; Pereira, L.S. Validation of the FAO methodology for computing ETo with limited data. Application to South Bulgaria. Irrig. Drain 2006, 55, 201–215. [Google Scholar] [CrossRef]
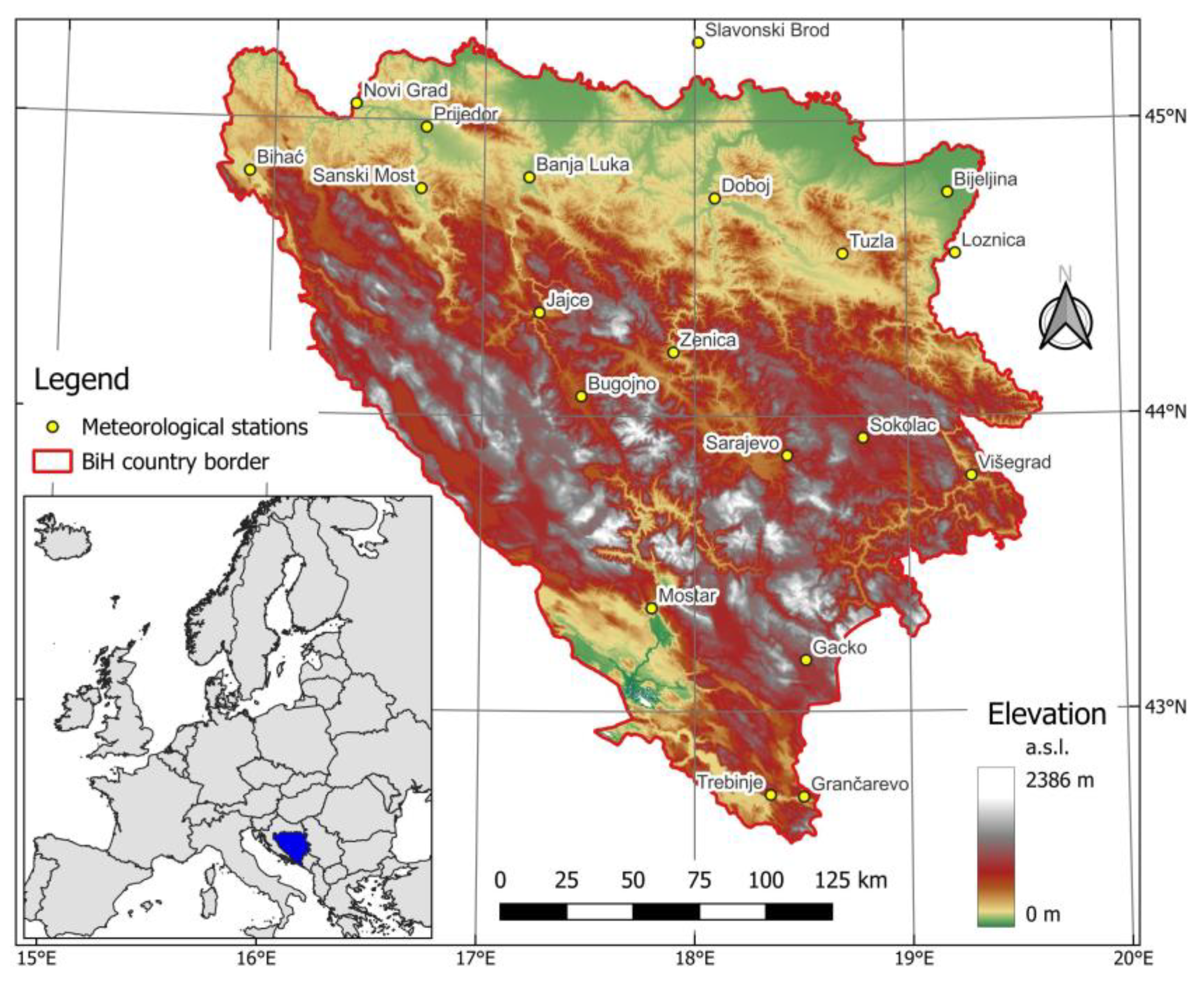
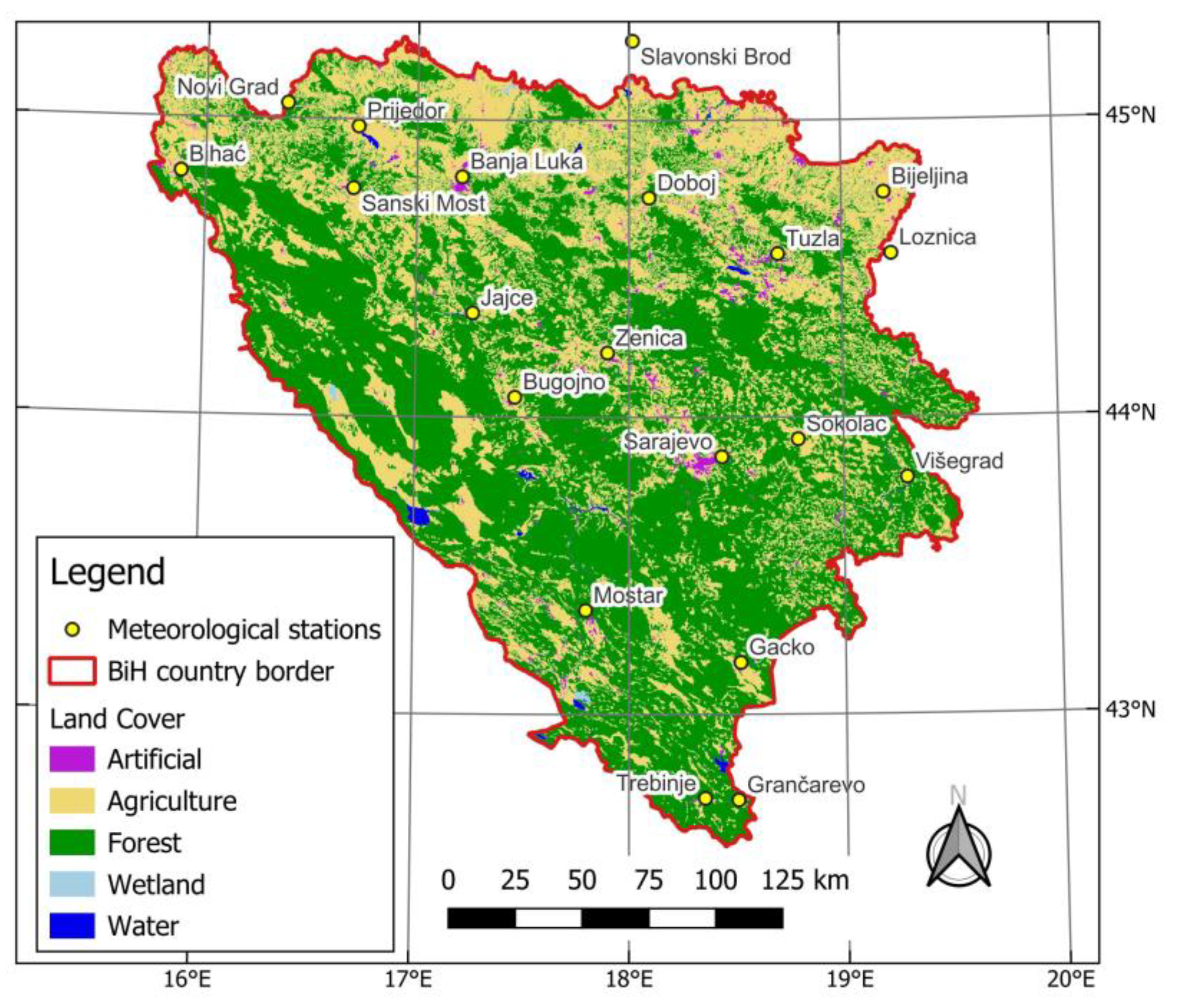

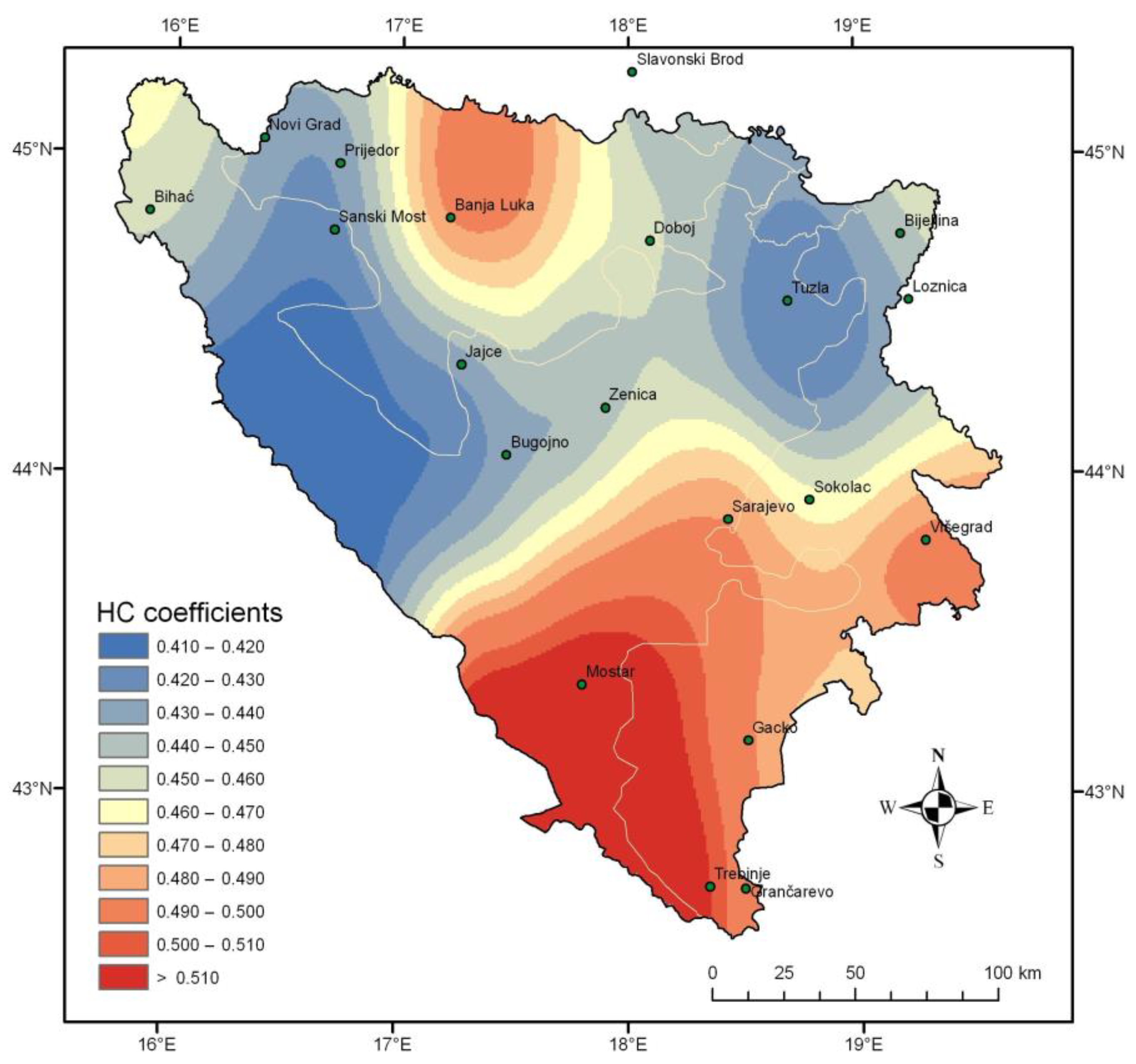
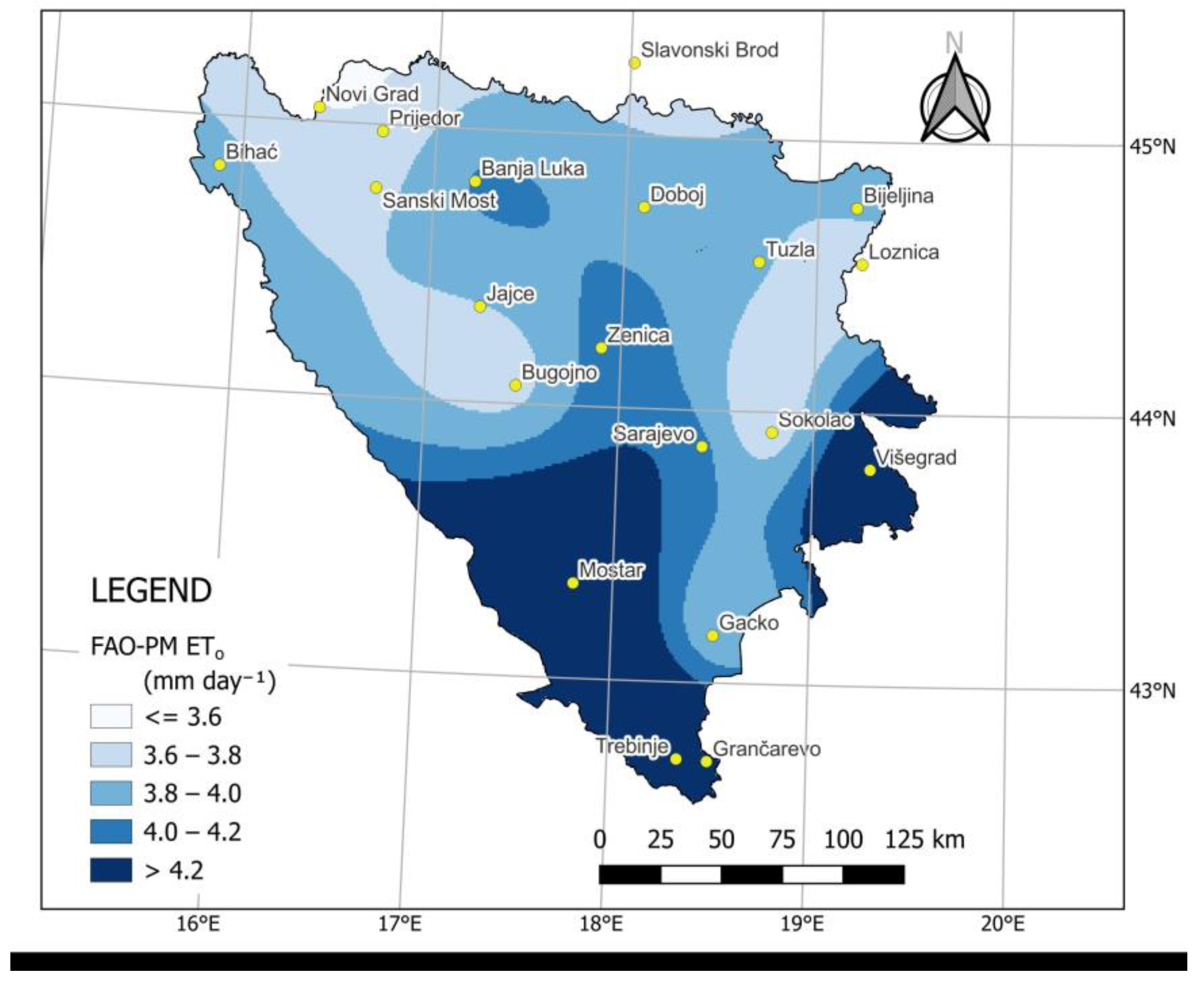
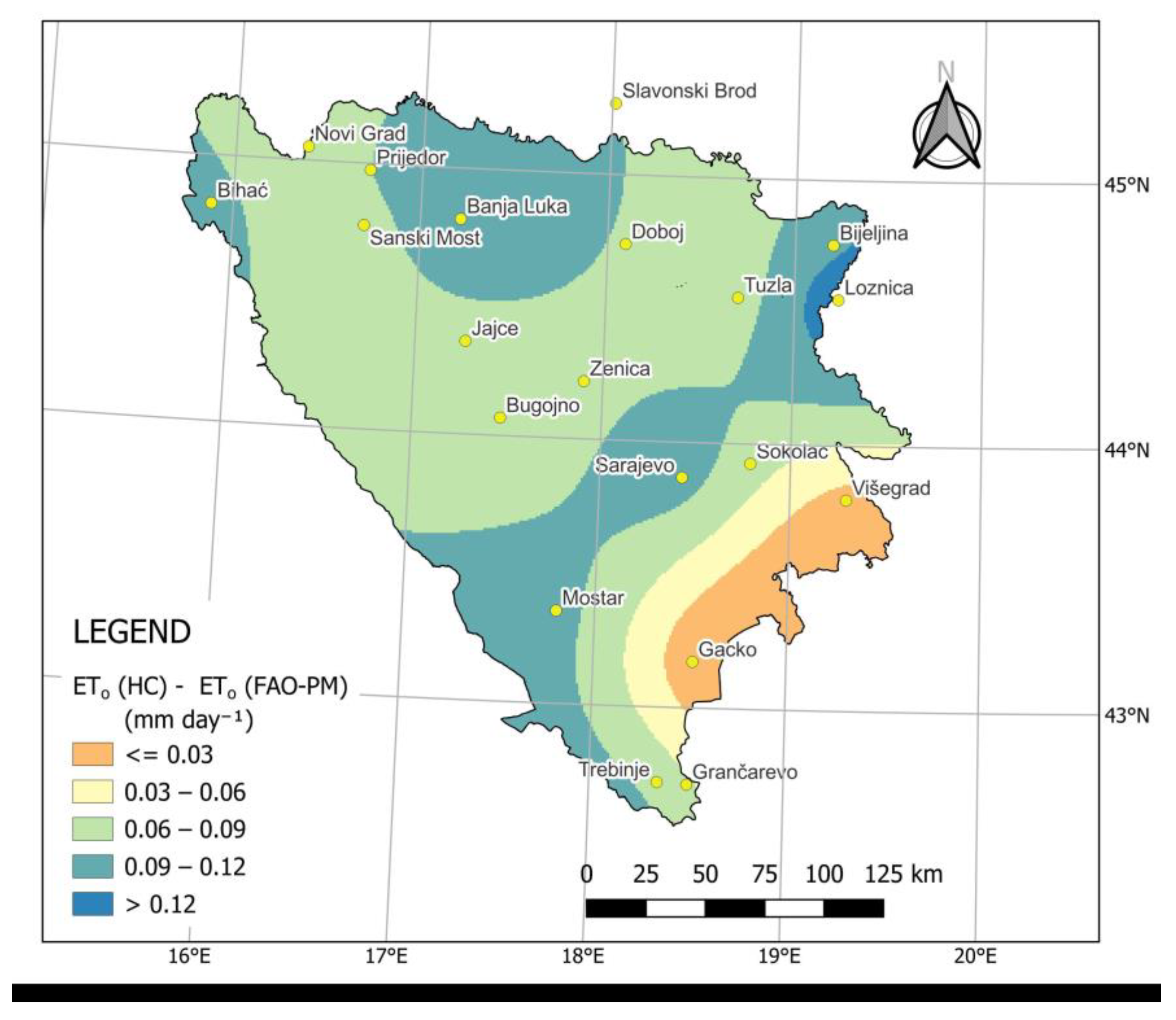

| Meteorological Station | ALT (m) | LAT | LONG | Meteorological Station | ALT (m) | LAT | LONG |
|---|---|---|---|---|---|---|---|
| Bijeljina | 97 | 44.756 | 19.201 | Mostar | 99 | 43.35 | 17.80 |
| Novi Grad | 134 | 45.051 | 16.384 | Sanski Most | 158 | 44.767 | 16.70 |
| Prijedor | 141 | 44.975 | 16.721 | Tuzla | 274 | 44.90 | 18.70 |
| Doboj | 147 | 44.739 | 18.095 | Jajce | 430 | 44.35 | 17.267 |
| Banja Luka | 159 | 44.808 | 17.213 | Sarajevo | 630 | 43.86 | 18.43 |
| Trebinje | 200 | 42.717 | 18.350 | Bihać | 246 | 44.81 | 15.88 |
| Višegrad | 416 | 43.796 | 19.295 | Bugojno | 562 | 44.06 | 17.46 |
| Grančarevo | 430 | 42.711 | 18.503 | Zenica | 344 | 44.21 | 17.90 |
| Sokolac | 913 | 43.926 | 18.789 | Loznica (RS) | 121 | 44.55 | 19.76 |
| Gacko | 947 | 43.174 | 18.516 | Slavonski Brod (RC) | 88 | 45.267 | 18.017 |
| Weather Station and Period | Average Weather Data and Climatic Zones | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tmax °C | Tmin °C | Tavg °C | RHmax % | RHmin % | RHm % | n h | Rs MJ m−2day−1 | u m∙s−1 | P mm | ETo mm | P/ETo | Climatic Zone | |
| 1 Bijeljina 2000–2005 | 25.3 | 12.7 | 18.9 | 84.5 | 64.4 | 75.6 | - | 21.5 | 2.9 | 484 | 799 | 0.61 | DSH |
| 2018–2022 | 26.5 | 13.2 | 19.9 | 84.6 | 55.8 | 72.0 | 1558.1 | 21.4 | 1.3 | 322 | 702 | 0.46 | SA |
| 1 Novi Grad 2000–2005 | 24.4 | 11.8 | 18.1 | 94.8 | 50.0 | 74.2 | - | 21.2 | 0.67 | 596 | 658 | 0.91 | MSH |
| 2018–2022 | 25.8 | 12.7 | 19.3 | 75.3 | 46.1 | 61.1 | 1522.0 | 21.9 | 0.4 | 549 | 660 | 0.83 | MSH |
| 1 Prijedor 2000–2005 | 24.9 | 11.9 | 18.4 | 89.6 | 52.8 | 73.4 | - | 21.2 | 0.7 | 507 | 663 | 0.76 | MSH |
| 2018–2022 | 26.4 | 12.4 | 19.4 | 89.5 | 51.2 | 71.7 | 1386.0 | 21.9 | 0.5 | 519 | 670 | 0.77 | MSH |
| 1 Doboj 2000–2005 | 24.3 | 12.0 | 18.2 | 89.8 | 52.8 | 74.1 | 1282.2 | 21.0 | 0.8 | 628 | 656 | 0.96 | MSH |
| 2018–2022 | 26.3 | 12.9 | 19.6 | 86.2 | 48.1 | 70.6 | 1380.8 | 21.7 | 1.1 | 495 | 715 | 0.69 | MSH |
| 1 Banja Luka 2000–2005 | 25.2 | 11.9 | 18.6 | 84.9 | 49.3 | 69.9 | 1369.7 | 20.3 | 1.7 | 536 | 735 | 0.73 | MSH |
| 2018–2022 | 26.7 | 12.9 | 19.8 | 84.1 | 47.2 | 68.0 | 1576.9 | 20.7 | 1.5 | 475 | 734 | 0.65 | DSH |
| 1 Trebinje 2000–2005 | 26.8 | 15.4 | 21.1 | 69.1 | 43.6 | 57.3 | - | 23.6 | 1.2 | 551 | 840 | 0.66 | DSH |
| 2018–2022 | 27.3 | 16.1 | 21.7 | 71.8 | 46.9 | 60.8 | 1805.5 | 24.1 | 2.2 | 444 | 897 | 0.49 | SA |
| 1 Višegrad 2000–2005 | 25.3 | 11.1 | 18.2 | 93.0 | 46.9 | 74.2 | - | 21.8 | 2.2 | 403 | 750 | 0.54 | DSH |
| 2018–2022 | 26.9 | 12.0 | 19.4 | 87.3 | 32.0 | 64.2 | 1377.5 | 21.5 | 1.1 | 361 | 878 | 0.41 | SA |
| 1 Grančarevo 2000–2005 | 26.2 | 12.7 | 19.5 | - | - | 55.7 | - | 23.5 | 1.5 | 456 | 834 | 0.55 | DSH |
| 1 Sokolac 2000–2005 | 20.8 | 7.1 | 14.0 | 93.8 | 50.7 | 74.8 | 1312.8 | 20.3 | 1.4 | 500 | 632 | 0.79 | MSH |
| 2018–2022 | 21.7 | 7.7 | 14.7 | 88.7 | 47.7 | 69.5 | 1417.6 | 21.6 | 1.7 | 452 | 673 | 0.67 | MSH |
| 1 Gacko 2000–2005 | 20.9 | 7.5 | 14.2 | 84.3 | 45.4 | 67.1 | 1446.7 | 20.3 | 2.3 | 599 | 677 | 0.88 | MSH |
| 2018–2022 | 22.1 | 9.1 | 15.6 | 91.9 | 47.2 | 70.1 | 1650.0 | 22.8 | 2.0 | 415 | 706 | 0.59 | DSH |
| 2 Mostar 2000–2005 | 28.0 | 16.0 | 22.0 | 71.4 | 40.6 | 56.8 | 1587.4 | 21.7 | 1.8 | 509 | 897 | 0.57 | DSH |
| 2018–2022 | 29.1 | 16.8 | 23.0 | 92.1 | 44.4 | 63.7 | 1591.9 | 22.7 | 2.2 | 440 | 879 | 0.50 | SA |
| 2 Sanski Most 2000–2005 | 24.7 | 10.9 | 17.8 | 95.8 | 49.9 | 75.3 | 1331.4 | 20.0 | 0.8 | 539 | 648 | 0.83 | MSH |
| 2018–2022 | 25.4 | 11.7 | 18.6 | 96.7 | 46.3 | 74.0 | 1519.2 | 21.2 | 1.1 | 511 | 685 | 0.75 | MSH |
| 2 Tuzla 2000–2005 | 24.6 | 11.1 | 17.8 | 87.7 | 47.0 | 71.5 | 1279.0 | 20.6 | 0.5 | 609 | 632 | 0.96 | MSH |
| 2018–2022 | 25.1 | 11.6 | 18.4 | 94.7 | 44.5 | 70.4 | 1166.1 | 21.4 | 1.2 | 490 | 701 | 0.70 | MSH |
| 2 Jajce 2000–2005 | 23.4 | 10.8 | 17.1 | 96.0 | 48.2 | 75.2 | 1107.0 | 18.5 | 1.4 | 550 | 624 | 0.88 | MSH |
| 2 Sarajevo 2000–2005 | 23.2 | 10.6 | 16.9 | 90.5 | 39.9 | 67.4 | 1244.4 | 13.8 | 1.4 | 509 | 721 | 0.71 | MSH |
| 2018–2022 | 25.1 | 11.6 | 18.3 | 97.7 | 44.7 | 63.3 | 1317.8 | 20.7 | 1.9 | 429 | 741 | 0.58 | MSH |
| 2 Bihać 2000–2005 | 24.1 | 11.3 | 17.7 | 90.3 | 54.6 | 72.2 | 1406.7 | 20.0 | 1.0 | 665 | 665 | 1.00 | MSH |
| 2018–2022 | 25.5 | 12.2 | 18.8 | 95.0 | 43.8 | 69.9 | 1518.2 | 20.8 | 1.4 | 608 | 708 | 0.86 | MSH |
| 2 Bugojno 2000–2005 | 25.3 | 11.4 | 18.3 | 94.5 | 37.5 | 68.4 | 1279.1 | 20.1 | 1.0 | 477 | 649 | 0.73 | MSH |
| 2018–2022 | 24.3 | 10.2 | 17.3 | 96.5 | 43.5 | 70.2 | 1319.3 | 20.9 | 1.3 | 407 | 682 | 0.60 | MSH |
| 2 Zenica 2000–2005 | 23.6 | 9.4 | 16.4 | 96.5 | 43.0 | 71.7 | 1204.9 | 19.4 | 1.1 | 477 | 700 | 0.68 | MSH |
| 2018–2022 | 27.1 | 11.8 | 19.5 | 96.9 | 41.6 | 68.4 | 1378.3 | 21.4 | 1.4 | 460 | 745 | 0.62 | MSH |
| 3 Loznica 2000–2005 | 24.7 | 11.5 | 18.1 | 93.5 | 41.6 | 69.7 | 1418.1 | 19.9 | 1.2 | 501 | 639 | 0.78 | MSH |
| 2018–2020 | 26.0 | 13.8 | 19.9 | - | - | 69.7 | 1437.7 | 19.9 | 1.3 | 481 | 671 | 0.72 | MSH |
| 4 Slavonski Brod 2000–2005 | 24.8 | 12.9 | 18.8 | - | - | 69.5 | 1419.9 | 19.5 | 0.8 | 508 | 666 | 0.76 | MSH |
| 2018–2020 | 25.8 | 12.1 | 19.0 | - | - | 71.8 | 1471.8 | 21.0 | 1.6 | 431 | 670 | 0.64 | DSH |
| Weather Stations and Meteorological Parameters | Input Daily Data Error (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| Tmax °C | Tmin °C | Tavg °C | RHmax % | RHmin % | RHm % | n h | u m∙s−1 | |
| Bijeljina | ||||||||
| 2000–2005 | 0.28 | 0.37 | - | - | - | - | 100 | - |
| 2018–2022 | - | - | - | - | - | - | - | - |
| Novi Grad | ||||||||
| 2000–2005 | - | - | - | 77 | 77 | 77 | 100 | - |
| 2018–2022 | - | - | - | - | - | - | 60 | - |
| Prijedor | ||||||||
| 2000–2005 | - | - | - | - | - | - | 100 | - |
| 2018–2022 | - | - | - | - | - | - | - | - |
| Doboj | ||||||||
| 2000–2005 | - | - | - | - | - | - | 5.6 | - |
| 2018–2022 | - | - | - | - | - | - | - | - |
| Banja Luka | ||||||||
| 2000–2005 | 1.1 | 1.1 | - | - | - | - | 2.1 | 0.5 |
| 2018–2022 | - | - | - | - | - | - | - | - |
| Trebinje | ||||||||
| 2000–2005 | 0.5 | 0.2 | - | - | - | - | 100 | - |
| 2018–2022 | - | - | - | - | - | - | 60 | - |
| Višegrad | ||||||||
| 2000–2005 | - | 25 | - | - | - | - | 100 | 3.5 |
| 2018–2022 | - | - | - | - | - | - | 60 | - |
| Grančarevo | ||||||||
| 2000–2005 | - | - | - | 100 | 100 | - | 100 | - |
| Sokolac | ||||||||
| 2000–2005 | - | - | - | - | - | - | - | - |
| 2018–2022 | - | - | - | - | - | - | - | - |
| Gacko | ||||||||
| 2000–2005 | - | - | - | - | - | - | - | - |
| 2018–2022 | - | - | - | 60 | 60 | 60 | 60 | - |
| Mostar | - | |||||||
| 2000–2005 | - | - | - | - | - | - | - | |
| 2018–2022 | - | - | - | 40 | 40 | - | - | 3.3 |
| Sanski Most | ||||||||
| 2000–2005 | - | - | - | - | - | - | - | - |
| Most 2018–2022 | - | - | - | 40 | 40 | - | - | 10.1 |
| Tuzla | ||||||||
| 2000–2005 | - | - | - | - | - | - | - | 16.9 |
| 2018–2022 | - | - | - | 40 | 40 | - | - | 8.0 |
| Jajce 2000–2005 | - | - | - | - | - | - | - | - |
| Sarajevo | ||||||||
| 2000–2005 | - | - | - | - | - | - | - | - |
| 2018–2022 | - | - | - | 40 | 40 | - | - | 2.7 |
| Bihać | ||||||||
| 2000–2005 | - | - | - | - | - | - | - | 12.2 |
| 2018–2022 | - | - | - | 40 | 40 | - | - | 0.6 |
| Bugojno | ||||||||
| 2000–2005 | - | - | - | - | - | - | - | - |
| 2018–2022 | - | - | - | 40 | 40 | - | - | 1.8 |
| Zenica | ||||||||
| 2000–2005 | - | - | - | - | - | - | - | - |
| 2018–2022 | - | - | - | 40 | 40 | - | - | 20.6 |
| Loznica | ||||||||
| 2000–2005 | - | - | - | 100 | 100 | - | - | - |
| 2018–2021 | - | - | - | 100 | 100 | - | - | - |
| Slavonski Brod | ||||||||
| 2000–2005 | - | - | - | - | - | - | - | - |
| 2018–2020 | - | - | - | 100 | 100 | - | - | - |
| Station | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2018 | 2019 | 2020 | 2021 | 2022 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bijeljina | n.a. | 1.05 | 1.05 | 1.03 | 1.07 | 1.07 | 1.06 | 1.07 | 1.07 | 1.07 | 1.07 |
| Novi Grad | n.a. | n.a. | 1.05 | 1.02 | 1.05 | 1.06 | 1.17 | 1.08 | 1.07 | 1.06 | 1.06 |
| Prijedor | n.a. | 1.06 | 1.04 | 1.01 | 1.03 | 1.04 | 1.16 | 1.16 | 1.16 | 1.18 | 1.18 |
| Doboj | 1.04 | 1.12 | 1.09 | 1.09 | 1.09 | 1.09 | 1.13 | 1.10 | 1.13 | 1.17 | 1.23 |
| Banja Luka | 1.08 | 1.08 | 1.08 | 1.08 | 1.08 | 1.08 | 1.03 | 1.03 | 1.01 | 1.01 | 1.01 |
| Trebinje | 1.17 | 1.17 | 1.20 | 1.20 | 1.22 | 1.22 | 1.25 | 1.25 | 1.24 | 1.05 | 1.05 |
| Višegrad | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | 1.07 | n.a. | 1.02 | 1.05 | 1.05 |
| Grančarevo | 1.07 | 1.07 | 1.12 | 1.12 | 1.10 | 1.10 | - | - | - | - | - |
| Sokolac | 1.10 | 1.10 | 1.10 | 1.10 | 1.09 | 1.09 | 1.17 | 1.10 | 1.10 | 1.10 | 1.10 |
| Gacko | 1.02 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.14 | 1.09 | 1.09 | 1.06 | 1.06 |
| Mostar | 1.06 | 1.06 | 1.06 | 1.06 | 1.06 | 1.06 | 1.08 | 1.08 | 1.13 | 1.11 | 1.11 |
| Sanski Most | 1.09 | 1.07 | 1.08 | 1.08 | 1.08 | 1.08 | 1.10 | 1.07 | 1.05 | 1.05 | 1.05 |
| Tuzla | 1.14 | 1.14 | 1.14 | 1.13 | 1.13 | 1.13 | 1.15 | 1.09 | 1.09 | 1.09 | 1.09 |
| Jajce | n.a. | 1.13 | 1.13 | 1.06 | 1.11 | 1.09 | - | - | - | - | - |
| Sarajevo | 1.09 | 1.11 | 1.13 | 1.12 | 1.10 | 1.12 | 1.17 | 1.13 | 1.06 | 1.08 | 1.08 |
| Bihać | 1.05 | 1.05 | 1.04 | 1.05 | 1.05 | 1.05 | 1.07 | 1.05 | 1.04 | 1.04 | 1.04 |
| Bugojno | 1.08 | 1.08 | 1.08 | 1.08 | 1.12 | 1.12 | 1.24 | 1.14 | 1.11 | 1.09 | 1.09 |
| Zenica | 1.09 | 1.11 | 1.11 | 1.10 | 1.10 | 1.09 | 1.21 | 1.12 | 1.11 | 1.11 | 1.11 |
| Loznica | 1.01 | 1.02 | 1.01 | 1.02 | 1.03 | 1.02 | 1.08 | 1.02 | 1.01 | - | - |
| Slavonski Brod | 1.03 | 1.06 | 1.04 | 1.04 | 1.07 | 1.04 | 1.11 | 1.08 | 1.06 | - | - |
| Statistical Parameters | ETo | b | R2 | RMSE | MAE | dIA | NSE | Emax | MRE | Rank |
|---|---|---|---|---|---|---|---|---|---|---|
| unit | mm·day−1 | mm·day−1 | mm·day−1 | % | No | |||||
| DSH | ||||||||||
| FAO-PM | 4.45 | |||||||||
| HS | 4.65 | 1.04 | 0.76 | 0.77 | 0.70 | 0.92 | 0.72 | 2.86 | 14.8 | 3 |
| HM 0.424 | 3.83 | 0.85 | 0.75 | 0.92 | 0.77 | 0.87 | 0.59 | 3.50 | 14.3 | 7 |
| HC 0.489 * | 4.54 | 1.00 | 0.76 | 0.65 | 0.63 | 0.94 | 0.79 | 2.91 | 12.2 | 1 |
| PT | 4.48 | 1.00 | 0.76 | 0.75 | 0.60 | 0.93 | 0.74 | 2.79 | 14.5 | 6 |
| MAK | 3.74 | 0.83 | 0.81 | 0.95 | 0.85 | 0.88 | 0.58 | 3.46 | 15.7 | 8 |
| COP | 4.92 | 1.10 | 0.83 | 0.93 | 0.68 | 0.91 | 0.57 | 3.26 | 17.0 | 9 |
| PMT2 | 4.33 | 0.96 | 0.75 | 0.76 | 0.64 | 0.92 | 0.73 | 3.12 | 12.7 | 2 |
| PMT1.3 | 4.04 | 0.90 | 0.76 | 0.80 | 0.66 | 0.90 | 0.68 | 3.31 | 12.4 | 5 |
| PMTlok(1.0) ** | 4.18 | 0.93 | 0.77 | 0.73 | 0.57 | 0.92 | 0.74 | 3.01 | 12.0 | 4 |
| MSH | ||||||||||
| FAO-PM | 3.63 | |||||||||
| HS | 4.36 | 1.18 | 0.79 | 0.98 | 0.83 | 0.89 | 0.46 | 3.29 | 25.7 | 9 |
| HM 0.424 | 3.61 | 0.97 | 0.77 | 0.57 | 0.42 | 0.94 | 0.82 | 2.71 | 13.0 | 2 |
| HC 0.441 | 3.74 | 1.00 | 0.78 | 0.56 | 0.43 | 0.95 | 0.83 | 2.57 | 13.7 | 3 |
| PT | 3.91 | 1.07 | 0.90 | 0.56 | 0.46 | 0.96 | 0.82 | 2.38 | 13.6 | 1 |
| MAK | 3.21 | 0.89 | 0.92 | 0.58 | 0.46 | 0.95 | 0.81 | 2.88 | 13.2 | 4 |
| COP | 4.01 | 1.11 | 0.87 | 0.76 | 0.58 | 0.94 | 0.68 | 2.86 | 16.1 | 7 |
| PMT2 | 4.08 | 1.10 | 0.77 | 0.82 | 0.65 | 0.91 | 0.63 | 3.08 | 19.9 | 8 |
| PMT1.3 | 3.81 | 1.03 | 0.78 | 0.65 | 0.50 | 0.94 | 0.77 | 3.06 | 15.5 | 5 |
| PMTlok (1.0) ** | 3.86 | 1.02 | 0.78 | 0.67 | 0.51 | 0.93 | 0.76 | 2.86 | 15.9 | 6 |
| Statistical Parameters | ETo | b | R2 | RMSE | MAE | dIA | NSE | Emax | MRE | Rank |
|---|---|---|---|---|---|---|---|---|---|---|
| unit | mm·day−1 | mm·day−1 | mm·day−1 | % | No | |||||
| SA | ||||||||||
| FAO-PM | 4.59 | |||||||||
| HS | 4.77 | 1.03 | 0.98 | 0.86 | 0.55 | 0.92 | 0.61 | 3.65 | 17.1 | 5 |
| HM 0.424 | 3.92 | 0.85 | 0.98 | 1.02 | 0.42 | 0.85 | 0.46 | 3.96 | 18.0 | 9 |
| HC 0.488 * | 4.58 | 1.00 | 0.98 | 0.67 | 0.32 | 0.93 | 0.75 | 2.94 | 13.2 | 1 |
| PT | 5.03 | 1.10 | 0.99 | 0.82 | 0.70 | 0.91 | 0.60 | 3.23 | 15.7 | 4 |
| MAK | 4.21 | 0.92 | 0.99 | 0.80 | 0.61 | 0.92 | 0.67 | 4.04 | 14.0 | 7 |
| COP | 4.90 | 1.08 | 0.98 | 0.87 | 0.47 | 0.92 | 0.61 | 3.33 | 16.1 | 3 |
| PMT2 | 4.49 | 0.97 | 0.97 | 0.89 | 0.55 | 0.89 | 0.60 | 3.61 | 16.5 | 6 |
| PMT1.3 | 4.16 | 0.90 | 0.98 | 0.89 | 0.47 | 0.89 | 0.59 | 3.57 | 15.9 | 8 |
| PMTlok(1.4) ** | 4.37 | 0.94 | 0.98 | 0.88 | 0.58 | 0.89 | 0.59 | 3.63 | 16.1 | 2 |
| DSH | ||||||||||
| FAO-PM | 3.93 | |||||||||
| HS | 4.44 | 1.12 | 0.99 | 0.73 | 0.60 | 0.93 | 0.70 | 2.54 | 17.3 | 7 |
| HM 0.424 | 3.65 | 0.91 | 0.99 | 0.61 | 0.50 | 0.94 | 0.79 | 2.47 | 13.3 | 6 |
| HC 0.461 * | 4.00 | 1.00 | 0.99 | 0.49 | 0.35 | 0.96 | 0.87 | 2.34 | 10.6 | 1 |
| PT | 4.17 | 1.06 | 0.99 | 0.50 | 0.40 | 0.96 | 0.86 | 2.53 | 11.0 | 4 |
| MAK | 3.45 | 0.88 | 1.00 | 0.61 | 0.51 | 0.95 | 0.79 | 2.86 | 13.5 | 8–9 |
| COP | 4.41 | 1.13 | 0.99 | 0.78 | 0.61 | 0.92 | 0.64 | 2.55 | 16.2 | 8–9 |
| PMT2 | 4.16 | 1.07 | 0.99 | 0.59 | 0.44 | 0.95 | 0.81 | 2.45 | 13.1 | 5 |
| PMT1.3 | 3.88 | 1.01 | 0.99 | 0.52 | 0.40 | 0.96 | 0.85 | 2.42 | 11.4 | 2 |
| PMTlok(1.4) ** | 4.01 | 1.03 | 0.99 | 0.56 | 0.41 | 0.95 | 0.82 | 2.52 | 11.5 | 3 |
| MSH | ||||||||||
| FAO-PM | 3.81 | |||||||||
| HS | 4.57 | 1.18 | 0.99 | 0.94 | 0.81 | 0.89 | 0.50 | 2.60 | 23.8 | 9 |
| HM 0.424 | 3.79 | 0.97 | 0.99 | 0.52 | 0.40 | 0.96 | 0.86 | 2.24 | 11.8 | 5 |
| HC 0.439 * | 3.90 | 1.00 | 0.99 | 0.50 | 0.39 | 0.96 | 0.87 | 2.18 | 11.8 | 1 |
| PT | 4.19 | 1.10 | 0.99 | 0.56 | 0.48 | 0.95 | 0.82 | 1.79 | 13.1 | 3 |
| MAK | 3.47 | 0.91 | 0.98 | 0.49 | 0.41 | 0.97 | 0.88 | 2.18 | 11.6 | 2 |
| COP | 4.38 | 1.16 | 0.98 | 0.90 | 0.71 | 0.91 | 0.50 | 2.97 | 19.2 | 8 |
| PMT2 | 4.29 | 1.11 | 0.98 | 0.75 | 0.61 | 0.92 | 0.68 | 2.45 | 17.8 | 7 |
| PMT1.3 | 3.99 | 1.03 | 0.99 | 0.56 | 0.44 | 0.96 | 0.83 | 2.69 | 12.2 | 6 |
| PMTlok(1.4) ** | 3.96 | 1.02 | 0.98 | 0.55 | 0.43 | 0.95 | 0.84 | 2.31 | 12.7 | 4 |
| Month/ Station | April | May | June | July | August | September | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S | α | S | α | S | α | S | α | S | α | S | α | |
| Trebinje | −6  | >0.1 | 2  | >0.1 | 6  | >0.1 | 8  | 0.1 | −8  | 0.1 | −4 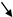 | >0.1 |
| Gacko | −6 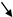 | >0.1 | 4  | >0.1 | 6  | >0.1 | 8  | 0.1 | −4 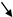 | >0.1 | −4 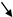 | >0.1 |
| Sanski Most | −6 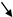 | >0.1 | 4  | >0.1 | 6  | >0.1 | 8  | 0.1 | −2 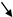 | >0.1 | 2  | >0.1 |
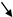 ; Increasing trend
; Increasing trend  ; S—Mann–Kendall S test statistic; α—significance level.
; S—Mann–Kendall S test statistic; α—significance level.Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srdić, S.; Srđević, Z.; Stričević, R.; Čereković, N.; Benka, P.; Rudan, N.; Rajić, M.; Todorović, M. Assessment of Empirical Methods for Estimating Reference Evapotranspiration in Different Climatic Zones of Bosnia and Herzegovina. Water 2023, 15, 3065. https://doi.org/10.3390/w15173065
Srdić S, Srđević Z, Stričević R, Čereković N, Benka P, Rudan N, Rajić M, Todorović M. Assessment of Empirical Methods for Estimating Reference Evapotranspiration in Different Climatic Zones of Bosnia and Herzegovina. Water. 2023; 15(17):3065. https://doi.org/10.3390/w15173065
Chicago/Turabian StyleSrdić, Sretenka, Zorica Srđević, Ružica Stričević, Nataša Čereković, Pavel Benka, Nada Rudan, Milica Rajić, and Mladen Todorović. 2023. "Assessment of Empirical Methods for Estimating Reference Evapotranspiration in Different Climatic Zones of Bosnia and Herzegovina" Water 15, no. 17: 3065. https://doi.org/10.3390/w15173065
APA StyleSrdić, S., Srđević, Z., Stričević, R., Čereković, N., Benka, P., Rudan, N., Rajić, M., & Todorović, M. (2023). Assessment of Empirical Methods for Estimating Reference Evapotranspiration in Different Climatic Zones of Bosnia and Herzegovina. Water, 15(17), 3065. https://doi.org/10.3390/w15173065








