Study on the Hydraulic Response of an Open-Channel Water Transmission Project after Flow Switching
Abstract
:1. Introduction
2. Research Methods
2.1. Governing Equations and Solutions
2.2. Model Internal Boundary Conditions’ Generalization
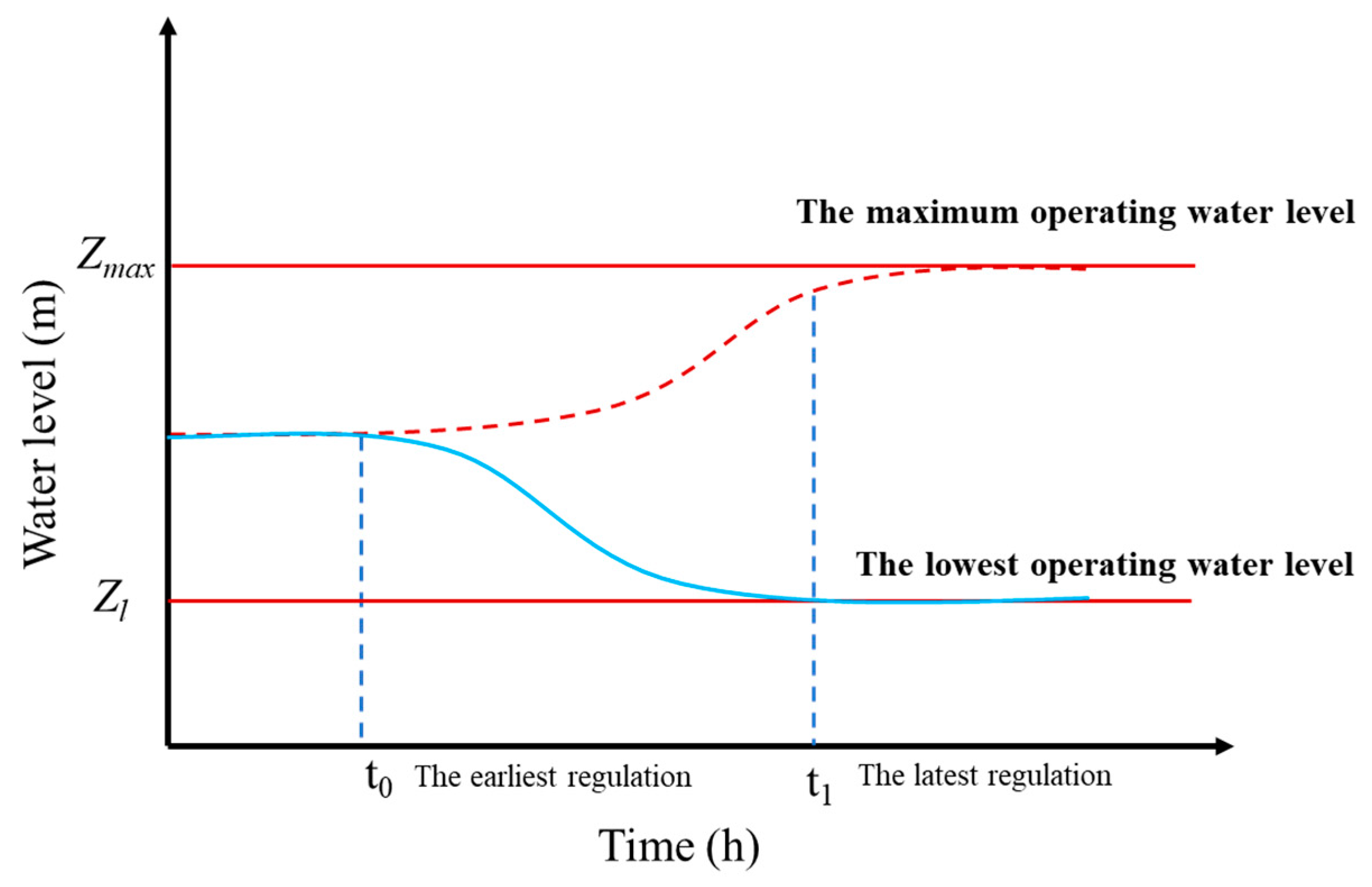
2.3. Safety Regulation Time Frame
2.4. Sobol Global Sensitivity Analysis
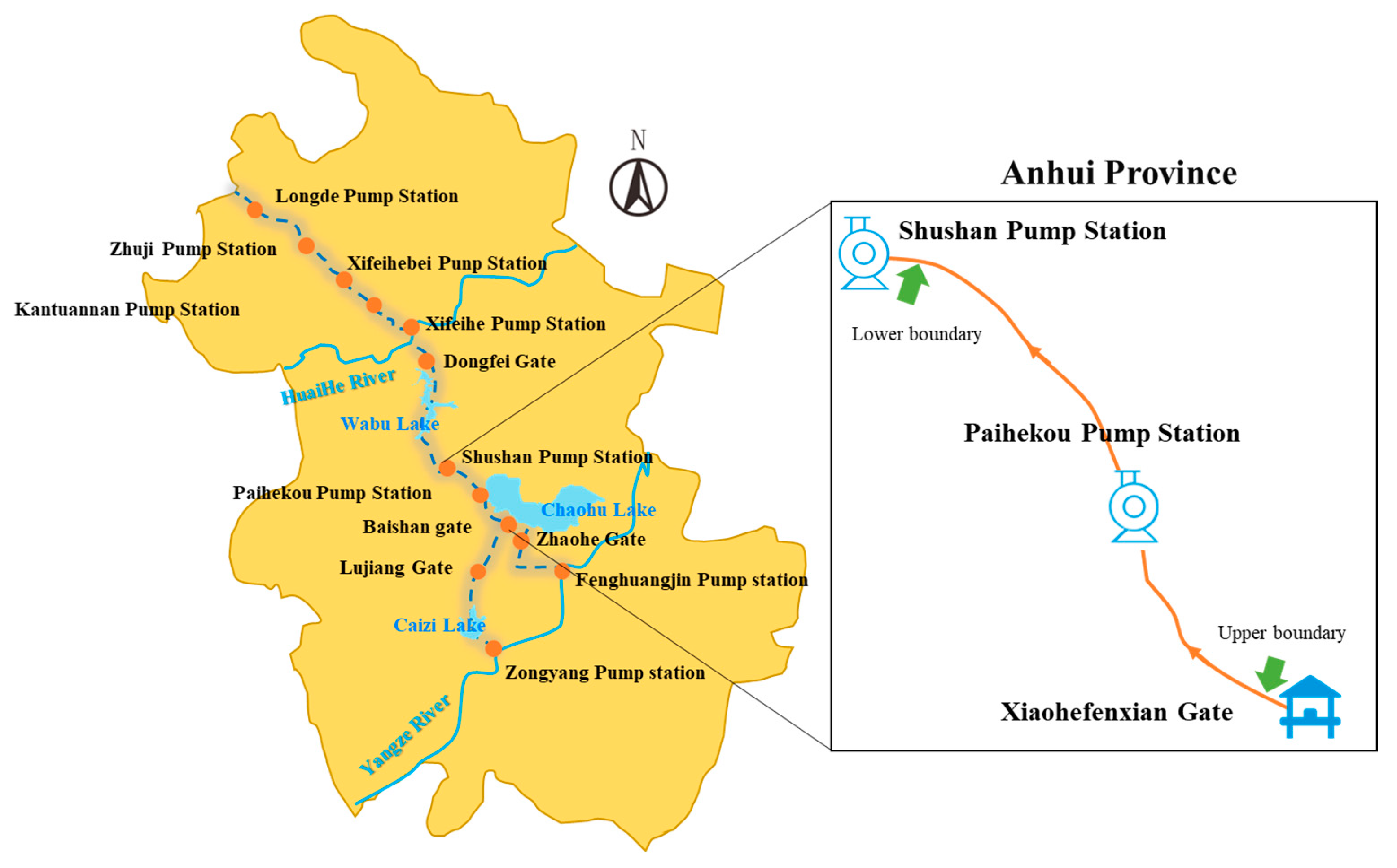
2.5. Overview of the Region
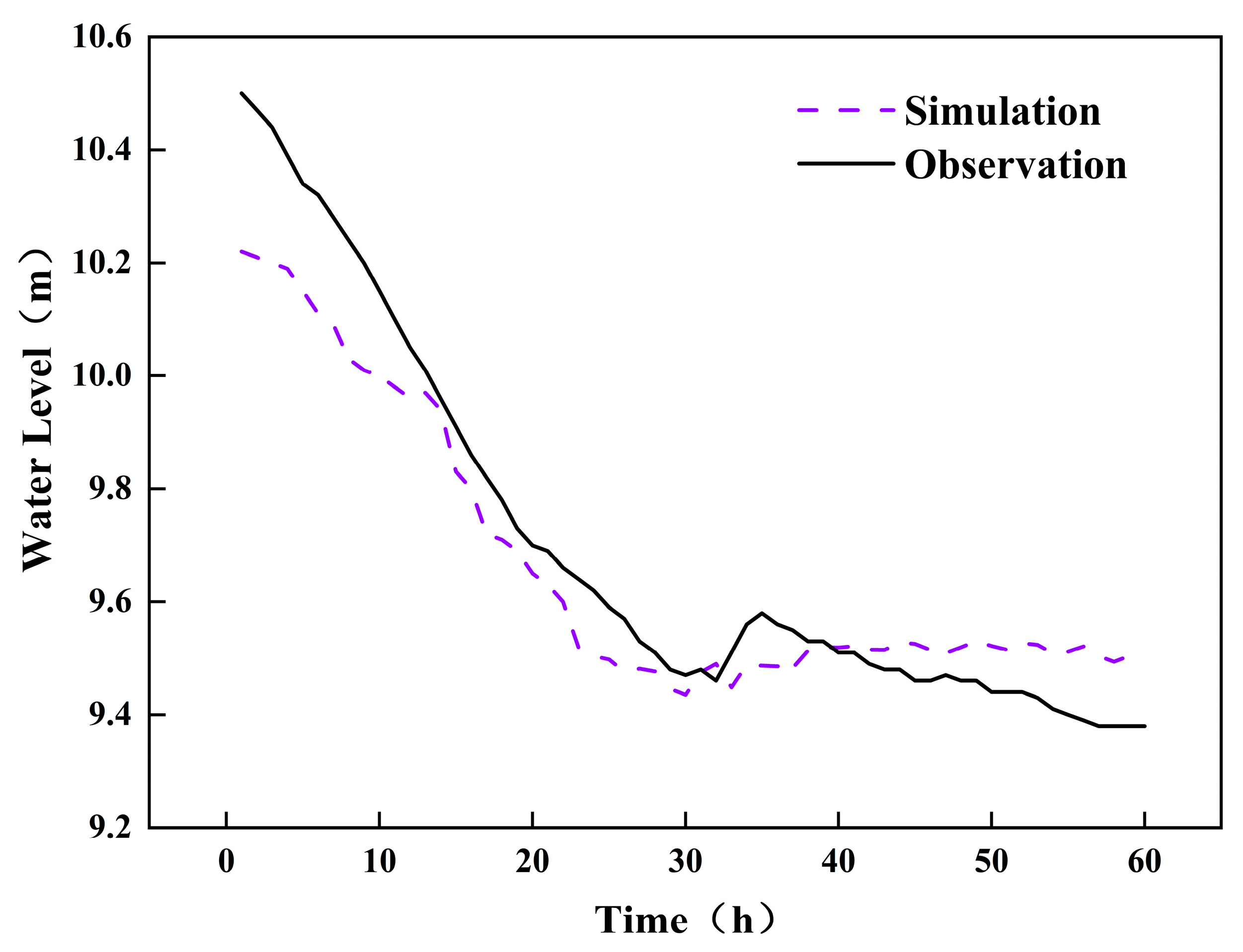
2.6. Hydrodynamic and Parameter Verification
3. Project Case
3.1. Operation Setting
3.2. Feasible Domain of Safety Regulation Time
3.3. Parametric Sensitivity Analysis
3.3.1. Sobol Global Sensitivity Analysis Method
3.3.2. Analysis of the Results of the Sobol Method
3.4. Fast Computational Equation Fitting
3.5. Test of the Fitting Equation
4. Conclusions
- (1)
- The latest regulation time at the Paihekou pumping station upstream and downstream was calculated in this study to determine the effects of the flow change, downstream water level, and upstream initial flow. It was found that, for the same initial flow and downstream water level, the regulation time decreased with the increase in the flow variation volume; for the same initial flow and flow variation volume, the latest regulation time decreased with the increase in the water level. The latest regulation time with the starting flow increased initially and subsequently reduced in a trending format for the same flow variation and downstream water level conditions.
- (2)
- The overall sensitivity index of the flow variation was found to be at the maximum when using the Sobol global sensitivity analysis method at the latest regulation time, which is connected to the starting upstream flow, the flow variation, and the downstream water level. At the same time, it was suggested for the method of the fitting equation to be used for the calculation of the most-recent regulation time in order to calculate it rapidly. The hydrodynamic model was used for testing, and the amount of flow change was chosen as a one variate to suit the computation of the most-recent regulation time. The results showed that the effect of the fit was better with the computed NSE = 0.98, and the fitting equation can be a perfect replacement.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.; Tian, Y.; Lei, X.H. Study and application of general unsteady flow simulation model for complex open channel water transfer Project. In Proceedings of the 2018 CHES Annual Conference, Amsterdam, The Netherlands, 9–12 September 2018. [Google Scholar]
- Litrico, X.; Fromion, V. Simplified Modeling of Irrigation Canals for Controller Design. J. Irrig. Drain. Eng. 2004, 130, 373–383. [Google Scholar] [CrossRef]
- Qi, J.S.; Cui, Y.R.; Wang, S.Y. Analysis of Hydraulic Response in Emergency Gate Control of the Water Supply Project in North Xinjiang. J. Water Resour. Archit. Eng. 2021, 19, 250–256. [Google Scholar]
- Li, K.B.; Shen, B.; Li, Z.L. Open channel hydraulic response characteristics in irrigation area based on unsteady flow simula-tion analysis. Trans. Chin. Soc. Agric. Eng. 2015, 31, 107–114. [Google Scholar]
- Schuurmans, J.; Clemmens, A.J.; Dijkstra, S.; Hof, A.; Brouwer, R. Modeling of Irrigation and Drainage Canals for Controller Design. J. Irrig. Drain. Eng. 1999, 125, 338–344. [Google Scholar] [CrossRef]
- Bautista, E.; Clemmens, A.J. Volume Compensation Method for Routing Irrigation Canal Demand Changes. J. Irrig. Drain. Eng. 2005, 131, 494–503. [Google Scholar] [CrossRef]
- Parrish, J. A Methodology for Automated Control of Sloping Canals; University of Iowa: Lowa City, IA, USA, 1997. [Google Scholar]
- Zheng, H.Z.; Tian, Y.; Wang, C. Study on the Predictive Control Method of Cascade Pumping Stations in Water Transfer System. Yellow River 2018, 40, 140–143. [Google Scholar]
- Wahlin, B.T.; Clemmens, A.J. Automatic downstream water-level feedback control of branching canal networks: Simula-tion results. J. Irrig. Drain. Eng. 2006, 132, 208–219. [Google Scholar] [CrossRef]
- Lu, L.B.; Lei, X.H.; Tian, Y. Research on the Characteristic of Hydraulic Response in Open Channel of the Cascade Pumping Station Project in an Emergent State. J. Basic Sci. Eng. 2018, 26, 263–275. [Google Scholar]
- Li, M.X.; Tian, Y.; Lei, X.H. Analysis onemergency response time for accidental pump—Stop at multi—Stage pumping station of Water Diversion Project from Yangtze River to Huaihe River. Yangtze River 2021, 52, 212–217. [Google Scholar]
- Liu, Z.Y.; Liu, M.Q. Analysis and Control of Pump-stopping Hydraulic Transient in Cascade Water Supply Pumping Station. China Rural Water Hydropower 2006, 7, 32–34. [Google Scholar]
- Zhang, Z.; Lei, X.; Tian, Y.; Wang, L.; Wang, H.; Su, K. Optimized Scheduling of Cascade Pumping Stations in Open-Channel Water Transfer Systems Based on Station Skipping. J. Water Resour. Plan. Manag. 2019, 145, 05019011. [Google Scholar] [CrossRef]
- Yan, P.; Zhang, Z.; Lei, X.; Zheng, Y.; Zhu, J.; Wang, H.; Tan, Q. A Simple Method for the Control Time of a Pumping Station to Ensure a Stable Water Level Immediately Upstream of the Pumping Station under a Change of the Discharge in an Open Channel. Water 2021, 13, 355. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, Z.; Lei, X.; Yue, X.; Xiang, X.; Wang, H.; Ye, M. Optimal Regulation of the Cascade Gates Group Water Diversion Project in a Flow Adjustment Period. Water 2021, 13, 2825. [Google Scholar] [CrossRef]
- Belaud, G.; Litrico, X.; Clemmens, A.J. Response Time of a Canal Pool for Scheduled Water Delivery. J. Irrig. Drain. Eng. 2013, 139, 300–308. [Google Scholar] [CrossRef]
- Burt, C.M.; Feist, K.E.; Piao, X.S. Accelerated Irrigation Canal Flow Change Routing. J. Irrig. Drain. Eng. 2018, 144, 6. [Google Scholar] [CrossRef]
- Liao, W.; Guan, G.; Tian, X. Exploring Explicit Delay Time for Volume Compensation in Feedforward Control of Canal Systems. Water 2019, 11, 1080. [Google Scholar] [CrossRef]
- Kong, L.; Li, Y.; Tang, H.; Yuan, S.; Yang, Q.; Ji, Q.; Li, Z.; Chen, R. Predictive control for the operation of cascade pumping stations in water supply canal systems considering energy consumption and costs. Appl. Energy 2023, 341, 121103. [Google Scholar] [CrossRef]
- Khatavkar, P.; Mays, L.W. Real-Time Operation of Water-Supply Canal Systems under Limited Electrical Power and/or Water Availability. J. Water Resour. Plan. Manag. 2020, 146, 04020012. [Google Scholar] [CrossRef]
- Kucuk, H.; Turan, M.; Yarali, K.; Al-Sanabani, H.; Iskefiyeli, M. A new algorithm for load shifting operation of water pumping stations. J. Fac. Eng. Archit. Gaz. 2021, 36, 2087–2093. [Google Scholar]
- Shahdany, S.M.H.; Maestre, J.M.; van Overloop, P.J. Equitable Water Distribution in Main Irrigation Canals with Constrained Water Supply. Water Resour. Manag. 2015, 29, 3315–3328. [Google Scholar] [CrossRef]
- Wang, J.P.; Lv, W.B.; Fan, Q.F. New Empirical Equations of Equilibrium Flow Scour Depth of Open Channel Outlet. Water Resour. Power 2013, 31, 139–140. [Google Scholar]
- Xia, W.Y.; Zhao, X.D.; Zhang, X.Z. Application of Empirical Equation of Sediment Transport Capacity in Forecast of Riv-erbed Erosion and Deposition of Jiaojiang River Estuary. Water Resour. Power 2017, 35, 101–103. [Google Scholar]
- Li, G.H.; Zhang, Z.; Kong, L.Z. Research on the Hydraulic Control Method of Shaping II Hydropower Station. China Rural Water Hydropower 2022, 1, 196–199. [Google Scholar]
- Malaterre, P.-O.; Rogers, D.C.; Schuurmans, J. Classification of Canal Control Algorithms. J. Irrig. Drain. Eng. 1998, 124, 3–10. [Google Scholar] [CrossRef]
- Mu, J.-B.; Zhang, X.-F. Real-Time Flood Forecasting Method With 1-D Unsteady Flow Model. J. Hydrodyn. 2007, 19, 150–154. [Google Scholar] [CrossRef]
- Wang, C.H.; Li, G.Z.; Xiang, X.H. Practical River Network Flow Calculation; Hohai University Press: Nanjing, China, 2015. [Google Scholar]
- Litrico, X.; Fromion, V.; Baume, J.-P.; Arranja, C.; Rijo, M. Experimental validation of a methodology to control irrigation canals based on Saint-Venant equations. Control Eng. Pract. 2005, 13, 1425–1437. [Google Scholar] [CrossRef]
- Mehmed, Y. Steady Non-Uniform Flow in Open Channel; Water Resources and Electric Power Press: Beijing, China, 1987. [Google Scholar]
- Wang, C.; Yang, J.; Nilsson, H. Simulation of Water Level Fluctuations in a Hydraulic System Using a Coupled Liquid-Gas Model. Water 2015, 7, 4446–4476. [Google Scholar] [CrossRef]
- Yan, P.; Zhang, Z.; Lei, X.; Hou, Q.; Wang, H. A multi-objective optimal control model of cascade pumping stations considering both cost and safety. J. Clean. Prod. 2022, 345, 131171. [Google Scholar] [CrossRef]
- Zhang, Z. Research on Perception and Regulation Model of Water Delivery Process in Open Channel Water Transfer Project. Ph.D. Thesis, Hohai University, Nanjing, China, 2020. [Google Scholar]
- Olszewski, P. Genetic optimization and experimental verification of complex parallel pumping station with centrifugal pumps. Appl. Energy 2016, 178, 527–539. [Google Scholar] [CrossRef]

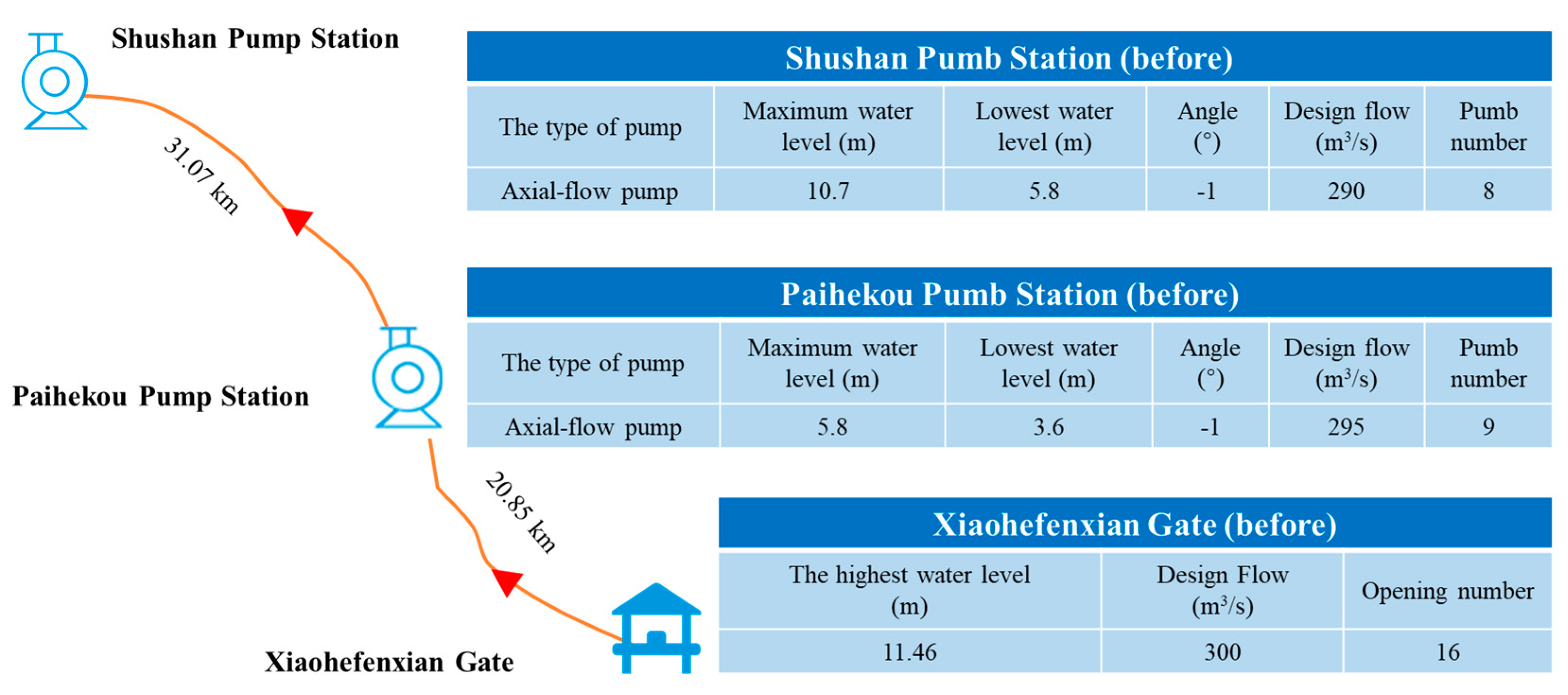
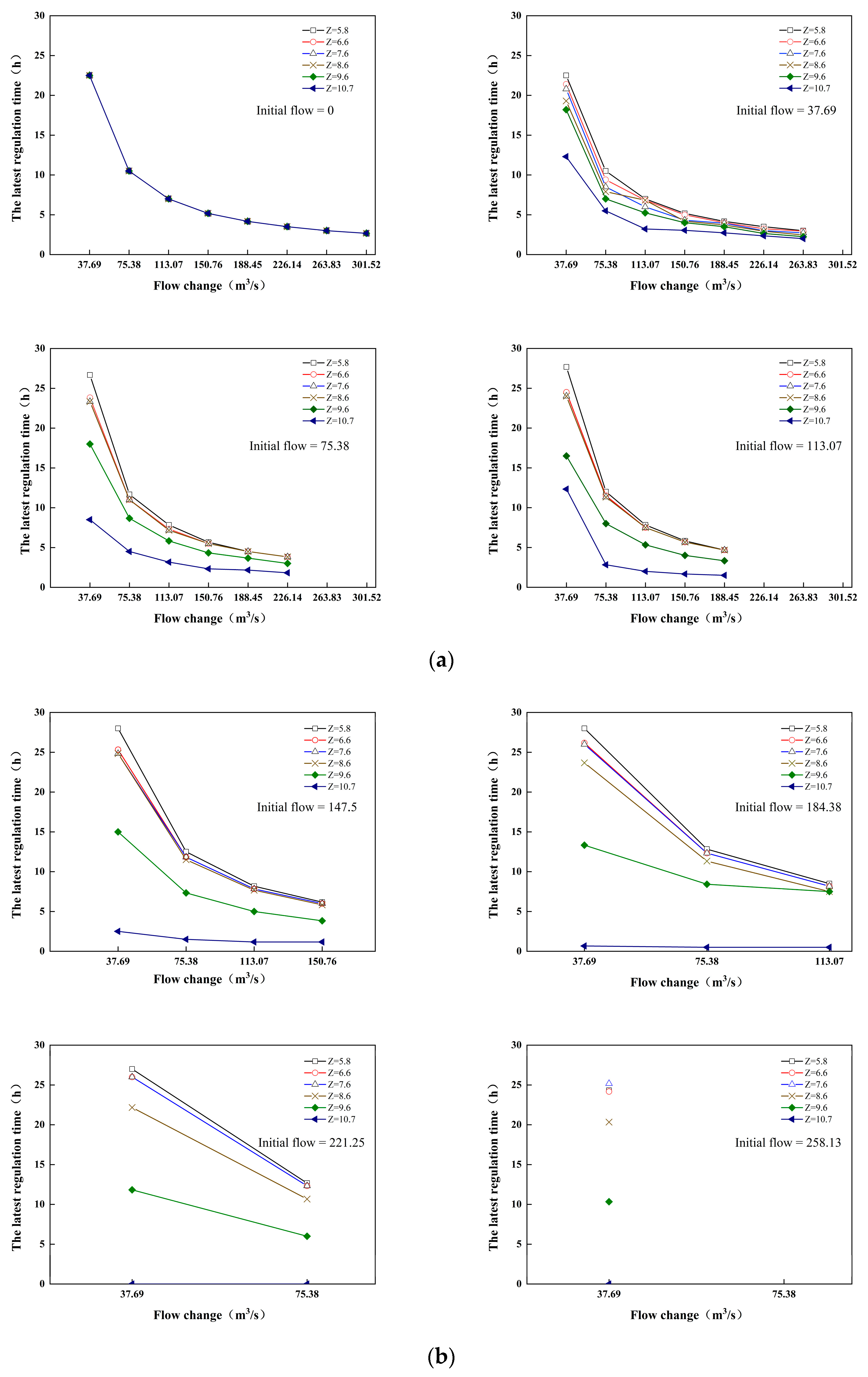
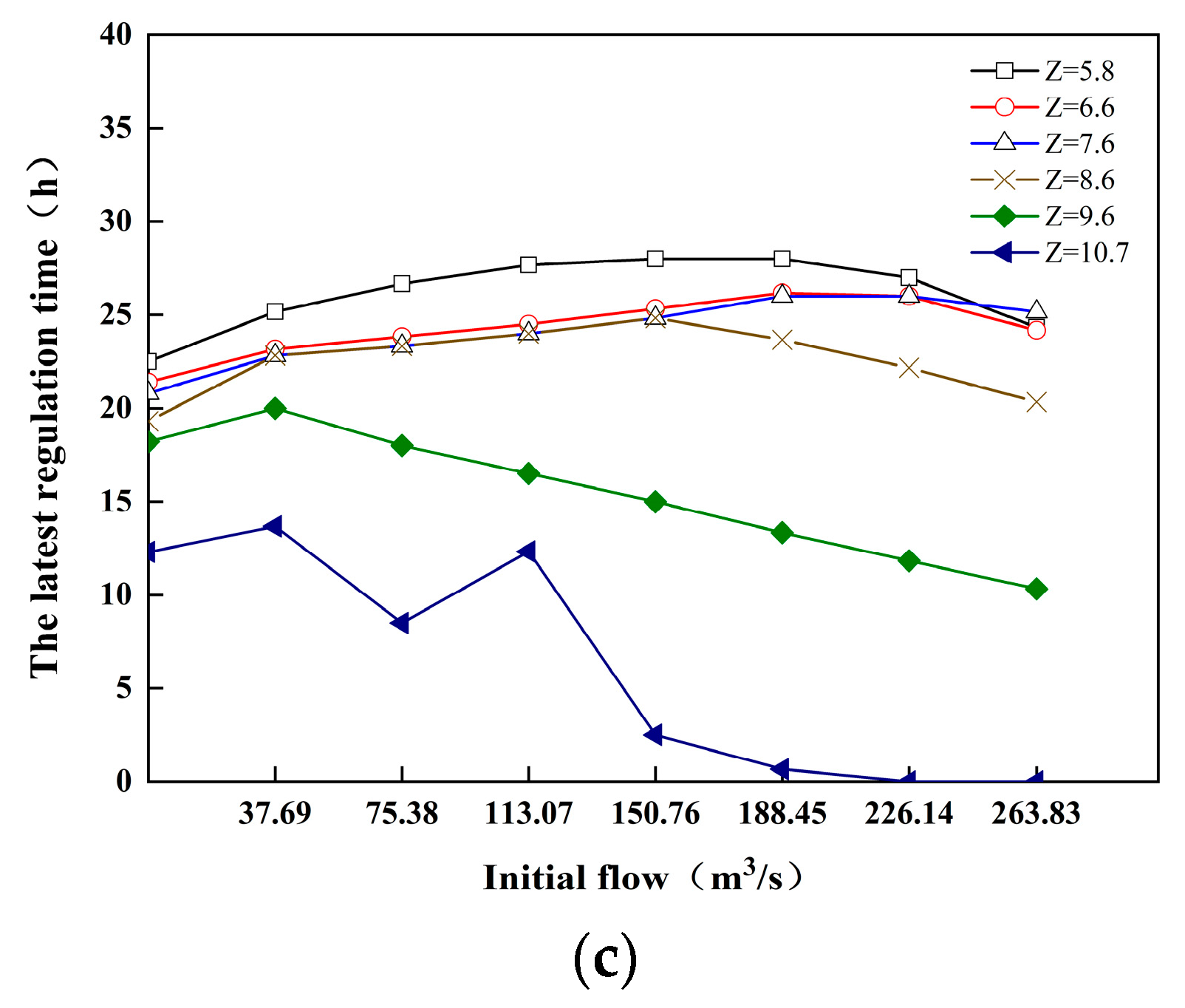
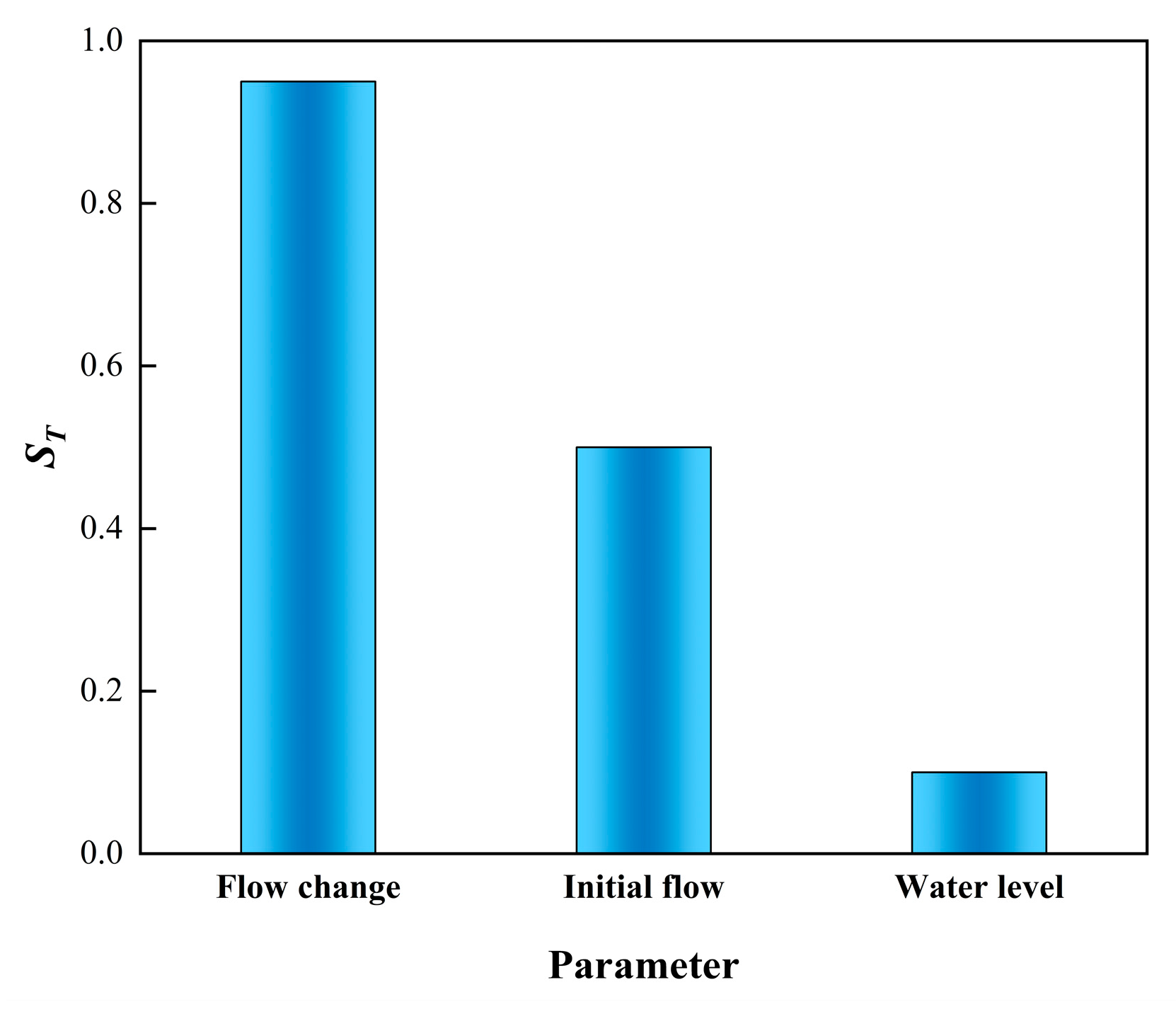
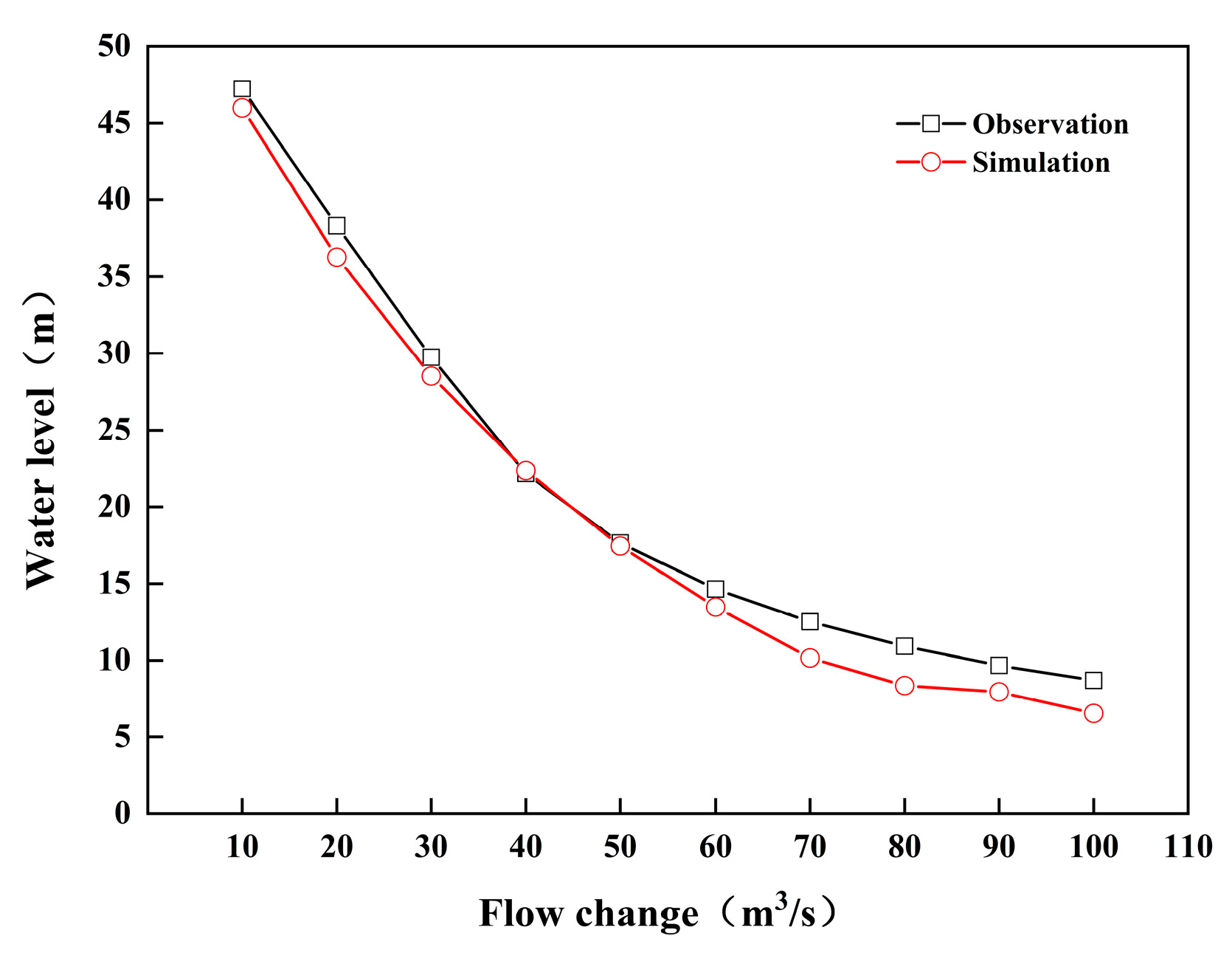
| The Pump Station | Type | Design Flow (m3/s) | Number | Design Flow (m3/s) | Water Level in Front of Station | ||
|---|---|---|---|---|---|---|---|
| Design (m) | Max (m) | Min (m) | |||||
| Paihekou | Axial flow | 37.69 | 9 | 301.5 | 4.10 | 5.80 | 3.60 |
| Shushan | Axial flow | 36.25 | 8 | 290 | 7.60 | 10.70 | 5.80 |
| Initial Upstream Flow (m3/s) | 0 | 37.69 | 75.38 | 113.07 | 150.76 | 188.45 | 226.14 | 263.83 |
|---|---|---|---|---|---|---|---|---|
| Flow change (m3/s) | 37.69 | − | − | − | − | − | − | − |
| 75.38 | 75.38 | − | − | − | − | − | − | |
| 113.07 | 113.07 | 113.07 | − | − | − | − | − | |
| 150.76 | 150.76 | 150.76 | 150.76 | − | − | − | − | |
| 188.45 | 188.45 | 188.45 | 188.45 | 188.45 | − | − | − | |
| 226.14 | 226.14 | 226.14 | 226.14 | 226.14 | 226.14 | − | − | |
| 263.83 | 263.83 | 263.83 | 263.83 | 263.83 | 263.83 | 263.83 | − | |
| 301.5 | 301.5 | 301.5 | 301.5 | 301.5 | 301.5 | 301.5 | 301.5 |
| Number | Variable | Fitting Equation Form | R2 |
|---|---|---|---|
| 1 | Flow change | Linear function fitting | 0.77 |
| 2 | Exponential function fitting | 0.92 | |
| 3 | Logarithmic function fitting | 0.90 | |
| 4 | Power function fitting | 0.99 |
| Number | Flow Change (m3/s) | Number | Flow Change (m3/s) |
|---|---|---|---|
| 1 | 10 | 6 | 60 |
| 2 | 20 | 7 | 70 |
| 3 | 30 | 8 | 80 |
| 4 | 40 | 9 | 90 |
| 5 | 50 | 10 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Ren, H.; Lin, F. Study on the Hydraulic Response of an Open-Channel Water Transmission Project after Flow Switching. Water 2023, 15, 3201. https://doi.org/10.3390/w15183201
Zhang N, Ren H, Lin F. Study on the Hydraulic Response of an Open-Channel Water Transmission Project after Flow Switching. Water. 2023; 15(18):3201. https://doi.org/10.3390/w15183201
Chicago/Turabian StyleZhang, Naifeng, Honglei Ren, and Fei Lin. 2023. "Study on the Hydraulic Response of an Open-Channel Water Transmission Project after Flow Switching" Water 15, no. 18: 3201. https://doi.org/10.3390/w15183201
APA StyleZhang, N., Ren, H., & Lin, F. (2023). Study on the Hydraulic Response of an Open-Channel Water Transmission Project after Flow Switching. Water, 15(18), 3201. https://doi.org/10.3390/w15183201






