Estimation of Hypoxic Areas in the Western Baltic Sea with Geostatistical Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Preparation
2.2. Geostatistical Methods
2.2.1. IPDW (Inverse Path Distance Weighting)
2.2.2. Ordinary Kriging
2.2.3. Quantile Regression Forest
3. Results
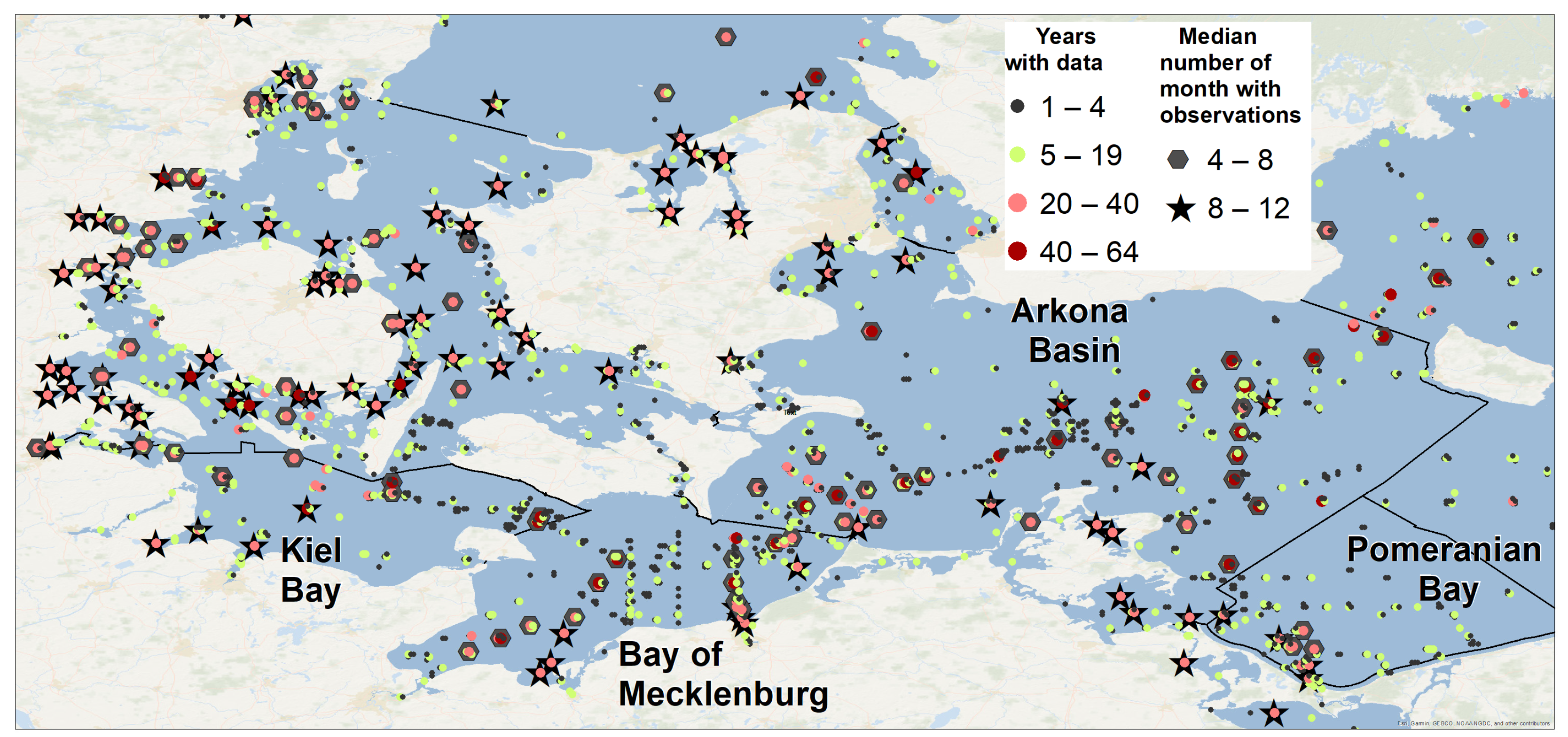
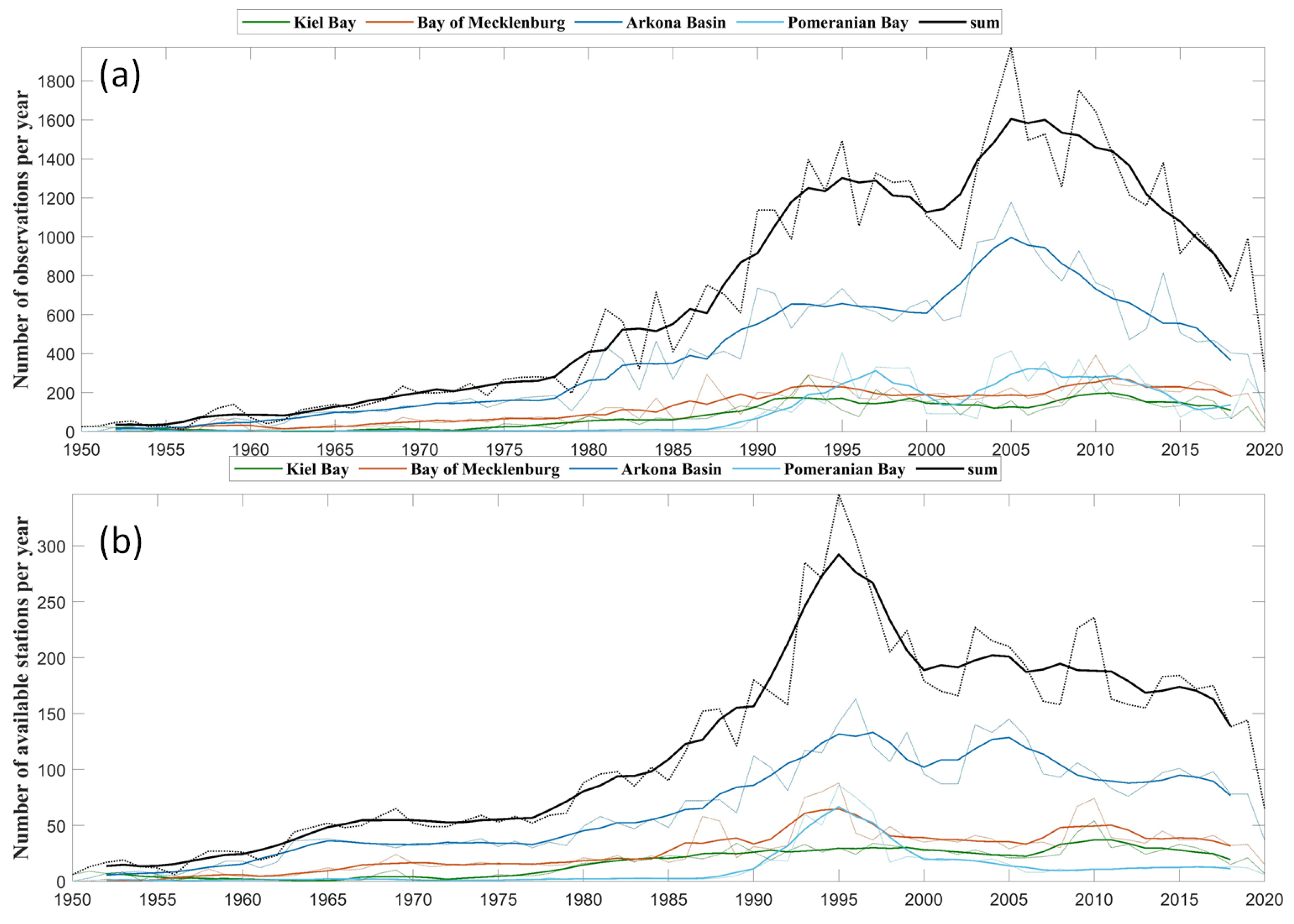
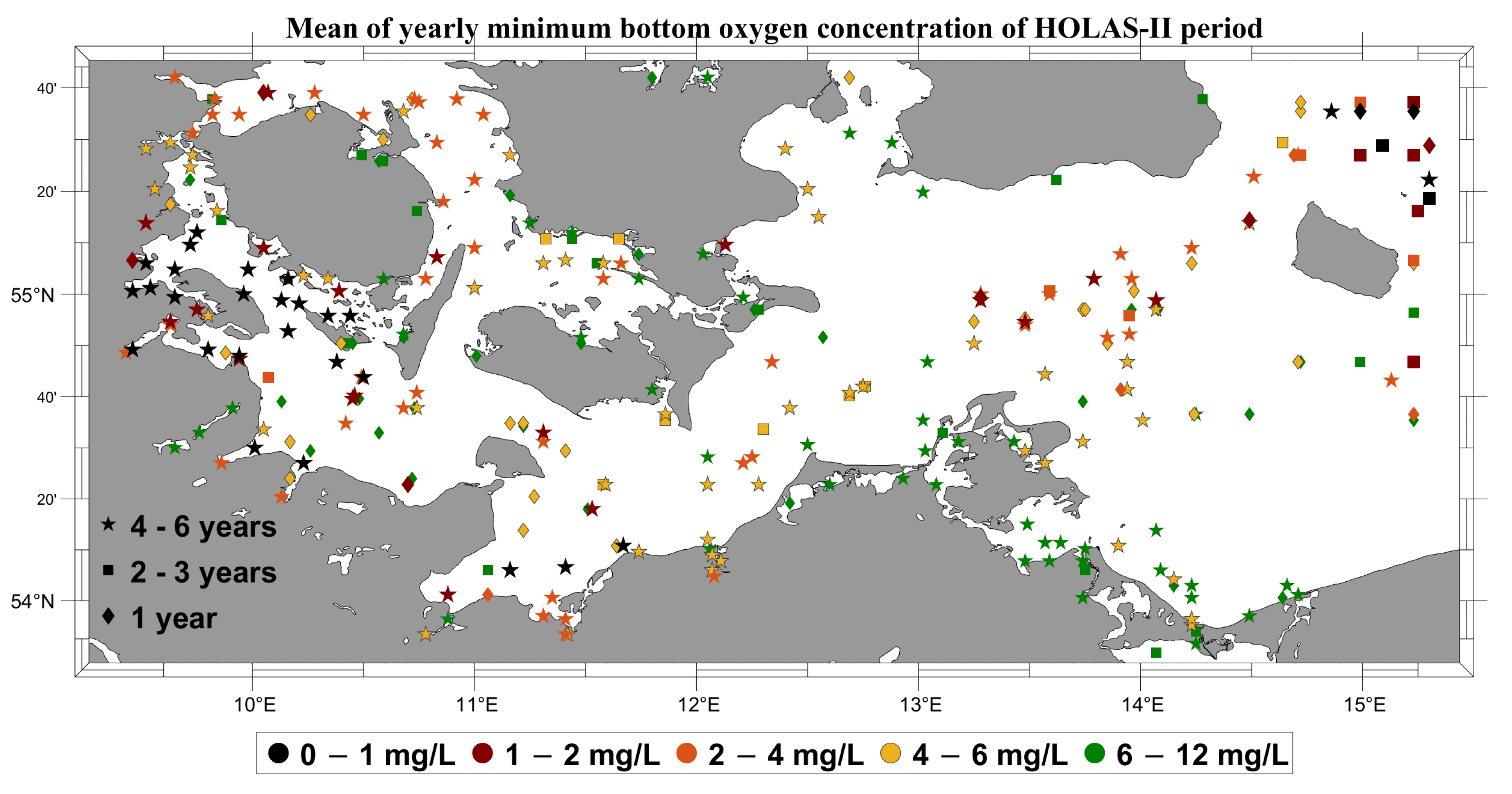
3.1. The Joint Dataset
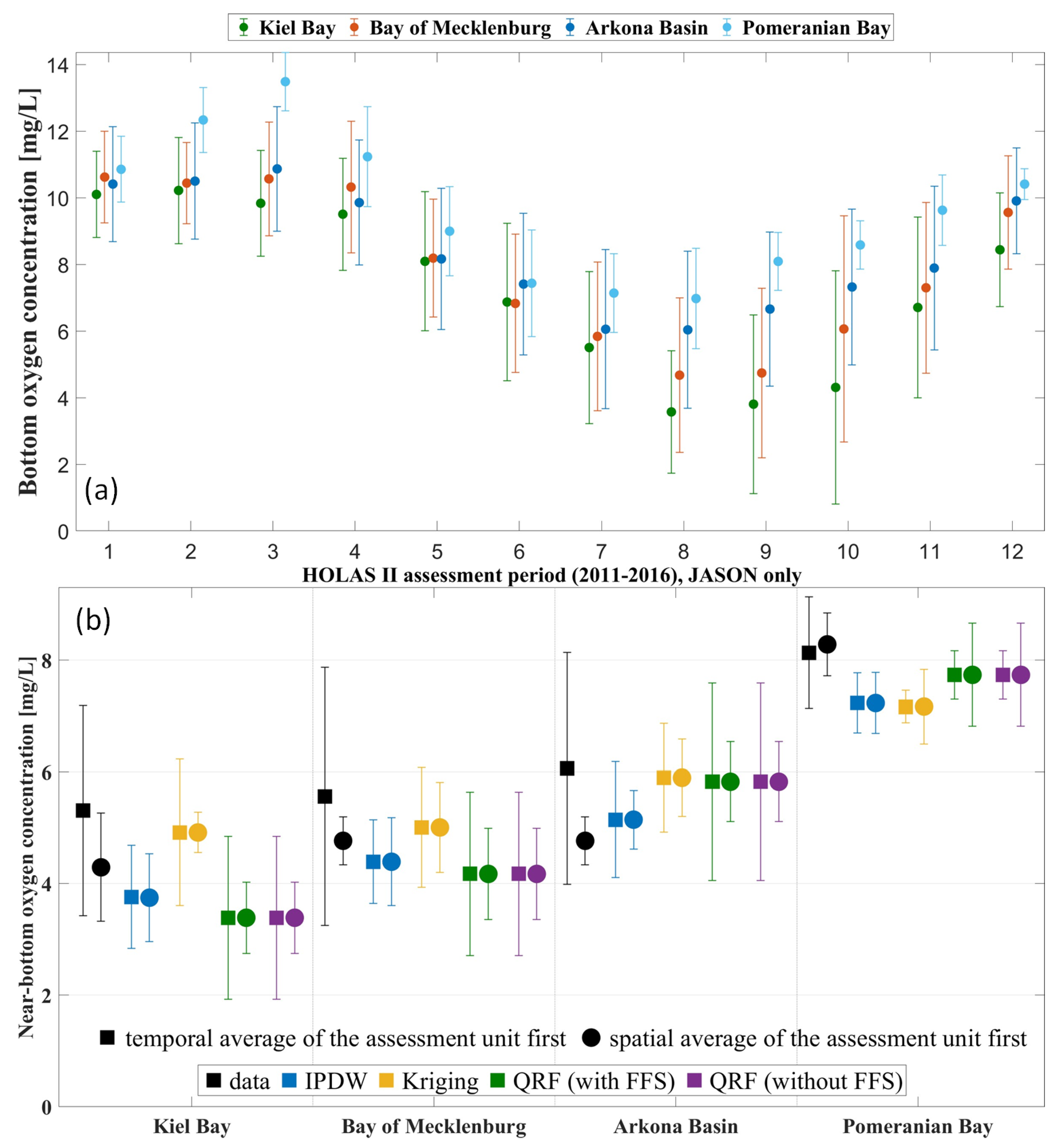
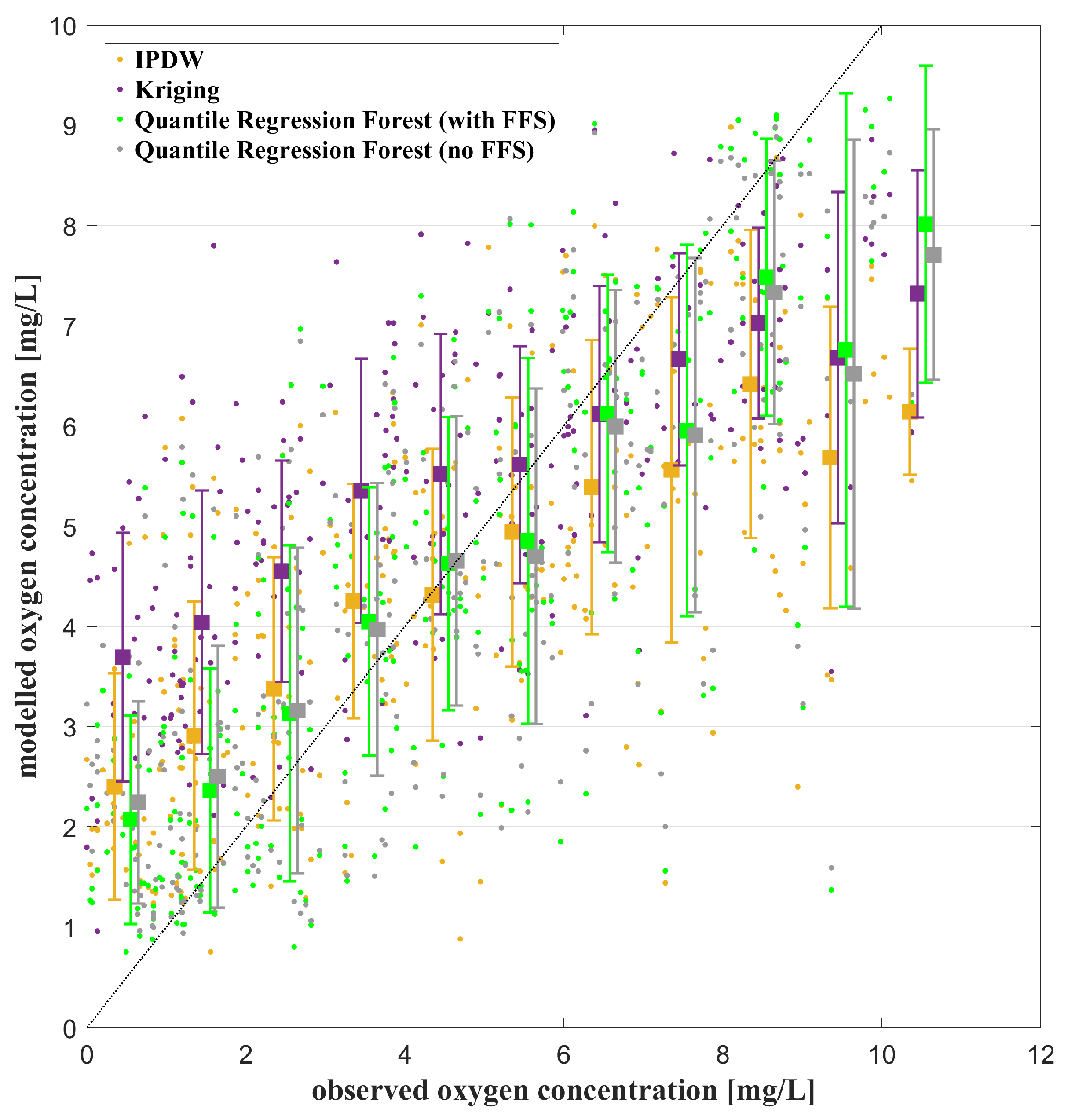
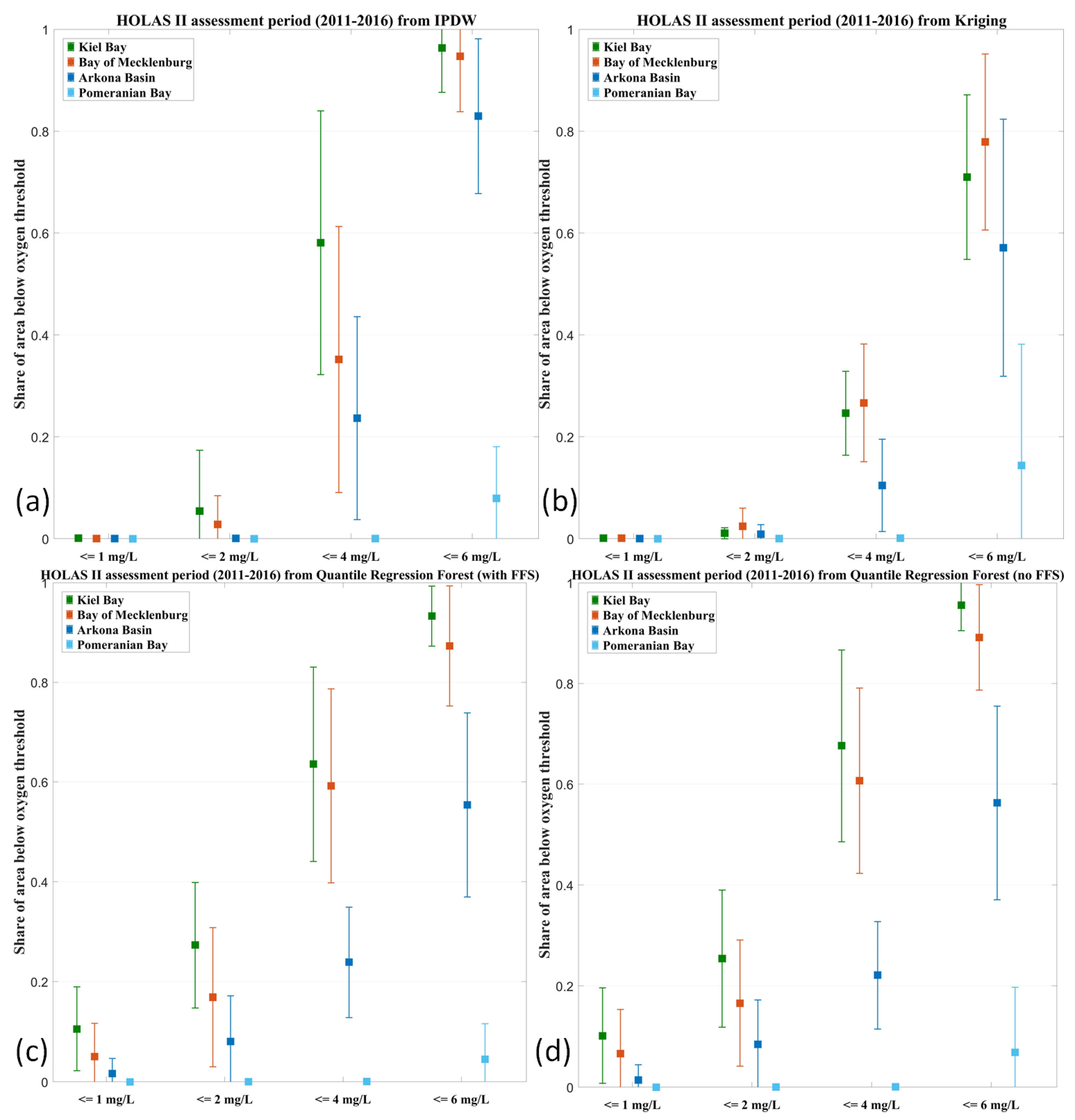
3.2. Comparison of the Different Geostatistical Methods for One Test Year (2015) and the HOLAS-II Assessment Period
3.3. Temporal Analysis for the Different Assessment Units
3.4. Training QRF with Data from 2015 and Applying It to the Whole Time Series
4. Discussion
4.1. The Joint Dataset
4.2. Potentials, Strengths and Weaknesses of the Geostatistical Methods Assessing the Critical Areas
4.3. Assessing the Pre-Eutrophic State and the Temporal Development since It
5. Summary and Conclusions
- A comprehensive dataset with freely available observations of near-bottom oxygen concentrations covering the western Baltic Sea was compiled.
- To estimate the hypoxic area (e.g., for environmental assessments like the EU-MSFD), gap-free spatial information is needed. We, therefore, applied two interpolation methods and the machine learning algorithm Quantile Random Forest (QRF).
- Our validation results indicated that QRF combined with feature forward selection gained the best results. The interpolation methods struggled to reproduce the very low oxygen concentrations, which led to substantially smaller hypoxic areas. Further, in years with only a few observations, the same spatial gaps were not closed by the interpolation method IPDW.
- QRF has the advantage that it is easily automatable and that the uncertainty can be estimated and combined with the area of applicability, gaining more robust results.
- The hypoxic areas increased in all applied methods drastically from the 1950s to the current situation, indicating a high anthropogenic pressure. To a lesser extent, they were also impacted by the hydrodynamic conditions, especially in the 1980s and 1990s. Nevertheless, our results indicate that even in the pre-eutrophic state, hypoxia occurred in the western Baltic Sea.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diaz, R.J.; Rosenberg, R. Spreading Dead Zones and Consequences for Marine Ecosystems. Science 2008, 321, 926–929. [Google Scholar] [CrossRef] [PubMed]
- Schmidtko, S.; Stramma, L.; Visbeck, M. Decline in global oceanic oxygen content during the past five decades. Nature 2017, 542, 335–339. [Google Scholar] [CrossRef] [PubMed]
- Brauko, K.M.; Cabral, A.; Costa, N.V.; Hayden, J.; Dias, C.E.P.; Leite, E.S.; Westphal, R.D.; Mueller, C.M.; Hall-Spencer, J.M.; Rodrigues, R.R.; et al. Marine Heatwaves, Sewage and Eutrophication Combine to Trigger Deoxygenation and Biodiversity Loss: A SW Atlantic Case Study. Front. Mar. Sci. 2020, 7, 590258. [Google Scholar] [CrossRef]
- Halpern, B.S.; Frazier, M.; Afflerbach, J.; Lowndes, J.S.; Micheli, F.; O’Hara, C.; Scarborough, C.; Selkoe, K.A. Recent pace of change in human impact on the world’s ocean. Sci. Rep. 2019, 9, 11609. [Google Scholar] [CrossRef] [PubMed]
- Vaquer-Sunyer, R.; Duarte, C.M. Thresholds of hypoxia for marine biodiversity. Proc. Natl. Acad. Sci. USA 2008, 105, 15452–15457. [Google Scholar] [CrossRef]
- 2008/56/EC; Directive 2008/56/EC of the European Parliament and of the Council of 17 June 2008. Establishing a Framework for Community Action in the Field of Marine Environmental Policy (Marine Strategy Framework Directive). Commission of the European Communities: Brussels, Belgium, 2008.
- Carstensen, J.; Andersen, J.H.; Gustafsson, B.G.; Conley, D.J. Deoxygenation of the Baltic Sea during the last century. Proc. Natl. Acad. Sci. USA 2014, 111, 5628–5633. [Google Scholar] [CrossRef] [PubMed]
- Breitburg, D.; Levin, L.A.; Oschlies, A.; Grégoire, M.; Chavez, F.P.; Conley, D.J.; Garçon, V.; Gilbert, D.; Gutiérrez, D.; Isensee, K.; et al. Declining oxygen in the global ocean and coastal waters. Science 2018, 359, eaam7240. [Google Scholar] [CrossRef]
- Schourup-Kristensen, V.; Larsen, J.; Maar, M. Drivers of hypoxia variability in a shallow and eutrophicated semi-enclosed fjord. Mar. Pollut. Bull. 2023, 188, 114621. [Google Scholar] [CrossRef]
- Dietze, H.; Löptien, U. Retracing hypoxia in Eckernförde Bight (Baltic Sea). Biogeosciences 2021, 18, 4243–4264. [Google Scholar] [CrossRef]
- Carstensen, J.; Conley, D.J. Baltic Sea Hypoxia Takes Many Shapes and Sizes. Limnol. Oceanogr. Bull. 2019, 28, 125–129. [Google Scholar] [CrossRef]
- Reissmann, J.H.; Burchard, H.; Feistel, R.; Hagen, E.; Lass, H.U.; Mohrholz, V.; Nausch, G.; Umlauf, L.; Wieczorek, G. Vertical mixing in the Baltic Sea and consequences for eutrophication—A review. Prog. Oceanogr. 2009, 82, 47–80. [Google Scholar] [CrossRef]
- Meier, H.E.M.; Eilola, K.; Almroth-Rosell, E.; Schimanke, S.; Kniebusch, M.; Höglund, A.; Pemberton, P.; Liu, Y.; Väli, G.; Saraiva, S. Disentangling the impact of nutrient load and climate changes on Baltic Sea hypoxia and eutrophication since 1850. Clim. Dyn. 2019, 53, 1145–1166. [Google Scholar] [CrossRef]
- Lennartz, S.T.; Lehmann, A.; Herrford, J.; Malien, F.; Hansen, H.P.; Biester, H.; Bange, H.W. Long-term trends at the Boknis Eck time series station (Baltic Sea), 1957–2013: Does climate change counteract the decline in eutrophication? Biogeosciences 2014, 11, 6323–6339. [Google Scholar] [CrossRef]
- Liblik, T.; Lips, U. Stratification Has Strengthened in the Baltic Sea—An Analysis of 35 Years of Observational Data. Front. Earth Sci. 2019, 7, 174. [Google Scholar] [CrossRef]
- Holt, J.; Harle, J.; Wakelin, S.; Jardine, J.; Hopkins, J. Why Is Seasonal Density Stratification in Shelf Seas Expected to Increase Under Future Climate Change? Geophys. Res. Lett. 2022, 49, e2022GL100448. [Google Scholar] [CrossRef]
- Rabouille, C.; Conley, D.J.; Dai, M.H.; Cai, W.J.; Chen, C.T.A.; Lansard, B.; Green, R.; Yin, K.; Harrison, P.J.; Dagg, M.; et al. Comparison of hypoxia among four river-dominated ocean margins: The Changjiang (Yangtze), Mississippi, Pearl, and Rhône rivers. Cont. Shelf Res. 2008, 28, 1527–1537. [Google Scholar] [CrossRef]
- Levin, L.A.; Ekau, W.; Gooday, A.J.; Jorissen, F.; Middelburg, J.J.; Naqvi, S.W.A.; Neira, C.; Rabalais, N.N.; Zhang, J. Effects of natural and human-induced hypoxia on coastal benthos. Biogeosciences 2009, 6, 2063–2098. [Google Scholar] [CrossRef]
- EEA. Oxygen Concentrations in Coastal and Marine Waters Surrounding Europe. Available online: https://www.eea.europa.eu/ims/oxygen-concentrations-in-coastal-and (accessed on 14 March 2023).
- Zettler, M.L.; Friedland, R.; Gogina, M.; Darr, A. Variation in benthic long-term data of transitional waters: Is interpretation more than speculation? PLoS ONE 2017, 12, e0175746. [Google Scholar] [CrossRef]
- LLUR. Sauerstoffmangel im Bodennahen Wasser der Westlichen Ostsee. 2020. Available online: https://www.schleswig-holstein.de/DE/Fachinhalte/M/meeresschutz/Downloads/Bericht_LLUR_Sauerstoff_2020.pdf (accessed on 28 August 2023).
- IOW. Data Product Baltic Thalweg (Level 4). Available online: https://www.io-warnemuende.de/baltic-thalweg-transect.html (accessed on 14 March 2023).
- HELCOM. State of the Baltic Sea—Second HELCOM Holistic Assessment 2011–2016. Available online: http://stateofthebalticsea.helcom.fi/ (accessed on 14 March 2023).
- HELCOM. State of the Baltic Sea—Second HELCOM Holistic Assessment 2011–2016. In Baltic Sea Environment Proceedings 2018; HELCOM: Lübeck, Germany, 2018. [Google Scholar]
- Piehl, S.; Friedland, R.; Heyden, B.; Leujak, W.; Neumann, T.; Schernewski, G. Modeling of Water Quality Indicators in the Western Baltic Sea: Seasonal Oxygen Deficiency. Environ. Model. Assess. 2022, 28, 429–446. [Google Scholar] [CrossRef]
- Testa, J.M.; Clark, J.B.; Dennison, W.C.; Donovan, E.C.; Fisher, A.W.; Ni, W.; Parker, M.; Scavia, D.; Spitzer, S.E.; Waldrop, A.M.; et al. Ecological Forecasting and the Science of Hypoxia in Chesapeake Bay. BioScience 2017, 67, 614–626. [Google Scholar] [CrossRef]
- Davis, B.J.K.; Curriero, F.C. Development and Evaluation of Geostatistical Methods for Non-Euclidean-Based Spatial Covariance Matrices. Math. Geosci. 2019, 51, 767–791. [Google Scholar] [CrossRef] [PubMed]
- Murphy, R.R.; Curriero, F.C.; Ball, W.P. Comparison of Spatial Interpolation Methods for Water Quality Evaluation in the Chesapeake Bay. J. Environ. Eng. 2010, 136, 160–171. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. Spatial interpolation methods applied in the environmental sciences: A review. Environ. Model. Softw. 2014, 53, 173–189. [Google Scholar] [CrossRef]
- Fang, S.; Del Giudice, D.; Scavia, D.; Binding, C.E.; Bridgeman, T.B.; Chaffin, J.D.; Evans, M.A.; Guinness, J.; Johengen, T.H.; Obenour, D.R. A space-time geostatistical model for probabilistic estimation of harmful algal bloom biomass and areal extent. Sci. Total Environ. 2019, 695, 133776. [Google Scholar] [CrossRef] [PubMed]
- Hengl, T.; Nussbaum, M.; Wright, M.N.; Heuvelink, G.B.; Gräler, B. Random forest as a generic framework for predictive modeling of spatial and spatio-temporal variables. PeerJ 2018, 6, e5518. [Google Scholar] [CrossRef] [PubMed]
- Guinness, J.; Stein, M.L. Interpolation of Nonstationary High Frequency Spatial—Temporal Temperature Data. Ann. Appl. Stat. 2013, 7, 1684–1708. [Google Scholar] [CrossRef]
- Gogina, M.; Morys, C.; Forster, S.; Gräwe, U.; Friedland, R.; Zettler, M.L. Towards benthic ecosystem functioning maps: Quantifying bioturbation potential in the German part of the Baltic Sea. Ecol. Indic. 2017, 73, 574–588. [Google Scholar] [CrossRef]
- Meyer, H.; Pebesma, E. Machine learning-based global maps of ecological variables and the challenge of assessing them. Nat. Commun. 2022, 13, 2208. [Google Scholar] [CrossRef]
- Kotta, J.; Kutser, T.; Teeveer, K.; Vahtmäe, E.; Pärnoja, M. Predicting Species Cover of Marine Macrophyte and Invertebrate Species Combining Hyperspectral Remote Sensing, Machine Learning and Regression Techniques. PLoS ONE 2013, 8, e63946. [Google Scholar] [CrossRef]
- Smoliński, S.; Radtke, K. Spatial prediction of demersal fish diversity in the Baltic Sea: Comparison of machine learning and regression-based techniques. ICES J. Mar. Sci. 2017, 74, 102–111. [Google Scholar] [CrossRef]
- Ross, A.C.; Stock, C.A. An assessment of the predictability of column minimum dissolved oxygen concentrations in Chesapeake Bay using a machine learning model. Estuar. Coast. Shelf Sci. 2019, 221, 53–65. [Google Scholar] [CrossRef]
- HELCOM. Approaches and Methods for Eutrophication Target Setting in the Baltic Sea Region; Helsinki Commission Press: Helsinki, Finland, 2013.
- Schernewski, G.; Friedland, R.; Carstens, M.; Hirt, U.; Leujak, W.; Nausch, G.; Neumann, T.; Petenati, T.; Sagert, S.; Wasmund, N.; et al. Implementation of European marine policy: New water quality targets for German Baltic waters. Mar. Policy 2015, 51, 305–321. [Google Scholar] [CrossRef]
- Börgel, F.; Neumann, T.; Rooze, J.; Radtke, H.; Barghorn, L.; Meier, H.E.M. Deoxygenation of the Baltic Sea during the last millennium. Front. Mar. Sci. 2023, 10, 1174039. [Google Scholar] [CrossRef]
- Radtke, H.; Börgel, F.; Brunnabend, S.-E.; Eggert, A.; Kniebusch, M.; Meier, H.E.M.; Neumann, D.; Neumann, T.; Placke, M. Validator—A Web-Based Interactive Tool for Validation of Ocean Models at Oceanographic Stations. J. Open Res. Softw. 2019, 7, 18. [Google Scholar] [CrossRef]
- Skogen, M.D.; Ji, R.; Akimova, A.; Daewel, U.; Hansen, C.; Hjøllo, S.S.; van Leeuwen, S.M.; Maar, M.; Macias, D.; Mousing, E.A.; et al. Disclosing the truth: Are models better than observations? Mar. Ecol. Prog. Ser. 2021, 680, 7–13. [Google Scholar] [CrossRef]
- HELCOM. Subbasins (Level 2) 2022. Available online: https://metadata.helcom.fi/geonetwork/srv/eng/catalog.search#/metadata/d4b6296c-fd19-462c-94d2-4c81b9313d77 (accessed on 14 March 2023).
- IOW. ODIN 2 (Oceanographic Database Search with Interactive Navigation). Available online: https://odin2.io-warnemuende.de/ (accessed on 14 March 2023).
- ICES. Oceanographic Database. Available online: https://www.ices.dk/data/data-portals/Pages/ocean.aspx (accessed on 19 December 2020).
- Boknis Eck. Available online: https://www.bokniseck.de/database-access (accessed on 14 March 2023).
- Copernicus Marine Service. Baltic Sea—Near Real-Time (NRT) In Situ Quality Controlled Observations, Hourly Updated and Distributed by INSTAC within 24–48 Hours from Acquisition in Average. Available online: https://data.marine.copernicus.eu/product/INSITU_BAL_PHYBGCWAV_DISCRETE_MYNRT_013_032/description (accessed on 6 May 2021).
- Weiss, R.F. The solubility of nitrogen, oxygen and argon in water and seawater. Deep Sea Res. Oceanogr. Abstr. 1970, 17, 721–735. [Google Scholar] [CrossRef]
- EMODnet. Bathymetry. Available online: https://emodnet.ec.europa.eu/en/bathymetry (accessed on 14 March 2023).
- Seifert, T.; Tauber, F.; Kayser, B. A High Resolution Spherical Grid Topography of the Baltic Sea, 2nd ed. Available online: www.io-warnemuende.de/iowtopo (accessed on 28 August 2023).
- Vock, C.; Friedland, R.; Piehl, S. Near-Bottom Oxygen Observations from the Western Baltic Sea. 2023. Available online: https://doi.org/10.5281/zenodo.8116592 (accessed on 28 August 2023).
- Suominen, T.; Tolvanen, H.; Kalliola, R. Surface layer salinity gradients and flow patterns in the archipelago coast of SW Finland, northern Baltic Sea. Mar. Environ. Res. 2010, 69, 216–226. [Google Scholar] [CrossRef]
- Stachelek, J. ipdw: Spatial Interpolation by Inverse Path Distance Weighting. 2023. Available online: https://cran.r-project.org/package=ipdw (accessed on 28 August 2023).
- Cressie, N. The origins of kriging. Math. Geol. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- Murphy, R.R.; Kemp, W.M.; Ball, W.P. Long-Term Trends in Chesapeake Bay Seasonal Hypoxia, Stratification, and Nutrient Loading. Estuaries Coasts 2011, 34, 1293–1309. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. A tutorial guide to geostatistics: Computing and modelling variograms and kriging. Catena 2014, 113, 56–69. [Google Scholar] [CrossRef]
- Negreiros, J.; Painho, M.; Aguilar, F.; Aguilar, M. Geographical information systems principles of ordinary kriging interpolator. J. Appl. Sci. 2010, 10, 852–867. [Google Scholar] [CrossRef]
- Ribeiro, P.J.; Diggle, P.J. geoR—A Package for Geostatistical Data Analysis Using the R Software. 2008. Available online: http://leg.ufpr.br/geoR/ (accessed on 28 August 2023).
- Muñoz, F. geoRcb: An Extension of Package geoR that Works with Cost-Based Distances; Zenodo: Genève, Switzerland, 2015. [Google Scholar] [CrossRef]
- López-Quílez, A.; Muñoz, F. Geostatistical computing of acoustic maps in the presence of barriers. Math. Comput. Model. 2009, 50, 929–938. [Google Scholar] [CrossRef]
- Curriero, F.C. On the Use of Non-Euclidean Distance Measures in Geostatistics. Math. Geol. 2006, 38, 907–926. [Google Scholar] [CrossRef]
- Murphy, R.R.; Perlman, E.; Ball, W.P.; Curriero, F.C. Water-Distance-Based Kriging in Chesapeake Bay. J. Hydrol. Eng. 2015, 20, 05014034. [Google Scholar] [CrossRef]
- Løland, A.; Høst, G. Spatial covariance modelling in a complex coastal domain by multidimensional scaling. Environmetrics 2003, 14, 307–321. [Google Scholar] [CrossRef]
- Meinshausen, N.; Ridgeway, G. Quantile regression forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. An Introduction to Feature Selection. In Applied Predictive Modeling; Kuhn, M., Johnson, K., Eds.; Springer: New York, NY, USA, 2013; pp. 487–519. [Google Scholar]
- Meyer, H. CAST: Caret Applications for Spatio-Temporal Models. 2023. Available online: https://hannameyer.github.io/CAST/ (accessed on 28 August 2023).
- Meyer, H.; Reudenbach, C.; Hengl, T.; Katurji, M.; Nauss, T. Improving performance of spatio-temporal machine learning models using forward feature selection and target-oriented validation. Environ. Model. Softw. 2018, 101, 1–9. [Google Scholar] [CrossRef]
- Große, F.; Greenwood, N.; Kreus, M.; Lenhart, H.J.; Machoczek, D.; Pätsch, J.; Salt, L.; Thomas, H. Looking beyond stratification: A model-based analysis of the biological drivers of oxygen deficiency in the North Sea. Biogeosciences 2016, 13, 2511–2535. [Google Scholar] [CrossRef]
- Neumann, T.; Siegel, H.; Moros, M.; Gerth, M.; Kniebusch, M.; Heydebreck, D. Ventilation of the northern Baltic Sea. Ocean Sci. 2020, 16, 767–780. [Google Scholar] [CrossRef]
- Meyer, H.; Pebesma, E. Predicting into unknown space? Estimating the area of applicability of spatial prediction models. Methods Ecol. Evol. 2021, 12, 1620–1633. [Google Scholar] [CrossRef]
- Kõuts, M.; Maljutenko, I.; Elken, J.; Liu, Y.; Hansson, M.; Viktorsson, L.; Raudsepp, U. Recent regime of persistent hypoxia in the Baltic Sea. Environ. Res. Commun. 2021, 3, 075004. [Google Scholar] [CrossRef]
- Grégoire, M.; Garçon, V.; Garcia, H.; Breitburg, D.; Isensee, K.; Oschlies, A.; Telszewski, M.; Barth, A.; Bittig, H.C.; Carstensen, J.; et al. A Global Ocean Oxygen Database and Atlas for Assessing and Predicting Deoxygenation and Ocean Health in the Open and Coastal Ocean. Front. Mar. Sci. 2021, 8, 724913. [Google Scholar] [CrossRef]
- Institute, W.R. Eutrophication & Hypoxia Map Data Set. Available online: https://www.wri.org/data/eutrophication-hypoxia-map-data-set (accessed on 14 March 2023).
- Krapf, K.; Naumann, M.; Dutheil, C.; Meier, H.E.M. Investigating Hypoxic and Euxinic Area Changes Based on Various Datasets From the Baltic Sea. Front. Mar. Sci. 2022, 9, 823476. [Google Scholar] [CrossRef]
- BSH. Available online: https://www.bsh.de/EN/TOPICS/Monitoring_systems/MARNET_monitoring_network/marnet_monitoring_network_node.html (accessed on 28 August 2023).
- Feistel, S.; Feistel, R.; Nehring, D.; Matthäus, W.; Nausch, G.; Naumann, M. Hypoxic and anoxic regions in the Baltic Sea, 1969-2015. Meereswiss Berichte 2016, 100, 1–85. [Google Scholar]
- Yu, X.; Shen, J.; Du, J. A Machine-Learning-Based Model for Water Quality in Coastal Waters, Taking Dissolved Oxygen and Hypoxia in Chesapeake Bay as an Example. Water Resour. Res. 2020, 56, e2020WR027227. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Rossiter, D.G. About regression-kriging: From equations to case studies. Comput. Geosci. 2007, 33, 1301–1315. [Google Scholar] [CrossRef]
- Ver Hoef, J.M. Kriging models for linear networks and non-Euclidean distances: Cautions and solutions. Methods Ecol. Evol. 2018, 9, 1600–1613. [Google Scholar] [CrossRef]
- Meng, Q.; Liu, Z.; Borders, B.E. Assessment of regression kriging for spatial interpolation—Comparisons of seven GIS interpolation methods. Cartogr. Geogr. Inf. Sci. 2013, 40, 28–39. [Google Scholar] [CrossRef]
- Meyer, H.; Reudenbach, C.; Wöllauer, S.; Nauss, T. Importance of spatial predictor variable selection in machine learning applications—Moving from data reproduction to spatial prediction. Ecol. Model. 2019, 411, 108815. [Google Scholar] [CrossRef]
- Ludwig, M.; Moreno-Martinez, A.; Hölzel, N.; Pebesma, E.; Meyer, H. Assessing and improving the transferability of current global spatial prediction models. Glob. Ecol. Biogeogr. 2023, 32, 356–368. [Google Scholar] [CrossRef]
- Leipe, T.; Naumann, M.; Tauber, F.; Radtke, H.; Friedland, R.; Hiller, A.; Arz, H.W. Regional distribution patterns of chemical parameters in surface sediments of the south-western Baltic Sea and their possible causes. Geo-Mar. Lett. 2017, 37, 593–606. [Google Scholar] [CrossRef]
- Mohrholz, V. Major Baltic Inflow Statistics—Revised. Front. Mar. Sci. 2018, 5, 384. [Google Scholar] [CrossRef]
- Börgel, F.; Gröger, M.; Meier, H.E.M.; Dutheil, C.; Radtke, H.; Borchert, L. The impact of Atlantic Multidecadal Variability on Baltic Sea temperatures limited to winter. npj Clim. Atmos. Sci. 2023, 6, 64. [Google Scholar] [CrossRef]
- Väli, G.; Meier, H.E.M.; Elken, J. Simulated halocline variability in the Baltic Sea and its impact on hypoxia during 1961–2007. J. Geophys. Res. Ocean. 2013, 118, 6982–7000. [Google Scholar] [CrossRef]
- Gustafsson, B.G.; Schenk, F.; Blenckner, T.; Eilola, K.; Meier, H.E.M.; Müller-Karulis, B.; Neumann, T.; Ruoho-Airola, T.; Savchuk, O.P.; Zorita, E. Reconstructing the Development of Baltic Sea Eutrophication 1850–2006. Ambio 2012, 41, 534–548. [Google Scholar] [CrossRef]
- Meier, H.E.M.; Edman, M.K.; Eilola, K.J.; Placke, M.; Neumann, T.; Andersson, H.C.; Brunnabend, S.-E.; Dieterich, C.; Frauen, C.; Friedland, R.; et al. Assessment of Eutrophication Abatement Scenarios for the Baltic Sea by Multi-Model Ensemble Simulations. Front. Mar. Sci. 2018, 5, 440. [Google Scholar] [CrossRef]
- Kuliński, K.; Rehder, G.; Asmala, E.; Bartosova, A.; Carstensen, J.; Gustafsson, B.; Hall, P.O.J.; Humborg, C.; Jilbert, T.; Jürgens, K.; et al. Biogeochemical functioning of the Baltic Sea. Earth Syst. Dynam. 2022, 13, 633–685. [Google Scholar] [CrossRef]




| R2 | Maximal Distance (d) | ||||||
| 22,750 | 45,500 | 79,500 | 114,000 | 148,000 | 182,000 | ||
| Inverse Distance Power (p) | 0.25 | 0.449 | 0.456 | 0.448 | 0.433 | 0.417 | 0.407 |
| 0.5 | 0.456 | 0.460 | 0.436 | 0.418 | 0.400 | 0.382 | |
| 0.875 | 0.448 | 0.459 | 0.453 | 0.449 | 0.445 | 0.443 | |
| 1.25 | 0.433 | 0.442 | 0.440 | 0.438 | 0.437 | 0.437 | |
| 1.625 | 0.417 | 0.425 | 0.425 | 0.424 | 0.424 | 0.424 | |
| 2 | 0.407 | 0.412 | 0.412 | 0.412 | 0.412 | 0.412 | |
| RMSE | Maximal Distance (d) | ||||||
| 22,750 | 45,500 | 79,500 | 114,000 | 148,000 | 182,000 | ||
| Inverse Distance Power (p) | 0.25 | 2.112 | 2.105 | 2.141 | 2.196 | 2.253 | 2.294 |
| 0.5 | 2.105 | 2.084 | 2.139 | 2.202 | 2.259 | 2.309 | |
| 0.875 | 2.141 | 2.091 | 2.097 | 2.108 | 2.118 | 2.125 | |
| 1.25 | 2.196 | 2.148 | 2.142 | 2.141 | 2.141 | 2.141 | |
| 1.625 | 2.253 | 2.211 | 2.204 | 2.203 | 2.202 | 2.202 | |
| 2 | 2.294 | 2.264 | 2.259 | 2.258 | 2.257 | 2.257 | |
| Method | RMSE | R2 |
|---|---|---|
| IPDW | 2.084 | 0.460 |
| Kriging | 2.142 | 0.433 |
| Quantile Regression Forest (with Forward Feature Selection) | 1.888 | 0.554 |
| Quantile Regression Forest (without Forward Feature Selection) | 1.943 | 0.545 |
| Decade | Share of Stations [%] | Share of Area [%] | |||||
|---|---|---|---|---|---|---|---|
| IPDW | Kriging | QRF (with FFS) | QRF (without FFS) | Kõuts, Maljutenko [72] | Piehl, Friedland [25] | ||
| Kiel Bay (NBO ≤ 2 mg/L) | |||||||
| 1950 | 9.9 | 0 | 0 | 0.6 | 0 | 0.3 | |
| 1960 | 9.5 | 47.0 | 0 | 4.9 | 0.3 | 2.0 | |
| 1970 | 12.1 | 0.7 | 0 | 7.7 | 2.9 | 6.6 | |
| 1980 | 26.8 | 0.1 | 0.8 | 17.2 | 15.4 | 11.6 | |
| 1990 | 17.2 | 0.1 | 0.5 | 20.4 | 24.1 | 0.7 | 9.0 |
| 2000 | 25.0 | 8.7 | 0.9 | 27.5 | 29.4 | 1.1 | 7.9 |
| 2010 | 21.1 | 0.9 | 1.0 | 23.9 | 21.0 | 0.6 | 4.0 |
| Bay of Mecklenburg (NBO ≤ 2 mg/L) | |||||||
| 1950 | 1.2 | 0 | 0 | 0 | 0 | 8.3 | |
| 1960 | 3.1 | 0 | 0 | 2.0 | 0.1 | 16.4 | |
| 1970 | 22.3 | 10.0 | 4.1 | 16.0 | 16.6 | 20.4 | |
| 1980 | 19.7 | 12.9 | 5.0 | 38.5 | 36.0 | 26.0 | |
| 1990 | 10.9 | 0 | 0.9 | 12.2 | 13.7 | 3.1 | 24.1 |
| 2000 | 16.3 | 1.1 | 0.6 | 16.1 | 21.2 | 1.9 | 22.6 |
| 2010 | 15.0 | 0.2 | 1.5 | 15.7 | 18.2 | 0.9 | 18.9 |
| Arkona Basin (NBO ≤ 4 mg/L) | |||||||
| 1950 | 5.8 | 0 | 0 | 5.7 | 0.2 | 2.8 | |
| 1960 | 17.4 | 0.2 | 0.8 | 10.3 | 9.1 | 4.6 | |
| 1970 | 27.1 | 6.5 | 10.0 | 16.2 | 15.5 | 6.2 | |
| 1980 | 23.5 | 27.6 | 14.8 | 25.6 | 26.6 | 7.8 | |
| 1990 | 16.3 | 15.0 | 16.0 | 18.3 | 20.0 | 3.4 | 7.4 |
| 2000 | 15.7 | 3.7 | 2.5 | 17.3 | 17.7 | 4.0 | 7.1 |
| 2010 | 16.3 | 15.8 | 5.6 | 21.7 | 20.5 | 2.4 | 6.4 |
| Pomeranian Bay (NBO ≤ 6 mg/L) | |||||||
| 1950 | 0 | 0 | 10.0 | 0 | 0 | 2.2 | |
| 1960 | 14.3 | 0.8 | 5.9 | 0 | 0 | 2.3 | |
| 1970 | 22.2 | 8.1 | 75.3 | 0 | 0 | 3.3 | |
| 1980 | 4.9 | 3.3 | 33.2 | 0 | 0 | 3.3 | |
| 1990 | 25.6 | 0.2 | 21.2 | 0 | 0.6 | 3.1 | 3.9 |
| 2000 | 8.5 | 4.0 | 2.6 | 0.4 | 0.4 | 2.2 | 3.3 |
| 2010 | 7.8 | 3.9 | 11.5 | 0.9 | 1.7 | 0.1 | 2.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Friedland, R.; Vock, C.; Piehl, S. Estimation of Hypoxic Areas in the Western Baltic Sea with Geostatistical Models. Water 2023, 15, 3235. https://doi.org/10.3390/w15183235
Friedland R, Vock C, Piehl S. Estimation of Hypoxic Areas in the Western Baltic Sea with Geostatistical Models. Water. 2023; 15(18):3235. https://doi.org/10.3390/w15183235
Chicago/Turabian StyleFriedland, René, Clarissa Vock, and Sarah Piehl. 2023. "Estimation of Hypoxic Areas in the Western Baltic Sea with Geostatistical Models" Water 15, no. 18: 3235. https://doi.org/10.3390/w15183235
APA StyleFriedland, R., Vock, C., & Piehl, S. (2023). Estimation of Hypoxic Areas in the Western Baltic Sea with Geostatistical Models. Water, 15(18), 3235. https://doi.org/10.3390/w15183235







