Numerical Modeling of Local Scour in the Vicinity of Bridge Abutments When Covered with Ice
Abstract
:1. Introduction
2. Experiment Setup
3. Numerical Model
3.1. Governing Equations
3.2. Turbulent Model
3.3. Sediment Scour Model
Deposition and Entrainment
3.4. Model Setup
3.4.1. Meshing
3.4.2. Boundary Conditions
4. Results and Discussion
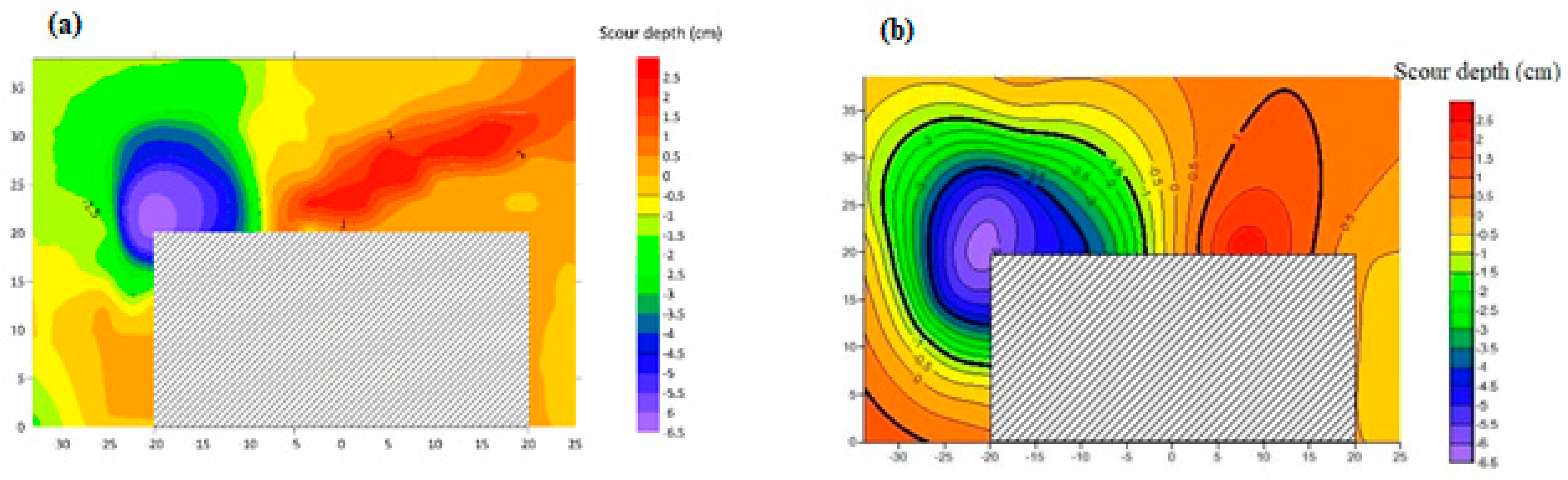
4.1. Local Scour around Square Abutment under Open Channel Flow Condition
4.2. Local Scour around Semi-Circular Abutment under Open Channel Flow Condition
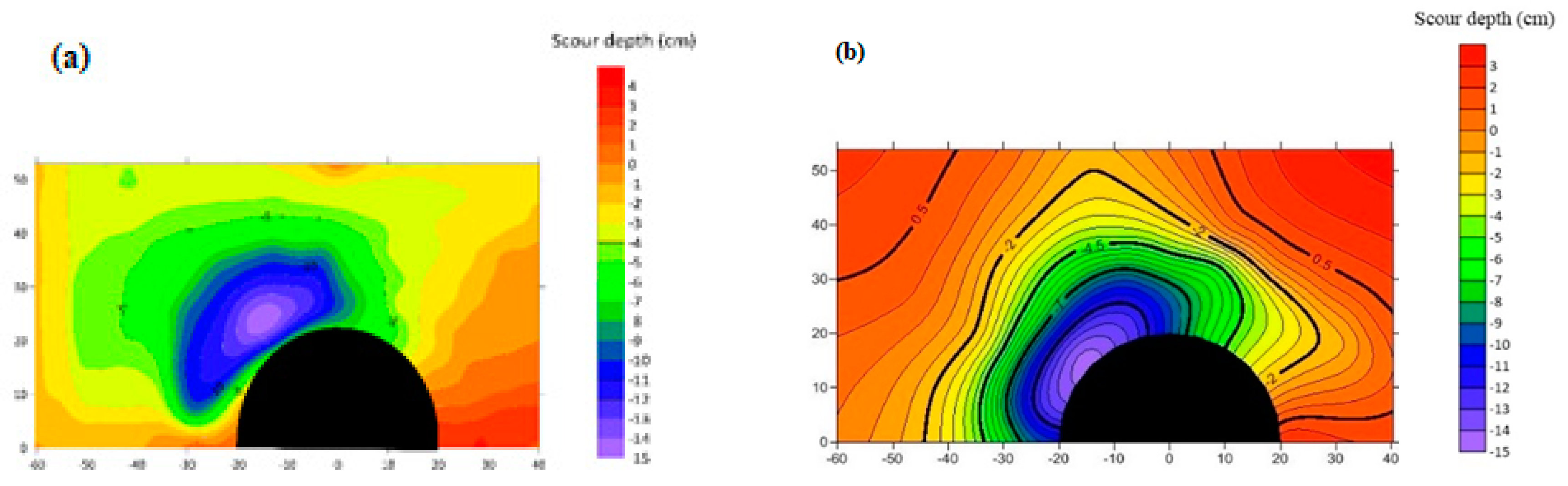
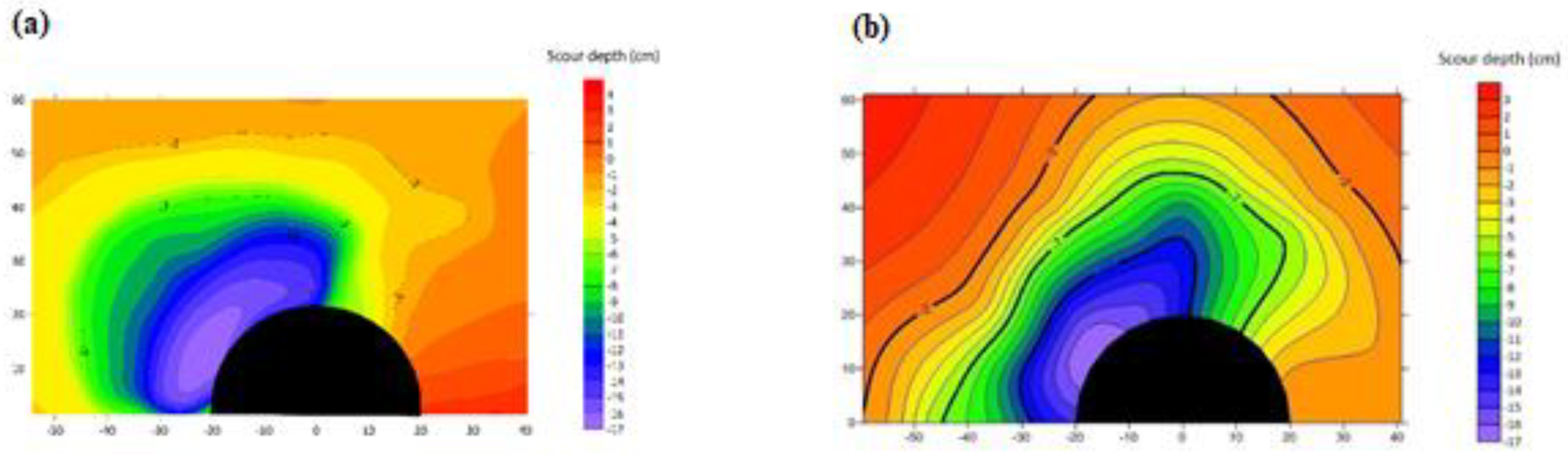
4.3. Local Scour around Square Abutment under Ice-Covered Flow Conditions
4.4. Local Scour around Semi-Circular Abutment under Ice-Covered Flow Conditions
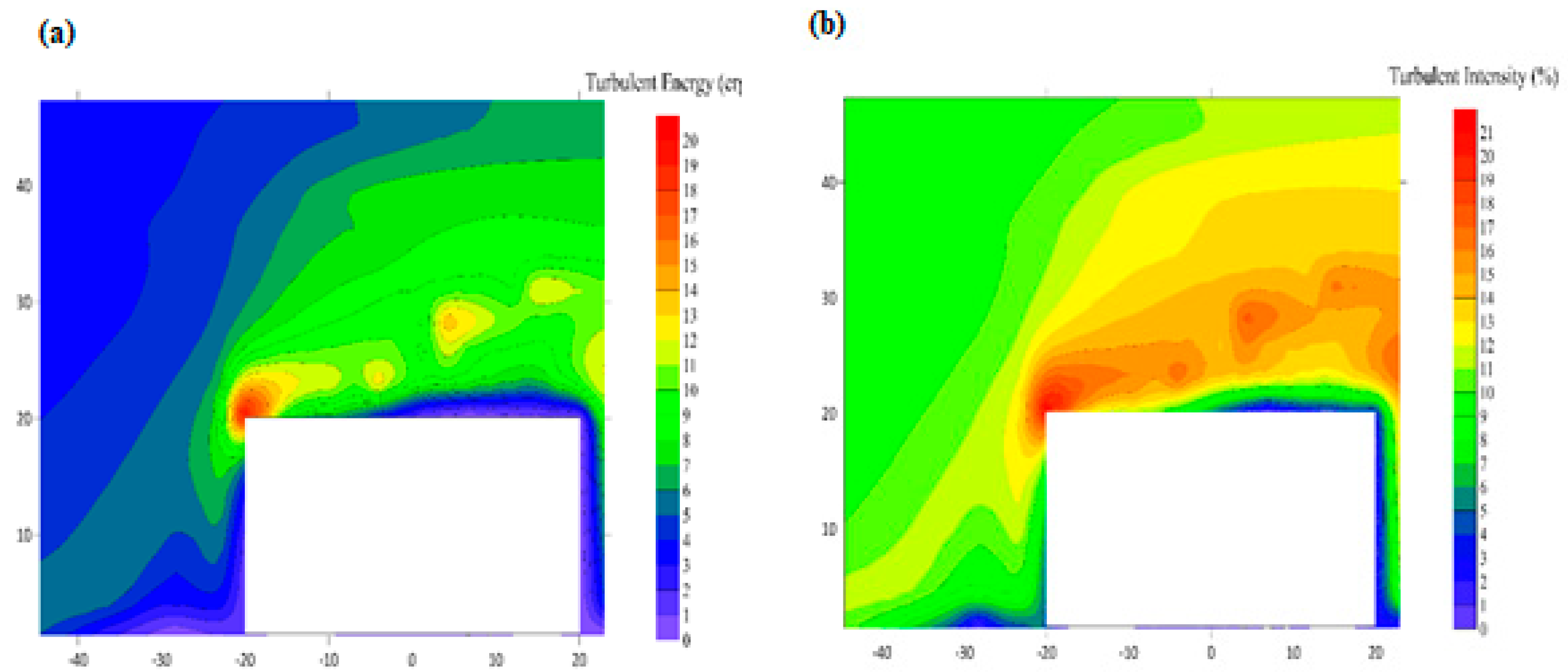
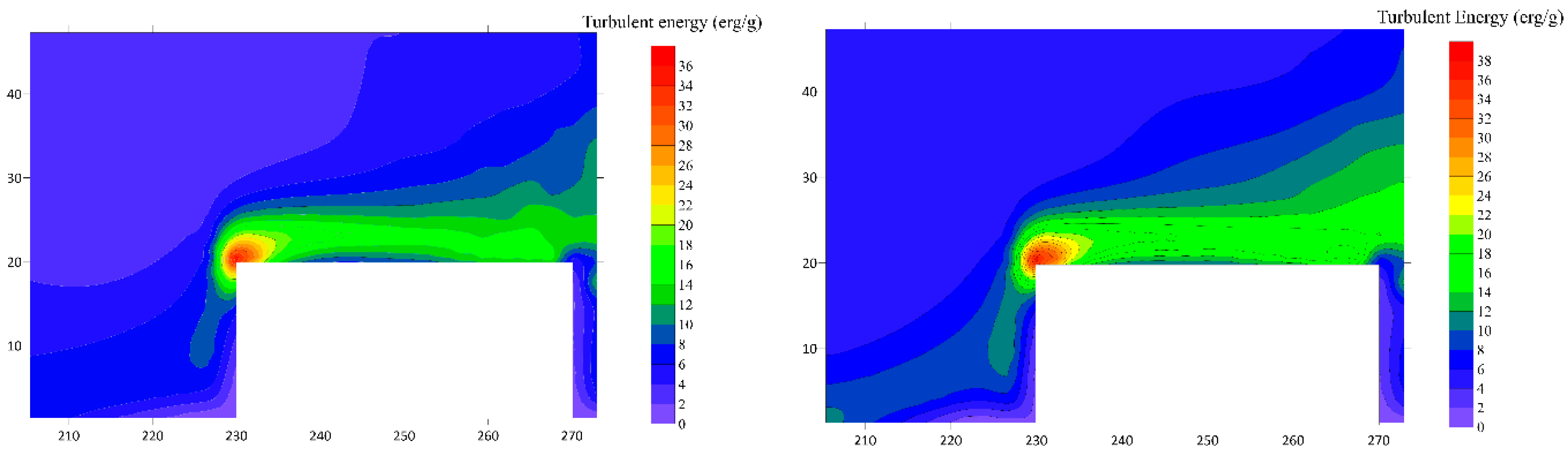
4.5. The Numerical Turbulent Energy Distribution around the Square Bridge Abutments
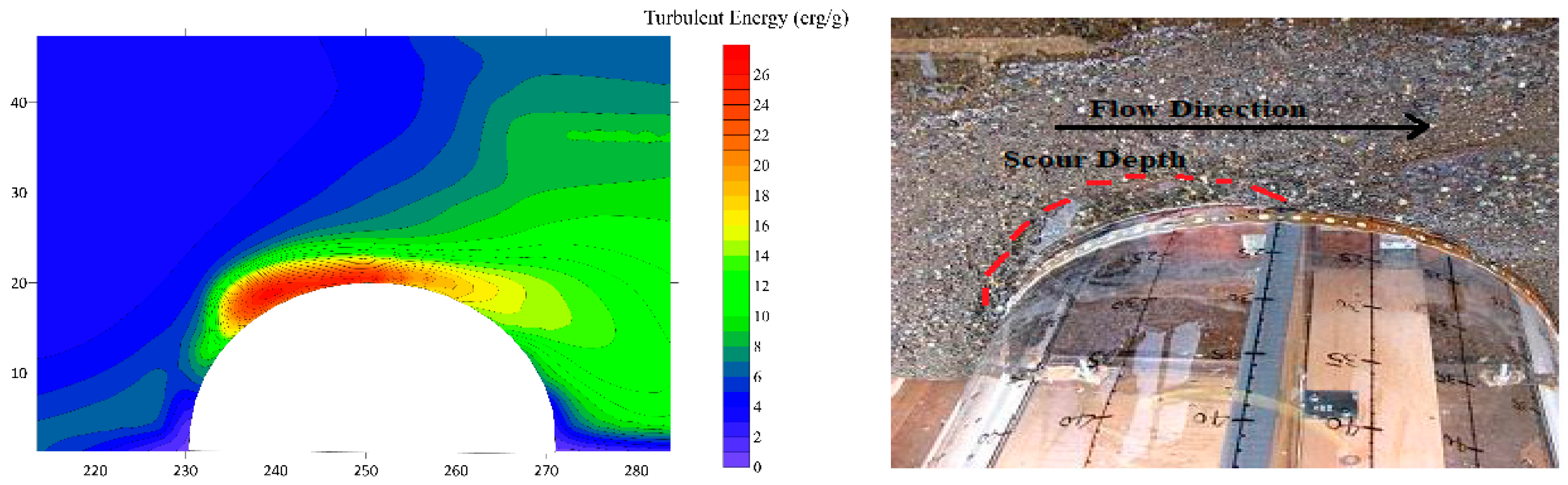
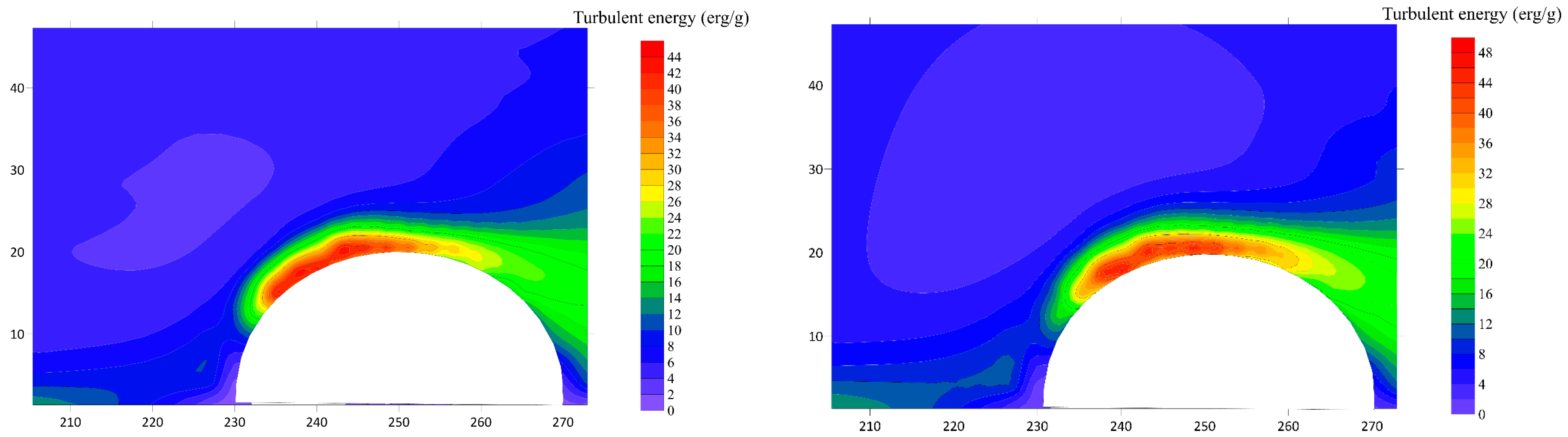
4.6. The Numerical Turbulent Energy Distribution around the Semi-Circular Bridge Abutments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barbhuiya, A.K.; Dey, S. Local scour at abutments: A review. Sadhana 2004, 29, 449–476. [Google Scholar] [CrossRef]
- Chang, H.H. Fluvial Processes in River Engineering; John Wiley: New York, NY, USA, 2008; 425p. [Google Scholar]
- Deng, L.; Cai, C.S. Bridge scour: Prediction, modeling, monitoring, and countermeasures. Pract. Period. Struct. Des. Constr. 2009, 15, 125–134. [Google Scholar] [CrossRef]
- Foti, S.; Sabia, D. Influence of foundation scour on the dynamic response of an existing bridge. J. Bridge Eng. 2010, 16, 295–304. [Google Scholar] [CrossRef]
- Zhu, S.; Levinson, D.M. Disruptions to transportation networks: A review. In Network Reliability in Practice; Springer: New York, NY, USA, 2012; pp. 5–20. [Google Scholar]
- Froehlich, D.C. Local scour at bridge abutments. In Proceedings of the 1989 National Conference on Hydraulic Engineering, New Orleans, LA, USA, 14–18 August 1989; pp. 13–18. [Google Scholar]
- Melville, B.W.; Chiew, Y.M. Time scale for local scour at bridge piers. J. Hydraul. Eng. 1999, 125, 59–65. [Google Scholar] [CrossRef]
- Coleman, S.E. Clearwater local scour at complex piers. J. Hydraul. Eng. 2005, 131, 330–334. [Google Scholar] [CrossRef]
- Dey, S.; Sarkar, A. Scour downstream of an apron due to submerged horizontal jets. J. Hydraul. Eng. 2006, 132, 246–257. [Google Scholar] [CrossRef]
- Shen, H.T.; Yapa, P.D. Flow resistance of river ice cover. J. Hydraul. Eng. 1986, 112, 142–156. [Google Scholar] [CrossRef]
- Kwan, R.T.; Melville, B.W. Local scour and flow measurements at bridge abutments. J. Hydraul. Res. 1994, 32, 661–673. [Google Scholar] [CrossRef]
- Zabilansky, L.J.; White, K.D. Ice-cover effects on scour in narrow rivers. In Proceedings of the Third International Conference on Remediation of Contaminated Sediment, New Orleans, LA, USA, 11–14 February 2005; pp. 24–27. [Google Scholar]
- Wu, P.; Balachandar, R.; Sui, J. Local scour around bridge piers under ice-covered conditions. J. Hydraul. Eng. 2015, 142, 04015038. [Google Scholar] [CrossRef]
- Wu, P.; Hirshfield, F.; Sui, J.Y. Local scour around bridge abutments under ice covered conditions-an experimental study. Int. J. Sediment. Res. 2015, 30, 39–47. [Google Scholar] [CrossRef]
- Namaee, M.R.; Sui, J.; Wu, Y.; Linklater, N. Three-dimensional numerical simulation of local scour around circular side-by-side bridge piers with ice cover. Can. J. Civ. Eng. 2021, 48, 1335–1353. [Google Scholar] [CrossRef]
- Toombes, L.; Chanson, H. Numerical limitations of hydraulic models. In Proceedings of the 34th IAHR World Congress, 33rd Hydrology and Water Resources Symposium and 10th Conference on Hydraulics in Water Engineering, Brisbane, Australia, 26 June–1 July 2011; pp. 2322–2329. [Google Scholar]
- Richardson, J.E.; Panchang, V.G. Three-dimensional simulation of scour-inducing flow at bridge piers. J. Hydraul. Eng. 1998, 124, 530–540. [Google Scholar] [CrossRef]
- Vasquez, J.A.; Walsh, B.W. CFD simulation of local scour in complex piers under tidal flow. In Proceedings of the 33rd IAHR Congress: Water Engineering for a Sustainable Environment, Vancouver, BC, Canada, 9–14 August 2009. [Google Scholar]
- Kim, H.S.; Nabi, M.; Kimura, I.; Shimizu, Y. Numerical investigation of local scour at two adjacent cylinders. Adv. Water Resour. 2014, 70, 131–147. [Google Scholar] [CrossRef]
- Dey, S.; Barbhuiya, A.K. Time variation of scour at abutments. J. Hydraul. Eng. 2005, 131, 11–23. [Google Scholar] [CrossRef]
- Melville, B.W. Local scour at bridge abutments. J. Hydraul. Eng. 1992, 118, 615–631. [Google Scholar] [CrossRef]
- Omara, H.; Elsayed, S.M.; Abdeelaal, G.M.; Abd-Elhamid, H.F.; Tawfik, A. Hydromorphological Numerical Model of the Local Scour Process Around Bridge Piers. Arab. J. Sci. Eng. 2019, 44, 4183–4199. [Google Scholar] [CrossRef]
- Hatton, K.A.; Foster, D.L.; Traykovski, P.; Smith, H.D. Numerical Simulations of the Flow and Sediment Transport Regimes Surrounding a Short Cylinder. IEEE J. Ocean. Eng. 2007, 32, 249–259. [Google Scholar] [CrossRef]
- Amini, A.; Parto, A.A. 3D Numerical Simulation of Flow Field around Twin Piles. ACTA Geophys. 2017, 65, 1243–1251. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Ghaderi, A.; Sattariyan, M.; Alinejad, B.; Asl, M.M.; Di Francesco, S. Investigation of Local Scouring around Hydrodynamic and Circular Pile Groups under the Influence of River Material Harvesting Pits. Water 2021, 13, 2192. [Google Scholar] [CrossRef]
- Nielsen, A.W.; Liu, X.F.; Sumer, B.M.; Fredsoe, J. Flow and Bed Shear Stresses in Scour Protections around a Pile in a Current. Coast. Eng. 2013, 72, 20–38. [Google Scholar] [CrossRef]
- Choufu, L.; Abbasi, S.; Pourshahbaz, H.; Taghvaei, P.; Tfwala, S. Investigation of Flow, Erosion, and Sedimentation Pattern around Varied Groynes under Different Hydraulic and Geometric Conditions: A Numerical Study. Water 2019, 11, 235. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Hirt, C.W.; Sicilian, J.M. A porosity technique for the definition of obstacles in rectangular cell meshes. In Proceedings of the 4th International Conference on Numerical Ship Hydrodynamics, Washington, DC, USA, 24–27 September 1985; pp. 1–19. [Google Scholar]
- Flow Sciences Inc. FLOW-3D User’s Manual Version 11.1; Flow Sciences Inc.: Santa Fe, NM, USA, 2015. [Google Scholar]
- Yakhot, V.; Orszag, S.A.; Thangam, S.; Gatski, T.B.; Speziale, C.G. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids A 1992, 4, 1510–1520. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The Numerical Computation of Turbulent Flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, X.L.; Wang, J.H. Numerical investigation of local scour around three adjacent piles with different arrangements under current. Ocean. Eng. 2017, 142, 625–638. [Google Scholar] [CrossRef]
- Mastbergen, D.R.; Von den Berg, J.H. Breaching in fine sands and the generation of sustained turbidity currents in submarine canyons. Sedimentology 2003, 50, 625–637. [Google Scholar] [CrossRef]
- Soulsby, R.L.; Whitehouse, R.J.S. Threshold of sediment motion in coastal environments. In Pacific Coasts and Ports’ 97, Proceedings of the 13th Australasian Coastal and Ocean Engineering Conference and the 6th Australasian Port and Harbour Conference, Melbourne, Australia, 18–21 April 1997; ; Centre for Advanced Engineering, University of Canterbury: Christchurch, New Zealand, 1997; Volume 1, p. 145. [Google Scholar]
- Meyer-Peter, E.; Müller, R. Formulas for bed-load transport. In Proceedings of the IAHSR 2nd Meeting, Stockholm, Sweden, 7–9 June 1948. appendix 2. IAHR. [Google Scholar]
- Nielsen, P. Coastal Bottom Boundary Layers and Sediment Transport; World Scientific Publishing Company: Singapore, 1992; Volume 4. [Google Scholar]
- Van Rijn, L. Sediment transport, Part I: Bed load transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
- Wu, P.; Hirshfield, F.; Sui, J.; Wang, J.; Chen, P.P. Impacts of ice cover on local scour around semi-circular bridge abutment. J. Hydrodyn. Ser. B 2014, 26, 10–18. [Google Scholar] [CrossRef]
- Tang, J.H.; Puspasari, A.D. Numerical simulation of local scour around three cylindrical piles in a tandem arrangement. Water 2021, 13, 3623. [Google Scholar] [CrossRef]
- Zhang, H.; Nakagawa, H.; Mizutani, H. Bed morphology and grain size characteristics around a spur dyke. Int. J. Sediment Res. 2012, 27, 141–157. [Google Scholar] [CrossRef]
- Ettema, R.; Kempema, E.W. River-Ice Effects on Gravel-Bed Channels. In Gravel-Bed Rivers: Processes, Tools, Environments; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 523–540. [Google Scholar]
- Sui, J.; Wang, J.; He, Y.; Krol, F. Velocity profiles and incipient motion of frazil particles under ice cover. Int. J. Sediment. Res. 2010, 25, 39–51. [Google Scholar] [CrossRef]
- Hains, D.; Zabilansky, L.J.; Weisman, R.N. An experimental study of ice effects on scour at bridge piers. In Proceedings of the Cold Regions Engineering and Construction Conference and Expo, Edmonton, AB, Canada, 16–19 May 2004. [Google Scholar]

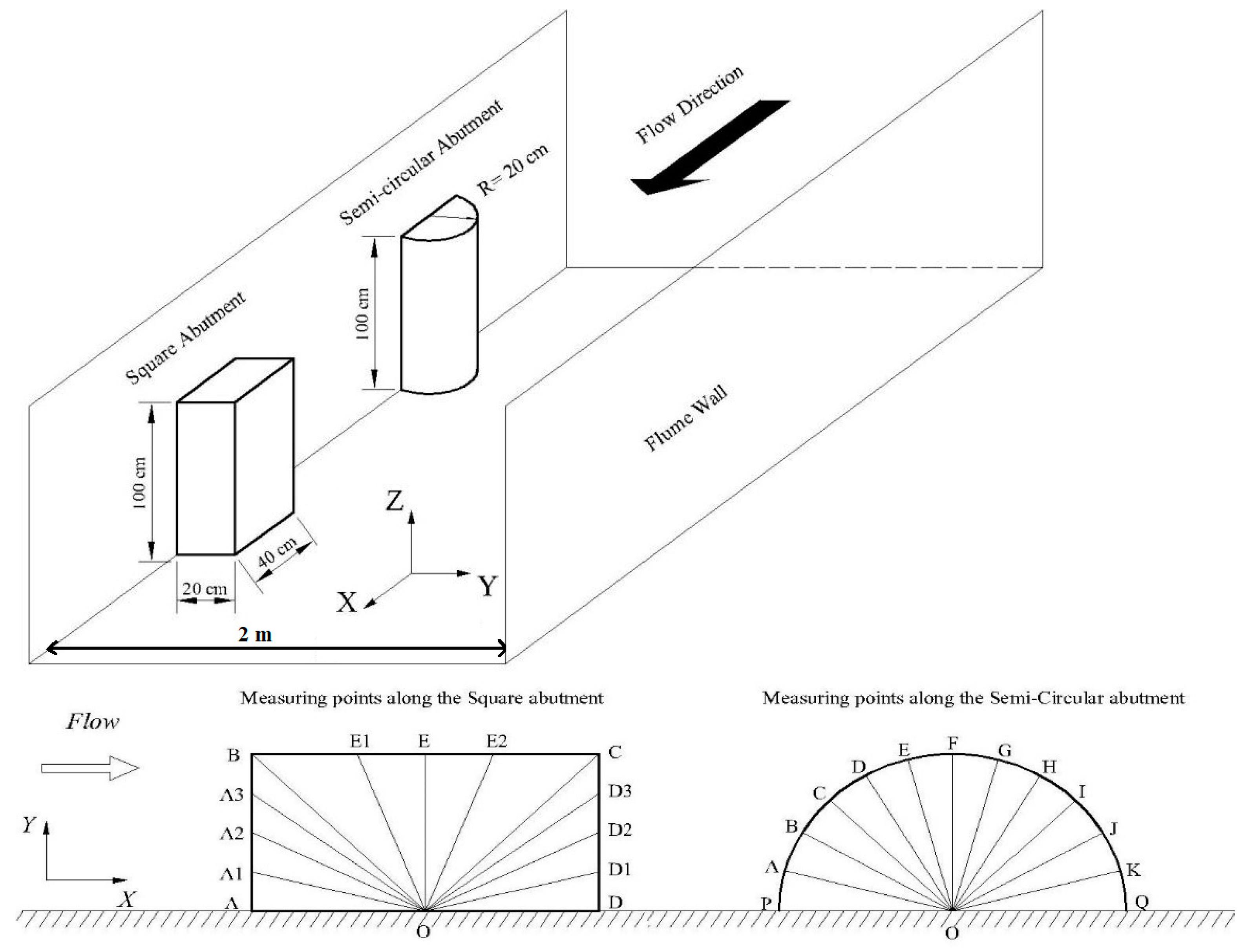






| Cover Condition | D50 (mm) | D16 (mm) | D84 (mm) | D90 (mm) | Depth (m) | Average Velocity (m/s) |
|---|---|---|---|---|---|---|
| Open Channel | 0.58 | 0.28 | 1.91 | 2.57 | 0.07 | 0.26 |
| 0.58 | 0.28 | 1.91 | 2.57 | 0.07 | 0.21 | |
| 0.58 | 0.28 | 1.91 | 2.57 | 0.19 | 0.21 | |
| 0.5 | 0.26 | 1.66 | 2.09 | 0.07 | 0.26 | |
| 0.5 | 0.26 | 1.66 | 2.09 | 0.07 | 0.21 | |
| 0.5 | 0.26 | 1.66 | 2.09 | 0.19 | 0.21 | |
| 0.47 | 0.23 | 0.82 | 1.19 | 0.07 | 0.26 | |
| 0.47 | 0.23 | 0.82 | 1.19 | 0.07 | 0.21 | |
| 0.47 | 0.23 | 0.82 | 1.19 | 0.19 | 0.21 | |
| Smooth Cover | 0.58 | 0.28 | 1.91 | 2.57 | 0.07 | 0.20 |
| 0.58 | 0.28 | 1.91 | 2.57 | 0.07 | 0.16 | |
| 0.58 | 0.28 | 1.91 | 2.57 | 0.19 | 0.23 | |
| 0.5 | 0.26 | 1.66 | 2.09 | 0.07 | 0.20 | |
| 0.5 | 0.26 | 1.66 | 2.09 | 0.07 | 0.16 | |
| 0.5 | 0.26 | 1.66 | 2.09 | 0.19 | 0.23 | |
| 0.47 | 0.23 | 0.82 | 1.19 | 0.07 | 0.20 | |
| 0.47 | 0.23 | 0.82 | 1.19 | 0.07 | 0.16 | |
| 0.47 | 0.23 | 0.82 | 1.19 | 0.19 | 0.23 | |
| Rough Cover | 0.58 | 0.28 | 1.91 | 2.57 | 0.07 | 0.22 |
| 0.58 | 0.28 | 1.91 | 2.57 | 0.07 | 0.2 | |
| 0.58 | 0.28 | 1.91 | 2.57 | 0.19 | 0.14 | |
| 0.5 | 0.26 | 1.66 | 2.09 | 0.07 | 0.22 | |
| 0.5 | 0.26 | 1.66 | 2.09 | 0.07 | 0.20 | |
| 0.5 | 0.26 | 1.66 | 2.09 | 0.19 | 0.14 | |
| 0.47 | 0.23 | 0.82 | 1.19 | 0.07 | 0.22 | |
| 0.47 | 0.23 | 0.82 | 1.19 | 0.07 | 0.20 | |
| 0.47 | 0.23 | 0.82 | 1.19 | 0.19 | 0.14 |
| Number of Cells in Mesh Blocks | |||
|---|---|---|---|
| Block 1 | Block 2 | Block 3 | Domain Size |
| 37,587 | 1,000,000 | 35,376 | 5.6 m × 2 m × 1 m |
| Abutment Type | Flow Cover | |||||
|---|---|---|---|---|---|---|
| Open Channel | Smooth Ice Cover | Uneven Ice Cover | ||||
| Experimental Study | Numerical Study | Experimental Study | Numerical Study | Experimental Study | Numerical Study | |
| Square Abutment | 65 mm | 66 mm | 65 mm | 65 mm | 80 mm | 80 mm |
| Semi-Circular | 14 mm | 14 mm | 15 mm | 15 mm | 17 mm | 17 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Namaee, M.R.; Wu, P.; Dziedzic, M. Numerical Modeling of Local Scour in the Vicinity of Bridge Abutments When Covered with Ice. Water 2023, 15, 3330. https://doi.org/10.3390/w15193330
Namaee MR, Wu P, Dziedzic M. Numerical Modeling of Local Scour in the Vicinity of Bridge Abutments When Covered with Ice. Water. 2023; 15(19):3330. https://doi.org/10.3390/w15193330
Chicago/Turabian StyleNamaee, Mohammad Reza, Peng Wu, and Mauricio Dziedzic. 2023. "Numerical Modeling of Local Scour in the Vicinity of Bridge Abutments When Covered with Ice" Water 15, no. 19: 3330. https://doi.org/10.3390/w15193330
APA StyleNamaee, M. R., Wu, P., & Dziedzic, M. (2023). Numerical Modeling of Local Scour in the Vicinity of Bridge Abutments When Covered with Ice. Water, 15(19), 3330. https://doi.org/10.3390/w15193330







