Planning and Evaluating Nature-Based Solutions for Watershed Investment Programs with a SMART Perspective Using a Distributed Modeling Tool
Abstract
:1. Introduction
2. Materials and Methods
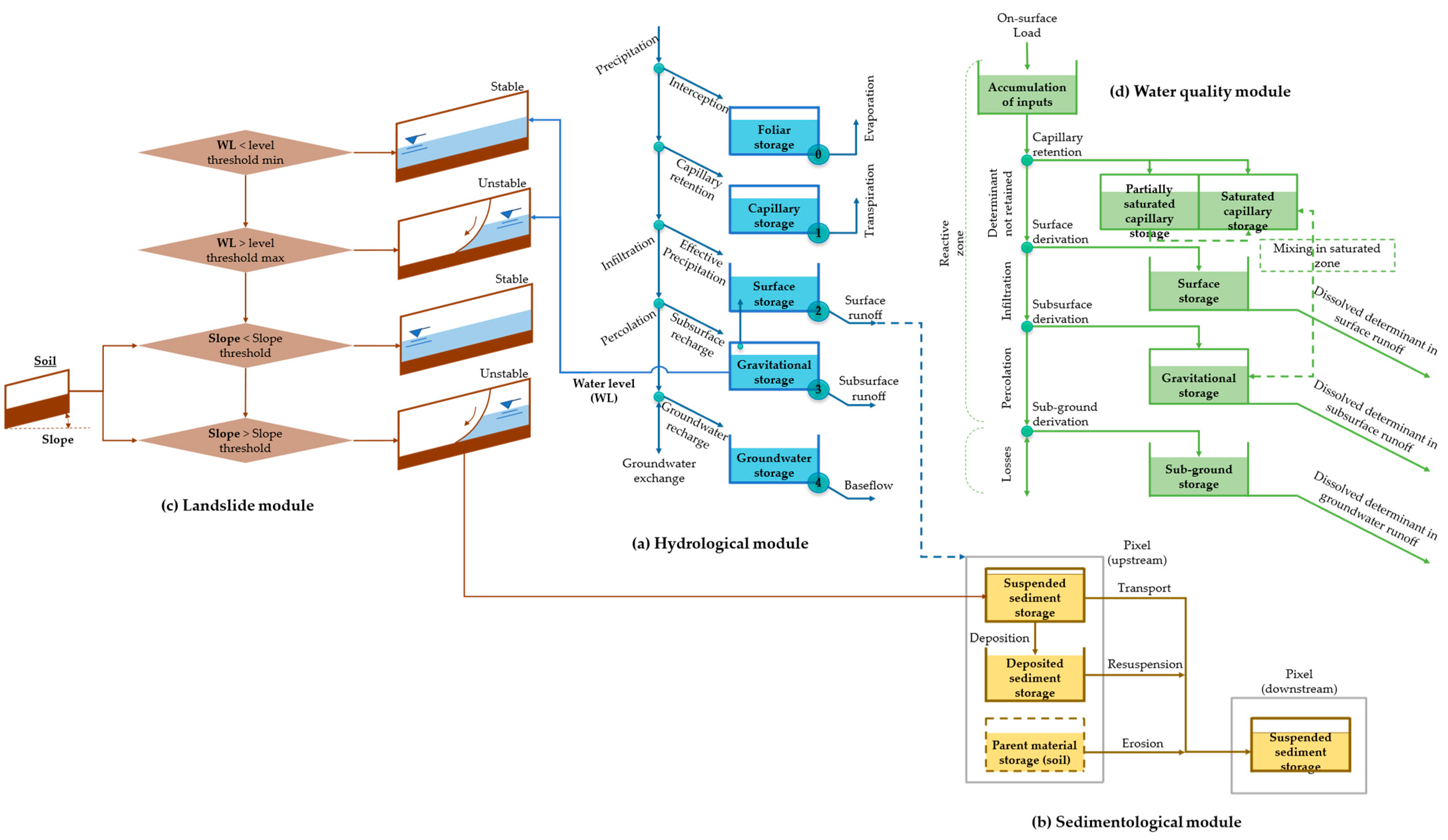
2.1. Modeling Framework Structure
2.2. Topological Representation of the Basin
2.3. Physical Processess Conceptualization
2.3.1. Meteorological Model
2.3.2. Phenological Model
2.3.3. Hydrological Model
2.3.4. Sedimentological Model
2.3.5. Landslide Model
2.3.6. Water Quality Model
2.4. NbS Portfolio and Potential NbS Interventions
2.5. Prioritization of Intervention Areas
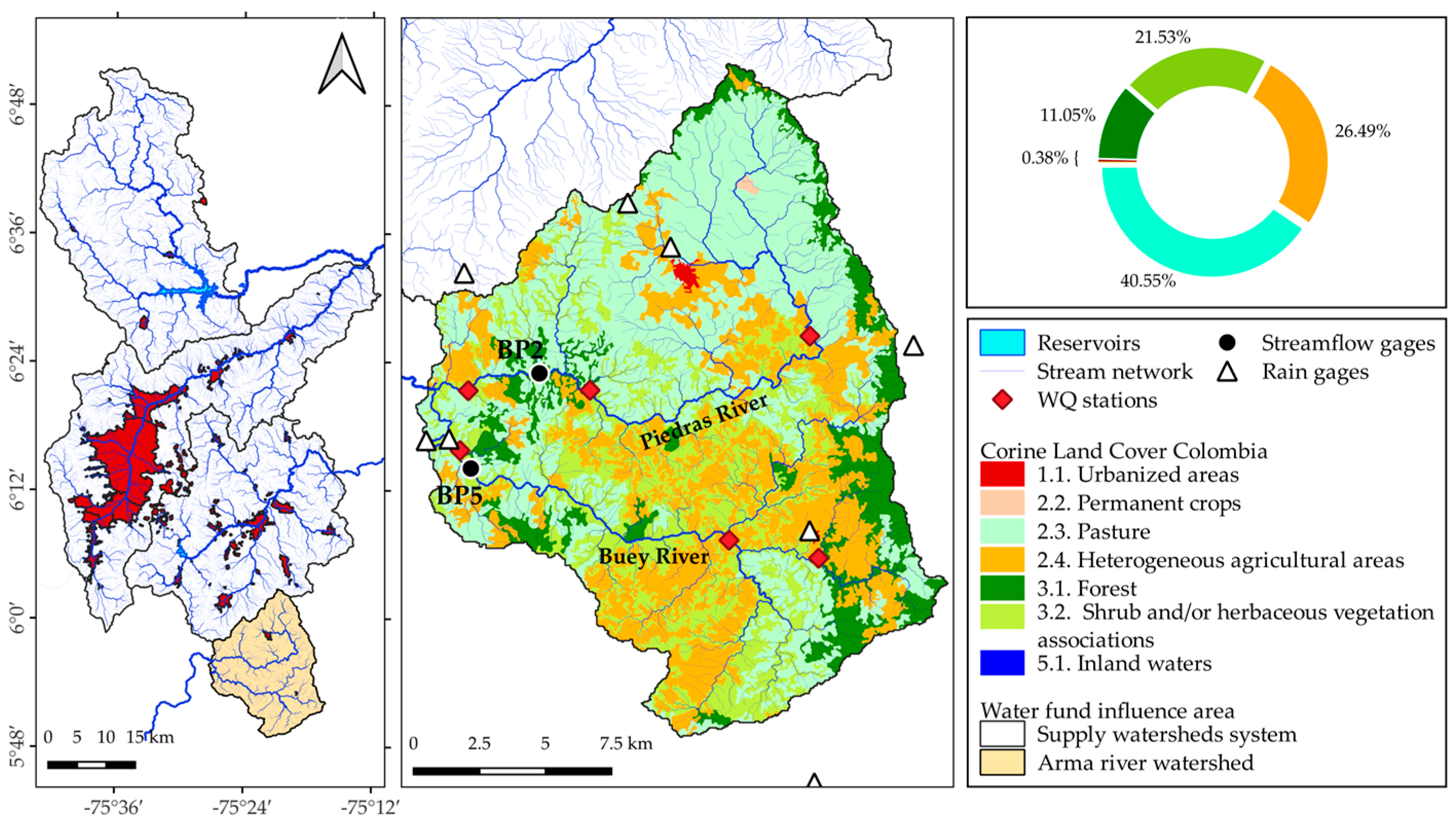
2.6. Basin of Study
2.7. Model Input Data
2.8. Model Calibration and Validation
3. Results and Discussion
3.1. NbS Spatial Allocation
3.2. SIGA-CALv1.0 Calibration
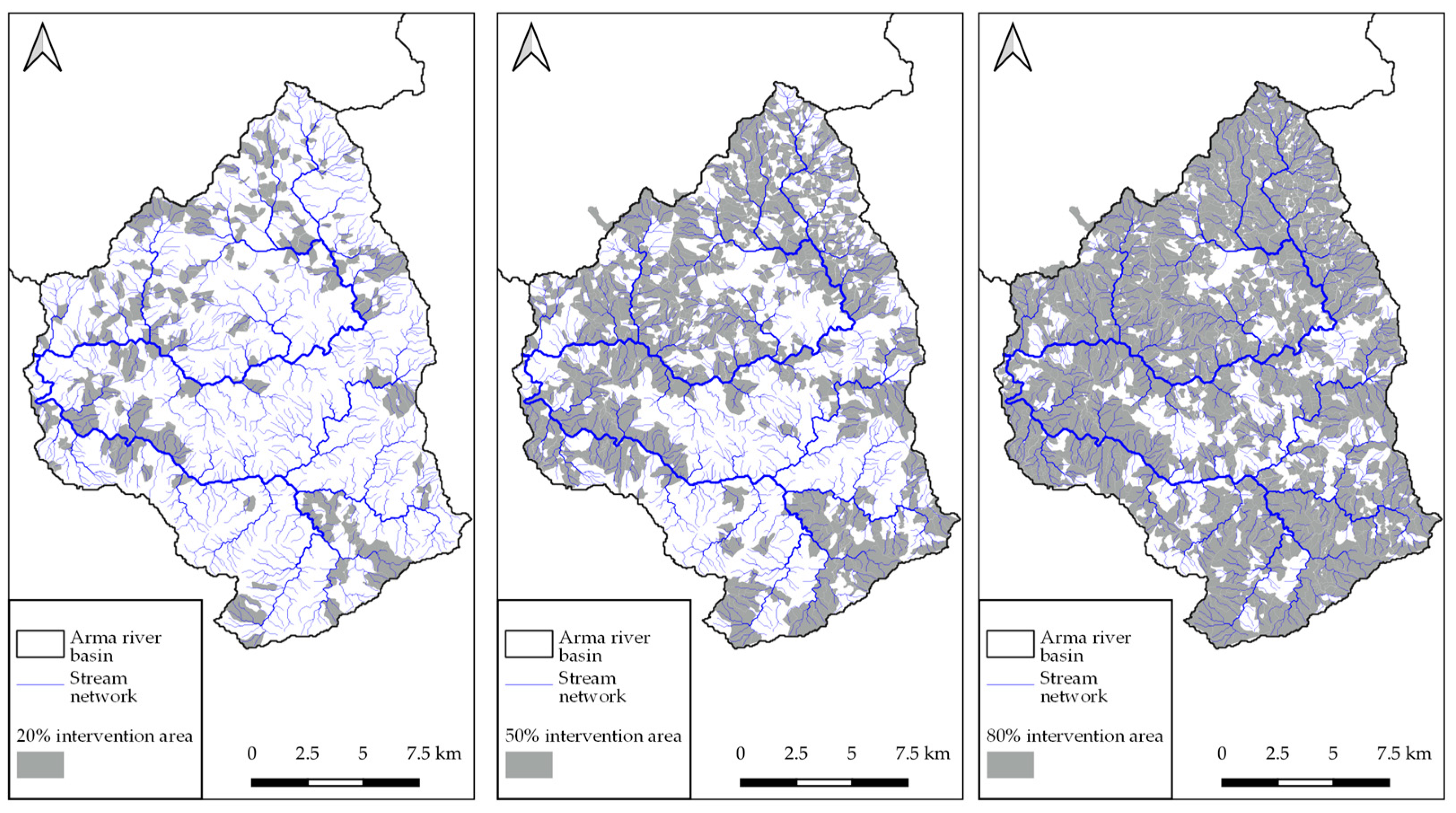
3.3. Priority Management Areas
3.4. NbS Intermediate Scenarios and Metrics Evaluation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ruangpan, L.; Vojinovic, Z.; Di Sabatino, S.; Leo, L.S.; Capobianco, V.; Oen, A.M.P.; McClain, M.E.; Lopez-Gunn, E. Nature-Based Solutions for Hydro-Meteorological Risk Reduction: A State-of-the-Art Review of the Research Area. Nat. Hazards Earth Syst. Sci. 2020, 20, 243–270. [Google Scholar] [CrossRef]
- Mosquera-Romero, S.; Ntagia, E.; Rousseau, D.P.L.; Esteve-Núñez, A.; Prévoteau, A. Water Treatment and Reclamation by Implementing Electrochemical Systems with Constructed Wetlands. Environ. Sci. Ecotechnol. 2023, 16, 100265. [Google Scholar] [CrossRef] [PubMed]
- Vörösmarty, C.J.; Stewart-Koster, B.; Green, P.A.; Boone, E.L.; Flörke, M.; Fischer, G.; Wiberg, D.A.; Bunn, S.E.; Bhaduri, A.; McIntyre, P.B.; et al. A Green-Gray Path to Global Water Security and Sustainable Infrastructure. Glob. Environ. Chang. 2021, 70, 102344. [Google Scholar] [CrossRef]
- Di Grazia, F.; Gumiero, B.; Galgani, L.; Troiani, E.; Ferri, M.; Loiselle, S.A. Ecosystem Services Evaluation of Nature-Based Solutions with the Help of Citizen Scientists. Sustainability 2021, 13, 10629. [Google Scholar] [CrossRef]
- Baustian, M.M.; Jung, H.; Bienn, H.C.; Barra, M.; Hemmerling, S.A.; Wang, Y.; White, E.; Meselhe, E. Engaging Coastal Community Members about Natural and Nature-Based Solutions to Assess Their Ecosystem Function. Ecol. Eng. 2020, 143, 100015. [Google Scholar] [CrossRef]
- Dutta, A.; Torres, A.S.; Vojinovic, Z. Evaluation of Pollutant Removal Efficiency by Small-Scale Nature-Based Solutions Focusing on Bio-Retention Cells, Vegetative Swale and Porous Pavement. Water 2021, 13, 2361. [Google Scholar] [CrossRef]
- Vigerstol, K.L.; Aukema, J.E. A Comparison of Tools for Modeling Freshwater Ecosystem Services. J. Environ. Manag. 2011, 92, 2403–2409. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, N.; Harper, R.; Li, Q.; Liu, K.; Wei, X.; Ning, D.; Hou, Y.; Liu, S. A Global Review on Hydrological Responses to Forest Change across Multiple Spatial Scales: Importance of Scale, Climate, Forest Type and Hydrological Regime. J. Hydrol. 2017, 546, 44–59. [Google Scholar] [CrossRef]
- Bremer, L.L.; Auerbach, D.A.; Goldstein, J.H.; Vogl, A.L.; Shemie, D.; Kroeger, T.; Nelson, J.L.; Benítez, S.P.; Calvache, A.; Guimarães, J.; et al. One Size Does Not Fit All: Natural Infrastructure Investments within the Latin American Water Funds Partnership. Ecosyst. Serv. 2016, 17, 217–236. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large Area Hydrologic Modeling and Assessment Part I: Model Development 1. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Tallis, H.T.; Ricketts, T.; Guerry, A.; Wood, S.A.; Sharp, R.; Nelson, E.; Ennaanay, D.; Wolny, S.; Olwero, N.; Vigerstol, K.; et al. InVEST 2.5.3 User′s Guide. The Natural Capital Project; Stanford University: Stanford, CA, USA, 2013. [Google Scholar]
- Francesconi, W.; Srinivasan, R.; Pérez-Miñana, E.; Willcock, S.P.; Quintero, M. Using the Soil and Water Assessment Tool (SWAT) to Model Ecosystem Services: A Systematic Review. J. Hydrol. 2016, 535, 625–636. [Google Scholar] [CrossRef]
- Ricci, G.F.; Jeong, J.; De Girolamo, A.M.; Gentile, F. Effectiveness and Feasibility of Different Management Practices to Reduce Soil Erosion in an Agricultural Watershed. Land Use Policy 2020, 90, 104306. [Google Scholar] [CrossRef]
- Ricci, G.F.; D’Ambrosio, E.; De Girolamo, A.M.; Gentile, F. Efficiency and Feasibility of Best Management Practices to Reduce Nutrient Loads in an Agricultural River Basin. Agric. Water Manag. 2022, 259, 107241. [Google Scholar] [CrossRef]
- Chen, L.; Zhong, Y.; Wei, G.; Cai, Y.; Shen, Z. Development of an Integrated Modeling Approach for Identifying Multilevel Non-Point-Source Priority Management Areas at the Watershed Scale. Water Resour. Res. 2014, 50, 4095–4109. [Google Scholar] [CrossRef]
- The Nature Conservancy What Is a Water Fund? Available online: https://waterfundstoolbox.org/getting-started/what-is-a-water-fund (accessed on 10 September 2023).
- Velásquez, N.; Vélez, J.I.; Álvarez-Villa, O.D.; Salamanca, S.P. Comprehensive Analysis of Hydrological Processes in a Programmable Environment: The Watershed Modeling Framework. Hydrology 2023, 10, 76. [Google Scholar] [CrossRef]
- Vélez, J.I. Desarrollo de Un Modelo Hidrológico Conceptual y Distribuido Orientado a La Simulación de Crecidas. Tesis de Doctorado, Universitat Politècnica de València, Valencia, Spain, 2001. [Google Scholar]
- Francés, F.; Vélez, J.I.; Vélez, J.J. Split-Parameter Structure for the Automatic Calibration of Distributed Hydrological Models. J. Hydrol. 2007, 332, 226–240. [Google Scholar] [CrossRef]
- Krysanova, V.; Müller-Wohlfeil, D.-I.; Becker, A. Development and Test of a Spatially Distributed Hydrological/Water Quality Model for Mesoscale Watersheds. Ecol. Model. 1998, 106, 261–289. [Google Scholar] [CrossRef]
- O’Callaghan, J.F.; Mark, D.M. The Extraction of Drainage Networks from Digital Elevation Data. Comput. Vis. Graph. Image Process. 1984, 28, 323–344. [Google Scholar] [CrossRef]
- Shepard, D. A Two-Dimensional Interpolation Function for Irregularly-Spaced Data. In Proceedings of the 1968 23rd ACM National Conference, New York, NY, USA, 27–29 August 1968; ACM Press: New York, NY, USA, 1968; pp. 517–524. [Google Scholar]
- Galton, F. Regression Towards Mediocrity in Hereditary Stature. J. Anthropol. Inst. Great Br. Irel. 1886, 15, 246. [Google Scholar] [CrossRef]
- Shuttleworth, W.J. Evaporation. In Handbook of Hydrology; McGraw-Hill: New York, NY, USA, 1993; Volume 1, pp. 4.1–4.53. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements. Food Agric. Organ. United Nations Rome 1998, 300, D05109. [Google Scholar]
- Gómez Elorza, Á. Herramientas de Modelación y Monitoreo Para La Hidrología de Alta Montaña Colombiana—Cuenca de La Quebrada Calostros—PNN Chingaza. Master’s Thesis, Universidad Nacional de Colombia Sede Bogotá, Bogotá, Colombia, 2016. [Google Scholar]
- Alemayehu, T.; van Griensven, A.; Woldegiorgis, B.T.; Bauwens, W. An Improved SWAT Vegetation Growth Module and Its Evaluation for Four Tropical Ecosystems. Hydrol. Earth Syst. Sci. 2017, 21, 4449–4467. [Google Scholar] [CrossRef]
- Waring, R.H.; Running, S.W. Water Cycle. In Forest Ecosystems; Elsevier: Amsterdam, The Netherlands, 2007; pp. 19–57. [Google Scholar]
- Kilinc, M.Y. Mechanics of Soil Erosion from Overland Flow Generated by Simulated Rainfall; Colorado State University: Fort Collins, CO, USA, 1972. [Google Scholar]
- Julien, P.Y. Erosion and Sedimentation; Cambridge University Press: Cambridge, UK, 1995; ISBN 9780521442374. [Google Scholar]
- Rojas, R.; Julien, P.; Johnson, B. A 2-Dimensional Rainfall-Runoff and Sediment Model; CASC2D-SED Reference Manual v1. 0; Colorado State University: Fort Collins, CO, USA, 2003. [Google Scholar]
- Wilkinson, S.N.; Dougall, C.; Kinsey-Henderson, A.E.; Searle, R.D.; Ellis, R.J.; Bartley, R. Development of a Time-Stepping Sediment Budget Model for Assessing Land Use Impacts in Large River Basins. Sci. Total Environ. 2014, 468–469, 1210–1224. [Google Scholar] [CrossRef] [PubMed]
- Engelund, F.; Hansen, E. A Monograph on Sediment Transport in Alluvial Streams. 1967. Available online: https://repository.tudelft.nl/islandora/object/uuid%3A81101b08-04b5-4082-9121-861949c336c9 (accessed on 25 September 2023).
- Osorio Yepes, S. Simulación de Sedimentos Mediante Un Modelo Hidrológico Distribuido Utilizando Información Indirecta. Master’s Thesis, Universidad Nacional de Colombia Sede Medellín, Medellín, Colombia, 2016. [Google Scholar]
- Aristizábal, E.; Vélez, J.I.; Martínez, H.E.; Jaboyedoff, M. SHIA_Landslide: A Distributed Conceptual and Physically Based Model to Forecast the Temporal and Spatial Occurrence of Shallow Landslides Triggered by Rainfall in Tropical and Mountainous Basins. Landslides 2016, 13, 497–517. [Google Scholar] [CrossRef]
- Arnone, E.; Noto, L.V.; Lepore, C.; Bras, R.L. Physically-Based and Distributed Approach to Analyze Rainfall-Triggered Landslides at Watershed Scale. Geomorphology 2011, 133, 121–131. [Google Scholar] [CrossRef]
- Taylor, D.W. Fundamentals of Soil Mechanics, 1st ed.; Wiley: New York, NY, USA, 1948; Volume 1. [Google Scholar]
- Tsai, Z.-X.; You, G.J.-Y.; Lee, H.-Y.; Chiu, Y.-J. Modeling the Sediment Yield from Landslides in the Shihmen Reservoir Watershed, Taiwan. Earth Surf. Process. Landf. 2013, 38, 661–674. [Google Scholar] [CrossRef]
- Wade, A.J.; Whitehead, P.G.; Butterfield, D. The Integrated Catchments Model of Phosphorus Dynamics (INCA-P), a New Approach for Multiple Source Assessment in Heterogeneous River Systems: Model Structure and Equations. Hydrol. Earth Syst. Sci. 2002, 6, 583–606. [Google Scholar] [CrossRef]
- Wade, A.J.; Durand, P.; Beaujouan, V.; Wessel, W.W.; Raat, K.J.; Whitehead, P.G.; Butterfield, D.; Rankinen, K.; Lepisto, A. A Nitrogen Model for European Catchments: INCA, New Model Structure and Equations. Hydrol. Earth Syst. Sci. 2002, 6, 559–582. [Google Scholar] [CrossRef]
- Whitehead, P.G.; Wilson, E.J.; Butterfield, D. A Semi-Distributed Integrated Nitrogen Model for Multiple Source Assessment in Catchments (INCA): Part I—Model Structure and Process Equations. Sci. Total Environ. 1998, 210–211, 547–558. [Google Scholar] [CrossRef]
- Vélez, J.; Francés, F.; Vélez, I. TETIS: A Catchment Hydrological Distributed Conceptual Model. Geophys. Res. Abstr. 2005, 7, 03503. [Google Scholar]
- Beer, T.; Young, P.C. Longitudinal Dispersion in Natural Streams. J. Environ. Eng. 1983, 109, 1049–1067. [Google Scholar] [CrossRef]
- Santos Santos, T.F. Development of an Environmental Multiscale Decision Support System (EMDSS) for Sustainable Water Management in Highly Complex Altered Catchments. Tesis de Doctorado, Universidad de los Andes, Bogotá, Colombia, 2020. [Google Scholar]
- Whitehead, P.G.; Williams, R.J.; Lewis, D.R. Quality Simulation along River Systems (QUASAR): Model Theory and Development. Sci. Total Environ. 1997, 194–195, 447–456. [Google Scholar] [CrossRef]
- Lees, M.J.; Camacho, L.; Whitehead, P. Extension of the QUASAR River Water Quality Model to Incorporate Dead-Zone Mixing. Hydrol. Earth Syst. Sci. 1998, 2, 353–365. [Google Scholar] [CrossRef]
- The Nature Conservancy. Gotta Ingeniería Caracterización y Modelamiento de La Hidrología y Sedimentología de 2 Cuencas Piloto En El Marco Del Proyecto Blue Energy Mechanism (BEM); The Nature Conservancy: Medellín, Colombia, 2021. [Google Scholar]
- Bossard, M.; Feranec, J.; Otahel, J. CORINE Land Cover Technical Guide: Addendum 2000; European Environment Agency: Copenhagen, Denmark, 2000; Volume 40. [Google Scholar]
- Instituto de Hidrología, Meteorología y Estudios Ambientales (IDEAM). Leyenda Nacional de Coberturas de La Tierra, Metodología Corine Land Cover Para Colombia, Escala 1:100.000; IDEAM: Bogotá, Colombia, 2010. [Google Scholar]
- Buytaert, W.; Célleri, R.; De Bièvre, B.; Cisneros, F.; Wyseure, G.; Deckers, J.; Hofstede, R. Human Impact on the Hydrology of the Andean Páramos. Earth-Sci. Rev. 2006, 79, 53–72. [Google Scholar] [CrossRef]
- Lu, H.; Moran, C.J.; Prosser, I.P.; DeRose, R. Investment Prioritization Based on Broadscale Spatial Budgeting to Meet Downstream Targets for Suspended Sediment Loads. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Water Fund CuencaVerde. Available online: https://www.cuencaverde.org/ (accessed on 25 September 2023).
- Alaska Satellite Facility Dataset: ASF DAAC 2015, ALOS PALSAR_Radiometric_Terrain_Corrected_high_res; Includes Material © JAXA/METI 2007. Available online: https://search.asf.alaska.edu/#/ (accessed on 25 September 2023).
- Rojas, R.; Velleux, M.; Julien, P.Y.; Johnson, B.E. Grid Scale Effects on Watershed Soil Erosion Models. J. Hydrol. Eng. 2008, 13, 793–802. [Google Scholar] [CrossRef]
- Sharma, A.; Tiwari, K.N.; Bhadoria, P.B.S. Determining the Optimum Cell Size of Digital Elevation Model for Hydrologic Application. J. Earth Syst. Sci. 2011, 120, 573–582. [Google Scholar] [CrossRef]
- Sistema de Información Ambiental de Colombia -SIAC- Catálogo de Mapas SIAC. Available online: www.siac.gov.co/catalogo-de-mapas (accessed on 10 September 2023).
- Panagos, P.; Borrelli, P.; Meusburger, K.; Alewell, C.; Lugato, E.; Montanarella, L. Estimating the Soil Erosion Cover-Management Factor at the European Scale. Land Use Policy 2015, 48, 38–50. [Google Scholar] [CrossRef]
- Bosco, C.; de Rigo, D. Land Cover and Soil Erodibility within the E-RUSLE Model. Scientific Topics Focus 1, MRI-11b13. Notes Transdiscipl. Model. Env., Maieutike Research Initiative. 2013. Available online: https://figshare.com/articles/dataset/Land_Cover_and_Soil_Erodibility_whithin_the_e_RUSLE_Model/856670/2 (accessed on 10 September 2023).
- Myneni, R.; Park, Y. MODIS Collection 6 (C6) LAI/FPAR Product User’s Guide. 2015. Available online: https://lpdaac.usgs.gov/documents/2/mod15_user_guide.pdf (accessed on 10 September 2023).
- Salata, S.; Garnero, G.; Barbieri, C.; Giaimo, C. The Integration of Ecosystem Services in Planning: An Evaluation of the Nutrient Retention Model Using InVEST Software. Land 2017, 6, 48. [Google Scholar] [CrossRef]
- Ward, A.S.; Kelleher, C.A.; Mason, S.J.K.; Wagener, T.; McIntyre, N.; McGlynn, B.; Runkel, R.L.; Payn, R.A. A Software Tool to Assess Uncertainty in Transient-Storage Model Parameters Using Monte Carlo Simulations. Freshw. Sci. 2017, 36, 195–217. [Google Scholar] [CrossRef]
- Xiong, L.; Wan, M.; Wei, X.; O’Connor, K.M. Indices for Assessing the Prediction Bounds of Hydrological Models and Application by Generalised Likelihood Uncertainty Estimation/Indices Pour Évaluer Les Bornes de Prévision de Modèles Hydrologiques et Mise En Œuvre Pour Une Estimation d’incertitude Par Vraisemblance Généralisée. Hydrol. Sci. J. 2009, 54, 852–871. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The Future of Distributed Models: Model Calibration and Uncertainty Prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Instituto de Hidrología, Meteorología y Estudios Ambientales (IDEAM). Anexos—Estudio Nacional Del Agua. 2022. Available online: http://www.ideam.gov.co/web/agua/estudio-nacional-del-agua (accessed on 10 September 2023).
- Water Fund CuencaVerde. Priorización de Áreas de Protección Hídrica en las Cuencas Abastecedoras del Sistema de Abastecimiento de Agua Potable de Empresas Públicas de Medellín; Water Fund CuencaVerde: Medelllín, Colombia, 2022. [Google Scholar]
- Razavi, T.; Coulibaly, P. Classification of Ontario Watersheds Based on Physical Attributes and Streamflow Series. J. Hydrol. 2013, 493, 81–94. [Google Scholar] [CrossRef]
- Strauch, M.; Lima, J.E.F.W.; Volk, M.; Lorz, C.; Makeschin, F. The Impact of Best Management Practices on Simulated Streamflow and Sediment Load in a Central Brazilian Catchment. J. Environ. Manag. 2013, 127, S24–S36. [Google Scholar] [CrossRef] [PubMed]
- Acosta, E.A.; Cho, S.J.; Klemz, C.; Reapple, J.; Barreto, S.; Ciasca, B.S.; León, J.; Rogéliz-Prada, C.A.; Bracale, H. Biophysical Benefits Simulation Modeling Framework for Investments in Nature-Based Solutions in São Paulo, Brazil Water Supply System. Water 2023, 15, 681. [Google Scholar] [CrossRef]
- Acreman, M.; Smith, A.; Charters, L.; Tickner, D.; Opperman, J.; Acreman, S.; Edwards, F.; Sayers, P.; Chivava, F. Evidence for the Effectiveness of Nature-Based Solutions to Water Issues in Africa. Environ. Res. Lett. 2021, 16, 063007. [Google Scholar] [CrossRef]
- Frei, C. Interpolation of Temperature in a Mountainous Region Using Nonlinear Profiles and Non-Euclidean Distances. Int. J. Climatol. 2014, 34, 1585–1605. [Google Scholar] [CrossRef]
- Shuttleworth, W.J. Putting the “Vap” into Evaporation. Hydrol. Earth Syst. Sci. 2007, 11, 210–244. [Google Scholar] [CrossRef]
- Tobón, C.; Morales, E.G.G. Capacidad de Interceptación de La Niebla Por La Vegetación de Los Páramos Andinos. Av. Recur. Hidráulicos 2007, 15, 35–46. [Google Scholar]
- Gultepe, I.; Isaac, G.A. Liquid Water Content and Temperature Relationship from Aircraft Observations and Its Applicability to GCMs. J. Clim. 1997, 10, 446–452. [Google Scholar] [CrossRef]
- Romps, D.M. Exact Expression for the Lifting Condensation Level. J. Atmos. Sci. 2017, 74, 3891–3900. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool—Theoretical Documentation—Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Francés, F.; Vélez, J.J.; Vélez, J.I.; Puricelli, M. Distributed Modelling of Large Basins for a Real Time Flood Forecasting System in Spain. In Proceedings of the Second Federal Interagency Hydrologic Modelling Conference, Gan, TY and Biftu, Las Vegas, NV, USA, 28 July–1 August 2002; pp. 3513–3524. [Google Scholar]
- Restrepo-Tamayo, C.A. Modelo Hidrológico Distribuido Orientado a La Gestión de La Utilización Conjunta de Aguas Superficiales y Subterráneas. Master’s Thesis, Universidad Nacional de Colombia, Sede Medellín, Medellín, Colombia, 2007. [Google Scholar]
- Velázquez, N. Simulación de Sedimentos a Partir de Un Modelo Conceptual y Distribuido No Lineal. Master’s Thesis, Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia, 2011. [Google Scholar]
- Cataño-Álvarez, S.; Vélez-Upegui, J.I. Modelo Conceptual Agregado de Transporte de Sedimentos Para Cuencas de Montaña En Antioquia-Colombia. Boletín Cienc. Tierra 2016, 38–48. [Google Scholar] [CrossRef]
- Sáenz, L.L.; Mulligan, M. Análisis Científico Detallado del Impacto del Cambio del Uso del Suelo en el Suministro de Recursos Hídricos Para la Ciudad de Bogotá e Implicaciones Para el Desarrollo de Esquemas PES; Department of Geography, King’s College London: London, UK, 2007. [Google Scholar]
- Hofstede, R.; Mondragon, M.; Rocha, C. Biomass of Grazed, Burned, and Undisturbed Paramo Grasslands, Colombia. I. Aboveground Vegetation. Artic Alp. Res. 1995, 27, 1–12. [Google Scholar] [CrossRef]
- Buytaert, W.; Célleri, R.; De Bièvre, B.; Cisneros, F. Hidrología del Páramo Andino: Propiedades, Importancia y Vulnerabilidad. 2005. Available online: https://www.researchgate.net/profile/felipe-cisneros/publication/228459137_hidrologia_del_paramo_andino_propiedades_importancia_y_vulnerabilidad/links/0deec528f8f8e65d5e000000/hidrologia-del-paramo-andino-propiedades-importancia-y-vulnerabilidad.pdf (accessed on 10 September 2023).
- Mulligan, M.; Torres, E.; Jarvis, A.; González, J.; Sáenz, L.L. Field and Laboratory Measurement of Rates and Processes of Clud Interception by Epiphytes, Leaves and Standard Collectors. In Forests in the Mist: Science for Conserving and Managing Tropical Montane Cloud Forests; Bruijnzeel, L.A., Juvik, J., Scatena, F.N., Hamilton, L.S., Bubb, P., Eds.; University of Hawaii: Honolulu, HI, USA, 2006. [Google Scholar]
- Bergström, S. The HBV Model. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Littleton, CO, USA, 1995. [Google Scholar]
- Arnaud, P.; Lavabre, J. Simulation du Functionnement Hydrologique d’une Retenue d’eau; Cemagref: Paris, France, 1996. [Google Scholar]
- Michel, C. Hydrologie Appliquée Aux Petits Bassins Ruraux; Cemagref: Paris, France, 1989. [Google Scholar]
- Singh, V.P.; Dickinson, W.T. An Analytical Method to Determine Daily Soil Moisture. In Proceedings of the Second World Congress on Water Resources, Delhi, India, 12–16 December 1975; pp. 355–365. [Google Scholar]
- Foster, G.R.; Lane, L.J. Modelling Rill Density. J. Irrig. Drain. Div. Proc. ASCE 1981, 107, 109–112. [Google Scholar] [CrossRef]
- Moor, I.D.; Burch, G.J. Sediment Transport Capacity o Sheet and Rill Flow: Application of Unit Stream Power Theory. Water Resour. Res. 1986, 22, 1350–1360. [Google Scholar] [CrossRef]
- Parsons, A.J.; Abrahams, A.D.; Wainwright, J. On Determining Resistance to Interrill Overland Flow. Water Resour. Res. 1994, 30, 3515–3521. [Google Scholar] [CrossRef]
- Boyd, J.P. Finding the Zeros of a Univariate Equation: Proxy Rootfinders, Chebyshev Interpolation, and the Companion Matrix. SIAM Rev. 2013, 55, 375–396. [Google Scholar] [CrossRef]
- Prosser, I.P.; Rustomji, P. Sediment Transport Capacity Relations for Overland Flow. Prog. Phys. Geogr. 2000, 24, 179–193. [Google Scholar] [CrossRef]
- Graham, S. Cuphea Fluviatilis (Lythraceae), a New Species from Antioquia, Colombia. Novon 2009, 19, 45–48. [Google Scholar] [CrossRef]
- Burton, A.; Bathurst, J.C. Physically Based Modelling of Shallow Landslide Sediment Yield at a Catchment Scale. Environ. Geol. 1998, 35, 89–99. [Google Scholar] [CrossRef]
- Bathurst, J.C.; Burton, A.; Ward, T.J. Debris Flow Run-out and Landslide Sediment Delivery Model Tests. J. Hydraul. Eng. 1997, 123, 410–419. [Google Scholar] [CrossRef]
- Bowles, D.S. Delineation of Landslide, Flash Flood, and Debris Flow Hazards in Utah. 1985. Available online: https://digitalcommons.usu.edu/water_rep/596/ (accessed on 10 September 2023).
- Larsen, M.C. Landslides and Sediment Budgets in Four Watersheds in Eastern Puerto Rico. In Water Quality and Landscape Processes of Four Watersheds in Eastern Puerto Rico; USGS: Reston, VA, USA, 2012; Volume 1789, pp. 153–178. [Google Scholar]
- Simonett, D.S.; Jennings, J.N.; Mabbutt, J.A. Landform Studies from Australia and New Guinea; ANU Press: Canberra, Australia, 1967. [Google Scholar]
- Lees, M.J.; Camacho, L.A.; Chapra, S. On the Relationship of Transient Storage and Aggregated Dead Zone Models of Longitudinal Solute Transport in Streams. Water Resour. Res. 2000, 36, 213–224. [Google Scholar] [CrossRef]
- Foster, G.R.; Huggins, L.F.; Meyer, L.D. A Laboratory Study of Rill Hydraulics: Velocitiy Relationships. Trans. Am. Soc. Agric. Eng. 1984, 25, 940–947. [Google Scholar]










| Model Aspect | Modeling Tools | ||
|---|---|---|---|
| SWAT | InVEST | SIGA-CALv1.0 (This Exercise) | |
| Time step | Daily | Annual | Daily |
| Scale | Subbasin | Cell-based size | Cell-based size |
| Water primary service | Water yield, stream flow, base flow, flood regulation, nitrogen load/concentration, phosphorus load/concentration, sediment load/concentration | Water yield, sediment yield, nutrient yie ld | Water yield, stream flow, base flow, flood regulation, nitrogen load/concentration, phosphorus load/concentration, sediment load/concentration, dissolved oxygen, biochemical oxygen demand, pH, pathogen indicators (total coliforms) |
| Criteria | Challenge | Goal |
|---|---|---|
| Specific | Linking improvements to NbS portfolios with modeled parametrization | To define potential NbS interventions based on the actual watershed Land Use/Land Cover (LULC), as well as relating the induced LULC change with hydrological and water quality processes |
| Measurable | NbS effects take time to materialize, thus monitoring and modeling allow for the assessment of the likely tendency and impact of outcomes in advance | To estimate attributes of water quantity and water quality and align them with Water Funds’ practical monitoring and evaluation programs |
| Achievable | WIPs targeting water security issues must define a realistic program(s) of NbS interventions that aim to achieve relevant outcomes | To identify how much NbS to implement based on established goals, and where |
| Relevant | Most WIPs and NbS are voluntary and may thus not deliver optimal interventions, particularly if not targeted precisely | To identify and prioritize management areas to best achieve the goals of the WIP |
| Time-bound | Few models enable a dynamic simulation of the temporal effects of NbS, which is important for assessing the timing of benefits of water quantity and quality | To give WIPs simulation capabilities to assess temporal trends in water quantity and water quality, while considering external factors that may cause deviations from expected outcomes |
| NbS | Definition |
|---|---|
| Best livestock practices | Active introduction of shrub and tree plants that serve to improve soils and provide fodder for livestock. This is generally associated with an improvement of previously compacted soils, as well as an improvement in pasture quality. About 200 plants are used for each single hectare of a system with best livestock practices. These plants are arranged linearly every 3 m along the boundaries of the property, or to separate paddocks. |
| Best agricultural practices | Active introduction of productive plants, usually shrubs or trees, often in combination with other species. Arrangements that contribute to greater productivity, such as live fences, are also often incorporated. For each single hectare of a system with best agricultural practices about 200 plants are used. These plants are dispersed throughout the property depending on drainage conditions, slope, and soil type. They can also be arranged as a corridor at the boundaries of the property. |
| Nucleation | A combination of actions aimed to aid the recovery of vegetative cover. Nucleation consists of installing cores of native plants that attract dispersers and facilitate natural regeneration. It should only be implemented in areas adjacent to natural areas. Nucleation requires planting approximately 800 trees per hectare. |
| Enrichment planting | A combination of actions aimed to aid the recovery of vegetative cover. Active restoration by enrichment planting consists of introducing native plants in the most degraded parts of an area where there are already traces of native vegetation. This approach requires the planting of approximately 390 trees per hectare. |
| Passive restoration | A combination of actions that facilitates the natural regeneration of vegetation. These actions are mainly aimed at removing the source of degradation of vegetative cover—the most common strategy is physical fencing (e.g., spike or electric fencing) to protect areas. Some passive restoration exercises also include installing structures that serve as perches or shelters for animals that are potential seed dispersers to attract them and expedite the process. No planting is carried out in this scheme. |
| NbS | Base LULC | Base LULC Code | Final LULC | Final LULC Code | (Years) | |
|---|---|---|---|---|---|---|
| Best livestock practices | Mosaic of pastures and crops | 242 | Mosaic of crops, pastures, and natural areas | 243 | 10 | 0 |
| Wooded pastures | 232 | Mosaic of pastures with natural spaces | 244 | 7 | 0.56 | |
| Weedy pastures | 233 | Mosaic of pastures with natural spaces | 244 | 10 | 0.56 | |
| Clean pastures | 231 | Mosaic of pastures with natural spaces | 244 | 12 | 0.56 | |
| Bare and degraded lands | 333 | Mosaic of pastures with natural spaces | 244 | 13 | 2.89 | |
| Best agricultural practices | Permanent shrub crops | 222 | Mosaic of crops and natural spaces | 245 | 10 | 0.6 |
| Permanent herbaceous crops | 221 | Mosaic of crops and natural spaces | 245 | 10 | 0.6 | |
| Crop mosaic | 241 | Mosaic of crops and natural spaces | 245 | 12 | 0 | |
| Pasture and crop mosaic | 242 | Mosaic of pastures and crops | 243 | 10 | 0 | |
| Other transitory crops | 211 | Mosaic of crops and natural spaces | 245 | 12 | 0.6 | |
| Tubers | 215 | Mosaic of crops and natural spaces | 245 | 12 | 0.6 | |
| Nucleation | Weeded pastures | 233 | Fragmented forest | 313 | 19 | 0.82 |
| Weeded pastures | 233 | Grassland | 321 | 19 | 1.01 | |
| Clean pasture | 231 | Fragmented forest | 313 | 21 | 0.82 | |
| Clean pasture | 231 | Grassland | 321 | 21 | 1.01 | |
| Bare and degraded land | 333 | Secondary or transitional vegetation | 323 | 22 | 1.72 | |
| Enrichment planting | Open forest | 312 | Dense forest | 311 | 19 | 0 |
| Fragmented forest | 313 | Open forest | 312 | 11 | 0 | |
| Mosaic of pastures with natural spaces | 244 | Fragmented forest | 313 | 14 | 0.26 | |
| Wooded pasture | 232 | Open forest | 312 | 16 | 0.82 | |
| Wooded pasture | 232 | Grassland | 321 | 16 | 1.01 | |
| Secondary or transitional vegetation | 323 | Open forest | 312 | 19 | −0.19 | |
| Passive restoration | Open forest | 312 | Dense forest | 311 | 19 | 0 |
| Fragmented forest | 313 | Open forest | 312 | 19 | 0 | |
| Mosaic of pastures with natural spaces | 244 | Secondary or transitional vegetation | 323 | 22 | 0 | |
| Secondary or transitional vegetation | 323 | Fragmented forest | 313 | 27 | −0.19 |
| Data Format | Description |
|---|---|
| Raster | Digital Elevation Model |
| Flow direction map | |
| Flow accumulation map | |
| Sand, silt and clay fraction in soil | |
| Soil depth and organic matter fraction | |
| Soil cohesion and angle of repose | |
| RUSLE erodibility and cropping practice factors | |
| Subterranean water interchange rate | |
| Paramo areas | |
| Level 3 CORINE LULC map | |
| Integer id representing nitrogen, phosphorus and total coliforms loads and their annual variations | |
| Environmental flow demand map | |
| Integer code representing a LULC transition from a base line to a desired final state according to the NbS portfolio | |
| Integer code representing the NbS intervention priority of each pixel | |
| Vector | Parcel of land owned by a single person or entity in the watershed |
| Text file | Water diversions |
| Point waste loads |
| Process | Calibration Factors Description | |
|---|---|---|
| Phenological model a | Maximum and minimum for each CLC class represented Total heat units required for plant maturity Fraction of heat units accumulated on a given date Soil humidity contents factors Temperature limits that contribute to vegetative development | |
| Hydrological model | Vertical precipitation depth Horizontal precipitation depth Maximum leaf storage Maximum capillary storage Maximum gravitational storage Subsurface permeability Groundwater permeability Subsurface exchange permeability Hillslope flow velocity Subsurface flow velocity Groundwater flow velocity Instream flow velocity | |
| Sedimentological model | Hillslope sediment transport capacity Stream sediment transport capacity Bank erosion Sediment supply disaggregation factor | |
| Landslide model | Soil cohesion and friction angle | |
| Water quality | BDO | Oxidation rate |
| DO | Reaeration model Reaeration factor | |
| Nitrogen forms | Nitrogen load factor on hillslopes Plant nitrogen uptake rates Nitrification rates from organic nitrogen to nitrites Nitrogen forms settling velocity | |
| Phosphorus forms | Phosphorus load factor on hillslopes Phosphorus mineralization rates Phosphorus immobilization rate Plant phosphorus uptake rate Organic/Inorganic phosphorus sorption Organic phosphorus hydrolysis Phosphorus forms settling velocity | |
| Total coliforms | Total coliforms load factor on hillslopes Growth and die-off bacteria ratesSediment fraction adsorption | |
| Temperature | Temperature correction factors | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiménez, M.; Usma, C.; Posada, D.; Ramírez, J.; Rogéliz, C.A.; Nogales, J.; Spiro-Larrea, E. Planning and Evaluating Nature-Based Solutions for Watershed Investment Programs with a SMART Perspective Using a Distributed Modeling Tool. Water 2023, 15, 3388. https://doi.org/10.3390/w15193388
Jiménez M, Usma C, Posada D, Ramírez J, Rogéliz CA, Nogales J, Spiro-Larrea E. Planning and Evaluating Nature-Based Solutions for Watershed Investment Programs with a SMART Perspective Using a Distributed Modeling Tool. Water. 2023; 15(19):3388. https://doi.org/10.3390/w15193388
Chicago/Turabian StyleJiménez, Mario, Cristian Usma, Daniela Posada, Juan Ramírez, Carlos A. Rogéliz, Jonathan Nogales, and Erik Spiro-Larrea. 2023. "Planning and Evaluating Nature-Based Solutions for Watershed Investment Programs with a SMART Perspective Using a Distributed Modeling Tool" Water 15, no. 19: 3388. https://doi.org/10.3390/w15193388
APA StyleJiménez, M., Usma, C., Posada, D., Ramírez, J., Rogéliz, C. A., Nogales, J., & Spiro-Larrea, E. (2023). Planning and Evaluating Nature-Based Solutions for Watershed Investment Programs with a SMART Perspective Using a Distributed Modeling Tool. Water, 15(19), 3388. https://doi.org/10.3390/w15193388





