An Improved Xin’anjiang Hydrological Model for Flood Simulation Coupling Snowmelt Runoff Module in Northwestern China
Abstract
:1. Introduction
2. Methodology
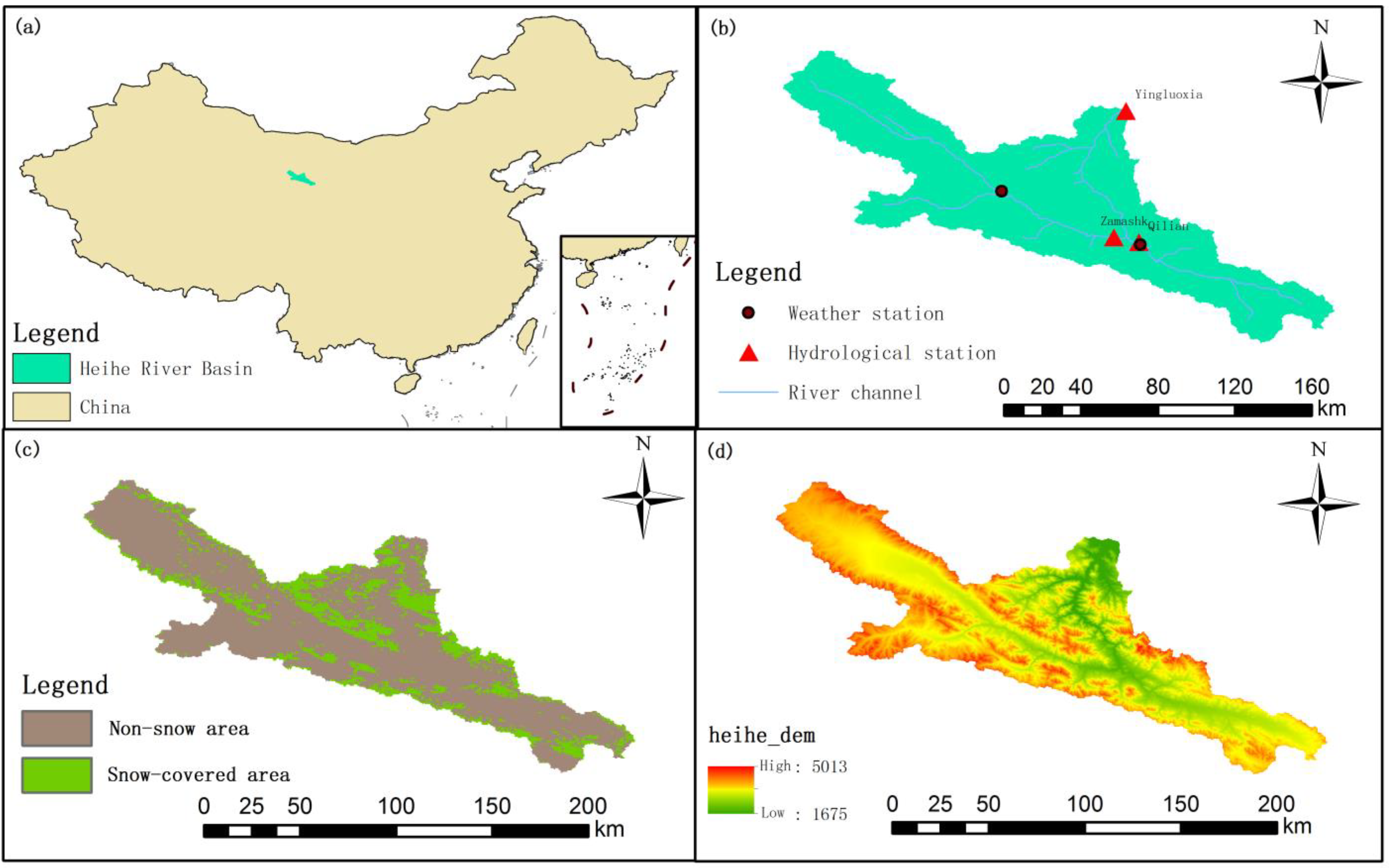
2.1. Study Area and Data
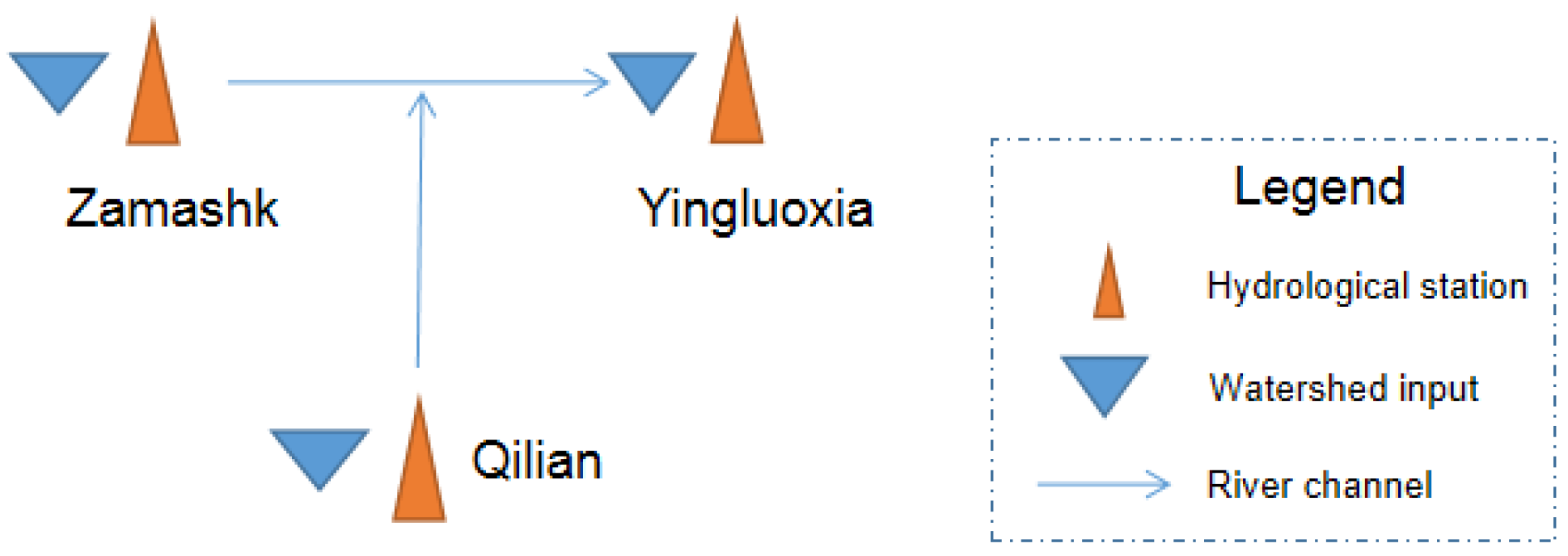
2.1.1. Study Area
2.1.2. Data Collection
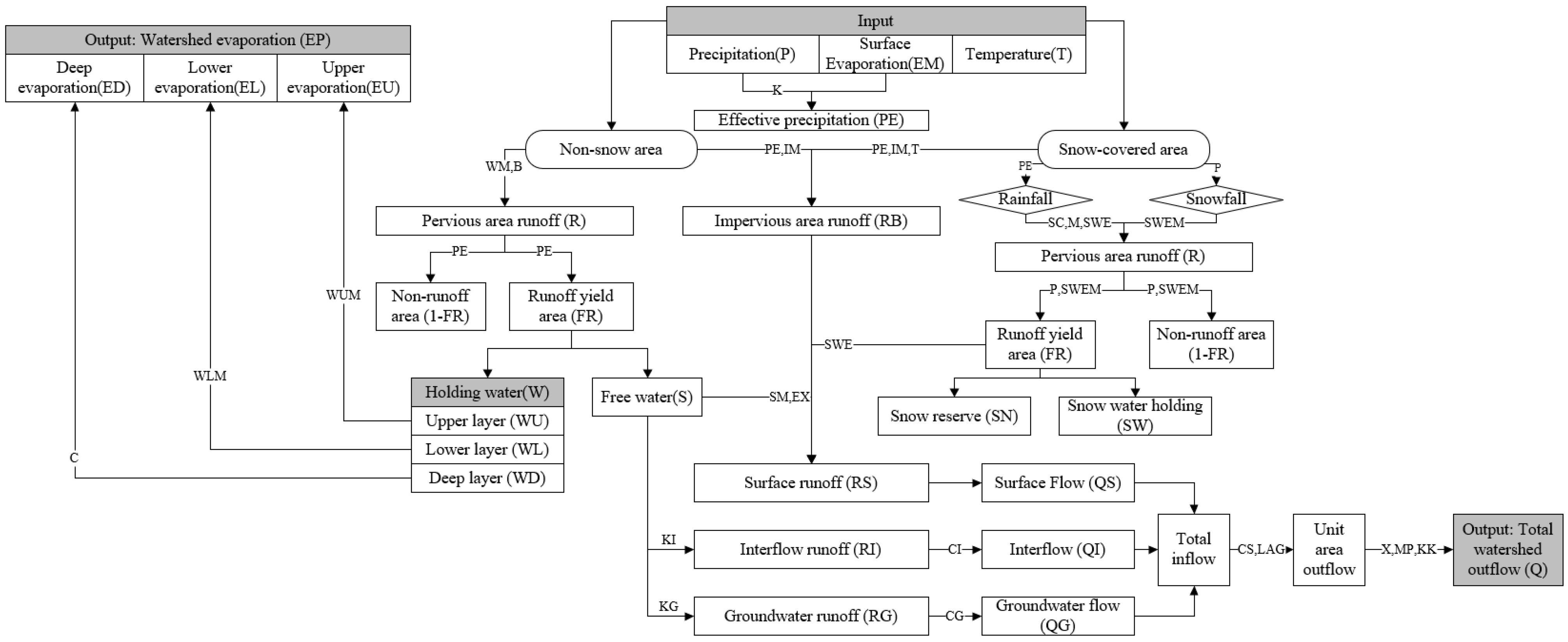
2.2. Model Description
2.2.1. Evaporation Sub-Model
2.2.2. Runoff Yield Sub-Model
- (1)
- Precipitation input processing
- (2)
- Snowmelt runoff module
- (3)
- Runoff production calculation considering snow melting
- Non-snow areas
- b.
- Snow-covered areas (considering glaciers)
- Case 1: the precipitation form is rainfall.
- If the threshold temperature for snow melting (Tmelt,snow) is between the temperature range of two adjacent days (hereby Tt and Tt−1), then
- If both Tt and Tt−1 are greater than Tmelt,snow then
- If both Tt and Tt−1 are less than Tmelt,snow then
- Case 2: the precipitation form is snowfall.
- Case 3: no precipitation.
2.2.3. Runoff Separation Sub-Model
2.2.4. Runoff Concentration Sub-Model
2.3. Model Calibration and Validation
2.3.1. Parameters Needing Calibration
2.3.2. Parameter Value Range Considering Snowmelt
- (1)
- Degree-day factor (a)
- (2)
- Snow cover storage (SN)
2.3.3. Parameter Calibration and Model Assessment
3. Results
3.1. Parameter Calibration Result
3.2. Model Simulation Result and Comparison
3.2.1. Model Efficiency Assessment
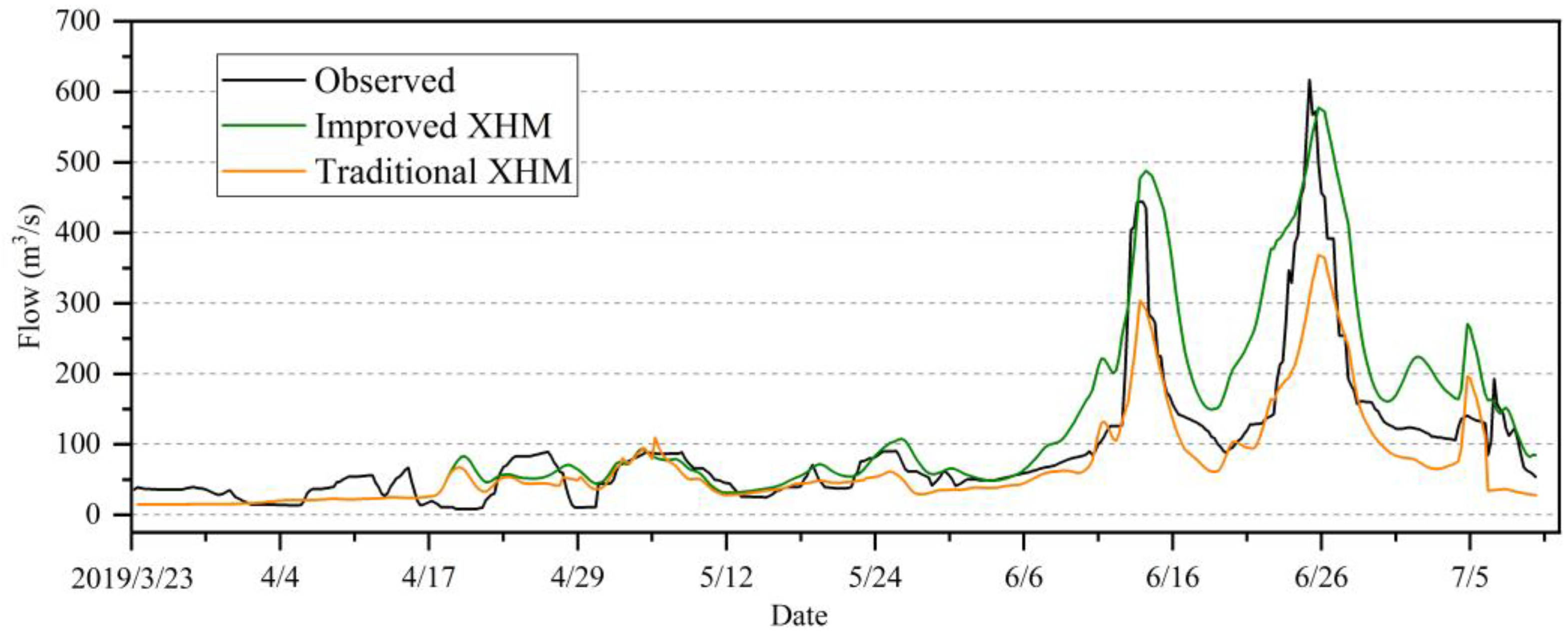
3.2.2. Comparison of Simulation Result with the Traditional Model
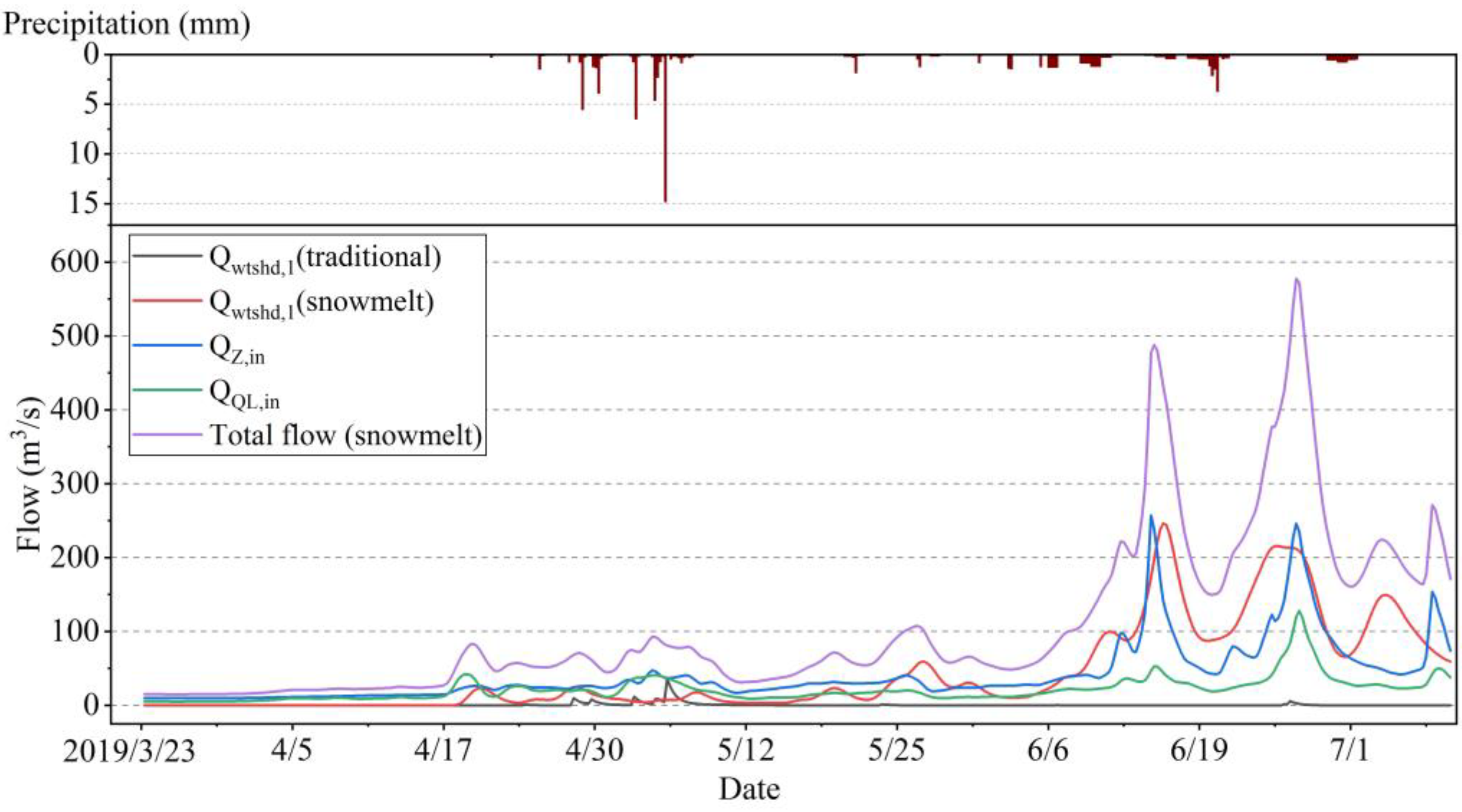
3.3. Flood Composition Analysis
4. Discussion
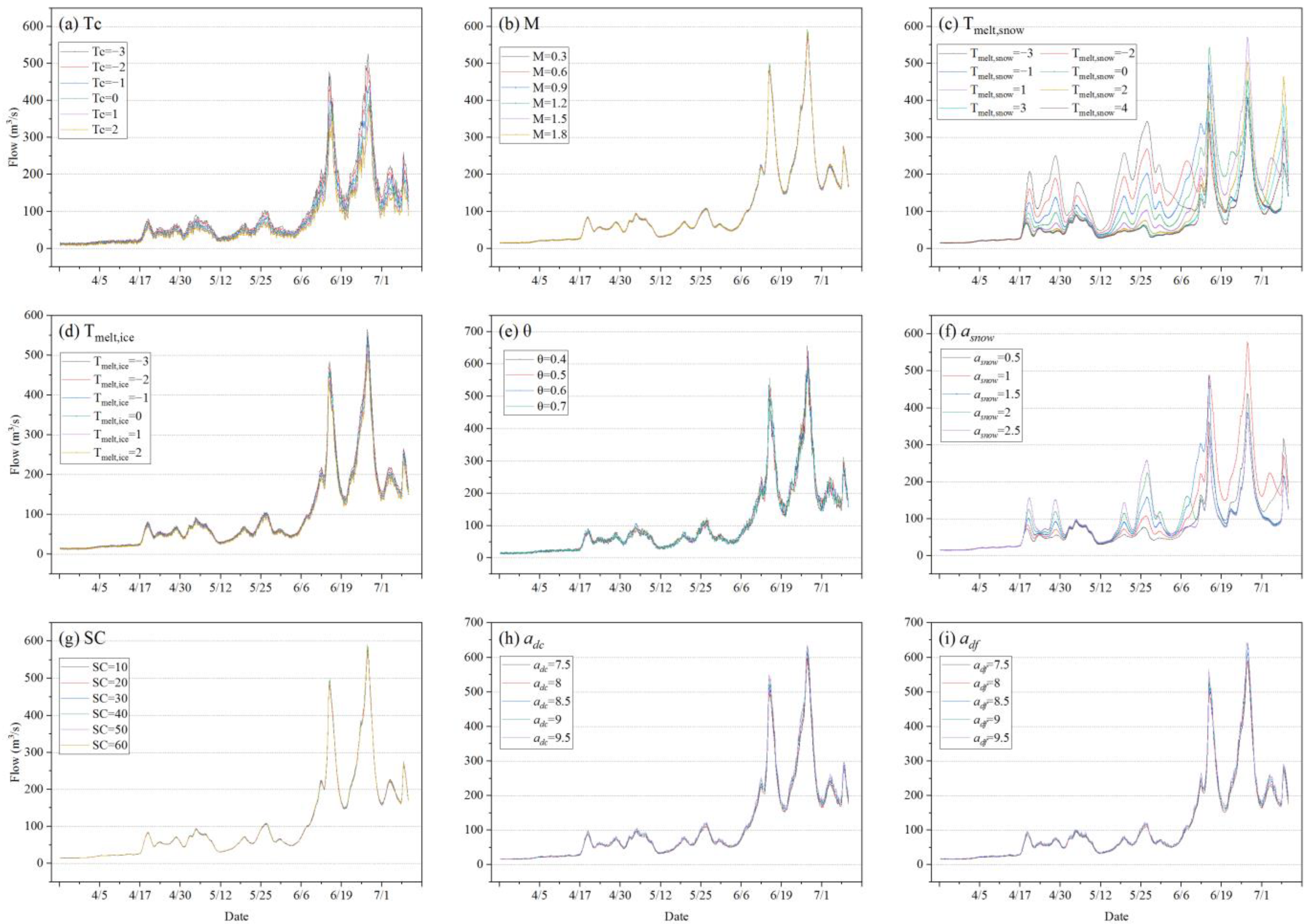
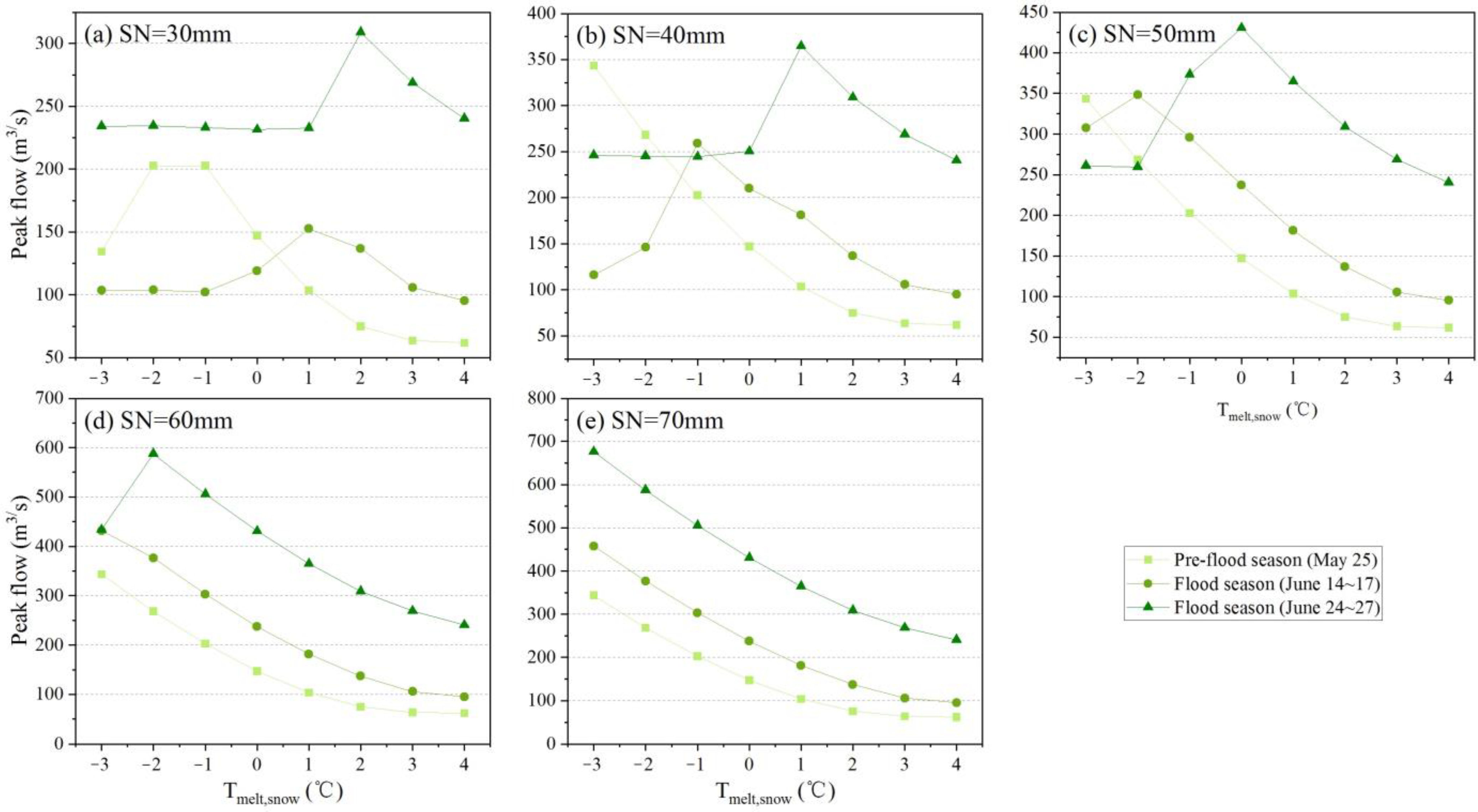
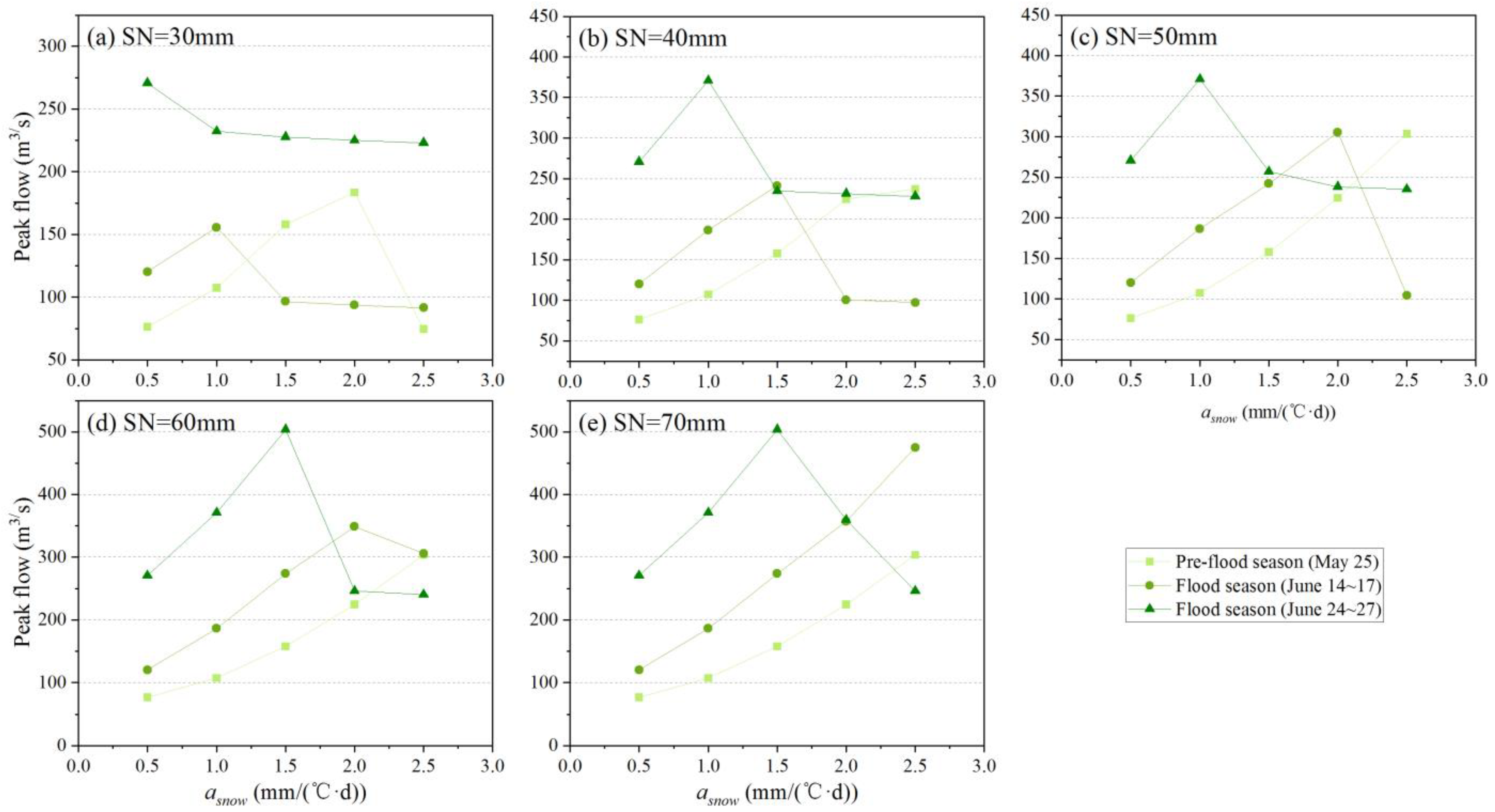
4.1. Sensitivity Analysis of Parameters
4.2. Effects of Model’s State
4.3. Model Comparisons and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mook, W.G. Environmental Isotopes in the Hydrological Cycle: Principles and Applications; UNESCO: Paris, France, 2000. [Google Scholar]
- Paz-Ríos, C.E.; Sosa-López, A.; Torres-Rojas, Y.E. Spatiotemporal Configuration of Hydrographic Variability in Terminos Lagoon: Implications for Fish Distribution. Estuaries Coasts 2023. [Google Scholar] [CrossRef]
- Shi, W.; Qiu, J.; Zhang, C.; Wang, Q.; Lai, J.; Li, B.; Mao, Z. Immersion mode and spatiotemporal distribution characteristic of water migration in loess tunnel. Arab. J. Geosci. 2022, 15, 654. [Google Scholar] [CrossRef]
- Bisht, N.; Chauhan, P.S. Excessive and disproportionate use of chemicals cause soil contamination and nutritional stress. In Soil Contamination-Threats and Sustainable Solutions; IntechOpen: London, UK, 2020; pp. 1–10. [Google Scholar]
- Zhu, G.; Wang, L.; Liu, Y.; Bhat, M.A.; Qiu, D.; Zhao, K.; Sang, L.; Lin, X.; Ye, L. Snow-melt water: An important water source for Picea crassifolia in Qilian Mountains. J. Hydrol. 2022, 613, 128441. [Google Scholar] [CrossRef]
- Meng, X.; Liu, Y.; Qin, Y.; Wang, W.; Zhang, M.; Zhang, K. Adaptability of MODIS Daily Cloud-Free Snow Cover 500 m Dataset over China in Hutubi River Basin Based on Snowmelt Runoff Model. Sustainability 2022, 14, 4067. [Google Scholar] [CrossRef]
- Marks, D.; Kimball, J.; Tingey, D.; Link, T. The sensitivity of snowmelt processes to climate conditions and forest cover during rain-on-snow: A case study of the 1996 Pacific Northwest flood. Hydrol. Process. 1998, 12, 1569–1587. [Google Scholar] [CrossRef]
- Li, M.; Weng, B.; Yan, D.; Bi, W.; Yang, Y.; Gong, X.; Wang, H. Spatiotemporal characteristics of surface water resources in the Tibetan plateau: Based on the produce water coefficient method considering snowmelt. Sci. Total Environ. 2022, 851, 158048. [Google Scholar] [CrossRef]
- Yang, W.; Chen, L.; Deng, F.; Lv, S. Application of an improved distributed Xin’anjiang hydrological model for flood prediction in a karst catchment in South-Western China. J. Flood Risk Manag. 2020, 13, e12649. [Google Scholar] [CrossRef]
- Hartmann, A.; Goldscheider, N.; Wagener, T.; Lange, J.; Weiler, M. Karst water resources in a changing world: Review of hydrological modeling approaches. Rev. Geophys. 2014, 52, 218–242. [Google Scholar] [CrossRef]
- Fleury, P.; Plagnes, V.; Bakalowicz, M. Modelling of the functioning of karst aquifers with a reservoir model: Application to Fontaine de Vaucluse (south of France). J. Hydrol. 2007, 345, 38–49. [Google Scholar] [CrossRef]
- Jukić, D.; Denić-Jukić, V. Nonlinear kernel functions for karst aquifers. J. Hydrol. 2006, 328, 360–374. [Google Scholar] [CrossRef]
- Hartmann, A.; Barberá, J.A.; Lange, J.; Andreo, B.; Weiler, M. Progress in the hydrologic simulation of time variant recharge areas of karst systems—Exemplified at a karst spring in Southern Spain. Adv. Water Resour. 2013, 54, 149–160. [Google Scholar] [CrossRef]
- Ronayne, M.J. Influence of conduit network geometry on solute transport in karst aquifers with a permeable matrix. Adv. Water Resour. 2013, 56, 27–34. [Google Scholar] [CrossRef]
- Usman, M.; Ndehedehe, C.E.; Farah, H.; Ahmad, B.; Wong, Y.; Adeyeri, O.E. Application of a Conceptual Hydrological Model for Streamflow Prediction Using Multi-Source Precipitation Products in a Semi-Arid River Basin. Water 2022, 14, 1260. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J.; Freer, J.E.; Lamb, R. A history of TOPMODEL. Hydrol. Earth Syst. Sci. 2021, 25, 527–549. [Google Scholar] [CrossRef]
- Ambroise, B.; Beven, K.; Freer, J. Toward a generalization of the TOPMODEL concepts: Topographic indices of hydrological similarity. Water Resour. Res. 1996, 32, 2135–2145. [Google Scholar] [CrossRef]
- McMichael, C.E.; Hope, A.S.; Loaiciga, H.A. Distributed hydrological modelling in California semi-arid shrublands: MIKE SHE model calibration and uncertainty estimation. J. Hydrol. 2006, 317, 307–324. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Z.; Sun, G.; Strauss, P.; Guo, J.; Tang, Y.; Yao, A. Multi-site calibration, validation, and sensitivity analysis of the MIKE SHE Model for a large watershed in northern China. Hydrol. Earth Syst. Sci. 2012, 16, 4621–4632. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; Van Liew, M.W. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Douglas-Mankin, K.R.; Srinivasan, R.; Arnold, J.G. Soil and Water Assessment Tool (SWAT) model: Current developments and applications. Trans. ASABE 2010, 53, 1423–1431. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, R.; Xie, J.; Zhao, Y.; Yan, D.; Yang, S. Soil and water assessment tool (SWAT) model: A systemic review. J. Coast. Res. 2019, 93, 22–30. [Google Scholar] [CrossRef]
- Gao, H.; Tang, Q.; Shi, X.; Zhu, C.; Bohn, T.; Su, F.; Sheffield, J.; Pan, M.; Lettenmaier, D.; Wood, E. Water budget record from Variable Infiltration Capacity (VIC) model. In Algorithm Theoretical Basis Document for Terrestrial Water Cycle Data Records; 2010; Available online: https://eprints.lancs.ac.uk/id/eprint/89407/1/Gao_et_al_VIC_2014.pdf (accessed on 8 August 2023).
- Zhang, Y.; You, Q.; Chen, C.; Ge, J.; Adnan, M. Evaluation of downscaled CMIP5 coupled with VIC model for flash drought simulation in a humid subtropical basin, China. J. Clim. 2018, 31, 1075–1090. [Google Scholar] [CrossRef]
- Kordilla, J.; Sauter, M.; Reimann, T.; Geyer, T. Simulation of saturated and unsaturated flow in karst systems at catchment scale using a double continuum approach. Hydrol. Earth Syst. Sci. 2012, 16, 3909–3923. [Google Scholar] [CrossRef]
- Reimann, T.; Rehrl, C.; Shoemaker, W.B.; Geyer, T.; Birk, S. The significance of turbulent flow representation in single-continuum models. Water Resour. Res. 2011, 47, W09503. [Google Scholar] [CrossRef]
- Okkan, U.; Ersoy, Z.B.; Kumanlioglu, A.A.; Fistikoglu, O. Embedding machine learning techniques into a conceptual model to improve monthly runoff simulation: A nested hybrid rainfall-runoff modeling. J. Hydrol. 2021, 598, 126433. [Google Scholar] [CrossRef]
- Hu, J.; Chen, S.; Behrangi, A.; Yuan, H. Parametric uncertainty assessment in hydrological modeling using the generalized polynomial chaos expansion. J. Hydrol. 2019, 579, 124158. [Google Scholar] [CrossRef]
- Zhang, D.; Quan, J.; Wang, F.; He, X. Flash flood simulation using geomorphic unit hydrograph method: Case study of headwater catchment of Xiapu River Basin, China. In Proceedings of the International Conference on Hydroinformatics, New York, NY, USA, 17–21 August 2014. [Google Scholar]
- Yao, C.; Ye, J.; He, Z.; Bastola, S.; Zhang, K.; Li, Z. Evaluation of flood prediction capability of the distributed Grid-Xin’anjiang model driven by weather research and forecasting precipitation. J. Flood Risk Manag. 2019, 12, e12544. [Google Scholar] [CrossRef]
- Zhao, Q.; Ye, B.; Ding, Y.; Zhang, S.; Yi, S.; Wang, J.; Shangguan, D.; Zhao, C.; Han, H. Coupling a glacier melt model to the Variable Infiltration Capacity (VIC) model for hydrological modeling in north-western China. Environ. Earth Sci. 2013, 68, 87–101. [Google Scholar] [CrossRef]
- Finsterwalder, S.; Schunk, H. Der suldenferner. Z. Des Dtsch. Und Oesterreichischen Alpenver. 1887, 18, 72–89. [Google Scholar]
- Singh, V.; Jain, S.K.; Shukla, S. Glacier change and glacier runoff variation in the Himalayan Baspa river basin. J. Hydrol. 2021, 593, 125918. [Google Scholar] [CrossRef]
- Matinec, J.; Rango, A. Parameter values for snowmelt runoff modeling. J. Hydrol. 1986, 84, 197–219. [Google Scholar] [CrossRef]
- Fathi, M.M.; Awadallah, A.G.; Aldahshoory, W. An Improved Monthly Water Balance GR2M Model with a Seasonally Variable Parameter. J. Hydrol. 2023, 617, 129127. [Google Scholar] [CrossRef]
- Maneechot, L.; Wong, Y.J.; Try, S.; Shimizu, Y.; Bharambe, K.P.; Hanittinan, P.; Ram-Indra, T.; Usman, M. Evaluating the necessity of post-processing techniques on d4PDF data for extreme climate assessment. Environ. Sci. Pollut. Res. 2023. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Landesa, E.; Rango, A. Operational snowmelt runoff forecasting in the Spanish Pyrenees using the snowmelt runoff model. Hydrol. Process. 2002, 16, 1583–1591. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Ge, Y.; Li, H.; Han, F.; Hu, X.; Tian, W.; Tian, Y.; Pan, X.; Nian, Y.; et al. Hydrological cycle in the Heihe River Basin and its implication for water resource management in endorheic basins. J. Geophys. Res. Atmos. 2018, 123, 890–914. [Google Scholar] [CrossRef]
- Yin, Z.; Feng, Q.; Liu, S.; Zou, S.; Li, J.; Yang, L.; Deo, R.C. The spatial and temporal contribution of glacier runoff to watershed discharge in the Yarkant River Basin, Northwest China. Water 2017, 9, 159. [Google Scholar] [CrossRef]
- Yan, W. Study on Variations of Runoff and Its Components in Three Sources Streams of Tarim River. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2021. [Google Scholar]
- Zhang, Y.; Liu, S.; Ding, Y. Observed degree-day factors and their spatial variation on glaciers in western China. Ann. Glaciol. 2006, 43, 301–306. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, C.; Yu, Q.; Zhao, C.; Quan, L.; Hu, C. Study on a Hybrid Hydrological Forecasting Model SCE-GUH by Coupling SCE-UA Optimization Algorithm and General Unit Hydrograph. Water 2023, 15, 2783. [Google Scholar] [CrossRef]
- Arsenault, R.; Poulin, A.; Côté, P.; Brissette, F. Comparison of stochastic optimization algorithms in hydrological model calibration. J. Hydrol. Eng. 2014, 19, 1374–1384. [Google Scholar] [CrossRef]
- Kan, G.; He, X.; Li, J.; Ding, L.; Hong, Y.; Zhang, H.; Liang, K.; Zhang, M. Computer aided numerical methods for hydrological model calibration: An overview and recent development. Arch. Comput. Methods Eng. 2019, 26, 35–59. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]


| Type of Parameter | Name of Parameter | Unit | Description | Default Range |
|---|---|---|---|---|
| Runoff yield sub-model in non-snow areas used in traditional XHM | WM | mm | Average tension water storage capacity of the basin | (80, 200) |
| K | / | Watershed evapotranspiration conversion coefficient | (0.7, 1.3) | |
| B | / | Coefficient of the unevenness of tension water storage capacity in the basin | (0.01, 0.4) | |
| C | / | Deep evapotranspiration conversion coefficient | (0.01, 0.15) | |
| IM | / | The proportion of impervious area in the whole basin area | (0.02, 0.1) | |
| EX | / | Coefficient of the unevenness of surface free water storage capacity | 1.5 | |
| SM | mm | Surface free water storage capacity | (15, 50) | |
| KG | / | Groundwater discharge coefficient | ||
| KI | / | Interflow discharge coefficient | ||
| Runoff yield sub-model in the snow-covered area used in improved XHM | SC | mm | Average water-holding capacity of snow cover | |
| M | / | Uneven coefficient of water-holding capacity of snow cover | ||
| Tc | °C | Critical temperature for rain and snow | ||
| Tmelt,snow | °C | Critical temperature of snow melt | (−2, 5) | |
| Tmelt,ice | °C | Critical temperature of ice melt | (−2, 5) | |
| θ | / | Coefficient of glacier melt runoff | (0.3, 0.7) | |
| asnow | mm/(°C·d) | Degree-day factor of snow | (0.6, 3.5) | |
| adf | mm/(°C·d) | Degree-day factor of debris-free glaciers | (7.5, 9.5) | |
| adc | mm/(°C·d) | Degree-day factor of debris-covered glaciers | (7.5, 9.5) | |
| Runoff concentration of slope and river network | F | km2 | Basin area | / |
| CI | / | Interflow extinction coefficient | ||
| CG | / | Groundwater extinction coefficient | ||
| CS | / | Surface flow extinction coefficient | ||
| KK | h | Time step (Δt) | ||
| L | / | The intermediate variable of the lag time represents how many KK’s, and the value multiplied by the value of KK is the lag time | (0, 20, N) | |
| Runoff concentration of river channel | X | / | Represents the shape of the flood process line | (−∞, 0.5) |
| KK | h | Time step (Δt) | ||
| MP | / | Flood traveling time represents how many KK’s. |
| Name of Parameter | Unit | Value | |
|---|---|---|---|
| Zamashk | Yingluoxia | ||
| WM | mm | 109.9 | 100.51 |
| K | / | 0.729 | 0.741 |
| B | / | 0.389 | 0.375 |
| C | / | 0.135 | 0.165 |
| IM | / | 0.041 | 0.035 |
| EX | / | 1.5 | 1.5 |
| SM | mm | 47.82 | 25.29 |
| KG | / | 0.497 | 0.362 |
| KI | / | 0.179 | 0.169 |
| SC | mm | 53.75 | 58.63 |
| M | / | 1.5 | 1.56 |
| Tc | °C | −2.54 | −1.89 |
| Tmelt,snow | °C | 3.65 | 4.09 |
| Tmelt,ice | °C | 1.53 | 1.06 |
| θ | / | 0.423 | 0.537 |
| asnow | mm/(°C·d) | 2.17 | 2.31 |
| adc | mm/(°C·d) | 7.98 | 8.56 |
| adf | mm/(°C·d) | 8.22 | 8.97 |
| F | km2 | 4589 | 2968 |
| CI | / | 0.66 | 0.597 |
| CG | / | 0.959 | 0.966 |
| CS | / | 0.8 | 0.452 |
| KK | h | 6 | 6 |
| L | / | 0 | 4 |
| Name of Parameter | Unit | Value | |
|---|---|---|---|
| From Zamashk | From Qilian | ||
| X | / | 0.264 | 0.244 |
| KK | h | 6 | 6 |
| MP | / | 1 | 2 |
| Model Type | Zamashk Station | Yingluoxia Station | |||||
|---|---|---|---|---|---|---|---|
| R2 | MSE (m3/s) | NSE | R2 | MSE (m3/s) | NSE | ||
| Traditional XHM | Calibration period (2010~2016) | 0.466 | 897 | 0.284 | 0.724 | 547 | 0.559 |
| Validation period (2017~2019) | 0.426 | 634 | 0.171 | 0.751 | 529 | 0.541 | |
| XHM considering snowmelt | Calibration period (2010~2016) | 0.792 | 524 | 0.589 | 0.884 | 465 | 0.785 |
| Validation period (2017~2019) | 0.764 | 435 | 0.582 | 0.861 | 397 | 0.794 | |
| Flood Process | 6/14~6/17 | 6/24~6/27 | |||
|---|---|---|---|---|---|
| Station | Zamashk | Yingluoxia | Zamashk | Yingluoxia | |
| Observed | Flow (m3/s) | 331 | 444 | 278 | 617 |
| Occur time | 6/14 15:00 | 6/15 4:00 | 6/26 3:00 | 6/26 16:00 | |
| Traditional XHM | Flow (m3/s) | 66 | 303 | 109 | 368 |
| Occur time | 6/15 6:00 | 6/15 2:00 | 6/26 12:00 | 6/27 2:00 | |
| Error (%) | −80 | −32 | −61 | −40 | |
| Improved XHM | Flow (m3/s) | 275 | 488 | 229 | 577 |
| Occur time | 6/15 0:00 | 6/15 8:00 | 6/26 12:00 | 6/27 2:00 | |
| Error (%) | −17 | 10 | −18 | −6 | |
| Date | 7 | 8 | 9 | 10 | 11 | 12 | 13 | … | 19 | 20 | 21 | 22 | 23 | 24 |
| Temperature | 12.2 | 13 | 11.9 | 11 | 12.9 | 14.5 | 17 | … | 12.3 | 13.8 | 14 | 14.2 | 13.5 | 15.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Y.; Dong, N.; Hou, A.; Yan, W. An Improved Xin’anjiang Hydrological Model for Flood Simulation Coupling Snowmelt Runoff Module in Northwestern China. Water 2023, 15, 3401. https://doi.org/10.3390/w15193401
Tan Y, Dong N, Hou A, Yan W. An Improved Xin’anjiang Hydrological Model for Flood Simulation Coupling Snowmelt Runoff Module in Northwestern China. Water. 2023; 15(19):3401. https://doi.org/10.3390/w15193401
Chicago/Turabian StyleTan, Yaogeng, Ningpeng Dong, Aizhong Hou, and Wei Yan. 2023. "An Improved Xin’anjiang Hydrological Model for Flood Simulation Coupling Snowmelt Runoff Module in Northwestern China" Water 15, no. 19: 3401. https://doi.org/10.3390/w15193401
APA StyleTan, Y., Dong, N., Hou, A., & Yan, W. (2023). An Improved Xin’anjiang Hydrological Model for Flood Simulation Coupling Snowmelt Runoff Module in Northwestern China. Water, 15(19), 3401. https://doi.org/10.3390/w15193401







