Dam System and Reservoir Operational Safety: A Meta-Research
Abstract
:1. Introduction
2. Quantitative Analysis
2.1. Data Collection
2.2. Pre-Processing
2.3. Latent Dirichlet Allocation (LDA)
- (1)
- The model user determines the analyzed documents (D);
- (2)
- Define the number of topics (K);
- (3)
- The algorithm randomly assigns a particular topic kdi to each word wdi based on:
- The word distribution for each topic k (ψk), evaluated by initial Dirichlet (β);
- The topic distribution for each document d (θd), evaluated by initial Dirichlet (α)
- where wdi is the word (i) in the word collection (wd) per document (d), d [1, D], i [1, Nd (number of words in wd)], and kdi is the topic assigned to the word i (wdi) in the document (d), kdi [1, K];
- (4)
- Using Gibbs sampling [35] with iteration j (j = 1000 in this study), the algorithm improves the topic assignment in terms of enhancing the values of β and α, where the algorithm can calculate the probability that word (wdi) is generated from the topic (kdi);
- (5)
- The algorithm re-assigns each word (wdi) with the new topic (kdi) based on the previous step calculations.
2.4. Perplexity
2.5. Topic Identification
3. Qualitative Analysis
3.1. Topic 1: Optimization Models
3.2. Topic 2: Climate Change
3.3. Topic 3: Flood Risk
3.4. Topic 4: Inflow Forecasting
3.5. Topic 5: Hydropower Generation
3.6. Topic 6: Water Supply Management
3.7. Topic 7: Risk-Based Assessment and Management
4. Research Gaps
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Herzog, M.A.M. Practical Dam Analysis; Thomas Telford Publishing: London, UK, 1998. [Google Scholar] [CrossRef]
- Zhang, J.; Shang, Y. Nexus of dams, reservoirs, climate, and the environment: A systematic perspective. Int. J. Environ. Sci. Technol. 2023. [Google Scholar] [CrossRef]
- Ma, C.; Xu, X.; Yang, J.; Cheng, L. Safety Monitoring and Management of Reservoir and Dams. Water 2023, 15, 1078. [Google Scholar] [CrossRef]
- Tajziehchi, S.; Karbassi, A.; Nabi, G.; Yoo, C.; Ifaei, P. A cost-benefit analysis of Bakhtiari hydropower dam considering the nexus between energy and water. Energies 2022, 15, 871. [Google Scholar] [CrossRef]
- Zohuri, B. Nuclear fuel cycle and decommissioning. In Nuclear Reactor Technology Development and Utilization; Woodhead Publishing: Cambridge, UK, 2020; pp. 61–120. [Google Scholar] [CrossRef]
- Boretti, A.; Rosa, L. Reassessing the projections of the World Water Development Report. npj Clean Water 2019, 2, 15. [Google Scholar] [CrossRef]
- Berga, L. The role of hydropower in climate change mitigation and adaptation: A review. Engineering 2016, 2, 313–318. [Google Scholar] [CrossRef]
- Fluixá-Sanmartín, J.; Escuder-Bueno, I.; Morales-Torres, A.; Castillo-Rodríguez Jesica, T. Accounting for climate change uncertainty in Long-Term dam risk management. J. Water Resour. Plan. Manag. 2021, 147, 04021012. [Google Scholar] [CrossRef]
- UNEP. The Future We Want. In Proceedings of the Outcome Document of the United Nations Conference on Sustainable Development, Rio, Brazil, 20–22 June 2012; Available online: https://www.un.org/ga/search/view_doc.asp?symbol=A/RES/66/288&Lang=E (accessed on 8 October 2021).
- Zarfl, C.; Lumsdon, A.; Tockner, K. A global boom in hydropower dam construction. Aquat. Sci. 2015, 77, 161–170. [Google Scholar] [CrossRef]
- Homeland Security, Cybersecurity and Infrastructure Security Agency. National Infrastructure Protection Plan (N.I.P.P.) Dams Sector-Estimating Loss of Life for Dam Failures Scenarios. 2011. Available online: https://damsafety.org/sites/default/files/files/DamsSectorConsequenceEstimation_LossOfLife.pdf (accessed on 7 October 2021).
- United Nations World Water Development Report (UN-WWDR). Water and Climate Change. 2020. Available online: https://unesdoc.unesco.org/ark:/48223/pf0000372985.locale=en (accessed on 7 October 2021).
- Ehsani, N.; Vörösmarty, C.J.; Fekete, B.M.; Stakhiv, E.Z. Reservoir operations under climate change: Storage capacity options to mitigate risk. J. Hydrol. 2017, 555, 435–446. [Google Scholar] [CrossRef]
- Regan, P.J. Dams as systems—A holistic approach to dam safety. In Proceedings of the U.S.S.D. Annual Meeting and Conference 2010, Sacramento, CA, USA, 12–16 April 2010; pp. 1307–1340. [Google Scholar]
- Kumar, K.; Saini, R.P. A review of operation and maintenance of hydropower plants. Sustain. Energy Technol. Assess. 2022, 49, 101704. [Google Scholar] [CrossRef]
- Hauera, C.; Wagnera, B.; Aignera, J.; Holzapfela, P.; Flödla, P.; Liedermanna, M.; Trittharta, M.; Sindelara, C.; Pulgb, U.; Klöscha, M.; et al. State of the art, shortcomings and future challenges for a sustainable sediment management in hydropower: A review. Renew. Sustain. Energy 2018, 98, 40–55. [Google Scholar] [CrossRef]
- Neboh, N.; Adeyemo, J.; Enitan, A.; Olugbara, O. A review of applications of evolutionary algorithms to reservoir operation for hydropower production. Int. J. Geol. Environ. Eng. 2015, 9, 1153–1159. Available online: https://zenodo.org/record/1109762#.YvAJqHbMK38 (accessed on 1 December 2022).
- You, L.; Li, C.; Min, X.; Xiaolei, T. Review of dam-break research of earth-rock dam combined with dam safety management. Procedia Eng. 2012, 28, 382–388. [Google Scholar] [CrossRef]
- Rani, D.; Moreira, M.M. Simulation–Optimization modeling: A survey and potential application in reservoir systems operation. Water Resour. Manag. 2010, 24, 1107–1138. [Google Scholar] [CrossRef]
- Sun, L.; Yin, Y. Discovering themes and trends in transportation research using topic modeling. Transp. Res. Part C Emerg. Technol. 2017, 77, 49–66. [Google Scholar] [CrossRef]
- Gatti, C.; Brooks, J.; Nurre, S. A historical analysis of the field of OR/MS using topic models. arXiv 2015, arXiv:1510.05154. [Google Scholar] [CrossRef]
- Haggag, M.; Ezzeldin, M.; El-Dakhakhni, W.; Hassini, E. Resilient cities critical infrastructure interdependence: Meta-research. Sustain. Resilient Infrastruct. 2020, 7, 291–312. [Google Scholar] [CrossRef]
- Ezzeldin, M.; El-Dakhakhni, W. Meta-researching structural engineering: Trend identification and knowledge gap discovery using text mining. J. Struct. Eng. 2020, 146, 1–22. [Google Scholar] [CrossRef]
- Islam, A.; Hassini, S.; El-Dakhakhni, W. A systematic bibliometric review of optimization and resilience within low impact development stormwater management practices. J. Hydrol. 2021, 599, 126457. [Google Scholar] [CrossRef]
- Das, S.; Sun, X.; Dutta, A. Text mining and topic modeling of compendiums of papers from transportation research board annual meetings. J. Transp. Res. Board 2016, 2552, 48–56. [Google Scholar] [CrossRef]
- Griffiths, T.L.; Steyvers, M. Finding scientific topics. Proc. Natl. Acad. Sci. USA 2004, 101, 5228–5235. [Google Scholar] [CrossRef]
- Salloum, S.A.; Al-Emran, M.; Abdel Monem, A.; Shaalan, K. Using text mining techniques for extracting information from research articles. In Intelligent Natural Language Processing: Trends and Applications; Springer: Cham, Switzerland, 2018; pp. 373–397. [Google Scholar] [CrossRef]
- Miner, G.; Elder, J.; Hill, T.; Delen, D.; Fast, A.; Nisbet, R.A. Practical Text Mining and Statistical Analysis for Non-Structured Text Data Applications; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar] [CrossRef]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent Dirichlet allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Hofmann, T. Probabilistic latent semantic indexing. In Proceedings of the 22nd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (S.I.G.I.R. ‘99), A.C.M., Berkeley, CA, USA, 15–19 August 1999; pp. 50–57. [Google Scholar] [CrossRef]
- Amado, A.; Cortez, P.; Rita, P.; Moro, S. Research trends on big data in marketing: A text mining and topic modeling-based literature analysis. Eur. Res. Manag. Bus. Econ. 2018, 24, 1–7. [Google Scholar] [CrossRef]
- Steyvers, M.; Griffiths, T. Probabilistic topic models. In Latent Semantic Analysis: A Road to Meaning; Landauer, T., McNamara, D., Dennis, S., Kintsch, W., Eds.; Laurence Erlbaum: Hillsdale, NJ, USA, 2007; Volume 427, pp. 424–440. [Google Scholar]
- Blei, D.M. Probabilistic topic models. Commun. ACM 2012, 55, 77–84. [Google Scholar] [CrossRef]
- Minka, T. Estimating a Dirichlet distribution. In Technical Rep.; Massachusetts Institute of Technology: Cambridge, MA, USA, 2000. [Google Scholar]
- Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, PAMI-6, 721–741. [Google Scholar] [CrossRef] [PubMed]
- Fayaed, S.S.; El-Shafie, A.; Jaafar, O. Reservoir-system simulation and optimization techniques. Stoch. Environ. Res. Risk Assess. 2013, 27, 1751–1772. [Google Scholar] [CrossRef]
- Taghian, M.; Rosbjerg, D.; Haghighi, A.; Madsen, H. Optimization of conventional rule curves coupled with hedging rules for reservoir operation. J. Water Resour. Plan. Manag. 2014, 140, 693–698. [Google Scholar] [CrossRef]
- Parvez, I.; Shen, J.; Hassan, I.; Zhang, N. Generation of hydro energy by using a data mining algorithm for the cascaded hydropower plant. Energies 2021, 14, 298. [Google Scholar] [CrossRef]
- Bozorg-Haddad, O.; Aboutalebi, M.; Ashofteh, P.S. Real-time reservoir operation using data mining techniques. Environ. Monit. Assess. 2018, 190, 594. [Google Scholar] [CrossRef]
- Raju, K.; Chandre, G.C.; Karthika, B.S. Optimization of reservoir operation using linear programming. Int. J. Recent Technol. Eng. 2020, 8, 2277–3878. [Google Scholar] [CrossRef]
- Ginting, B.M.; Harlan, D.; Taufik, A. Optimization of reservoir operation using the linear program, a case study of Riam Jerawi Reservoir, Indonesia. Int. J. River Basin Manag. 2017, 15, 187–198. [Google Scholar] [CrossRef]
- Heydari, M.; Othman, F.; Qaderi, K. Developing optimal reservoir operation for multiple and multipurpose reservoirs using mathematical programming. Math. Probl. Eng. 2015, 2015, 435752. [Google Scholar] [CrossRef]
- Needham, J.T.; David, W.; Watkins, D.W.; Lund, J.R.; Nanda, S.K. Linear programming for flood control in the Iowa and Des Moines rivers. Water Resour. Plan. Manag. 2000, 126, 118–127. [Google Scholar] [CrossRef]
- Houck, M.H.; Cohon, J.L. Sequential explicitly stochastic linear programming models: A proposed method for design and management of multi-purpose reservoir system. Water Resour. Res. 1978, 14, 161–168. [Google Scholar] [CrossRef]
- Wu, X.; Wu, Y.; Cheng, X.; Chuntian Cheng Li, Z.; Wu, Y. A mixed-integer linear programming model for hydro unit commitment considering operation constraint priorities. Renew. Energy 2023, 204, 507–520. [Google Scholar] [CrossRef]
- Dogan, M.S.; Lund, J.R.; Josue Medellin-Azuara, J.M. Hybrid linear and nonlinear programming model for hydropower reservoir optimization. J. Water Resour. Plan. Manag. 2021, 147, 06021001. [Google Scholar] [CrossRef]
- Arunkumar, R.; Jothiprakash, V. Optimal reservoir operation for hydropower generation using a non-linear programming model. J. Inst. Eng. Ser. A 2012, 93, 111–120. [Google Scholar] [CrossRef]
- Gu, J.J.; Guo, P.; Huang, G.H.; Shen, N. Optimization of the industrial structure facing sustainable development in resource-based cities subjected to water resources under uncertainty. Stoch. Environ. Res. Risk Assess. 2012, 27, 659–673. [Google Scholar] [CrossRef]
- Simonovic, S.P.; Marino, M.A. Reliability programming in reservoir management, single multipurpose reservoir. Water Resour. Res. 1980, 16, 844–848. [Google Scholar] [CrossRef]
- Nandalal, K.D.W.; Bogardi, J.J. Dynamic Programming-Based Operation of Reservoirs: Applicability and Limits; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Labadie, J.W. Optimal operation of multi-reservoir systems: A state-of-the-art review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Shim, K.-C.; Fontane, D.; Labadie, J. Spatial decision support system for integrated river basin flood control. J. Water Resour. Plan. Manag. 2002, 128, 190–201. [Google Scholar] [CrossRef]
- Yakowitz, S. Dynamic programming applications in water resources. Water Resour. Res. 1982, 18, 673–696. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957; ISBN 0-691-07951-X. [Google Scholar]
- Mizyed, N.; Loftis, J.; Fontane, D. Operation of large multi-reservoir systems using optimal-control theory. J. Water Resour. Plan. Manag. 1992, 118, 371–387. [Google Scholar] [CrossRef]
- Pontryagin, L.; Boltyanskii, V.; Gamdrelidze, R.; Mishchenko, E. The Mathematical Theory of Optimal Processes; Interscience: New York, NY, USA, 1962. [Google Scholar]
- Chen, C.; Kang, C.; Wang, J. Stochastic linear programming for reservoir operation with constraints on reliability and vulnerability. Water 2018, 10, 175. [Google Scholar] [CrossRef]
- Lee, Y.; Kim, S.K.K.; Ko, I.H. Two-stage stochastic linear programming model for coordinated multi-reservoir operation. In Proceedings of the Operations Management 2006: Operating Reservoirs in Changing Conditions, Sacramento, CA, USA, 14–16 August 2006; Zimbelman, D., Loehlein, W.C., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2006; pp. 400–410, ISBN 978-0-7844-0875-9. [Google Scholar] [CrossRef]
- Seifi, A.; Hipel, K. Interior-point method for reservoir operation with stochastic inflows. J. Water Resour. Plan. Manag. 2001, 127, 48–57. [Google Scholar] [CrossRef]
- Juárez ML, A.; Ramírez, R.M.; Mora, R.D.; Reséndiz, A.M.; Esteban, R.V.; De la Cruz Courtois, O.A.; Elizondo, E.C. Guide curves in stochastic dynamic programming to optimize operation policies in sequential hydropower dams. Stoch. Environ. Res. Risk Assess. 2023. [Google Scholar] [CrossRef]
- Fayaed, S.S.; Fiyadh, S.S.; Khai, W.J.; Ahmed, A.N.; Afan, H.A.; Ibrahim, R.K.; Fai, C.M.; Koting, S.; Mohd, N.S.; Jaafar, W.Z.B.; et al. Improving dam and reservoir operation rules using stochastic dynamic programming and artificial neural network integration model. Sustainability 2019, 11, 5367. [Google Scholar] [CrossRef]
- Liu, P.; Zhao, J.; Li, L.; Shen, Y. Optimal reservoir operation using stochastic dynamic programming. J. Water Resour. Prot. 2012, 4, 342–345. [Google Scholar] [CrossRef]
- Tilmant, A.; Faouzi, E.H.; Vanclooster, M. Optimal operation of multi-purpose reservoirs using flexible stochastic dynamic programming. Appl. Soft Comput. 2002, 2, 61–74. [Google Scholar] [CrossRef]
- Azaiez, M.N.; Hariga, M.; Al-Harkan, I. A chance-constrained multi-period model for a special multi-reservoir system. Comput. Oper. Res. 2005, 32, 1337–1351. [Google Scholar] [CrossRef]
- Ouarda, T.; Labadie, J. Chance-constrained optimal control for multi-reservoir system optimization and risk analysis. Stoch. Environ. Res. Risk Assess. 2001, 15, 185–204. [Google Scholar] [CrossRef]
- Kitanidis, P.K. A first-order approximation to stochastic optimal control of reservoirs. Stoch. Hydrol. Hydraul. 1987, 1, 169–184. [Google Scholar] [CrossRef]
- Mezenner, N.; Dechemi, N.; Bermad, A.; Benkaci, T. Optimized reservoir operation using genetic algorithm and simulated inflows to reservoir based principal components analysis: The case of Cheffia reservoir—Algeria. Model. Earth Syst. Environ. 2023. [Google Scholar] [CrossRef]
- Chandra, V.S.S.; Hareendran, S.A.; Sankar, S.S. Optimal reservoir optimization using multiobjective genetic algorithm. In Advances in Swarm Intelligence. I.C.S.I. 2020; Tan, Y., Shi, Y., Tuba, M., Eds.; Lecture Notes in Computer Science 12145; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Olukanni, D.O.; Adejumo, T.A.; Salami, A.W.; Adedeji, A.A.; Alavi, A.H. Optimization-based reliability of a multipurpose reservoir by genetic algorithms: Jebba hydropower dam, Nigeria. Cogent Eng. 2018, 5, 143874. [Google Scholar] [CrossRef]
- Al-Aqeeli, Y.H.; Lee, T.S.; Abd Aziz, S. Enhanced genetic algorithm optimization model for a single reservoir operation based on hydropower generation: A case study of Mosul reservoir, northern Iraq. SpringerPlus 2016, 5, 797. [Google Scholar] [CrossRef]
- Sharif, M.; Wardlaw, R. Multireservoir systems optimization using genetic algorithms: Case study. J. Comput. Civ. Eng. 2000, 14, 255–263. [Google Scholar] [CrossRef]
- Kumar, D.N.; Reddy, M.J. Ant colony optimization for multi-purpose reservoir operation. Water Resour. Manag. 2006, 20, 879–898. [Google Scholar] [CrossRef]
- Al-Aqeeli, Y.H.; Mahmood Agha, O.M. Optimal operation of a multi-reservoir system for hydropower production using particle swarm optimization algorithm. Water Resour. Manag. 2020, 34, 3099–3112. [Google Scholar] [CrossRef]
- Moradi, A.M.; Dariane, A.B. Particle swarm optimization: Application to reservoir operation problems. In Proceedings of the IEEE International Advance Computing Conference, Patiala, India, 6–7 March 2009; pp. 1048–1051. [Google Scholar] [CrossRef]
- Georgiou, P.E.; Papamichail, D.M.; Vougioukas, S.G. Optimal irrigation reservoir operation and simultaneous multi-crop cultivation area selection using simulated annealing. Irrig. Drain. 2006, 55, 129–144. [Google Scholar] [CrossRef]
- Teegavarapu, R.S.; Simonovic, S.P. Optimal operation of reservoir systems using simulated annealing. Water Resour. Manag. 2002, 16, 401–428. [Google Scholar] [CrossRef]
- Haddad, O.B.; Afshar, A.; Mariño, M.A. Honeybees mating optimization (H.B.M.O.) algorithm: A new heuristic to roach for water resources optimization. J. Water Resour. Manag. 2006, 20, 661–680. [Google Scholar] [CrossRef]
- Beiranvand, B.; Ashofteh, P.S. A Systematic Review of Optimization of Dams Reservoir Operation Using the Meta-heuristic Algorithms. Water Resour. Manag. 2023, 37, 3457–3526. [Google Scholar] [CrossRef]
- Sharifi, M.R.; Akbarifard, S.; Qaderi, K. Comparative analysis of some evolutionary-based models in optimization of dam reservoir operation. Sci. Rep. 2021, 11, 15611. [Google Scholar] [CrossRef] [PubMed]
- Azad, A.S.; Rahaman Md, S.A.; Watada, J.; Vasant, P.; Vintaned, J.A.G. Optimization of the hydropower energy generation using meta-heuristic approaches: A review. Energy Rep. 2020, 6, 2230–2248. [Google Scholar] [CrossRef]
- Ahmad, A.; El-Shafie, A.; Razali, S.F.M.; Mohamad, Z.S. Reservoir optimization in water resources: A review. Water Resour. Manag. 2014, 28, 3391–3405. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Neural Networks and Deep Learning: A Textbook; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Zhanga, D.; Lina, J.; Penga, Q.; Wangb, D.; Yang, T.; Sorooshian, S.; Liua, X.; Zhuang, J. Modeling and simulating reservoir operation using the artificial neural network, support vector regression, and deep learning algorithm. J. Hydrol. 2018, 565, 720–736. [Google Scholar] [CrossRef]
- Moorthi, P.V.P.; Singh, A.P.; Agnivesh, P. Regulation of water resources systems using fuzzy logic: A case study of Amaravathi dam. Appl. Water Sci. 2018, 8, 132. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Bellman, R.E.; Zadeh, L.A. Decision-making in a fuzzy environment. Manag. Sci. 1970, 17, B-141–B-273. [Google Scholar] [CrossRef]
- Mousavi, S.J.; Karamouz, M.; Menhadj, M.B. Fuzzy-State Stochastic Dynamic Programming for Reservoir Operation. J. Water Resour. Plan. Manag. 2004, 130, 460–470. [Google Scholar] [CrossRef]
- Dehghani, M.; Riahi-Madvar, H.; Hooshyaripor, F.; Mosavi, A.; Shamshirband, S.; Zavadskas, E.K.; Chau, K.-W. Prediction of Hydropower Generation Using Grey Wolf Optimization AdaptiveNeuro-Fuzzy Inference System. Energies 2019, 12, 289. [Google Scholar] [CrossRef]
- Trillas, E.; Eciolaza, L. Fuzzy Logic, An Introductory Course for Engineering Students; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Ferdowsi, A.; Singh, V.P.; Ehteram, M.; Mirjalili, S. Multi-objective optimization approaches for design, planning, and management of water resource systems. In Essential Tools for Water Resources Analysis, Planning, and Management; Bozorg-Haddad, O., Ed.; Springer Water: Singapore, 2021. [Google Scholar] [CrossRef]
- Goicoechea, A.; Hansen, D.; Duckstein, L. Multiobjective Decision Analysis with Engineering and Business Applications; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Cohon, J.L. Multiobjective Programming and Planning; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Zhu, F.; Zhong, P.-A.; Xu, B.; Chen, J.; Sun, Y.; Liu, W.; Li, T. Stochastic multi-criteria decision-making based on stepwise weight information for real-time reservoir operation. J. Clean. Prod. 2020, 257, 120554. [Google Scholar] [CrossRef]
- Zhu, F.; Zhong, P.-A.; Sun, Y.; Xu, B. Selection of criteria for multi-criteria decision-making of reservoir flood control operation. J. Hydro Inform. 2017, 19, 558–571. [Google Scholar] [CrossRef]
- Malekmohammadi, B.; Zahraie, B.; Kerachian, R. Ranking solutions of multi-objective reservoir operation optimization models using multi-criteria decision analysis. Expert Syst. Appl. 2011, 38, 7851–7863. [Google Scholar] [CrossRef]
- Wu, X.; Li, S.; Cheng, C.; Miao, S. Simulation-Optimization model to derive operation rules of multiple cascaded reservoirs for Nash equilibrium. J. Water Resour. Plan. Manag. 2019, 145, 04019013. [Google Scholar] [CrossRef]
- Jamali, S.; Jamali, B. Cascade hydropower systems optimal operation: Implications for Iran’s Great Karun hydropower systems. Appl. Water Sci. 2019, 9, 66. [Google Scholar] [CrossRef]
- Niewiadomska-Szynkiewicz, E.; Blaszczyk, J. Simulation-based optimization methods applied to large-scale water systems control. In Proceedings of the Intl IEEE Conferences on Ubiquitous Intelligence and Computing, Advanced and Trusted Computing, Scalable Computing and Communications, Cloud and Big Data Computing, Internet of People, and Smart World Congress (UIC/ATC/ScalCom/CBDCom/IoP/SmartWorld), Toulouse, France, 18–21 July 2016; pp. 649–656. [Google Scholar] [CrossRef]
- Chaturvedi, M.C.; Srivastava, D.K. Study of complex water-resources system with screening and simulation models. Water Resour. Res. 1981, 17, 783–794. [Google Scholar] [CrossRef]
- Anand, J.; Gosain, A.K.; Khosa, R. Optimization of multipurpose reservoir operation by coupling soil and water assessment tool (SWAT) and genetic algorithm for optimal operating policy (Case study: Ganga River Basin). Sustainability 2018, 10, 1660. [Google Scholar] [CrossRef]
- Suiadee, W.; Tingsanchali, T. A combined simulation-genetic algorithm optimization model for optimal rule curves of a reservoir: A case study of the Nam on Irrigation Project, Thailand. Hydrol. Process 2007, 21, 3211–3225. [Google Scholar] [CrossRef]
- Lai, V.; Huang, Y.F.; Koo, C.H.; Ahmed, A.N.; El-Shafie, A. A Review of Reservoir Operation Optimisations: From Traditional Models to Metaheuristic Algorithms. Arch Comput. Methods Eng 2022, 29, 3435–3457. [Google Scholar] [CrossRef]
- Saab, S.M.; Othman, F.B.; Tan, C.G.; Allawi, M.F.; El-Shafie, A. Review of generating optimal operation for dam and reservoir water system: Simulation models and optimization algorithms. Appl. Water Sci. 2022, 12, 73. [Google Scholar] [CrossRef]
- Dobson, B.; Wagener, T.; Pianosi, F. An argument-driven classification and comparison of reservoir operation optimization methods. Adv. Water Resour. 2019, 128, 74–86. [Google Scholar] [CrossRef]
- Macian-Sorribes, H.; Pulido-Velazquez, M. Inferring efficient operating rules in multi-reservoir water resource systems: A review. WIREs Water 2020, 7, e1400. [Google Scholar] [CrossRef]
- Giuliani, M.; Lamontagne, J.R.; Reed, P.M.; Castelletti, A. A state-of-the-art review of optimal reservoir control for managing conflicting demands in a changing world. Water Resour. Res. 2021, 57, e2021WR029927. [Google Scholar] [CrossRef]
- Dalcin, A.P.; Brêda, J.; Marques, G.; Tilmant, A.; de Paiva, R.; Kubota, P. The Role of Reservoir Reoperation to Mitigate Climate Change Impacts on Hydropower and Environmental Water Demands. J. Water Resour. Plan. Manag. 2023, 149, 04023005. [Google Scholar] [CrossRef]
- Aljoda, A.; Jain, S. Uncertainties and risks in reservoir operations under changing hydroclimatic conditions. J. Water Clim. Change 2021, 12, 1708–1723. [Google Scholar] [CrossRef]
- Zhong, W.; Guo, J.; Chen, L.; Zhou, J.; Zhang, J.; Wang, D. Future hydropower generation prediction of large-scale reservoirs in the upper Yangtze River basin under climate change. J. Hydrol. 2020, 588, 125013. [Google Scholar] [CrossRef]
- Liu, B.; Lund, J.R.; Liu, L.; Liao, S.; Li, G.; Cheng, C. Climate change impacts on hydropower in Yunnan, China. Water 2020, 12, 197. [Google Scholar] [CrossRef]
- Fluixá-Sanmartín, J.; Morales-Torres, A.; Escuder-Bueno, I. Quantification of climate change impact on dam failure risk under hydrological scenarios: A case study from a Spanish dam. Nat. Hazards Earth Syst. Sci. 2019, 19, 2117–2139. [Google Scholar] [CrossRef]
- Zolghadr-Asli, B.; Bozorg-Haddad, O.; Chu, X. Effects of the uncertainties of climate change on the performance of hydropower systems. J. Water Clim. Change 2019, 10, 591–609. [Google Scholar] [CrossRef]
- Boehlert, B.; Strzepek, K.M.; Gebretsadik, Y.; Swanson, R.; McCluskey, A.; Neumann, J.E.; McFarland, J.; Martinich, J. Climate change impacts and greenhouse gas mitigation effects on U.S. hydropower generation. Appl. Energy 2016, 183, 1511–1519. [Google Scholar] [CrossRef]
- Fluixá-Sanmartín, J.; Altarejos-García, L.; Morales-Torres, A.; Escuder-Bueno, I. Review article: Climate change impacts on dam safety. Nat. Hazards Earth Syst. Sci. 2018, 18, 2471–2488. [Google Scholar] [CrossRef]
- Watts, R.J.; Richter, B.D.; Opperman, J.J.; Bowmer, K.H. Dam reoperation in an era of climate change. Mar. Freshw. Res. 2011, 62, 321–327. [Google Scholar] [CrossRef]
- Li, W.; Li, Z.; Ge, W.; Wu, S. Risk evaluation model of life loss caused by dam-break flood and its application. Water 2019, 11, 1359. [Google Scholar] [CrossRef]
- Chernet, H.; Knut Alfredsen, M.; Midttømme, G. Safety of hydropower dams in a changing climate. J. Hydraul. Eng. 2014, 19, 569–582. [Google Scholar] [CrossRef]
- Ahmadi, M.; Bozorg Haddad, O.; Loáiciga, H.A. Adaptive reservoir operation rules under climatic change. Water Resour. Manag. 2014, 29, 1247–1266. [Google Scholar] [CrossRef]
- Lompi, M.; Mediero, L.; Soriano, E.; Caporali, E. Climate change and hydrological dam safety: A stochastic methodology based on climate projections. Hydrol. Sci. J. 2023, 68, 745–763. [Google Scholar] [CrossRef]
- Nourani, V.; Rouzegaria, N.; Molajouc, A.; Baghanama, A.H. An integrated simulation-optimization framework to optimize the reservoir operation adapted to climate change scenarios. J. Hydrol. 2020, 587, 125018. [Google Scholar] [CrossRef]
- Tukimat, N.N.A.; Harun, S. Comparative study on the reservoir operation planning with the climate change adaptation. SN Appl. Sci. 2019, 1, 1449. [Google Scholar] [CrossRef]
- Chang, J.; Wang, X.; Li, Y.Y.; Wang, Y.; Zhang, H. Hydropower plant operation rules optimization response to climate change. Energy 2018, 160, 886–897. [Google Scholar] [CrossRef]
- Ehteram, M.; Mousavi, S.F.; Karami, H.; Farzin, S.; Singh, V.P.; Chau, K.-W.; El-Shafie, A. Reservoir operation based on evolutionary algorithms and multi-criteria decision-making under climate change and uncertainty. J. Hydro Inform. 2018, 20, 332–355. [Google Scholar] [CrossRef]
- Yang, G.; Guo, S.; Li, L.; Hong, X.; Wang, L. Multi-objective operating rules for Danjiangkou reservoir under climate change. Water Resour. Manag. 2016, 30, 1183–1202. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S. Incorporating ecological requirements into multipurpose reservoir operating rule curves for adaptation to climate change. J. Hydrol. 2013, 498, 153–164. [Google Scholar] [CrossRef]
- Forrest, K.; Tarroja, B.; Chiang, F.; AghaKouchak, A.; Samuelsen, S. Assessing climate change impacts on California hydropower generation and ancillary services provision. Clim. Change 2018, 151, 395–412. [Google Scholar] [CrossRef]
- Anaraki, M.V.; Farzin, S.; Mousavi, S.F.; Karami, H. Uncertainty analysis of climate change impacts on flood frequency by using hybrid machine learning methods. Water Resour. Manag. 2021, 35, 199–223. [Google Scholar] [CrossRef]
- Wang, J.; Fonseca, R.M.; Rutledge, K. A hybrid statistical-dynamical downscaling of air temperature over Scandinavia using the W.R.F. Model. Adv. Atmos. Sci. 2020, 37, 57–74. [Google Scholar] [CrossRef]
- Tang, J.; Niu, X.; Wang, S.; Gao, H.; Wang, X.; Wu, J. Statistical downscaling and dynamical downscaling of regional climate in China: Present climate evaluations and future climate projections. J. Geophys. Res. Atmos. 2016, 121, 2110–2129. [Google Scholar] [CrossRef]
- Xu, Z.; Han, Y.; Yang, Z. Dynamical downscaling of regional climate: A review of methods and limitations. Sci. China Earth Sci. 2019, 62, 365–375. [Google Scholar] [CrossRef]
- Tabari, H.; Paz, S.M.; Buekenhout, D.; Willems, P. Comparison of statistical downscaling methods for climate change impact analysis on precipitation-driven drought. Hydrol. Earth Syst. Sci. 2021, 25, 3493–3517. [Google Scholar] [CrossRef]
- Trzaska, S.; Schnarr, E. A Review of Downscaling Methods for Climate Change Projections; Center for International Earth Science, Information Network (C.I.E.S.I.N.): Burlington, VT, USA, 2014. [Google Scholar]
- Dang, T.D.; Vu, D.T.; Chowdhury, A.F.M.K.; Galelli, S. A software package for the representation and optimization of water reservoir operations in the V.I.C. hydrologic model. Environ. Model. Softw. 2020, 126, 104673. [Google Scholar] [CrossRef]
- Dang, T.D.; Vu, D.T.; Chowdhury, A.F.M.K.; Galelli, S. On the representation of water reservoir storage and operations in large-scale hydrological models: Implications on model parameterization and climate change impact assessments. Hydrol. Earth Syst. Sci. 2020, 24, 397–416. [Google Scholar] [CrossRef]
- Beharry, S.L.; Gabriels, D.; Lobo, D.; Ramsewak, D.; Clarke, R.M. Use of the SWAT model for estimating reservoir volume in the Upper Navet watershed in Trinidad. Appl. Sci. 2021, 3, 163. [Google Scholar] [CrossRef]
- Shrestha, J.P.; Pahlow, M.; Cochrane, T.A. Development of a SWAT hydropower operation routine and its application to assessing hydrological alterations in the Mekong. Water 2020, 12, 2193. [Google Scholar] [CrossRef]
- Wilby, R.L.; Dessai, S. Robust adaptation to climate change. Weather 2010, 65, 180–185. [Google Scholar] [CrossRef]
- Brown, C.; Ghile, Y.; Laverty, M.; Li, K. Decision scaling: Linking bottom-up vulnerability analysis with climate projections in the water sector. Water Resour. Res. 2012, 48, W09537. [Google Scholar] [CrossRef]
- Mateus, M.C.; Tullos, D. Reliability, sensitivity, and vulnerability of reservoir operations under climate change. J. Water Resour. Plan. Manag. 2017, 143, 04016085. [Google Scholar] [CrossRef]
- Becker, B.; Ochterbeck, D.; Piovesan, T. A comparison of the homotopy method with linearization approaches for a non-linear optimization problem of operations in a reservoir cascade. Energy Syst. 2023. [Google Scholar] [CrossRef]
- Şen, Z. Reservoirs for Water Supply Under Climate Change Impact—A Review. Water Resour. Manag. 2021, 35, 3827–3843. [Google Scholar] [CrossRef]
- Lu, S.; Dai, W.; Tang, Y.; Guo, M. A review of the impact of hydropower reservoirs on global climate change. Sci. Total Environ. 2020, 711, 134996. [Google Scholar] [CrossRef]
- United Nations Office for Disaster Risk Reduction (UNDRR). Flood Hazard and Risk Assessment, in Words into Action Guidelines: National Disaster Risk Assessment, Hazard Specific Risk Assessment. 2017. Available online: www.preventionweb.net/files/52828_04floodhazardandriskassessment.pdf (accessed on 8 November 2021).
- Zhang, X.; Luo, J.; Sun, X.; Xie, J. Optimal reservoir flood operation using a decomposition-based multi-objective evolutionary algorithm. Eng. Optim. 2019, 51, 42–62. [Google Scholar] [CrossRef]
- Qi, Y.; Yu, J.; Li, X.; Wei, Y.; Miao, Q. Reservoir flood control operation using a multi-objective evolutionary algorithm with decomposition and preferences. Appl. Soft Comput. 2016, 50, 21–33. [Google Scholar] [CrossRef]
- Hsu, N.S.; Wei, C.C. A multipurpose reservoir real-time operation model for flood control during typhoon invasion. J. Hydrol. 2007, 336, 282–293. [Google Scholar] [CrossRef]
- Jain, S.K.; Shilpa, L.S.; Rani, D.; Sudheer, K.P. State-of-the-art review: Operation of multi-purpose reservoirs during flood season. J. Hydrol. 2023, 618, 129165. [Google Scholar] [CrossRef]
- Güvengir, U.; Savasaneril, S.; Altan-Sakarya, A.B.; Buhan, S. Short-term flood control and Long-Term energy maximization in multi-reservoir systems using improved particle swarm optimization. Water Resour. Manag. 2021, 35, 4293–4307. [Google Scholar] [CrossRef]
- Xu, B.; Zhong, P.-A.; Lu, Q.; Zhu, F.; Huang, X.; Ma, Y.; Fu, J. Multiobjective stochastic programming with recourses for real-time flood water conservation of a multi-reservoir system under uncertain forecasts. J. Hydrol. 2020, 590, 125513. [Google Scholar] [CrossRef]
- Maliwal, S.; Murmu, M.; Yadu, L.K.; Verma, M.K. Multi-reservoir flood control operation by optimization technique: A Review. Int. J. Eng. Res. Technol. 2019, 8, 681–685. [Google Scholar]
- Lei, X.; Zhang, J.; Wang, H.; Wang, M.; Khu, S.-T.; Li, Z.; Tan, Q. Deriving mixed reservoir operating rules for flood control based on weighted non-dominated sorting genetic algorithm II. J. Hydrol. 2018, 564, 967–983. [Google Scholar] [CrossRef]
- Zhou, C.; Sun, N.; Chen, L.; Ding, Y.; Zhou, J.; Zha, G.; Luo, G.; Dai, L.; Yang, X. Optimal operation of cascade reservoirs for flood control of multiple areas downstream: A case study in the Upper Yangtze River basin. Water 2018, 10, 1250. [Google Scholar] [CrossRef]
- Chou, F.N.; Wu, C.-W. Stage-wise optimizing operating rules for flood control in a multi-purpose reservoir. J. Hydrol. 2014, 521, 245–260. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, H.; Mo, L.; Wang, Y.; Chen, D.; Pang, S.; Yin, X. Hierarchical flood operation rules optimization using a multi-objective cultured evolutionary algorithm based on decomposition. Water Resour. Manag. 2019, 33, 337–354. [Google Scholar] [CrossRef]
- Zhang, J.; Cai, X.; Lei, X.; Liu, P.; Wang, H. Real-time reservoir flood control operation enhanced by data assimilation. J. Hydrol. 2021, 598, 126426. [Google Scholar] [CrossRef]
- Cuevas-Velásquez, V.; Sordo-Ward, A.; García-Palacios, J.H.; Bianucci, P.; Garrote, L. A probabilistic model for real-time flood operation of a dam based on a deterministic optimization model. Water 2020, 12, 3206. [Google Scholar] [CrossRef]
- Rahimi, H.; Ardakani, M.K.; Ahmadian, M.; Tang, X. Multi-reservoir utilization planning to optimize hydropower energy and flood control simultaneously. Environ. Process. 2020, 7, 41–52. [Google Scholar] [CrossRef]
- Porse, E.; Sandoval-Solis, S.; Lane, B. Integrating environmental flows into multi-objective reservoir management for a transboundary, water-scarce river basin: Rio Grande/bravo. Water Resour. Manag. 2015, 29, 2471–2484. [Google Scholar] [CrossRef]
- Li, Q.; Ouyang, S. Research on multi-objective joint optimal flood control model for cascade reservoirs in river basin system. Nat. Hazards 2015, 77, 2097–2115. [Google Scholar] [CrossRef]
- Wan, X.; Xue, Y.; Hua, L.; Wu, Q. Multi-objective collaborative decision-making for flood resource utilization in a reservoir. Stoch. Environ. Res. Risk Assess. 2023. [Google Scholar] [CrossRef]
- Wan, W.; Liu, Y.; Zheng, H.; Zhao, J.; Zhao, F.; Lu, Y. Optimization of Multi-Reservoir Flood Control Operating Rules: A Case Study for the Chaobai River Basin in China. Water 2023, 15, 2817. [Google Scholar] [CrossRef]
- Hu, H.-X.; Shao, L.-H.; Hu, Q.; Zhang, Y.; Hu, Z.-Y. Multi-objective reservoir optimal operation based on GCN and NSGA-II algorithm. In Proceedings of the 4th International Conference on Advanced Electronic Materials, Computers and Software Engineering (A.E.M.C.S.E.), Changsha, China, 26–28 March 2021; pp. 546–551. [Google Scholar] [CrossRef]
- Liu, X.; Luo, J. A dynamic multi-objective optimization model with interactivity and uncertainty for real-time reservoir flood control operation. Appl. Math. Model. 2019, 74, 606–620. [Google Scholar] [CrossRef]
- Moridi, A.; Yazdi, J. Optimal allocation of flood control capacity for multi-reservoir systems using a multi-objective optimization approach. Water Resour. Manag. 2017, 31, 4521–4538. [Google Scholar] [CrossRef]
- Zhu, F.; Zhong, P.-A.; Sun, Y. Multi-criteria group decision making under uncertainty: Application in reservoir flood control operation. Environ. Model. Softw. 2018, 100, 236–251. [Google Scholar] [CrossRef]
- Zhu, F.; Zhong, P.-A.; Wu, Y.-N.; Sun, Y.; Chen, J.; Jia, B. SMAA-based stochastic multi-criteria decision-making for reservoir flood control operation. Stoch. Environ. Res. Risk Assess. 2017, 31, 1485–1497. [Google Scholar] [CrossRef]
- Yu, X.; Xu, Y.-P.; Gu, H.; Guo, Y. Multi-objective robust optimization of reservoir operation for real-time flood control under forecasting uncertaint. J. Hydrol. Part A 2023, 620, 129421. [Google Scholar] [CrossRef]
- Huang, X.; Xu, B.; Zhong, P.-A.; Yao, H.; Yue, H.; Zhu, F.; Lu, Q.; Sun, Y.; Mo, R.; Li, Z.; et al. Robust multiobjective reservoir operation and risk decision-making model for real-time flood control coping with forecast uncertainty. J. Hydrol. 2022, 605, 127334. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, J.; Dai, L.; Huang, K.; Zha, G. Risk assessment of multi-reservoir joint flood control system under multiple uncertainties. J. Flood Risk Manag. 2021, 14, e12740. [Google Scholar] [CrossRef]
- Lu, Q.; Zhong, P.-A.; Xu, B.; Zhu, F.; Ma, Y.; Wang, H.; Xu, S. Risk analysis for reservoir flood control operation considering two-dimensional uncertainties based on Bayesian network. J. Hydrol. 2020, 589, 125353. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, J.; Huang, K.; Dai, L.; Zha, G.; Chen, L.; Qin, H. Risk assessment and decision-making based on Mean-CVaR-Entropy for flood control operation of large-scale reservoirs. Water 2019, 11, 649. [Google Scholar] [CrossRef]
- Chen, J.; Zhong, P.-A.; An, R.; Zhu, F.-L.; Xu, B. Risk analysis for real-time flood control operation of a multi-reservoir system using a dynamic Bayesian network. Environ. Model. Softw. 2019, 111, 409–420. [Google Scholar] [CrossRef]
- Huang, K.; Ye, L.; Chen, L.; Wang, Q.; Dai, L.; Zhou, J.; Singh, V.P.; Huang, M.; Zhang, J. Risk analysis of flood control reservoir operation considering multiple uncertainties. J. Hydrol. 2018, 565, 672–684. [Google Scholar] [CrossRef]
- Chen, J.; Zhong, P.-A.; Wang, M.-L.; Zhu, F.-L.; Wan, X.-Y.; Zhang, Y. A risk-based model for real-time flood control operation of a cascade reservoir system under emergency conditions. Water 2018, 10, 167. [Google Scholar] [CrossRef]
- Zhu, F.; Zhong, P.-A.; Sun, Y.; Yeh, W.W.-G. Real-time optimal flood control decision-making and risk propagation under multiple uncertainties. Water Resour. Res. 2017, 53, 10635–10654. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S. Risk analysis for flood control operation of seasonal flood-limited water level incorporating inflow forecasting error. Hydrol. Sci. J. 2014, 59, 1006–1019. [Google Scholar] [CrossRef]
- Yan, B.; Guo, S.; Chen, L. Estimation of reservoir flood control operation risks while considering inflow forecasting errors. Stoch. Environ. Res. Risk Assess. 2014, 28, 359–368. [Google Scholar] [CrossRef]
- Chen, J.; Zhong, P.-A.; Zhang, W.; Zhu, F.; Zhang, Y. Improved risk-assessment model for real-time reservoir flood-control operation. J. Water Resour. Plan. Manag. 2020, 146, 04020007. [Google Scholar] [CrossRef]
- Sun, Y.; Zhu, F.; Chen, J.; Li, J. Risk analysis for reservoir real-time optimal operation using the scenario tree-based stochastic optimization method. Water 2018, 10, 606. [Google Scholar] [CrossRef]
- Chen, J.; Zhong, P.-A.; Zhang, Y.; Navar, D.; Yeh, W.W.-G. A decomposition-integration risk analysis method for real-time operation of a complex flood control system. Water Resour. Res. 2017, 53, 2490–2506. [Google Scholar] [CrossRef]
- Zhao, Q.; Cai, X.; Li, Y. Determining inflow forecast horizon for reservoir operation. Water Resour. Res. 2019, 55, 4066–4081. [Google Scholar] [CrossRef]
- Kim, T.; Shin, J.-Y.; Kim, H.; Kim, S.; Heo, J.-H. The use of large-scale climate indices in monthly reservoir inflow forecasting and its application on time series and artificial intelligence models. Water 2019, 11, 374. [Google Scholar] [CrossRef]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Comparison of the A.R.M.A., A.R.I.M.A., and the autoregressive artificial neural network models in forecasting the monthly inflow of the Dez dam reservoir. J. Hydrol. 2013, 476, 433–441. [Google Scholar] [CrossRef]
- Karamouz, M.; Araghinejad, S. Advanced Hydrology; Amirkabir University Press: Tehran, Iran, 2005. [Google Scholar]
- Liang, Z.; Tang, T.; Li, B.; Liu, T.; Wang, J.; Hu, Y. Long-term streamflow forecasting using SWAT through the integration of the random forest’s precipitation generator: A case study of Danjiangkou. Reserv. Hydrol. Res. 2018, 49, 1513–1527. [Google Scholar] [CrossRef]
- Jaiswal, R.K.; Ali, S.; Bharti, B. Comparative evaluation of conceptual and physical rainfall–runoff models. Appl. Water Sci. 2020, 10, 48. [Google Scholar] [CrossRef]
- Tegegne, G.; Park, D.K.; Kim, Y.-O. Comparison of hydrological models for the assessment of water resources in a data-scarce region, the Upper Blue Nile River Basin. J. Hydrol. 2017, 14, 49–66. [Google Scholar] [CrossRef]
- Apaydin, H.; Feizi, H.; Sattari, M.T.; Colak, M.S.; Shamshirband, S.; Chau, K.-W. Comparative analysis of recurrent neural network architectures for reservoir inflow forecasting. Water 2020, 12, 1500. [Google Scholar] [CrossRef]
- Babaei, M.; Moeini, R.; Ehsanzadeh, E. Artificial neural network and support vector machine models for inflow prediction of dam reservoir (Case study: Zayandehroud dam reservoir). Water Resour. Manag. 2019, 33, 2203–2218. [Google Scholar] [CrossRef]
- Charoenporn, P. Reservoir inflow forecasting using ID3 and C4.5 decision tree model. In Proceedings of the 2017 3rd IEEE International Conference on Control Science and Systems Engineering (ICCSSE), Beijing, China, 17–19 August 2017; pp. 698–701. [Google Scholar] [CrossRef]
- Noorbeh, P.; Roozbahani, A.; Kardan Moghaddam, H. Annual and Monthly Dam Inflow Prediction Using Bayesian Networks. Water Resour. Manag. 2020, 34, 2933–2951. [Google Scholar] [CrossRef]
- Lin, Y.H.; Chiu, C.C.; Lee, P.C.; Lin, Y.J. Applying fuzzy grey modification model on inflow forecasting. Eng. Appl. Artif. Intell. 2012, 25, 734–743. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Souag-Gamane, D.; Ahmed, A.N.; Kisi, O.; El-Shafie, A. Improving artificial intelligence models accuracy for monthly streamflow forecasting using grey Wolf optimization (G.W.O.) algorithm. J. Hydrol. 2020, 582, 124435. [Google Scholar] [CrossRef]
- Ashrafi, S.M.; Mostaghimzadeh, E.; Adib, A. Applying wavelet transformation and artificial neural networks to develop forecasting-based reservoir operating rule curves. Hydrol. Sci. J. 2020, 65, 2007–2021. [Google Scholar] [CrossRef]
- Ebrahimi, E.; Shourian, M. River flow prediction using dynamic method for selecting and prioritizing K-Nearest Neighbors based on data features. J. Hydrol. Eng. 2020, 25, 04020010. [Google Scholar] [CrossRef]
- Latif, S.D.; Ahmed, A.N.; Sathiamurthy, E.; Huang, Y.F.; El-Shafie, A. Evaluation of deep learning algorithm for inflow forecasting: A case study of Durian Tunggal Reservoir, Peninsular Malaysia. Nat. Hazards 2021, 109, 351–369. [Google Scholar] [CrossRef]
- Chua, L.H.C. Considerations for data-driven and physically based hydrological models in flow forecasting. IFAC Proc. Vol. 2012, 45, 1025–1030. [Google Scholar] [CrossRef]
- Längkvist, M.; Karlsson, L.; Loutfi, A. A review of unsupervised feature learning and deep learning for time-series modeling. Pattern Recognit. Lett. 2014, 42, 11–24. [Google Scholar] [CrossRef]
- Bai, Y.; Chen, Z.; Xie, J.; Li, C. Daily reservoir inflow forecasting using multiscale deep feature learning with hybrid models. J. Hydrol. 2016, 532, 193–206. [Google Scholar] [CrossRef]
- Dong, N.; Guan, W.; Cao, J.; Zou, Y.; Yang, M.; Wei, J.; Chen, L.; Wang, H. A hybrid hydrologic modeling framework with data-driven and conceptual reservoir operation schemes for reservoir impact assessment and predictions. J. Hydrol. 2023, 619, 129246. [Google Scholar] [CrossRef]
- Khorram, S.; Jehbez, N. A Hybrid CNN-LSTM Approach for Monthly Reservoir Inflow Forecasting. Water Resour. Manag. 2023, 37, 4097–4121. [Google Scholar] [CrossRef]
- Tian, D.; He, X.; Srivastava, P.K.; Kalin, L. A hybrid framework for forecasting monthly reservoir inflow based on machine learning techniques with dynamic climate forecasts, satellite-based data, and climate phenomenon information. Stoch. Environ. Res. Risk Assess. 2022, 36, 2353–2375. [Google Scholar] [CrossRef]
- Attar, N.F.; Pham, Q.B.; Nowbandegani, S.F.; Rezaie-Balf, M.; Fai, C.M.; Ahmed, A.N.; Pipelzadeh, S.; Dung, T.D.; Nhi, P.T.T.; Khoi, D.N.; et al. Enhancing the prediction accuracy of data-driven models for monthly streamflow in the Urmia Lake basin based upon the autoregressive conditionally heteroskedastic time-series model. Appl. Sci. 2020, 10, 571. [Google Scholar] [CrossRef]
- Banihabib, M.E.; Bandari, R.; Valipour, M. Improving daily peak flow forecasts using hybrid Fourier-series autoregressive integrated moving average and recurrent artificial neural network models. AI 2020, 1, 263–275. [Google Scholar] [CrossRef]
- Luo, B.; Fang, Y.; Wang, H.; Zang, D. Reservoir inflow prediction using a hybrid model based on deep learning. IOP Conf. Ser. Mater. Sci. Eng. 2020, 715, 012044. [Google Scholar] [CrossRef]
- Chen, N.; Xiong, C.; Du, W.; Wang, C.; Lin, X.; Chen, Z. An improved genetic algorithm coupling a Back-Propagation neural network model (IGA-BPNN) for Water-Level predictions. Water 2019, 11, 1795. [Google Scholar] [CrossRef]
- Banihabib, M.E.; Ahmadian, A.; Valipour, M. Hybrid MARMA-NARX model for flow forecasting based on large-scale climate signals, sea-surface temperatures, and rainfall. Hydrol. Res. 2018, 49, 1788–1803. [Google Scholar] [CrossRef]
- Awan, J.A.; Bae, D. Application of adaptive neuro-fuzzy inference system for dam inflow prediction using long-range weather forecast. In Proceedings of the Eighth International Conference on Digital Information Management (ICDIM 2013), Islamabad, Pakistan, 10–12 September 2013; pp. 247–251. [Google Scholar] [CrossRef]
- Alquraish, M.M.; Abuhasel, K.A.; Alqahtani, A.S.; Khadr, M. A comparative analysis of hidden Markov model, hybrid support vector machines, and hybrid artificial neural fuzzy inference system in reservoir inflow forecasting (Case study: King Fahd Dam, Saudi Arabia). Water 2021, 13, 1236. [Google Scholar] [CrossRef]
- Ibrahim, K.S.M.H.; Huang, Y.F.; Ahmed, A.N.; Koo, C.H.; El-Shafie, A. A review of the hybrid artificial intelligence and optimization modeling of hydrological streamflow forecasting. Alex. Eng. J. 2022, 61, 279–303. [Google Scholar] [CrossRef]
- You, J.Y.; Cai, X. Determining forecast and decision horizons for reservoir operations under hedging policies. Water Resour. Res. 2008, 44, W11430. [Google Scholar] [CrossRef]
- Zhao, T.; Yang, D.; Cai, X.; Zhao, J.; Wang, H. Identifying effective forecast horizon for real-time reservoir operation under a limited inflow forecast. Water Resour. Res. 2012, 48, W01540. [Google Scholar] [CrossRef]
- Turner, S.W.D.; Xu, W.; Voisin, N. Inferred inflow forecast horizons guiding reservoir release decisions across the United States. Hydrol. Earth Syst. Sci. 2020, 24, 1275–1291. [Google Scholar] [CrossRef]
- Zhao, T.; Cai, X.; Yang, D. Effect of streamflow forecast uncertainty on real-time reservoir operation. Adv. Water Resour. 2011, 34, 495–504. [Google Scholar] [CrossRef]
- Zhong, Y.; Guo, Y.; Xiong, F.; Liu, D.; Ba, H.; Wu, X. Probabilistic forecasting based on ensemble forecasts and EMOS method for T.G.R. inflow. Front. Earth Sci. 2020, 14, 188–200. [Google Scholar] [CrossRef]
- Bourdin, D.R.; Nipen, T.N.; Stull, R.B. Reliable probabilistic forecasts from an ensemble reservoir inflow forecasting system. Water Resour. Res. 2014, 50, 3108–3130. [Google Scholar] [CrossRef]
- Barbetta, B.; Sahoo, B.; Bonaccorsi, B.; Nanda, T.; Chatterjee, C.; Moramarco, T.; Todini, E. Addressing effective real-time forecasting inflows to dams through predictive uncertainty estimate. J. Hydrol. 2023, 620, 129512. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S.; Xu, C.-Y.; Chang, F.-J.; Yin, J. Improving the reliability of probabilistic multi-step-ahead flood forecasting by fusing an unscented Kalman filter with a recurrent neural network. Water 2020, 12, 578. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Z.; He, H.; Lu, G. Deterministic and probabilistic evaluation of sub-seasonal precipitation forecasts at various spatiotemporal scales over China during the boreal summer monsoon. Atmosphere 2021, 12, 1049. [Google Scholar] [CrossRef]
- Zhong, Y.; Guo, S.; Ba, H.; Xiong, F.; Chang, F.-J.; Lin, K. Evaluation of the B.M.A. probabilistic inflow forecasts using T.I.G.G.E. numeric precipitation predictions based on artificial neural network. Hydrol. Res. 2018, 49, 1417–1433. [Google Scholar] [CrossRef]
- Bourdin, D.R.; Stull, R.B. Bias-corrected short-range Member-to-Member ensemble forecasts of reservoir inflow. J. Hydrol. 2013, 502, 77–88. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, J.; Fang, W.; Wang, Y. An ensemble flow forecast method based on an autoregressive model and hydrological uncertainty processer. Water 2020, 12, 3138. [Google Scholar] [CrossRef]
- Thi, P.C.; Ball, J.E.; Dao, N.H. Uncertainty estimation using the Glue and Bayesian approaches in flood estimation: A case study—Ba River, Vietnam. Water 2018, 10, 1641. [Google Scholar] [CrossRef]
- Thiemann, M.; Trosset, M.; Gupta, H.; Sorooshian, S. Bayesian recursive parameter estimation for hydrologic models. Water Resour. Res. 2001, 37, 2521–2535. [Google Scholar] [CrossRef]
- Parrish, M.A.; Moradkhani, H.; DeChant, C.M. Toward reduction of model uncertainty: Integration of Bayesian model averaging and data assimilation. Water Resour. Res. 2012, 48, W03519. [Google Scholar] [CrossRef]
- Hamill, T.M. Interpretation of rank histograms for verifying ensemble forecasts. Mon. Weather Rev. 2001, 129, 550–560. Available online: http://n2t.net/ark:/85065/d71z450p (accessed on 1 January 2022). [CrossRef]
- Hamill, T.M.; Colucci, S.J. Verification of Eta-RSM short-range ensemble forecasts. Mon. Weather Rev. 1997, 125, 1312–1327. [Google Scholar] [CrossRef]
- CAIT (Climate Analysis Indicators Tool). Climate Data Explorer; Data for the Year 2016; World Resources Institute: Washington, DC, USA, 2016; Available online: http://cait2.wri.org/ (accessed on 1 October 2020).
- Kumar, P.; Dhanya, T.; Chahar, B. A PSO approach for optimum design of dynamic inversion controller in water distribution systems. J. Water Supply Res. Technol. AQUA 2016, 65, 580–591. [Google Scholar] [CrossRef]
- Fallah-Mehdipour, E.; Bozorg Haddad, O.; Mariño, M.A. Developing reservoir operational decision rule by genetic programming. J. Hydro Inform. 2013, 15, 103–119. [Google Scholar] [CrossRef]
- Dias, V.; da Luz, M.P.; Medero, G.M.; Nascimento, D.T.F. An overview of hydropower reservoirs in Brazil: Current situation, Future perspectives and impacts of climate change. Water 2018, 10, 592. [Google Scholar] [CrossRef]
- Tkáč, S. Hydropower plants, an overview of the current types and technology. J. Civ. Eng. 2018, 13, 115–126. [Google Scholar] [CrossRef]
- McManamay, R.A.; Oigbokie, C.O.; Kao, S.-C.; Bevelhimer, M.S. Classification of US Hydropower Dams by their Modes of Operation. River Res. Appl. 2016, 32, 1450–1468. [Google Scholar] [CrossRef]
- Das, P.; Das, B.K.; Mustafi, N.N.; Sakir, T. A review on pump-hydro storage for renewable and hybrid energy systems applications. Energy 2020, 3, e223. [Google Scholar] [CrossRef]
- Pitorac, L.; Vereide, K.; Lia, L. Technical Review of Existing Norwegian Pumped Storage Plants. Energies 2020, 13, 4918. [Google Scholar] [CrossRef]
- Hoffstaedt, J.P.; Truijen, D.P.K.; Fahlbeck, J.; Gans, L.H.A.; Qudaih, M.; Laguna, A.J.; De Kooning, J.D.M.; Stockman, K.; Nilsson, H.; Storli, P.-T.; et al. Low head pumped hydro storage: A review of applicable technologies for design, grid integration, control, and modeling. Renew. Sustain. Energy 2022, 158, 112119. [Google Scholar] [CrossRef]
- Blakers, A.; Stocks, M.; Lu, B.; Cheng, C. A review of pumped hydro energy storage. Prog. Energy 2021, 3, 022003. [Google Scholar] [CrossRef]
- Pérez-Díaz, J.I.; Chazarra, M.; García-González, J.; Cavazzini, G.; Stoppato, A. Trends and challenges in the operation of pumped-storage hydropower plants. Renew. Sustain. Energy 2015, 44, 767–784. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, G.; Wen, X.; Tan, Q.; Zhang, P.; Liu, Z. Coordinated operation of conventional hydropower plants as hybrid pumped storage hydropower with wind and photovoltaic plants. Energy Convers. Manag. 2023, 277, 116654. [Google Scholar] [CrossRef]
- Ge, X.; Ma, Y.; Li, Y.; Jiao, Y.; Wang, Z.; Wu, F.; Zhao, B.; Xue, X. Daily peak shaving operation of mixed pumped-storage hydro plants considering cascade hydraulic coupling. In Proceedings of the 3rd International Conference on Power and Electrical Engineering (ICPEE 2022), Singapore 29–31 December 2022; pp. 971–978. [Google Scholar] [CrossRef]
- Bredeson, L.; Cicilio, P. Hydropower and Pumped Storage Hydropower Resource Review and Assessment for Alaska’s Railbelt Transmission System. Energies 2023, 16, 5494. [Google Scholar] [CrossRef]
- Nasab, M.A.; Zand, M.; Padmanabhan, S.; Bhaskar, M.S.; Guerrero, J.M. An efficient, robust optimization model for the unit commitment considering renewable uncertainty and pumped-storage hydropower. Comput. Electr. Eng. 2022, 100, 107846. [Google Scholar] [CrossRef]
- Nasir, J.; Javed, A.; Ali, M.; Ullah, K.; Kazmi, S.A.A. Capacity optimization of pumped storage hydropower and its impact on an integrated conventional hydropower plant operation. Appl. Energy 2022, 323, 119561. [Google Scholar] [CrossRef]
- Zhao, J.-F.; Oh, U.-J.; Park, J.-C.; Park, E.S.; Im, H.-B.; Lee, K.Y.; Choi, J.-S. A Review of World-wide Advanced Pumped Storage Hydropower Technologies. IFAC-Pap. 2022, 55, 170–174. [Google Scholar] [CrossRef]
- Yuan, W.; Xin, W.; Su, C.; Cheng, C.; Yan, D.; Wu, Z. Cross-regional integrated transmission of wind power and pumped-storage hydropower considering the peak shaving demands of multiple power grids. Renew. Energy 2022, 190, 1112–1126. [Google Scholar] [CrossRef]
- Li, Y.; Wu, F.; Li, J.; Yin, Y.; Li, Z.; Ai, L. Chance-constrained energy management for pumped storage hydropower plant to compensate for wind power uncertainties. In Proceedings of the 2021 IEEE Power & Energy Society General Meeting (PESGM), Washington, DC, USA, 26–29 July 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Dong, Z.; Tan, J.; Muljadi, E.; Nelms, R.M.; St-Hilaire, A.; Pevarnik, M.; Jacobson, M.D. Developing of Quaternary Pumped Storage Hydropower for Dynamic Studies. In IEEE Transactions on Sustainable Energy; IEEE: New York, NY, USA, 2020; Volume 11, pp. 2870–2878. [Google Scholar] [CrossRef]
- Bayazıt, Y.; Bakış, R.; Koç, C. A study on the transformation of multi-purpose dams into pumped storage hydroelectric power plants by using GIS model. Int. J. Green Energy 2021, 18, 308–318. [Google Scholar] [CrossRef]
- Alvarez, G.E. Operation of pumped storage hydropower plants through optimization for power systems. Energy 2020, 202, 17797. [Google Scholar] [CrossRef]
- Ma, X.; Wu, D.; Wang, D.; Huang, B.; Desomber, K.; Fu, T.; Weimar, M. Optimizing pumped storage hydropower for multiple grid services. J. Energy Storage 2022, 51, 104440. [Google Scholar] [CrossRef]
- Hunt, J.D.; Zakeri, B.; Lopes, R.; Barbosa, P.S.F.; Nascimento, A.; de Castro, N.J.; Brandão, R.; Schneider, P.S.; Wada, Y. Reviews Existing and new arrangements of pumped-hydro storage plants. Renew. Sustain. Energy 2020, 129, 109914. [Google Scholar] [CrossRef]
- Villeneuve, Y.; Séguin, S.; Chehri, A. AI-Based Scheduling Models, Optimization, and Prediction for Hydropower Generation: Opportunities, Issues, and Future Directions. Energies 2023, 16, 3335. [Google Scholar] [CrossRef]
- Bernardes, J., Jr.; Santos, M.; Abreu, T.; Prado, L., Jr.; Miranda, D.; Julio, R.; Viana, P.; Fonseca, M.; Bortoni, E.; Bastos, G.S. Hydropower Operation Optimization Using Machine Learning: A Systematic Review. AI 2022, 3, 78–99. [Google Scholar] [CrossRef]
- Bordin, C.; Skjelbred, H.I.; Kong, J.; Yang, Z. Machine learning for hydropower scheduling: State of the art and future research directions. Procedia Comput. Sci. 2020, 176, 1659–1668. [Google Scholar] [CrossRef]
- Hammid, A.T.; Awad, O.I.; Sulaiman, M.H.; Gunasekaran, S.S.; Mostafa, S.A.; Kumar, N.M.; Khalaf, B.A.; Al-Jawhar, Y.A.; Abdulhasan, R.A. A review of optimization algorithms in solving hydro generation scheduling problems. Energies 2020, 13, 2787. [Google Scholar] [CrossRef]
- Singh, V.K.; Singal, S.K. Operation of hydropower plants review. Renew. Sustain. Energy Rev. 2017, 69, 610–619. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, S.; Wen, X.; Jing, Z. Refined Scheduling Based on Dynamic Capacity Model for Short-term Hydropower Generation. Water Resour Manag. Manag. 2023, 37, 21–35. [Google Scholar] [CrossRef]
- Brito, B.H.; Finardi, E.C.; Takigawa, F.Y.K.; Pereira, A.I. Exploring symmetry in a short-term hydro scheduling problem: The case of the Santo Antônio hydro plant. J. Water Resour. Plan. Manag. 2022, 148, 05021026. [Google Scholar] [CrossRef]
- Daadaa, M.; Séguin, S.; Demeester, K.; Anjos, M.F. An optimization model to maximize energy generation in short-term hydropower unit commitment using efficiency points. Int. J. Electr. Power Energy Syst. 2021, 125, 106419. [Google Scholar] [CrossRef]
- Mathur, P.; Swartz, C.L.E.; Zyngier, D.; Welt, F. Robust online scheduling for optimal short-term operation of cascaded hydropower systems under uncertainty. J. Process Control 2021, 98, 52–65. [Google Scholar] [CrossRef]
- Guisández, I.; Pérez-Díaz, J.I. Mixed integer linear programming formulations for the hydro production function in a unit-based short-term scheduling problem. Int. J. Electr. Power Energy Syst. 2021, 128, 106747. [Google Scholar] [CrossRef]
- Skjelbred, H.I.; Kong, J.; Fosso, O.B. Dynamic incorporation of nonlinearity into M.I.L.P. formulation for short-term hydro scheduling. Int. J. Electr. Power Energy Syst. 2020, 116, 105530. [Google Scholar] [CrossRef]
- Su, C.; Yuan, W.; Cheng, C.; Wang, P.; Sun, L.; Zhang, T. Short-term generation scheduling of cascade hydropower plants with strong hydraulic coupling and head-dependent prohibited operating zones. J. Hydrol. 2020, 591, 125556. [Google Scholar] [CrossRef]
- Zhou, L.; Cheng, C.; Liao, S.; Wang, J. Multiobjective scheduling method for short-term peak shaving operation of cascade hydro plants. J. Water Resour. Plan. Manag. 2020, 146, 04020073. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, K.; Wang, Y.; Su, L.; Hu, H. multi-objective short-term hydropower generation operation for cascade reservoirs and stochastic decision-making under multiple uncertainties. J. Clean. Prod. 2020, 276, 122995. [Google Scholar] [CrossRef]
- Shang, L.; Shang, Y.; Hu, L.; Li, J. Performance of genetic algorithms with different selection operators for solving short-term optimized reservoir scheduling problems. Soft Comput. 2020, 24, 6771–6785. [Google Scholar] [CrossRef]
- Cheng, X.; Tang, Y.-L.; Liu, J.; Zhong, H.; Li, W.-W.; Wu, Y.-L. Ultrashort-Term scheduling of inter-basin cascaded hydropower plants to rapidly balance the load demand. IEEE Access 2020, 8, 32737–32756. [Google Scholar] [CrossRef]
- Liao, S.; Zhang, Y.; Liu, B.; Liu, Z.; Fang, Z.; Li, S. Short-term peak-shaving operation of head-sensitive cascaded hydropower plants based on spillage adjustment. Water 2020, 12, 3438. [Google Scholar] [CrossRef]
- Hu, H.; Yang, K.; Liu, L.; Su, L.; Yang, Z. Short-term hydropower generation scheduling using an improved cloud adaptive quantum-inspired binary social spider optimization algorithm. Water Resour. Manag. 2019, 33, 2357–2379. [Google Scholar] [CrossRef]
- Hermida, G.; Castronuovo, E.D. On the hydropower short-term scheduling of large basins, considering nonlinear programming, stochastic inflows, and heavy ecological restrictions. Int. J. Electr. Power Energy Syst. 2018, 97, 408–417. [Google Scholar] [CrossRef]
- Ge, X.; Xia, S.; Lee, W.-J.; Chung, C.Y. A successive approximation approach for short-term cascaded hydro scheduling with variable water flow delay. Electr. Power Syst. Res. 2018, 154, 213–222. [Google Scholar] [CrossRef]
- Wang, J.; Hu, W.; Liu, S. Short-term hydropower scheduling model with two coupled temporal scales. J. Water Resour. Plan. Manag. 2018, 144, 04017095. [Google Scholar] [CrossRef]
- Liu, S.; Luo, J.; Chen, H.; Wang, Y.; Li, X.; Zhang, J.; Wang, J. Third-Monthly Hydropower Scheduling of Cascaded Reservoirs Using Successive Quadratic Programming in Trust Corridor. Water 2023, 15, 716. [Google Scholar] [CrossRef]
- Li, G.; Lu, J.; Yang, R.; Cheng, C. Igdt-based medium-term optimal cascade hydropower operation in multimarket with hydrologic and economic uncertainties. J. Water Resour. Plan. Manag. 2021, 147, 05021015. [Google Scholar] [CrossRef]
- Beltrán, F.; Finardi, E.C.; de Oliveira, W. Two-stage and multi-stage decompositions for the medium-term hydrothermal scheduling problem: A computational comparison of solution techniques. Int. J. Electr. Power Energy Syst. 2021, 127, 106659. [Google Scholar] [CrossRef]
- Pérez-Díaz, J.I.; Guisández, I.; Chazarra, M.; Helseth, A. Medium-term scheduling of a hydropower plant participating as a price-maker in the automatic frequency restoration reserve market. Electr. Power Syst. Res. 2020, 185, 106399. [Google Scholar] [CrossRef]
- Ge, X.; Xia, S.; Lee, W. An efficient stochastic algorithm for mid-term scheduling of cascaded hydro systems. J. Mod. Power Syst. Clean Energy 2019, 7, 163–173. [Google Scholar] [CrossRef]
- Hjelmeland, M.N.; Zou, J.; Helseth, A.; Ahmed, S. Nonconvex medium-term hydropower scheduling by stochastic dual dynamic integer programming. IEEE Trans. Sustain. Energy 2019, 10, 481–490. [Google Scholar] [CrossRef]
- Feng, S.; Zheng, H.; Qiao, Y.; Yang, Z.; Wang, J.; Liu, S. Weekly hydropower scheduling of cascaded reservoirs with hourly power and capacity balances. Appl. Energy 2022, 311, 118620. [Google Scholar] [CrossRef]
- He, Z.; Wang, C.; Wang, Y.; Wei, B.; Zhou, J.; Zhang, H.; Qin, H. Dynamic programming with successive approximation and relaxation strategy for long-term joint power generation scheduling of large-scale hydropower station group. Energy 2021, 222, 119960. [Google Scholar] [CrossRef]
- Mbeutcha, Y.; Gendreau, M.; Emiel, G. The benefit of PARMA modeling for long-term hydroelectric scheduling using stochastic dual dynamic programming. J. Water Resour. Plan. Manag. 2021, 147, 05021002. [Google Scholar] [CrossRef]
- Ding, X.; Mo, X.; Zhou, J.; Bi, S.; Jia, B.; Liao, X. Long-term scheduling of cascade reservoirs considering inflow forecasting uncertainty based on a disaggregation model. Water Resour. Manag. 2021, 35, 645–660. [Google Scholar] [CrossRef]
- He, Z.; Zhou, J.; Qin, H.; Jia, B.; He, F.; Liu, G.; Feng, K. A fast water level optimal control method based on two-stage analysis for long-term power generation scheduling of hydropower station. Energy 2020, 210, 118531. [Google Scholar] [CrossRef]
- Yan, Z.; Liao, S.; Cheng, C.; Zhou, L. Long-term optimization of large-scale hydropower system operations based on decomposition coordination. J. Water Resour. Plan. Manag. 2020, 146, 04020078. [Google Scholar] [CrossRef]
- Hu, H.; Yang, K. Multiobjective long-term generation scheduling of cascade hydroelectricity system using a quantum-behaved particle swarm optimization based on decomposition. IEEE Access 2020, 8, 100837–100856. [Google Scholar] [CrossRef]
- Cao, R.; Shen, J.; Cheng, C.; Wang, J. Optimization model for the Long-Term operation of an interprovincial hydropower plant incorporating peak shaving demands. Energies 2020, 13, 4804. [Google Scholar] [CrossRef]
- Su, L.; Yang, K.; Hu, H.; Yang, Z. Long-term hydropower generation scheduling of large-scale cascade reservoirs using chaotic adaptive multi-objective bat algorithm. Water 2019, 11, 2373. [Google Scholar] [CrossRef]
- Hu, H.; Yang, K.; Su, L.; Yang, Z. A novel adaptive multi-objective particle swarm optimization based on decomposition and dominance for long-term generation scheduling of cascade hydropower system. Water Resour. Manag. 2019, 33, 4007–4026. [Google Scholar] [CrossRef]
- Wen, X.; Zhou, J.; He, Z.; Wang, C. Long-term scheduling of large-scale cascade hydropower stations using improved differential evolution algorithm. Water 2018, 10, 383. [Google Scholar] [CrossRef]
- Hammid, A.T.; Bin Sulaiman, M.H. Series division method based on PSO and F.A. to optimize Long-Term Hydro Generation Scheduling. Sustain. Energy Technol. Assess. 2018, 29, 106–118. [Google Scholar] [CrossRef]
- Luo, B.; Miao, S.; Cheng, C.; Lei, Y.; Chen, G.; Gao, L. Long-term generation scheduling for cascade hydropower plants considering price correlation between multiple markets. Energies 2019, 12, 2239. [Google Scholar] [CrossRef]
- Kang, C.; Chen, C.; Wang, J. An efficient linearization method for long-term operation of cascaded hydropower reservoirs. Water Resour. Manag. 2018, 32, 3391–3404. [Google Scholar] [CrossRef]
- Ehteram, M.; Karami, H.; Mousavi, S.F.; Farzin, S.; Kisi, O. Evaluation of contemporary evolutionary algorithms for optimization in reservoir operation and water supply. J. Water Supply Res. Technol. 2018, 67, 54–67. [Google Scholar] [CrossRef]
- UN-Water. Coping with Water Scarcity—The Challenge of the Twenty-First Century. 2007. Available online: www.fao.org/3/aq444e/aq444e.pdf (accessed on 8 November 2021).
- Syme, G.J. Acceptable risk and social values: Struggling with uncertainty in Australian water allocation. Stoch. Environ. Res. Risk Assess. 2013, 28, 113–121. [Google Scholar] [CrossRef]
- Chen, J.; Shi, H.Y.; Sivakumar, B.; Peart, M.R. Population, water, food, energy, and dams. Renew. Sustain. Energy Rev. 2016, 56, 18–28. [Google Scholar] [CrossRef]
- Chang, F.; Wang, K.W. A systematical water allocation scheme for drought mitigation. J. Hydrol. 2013, 507, 124–133. [Google Scholar] [CrossRef]
- Payus, C.; Huey, L.A.; Adnan, F.; Rimba, A.B.; Mohan, G.; Chapagain, S.K.; Roder, G.; Gasparatos, A.; Fukushi, K. Impact of extreme drought climate on water security in north Borneo: Case study of Sabah. Water 2020, 12, 1135. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Yao, H.; Gao, L.; Chen, Y.; Liu, M. Non-linear relationship of hydrological drought responding to meteorological drought and impact of a large reservoir. J. Hydrol. 2017, 551, 495–507. [Google Scholar] [CrossRef]
- World Meteorological Organization. Drought Monitoring and Warning: Concepts, Progress and Future Challenges; No. 1006; WMO Publication: Geneva, Switzerland, 2006; pp. 6–9. Available online: http://www.wamis.org/agm/pubs/brochures/WMO1006e.pdf (accessed on 1 August 2022).
- Huang, C.; Zhao, J.; Wang, Z.; Shang, W. Optimal hedging rules for two-objective reservoir operation: Balancing water supply and environmental flow. J. Water Resour. Plan. Manag. 2016, 142, 04016053. [Google Scholar] [CrossRef]
- Ji, Y.; Lei, X.; Cai, S.; Wang, X. Hedging rules for water supply reservoirs based on the model of simulation and optimization. Water 2016, 8, 249. [Google Scholar] [CrossRef]
- Ngamsert, R.; Techarungruengsakul, R.; Kaewplang, S.; Hormwichian, R.; Prasanchum, H.; Sivanpheng, O.; Kangrang, A. Optimizing Solution in Decision Supporting System for River Basin Management Consisting of a Reservoir System. Water 2023, 15, 2510. [Google Scholar] [CrossRef]
- Choi, Y.; Ji, J.; Lee, E.; Lee, S.; Yi, S.; Yi, J. Developing Optimal Reservoir Rule Curve for Hydropower Reservoir with an add-on Water Supply Function Using Improved Grey Wolf Optimizer. Water Resour. Manag. 2023, 37, 2063–2082. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, C.; Wu, X.; Shen, J. Optimal Hedging for Hydropower Operation and End-of-Year Carryover Storage Values. J. Water Resour. Plan. Manag. 2019, 145, 04019003. [Google Scholar] [CrossRef]
- Xu, B.; Zhong, P.-A.; Huang, Q.; Wang, J.; Yu, Z.; Zhang, J. Optimal Hedging Rules for Water Supply Reservoir Operations under Forecast Uncertainty and Conditional Value-at-Risk Criterion. Water 2017, 9, 568. [Google Scholar] [CrossRef]
- Felfelani, F.; Movahed, A.J.; Zarghami, M. Simulating hedging rules for effective reservoir operation by using system dynamics: A case study of Dez Reservoir, Iran. Lake Reserv. Manag. 2013, 29, 126–140. [Google Scholar] [CrossRef]
- Thiha, S.; Shamseldin, A.Y.; Melville, B.W. Optimal reservoir operation using the improved multi-step-ahead time-varying hedging rule under climate and land-use changes. Hydrol. Sci. J. 2023, 68, 1139–1161. [Google Scholar] [CrossRef]
- Chang, J.; Guo, A.; Wang, Y.; Ha, Y.; Zhang, R.; Xue, L.; Tu, Z. Reservoir operations to mitigate drought effects with a hedging policy triggered by the drought prevention limiting water level. Water Resour. Res. 2019, 55, 904–922. [Google Scholar] [CrossRef]
- Hu, T.; Zhang, X.-Z.; Zeng, X.; Wang, J. A two-step approach for analytical optimal hedging with two triggers. Water 2016, 8, 52. [Google Scholar] [CrossRef]
- Neelakantan, T.R.; Sasireka, K. Hydropower reservoir operation using standard operating and standard hedging policies. Int. J. Eng. Technol. 2013, 5, 1191–1196. [Google Scholar]
- You, J.Y.; Cai, X. Hedging rules for reservoir operations: 1. A theoretical analysis. Water Resour. Res. 2008, 44, W01415. [Google Scholar] [CrossRef]
- You, J.Y.; Cai, X. Hedging rules for reservoir operations: 2. A numerical model. Water Resour. Res. 2008, 44, W01416. [Google Scholar] [CrossRef]
- Kumar, K.; Kasthurirengan, S. Generalized linear two-point hedging rule for water supply reservoir operation. J. Water Resour. Plan. Manag. 2018, 144, 04018051. [Google Scholar] [CrossRef]
- Shih, J.S.; ReVelle, C. Water-supply operations during drought: Continuous hedging rule. J. Water Resour. Plan. Manag. 1994, 120, 613–629. [Google Scholar] [CrossRef]
- Shiau, J.T. Analytical optimal hedging with explicit incorporation of reservoir release and carryover storage targets. Water Resour. Res. 2011, 47, W01515. [Google Scholar] [CrossRef]
- Rittima, A. Hedging policy for reservoir system operation: A case study of Mun Bon and Lam Chae reservoirs. J. Nat. Sci. 2009, 43, 833–842. [Google Scholar]
- Seo, S.B.; Kim, Y.O.; Kang, S.U. Time-varying discrete hedging rules for drought contingency plan considering long-range dependency in streamflow. Water Resour. Manag. 2019, 33, 2791–2807. [Google Scholar] [CrossRef]
- Jin, Y.; Lee, S. Comparative effectiveness of reservoir operation applying hedging rules based on available water and beginning storage to cope with droughts. Water Resour. Manag. 2019, 33, 1897–1911. [Google Scholar] [CrossRef]
- Men, B.; Wu, Z.; Liu, H.; Li, Y.; Zhao, Y. Research on hedging rules based on water supply priority and benefit loss of water shortage—A case study of Tianjin, China. Water 2019, 11, 778. [Google Scholar] [CrossRef]
- Tayebiyan, A.; Mohammad, T.A.; Al-Ansari, N.; Malakootian, M. Comparison of optimal hedging policies for hydropower reservoir system operation. Water 2019, 11, 121. [Google Scholar] [CrossRef]
- Lee, S.; Jin, Y.; Park, J. Comparison of hedging rule curves depending on available water and current storage in reservoir operation under droughts. Eur. Water 2017, 60, 227–232. [Google Scholar]
- Mansouri, S.; Fathian, H.; Nikbakht Shahbazi, A.; Asadi Lour, M.; Asareh, A. Multi-objective simulation–optimization operation of dam reservoir in low water regions based on hedging principles. Environ. Sci. Pollut. Res. 2023, 30, 41581–41590. [Google Scholar] [CrossRef]
- Jalilian, A.; Heydari, M.; Azari, A.; Shabanlou, S. Extracting optimal rule curve of dam reservoir based on stochastic inflow. Water Resour. Manag. 2022, 36, 1763–1782. [Google Scholar] [CrossRef]
- Bayesteh, M.; Azari, A. Stochastic optimization of reservoir operation by applying hedging rules. J. Water Resour. Plan. Manag. 2021, 147, 04020099. [Google Scholar] [CrossRef]
- Jamshidi, J.; Shourian, M. Hedging rules-based optimal reservoir operation using bat algorithm. Water Resour. Manag. 2019, 33, 4525–4538. [Google Scholar] [CrossRef]
- Srinivasan, K.; Kumar, K. Multi-Objective Simulation-Optimization Model for Long-term Reservoir Operation using Piecewise Linear Hedging Rule. Water Resour Manag. 2018, 32, 1901–1911. [Google Scholar] [CrossRef]
- Srivastava, A. A computational framework for dam safety risk Assessment with uncertainty analysis. In All Graduate Theses and Dissertations; Utah State University: Logan, UT, USA, 2013; p. 1480. [Google Scholar] [CrossRef]
- Neelakantan, T.R.; Sasireka, K. Review of hedging rules applied to reservoir operation. Int. J. Eng. Technol. 2015, 7, 1571–1580. [Google Scholar]
- Baecher, G. Uncertainty in dam safety risk analysis. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2016, 10, 92–108. [Google Scholar] [CrossRef]
- ICOLD. Bulletin 130: Risk Assessment in Dam Safety Management; International Commission on Large Dams: Paris, France, 2005. [Google Scholar]
- Ljungqvist, K. A Probabilistic Approach to Risk Analysis. A Comparison between Undesirable Indoor Events and Human Sensitivity. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2005. [Google Scholar]
- Stedinger, J.R.; Heath, D.C.; Thompson, K. Risk Analysis for Dam Safety Evaluation: Hydrologic Risk; IWR Report 96-R-13.1996; Cornell University: Ithaca, NY, USA, 1996. [Google Scholar]
- Babu, G.L.S.; Srivastava, A. Reliability Analysis of Earth Dams. J. Geotech. Geoenviron. Eng. 2010, 136, 995–998. [Google Scholar] [CrossRef]
- Federal Energy Regulatory Commission (FERC). Risk-Informed Decision-Making Guidelines. Version 4.1. 2016. Available online: https://www.ferc.gov/sites/default/files/2020-04/Introduction-to-Risk-Informed-Decision-Making.pdf (accessed on 1 August 2022).
- Hartford, D.N.D.; Baecher, G.B. Risk and Uncertainty in Dam Safety; Thomas Telford Publishing: London, UK, 2004. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency (FEMA). Federal Guidelines for Dam Safety Risk Management. FEMA P-1025. 2015. Available online: https://www.fema.gov/sites/default/files/2020-08/fema_dam-safety_risk-management_P-1025.pdf (accessed on 27 August 2022).
- Simonovic, S.P. From risk management to quantitative disaster resilience- A paradigm shift. Int. J. Saf. Secur. Eng. 2016, 6, 85–95. [Google Scholar] [CrossRef]
- Tong, H. A Network Approach to Interdependent Infrastructure Resilience Assessment for Natural Hazards. Ph.D. Thesis, The University of Western Ontario, London, ON, Canada, 2019; p. 6047. Available online: https://ir.lib.uwo.ca/etd/6047 (accessed on 27 August 2023).
- Fuller, W. Flood flows. Trans. Am. Soc. Civ. Eng. 1914, 77, 564–617. [Google Scholar] [CrossRef]
- Du, T.; Xiong, L.; Xu, C.; Gippel, C.; Guo, S.; Liu, P. Return period and risk analysis of nonstationary low-flow series under climate change. J. Hydrol. 2015, 527, 234–250. [Google Scholar] [CrossRef]
- Read, L.K.; Vogel, R.M. Reliability, return periods, and risk under nonstationary. Water Resour. Res. 2015, 51, 6381–6398. [Google Scholar] [CrossRef]
- Poduje, A.C.C.; Belli, A.; Haberlandt, U. Dam risk assessment based on univariate versus bivariate statistical approaches: A case study for Argentina. Hydrol. Sci. J. 2014, 59, 2216–2232. [Google Scholar] [CrossRef]
- Volpi, E.; Fiori, A.; Grimaldi, S.; Lombardo, F.; Koutsoyiannis, D. One hundred years of return period: Strengths and limitations. Water Resour. Res. 2015, 51, 8570–8585. [Google Scholar] [CrossRef]
- Dai, L.; Zhou, J.; Chen, L.; Huang, K.; Wang, Q.; Zha, G. Flood-risk analysis based on a stochastic differential equation method. J. Flood Risk Manag. 2019, 12, e12515. [Google Scholar] [CrossRef]
- Jiang, S. Application of stochastic differential equations in risk assessment for flood releases. Hydrol. Sci. J. 1998, 43, 349–360. [Google Scholar] [CrossRef]
- Adarsh, S.; Janga Reddy, M. Reliability analysis of composite channels using first-order approximation and Monte-Carlo simulations. Stoch. Environ. Res. Risk Assess. 2013, 27, 477–487. [Google Scholar] [CrossRef]
- Marengo, H.; Arreguin, F.; Aldama, A.; Morales, V. Case study: Risk analysis by overtopping of diversion works during dam construction: The La Yesca hydroelectric project, Mexico. Struct. Saf. 2013, 42, 26–34. [Google Scholar] [CrossRef]
- Park, Y.; Yeghiazarian, L.; Stedinger, J.; Montemagno, C.D. Numerical approach to cryptosporidium risk assessment using reliability method. Stoch. Environ. Res. Risk Assess. 2008, 22, 169–183. [Google Scholar] [CrossRef]
- Ganji, A.; Jowkarshorijeh, L. Advance first order second moment (A.F.O.S.M.) method for single reservoir operation reliability analysis: A case study. Stoch. Environ. Res. Risk Assess. 2012, 26, 33–42. [Google Scholar] [CrossRef]
- Xin, C.; Chongshim, G. Risk analysis of gravity dam instability using credibility theory Monte Carlo simulation model. SpringerPlus 2016, 5, 778. [Google Scholar] [CrossRef]
- Goodarzi, E.; Teang, M.; Ziaei, L. Risk and uncertainty analysis for dam overtopping Case Study: The Doroudzan dam, Iran. J. Hydro-Environ. Res. 2013, 8, 50–61. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A. Risk, Reliability, Resilience (R3) and beyond in dam engineering: A state-of-the-art review. Int. J. Disaster Risk Reduct. 2018, 31, 806–831. [Google Scholar] [CrossRef]
- Baecher, G.B.; Christian, J.T. Reliability and Statistics in Geotechnical Engineering; Wiley: New York, NY, USA, 2003; ISBN 978-0-471-49833-9. [Google Scholar]
- Chen, S.T. Statistics on dam failure. In Reliability and Uncertainty Analyses in Hydraulic Design; Yen, B., Tung, Y., Eds.; ASCE: New York, NY, USA, 1993; pp. 97–105. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems; Morgan-Kaufmann: San Mateo, CA, USA, 1988. [Google Scholar] [CrossRef]
- Hanea, M.; Remus, G. Non-parametric Bayesian networks for parameter estimation in reservoir simulation: A graphical take on the ensemble Kalman filter (Part I). Comput. Geosci. 2013, 17, 929–949. [Google Scholar] [CrossRef]
- Tang, X.; Chen, A.; He, J. Optimized variable selection of Bayesian network for dam risk analysis: A case study of earth dams in the United States. J. Hydrol. 2023, 61, 129091. [Google Scholar] [CrossRef]
- Wang, T.; Li, Z.; Ge, W.; Zhang, Y.; Jiao, Y.; Sun, H.; Zhang, H. Calculation of dam risk probability of cascade reservoirs considering risk transmission and superposition. J. Hydrol. 2022, 609, 127768. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, P. Bayesian network of risk assessment for a super-large dam exposed to multiple natural risk sources. Stoch. Environ. Res. Risk Assess. 2018, 33, 581–592. [Google Scholar] [CrossRef]
- Zhang, L.M.; Xu, Y.; Jia, J.; Zhao, C. Diagnosis of embankment dam distresses using Bayesian networks Part, I. Global-level characteristics based on a dam distress database. Can. Geotech. J. 2011, 48, 1630–1644. [Google Scholar] [CrossRef]
- El-Awady, A.; Ponnambalam, K. Integration of simulation and Markov Chains to support Bayesian Networks for probabilistic failure analysis of complex systems. Reliab. Eng. Syst. Saf. 2021, 211, 107511. [Google Scholar] [CrossRef]
- Badr, A.; Yosri, A.; Hassini, S.; El-Dakhakhni, W. Coupled Continuous-Time Markov Chain–Bayesian Network Model for Dam Failure Risk Prediction. J. Infrastruct. Syst. 2021, 27, 04021041. [Google Scholar] [CrossRef]
- Gill, J.C.; Malamud, B.D. Reviewing and visualizing the interactions of natural hazards. Rev. Geophys. 2014, 52, 680–722. [Google Scholar] [CrossRef]
- King, L.M.; Simonovic, S.P.; Hartford, D.N.D. Using system dynamics simulation for assessment of hydropower system safety. Water Resour. Res. 2017, 53, 7148–7174. [Google Scholar] [CrossRef]
- Hartford, D.N.D.; Baecher, G.B.; Zielinski, P.A.; Patev, R.C.; Ascila, R.; Rytters, K. Operational Safety of Dams Reservoirs; ICE Publishing: London, UK, 2016. [Google Scholar] [CrossRef]
- Komey, A.; Deng, Q.; Baecher, G.B.; Zielinski, P.A.; Atkinson, T. Systems Reliability of Flow Control in Dam Safety. In Proceedings of the 12th International Conference on Application of Statistics and Probability in Civil Engineering, ICASP12, Vancouver, BC, Canada, 12–15 July 2015; pp. 1–8. [Google Scholar]
- Kwag, S.; Gupta, A. Probabilistic risk assessment framework for structural systems under multiple hazards using Bayesian statistics. Nucl. Eng. Des. 2017, 315, 20–34. [Google Scholar] [CrossRef]
- Zomorodian, M.; Lai, S.H.; Homayounfar, M.; Ibrahim, S.; Fatemi, S.E.; El-Shafie, A. The state-of-the-art system dynamics application in integrated water resources modeling. J. Environ. Manag. 2018, 227, 294–304. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Kang, D. Analyzing the Effectiveness of a Multi-Purpose Dam Using a System Dynamics Model. Water 2020, 12, 1062. [Google Scholar] [CrossRef]
- Ignjatovic, L.; Stojkovic, M.; Ivetic, D.; Milašinovic, M.; Milivojevic, N. Quantifying multi-parameter dynamic resilience for complex reservoir systems using failure simulations: A case study of the Pirot reservoir system. Water 2021, 13, 3157. [Google Scholar] [CrossRef]
- Salem, S.; Siam, A.; El-Dakhakhni, W.; Tait, M. Probabilistic resilience-guided infrastructure risk management. J. Manag. Eng. 2020, 36, 04020073. [Google Scholar] [CrossRef]
- Linkov, I.; Bridges, T.; Creutzig, F.; Decker, J.; Fox-Lent, C.; Kröger, W.; Lambert, J.H.; Levermann, A.; Montreuil, B.; Nathwani, J.; et al. Changing the resilience paradigm. Nat. Clim. Change 2014, 4, 407–409. [Google Scholar] [CrossRef]
- Lewis, T. Critical Infrastructure Protection in Homeland Security: Defending a Networked Nation; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Simonovic, S.P.; Arunkumar, R. Comparison of static and dynamic resilience for a multipurpose reservoir operation. Water Resour. Res. 2016, 52, 8630–8649. [Google Scholar] [CrossRef]
- Badr, A.; Zoe, L.; El-Dakhakhni, W. Dynamic Resilience Quantification of Hydropower Infrastructure in Multihazard Environments. J. Infrastruct. Syst. 2023, 29, 04023012. [Google Scholar] [CrossRef]

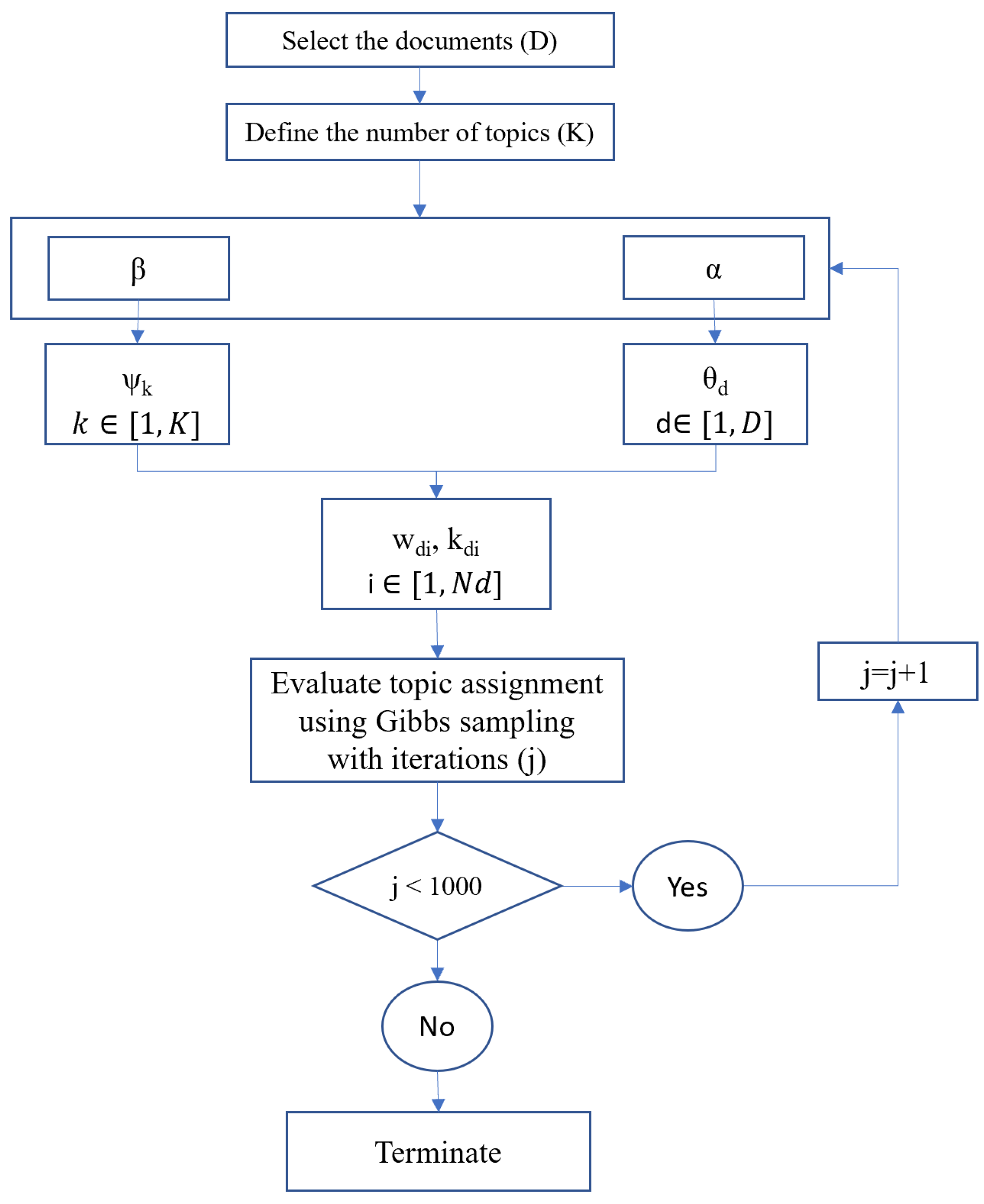



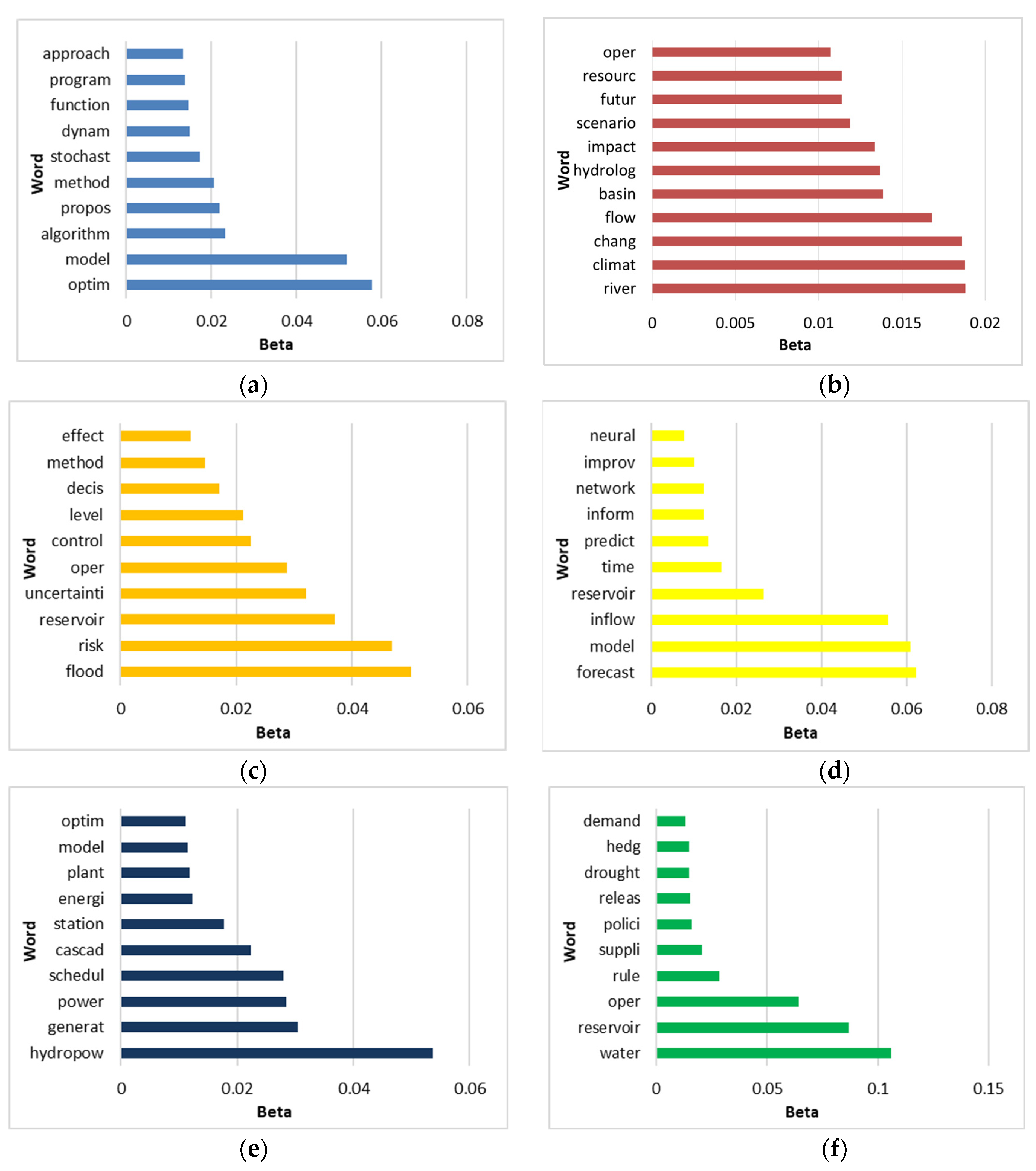
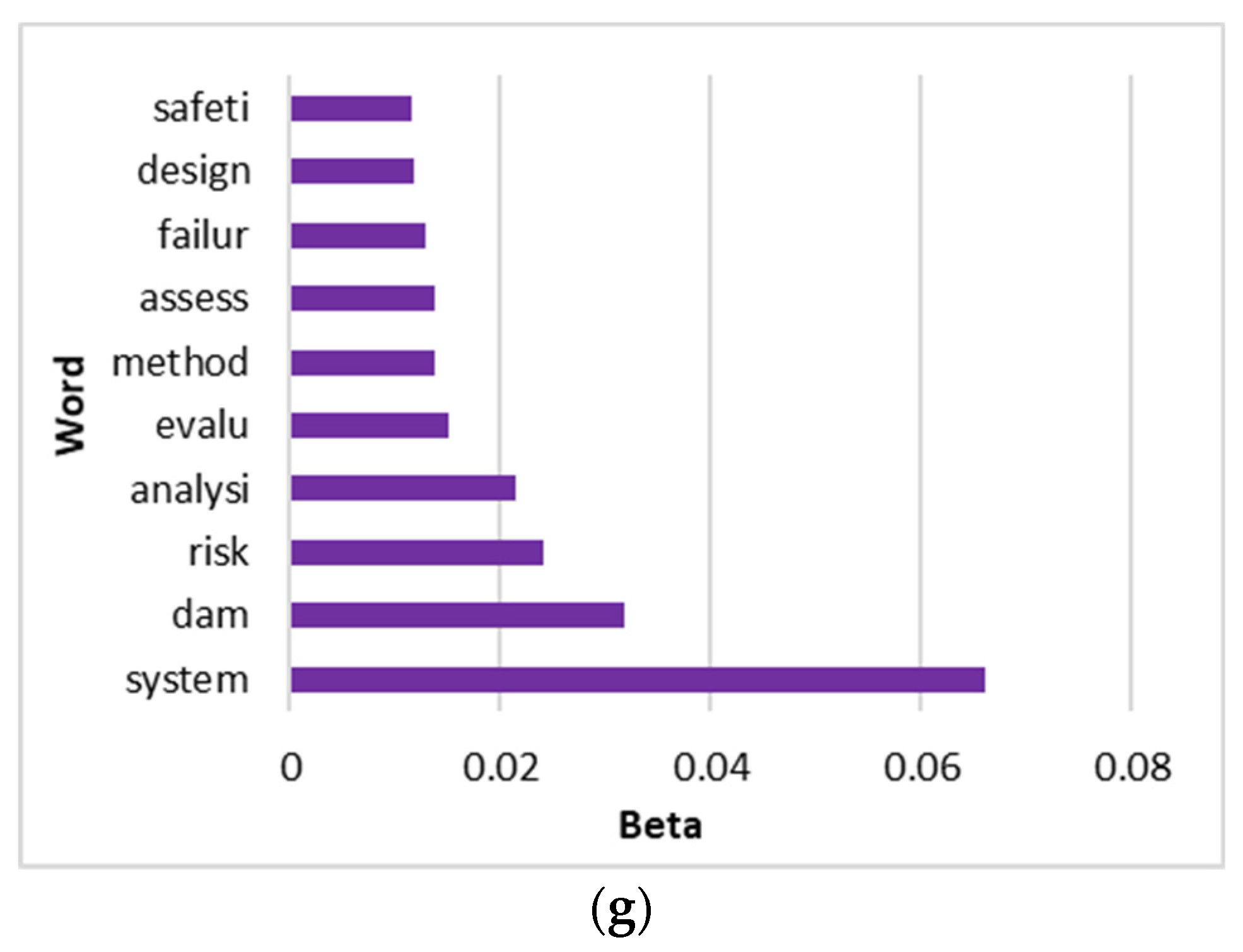
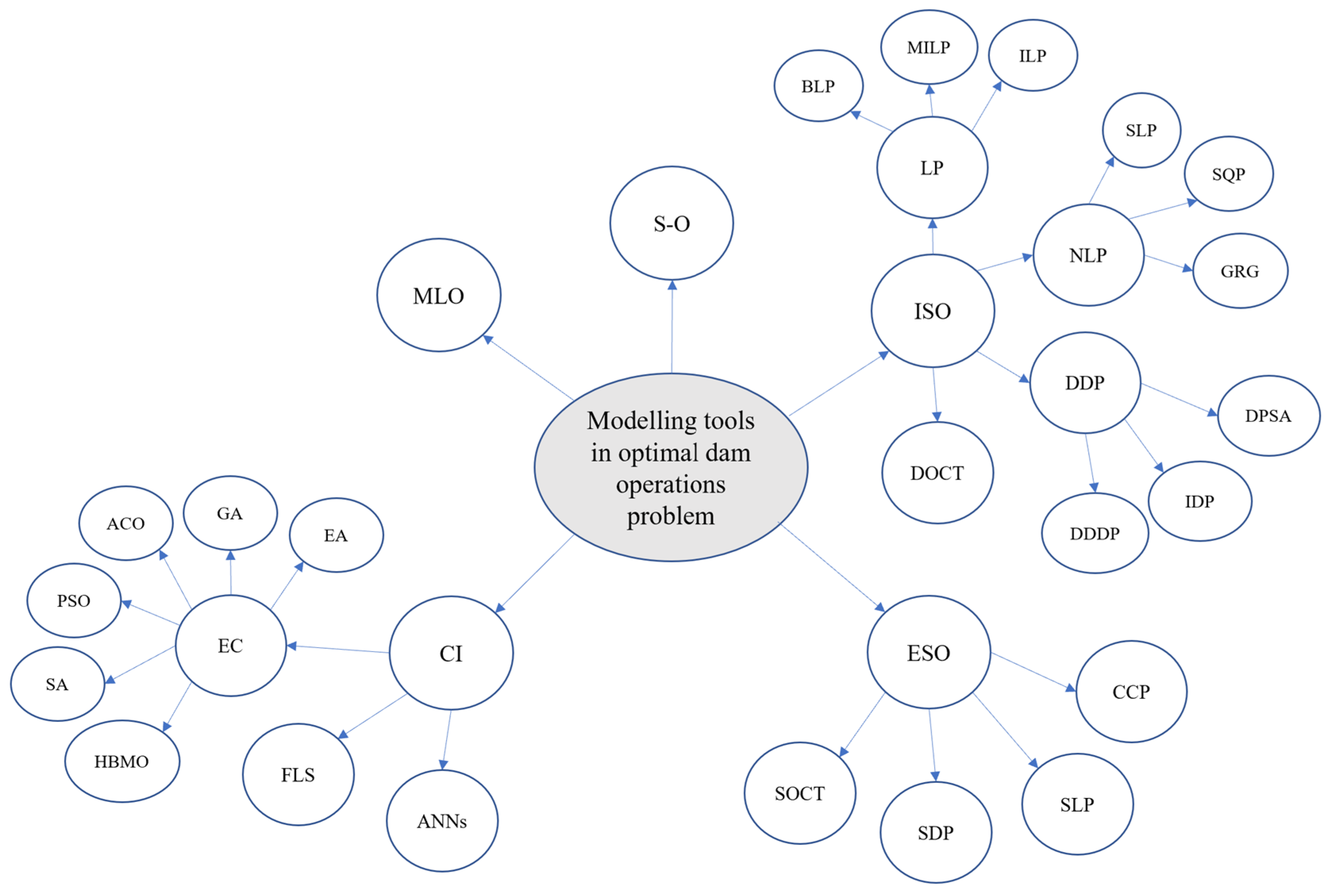
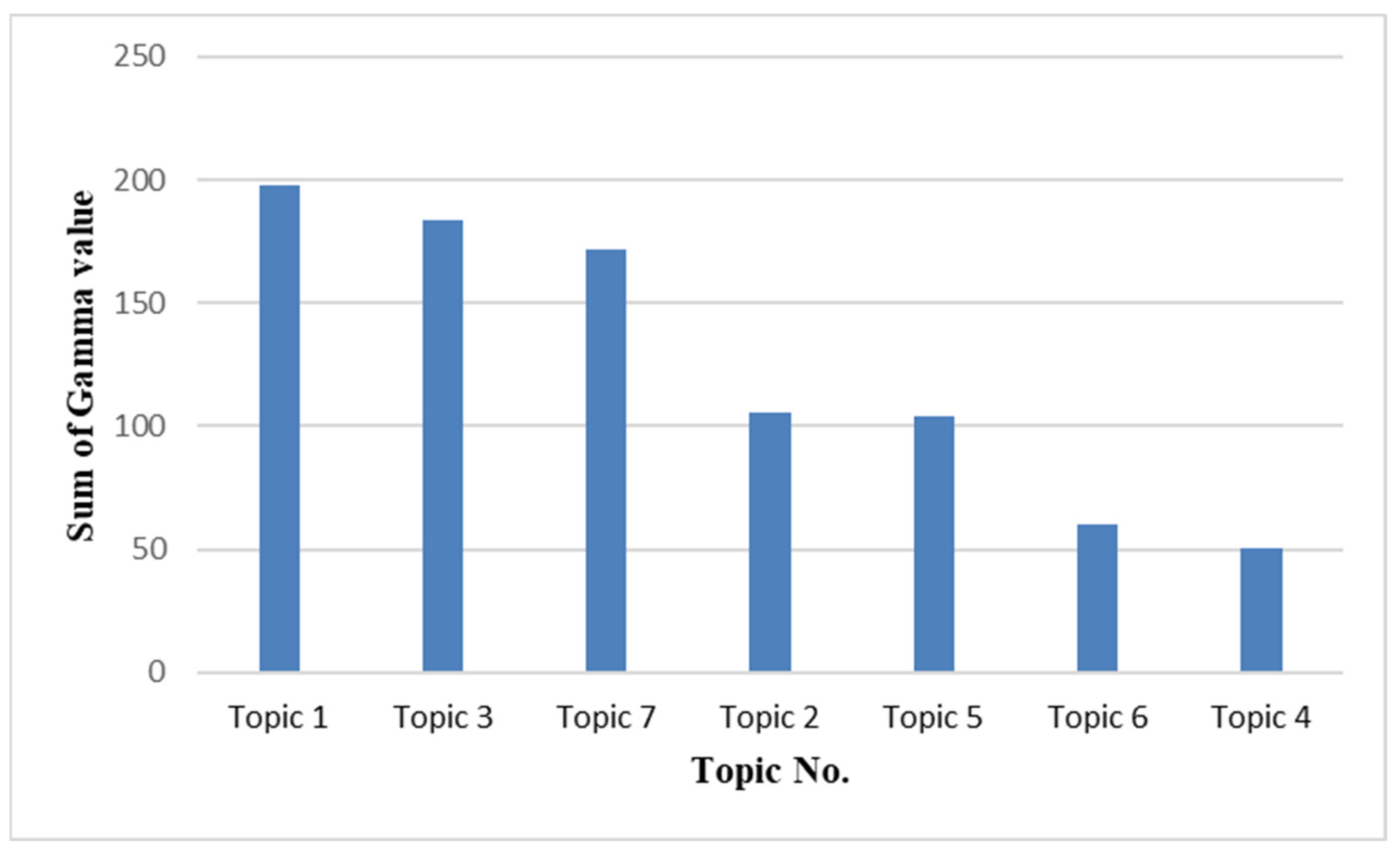
| Ref. | Main Goal | Case Study |
|---|---|---|
| [239] | Investigate the economic and energy efficiency of the coordinated operations between a hybrid PSH, integrating a pumping station between cascading conventional hydropower stations, with wind and photovoltaic systems at different time scales. | Wujiang River, China |
| [240] | Investigate the peak shaving of cascade hydropower with mixed PSH to decrease the variation of the residual load of the external power grid, considering the hydraulic coupling of multiple reservoirs and water delay time in the hydropower model. | Southwest China |
| [241] | Review and assess the research conducted on the operation, cost, and desired locations of PSH resources in the Railbelt transmission system. | Alaska, USA |
| [242] | Develop a new mixed-integer linear optimization model for allocating the PSH unit on the next day of the unit commitment program, using the Autoregressive integral Moving Average (ARIMA) and Stationary Autoregressive integral Moving Average (SARIMA) to predict the market prices of the next day, considering the electricity market uncertainties. | Ontario, Canada |
| [243] | Develop a comprehensive power and energy model for PSH integrated with conventional hydropower (CH), aiming to maximize the energy production of the CH, improve PSH operations to consider the discharge variation, achieve a monthly balance between PSH and CH operations, determine the optimum value for PSH and CH based on the range of the charge and discharge ratio, compare capacity optimization of PSH and CH with and without water stream. | Balakot hydropower plant, Pakistan |
| [244] | Review the recent advanced pumped storage hydropower technologies, including conventional pumped storage hydropower, adjustable speed pumped storage hydropower, and ternary pumped storage hydropower. | N.A. |
| [245] | Investigate the short-term operation of a hybrid wind farm-PSH system transmitting power to multiple cross-regional power grids through ultra-high-voltage transmission lines. | Eastern China |
| [246] | Propose an optimal unit model for a coordinated wind-PSH generation system, considering wind uncertainties using a chance-constrained optimization model. | Northwest, China |
| [247] | Develop a Quaternary PSH combining the Conventional-PSH and Adjustable speed-PSH technologies, aiming to provide fast power support and efficiently consider the uncertainties of power generation. | N.A. |
| [248] | Develop a GIS-based model to transfer a conventional hydropower dam to PSH, determining the most suitable second reservoir location, and calculating its hydroelectricity energy potential. | Porsuk Dam, Turkey |
| [249] | Develop a new mixed integer linear programming model for PSH, allowing a greater number of breakpoints, leading to more realistic solutions, and reducing computational efforts. | Argentine Republic |
| [250] | Proposed a generic method to model and optimize small-scale PSH that can be applied to different PSH technologies, including adjustable-speed and hydraulic short circuits and PSH configurations such as ternary, reversible, and separate turbines and pumps. | Shell Energy North America (SENA) modular PSH concept |
| [251] | Review the existing types of PSH, highlighting the advantages and disadvantages of each PSH system. | N.A. |
| Ref. | Main Goal | Case Study |
|---|---|---|
| Short-Term Hydropower Scheduling (STHS) | ||
| [257] | Propose a dynamic capacity short-term scheduling model based on one-dimensional unsteady flow for Three Gorges in China. | Three Gorges, China |
| [258] | Propose a two-step technique based on mixed-integer linear programming (MILP) to solve the STHS by exploring the symmetry related to the identical generating units in San Antonio and obtaining the optimal load distribution. | San Antonio, Brazil |
| [259] | Develop a linear mixed-integer optimization model to maximize total hydropower generation among all periods of the operation year, considering the production rate at the maximum storage for all possible operational scenarios of the turbine and the most efficient point of water discharge. | Saguenay-Lac-St-Jean, Quebec, Canada. |
| [260] | Develop a rolling horizon robust online scheduling scheme that employs stochastic optimization within a feedback model to consider the uncertainties in hydropower operation, including electricity prices, power demand, inflow, and model parameters. | Ontario, Canada |
| [261] | Compare five mixed-integer linear programming formulations for efficient STHS. | Hypothetical three hydropower plant system |
| [38] | Identify a quick decision approach for STHS for cascaded hydropower plants using data mining algorithms. | Tianshengqiao, Guangdong, China. |
| [262] | Propose a dynamic determination process for the breakpoints of the piecewise linear approximation method for solving STHS, considering the intake loss, efficiency of the head-dependent turbine, penstock loss, the varying time head effect, and tailrace loss. | Northern Norway |
| [263] | Develop mixed-linear programming for hourly hydropower scheduling applied to a cascading hydropower system with hydraulic coupling and multiple prohibited zones for head-dependent operation. | Tianshengqiao, Hongshui River, southwest China |
| [264] | Develop a multi-objective mixed-integer non-linear programming for the peak shaving operations to enhance power efficiency and control the peak loads. | Beipanjiang, China |
| [265] | Propose a stochastic multicriteria decision-making framework for STHS under multiple uncertainties. | Qingjiang, Hubei, China |
| [266] | Determine the efficiency of genetic algorithms with different selection operators for optimizing the STHS problem. | Gezhouba, China |
| [267] | Develop a rolling optimal operation model for hourly (ultra) STHS in real-time for cascading hydropower dam system. | Yunnan, China |
| [268] | Develop a short-term peak-shaving method using fuzzy clustering analysis and linear mixed-integer programming for cascading hydropower systems with sensitive heads, considering water spillage adjustments. | Hongshui, China |
| [269] | Develop an improved cloud adaptive quantum-inspired binary social spider optimization model to optimize short-term scheduling sub-problems, economic load dispatch, and unit commitment. | Three Gorges hydropower station, Yangtze, China. |
| [270] | Develop an advanced optimization model to improve the hydropower economic profit of a large chain of reservoirs, considering ecological restrictions, European regulations, and operation uncertainties. | Guadalquivir, southern Spain. |
| [271] | Develop a successive approximation approach to consider the STHS non-linear characteristics. | Ten Reservoir System, China |
| [272] | Used linear and dynamic programming to determine the number of operating units and the power in each quarter-hour and for each hydro plant. | Yunnan, China |
| Mid-Term Hydropower Scheduling (MTHS) | ||
| [273] | Develop a successive quadratic programming model with linearization updated by the non-linear constraints of the hydropower facility composed of cascading reservoirs. | Jinsha River, China |
| [274] | Develop a bi-level stochastic model based on information gap decision-making theory for MTHS of cascading hydropower systems, considering the economic and hydrologic uncertainties in hydropower market participation. | Southwest China |
| [275] | Develop a two-stage decomposition approach for the MTHS problem, where every state is represented as a multi-period stochastic model. | Brazil |
| [276] | Develop an MTHS approach acting as a price-maker in the automatic frequency restoration reserve market. | Northwest Spain |
| [277] | Develop a stochastic optimization model for mid-term scheduling using Latin hypercube sampling and Cholesky decomposition coupled with sensitivity analysis, considering the uncertainty of natural inflows. | China |
| [278] | Apply stochastic dual dynamic integer programming (SDDIP) to a non-convex MTHS problem. | Norwegian hydropower |
| Long-Term Hydropower Scheduling (LTHS) | ||
| [279] | Improves the traditional weekly hydropower scheduling by integrating the hourly power and capacity balances (HPCB), which are formulated in the form of mixed-integer linear constraints involving the spare, reserve, maintenance, disabled, and working capacities, besides optimizing the levels and orders of hydro plants in peak-shaving the hourly power load curve. | Lancang River, China |
| [280] | Develop improved dynamic programming with successive approximation at each stage and relaxation strategy to solve the joint optimal operation problem of the large-scale hydropower plan groups. | Yangtze River, China |
| [281] | Illustrate the advantages of coupling the periodic autoregressive and the moving average (PARMA) over using only the periodic autoregressive (PAR) model to represent inflow uncertainties within the SDDP optimization model of LTHS. | Quebec, Canada |
| [46] | Develop a hybrid linear and nonlinear hydropower reservoir optimization model to provide an efficient and faster solution for the LTHS problem. | California, USA |
| [282] | Develop the LHTS approach to consider inflow forecasting uncertainty based on the adaptive nearest neighbor Gaussian temporal disaggregation method. | Xiluodu-Xiangjiaba, China |
| [283] | Develop an improved optimal method to control water levels, considering the two-stage analysis of LTHS and adjustable policy for the target outflow. | Xiluodu and Three Gorges, China |
| [284] | Develop a hybrid decomposition-coordination and discrete differential dynamic programming model (IDC–DDDP) for solving the LTHS for large-scale hydropower systems. | Southwestern China |
| [285] | Develop a multi-objective quantum-behaved particle swarm optimization model based on improved Tchebycheff decomposition with a modified generator of direction vectors to maximize the total production rate and firm the hydropower output. | Three Gorges and Gezhouba, China |
| [286] | Develop a linear mixed-integer optimization model to consider peak shaving demands, aiming to maximize the power generation profit within the LTHS of an interprovincial hydropower plant. | Xiluodu, China |
| [287] | Develop a chaotic adaptive multi-objective bat algorithm for cascade hydropower dams. | Qingjiang, southern China |
| [288] | Develop an adaptive multi-objective particle swarm optimization model based on the dominance and decomposition of a multi-objective long-term generation. | Three Gorges, China |
| [289] | Develop an improved differential evolution algorithm based on the LSHADE evolutionary algorithm, using new mutation strategies to provide a wider search range and accelerate convergence. | Jinsha River, western China. |
| [290] | Develop a series division method based on particle swarm optimization and firefly algorithm for the LTHS problem. | Himreen lake, Diyala/Iraq |
| [291] | Develop a novel optimization model based on copula theory to consider the uncertainty of electricity prices and the correlation between multiple markets. | Wu river, southwestern |
| [292] | Develop a novel piecewise linearization method for LTHS that converts the non-linear problem to a linear programming problem without using integer variables. | Lancang River, southwest of China. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badr, A.; Li, Z.; El-Dakhakhni, W. Dam System and Reservoir Operational Safety: A Meta-Research. Water 2023, 15, 3427. https://doi.org/10.3390/w15193427
Badr A, Li Z, El-Dakhakhni W. Dam System and Reservoir Operational Safety: A Meta-Research. Water. 2023; 15(19):3427. https://doi.org/10.3390/w15193427
Chicago/Turabian StyleBadr, Ahmed, Zoe Li, and Wael El-Dakhakhni. 2023. "Dam System and Reservoir Operational Safety: A Meta-Research" Water 15, no. 19: 3427. https://doi.org/10.3390/w15193427
APA StyleBadr, A., Li, Z., & El-Dakhakhni, W. (2023). Dam System and Reservoir Operational Safety: A Meta-Research. Water, 15(19), 3427. https://doi.org/10.3390/w15193427








