Modeling Wetland Functions: Is Space-to-Time Substitution of the Perimeter–Area Relationship Appropriate?
Abstract
:1. Introduction
2. Materials and Methods
2.1. Metrics Used to Track the Perimeter–Area Covariation
2.1.1. Perimeter–Area (P:A) Ratio
2.1.2. Shoreline Fractal Dimension
2.1.3. Shoreline Irregularity
2.2. Tracking the Dynamics of Perimeter-Area Covariation
2.3. Assessing the Representativeness of Dynamic Perimeter-Area Covariation Based on Static Wetland Data
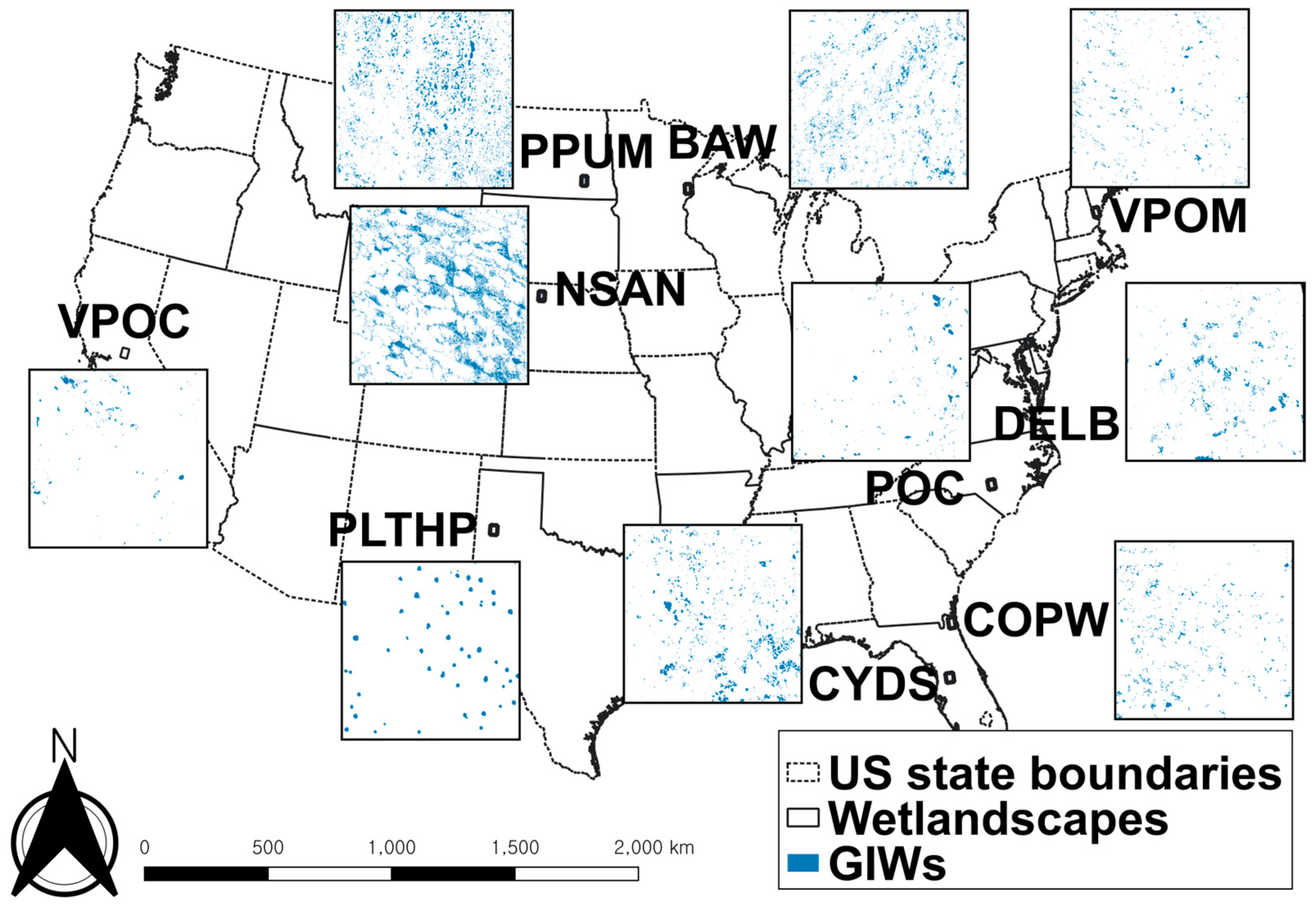
2.4. Data
3. Results
3.1. Covariation of Perimeter and Area Based on Static Wetland Data
3.2. Dynamic Covariation of Perimeter and Area
3.3. Discrepancies between Observed Dynamic P vs. A Variation and One Estimated from Static Data
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Whigham, D.F.; Chitterling, C.; Palmer, B. Impacts of Freshwater Wetlands on Water Quality: A Landscape Perspective. Environ. Manag. 1988, 12, 663–671. [Google Scholar] [CrossRef]
- Wamsley, T.V.; Cialone, M.A.; Smith, J.M.; Atkinson, J.H.; Rosati, J.D. The Potential of Wetlands in Reducing Storm Surge. Ocean Eng. 2010, 37, 59–68. [Google Scholar] [CrossRef]
- Ogawa, H.; Male, J.W. Simulating the Flood Mitigation Role of Wetlands. J. Water Resour. Plan. Manag. 1986, 112, 114–128. [Google Scholar] [CrossRef]
- Junk, W.J.; Brown, M.; Campbell, I.C.; Finlayson, M.; Gopal, B.; Ramberg, L.; Warner, B.G. The Comparative Biodiversity of Seven Globally Important Wetlands: A Synthesis. Aquat. Sci. 2006, 68, 400–414. [Google Scholar] [CrossRef]
- Pant, H.; Rechcigl, J.E.; Adjei, M. Carbon Sequestration in Wetlands: Concept and Estimation. Food Agric. Environ. 2003, 1, 308–313. [Google Scholar]
- Cheng, F.Y.; Van Meter, K.J.; Byrnes, D.K.; Basu, N.B. Maximizing US Nitrate Removal through Wetland Protection and Restoration. Nature 2020, 588, 625–630. [Google Scholar] [CrossRef]
- Cheng, F.Y.; Basu, N.B. Biogeochemical Hotspots: Role of Small Water Bodies in Landscape Nutrient Processing. Water Resour. Res. 2017, 53, 5038–5056. [Google Scholar] [CrossRef]
- Laterra, P.; Booman, G.C.; Picone, L.; Videla, C.; Orúe, M.E. Indicators of Nutrient Removal Efficiency for Riverine Wetlands in Agricultural Landscapes of Argentine Pampas. J. Environ. Manag. 2018, 222, 148–154. [Google Scholar] [CrossRef]
- Ligi, T.; Truu, M.; Truu, J.; Nõlvak, H.; Kaasik, A.; Mitsch, W.J.; Mander, Ü. Effects of Soil Chemical Characteristics and Water Regime on Denitrification Genes (NirS, NirK, and NosZ) Abundances in a Created Riverine Wetland Complex. Ecol. Eng. 2014, 72, 47–55. [Google Scholar] [CrossRef]
- Moreno-Mateos, D.; Mander, Ü.; Comín, F.A.; Pedrocchi, C.; Uuemaa, E. Relationships between Landscape Pattern, Wetland Characteristics, and Water Quality in Agricultural Catchments. J. Environ. Qual. 2008, 37, 2170–2180. [Google Scholar] [CrossRef]
- Bloom, A.A.; Bowman, K.W.; Lee, M.; Turner, A.J.; Schroeder, R.; Worden, J.R.; Weidner, R.; McDonald, K.C.; Jacob, D.J. A Global Wetland Methane Emissions and Uncertainty Dataset for Atmospheric Chemical Transport Models (WetCHARTs Version 1.0). Geosci. Model Dev. 2017, 10, 2141–2156. [Google Scholar] [CrossRef]
- Hondula, K.L.; DeVries, B.; Jones, C.N.; Palmer, M.A. Effects of Using High Resolution Satellite-Based Inundation Time Series to Estimate Methane Fluxes From Forested Wetlands. Geophys. Res. Lett. 2021, 48, e2021GL092556. [Google Scholar] [CrossRef]
- Melton, J.R.; Wania, R.; Hodson, E.L.; Poulter, B.; Ringeval, B.; Spahni, R.; Bohn, T.; Avis, C.A.; Beerling, D.J.; Chen, G.; et al. Present State of Global Wetland Extent and Wetland Methane Modelling: Conclusions from a Model Inter-Comparison Project (WETCHIMP). Biogeosciences 2013, 10, 753–788. [Google Scholar] [CrossRef]
- Zhang, Z.; Zimmermann, N.E.; Stenke, A.; Li, X.; Hodson, E.L.; Zhu, G.; Huang, C.; Poulter, B. Emerging Role of Wetland Methane Emissions in Driving 21st Century Climate Change. Proc. Natl. Acad. Sci. USA 2017, 114, 9647–9652. [Google Scholar] [CrossRef]
- Fairbairn, S.E.; Dinsmore, J.J. Local and Landscape-Level Influences on Wetland Bird Communities of the Prairie Pothole Region of Iowa, USA. Wetlands 2001, 21, 41–47. [Google Scholar] [CrossRef]
- Murray, C.G.; Kasel, S.; Loyn, R.H.; Hepworth, G.; Hamilton, A.J. Waterbird Use of Artificial Wetlands in an Australian Urban Landscape. Hydrobiologia 2013, 716, 131–146. [Google Scholar] [CrossRef]
- Santoro, A.; Chambers, J.M.; Robson, B.J.; Beatty, S.J. Land Use Surrounding Wetlands Influences Urban Populations of a Freshwater Turtle. Aquat. Conserv. Mar. Freshw. Ecosyst. 2020, 30, 1050–1060. [Google Scholar] [CrossRef]
- Wu, H.; Dai, J.; Sun, S.; Du, C.; Long, Y.; Chen, H.; Yu, G.; Ye, S.; Chen, J. Responses of Habitat Suitability for Migratory Birds to Increased Water Level during Middle of Dry Season in the Two Largest Freshwater Lake Wetlands of China. Ecol. Indic. 2021, 121, 107065. [Google Scholar] [CrossRef]
- Arp, C.D.; Jones, B.M.; Grosse, G. Recent Lake Ice-out Phenology within and among Lake Districts of Alaska, USA. Limnol. Oceanogr. 2013, 58, 2013–2028. [Google Scholar] [CrossRef]
- Bajer, P.G.; Beck, M.W.; Hundt, P.J. Effect of Non-Native versus Native Invaders on Macrophyte Richness: Are Carp and Bullheads Ecological Proxies? Hydrobiologia 2018, 817, 379–391. [Google Scholar] [CrossRef]
- Bélanger, L.; Couture, R. Use of Man-Made Ponds by Dabbling Duck Broods. J. Wildl. Manag. 1988, 52, 718–723. [Google Scholar] [CrossRef]
- Bowerman, W.W.; Grubb, T.G.; Bath, A.J.; Giesy, J.P.; Weseloh, D.V.C. A Survey of Potential Bald Eagle Nesting Habitat along the Great Lakes Shoreline; U.S. Department of Agriculture: Fort Collins, CO, USA, 2005; p. 6. [Google Scholar]
- Fox, B.J.; Holland, W.B.; Boyd, F.L.; Blackwell, B.F.; Armstrong, J.B. Use of Stormwater Impoundments near Airports by Birds Recognized as Hazardous to Aviation Safety. Landsc. Urban Plan. 2013, 119, 64–73. [Google Scholar] [CrossRef]
- Grubb, T.G.; Bowerman, W.W.; Bath, A.J.; Giesy, J.P.; Weseloh, D.V.C. Evaluating Great Lakes Bald Eagle Nesting Habitat with Bayesian Inference; RMRS-RP; U.S. Department of Agriculture: Fort Collins, CO, USA, 2003. [Google Scholar]
- Longcore, J.R.; Gibbs, J.P. Distribution and Numbers of American Black Ducks along the Maine Coast during the Severe Winter of 1980–1981. In Waterfowl in Winter; University of Minnesota Press: Minneapolis, MN, USA, 1988; pp. 377–389. [Google Scholar]
- Merendino, M.T.; Ankney, C.D.; Dennis, D.G. Increasing Mallards, Decreasing American Black Ducks: More Evidence for Cause and Effect. J. Wildl. Manag. 1993, 57, 199–208. [Google Scholar] [CrossRef]
- Merendino, M.T.; Ankney, C.D. Habitat Use by Mallards and American Black Ducks Breeding in Central Ontario. Condor 1994, 96, 411–421. [Google Scholar] [CrossRef]
- Oertli, B.; Parris, K.M. Review: Toward Management of Urban Ponds for Freshwater Biodiversity. Ecosphere 2019, 10, e02810. [Google Scholar] [CrossRef]
- Patton, D.R. A Diversity Index for Quantifying Habitat “Edge”. Wildl. Soc. Bull. 1975, 3, 171–173. [Google Scholar]
- Politi, E.; MacCallum, S.; Cutler, M.E.J.; Merchant, C.J.; Rowan, J.S.; Dawson, T.P. Selection of a Network of Large Lakes and Reservoirs Suitable for Global Environmental Change Analysis Using Earth Observation. Int. J. Remote Sens. 2016, 37, 3042–3060. [Google Scholar] [CrossRef]
- Roni, P.; Morley, S.A.; Garcia, P.; Detrick, C.; King, D.; Beamer, E. Coho Salmon Smolt Production from Constructed and Natural Floodplain Habitats. Trans. Am. Fish. Soc. 2006, 135, 1398–1408. [Google Scholar] [CrossRef]
- Willén, E. Phytoplankton and Water Quality Characterization: Experiences from the Swedish Large Lakes Mälaren, Hjälmaren, Vättern and Vänern. Ambio 2001, 30, 529–537. [Google Scholar] [CrossRef]
- Håkanson, L. The Length of Closed Geomorphic Lines. Math. Geol. 1978, 10, 141–167. [Google Scholar] [CrossRef]
- Håkanson, L. On Lake Bottom Dynamics—The Energy–Topography Factor. Can. J. Earth Sci. 1981, 18, 899–909. [Google Scholar] [CrossRef]
- Håkanson, L. Lake Bottom Dynamics and Morphometry: The Dynamic Ratio. Water Resour. Res. 1982, 18, 1444–1450. [Google Scholar] [CrossRef]
- Håkanson, L. Considerations on Representative Water Quality Data. Int. Rev. Der Gesamten Hydrobiol. Und Hydrogr. 1992, 77, 497–505. [Google Scholar] [CrossRef]
- Håkanson, L. Models to Predict Organic Content of Lake Sediments. Ecol. Model. 1995, 82, 233–245. [Google Scholar] [CrossRef]
- Håkanson, L. Error Propagations in Step-by-Step Predictions: Examples for Environmental Management Using Regression Models for Lake Ecosystems. Environ. Model. Softw. 1998, 14, 49–58. [Google Scholar] [CrossRef]
- Håkanson, L.; Kvarnäs, H.; Karlsson, B. Coastal Morphometry as Regulator of Water Exchange—A Swedish Example. Estuar. Coast. Shelf Sci. 1986, 23, 873–887. [Google Scholar] [CrossRef]
- Persson, J.; Håkanson, L.; Pilesjö, P. Prediction of Surface Water Turnover Time in Coastal Waters Using Digital Bathymetric Information. Environmetrics 1994, 5, 433–449. [Google Scholar] [CrossRef]
- Bernhardt, E.S.; Blaszczak, J.R.; Ficken, C.D.; Fork, M.L.; Kaiser, K.E.; Seybold, E.C. Control Points in Ecosystems: Moving Beyond the Hot Spot Hot Moment Concept. Ecosystems 2017, 20, 665–682. [Google Scholar] [CrossRef]
- Cohen, M.J.; Creed, I.F.; Alexander, L.; Basu, N.B.; Calhoun, A.J.K.; Craft, C.; D’Amico, E.; DeKeyser, E.; Fowler, L.; Golden, H.E.; et al. Do Geographically Isolated Wetlands Influence Landscape Functions? Proc. Natl. Acad. Sci. USA 2016, 113, 1978–1986. [Google Scholar] [CrossRef] [PubMed]
- Marton, J.M.; Creed, I.F.; Lewis, D.B.; Lane, C.R.; Basu, N.B.; Cohen, M.J.; Craft, C.B. Geographically Isolated Wetlands Are Important Biogeochemical Reactors on the Landscape. BioScience 2015, 65, 408–418. [Google Scholar] [CrossRef]
- McLaughlin, D.L.; Kaplan, D.A.; Cohen, M.J. A Significant Nexus: Geographically Isolated Wetlands Influence Landscape Hydrology. Water Resour. Res. 2014, 50, 7153–7166. [Google Scholar] [CrossRef]
- Van Meter, K.J.; Basu, N.B. Signatures of Human Impact: Size Distributions and Spatial Organization of Wetlands in the Prairie Pothole Landscape. Ecol. Appl. 2015, 25, 451–465. [Google Scholar] [CrossRef] [PubMed]
- Creed, I.F.; Lane, C.R.; Serran, J.N.; Alexander, L.C.; Basu, N.B.; Calhoun, A.J.K.; Christensen, J.R.; Cohen, M.J.; Craft, C.; D’Amico, E.; et al. Enhancing Protection for Vulnerable Waters. Nat. Geosci. 2017, 10, 809–815. [Google Scholar] [CrossRef] [PubMed]
- Walsh, R.; Ward, A.S. An Overview of the Evolving Jurisdictional Scope of the U.S. Clean Water Act for Hydrologists. WIREs Water 2022, 9, e1603. [Google Scholar] [CrossRef]
- Duan, H.; Xu, M.; Cai, Y.; Wang, X.; Zhou, J.; Zhang, Q. A Holistic Wetland Ecological Water Replenishment Scheme with Consideration of Seasonal Effect. Sustainability 2019, 11, 930. [Google Scholar] [CrossRef]
- Fu, Y.; Zhao, J.; Peng, W.; Zhu, G.; Quan, Z.; Li, C. Spatial Modelling of the Regulating Function of the Huangqihai Lake Wetland Ecosystem. J. Hydrol. 2018, 564, 283–293. [Google Scholar] [CrossRef]
- Hayashi, M.; van der Kamp, G. Simple Equations to Represent the Volume–Area–Depth Relations of Shallow Wetlands in Small Topographic Depressions. J. Hydrol. 2000, 237, 74–85. [Google Scholar] [CrossRef]
- Helzer, C.J.; Jelinski, D.E. The Relative Importance of Patch Area and Perimeter-Area Ratio to Grassland Breeding Birds. Ecol. Appl. 1999, 9, 1448–1458. [Google Scholar] [CrossRef]
- Yu, M.; Hu, G.; Feeley, K.J.; Wu, J.; Ding, P. Richness and Composition of Plants and Birds on Land-Bridge Islands: Effects of Island Attributes and Differential Responses of Species Groups. J. Biogeogr. 2012, 39, 1124–1133. [Google Scholar] [CrossRef]
- Krummel, J.R.; Gardner, R.H.; Sugihara, G.; O’Neill, R.V.; Coleman, P.R. Landscape Patterns in a Disturbed Environment. Oikos 1987, 48, 321–324. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Stochastic Models for the Earth’s Relief, the Shape and the Fractal Dimension of the Coastlines, and the Number-Area Rule for Islands. Proc. Natl. Acad. Sci. USA 1975, 72, 3825–3828. [Google Scholar] [CrossRef] [PubMed]
- Sugihara, G.; May, R.M. Applications of Fractals in Ecology. Trends Ecol. Evol. 1990, 5, 79–86. [Google Scholar] [CrossRef] [PubMed]
- Bertassello, L.E.; Rao, P.S.C.; Jawitz, J.W.; Botter, G.; Le, P.V.V.; Kumar, P.; Aubeneau, A.F. Wetlandscape Fractal Topography. Geophys. Res. Lett. 2018, 45, 6983–6991. [Google Scholar] [CrossRef]
- Gilbert, M.C.; Whited, P.M.; Clairain, J.; Smith, R.D. A Regional Guidebook for Applying the Hydrogeomorphic Approach to Assessing Wetland Functions of Prairie Potholes; U.S. Army Corps of Engineers: Washington, DC, USA, 2006. [Google Scholar]
- Wetzel, R.G. Limnology; W. B. Sauders Company: Philadelphia, 1975. [Google Scholar]
- Seekell, D.; Cael, B.B.; Byström, P. Problems with the Shoreline Development Index—A Widely Used Metric of Lake Shape. Geophys. Res. Lett. 2022, 49, e2022GL098499. [Google Scholar] [CrossRef]
- Jones, C.N.; Evenson, G.R.; McLaughlin, D.L.; Vanderhoof, M.K.; Lang, M.W.; McCarty, G.W.; Golden, H.E.; Lane, C.R.; Alexander, L.C. Estimating Restorable Wetland Water Storage at Landscape Scales. Hydrol. Process. 2018, 32, 305–313. [Google Scholar] [CrossRef] [PubMed]
- Lai, X.J.; Huang, Q.; Jiang, J.H. Wetland Inundation Modeling of Dongting Lake Using Two-Dimensional Hydrodynamic Model on Unstructured Grids. Procedia Environ. Sci. 2012, 13, 1091–1098. [Google Scholar] [CrossRef]
- Liu, Y.; Kumar, M. Role of Meteorological Controls on Interannual Variations in Wet-Period Characteristics of Wetlands. Water Resour. Res. 2016, 52, 5056–5074. [Google Scholar] [CrossRef]
- Sorribas, M.V.; Paiva, R.C.D.; Melack, J.M.; Bravo, J.M.; Jones, C.; Carvalho, L.; Beighley, E.; Forsberg, B.; Costa, M.H. Projections of Climate Change Effects on Discharge and Inundation in the Amazon Basin. Clim. Chang. 2016, 136, 555–570. [Google Scholar] [CrossRef]
- Wilson, M.; Bates, P.; Alsdorf, D.; Forsberg, B.; Horritt, M.; Melack, J.; Frappart, F.; Famiglietti, J. Modeling Large-Scale Inundation of Amazonian Seasonally Flooded Wetlands. Geophys. Res. Lett. 2007, 34, L15404. [Google Scholar] [CrossRef]
- Huang, C.; Peng, Y.; Lang, M.; Yeo, I.-Y.; McCarty, G. Wetland Inundation Mapping and Change Monitoring Using Landsat and Airborne LiDAR Data. Remote Sens. Environ. 2014, 141, 231–242. [Google Scholar] [CrossRef]
- Krapu, C.; Kumar, M.; Borsuk, M. Identifying Wetland Consolidation Using Remote Sensing in the North Dakota Prairie Pothole Region. Water Resour. Res. 2018, 54, 7478–7494. [Google Scholar] [CrossRef]
- Li, L.; Chen, Y.; Xu, T.; Liu, R.; Shi, K.; Huang, C. Super-Resolution Mapping of Wetland Inundation from Remote Sensing Imagery Based on Integration of Back-Propagation Neural Network and Genetic Algorithm. Remote Sens. Environ. 2015, 164, 142–154. [Google Scholar] [CrossRef]
- Shaeri Karimi, S.; Saintilan, N.; Wen, L.; Valavi, R. Application of Machine Learning to Model Wetland Inundation Patterns Across a Large Semiarid Floodplain. Water Resour. Res. 2019, 55, 8765–8778. [Google Scholar] [CrossRef]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-Resolution Mapping of Global Surface Water and Its Long-Term Changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
- Jones, J.W. Efficient Wetland Surface Water Detection and Monitoring via Landsat: Comparison with in Situ Data from the Everglades Depth Estimation Network. Remote Sens. 2015, 7, 12503–12538. [Google Scholar] [CrossRef]
- Jones, J.W. Improved Automated Detection of Subpixel-Scale Inundation—Revised Dynamic Surface Water Extent (DSWE) Partial Surface Water Tests. Remote Sens. 2019, 11, 374. [Google Scholar] [CrossRef]
- Allen, G.H.; Pavelsky, T.M. Global Extent of Rivers and Streams. Science 2018, 361, 585–588. [Google Scholar] [CrossRef] [PubMed]
- Luijendijk, A.; Hagenaars, G.; Ranasinghe, R.; Baart, F.; Donchyts, G.; Aarninkhof, S. The State of the World’s Beaches. Sci Rep 2018, 8, 6641. [Google Scholar] [CrossRef]
- Mentaschi, L.; Vousdoukas, M.I.; Pekel, J.-F.; Voukouvalas, E.; Feyen, L. Global Long-Term Observations of Coastal Erosion and Accretion. Sci Rep 2018, 8, 12876. [Google Scholar] [CrossRef]
- Park, J.; Kumar, M.; Lane, C.R.; Basu, N.B. Seasonality of Inundation in Geographically Isolated Wetlands across the United States. Environ. Res. Lett. 2022, 17, 054005. [Google Scholar] [CrossRef]
- Lane, C.R.; D’Amico, E. Identification of Putative Geographically Isolated Wetlands of the Conterminous United States. J. Am. Water Resour. Assoc. 2016, 52, 705–722. [Google Scholar] [CrossRef]
- Cheng, F.Y.; Park, J.; Kumar, M.; Basu, N.B. Disconnectivity Matters: The Outsized Role of Small Ephemeral Wetlands in Landscape-Scale Nutrient Retentions. Environ. Res. Lett. 2022, 18, 024018. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Kumar, M.; Jones, C.N. Modeling Wetland Functions: Is Space-to-Time Substitution of the Perimeter–Area Relationship Appropriate? Water 2023, 15, 3445. https://doi.org/10.3390/w15193445
Park J, Kumar M, Jones CN. Modeling Wetland Functions: Is Space-to-Time Substitution of the Perimeter–Area Relationship Appropriate? Water. 2023; 15(19):3445. https://doi.org/10.3390/w15193445
Chicago/Turabian StylePark, Junehyeong, Mukesh Kumar, and C. Nathan Jones. 2023. "Modeling Wetland Functions: Is Space-to-Time Substitution of the Perimeter–Area Relationship Appropriate?" Water 15, no. 19: 3445. https://doi.org/10.3390/w15193445
APA StylePark, J., Kumar, M., & Jones, C. N. (2023). Modeling Wetland Functions: Is Space-to-Time Substitution of the Perimeter–Area Relationship Appropriate? Water, 15(19), 3445. https://doi.org/10.3390/w15193445







