Applying Multivariate Analysis and Machine Learning Approaches to Evaluating Groundwater Quality on the Kairouan Plain, Tunisia
Abstract
:1. Introduction
2. Methodology
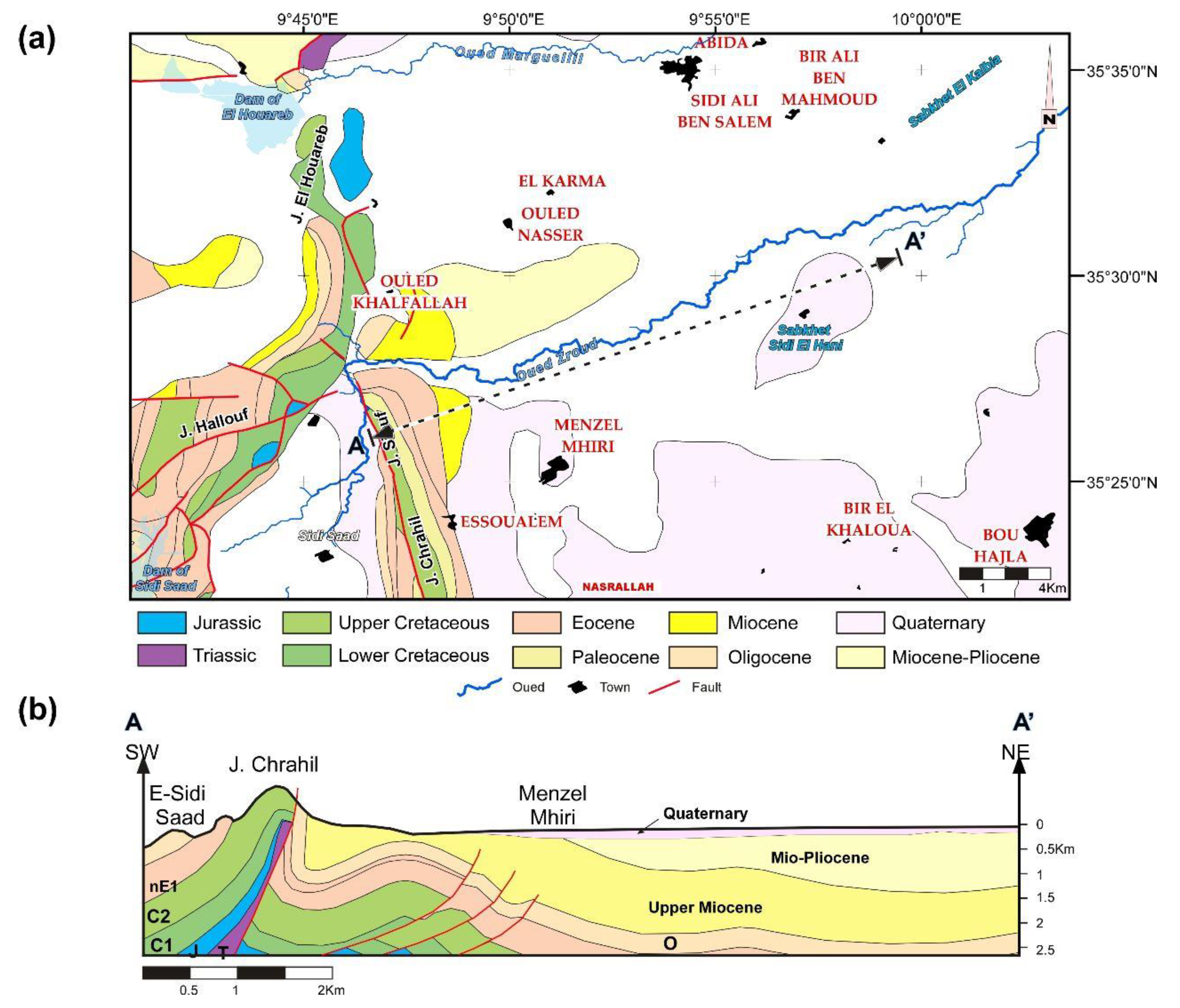
2.1. Area of Investigation
2.2. Geology and Hydrogeology
2.3. Sampling and Analysis
2.4. Multivariate Statistical Analysis
2.4.1. Cluster Analysis (CA)
2.4.2. Principal Component Analysis (PCA)
2.5. Indexing Approach
2.5.1. Chloro-Alkaline Indexes (CAIs)
2.5.2. Irrigation Water Quality Indices (IWQIs)
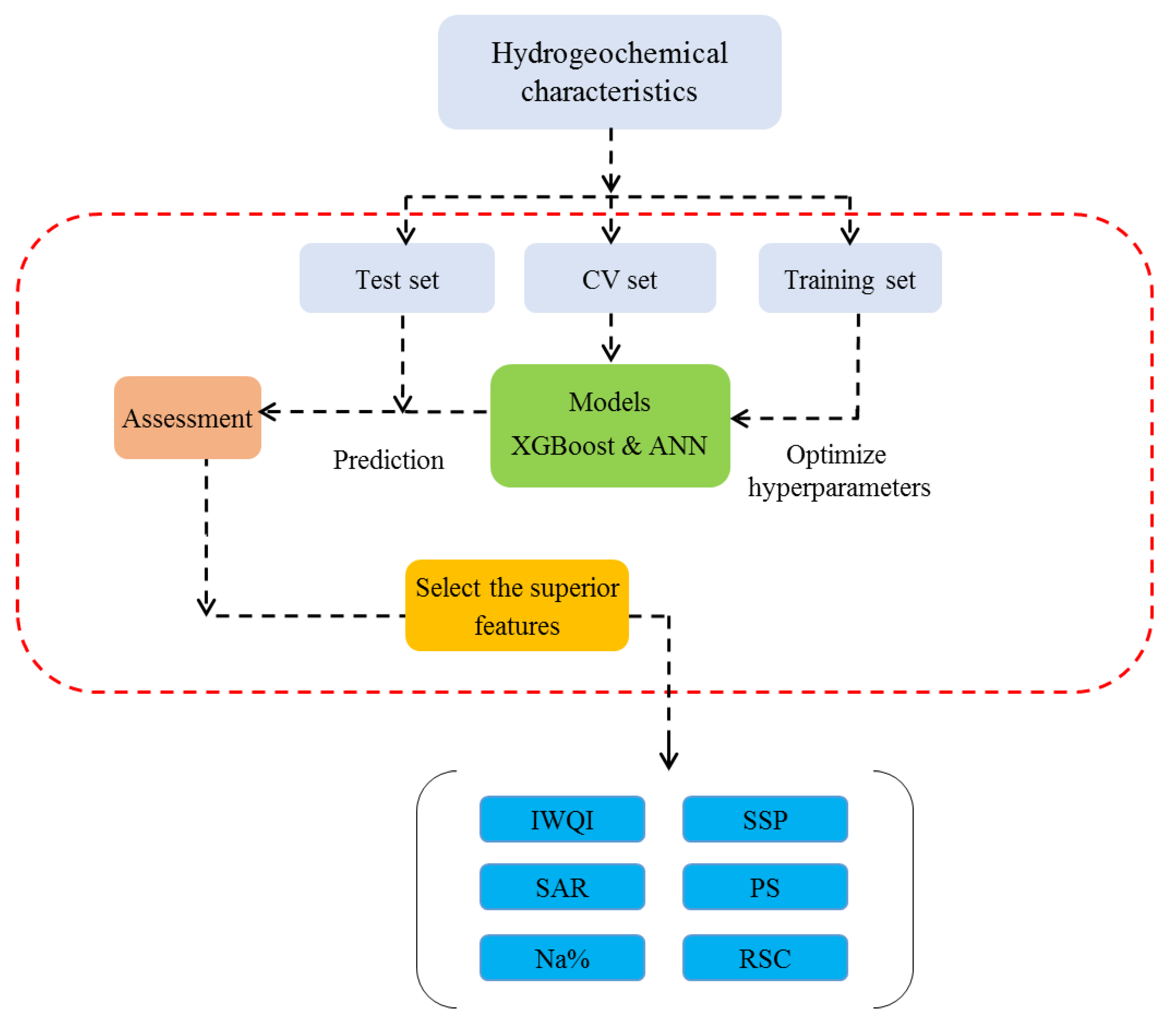
2.6. Machine Learning Approaches
2.6.1. Back-Propagation neural network (BPNN)
2.6.2. XGBoost Regression
2.7. Datasets and Software for Data Analysis and Processing
2.8. Model Evaluation
3. Results and Discussion
3.1. Groundwater Hydrochemical Properties
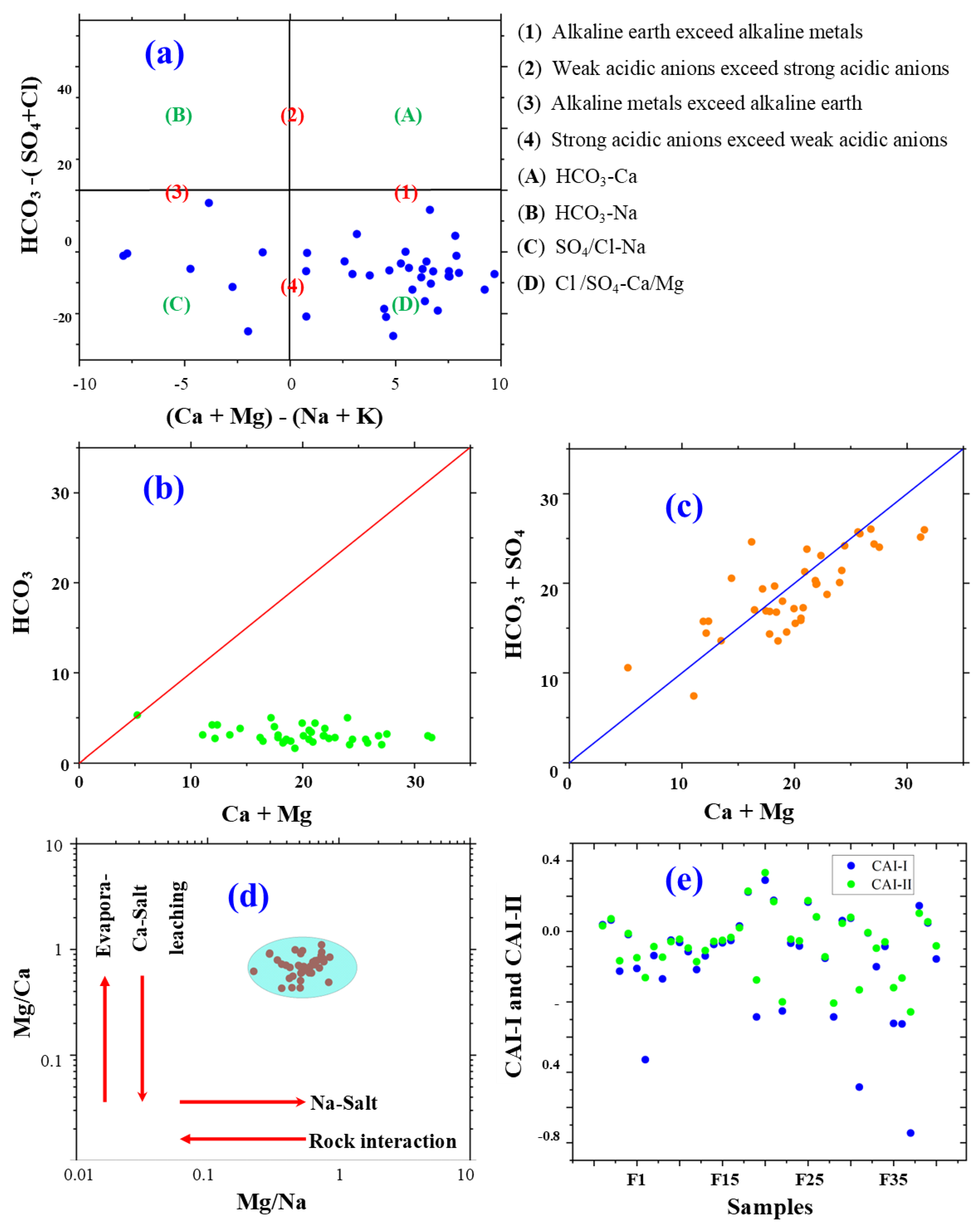
3.2. Groundwater Facies and Source Identification
3.2.1. Groundwater Type
3.2.2. Ion Exchange Processes
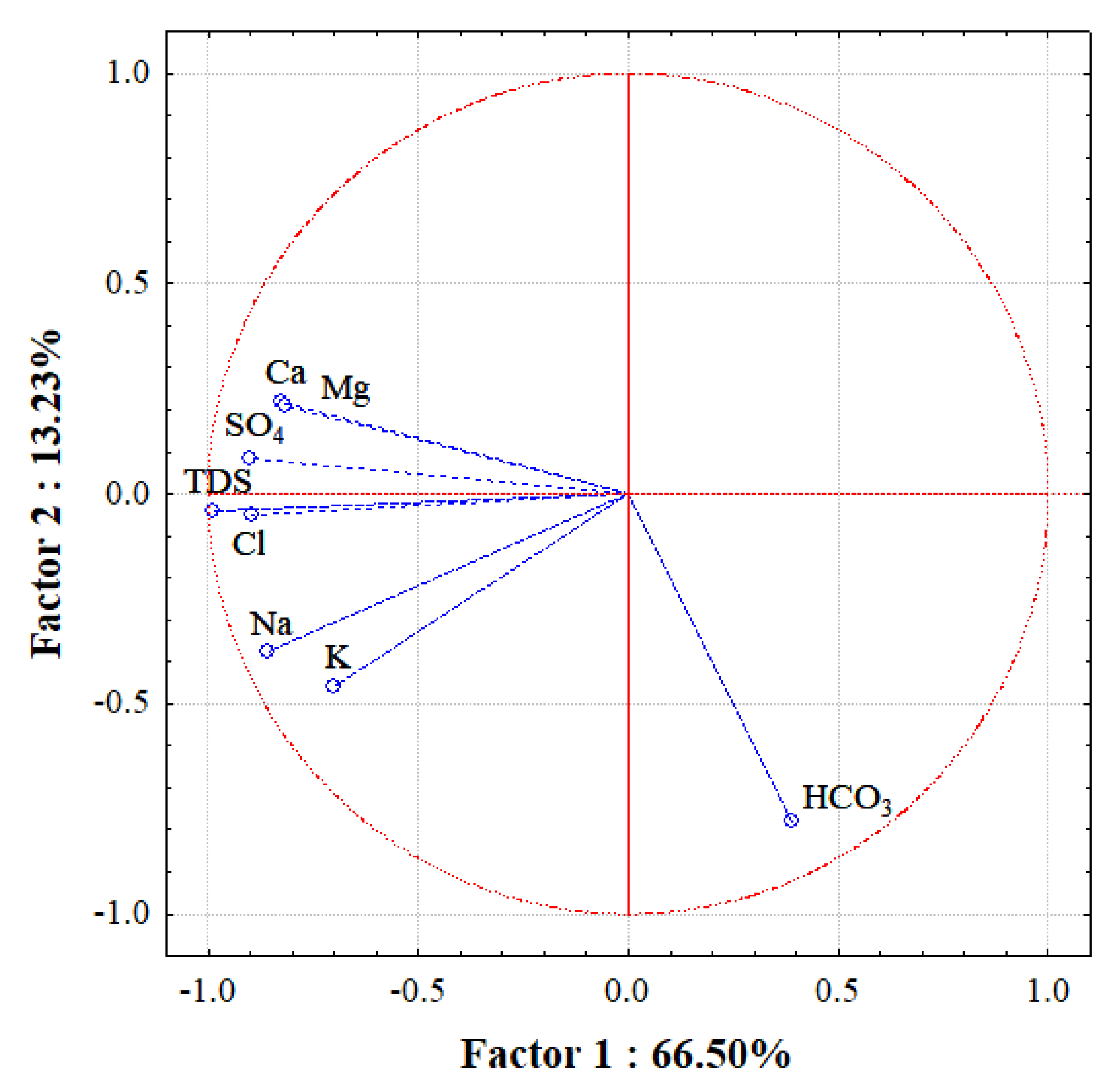
3.3. Analysis of Multivariate Statistics
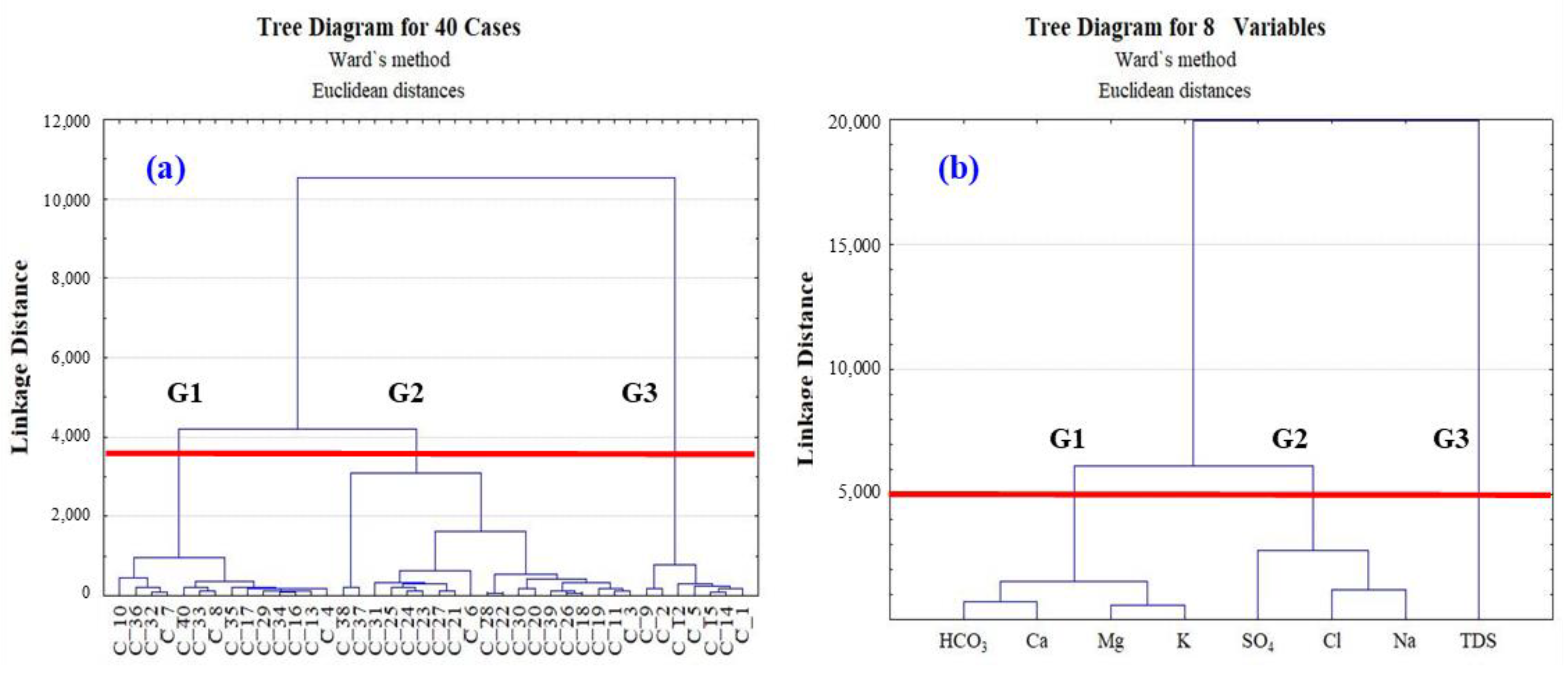
3.3.1. Cluster Analysis (CA)
3.3.2. Principal Component Analysis (PCA)
3.4. Irrigation Water Quality Indices (IWQIs)
3.4.1. The IWQI Classification
3.4.2. Impact on Soil Composition
3.4.3. Precipitation of Alkali Elements and RSC
3.4.4. Potential Salinity Index (PS)
3.5. Machine Learning Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tramblay, Y.; Koutroulis, A.; Samaniego, L.; Vicente-Serrano, S.M.; Volaire, F.; Boone, A.; Le Page, M.; Llasat, M.C.; Albergel, C.; Burak, S.; et al. Challenges for drought assessment in the Mediterranean region under future climate scenarios. Earth-Sci. Rev. 2020, 210, 103348. [Google Scholar] [CrossRef]
- Derwich, L.J.; Zouar, K.; Michelot, J.L. Recharge and paleorecharge of the deep groundwater aquifer system in the Zeroud Basin (Kairouan plain, Central Tunisia). Quat. Int. 2012, 257, 56–63. [Google Scholar] [CrossRef]
- Alexakis, D.E. Meta-Evaluation of Water Quality Indices. Application into Groundwater Resources. Water 2020, 12, 1890. [Google Scholar] [CrossRef]
- Ismail, E.; Snousy, M.G.; Alexakis, D.E.; Gamvroula, D.E.; Howard, G.; El Sayed, E.; Ahmed, M.S.; Ali, A.; Abdelhalim, A. Multivariate Statistical Analysis and Geospatial Mapping for Assessing Groundwater Quality in West El Minia District, Egypt. Water 2023, 15, 2909. [Google Scholar] [CrossRef]
- Biswas, M.R.; Alzubaidi, M.S.; Shah, U.; Abd-Alrazaq, A.A.; Shah, Z. A Scoping Review to Find out Worldwide COVID-19 Vaccine Hesitancy and Its Underlying Determinants. Vaccines 2021, 9, 1243. [Google Scholar] [CrossRef] [PubMed]
- Ismail, E.; Snousy, M.G.; Alexakis, D.E.; Abdelhalim, A.; Ahmed, M.S.; Elsayed, E. Diagnosis of Groundwater Quality in North Assiut Province, Egypt, for Drinking and Irrigation Uses by Applying Multivariate Statistics and Hydrochemical Methods. Water 2023, 15, 2812. [Google Scholar] [CrossRef]
- Salem, S.B.H.; Chkir, N.; Zouari, K.; Cognard-Plancq, A.L.; Valles, V.; Marc, V. Natural and artificial recharge investigation in the Zéroud Basin, Central Tunisia: Impact of Sidi Saad Dam storage. Environ. Earth Sci. 2011, 66, 1099–1110. [Google Scholar] [CrossRef]
- Gaagai, A.; Boudoukha, A.; Benaabidate, L. Failure Simulation of Babar Dam–Algeria and Its Impact on the Valley Downstream Section. J. Water Land Dev. 2020, 44, 75–89. [Google Scholar] [CrossRef]
- Meng, S.X.; Maynard, J. Use of statistical analysis to formulate conceptual models of geochemical behavior: Water chemical data from the Botucatu aquifer in São Paulo state, Brazil. J. Hydrol. 2001, 250, 78–97. [Google Scholar] [CrossRef]
- Farnham, I.M.; Johannesson, K.H.; Singh, A.K.; Hodge, V.F.; Stetzenbach, K.J. Factor analytical approaches for evaluating groundwater trace element chemistry data. Anal. Chim. Acta 2003, 490, 123–138. [Google Scholar] [CrossRef]
- Roubil, A.; El Ouali, A.; Bülbül, A.; Lahrach, A.; Mudry, J.; Mamouch, Y.; Essahlaoui, A.; El Hmaidi, A.; El Ouali, A. Groundwater Hydrochemical and Isotopic Evolution from High Atlas Jurassic Limestones to Errachidia Cretaceous Basin (Southeastern Morocco). Water 2022, 14, 1747. [Google Scholar] [CrossRef]
- Lu, Y.; Tang, C.; Chen, J.; Chen, J. Groundwater Recharge and Hydrogeochemical Evolution in Leizhou Peninsula, China. J. Chem. 2015, 2015, 1–12. [Google Scholar] [CrossRef]
- Yang, M.; Zhao, A.; Ke, H.; Chen, H. Geo-Environmental Factors’ Influence on the Prevalence and Distribution of Dental Fluorosis: Evidence from Dali County, Northwest China. Sustainability 2023, 15, 1871. [Google Scholar] [CrossRef]
- Kumar, P.J.S.; James, E.J. Geostatistical and geochemical model-assisted hydrogeochemical pattern recognition along the groundwater flow paths in Coimbatore district, South India. Environ. Dev. Sustain. 2017, 21, 369–384. [Google Scholar] [CrossRef]
- Gaagai, A.; Boudoukha, A.; Boumezbeur, A.; Benaabidate, L. Hydrochemical characterization of surface water in the Babar watershed (Algeria) using environmetric techniques and time series analysis. Int. J. River Basin Manag. 2017, 15, 361–372. [Google Scholar] [CrossRef]
- Shakeri, A.; Ghoreyshinia, S.; Mehrabi, B. Surface and Groundwater Quality in Taftan Geothermal Field, SE Iran. Water Qual. Expo. Heal. 2014, 7, 205–218. [Google Scholar] [CrossRef]
- Gad, M.; El-Hendawy, S.; Al-Suhaibani, N.; Tahir, M.U.; Mubushar, M.; Elsayed, S. Combining Hydrogeochemical Characterization and a Hyperspectral Reflectance Tool for Assessing Quality and Suitability of Two Groundwater Resources for Irrigation in Egypt. Water 2020, 12, 2169. [Google Scholar] [CrossRef]
- Elsayed, S.; Hussein, H.; Moghanm, F.S.; Khedher, K.M.; Eid, E.M.; Gad, M. Application of Irrigation Water Quality Indices and Multivariate Statistical Techniques for Surface Water Quality Assessments in the Northern Nile Delta, Egypt. Water 2020, 12, 3300. [Google Scholar] [CrossRef]
- Zhai, Y.; Zheng, F.; Zhao, X.; Xia, X.; Teng, Y. Identification of hydrochemical genesis and screening of typical groundwater pollutants impacting human health: A case study in Northeast China. Environ. Pollut. 2019, 252, 1202–1215. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Du, D.; Ji, D.; Bai, Y.; Jiang, W. Multivariate Analysis of Soil Salinity in a Semi-Humid Irrigated District of China: Concern about a Recent Water Project. Water 2020, 12, 2104. [Google Scholar] [CrossRef]
- Liu, S.; Li, H.; Yang, J.; Ma, M.; Shang, J.; Tang, Z.; Liu, G. Using Self-Organizing Map and Multivariate Statistical Methods for Groundwater Quality Assessment in the Urban Area of Linyi City, China. Water 2023, 15, 3463. [Google Scholar] [CrossRef]
- Piper, A.M. A graphic procedure in the geochemical interpretation of water-analyses. Eos Trans. Am. Geophys. Union 1944, 25, 914–928. [Google Scholar] [CrossRef]
- Gad, M.; Saad, A. Hydrogeochemical evaluation of fractured Limestone aquifer by applying a geochemical model in eastern Nile Valley, Egypt. Environ. Earth Sci. 2017, 76, 1–11. [Google Scholar] [CrossRef]
- Parra, V.; Muñoz, E.; Arumí, J.L.; Medina, Y. Analysis of the Behavior of Groundwater Storage Systems at Different Time Scales in Basins of South Central Chile: A Study Based on Flow Recession Records. Water 2023, 15, 2503. [Google Scholar] [CrossRef]
- Al-Ruwaih, F.M. Hydrogeology and Groundwater Geochemistry of the Clastic Aquifer and Its Assessment for Irrigation, Southwest Kuwait. In Aquifers–Matrix and Fluids; IntechOpen Limited: London, UK, 2018. [Google Scholar] [CrossRef]
- Flores, Y.G.; Eid, M.H.; Szűcs, P.; Szőcs, T.; Fancsik, T.; Szanyi, J.; Kovács, B.; Markos, G.; Újlaki, P.; Tóth, P.; et al. Integration of Geological, Geochemical Modelling and Hydrodynamic Condition for Understanding the Geometry and Flow Pattern of the Aquifer System, Southern Nyírség–Hajdúság, Hungary. Water 2023, 15, 2888. [Google Scholar] [CrossRef]
- Al-Mashreki, M.H.; Eid, M.H.; Saeed, O.; Székács, A.; Szűcs, P.; Gad, M.; Abukhadra, M.R.; AlHammadi, A.A.; Alrakhami, M.S.; Alshabibi, M.A.; et al. Integration of Geochemical Modeling, Multivariate Analysis, and Irrigation Indices for Assessing Groundwater Quality in the Al-Jawf Basin, Yemen. Water 2023, 15, 1496. [Google Scholar] [CrossRef]
- Eid, M.H.; Elbagory, M.; Tamma, A.A.; Gad, M.; Elsayed, S.; Hussein, H.; Moghanm, F.S.; Omara, A.E.-D.; Kovács, A.; Péter, S. Evaluation of Groundwater Quality for Irrigation in Deep Aquifers Using Multiple Graphical and Indexing Approaches Supported with Machine Learning Models and GIS Techniques, Souf Valley, Algeria. Water 2023, 15, 182. [Google Scholar] [CrossRef]
- Athamena, A.; Menani, M.R. Nitrogen flux and hydrochemical characteristics of the calcareous aquifer of the Zana plain, north east of Algeria. Arab. J. Geosci. 2018, 11, 356. [Google Scholar] [CrossRef]
- Aravinthasamy, P.; Karunanidhi, D.; Rao, N.S.; Subramani, T.; Srinivasamoorthy, K. Irrigation risk assessment of groundwater in a non-perennial river basin of South India: Implication from irrigation water quality index (IWQI) and geographical information system (GIS) approaches. Arab. J. Geosci. 2020, 13, 1–14. [Google Scholar] [CrossRef]
- Kawo, N.S.; Karuppannan, S. Groundwater quality assessment using water quality index and GIS technique in Modjo River Basin, central Ethiopia. J. Afr. Earth Sci. 2018, 147, 300–311. [Google Scholar] [CrossRef]
- Nagaraju, A.; Muralidhar, P.; Sreedhar, Y. Hydrogeochemistry and Groundwater Quality Assessment of Rapur Area, Andhra Pradesh, South India. J. Geosci. Environ. Prot. 2016, 04, 88–99. [Google Scholar] [CrossRef]
- El Osta, M.; Hussein, H.; Tomas, K. Numerical Simulation of Groundwater Flow and Vulnerability in Wadi El-Natrun Depression and Vicinities, West Nile Delta, Egypt. J. Geol. Soc. India 2018, 92, 235–247. [Google Scholar] [CrossRef]
- Meireles, A.C.M.; de Andrade, E.M.; Chaves, L.C.G.; Frischkorn, H.; Crisostomo, L.A. A new proposal of the classification of irrigation water. Rev. Ciência Agronômica 2010, 41, 349–357. [Google Scholar] [CrossRef]
- Gharbi, A.; Ibn Ali, Z.; Zairi, M. Groundwater suitability for drinking and agriculture purposes using irrigation water quality index and multivariate analysis: Case of Sidi Bouzid aquifer, central Tunisia. Environ. Earth Sci. 2019, 78, 692. [Google Scholar] [CrossRef]
- Khouni, I.; Louhichi, G.; Ghrabi, A. Use of GIS based Inverse Distance Weighted interpolation to assess surface water quality: Case of Wadi El Bey, Tunisia. Environ. Technol. Innov. 2021, 24, 101892. [Google Scholar] [CrossRef]
- Beltrán, N.; Duarte-Mermoud, M.; Salah, S.; Bustos, M.; Peña-Neira, A.; Loyola, E.; Jalocha, J. Feature selection algorithms using Chilean wine chromatograms as examples. J. Food Eng. 2005, 67, 483–490. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Schulze, F.; Wolf, H.; Jansen, H.; van der Veer, P. Applications of artificial neural networks in integrated water management: Fiction or future? Water Sci. Technol. 2005, 52, 21–31. [Google Scholar] [CrossRef] [PubMed]
- ElMasry, G.; Sun, D.-W.; Allen, P. Near-infrared hyperspectral imaging for predicting colour, pH and tenderness of fresh beef. J. Food Eng. 2012, 110, 127–140. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.-L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef]
- Glorfeld, L.W. A Methodology for simplification and interpretation of backpropagation-based neural network models. Expert Syst. Appl. 1996, 10, 37–54. [Google Scholar] [CrossRef]
- Melis, G.; Dyer, C.; Blunsom, P. On the State of the Art of Evaluation in Neural Language Models. arXiv 2017. [Google Scholar] [CrossRef]
- Bergstra, J.; Yamins, D.; Cox, D. Making a Science of Model Search: Hyperparameter Optimization in Hundreds of Dimensions for Vision Architectures. In Proceedings of the International Conference on Machine Learning, PMLR, Atlanta, GA, USA, 17–19 June 2013; pp. 115–123. [Google Scholar]
- Wu, J.; Chen, X.-Y.; Zhang, H.; Xiong, L.-D.; Lei, H.; Deng, S.-H. Hyperparameter optimization for machine learning models based on Bayesian optimization b. J. Electron. Sci. 2019, 17, 26–40. [Google Scholar] [CrossRef]
- Khomsi, S.; Ben Jemia, M.G.; de Lamotte, D.F.; Maherssi, C.; Echihi, O.; Mezni, R. An overview of the Late Cretaceous–Eocene positive inversions and Oligo-Miocene subsidence events in the foreland of the Tunisian Atlas: Structural style and implications for the tectonic agenda of the Maghrebian Atlas system. Tectonophysics 2009, 475, 38–58. [Google Scholar] [CrossRef]
- Soumaya, A.; Ben Ayed, N.; Delvaux, D.; Ghanmi, M. Spatial variation of present-day stress field and tectonic regime in Tunisia and surroundings from formal inversion of focal mechanisms: Geodynamic implications for central Mediterranean. Tectonics 2015, 34, 1154–1180. [Google Scholar] [CrossRef]
- Gharbi, M.; Bellier, O.; Masrouhi, A.; Espurt, N. Recent spatial and temporal changes in the stress regime along the southern Tunisian Atlas front and the Gulf of Gabes: New insights from fault kinematics analysis and seismic profiles. Tectonophysics 2014, 626, 120–136. [Google Scholar] [CrossRef]
- Bahrouni, N.; Bouaziz, S.; Soumaya, A.; Ben Ayed, N.; Attafi, K.; Houla, Y.; El Ghali, A.; Rebai, N. Neotectonic and seismotectonic investigation of seismically active regions in Tunisia: A multidisciplinary approach. J. Seism. 2013, 18, 235–256. [Google Scholar] [CrossRef]
- Bédir, M. Mécanismes Géodynamiques Des Bassins Associés Aux Couloirs de Coulissements de La Marge Atlasique de La Tunisie: Seismo-Stratigraphie, Séismo-Tectonique et Implications Pétrolières. Ph.D. Thesis, Faculté des Sciences Mathématiques, Physiques et Naturelles de Tunis, Tunis, Tunisia, 1995. [Google Scholar]
- Lachaal, F.; Azaiez, H.; Bruni, R.; Gabtni, H.; Bedir, M. Aquifer Structuring and Hydrogeological Investigation in North African Regions Using Geophysical Methods: Case Study of the Aquifer System in the Kairouan Plain (Central Tunisia). In Geology of North Africa and the Mediterranean: Sedimentary Basins and Georesources; Springer: Cham, Switzerland, 2023; pp. 247–260. [Google Scholar] [CrossRef]
- Bédir, M.; El Asmi, A.M. New insights into Upper Cretaceous hydrocarbon traps of platform-basin flanks in the Sahel Eastern Tunisian petroleum province: Inferred optimal hydrocarbon reserves accumulations. J. Pet. Sci. Eng. 2023, 220. [Google Scholar] [CrossRef]
- Nazoumou, Y. Modélisation de La Recharge Artificielle Des Nappes de La Plaine de Kairouan. Ph.D. Thesis, Ecole Nationale d’Ingénieurs de Tunis, Tunis, Tunisia, 1996. [Google Scholar]
- Castany, G.; Mathieu, G. Les Fosses d’effondrement de Tunisie: Géologie & Hydrologie. In Régence de Tunis (Protectorat Français), Direction des Travaux Publics; Impr. S.A.P.I. Tunis: Tunis, Tunisia, 1948. [Google Scholar]
- Besbes, M. Etude Hydrogéologique de La Plaine de Kairouan Sur Modèles Mathématiques.; DRE: Tunis, Tunisia, 1975. [Google Scholar]
- Chaudhry, A.K.; Kumar, K.; Alam, M.A. Groundwater contamination characterization using multivariate statistical analysis and geostatistical method. Water Supply 2019, 19, 2309–2322. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Jha, P.V.N.; Sahoo, S.K.; Ranjan, R.K. Groundwater quality and its suitability for drinking and irrigational purpose in Bhojpur district: Middle Gangetic plain of Bihar, India. Water Supply 2022, 22, 7072–7084. [Google Scholar] [CrossRef]
- Gaagai, A. Etude de l’évolution de la qualité des eaux du barrage de Babar (Sud-Est Algérien) et l’impact de la rupture de la digue sur l’environnement. Ph.D. Thesis, University of Batna 2, Batna, Algeria, 2017. [Google Scholar] [CrossRef]
- Dash, S.; Kalamdhad, A.S. Hydrochemical dynamics of water quality for irrigation use and introducing a new water quality index incorporating multivariate statistics. Environ. Earth Sci. 2021, 80, 1–21. [Google Scholar] [CrossRef]
- Athamena, A.; Gaagai, A.; Aouissi, H.A.; Burlakovs, J.; Bencedira, S.; Zekker, I.; Krauklis, A.E. Chemometrics of the Environment: Hydrochemical Characterization of Groundwater in Lioua Plain (North Africa) Using Time Series and Multivariate Statistical Analysis. Sustainability 2022, 15, 20. [Google Scholar] [CrossRef]
- Ghodbane, M.; Benaabidate, L.; Boudoukha, A.; Gaagai, A.; Adjissi, O.; Chaib, W.; Aouissi, H.A. Analysis of Groundwater Quality in the Lower Soummam Valley, North-East of Algeria. J. Water Land Dev. 2022, 54, 1–12. [Google Scholar]
- Hinge, G.; Bharali, B.; Baruah, A.; Sharma, A. Integrated groundwater quality analysis using Water Quality Index, GIS and multivariate technique: A case study of Guwahati City. Environ. Earth Sci. 2022, 81, 1–15. [Google Scholar] [CrossRef]
- Elsayed, S.; Gad, M.; Farouk, M.; Saleh, A.H.; Hussein, H.; Elmetwalli, A.H.; Elsherbiny, O.; Moghanm, F.S.; Moustapha, M.E.; Taher, M.A.; et al. Using Optimized Two and Three-Band Spectral Indices and Multivariate Models to Assess Some Water Quality Indicators of Qaroun Lake in Egypt. Sustainability 2021, 13, 10408. [Google Scholar] [CrossRef]
- Patil, V.B.B.; Pinto, S.M.; Govindaraju, T.; Hebbalu, V.S.; Bhat, V.; Kannanur, L.N. Multivariate statistics and water quality index (WQI) approach for geochemical assessment of groundwater quality—a case study of Kanavi Halla Sub-Basin, Belagavi, India. Environ. Geochem. Heal. 2020, 42, 2667–2684. [Google Scholar] [CrossRef]
- Schoeller, H. Geochemistry of Groundwater. In Groundwater Studies—An International Guide for Research and Practice; UNESCO: Paris, France, 1977; pp. 1–18. [Google Scholar]
- Dimri, D.; Daverey, A.; Kumar, A.; Sharma, A. Monitoring water quality of River Ganga using multivariate techniques and WQI (Water Quality Index) in Western Himalayan region of Uttarakhand, India. Environ. Nanotechnology, Monit. Manag. 2020, 15, 100375. [Google Scholar] [CrossRef]
- Pak, H.Y.; Chuah, C.J.; Tan, M.L.; Yong, E.L.; Snyder, S.A. A framework for assessing the adequacy of Water Quality Index – Quantifying parameter sensitivity and uncertainties in missing values distribution. Sci. Total. Environ. 2020, 751, 141982. [Google Scholar] [CrossRef] [PubMed]
- Richards, L.A. Diagnosis and Improvement of Saline and Alkali Soils; US Department of Agriculture: Washington, DC, USA, 1954; Volume 78, ISBN 0038-075X. [Google Scholar]
- Ravikumar, P.; Mehmood, M.A.; Somashekar, R.K. Water quality index to determine the surface water quality of Sankey tank and Mallathahalli lake, Bangalore urban district, Karnataka, India. Appl. Water Sci. 2013, 3, 247–261. [Google Scholar] [CrossRef]
- Eaton, F.M. SIGNIFICANCE OF CARBONATES IN IRRIGATION WATERS. Soil Sci. 1950, 69, 123–134. [Google Scholar] [CrossRef]
- Doneen, L.D. Water Quality for Agriculture, Department of Irrigation; University of California: Davis, CA, USA, 1964; 48. [Google Scholar]
- Schalkoff, R.J. Artificial Neural Networks; McGraw-Hill Higher Education: New York, NY, USA, 1997; ISBN 0-07-057118-X. [Google Scholar]
- Haykin, S. Self-Organizing Maps. In Neural Networks–A Comprehensive Foundation; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1999; pp. 443–483. [Google Scholar]
- Li, J.; Yoder, R.E.; Odhiambo, L.O.; Zhang, J. Simulation of nitrate distribution under drip irrigation using artificial neural networks. Irrig. Sci. 2004, 23, 29–37. [Google Scholar] [CrossRef]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A Limited Memory Algorithm for Bound Constrained Optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Elsayed, S.; Gupta, M.; Chaudhary, G.; Taneja, S.; Gaur, H.; Gad, M.; Hamdy Eid, M.; Kovács, A.; Péter, S.; Gaagai, A.; et al. Interpretation the Influence of Hydrometeorological Variables on Soil Temperature Prediction Using the Potential of Deep Learning Model. Knowl. Based Eng. Sci. 2023, 4, 55–77. [Google Scholar] [CrossRef]
- Bai, B.; Rao, D.; Chang, T.; Guo, Z. A nonlinear attachment-detachment model with adsorption hysteresis for suspension-colloidal transport in porous media. J. Hydrol. 2019, 578, 124080. [Google Scholar] [CrossRef]
- Yang, M.; Wang, H.; Hu, K.; Yin, G.; Wei, Z. IA-Net$:$ An Inception–Attention-Module-Based Network for Classifying Underwater Images From Others. IEEE J. Ocean Eng. 2022, 47, 704–717. [Google Scholar] [CrossRef]
- Nong, X.; Lai, C.; Chen, L.; Shao, D.; Zhang, C.; Liang, J. Prediction modelling framework comparative analysis of dissolved oxygen concentration variations using support vector regression coupled with multiple feature engineering and optimization methods: A case study in China. Ecol. Indic. 2023, 146. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, San Francisco, CA, USA, 13 August 2016; pp. 785–794. [Google Scholar]
- Chen, R.-C.; Caraka, R.E.; Arnita, N.E.G.; Pomalingo, S.; Rachman, A.; Toharudin, T.; Tai, S.-K.; Pardamean, B. An End to End of Scalable Tree Boosting System. Sylwan 2020, 165, 1–11. [Google Scholar]
- Lee, C.; Lee, S. Exploring the Contributions by Transportation Features to Urban Economy: An Experiment of a Scalable Tree-Boosting Algorithm with Big Data. Land 2022, 11, 577. [Google Scholar] [CrossRef]
- Chadha, D.K. A proposed new diagram for geochemical classification of natural waters and interpretation of chemical data. Hydrogeol. J. 1999, 7, 431–439. [Google Scholar] [CrossRef]
- Vasanthavigar, M.; Srinivasamoorthy, K.; Prasanna, M.V. Evaluation of groundwater suitability for domestic, irrigational, and industrial purposes: A case study from Thirumanimuttar river basin, Tamilnadu, India. Environ. Monit. Assess. 2011, 184, 405–420. [Google Scholar] [CrossRef]
- Gibbs, R.J. Mechanisms Controlling World Water Chemistry. Science 1970, 170, 1088–1090. [Google Scholar] [CrossRef]
- Rakotondrabe, F.; Ngoupayou, J.R.N.; Mfonka, Z.; Rasolomanana, E.H.; Abolo, A.J.N.; Ako, A.A. Water quality assessment in the Bétaré-Oya gold mining area (East-Cameroon): Multivariate Statistical Analysis approach. Sci. Total. Environ. 2018, 610-611, 831–844. [Google Scholar] [CrossRef]
- Malone, B.P.; Styc, Q.; Minasny, B.; McBratney, A.B. Digital soil mapping of soil carbon at the farm scale: A spatial downscaling approach in consideration of measured and uncertain data. Geoderma 2017, 290, 91–99. [Google Scholar] [CrossRef]
- Saggi, M.K.; Jain, S. Reference evapotranspiration estimation and modeling of the Punjab Northern India using deep learning. Comput. Electron. Agric. 2019, 156, 387–398. [Google Scholar] [CrossRef]
- Ayers, R.S.; Westcot, D.W. Water Quality for Agriculture; FAO Irrigation and Drainage Paper; FAO: Rome, Italy, 1985; ISBN 978-92-5-102263-4. [Google Scholar]
- Moussa, R.S.; Alma, M.M.M.; Laouli, M.S.; Natatou, I.; Habou, I. Caractérisation physico-chimique des eaux des aquifères du Continental Intercalaire/Hamadien et du Continentalsiems Terminal de la région de Zinder (Niger). Int. J. Biol. Chem. Sci. 2019, 12, 2395. [Google Scholar] [CrossRef]
- Ayers, R.; Westcott, D. Water Quality for Agriculture. FAO Irrigation and Drainage Paper 29 Rev. 1; FAO: Rome, Italy, 1994. [Google Scholar]
- Mhamdi, A.; Moussaoui, I.; Khalfi, C.; Tarki, M.; Dassi, L. Assessment of groundwater mineralization processes in the Garâat Douza-Tebeddit shallow aquifer, Southwestern Tunisia: An integrated geoelectrical and hydrochemical approach. Carbonates Evaporites 2022, 37, 1–16. [Google Scholar] [CrossRef]
- Ben Moussa, A.; Chandoul, S.; Mzali, H.; Salem, S.B.H.; Elmejri, H.; Zouari, K.; Hafiane, A.; Mrabet, H. Hydrogeochemistry and evaluation of groundwater suitability for irrigation purpose in the Mornag region, northeastern Tunisia. Environ. Dev. Sustain. 2020, 23, 2698–2718. [Google Scholar] [CrossRef]
- Gaagai, A.; Aouissi, H.A.; Bencedira, S.; Hinge, G.; Athamena, A.; Heddam, S.; Gad, M.; Elsherbiny, O.; Elsayed, S.; Eid, M.H.; et al. Application of Water Quality Indices, Machine Learning Approaches, and GIS to Identify Groundwater Quality for Irrigation Purposes: A Case Study of Sahara Aquifer, Doucen Plain, Algeria. Water 2023, 15, 289. [Google Scholar] [CrossRef]
- Jacobson, A.; Wasserburg, G. Anhydrite and the Sr isotope evolution of groundwater in a carbonate aquifer. Chem. Geol. 2005, 214, 331–350. [Google Scholar] [CrossRef]
- El Mejri, H.; Ben Moussa, A.; Zouari, K. The use of hydrochemical and environmental isotopic tracers to understand the functioning of the aquifer system in the Bou Hafna and Haffouz regions, Central Tunisia. Quat. Int. 2014, 338, 88–98. [Google Scholar] [CrossRef]
- Blubaugh, D.J.; Atamian, M.; Babcock, G.T.; Golbeck, J.H.; Cheniae, G.M. Photoinhibition of hydroxylamine-extracted photosystem II membranes: Identification of the sites of photodamage. Biochemistry 1991, 30, 7586–7597. [Google Scholar] [CrossRef]
- Gamvroula, D.; Alexakis, D.; Stamatis, G. Diagnosis of groundwater quality and assessment of contamination sources in the Megara basin (Attica, Greece). Arab. J. Geosci. 2012, 6, 2367–2381. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, J.; Long, A.; Xu, S.; Guo, T.; Gu, X.; Deng, X.; Zhang, P. Hydrochemical Characteristics and Formation Mechanism of Quaternary Groundwater in Baoshan Basin, Western Yunnan, China. Water 2023, 15, 2736. [Google Scholar] [CrossRef]
- Gad, M.; El-Safa, M.M.A.; Farouk, M.; Hussein, H.; Alnemari, A.M.; Elsayed, S.; Khalifa, M.M.; Moghanm, F.S.; Eid, E.M.; Saleh, A.H. Integration of Water Quality Indices and Multivariate Modeling for Assessing Surface Water Quality in Qaroun Lake, Egypt. Water 2021, 13, 2258. [Google Scholar] [CrossRef]
- El Osta, M.; Masoud, M.; Alqarawy, A.; Elsayed, S.; Gad, M. Groundwater Suitability for Drinking and Irrigation Using Water Quality Indices and Multivariate Modeling in Makkah Al-Mukarramah Province, Saudi Arabia. Water 2022, 14, 483. [Google Scholar] [CrossRef]
- Qian, C.; Wu, X.; Mu, W.-P.; Fu, R.-Z.; Zhu, G.; Wang, Z.-R.; Wang, D.-D. Hydrogeochemical characterization and suitability assessment of groundwater in an agro-pastoral area, Ordos Basin, NW China. Environ. Earth Sci. 2016, 75, 1–16. [Google Scholar] [CrossRef]
- Wu, J.; Li, P.; Qian, H. Hydrochemical characterization of drinking groundwater with special reference to fluoride in an arid area of China and the control of aquifer leakage on its concentrations. Environ. Earth Sci. 2015, 73, 8575–8588. [Google Scholar] [CrossRef]
- Mustapha, A.; Aris, A.Z.; Ramli, M.F.; Juahir, H. Spatial-temporal variation of surface water quality in the downstream region of the Jakara River, north-western Nigeria: A statistical approach. J. Environ. Sci. Heal. Part A 2012, 47, 1551–1560. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Wu, J.; Qian, H. Assessment of groundwater quality for irrigation purposes and identification of hydrogeochemical evolution mechanisms in Pengyang County, China. Environ. Earth Sci. 2012, 69, 2211–2225. [Google Scholar] [CrossRef]
- RamyaPriya, R.; Elango, L. Evaluation of geogenic and anthropogenic impacts on spatio-temporal variation in quality of surface water and groundwater along Cauvery River, India. Environ. Earth Sci. 2017, 77, 2. [Google Scholar] [CrossRef]
- Todd, D.K.; Mays, L.W. Groundwater Hydrology; John Wiley & Sons: Hoboken, NJ, USA, 2004; ISBN 0-471-05937-4. [Google Scholar]
- Pyrcz, M.J.; Deutsch, C.V. Geostatistical Reservoir Modeling; Oxford University Press: Oxford, UK, 2014; ISBN 0-19-973144-6. [Google Scholar]
- Zhang, T.; Song, B.; Han, G.; Zhao, H.; Hu, Q.; Zhao, Y.; Liu, H. Effects of coastal wetland reclamation on soil organic carbon, total nitrogen, and total phosphorus in China: A meta-analysis. Land Degrad. Dev. 2023, 34, 3340–3349. [Google Scholar] [CrossRef]
- Prasad, A.; Kumar, D.; Singh, D. Effect of residual sodium carbonate in irrigation water on the soil sodication and yield of palmarosa (Cymbopogon martinni) and lemongrass (Cymbopogon flexuosus). Agric. Water Manag. 2001, 50, 161–172. [Google Scholar] [CrossRef]
- Wu, M.-L.; Wang, Y.-S. Using Chemometrics to Evaluate Anthropogenic Effects in Daya Bay, China. Estuar. Coast. Shelf Sci. 2007, 72, 732–742. [Google Scholar] [CrossRef]




| IWQIs | Formula | References |
|---|---|---|
| IWQI | [34] | |
| SAR | [68] | |
| Na % | [69] | |
| SSP | [70] | |
| PS | [71] | |
| RSC | [70] |
| Qi | SAR | EC (µs/cm) | HCO3− (meq/L) | Na+ (meq/L) | Cl− (meq/L) |
|---|---|---|---|---|---|
| 0–35 | SAR > 2 or SAR ≥ 12 | E C< 200 or EC ≥ 3000 | HCO3 < 1 or HCO3 ≥ 8.5 | Na < 2 or Na ≥ 9 | Cl < 1 or Cl ≥ 10 |
| 35–60 | 6 ≤ SAR < 12 | 1500 ≤ EC < 3000 | 4.5 ≤ HCO3 < 8.5 | 6 ≤ Na< 9 | 7 ≤ Cl < 10 |
| 60–85 | 3 ≤ SAR < 6 | 750 ≤ EC < 1500 | 1.5 ≤ HCO3 < 4.5 | 3 ≤ Na < 6 | 4 ≤ Cl < 7 |
| 85–100 | 2 ≤ SAR < 3 | 200 ≤ EC< 750 | 1 ≤ HCO3 < 1.5 | 2 ≤ Na < 3 | 1 ≤ Cl < 4 |
| Parameters | FAO * | Minimum | Maximum | Average | Standard Deviation |
|---|---|---|---|---|---|
| pH | 8.5 | 6.7 | 7.73 | 7.286 | 0.31 |
| TDS | 2000 | 969.43 | 3319 | 2203.133 | 542.43 |
| EC | 3000 | 1514.74 | 5185.93 | 3442.39 | 847.55 |
| K+ | 2 | 0.275 | 26.675 | 13.43 | 5.95 |
| Na+ | 919 | 99.86 | 663.8 | 357.77 | 109.15 |
| Ca2⁺ | 400 | 64.36 | 419.05 | 237.36 | 76.01 |
| Mg2⁺ | 60 | 24.25 | 156.2 | 99.03 | 26.21 |
| SO42– | 960 | 206.93 | 1121.13 | 764.20 | 230.01 |
| Cl− | 1036 | 149.80 | 997.55 | 512.20 | 180.72 |
| HCO₃− | 610 | 97.6 | 323.3 | 190.76 | 53.57 |
| Criteria | Min | Max | Mean | Range | Class | Number of Samples (%) |
|---|---|---|---|---|---|---|
| IWQI | 22.1 | 80.3 | 42.4 | 85–100 | No restriction | 0 (0%) |
| 70–85 | Low restriction | 1 (2.5%) | ||||
| 55–70 | Moderate restriction | 3 (7.5%) | ||||
| 40–55 | High restriction | 18 (45%) | ||||
| 0–40 | Severe restriction | 18 (45%) | ||||
| SAR | 1.8 | 8 | 5 | <10 | Excellent | 40 (100%) |
| 10–18 | Good | 0 (0%) | ||||
| 19–26 | Fair-to-poor | 0 (0%) | ||||
| >26 | Unsuitable | 0 (0%) | ||||
| Na% | 28.6 | 63.5 | 44.4 | <20% | Excellent | 4 (10%) |
| 21–40% | Good | 12 (30%) | ||||
| 41–60% | Permissible | 21 (52.5%) | ||||
| 61–80% | Doubtful | 3 (7.5%) | ||||
| >80% | Unsuitable | 0 (0%) | ||||
| SSP | 28.2 | 63 | 43.8 | <60 | Suitable | 37 (92.5%) |
| >60 | Unsuitable | 3 (7.5 %) | ||||
| PS | 6.9 | 39.2 | 22.4 | PS < 3.0 | Excellent-to-good | 0 (0%) |
| PS = 3.0–5.0 | Good-to-injurious | 0 (0%) | ||||
| PS > 5.0 | Injurious-to-unsatisfactory | 40 (100%) | ||||
| RSC | −28.7 | 0.1 | −16.8 | <1.25 | Good | 40 (100%) |
| 1.25−2.5 | Doubtful | 0 (0%) | ||||
| >2.5 | Unsuitable | 0 (0%) |
| IWQIs | Optimal Features | Hyperparameters | Training | Cross-Validation | Testing | |||
|---|---|---|---|---|---|---|---|---|
| (h1, h2, Fn) | R2 | RMSE | R2 | RMSE | R2 | RMSE | ||
| IWQI | CO3, K, Ca, EC, Mg, Cl, Na, HCO3, SO4 | (8, 5, relu) | 0.999 | 0.375 | 0.917 | 2.259 | 0.823 | 3.168 |
| SAR | Ca, Mg, Na | (10, 9, tanh) | 0.999 | 0.003 | 0.999 | 0.012 | 0.999 | 0.005 |
| Na% | Cl, SO4, K, Mg, Ca, Na | (12, 13, tanh) | 0.999 | 0.015 | 0.995 | 0.261 | 0.999 | 0.167 |
| SSP | Ca, Mg, Na | (10, 1, tanh) | 0.999 | 0.023 | 0.999 | 0.094 | 0.999 | 0.056 |
| PS | SO4, CO3, Cl | (12, 11, relu) | 0.999 | 0.003 | 0.999 | 0.003 | 0.999 | 0.003 |
| RSC | HCO3, Cl, Mg, Ca | (10, 11, identity) | 0.999 | 0.003 | 0.999 | 0.003 | 0.999 | 0.003 |
| IWQIs | Optimal Features | Hyperparameters | Training | Cross-Validation | Testing | |||
|---|---|---|---|---|---|---|---|---|
| (LR, Ne, Md) | R2 | RMSE | R2 | RMSE | R2 | RMSE | ||
| IWQI | EC, Na, Cl | (0.1, 500, 9) | 0.999 | 0.001 | 0.823 | 3.625 | 0.913 | 2.217 |
| SAR | Ca, Na, SO4 | (0.1, 100, 3) | 0.999 | 0.039 | 0.682 | 0.479 | 0.888 | 0.371 |
| Na% | Na, Ca | (0.1, 500, 7) | 0.999 | 0.001 | 0.614 | 3.522 | 0.786 | 2.212 |
| SSP | Na, Ca | (0.1, 500, 7) | 0.999 | 0.001 | 0.615 | 3.450 | 0.803 | 2.118 |
| PS | SO4, Na, Cl, EC | (0.01, 1000, 7) | 0.999 | 0.031 | 0.947 | 1.192 | 0.689 | 2.615 |
| RSC | Mg, Ca | (0.1, 500, 3) | 0.999 | 0.002 | 0.917 | 1.191 | 0.874 | 1.161 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salem, S.B.H.; Gaagai, A.; Ben Slimene, I.; Moussa, A.B.; Zouari, K.; Yadav, K.K.; Eid, M.H.; Abukhadra, M.R.; El-Sherbeeny, A.M.; Gad, M.; et al. Applying Multivariate Analysis and Machine Learning Approaches to Evaluating Groundwater Quality on the Kairouan Plain, Tunisia. Water 2023, 15, 3495. https://doi.org/10.3390/w15193495
Salem SBH, Gaagai A, Ben Slimene I, Moussa AB, Zouari K, Yadav KK, Eid MH, Abukhadra MR, El-Sherbeeny AM, Gad M, et al. Applying Multivariate Analysis and Machine Learning Approaches to Evaluating Groundwater Quality on the Kairouan Plain, Tunisia. Water. 2023; 15(19):3495. https://doi.org/10.3390/w15193495
Chicago/Turabian StyleSalem, Sarra Bel Haj, Aissam Gaagai, Imed Ben Slimene, Amor Ben Moussa, Kamel Zouari, Krishna Kumar Yadav, Mohamed Hamdy Eid, Mostafa R. Abukhadra, Ahmed M. El-Sherbeeny, Mohamed Gad, and et al. 2023. "Applying Multivariate Analysis and Machine Learning Approaches to Evaluating Groundwater Quality on the Kairouan Plain, Tunisia" Water 15, no. 19: 3495. https://doi.org/10.3390/w15193495
APA StyleSalem, S. B. H., Gaagai, A., Ben Slimene, I., Moussa, A. B., Zouari, K., Yadav, K. K., Eid, M. H., Abukhadra, M. R., El-Sherbeeny, A. M., Gad, M., Farouk, M., Elsherbiny, O., Elsayed, S., Bellucci, S., & Ibrahim, H. (2023). Applying Multivariate Analysis and Machine Learning Approaches to Evaluating Groundwater Quality on the Kairouan Plain, Tunisia. Water, 15(19), 3495. https://doi.org/10.3390/w15193495














