Impact of Elastic Diaphragm Hardness and Structural Parameters on the Hydraulic Performance of Automatic Flushing Valve
Abstract
:1. Introduction
2. Materials and Methods
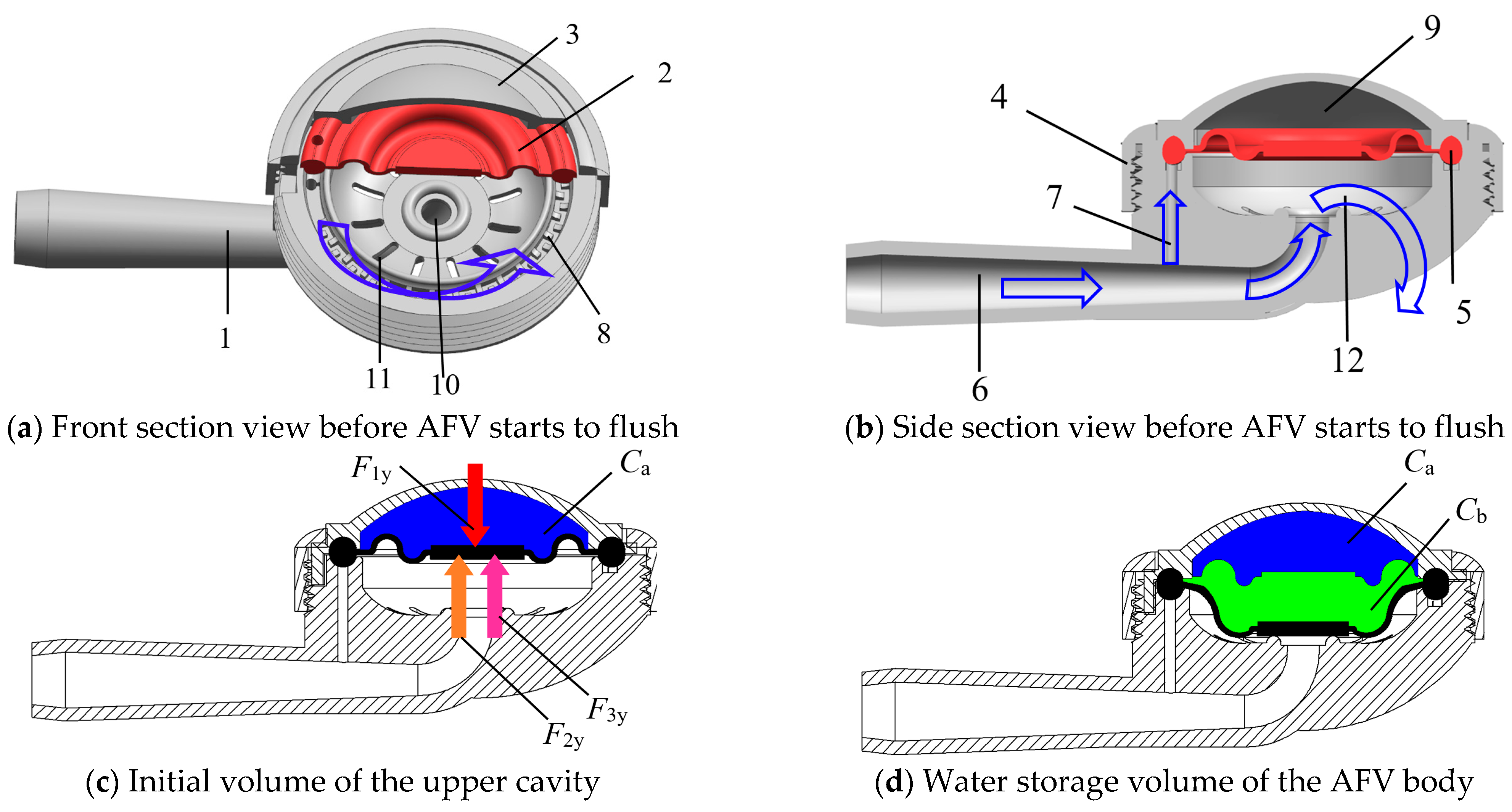
2.1. The Working Principle of the Automatic Flushing Valve
2.2. Analysis of Parameters Affecting the Hydraulic Performance of AFVs
2.2.1. Experimental Design
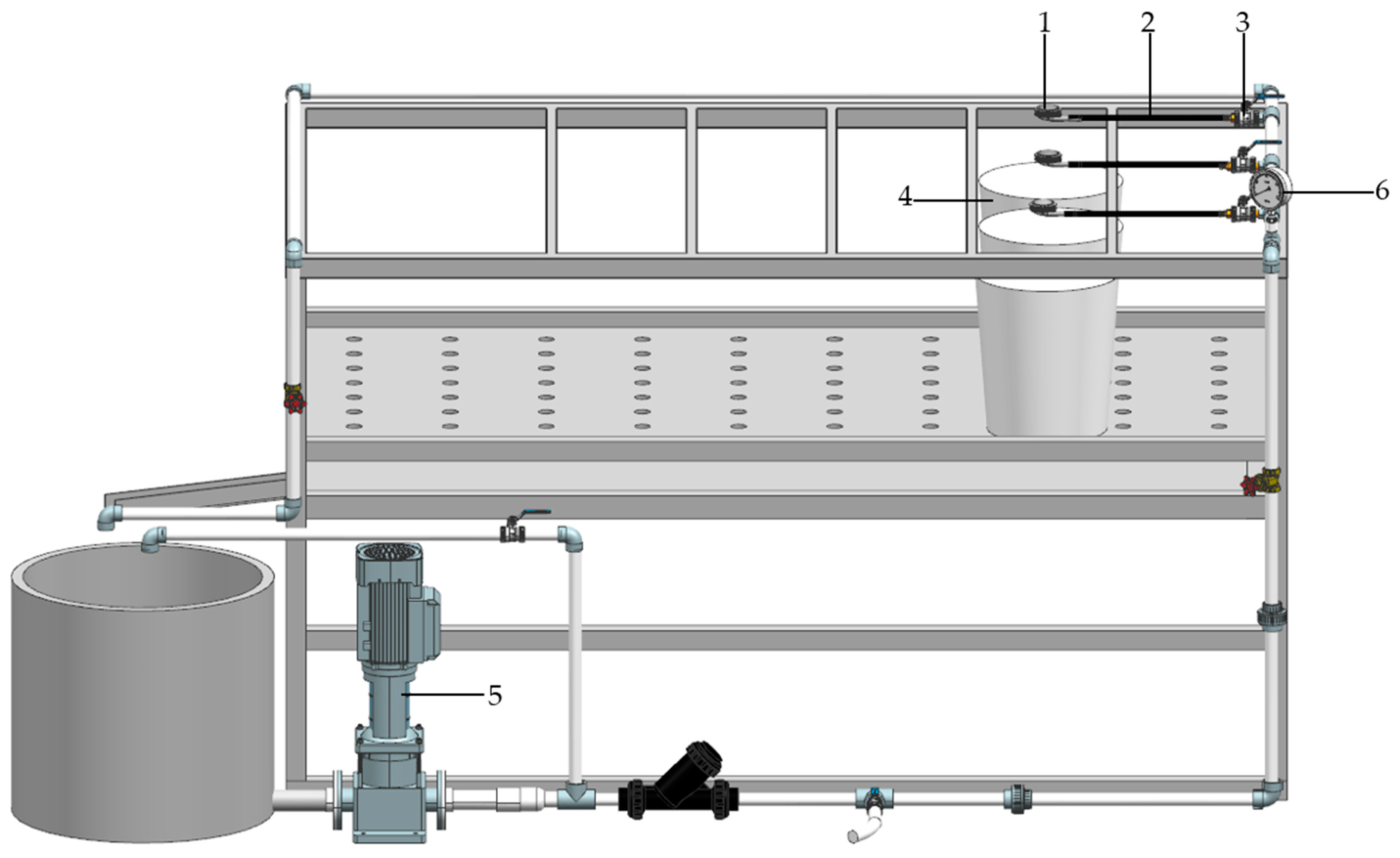
2.2.2. Experimental Method and Measurement Index
2.3. Data Analysis
3. Results and Analysis
3.1. Hydraulic Performance Experimental Results
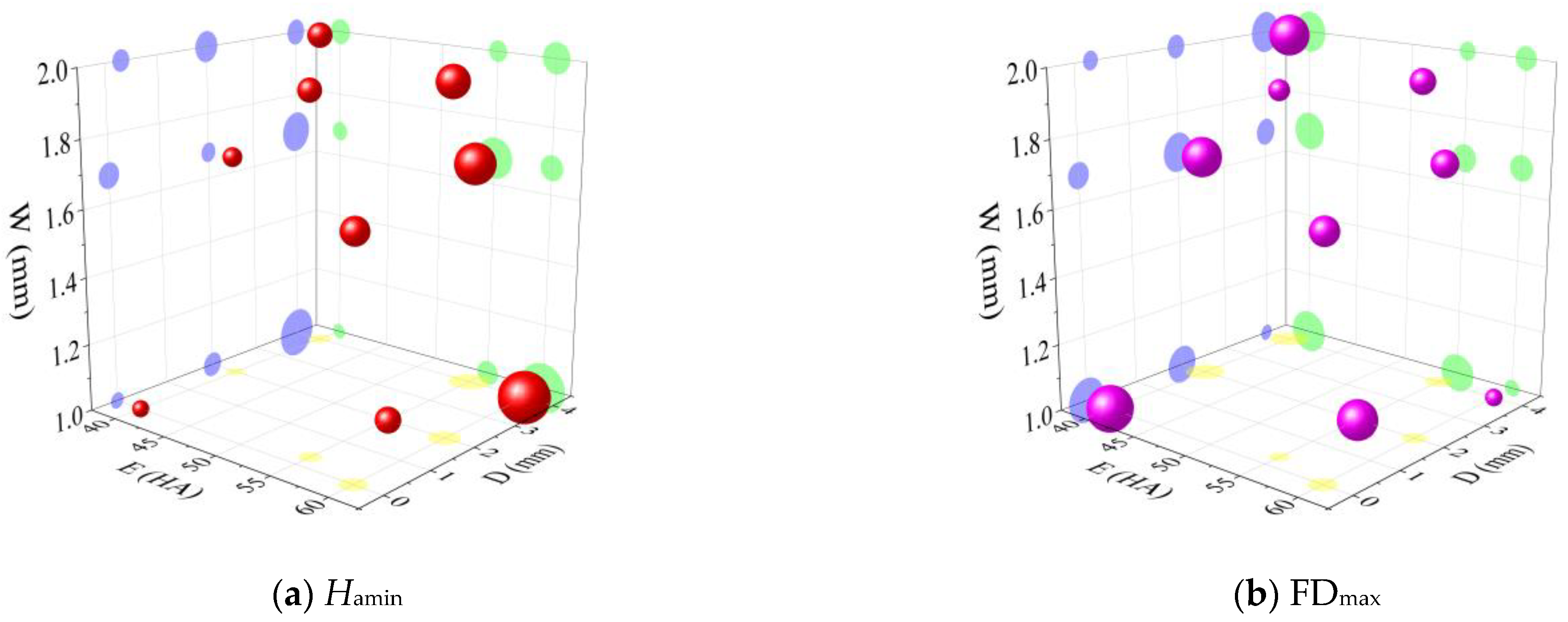
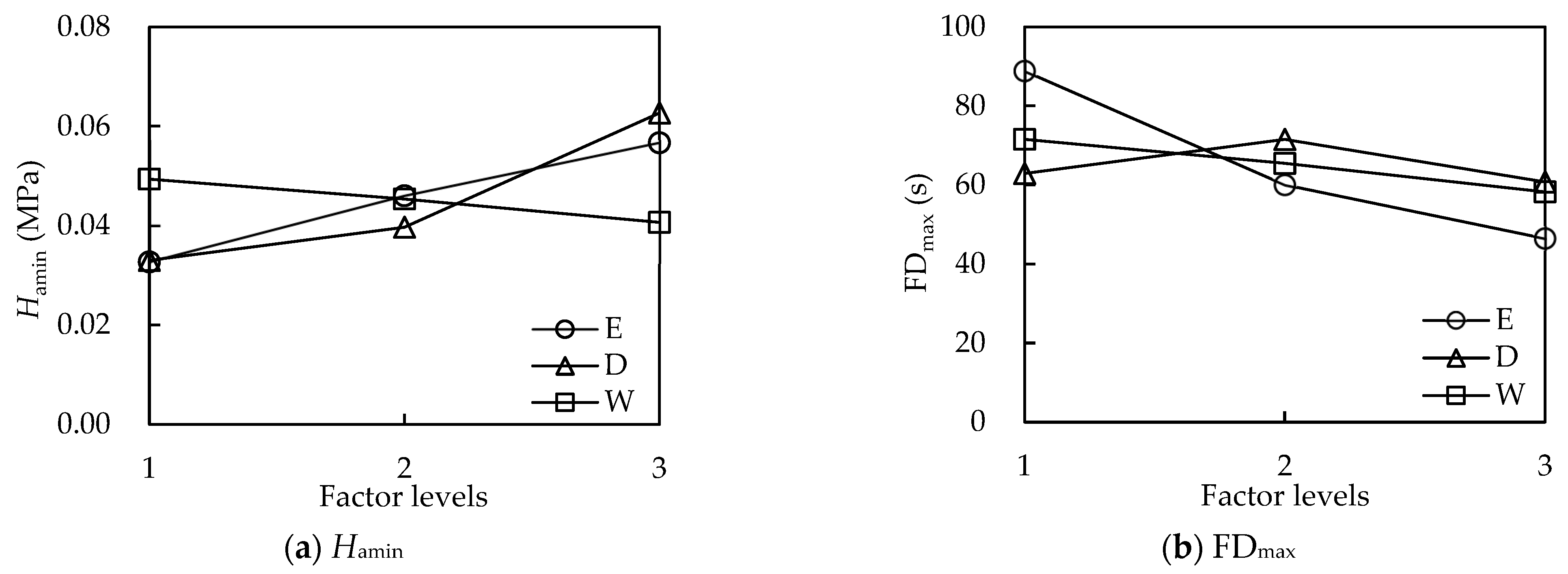
3.2. Analysis of the Hydraulic Performance Range of AFVs
3.3. Variance Analysis of the Hydraulic Performance of the Automatic Flushing Valve
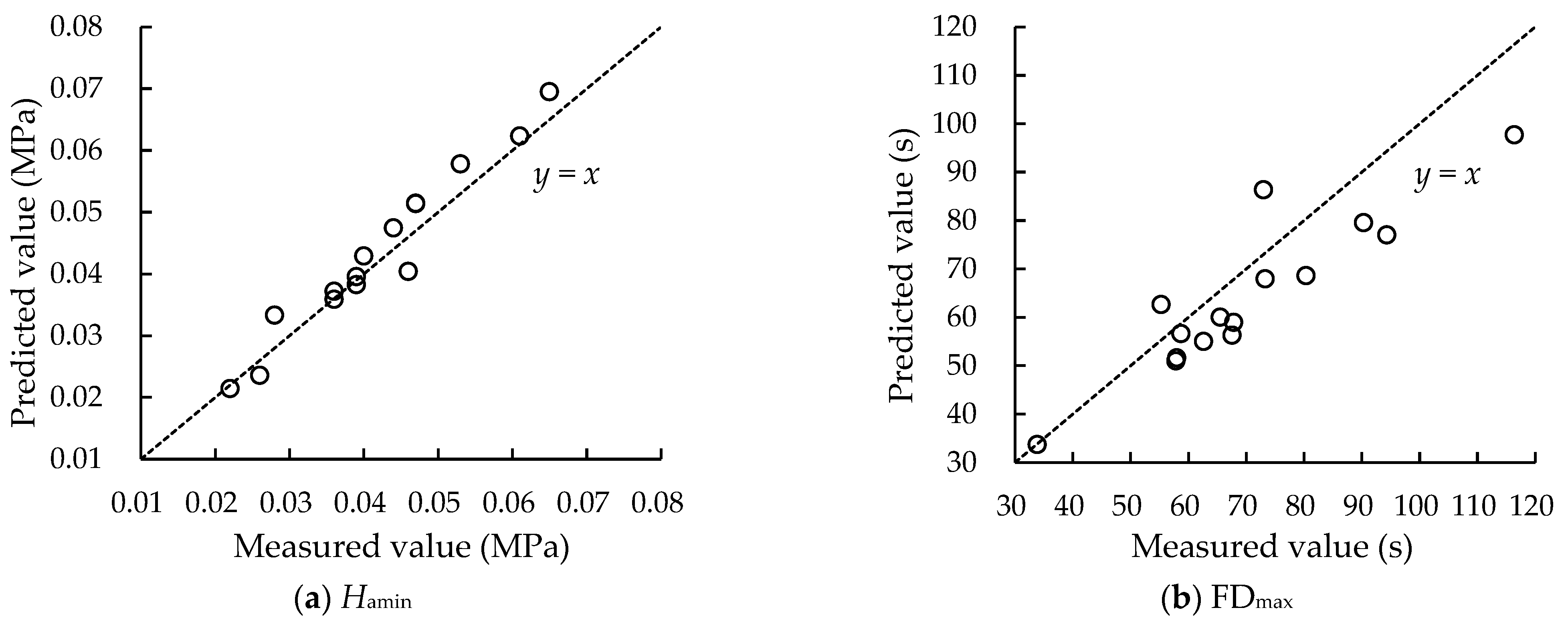
3.4. Construction and Verification of a Mathematical Regression Model for Hydraulic Performance of AFV
4. Discussion
5. Conclusions
- The physical relationship model between Hamin and FDmax and the elastic diaphragm hardness and structural parameters and the measured results of hydraulic performance show that Hamin increases with increasing E and D and decreases with increasing W, FDmax decreases with increasing E and W, and E, D and W have a significant effect on Hamin. E and W have significant effects on FDmax (p < 0.05);
- Based on range analysis, the minimum Hamin is 0.022 MPa, which is lower than the Hamin of the existing AFV by 63.3%. And the maximum FDmax is 116.4 s, which is higher than that of the existing AFV by 71.2%.
- The ternary nonlinear regression equation of hydraulic performance and elastic diaphragm hardness and structural parameters of the AFV has a good prediction accuracy, which can quickly give the structural parameter combination of the AFV required by the actual project and shorten the research and development time.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| AFV | Automatic flushing valve |
| Ha | The inlet pressure, (MPa) |
| Hamin | The minimum inlet pressure, (MPa) |
| FD | The flushing duration, (s) |
| FDmax | The maximum flushing duration, (s) |
| E | Elastic diaphragm hardness, (HA) |
| D | Ascending channel offset distance, (mm) |
| W | Drain hole width, (mm) |
| AFDS | Automatic flushing drip irrigation system |
| F1y | The downwards vertical force exerted by water in the upper cavity on the elastic diaphragm, (N) |
| F2y | The vertical upwards force of water in the lower cavity on the elastic diaphragm, (N) |
| F3y | The vertical elastic force of the elastic diaphragm, (N) |
| Fy | The vertical downwards resultant force of the elastic diaphragm, (N) |
| hf1 | The water loss generated in the water inlet, (MPa) |
| hf2 | The water loss generated in the ascending channel and delay channel, (MPa) |
| Sx | The projection area of the elastic diaphragm on the horizontal plane, (m2) |
| Sdrain x | The projection area of the drain hole on the horizontal plane, (m2) |
| Cw | The water storage volume of the AFV body, (mL) |
| Ca | The initial volume of the upper cavity, (mL) |
| Cb | The volume added by the downwards movement of the elastic diaphragm, (mL) |
| Cair | The volume of air in the upper cavity, (mL) |
| q | The average flow rate of water entering the upper cavity from the end of the delay channel, (mL/s) |
| m | The number of driplines controlled by one AFV |
| T | The flushing duration per unit length of dripline, (s/m) |
| H | The pump water supply pressure of AFDS, (MPa) |
| RMSE | Root mean square error |
| nRMSE | The normalized root mean square error |
| hf | The head loss between the pump and the AFVs inlet, (MPa) |
References
- Fan, J.L.; Wu, L.F.; Zhang, F.C.; Yan, S.C.; Xiang, Y.Z. Evaluation of drip fertigation uniformity affected by injector type, pressure difference and lateral layout. Irrig. Drain. 2017, 66, 520–529. [Google Scholar] [CrossRef]
- Kiboi, M.N.; Ngetich, K.F.; Fliessbach, A.; Muriuki, A.; Mugendi, D.N. Soil fertility inputs and tillage influence on maize crop performance and soil water content in the central highlands of Kenya. Agric. Water Manag. 2019, 217, 316–331. [Google Scholar] [CrossRef]
- Sun, G.Z.; Hu, T.T.; Liu, X.G.; Peng, Y.L.; Leng, X.X.; Li, Y.L.; Yang, Q.L. Optimizing irrigation and fertilization at various growth stages to improve mango yield, fruit quality and water-fertilizer use efficiency in xerothermic regions. Agric. Water Manag. 2022, 260, 107296. [Google Scholar] [CrossRef]
- Liu, C.Y.; Wang, R.; Wang, W.E.; Hu, X.T.; Wu, W.Y.; Liu, F.L. Different irrigation pressure and filter on emitter clogging in drip phosphate fertigation systems. Water 2022, 14, 853. [Google Scholar] [CrossRef]
- Guan, Y.H.; Niu, W.Q.; Liu, L.; Li, X.K.; Zhang, W.Q. Effect of fertilizer type and concentration on sediment transport capacity of dripper in drip fertigation with muddy water. Trans. Chin. Soc. Agric. Eng. 2018, 34, 78–84, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Khaled, E.M.; Stucki, J.W. Iron oxidation state effects on cation fixation in smectites. Soil Sci. Soc. Am. J. 1991, 55, 550–554. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Wang, W.L.; Tian, S.M. Mineral composition and distribution of the sediment in the Yellow River Basin. J. Sediment Res. 2007, 5, 3–10, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Chen, Z.J.; Gao, J.J.; Zhao, W.Y.; Wang, C.Y.; Zhou, J.B. Effects of application of phosphorus and potassium fertilizers on ion compositions of soil solution in solar greenhouse. Trans. CSAE 2011, 27, 261–266, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Wang, X.Y.; Wang, W.E.; Hu, X.T. Research on the emitter anti-clogging performance and system uniformity caused by fertigation. China Rural. Water Hydropower. 2015, 11, 1–5, (In Chinese with English abstract). [Google Scholar]
- Liu, L.; Niu, W.Q.; Wu, Z.G.; Guan, Y.H.; Li, Y. Risk and inducing mechanism of acceleration emitter clogging with fertigation through drip irrigation systems. Trans. Chin. Soc. Agric. Mach. 2017, 48, 228–236, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Tajrishy, M.A.; Hills, D.J.; Tchobanoglous, G. Pretreatment of secondary effluent for drip irrigation. J. Irrig. Drain. Eng. 1994, 120, 716–731. [Google Scholar] [CrossRef]
- Li, J.S.; Chen, L.; Li, Y.F. Effect of chlorination on emitter clogging and system performance for drip irrigation with sewage effluent. Trans. Chin. Soc. Agric. Eng. 2010, 26, 7–13. [Google Scholar] [CrossRef]
- Song, P.; Li, Y.K.; Li, J.S.; Pei, Y.T. Chlorination with lateral flushing controling drip irrigation emitter clogging using reclaimed water. Trans. Chin. Soc. Agric. Eng. 2017, 33, 80–86, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Vermeiren, T. Magnetic treatment of liquids for scale and corrosion prevention. Anti-Corros. Methods Mater. 1958, 5, 215–219. [Google Scholar] [CrossRef]
- Wang, Z.X.; Zhao, X.; Zhang, W.Q.; Niu, W.Q. Effect of magnetization of irrigation water on the clogging of drip irrigation emitters with integrated water and fertilizer. Trans. Chin. Soc. Agric. Eng. 2021, 37, 127–135, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Rav-Acha, C.; Kummel, M.; Salamon, I.; Adin, A. The effect of chemical oxidants on effluent constituents for drip irrigation. Water Res. 1995, 29, 119–129. [Google Scholar] [CrossRef]
- Li, Y.K.; Zhou, B.; Yang, P.L. Research advances in drip irrigation emitter clogging mechanism and controlling methods. J. Hydraul. Eng. 2018, 49, 103–114. [Google Scholar] [CrossRef]
- Tayel, M.Y.; Pibars, S.K.; Mansour, A.G. Effect of drip irrigation method, nitrogen source, and flushing schedule on emitter clogging. Agric. Syst. 2013, 4, 131–137. [Google Scholar] [CrossRef]
- Zhou, B.; Li, Y.K.; Liu, Y.Z.; Xu, F.P.; Pei, Y.T.; Wang, Z.H. Effect of drip irrigation frequency on emitter clogging using reclaimed water. Irrig. Sci. 2015, 33, 221–234. [Google Scholar] [CrossRef]
- Al-Mefleh, N.K.; Talozi, S.; Naser, K.A. Assessment of treated wastewater reuse in drip irrigation under different pressure conditions. Water 2021, 13, 1033. [Google Scholar] [CrossRef]
- Feng, D.; Kang, Y.H.; Wan, S.Q.; Liu, S.P. Lateral flushing regime for managing emitter clogging under drip irrigation with saline groundwater. Irrig. Sci. 2017, 35, 217–225. [Google Scholar] [CrossRef]
- Liu, J.S.; Li, Y.F.; Wang, J.; Wang, Z. Microirrigation in China: History, current situation and prospects. J. Hydraul. Eng. 2016, 47, 373–381. [Google Scholar] [CrossRef]
- Zhao, X.K.; Mo, Y.; Xia, H.; Gong, Y.T.; Wang, J.D.; Zhang, Y.Q.; Gong, S.H.; Li, Q.L. Hydraulic performance of automatic flushing valve at the end of dripline. J. Irrig. Drain. 2021, 40, 105–112. [Google Scholar] [CrossRef]
- Mo, Y.; Zhao, X.K.; Wang, J.D.; Zhang, Y.Q.; Gong, S.H.; Xia, H.; Li, Q.L.; Wang, Y. Design and structural optimization of the automatic flushing valve with exhaust function. Trans. Chin. Soc. Agric. Eng. 2022, 38, 72–79, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Puig-Bargues, J.; Lamm, F.R.; Trooien, T.P.; Clark, G.A. Effect of dripline flushing on subsurface drip irrigation systems. Trans. ASABE 2010, 53, 147–155. [Google Scholar] [CrossRef]
- Han, S.Q.; Li, Y.K.; Xu, F.P.; Sun, D.X.; Feng, J.; Liu, Z.Y.; Wu, R.N.; Wang, Z.H. Effect of lateral flushing on emitter clogging under drip irrigation with Yellow River water and a suitable method. Irrig. Drain. 2018, 67, 199–209. [Google Scholar] [CrossRef]
- Yu, L.M.; Li, N.; Liu, X.G.; Yang, Q.L.; Long, J. Influence of flushing pressure, flushing frequency and flushing time on the service life of a labyrinth-channel emitter. Biosyst. Eng. 2018, 172, 154–164. [Google Scholar] [CrossRef]
- Zhang, W.Q.; Niu, W.Q.; Li, X.K.; Lu, M.; Yang, X.K.; Wen, S.L. Determination of first lateral flushing time and period to mitigate risk of emitter clogging in drip irrigation. Trans. Chin. Soc. Agric. Eng. 2019, 35, 70–77, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Zhao, X.K. Research on Hydraulic Performance Test of Flushing Valve at End of Capillary and Its Application in Sandy Drip Irrigation System. Master’s Thesis, Hebei Agricultural University, Baoding, China, 2016. [Google Scholar]
- Li, W.J. Research on Hydrological Frequency of Rivers in Arid Areas Based on Normal Transformation. Master’s Thesis, Shihezi University, Shihezi, China, 2022. [Google Scholar]
- GB/T 2411-2008/ISO 868: 2003; Plastics and Ebonite—Determination of Indentation Hardness by Means of a Durometer (Shore Hardness), 1st ed. Standards Press of China: Beijing, China, 2008.
- GB/T 17187-2009/ISO 9261: 2004; Agricultural Irrigation Equipment—Emitters and Emitting Pipe—Specification and Test Methods. Standards Press of China: Beijing, China, 2010.
- GB/T 19812. 2-2017; Plastic Equipment for Water Saving Irrigation—Part 2: Pressure Compensating Emitter and Emitting Pipe. Standards Press of China: Beijing, China, 2017.
- Bannayan, M.; Hoogenboom, G. Using pattern recognition for estimating cultivar coefficients of a crop simulation model. Field. Crop. Res. 2009, 111, 290–302. [Google Scholar] [CrossRef]
- Dettori, M.; Cesaraccio, C.; Motroni, A.; Spano, D.; Duce, P. Using ceres-wheat to simulate durum wheat production and phenology in Southern Sardinia. Field. Crop. Res. 2011, 120, 179–188. [Google Scholar] [CrossRef]
- Xu, Y.B.; Zhang, J.; Long, Z.Q.; Tang, H.Z.; Zhang, X.G. Hourly urban water demand forecasting using the continuous deep belief echo state network. Water 2019, 11, 351. [Google Scholar] [CrossRef] [Green Version]
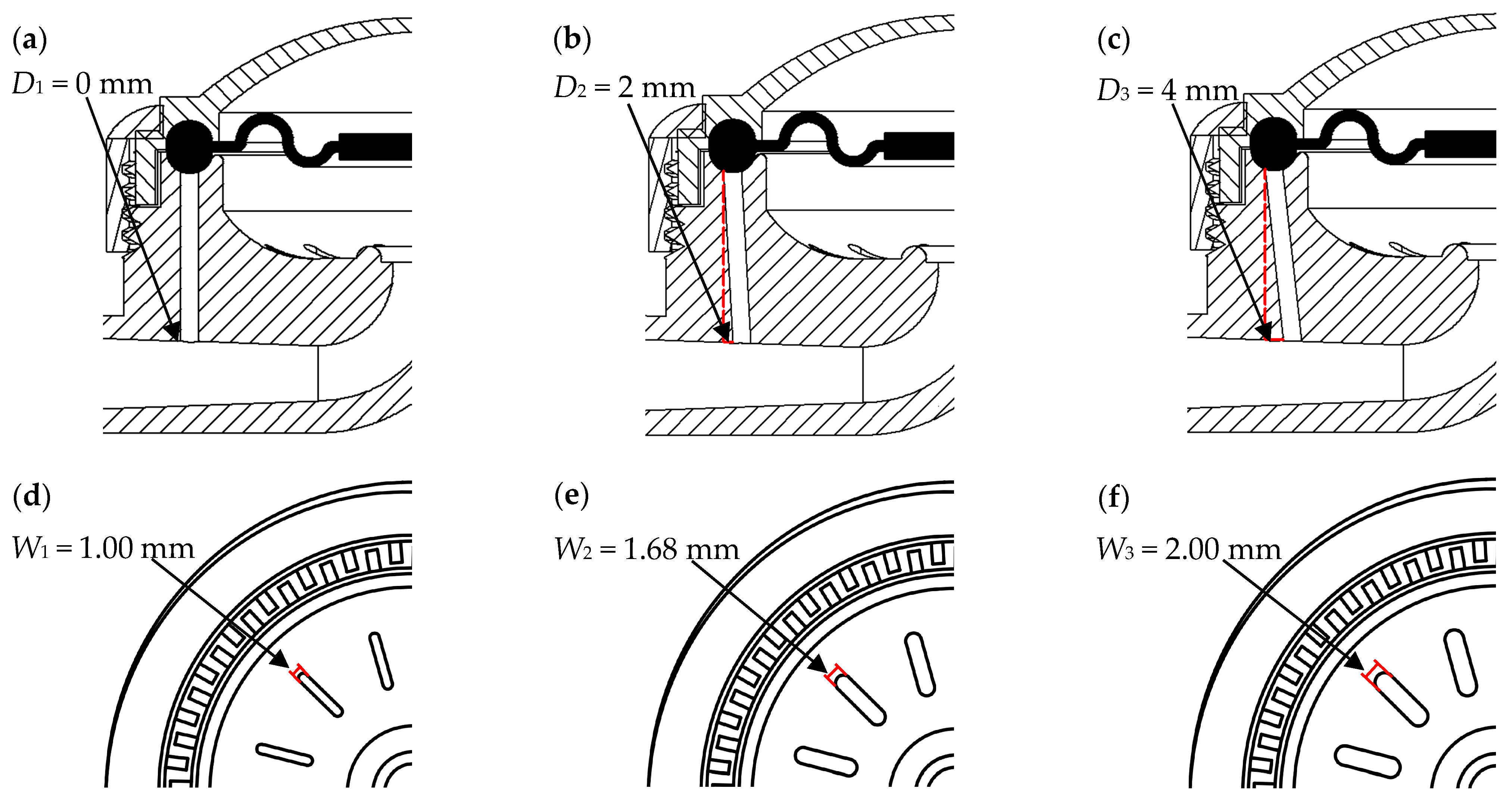
| Order | Treatments | Experimental Factors | ||
|---|---|---|---|---|
| E (HA) | D (mm) | W (mm) | ||
| 1 | E1D1W1 | 40 | 0 | 1.00 |
| 2 | E1D2W2 | 40 | 2 | 1.68 |
| 3 | E1D3W3 | 40 | 4 | 2.00 |
| 4 | E2D1W3 | 55 | 0 | 2.00 |
| 5 | E2D2W1 | 55 | 2 | 1.00 |
| 6 | E2D3W2 | 55 | 4 | 1.68 |
| 7 | E3D1W2 | 60 | 0 | 1.68 |
| 8 | E3D2W3 | 60 | 2 | 2.00 |
| 9 | E3D3W1 | 60 | 4 | 1.00 |
| Treatments | Hamin (MPa) | FDmax (s) |
|---|---|---|
| E1D1W1 | 0.026 | 95.7 |
| E1D2W2 | 0.031 | 83.3 |
| E1D3W3 | 0.041 | 87.3 |
| E2D1W3 | 0.033 | 38.7 |
| E2D2W1 | 0.040 | 82.7 |
| E2D3W2 | 0.065 | 58.7 |
| E3D1W2 | 0.040 | 54.3 |
| E3D2W3 | 0.048 | 48.7 |
| E3D3W1 | 0.082 | 36.3 |
| Experimental Indexes | Experimental Factors | |||
|---|---|---|---|---|
| E (HA) | D (mm) | W (mm) | ||
| Hamin | Hamin1 | 0.033 | 0.033 | 0.049 |
| Hamin2 | 0.046 | 0.040 | 0.045 | |
| Hamin3 | 0.057 | 0.063 | 0.041 | |
| R | 0.024 | 0.030 | 0.008 | |
| FDmax | FDmax1 | 88.8 | 62.9 | 71.6 |
| FDmax2 | 60.0 | 71.6 | 65.4 | |
| FDmax3 | 46.4 | 60.8 | 58.2 | |
| R | 42.4 | 10.8 | 13.4 | |
| Experimental Indexes | E | D | W |
|---|---|---|---|
| Hamin | 78.236 ** | 131.082 ** | 10.180 ** |
| FDmax | 33.773 ** | 2.357 | 3.219 * |
| Treatments | E (HA) | D (mm) | W (mm) | Hamin | FDmax | ||||
|---|---|---|---|---|---|---|---|---|---|
| Predicted Value (MPa) | Measured Value (MPa) | Relative Error (%) | Predicted Value (s) | Measured Value (s) | Relative Error (%) | ||||
| E1D1W2 | 40 | 0 | 1.68 | 0.024 | 0.026 | −9.3 | 86.4 | 73.0 | 18.3 |
| E1D1W3 | 40 | 0 | 2.00 | 0.021 | 0.022 | −2.7 | 77.0 | 94.3 | −18.4 |
| E1D2W1 | 40 | 2 | 1.00 | 0.033 | 0.028 | 19.0 | 97.7 | 116.4 | −16.1 |
| E1D3W2 | 40 | 4 | 1.68 | 0.051 | 0.047 | 9.3 | 79.6 | 90.3 | −11.9 |
| E2D1W1 | 55 | 0 | 1.00 | 0.036 | 0.036 | −0.4 | 68.6 | 80.4 | −14.6 |
| E2D1W2 | 55 | 0 | 1.68 | 0.037 | 0.036 | 3.3 | 56.6 | 58.7 | −3.5 |
| E2D2W2 | 55 | 2 | 1.68 | 0.043 | 0.040 | 7.3 | 68.0 | 73.3 | −7.3 |
| E2D2W3 | 55 | 2 | 2.00 | 0.038 | 0.039 | −1.9 | 62.6 | 55.3 | 13.3 |
| E2D3W3 | 55 | 4 | 2.00 | 0.058 | 0.053 | 9.1 | 60.0 | 65.5 | −8.4 |
| E3D1W1 | 60 | 0 | 1.00 | 0.040 | 0.046 | −12.2 | 55.0 | 62.7 | −12.2 |
| E3D1W3 | 60 | 0 | 2.00 | 0.040 | 0.039 | 1.4 | 33.7 | 33.9 | −0.4 |
| E3D2W1 | 60 | 2 | 1.00 | 0.051 | 0.047 | 9.5 | 59.0 | 67.8 | −13.1 |
| E3D2W2 | 60 | 2 | 1.68 | 0.047 | 0.044 | 7.8 | 56.3 | 67.6 | −16.7 |
| E3D3W2 | 60 | 4 | 1.68 | 0.070 | 0.065 | 6.9 | 51.6 | 58.0 | −11.0 |
| E3D3W3 | 60 | 4 | 2.00 | 0.062 | 0.061 | 2.2 | 51.0 | 57.8 | −11.8 |
| RMSE | 0.003 MPa | 10.2 s | |||||||
| nRMSE (%) | 8.0 | 14.5 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Mo, Y.; Wu, F.; Wang, J.; Gong, S. Impact of Elastic Diaphragm Hardness and Structural Parameters on the Hydraulic Performance of Automatic Flushing Valve. Water 2023, 15, 287. https://doi.org/10.3390/w15020287
Gao H, Mo Y, Wu F, Wang J, Gong S. Impact of Elastic Diaphragm Hardness and Structural Parameters on the Hydraulic Performance of Automatic Flushing Valve. Water. 2023; 15(2):287. https://doi.org/10.3390/w15020287
Chicago/Turabian StyleGao, Hao, Yan Mo, Feng Wu, Jiandong Wang, and Shihong Gong. 2023. "Impact of Elastic Diaphragm Hardness and Structural Parameters on the Hydraulic Performance of Automatic Flushing Valve" Water 15, no. 2: 287. https://doi.org/10.3390/w15020287
APA StyleGao, H., Mo, Y., Wu, F., Wang, J., & Gong, S. (2023). Impact of Elastic Diaphragm Hardness and Structural Parameters on the Hydraulic Performance of Automatic Flushing Valve. Water, 15(2), 287. https://doi.org/10.3390/w15020287








