Next Article in Journal
Tea-Waste-Mediated Magnetic Oxide Nanoparticles as a Potential Low-Cost Adsorbent for Phosphate (PO43−) Anion Remediation
Previous Article in Journal
Machine Learning Algorithms for Predicting the Water Quality Index
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 15
Issue 20
10.3390/w15203542
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Development of a Coupled Soil Water Assessment Tool-MODFLOW Model for Studying the Impact of Irrigation on a Regional Water Cycle

by
Fuli Liang
,
Sheng Li
*,
Feilong Jie
,
Yanyan Ge
,
Na Liu
and
Guangwei Jia
School of Geology and Mining Engineering, Xinjiang University, Urumqi 830017, China
*
Author to whom correspondence should be addressed.
Water 2023, 15(20), 3542; https://doi.org/10.3390/w15203542
Submission received: 19 September 2023 / Revised: 29 September 2023 / Accepted: 10 October 2023 / Published: 11 October 2023
Browse Figures
Versions Notes

Abstract

:
In regions with arid and semi-arid climates, water consumption for agricultural irrigation is much higher than that used for urban and industrial purposes. Intensive irrigation plays a vital role in influencing the interaction between groundwater and surface water. Understanding the impact of irrigation on the local hydrological cycle is of great significance for maintaining regional food production and -security. In order to study the impact of irrigation on the regional hydrological cycle, the present study employed the SWAT-MODFLOW coupled model to analyze the Weigan River Basin from 2002 to 2016. In the modeling process, detailed agricultural management measures were considered, including the zoning of crop types, amount of irrigation water for different crops, irrigation methods, and different sources of irrigation water. Before coupling, each model was set, calibrated, and validated separately. After coupling, the irrigation pumps and drainage units were mapped with the SWAT automatic irrigation and subbasins. Calibration and validation studies showed that the SWAT-MODFLOW coupled model could simulate the river flow and groundwater levels in the Weigan River Basin well. The model simulation results showed that the sources of water in the soil included groundwater irrigation (1147.5 mm) and surface water irrigation (68.4 mm), as well as precipitation and snowmelt recharge (97.62 mm). The groundwater balance was influenced by the river leakage (75.6 mm), lateral inflow from surrounding areas (3.6 mm), unsaturated zone infiltration (197.7 mm), and irrigation pumping (1275 mm). When compared with the scenario without irrigation, the surface runoff, groundwater infiltration, soil moisture content, and evapotranspiration increased by 7.9%, 3.2%, 4.1%, and 2.3%, respectively. Irrigation activities increased the soil moisture content and permeability, resulting in more groundwater recharge and evaporation, as well as a higher surface runoff. This model provides guidance for evaluating drought irrigation systems in future sustainable water resource management.

1. Introduction

Irrigation is the largest single use of water in the world, accounting for over 70% of global freshwater consumption [1]. The area of irrigated farmland exceeds 300 million hectares [2]. The demand for water resources is continuously increasing with social and economic developments and population growth [3]. Water scarcity has posed a serious threat to the sustainable development of agriculture in many arid regions of the world [4]. In the past 50 years, the area of oases in Xinjiang has continuously expanded [5] from 36,900 km2 to 147,600 km2, with an annual expansion rate of 114.33 km2/yr [6,7]. The development of agricultural land has led to an increasing imbalance between the irrigation demand and water supply. Unlike the year-round water extraction in urban areas, agricultural irrigation exhibits obvious seasonal differences [8,9], increasing the complexity of water resource management in regions with agriculture as the main focus. For example, the Weigan River Basin in the central part of the Xinjiang Uygur Autonomous Region is a typical area for intensive irrigation in arid regions. The Weigan River Irrigation District is an important grain production area in southern Xinjiang, with 67% of the area being farmland, growing crops including cotton, corn, and wheat. In recent years, the area of agricultural land in this region has been rapidly expanding, and the strong demand for agricultural irrigation has led to continuous groundwater extraction, resulting in a decline in the groundwater levels. The unreasonable use of groundwater for irrigation in the Weigan River Irrigation District has threatened the environment, ecological water supply, and the safety of drinking water for residents. As a result, the disturbance of the equilibrium between domestic water use, ecological water use, and agricultural irrigation water use has become more prominent. Therefore, a study on the impact of irrigation activities on the regional hydrological cycle is of great importance.
The use of hydrological models is a common method for evaluating the impact of irrigation activities on the evolution of groundwater and surface water cycle. Nakayama [10] used the NICE-DRY model to study the impact of irrigation on the hydrological cycle in the Yellow River Basin. Wei [11] used SWAT to study the impact of intensive irrigation in the Majes agricultural area in southern Peru from 2009 to 2020, with detailed field scale and agricultural management measures as input parameters in the regional scale model. Shu [12] employed MIKE SHE to construct a comprehensive hydrological model of the North China Plain to predict the groundwater resources under different crop rotation and irrigation intensity scenarios. Liu [13] proposed the multi-factor attribution (MFA) method for evaluating the impact of climate change and various human activities on the water cycle process. Li [14] and others quantitatively clarified the impact of reservoirs, precipitation, temperature, and farmland changes on runoff changes in the Yellow River Basin. The focus of the above studies mainly lies on the impact of climate change on river runoff, the prediction of agricultural management scenarios, and the relationship between groundwater extraction and the ecological environment. However, for densely irrigated areas, the human influence dominates the other influencing factors, and using a complete surface water–groundwater system can more clearly demonstrate the impact of irrigation on water resources.
Among the various models, SWAT [15] and MODFLOW-NWT [16] are the most widely used public domain codes for water resources assessment, development, and management, especially for agricultural watersheds [17]. The SWAT model [18,19,20] has been widely used for watershed-scale agricultural catchments. The model is based on physical processes and is used to partition the total flow into various flow components. Additionally, SWAT implements detailed soil water dynamics and allows for the detailed manipulation of agricultural management measures. For example, Wen et al. [21] used the SWAT model to study the water cycle simulation problem in the Wanyao irrigation area of Zhejiang Province, which was also used to simulate the process of reservoir runoff and sediment [22]. However, SWAT has several limitations in simulating the groundwater flow. In addition, SWAT uses the lumped linear reservoir approach, which may lead to modeling inaccuracies in the simulation of lowland areas with thin unsaturated zones. Groundwater has a significant impact on runoff [23]. The MODFLOW-NWT [24] model is one of the most commonly used three-dimensional, physically based, fully distributed groundwater flow models in the world and was developed by the U.S. Geological Survey. It can effectively solve the scenarios of drying and rewetting in unconfined aquifers [25].
Bailey [26] combined SWAT with MODFLOW-NWT to complete the conversion of variable values between HRU and CELL and modeled and simulated the Sprague River Basin in the Upper Klamath Basin of Oregon, USA, from 1970 to 2003 to evaluate the spatiotemporal patterns of groundwater and surface water exchange in the selected region. The simulation results showed that the coupled model could represent the actual situation well. Eugenio [27] and Liu [28] compared the simulation of groundwater pumping processes between SWAT and SWAT-MODFLOW, and the results indicated that the SWAT-MODFLOW provided more realistic outputs, with a decrease in the flow similar to the volume of the extracted water. Chunn [29] used SWAT-MODFLOW to study the hydrogeological conditions, climate change, and groundwater extraction of the surface water–groundwater interaction in the western region of Canada at a regional scale. Aliyari [30] established the connection between MODFLOW pumping and SWAT HRU irrigation in the SWAT-MODFLOW modeling code and proposed a comprehensive hydrological modeling code suitable for large basins with complex water transfer processes associated with agricultural–urban mixed land use types. Further, the model was validated and applied in the South Platte River Basin in the United States. Tina [31] conducted an in-depth study on the joint calibration of the SWAT-MODFLOW coupled model, based on the sensitivity analysis of groundwater and surface water parameters, and employed a “GW calibrator” tool to improve the efficiency of model calibration, which was successfully applied to the Sira Watershed in southwestern Iran. The above studies prove that the SWAT-MODFLOW coupled model can exhibit a good ability to simulate the interactions between the surface water and groundwater. SWAT-MODFLOW has been continuously enhanced in the past twenty years [23]. It links the surface and groundwater flow processes to better understand the complex hydrological processes in large agricultural basins. Moreover, SWAT-MODFLOW can assess the hydrological response of the fully integrated river–aquifer systems to land use changes, climate change, and agricultural management practices, and is beneficial for the management of water resources. Although previous studies have investigated the impact of irrigation on regional hydrological cycles, few have considered more refined agricultural measures.
In the present study, the SWAT-MODFLOW coupled model was used to investigate the impact of intensive irrigation in arid areas on the regional hydrological cycle at the watershed scale. The agricultural management measures incorporated in the modeling process were more detailed, thereby allowing a precise depiction of the irrigation water quantity, irrigation methods, and irrigation water sources for different crops. This makes the model more realistic and provides a basis for the sustainable development of agriculture in the region.

2. Materials and Methods

2.1. Research Area

The Weigan River Basin is located in the northeastern part of Aksu, Xinjiang, China, with an area of about 4178 km2 and an elevation of 898–2370 m (Figure 1). The agricultural irrigation area is mainly located in the downstream of the basin, with an area of about 2042 km2. During the simulated period from 2000 to 2016, the average temperature was 10.6 °C. The average temperature in July and August was 32.6 °C, the weather was hot and dry, and the average temperature in January and February was −9.2 °C, with cold and dry weather. The annual rainfall in the basin is 56.5 mm. The winter and summer seasons are clearly semi-arid continental climates. The main land cover types are bare land (55%), agricultural land (23.5%), water bodies (1.8%), towns (17%), and others (2.7%). The main soil type is loamy soil, and the desert area is covered by reeds and saltworts [32]. The Yinda River and Weigan River are the long-term surface water sources for the irrigation area. The upstream of the river is the Tianshan Mountains, and the water source is mainly contributed to by the snow melt and rainfall, with uneven distribution throughout the year. The spring runoff is small, and the summer (June to September) runoff accounts for more than 70% of the whole year. Therefore, relying solely on the surface water cannot meet the agricultural irrigation needs throughout the year, and groundwater is exploited for irrigation in this irrigation area.
The main crops in the irrigation area are cotton, corn, and wheat. The differences in crops and rainfall lead to different irrigation needs. The main growing season for cotton crops in the Weigan River Basin is from May to September, with a designated irrigation water requirement of 150 mm. The growing season for winter wheat is from September to November and from March to May of the following year, with an irrigation water requirement of 615 mm. The growing season for corn is from March to September, with an irrigation water requirement of 510 mm. In order to meet these different irrigation needs, both surface water and groundwater are used. Before the year 2000, most of the irrigation water in the region was obtained from the rivers and reservoirs, but in recent years, groundwater irrigation has rapidly expanded due to the reclamation of wasteland. By 2010, over 90% of the groundwater extracted in the Weigan River Basin was used for irrigation, and in 2016, the groundwater accounted for over 70% of the total irrigation water volume.

2.2. SWAT Model

SWAT [23] is a physically based semi-distributed model that can simulate the flow of water, sediment, nutrients, and pesticides within a watershed and predict the impact of climate change and best management practices on the quantity and quality of watershed water. The model divides the watershed into subwatersheds, with each subwatershed further divided into hydrologic response units (HRUs), which are unique combinations of land use, soil, and management. The overall hydrological balance of each HRU is simulated, such as precipitation, meltwater, surface runoff, water redistribution within the soil profile, precipitation interception, and evapotranspiration. The output of the HRU is further concentrated in the river network system.
The SWAT model establishes the geographical spatial dataset setting and data source (Table 1). Daily rainfall, sunshine hours, wind speed, daily maximum temperature, daily minimum temperature, and relative humidity were sourced from the China Meteorological Data Network, and the missing data were supplemented using a weather generator. Land use involves the combination of different crops, and GlobeLand30 land use data and remote sensing data were used to reclassify different crop types into winter wheat–cotton rotation areas and corn areas using ENVI 5.3 software for supervised classification, generating a new land use map. Soil properties were sourced from the Harmonized World Soil Database (HWSD) 500 m resolution two-layer (0–30 cm, 30–100 cm) soil database and combined with DEM data, land use, and soil classification to define hydrological response units (HRUs) using two slope classifications of 0–20% and >20% to define the HRUs (Figure 2). The unique combination of land use, soil type, and slope resulted in a total of 641 HRUs in the entire basin. Based on actual field visits and collected agricultural water management reports for the irrigation district, crop management operations including planting, harvesting, and irrigation were included for corn, cotton, and winter wheat (Table 2). The agricultural management measures of SWAT were represented by setting the value of IRR_SC (0—no irrigation; 1—river canal system; 2—reservoir; 3—shallow groundwater; 4—deep groundwater; 5—external water source for the model) to indicate the different irrigation water sources, thus achieving the setting of multiple irrigation water sources. The difference in the irrigation methods was achieved by defining the irrigation efficiency and surface runoff ratio.
The Sequential Uncertainty Fitting (SUFI2) algorithm from the SWAT-CUP 2012 software was used to calibrate and adjust the model parameters of the SWAT model. By referring to previous studies and considering the characteristics of this study, 29 parameters that were most closely related to the SWAT model were determined [33,34]. The model was run 500 times, and the global sensitivity was prioritized using p-value and t-statistics (the larger the absolute value of t-stat, and the closer the p-value to 0, the more sensitive the parameter is). The top 15 parameters in terms of high sensitivity were selected for analysis and adjustment (Table 3), including river parameters (CH_K2, ALPHA_BNK, CH_N2), groundwater parameters (ALPHA_BF, RCHRG_DP), surface runoff parameters (TRNSRCH, CNCOEF, SURLAG), soil moisture parameters (SOL_AWC, SOL_K, CN2), hydrological response unit parameters (DEP_IMP, EPCO), an irrigation efficiency parameter (IRR_EFF), and an average slope parameter (CH_S1). Among them, TRNSRCH (river transmission loss) and CH_K2 (riverbed hydraulic conductivity) were the two most sensitive parameters in this model, as they were related to river runoff. The reason is that the Weigan River study area is located in a drought-prone region with distinct seasonal hydrological characteristics, and the riverbed leakage was the main factor affecting the runoff loss during the propagation process. The high sensitivity of IRR_EFF (irrigation efficiency) in the model indicates that intensive irrigation activities have a significant impact on the spatial variation of the watershed hydrology. CNCOEF (plant ET curve coefficient) represents the surface water evaporation, and the coefficient was influenced by strong crop evapotranspiration in arid regions.

2.3. MODFLOW Model

In this study, the MODFLOW groundwater flow model was established using GMS 10.0. MODFLOW is a finite difference model for predicting three-dimensional groundwater flow in porous media [16]. The MODFLOW-NWT version was used in this study, along with the UPW package. MODFLOW-NWT can effectively simulate the flow of unconfined groundwater, while the UPW package allows the setting of zero flow out of dry cells and the calculation of groundwater head inflow into dry cells.
Initially, a steady-state MODFLOW model was established for the Weigan River Basin as the basis for model operation. The aquifer was generalized as a single-layer unconfined aquifer, and MODFLOW was discretized into 320 × 191 grids with a grid size of 1000 m × 1000 m. Assuming that the groundwater flow occurred near the Qianfodong outlet, and irrigation activities were only undertaken in the irrigation area, the active cells of the MODFLOW model included only the downstream oasis plain area. The SWAT model range was larger than the MODFLOW simulation range, as shown in Figure 3. The elevation of the model top was extracted from a 30 m resolution DEM, and the bottom elevation was 50–150 m below the ground surface. The model considered the main sources and sinks of the aquifer, including precipitation recharge, surface water and groundwater irrigation, irrigation pumping, river discharge and infiltration, lateral boundary inflow and outflow, and evaporation model settings. The MODFLOW recharge package (RCH) was used to provide precipitation and irrigation recharge outside the active grid cells, while the well package (WEL) included the groundwater pumping, lateral boundary inflow, and outflow. The MODFLOW evapotranspiration package (ET) was used to simulate the evaporation in the model. The river package was used to simulate river infiltration and discharge, but this was covered by the new river package in the SWAT-MODFLOW setting, which was used to calculate the exchange of groundwater and surface water between the aquifer and the river. The model was calibrated and validated using PEST combined with manual calibration, as shown in Figure 4, to obtain a transient model that matched the actual conditions as the basis for coupling. The observation and simulation results show that the spatial distribution of the groundwater in the Weigan River was basically consistent. After the steady-state simulation results were successfully obtained, the transient model was set up, considering the temporal variation of irrigation pumping, and artificially divided into two periods: an irrigation period (March to November) and a non-irrigation period (December to February of the following year).

2.4. Coupling of SWAT and MODFLOW

Coupled SWAT-MODFLOW consists of a mutual transfer of the variables between SWAT and MODFLOW during the simulation process. The calculation process generates daily, and the variable transfer of the two models is calculated by SWAT through hydrological response units (HRUs) to calculate the soil infiltration at each time step, which is then supplied to the corresponding grid unit of MODFLOW. At the same time, the discharge calculated by MODFLOW enters the corresponding HRUs, thus achieving bidirectional transfer of the calculation results of the two models. In addition, the MODFLOW river unit (estimating the exchange rate of volume flow between the aquifer and the river) intersects with the SWAT subbasin to transfer the groundwater return flow to the correct subbasin river. This model uses the QSWATMOD [35] plugin of the QGIS 3.28.1 software, which is a GIS-based GUI plugin that allows linking of the existing SWAT and the MODFLOW models in a GIS setup, thus providing a geographical background with maps and output post-processing pages. This link is based on Bailey et al.’s SWATMODFLOW modeling code [26], in which MODFLOW-NWT was embedded into the SWAT 2012 modeling code to simulate the groundwater flow and the groundwater–surface water interaction. In addition, SWAT-MODFLOW can also be applied to managed watersheds. These functions include connecting the MODFLOW groundwater pumping to SWAT irrigation and connecting the MODFLOW groundwater drainage to the SWAT channel flow (Figure 5).
To achieve the coupling of the model, an input of the necessary files was carried out, including subbasin, HRU, and river network shape files in the SWAT model, as well as grid shape files and source-sink files in the MODFLOW simulation. The purpose of creating the individual .nam files was to provide an identification of the model coupling. The river grid selected SWAT to regenerate the MODFLOW grid before describing river coverage. At the same time, HRU was decomposed into dhu and coupled with MODFLOW grid cells. After the model coupling was completed, a link file was successfully created to activate the irrigation and pumping function of the model. Pumping wells can be directly mapped from the MODFLOW well package in the coupled model, and the number of wells can be added, deleted, or modified according to actual conditions. Due to the existence of river irrigation in this model, the improved SWAT-MODFLOW [30,36,37] model was used to connect MOFDLOW pumping wells and rivers with groundwater irrigation of SWAT HRU. At the same time, the coupling of the model retained the functions of the areas outside the overlap between the SWAT and MODFLOW models.

2.5. Calibration and Validation of the Model

The calibration of this model relies on the combination of the manual and automatic adjustments of parameters. The main goal of model calibration was to constrain the river flow, groundwater head in the saturated zone, and actual evapotranspiration. The performance of the model was evaluated through regression analysis using the coefficient of determination (R2) and the Nash–Sutcliffe coefficient (NSE) as the objective functions to assess the goodness of fit of the model.
R 2 = ∑ i = 1 n ( Q O , i − Q ¯ O ) ( Q s , i − Q ¯ s ) ∑ i = 1 n ( Q O , i − Q ¯ O ) 2 ∑ i = 1 n ( Q s , i − Q ¯ s ) 2 2
N S E = 1 − ∑ i = 1 n ( Q s , i − Q O , i ) 2 ∑ i = 1 n ( Q O , i − Q ¯ O ) 2
where Q s is the simulated flow of SWAT; Q o is the observed flow; Q ¯ s is the average value of the simulated flow over multiple years; Q ¯ O is the average value of the observed flow; and n is the length of time. These measurement results were widely used in hydrological simulations and therefore served as benchmarks for performance evaluation. The range of NSE values was from −∞ to 1, with values close to 1 indicating better model performance. R2 is an indicator used to study the degree of linear relationship between the observed and simulated data, with values ranging from 0 to 1, and values close to 1 indicating a good fit.
By comparing the monthly monitoring data from Qianfodong Station from January 2002 to December 2011, the model was calibrated. Subsequently, from January 2012 to December 2016, the calibrated model was validated. The simulation results of the numerical model were in good agreement with the observed values at Qianfodong during the calibration and validation periods. The R2 of the model during the calibration period was 0.86 and the NSE coefficient was 0.84, while during the validation period, the R2 was 0.87 and the NSE coefficient was 0.82 (Figure 6). The match between simulated flow and observed flow was “very good”, indicating that the model was able to capture the timing and magnitude of the changes in flow. To further validate the performance of the model, the ET values in the Weigan River irrigation area were also verified. Due to the huge workload of in situ evaporation experiments, the monthly output of the model was verified by comparing it with the measured monthly evaporation data from the Shaya meteorological station’s small evaporation dish. From Figure 7, the calculated R2 and NSE were found to be 0.8 and 0.61, respectively, indicating a good performance of the model. The simulated results of the actual evapotranspiration were consistent with the observed values, and the seasonal variation of simulated evapotranspiration was consistent with the growth seasons of winter wheat and summer corn. Overall, the performance standards indicated that the model exhibited reasonable calibration.
After the model coupling, the groundwater module of the SWAT model was replaced by MODFLOW. The calibration period for the groundwater level of the coupled model was from January 2009 to December 2012, and the validation period was from January 2013 to December 2013. There were a total of four observation wells, and the measurement time of these wells was relatively continuous. The SW3 and SW4 (in Figure 8) present the short-term fluctuations in water level that do not match the observation results, which may be due to inaccurate supply provided by SWAT. Overall, the simulated groundwater dynamics of the model showed a good consistency with the observation results, thereby accurately capturing the seasonal and long-term variations in groundwater elevation.

3. Results and Discussion

3.1. Water Balance and Hydrological Response Analysis under Irrigation Activities

In order to investigate the impact of irrigation on regional water circulation and to compare and analyze the differences caused by various balances, a numerical scenario without the irrigation occurrence was set up. This was done to better understand the hydrological response process of irrigation in the Weigan area. The calibrated model results were used to analyze the water balance of the Weigan irrigation area from 2002 to 2016. The flux value (mm) is the normalized result divided by the watershed area, as shown in Figure 9. The results show that the main source of the water in the soil was irrigation, including groundwater irrigation (1147.5 mm) and surface water irrigation (68.4 mm), accounting for more than 80% of the supply. This was followed by the rainfall and snowmelt supply (97.62 mm). Due to the influence of a drought climate, the annual average evaporation was the main factor for soil water loss (783.1 mm). The groundwater balance was mainly affected by the river leakage (75.6 mm), lateral inflow from surrounding areas (3.6 mm), infiltration in the unsaturated zone (197.7 mm), and irrigation pumping (1275 mm).
As shown in Figure 10, in this region, due to intensive irrigation activities, there have been significant changes in both the surface water runoff and groundwater balance components. Compared with the non-irrigation scenario at an annual scale, it was observed that the surface runoff, groundwater infiltration, soil moisture content, and evapotranspiration (ET) increased by 7.9%, 3.2%, 4.1%, and 2.3%, respectively. It can be inferred that the irrigation activities increased the soil moisture content and permeability, resulting in more groundwater recharge and evaporation, as well as higher surface runoff. On a monthly scale, intensive irrigation months (May-August) showed significant increases in the seasonal surface runoff, evaporation, soil moisture content, and groundwater infiltration. These results are similar to the studies conducted by Wei [36] and Bailey in the Arkansas River Valley region, as well as Aliyari [30] in the South Platte River Basin in arid areas.

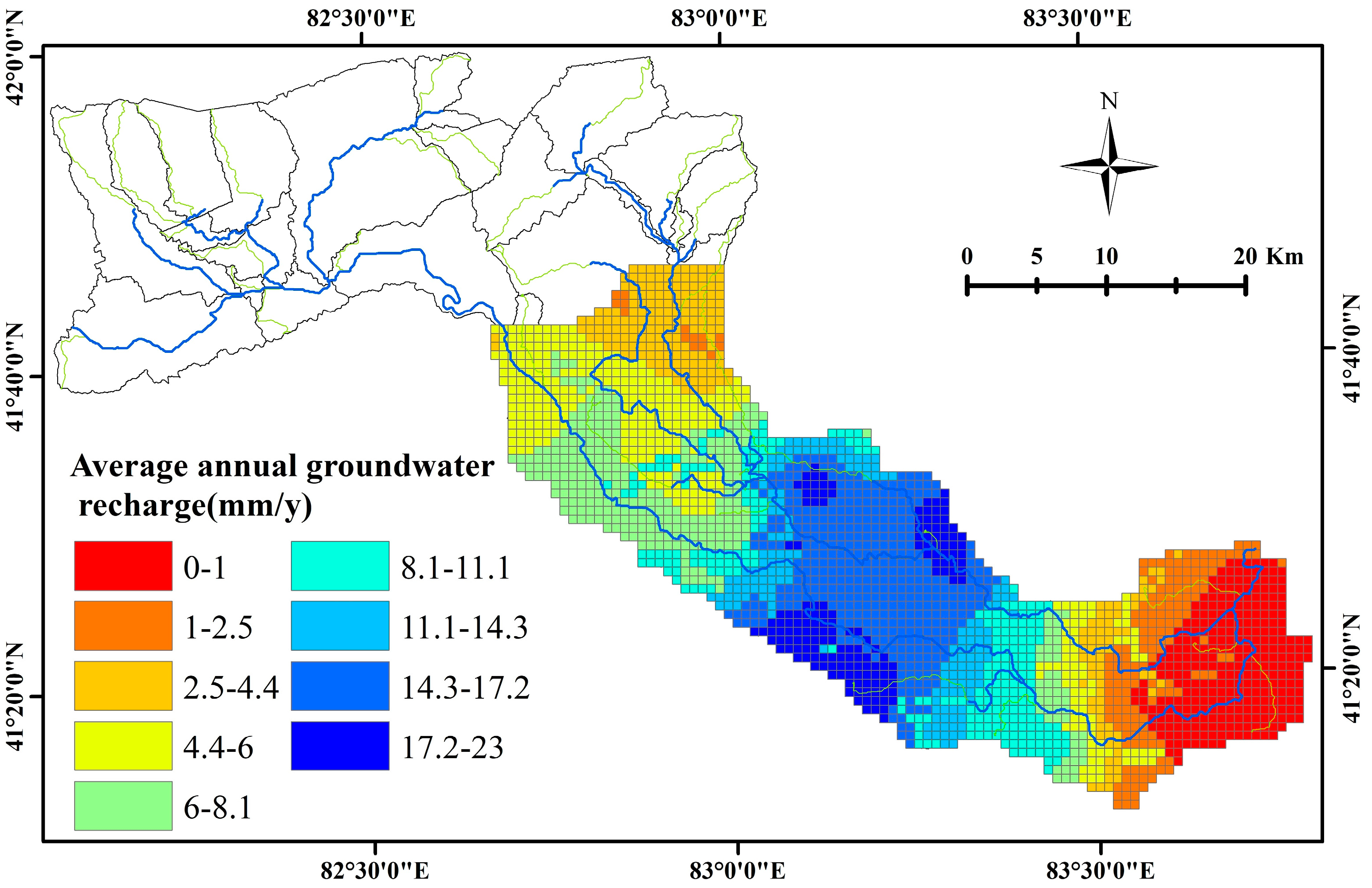
3.2. Impact of Irrigation Activities on Groundwater Recharge

The rate of groundwater recharge was mainly influenced by vegetation, soil type, and spatial variations in climate. Firstly, under current land and water resource management practices, the groundwater recharge in the region was calculated and compared with the non-irrigation scenario to analyze the overall impact of irrigation on groundwater recharge.
Figure 11 shows the spatial distribution of the average groundwater recharge rates from 2002 to 2016. The groundwater recharge rate in the entire irrigation area ranged from 0 to 164.3 mm. There was a significant spatial variation in the groundwater recharge, with the northern part near the mountain pass mainly covered by sediment types such as red loam and gravelly loam, accounting for more than 90% of the total soil. The crops grown in this area were mainly corn, and the irrigation method was traditional flood irrigation, which easily led to vertical leakage into the aquifer. The groundwater recharge in this area ranged from 100 to 164.3 mm. In the middle reaches, the lithology was alluvial soil and soft saline soil, with loamy sand accounting for 82%. The main crops in this area were winter wheat and cotton rotation. The use of subsurface drip irrigation for cotton could effectively reduce irrigation water usage, resulting in an annual recharge rate of 50–100 mm. In the downstream area, the main land use type was wasteland that mainly relied on rainfall recharge, with an annual recharge rate of less than 20 mm. Figure 12 represents the differences in the annual groundwater recharge compared with the no-irrigation scenario, with differences ranging from 0 to 23 mm. The northern and central parts of the irrigation area exhibited higher irrigation demands, resulting in larger recharge differences, while the southern non-irrigated area showed smaller differences.

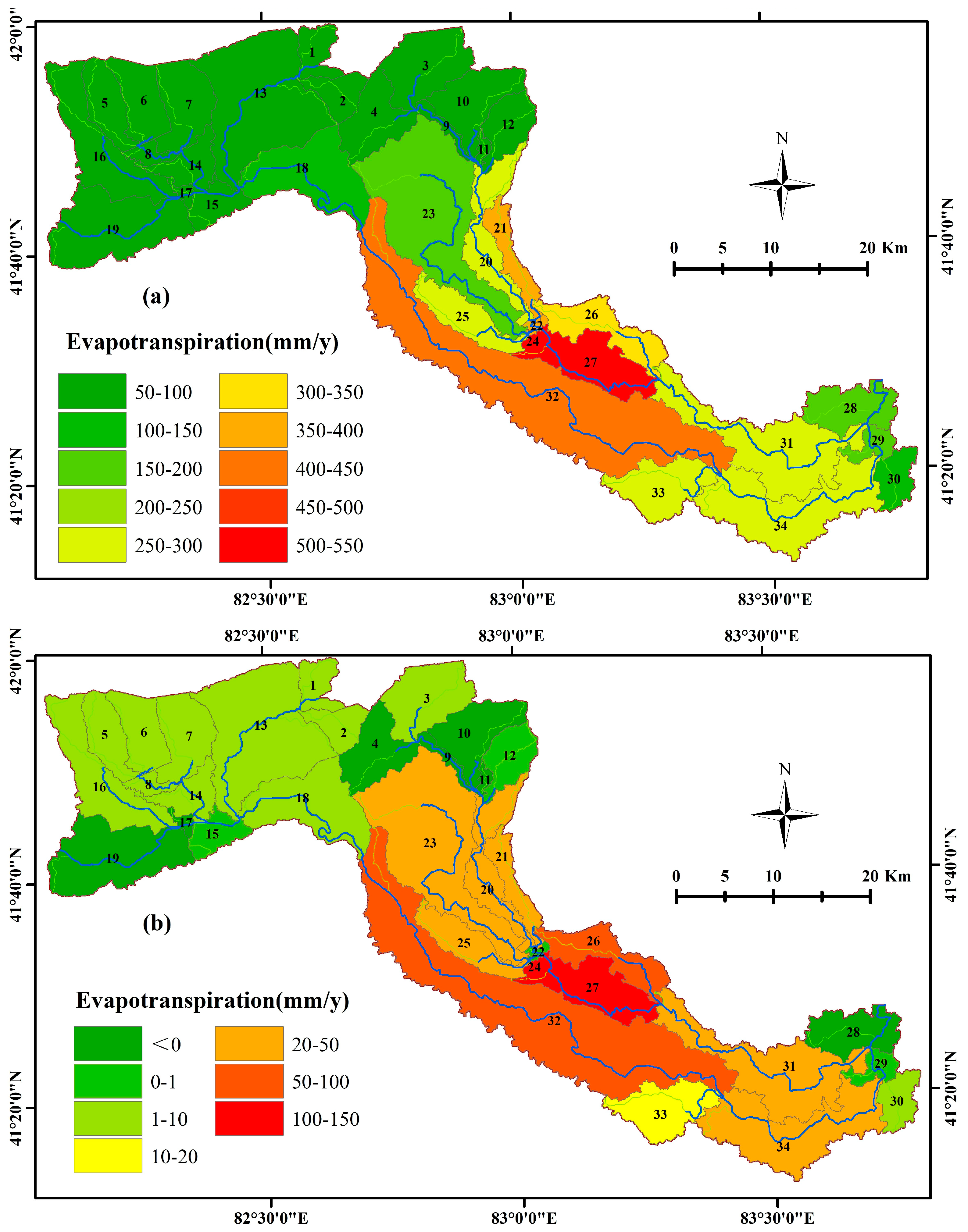
3.3. Impact of Irrigation Activities on Evaporation

The annual average evaporation amount simulated by the model was found to be 105.6 mm. Figure 13 shows that there were significant differences in the spatial distribution of evaporation. The annual evaporation in the northern mountainous area of the study area was between 50 and 100 mm, while evaporation mainly occurred in the southern oasis plain area, ranging from 300 to 528 mm. Due to the high irrigation demand in these subbasins covered by farmland, a large amount of groundwater was extracted for agricultural irrigation, resulting in a higher surface runoff and higher annual average evaporation in this region in high summer temperatures and intense solar radiation. Compared with the scenario without irrigation, it can be found that the areas with the largest differences in evaporation were the densely irrigated areas, with evaporation differences ranging from 20 to 132.3 mm. The studies by Wei [36] and Sijal [37] also confirm that regions with large differences in evaporation were mostly in areas with a high irrigation demand for irrigated crops.

3.4. Impact of Irrigation Activities on the Exchange of Surface Water and Groundwater

River–aquifer interaction is an important component of the watershed water balance, and understanding its spatial and temporal distribution is a necessary condition for effective water resources management. The SWAT-MODFLOW model has the ability to calculate the river–aquifer interaction, while evaluating the groundwater recharge. Based on the river package in the MODFLOW model code, SWAT-MODFLOW uses Darcy’s law to estimate the aquifer–river interactions (infiltration from the river to the aquifer and from the aquifer to the river). This method compares the groundwater head with the water level in the river cells to determine the direction and magnitude of water flow. The exchange of water also depends on the permeability of the riverbed and the hydraulic conductivity of the aquifer [38].
Figure 14 presents the spatial and temporal distribution of the river–groundwater exchange in each subbasin. The simulation results indicate that the surface water replenished the groundwater with a flow rate of 270–5902 m3/d. The temporal distribution varied significantly by month, with an average flow rate of 3735 m3/d from May to September, and an average flow rate of 699 m3/d in other months. On the other hand, the groundwater discharge to the river ranged from 1135 to 7366 m3/d, with an average flow rate of 6211 m3/d in summer and an average flow rate of 2124 m3/d in other months. The subbasins clearly reveal the spatial variability of the interaction between aquifers and rivers. River leakage was mainly concentrated in basins 23, 20, and 21, where the groundwater depth was greater and the aquifer was disconnected from the river, resulting in a dominant river recharge to groundwater. The highest groundwater discharge to the river occurred in subbasins 28, 29, 30, 31, and 34, as the groundwater level gradually rose and was discharged into the river. The middle and lower reaches were the locations with the closest interaction between the river and aquifer, and the maximum intensity of their interaction occurred from May to August (Figure 15). A study by Yifru [34] on the southern part of Seoul, South Korea, also demonstrated a strong river–aquifer exchange during months with intensive irrigation, and revealed the spatial variability of the aquifer–river interaction. However, unlike this study, there was no apparent zoning difference in the surface water–groundwater interaction between upstream and downstream areas, which can be attributed to the decisive role of groundwater depth in the exchange between surface water and groundwater.
Figure 16 shows the differences in the water exchange between surface water and groundwater during the simulation period compared with the scenario without irrigation. The red line represents the difference in the groundwater discharge between the scenario with irrigation and the scenario without irrigation, while the green line represents the difference in surface water leakage to groundwater. It can be observed that the maximum difference in groundwater discharge downstream occurred at groundwater levels of 1025.6–2562.8 m3/d, where the decrease in pumping affected the rise in groundwater levels. This was especially in areas with shallow groundwater depth, leading to more groundwater entering the river network. The difference in the surface water leakage to groundwater also decreased, ranging from 9.9 to 567.4 m3/d. Although the decrease in the surface water irrigation increased the river runoff, the overall impact of reduced irrigation was smaller than the impact of groundwater pumping on water exchange. The rise in groundwater levels reduced the river leakage. Therefore, pumping has an important impact on river runoff and groundwater levels.
The simulation of the Weigan River Basin in this study achieved good results. However, during the period from 2002 to 2016, due to continuous agricultural development and reclamation of the wasteland in the Weigan River Basin, the model did not consider the changes in land use and land cover during the simulation period. It is difficult to accurately estimate the irrigation demand and irrigation system, which is a limitation of this model. Therefore, the study of dynamic land use changes in the model can better represent the spatio-temporal changes in the regional hydrological cycle under intensive irrigation activities. Moreover, this coupled model involved a large number of parameters. Although SWATCUP can adjust the surface runoff and evaporation-related parameters using algorithms, and PEST can assist with the inversion of groundwater-flow-related parameters, sometimes the results of the coupled model do not match the actual observed values, requiring further adjustments in the individual models. This requires a lot of time and effort. Therefore, it is necessary to develop an algorithm for the comprehensive adjustment of parameters in the coupled model, which can greatly reduce the computational resources required for running the coupled model, allowing for multiple model runs and better understanding of the uncertainties related to parameters and input data.

4. Conclusions

The present study employed the SWAT-MODFLOW coupled model to simulate the hydrological cycle in the Weigan River area under intensive irrigation from 2002 to 2016. The model accurately characterized the agricultural management measures, including irrigation methods, irrigation water volume, and irrigation water sources. The validation results showed that the model could effectively describe the flow processes of surface water and groundwater. By comparing the simulation results with the scenario of no irrigation, it was found that irrigation activities increased the surface runoff by 7.9%, groundwater infiltration by 3.2%, soil moisture content by 4.1%, and evapotranspiration by 2.3%. Furthermore, irrigation also caused changes in the groundwater recharge rate and groundwater–surface water exchange rate, with significant spatial differences. The study demonstrates that the SWAT-MODFLOW model can provide quantitative results for the rational development, utilization, and management of agricultural irrigation water in this area.

Author Contributions

Conceptualization, F.L. and S.L.; methodology, F.L.; software, F.L.; validation, F.L.; formal analysis, F.L.; investigation, F.L., F.J., Y.G., N.L. and G.J.; resources, F.L.; data curation, F.L.; writing—original draft preparation, F.L.; writing—review and editing, F.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China, grant number U1603243.

Data Availability Statement

The general data are included in the article. Additional data are available on request.

Acknowledgments

The authors thank the valuable contributions from the National Natural Science Foundation of China for funding this project.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Khokhar, T. Chart: Globally, 70% of Freshwater is Used for Agriculture. World Bank Data Blog. 2017. Available online: https://blogs.worldbank.org/opendata/chart-globally-70-freshwater-used-agriculture. (accessed on 6 August 2023).
  2. Frenken, K.; Gillet, V. Irrigation Water Requirement and Water Withdrawal by Country; Food and Agriculture Organization (FAO) of the United Nations: Rome, Italy, 2012. [Google Scholar]
  3. Samimi, M.; Mirchi, A.; Moriasi, D.; Ahn, S.; Alian, S.; Taghvaeian, S.; Sheng, Z. Modeling Arid/Semi-arid Irrigated Agricultural Watersheds with SWAT: Applications, Challenges, and Solution Strategies. J. Hydrol. 2020, 590, 125418. [Google Scholar] [CrossRef]
  4. AghaKouchak, A.; Feldman, D.; Hoerling, M.; Huxman, T.; Lund, J. Water and climate: Recognize anthropogenic drought. Nature 2015, 524, 409–411. [Google Scholar] [CrossRef] [PubMed]
  5. Sun, C.-Z.; Wei, Y.-Q.; Zhao, L.-S. Co-evolution of water-energy-food nexus in arid areas: Take Northwest China as an example. J. Nat. Resour. 2022, 37, 320–333. [Google Scholar] [CrossRef]
  6. Zhu, L.; Xia, X.-X.; Yang, A.-M.; Jin, H. Expansion of cultivated land in the oasis area of the Manas River Basin sensitivity analysis of CA-Markov model parameters. Arid Zone Res. 2020, 37, 1327–1336. [Google Scholar]
  7. Yan, X.; Wang, Y.; Chen, Y.; Yang, G.; Xia, B.; Xu, H. Study on the Spatial Allocation of Receding Land and Water Reduction under Water Resource Constraints in Arid Zones. Agriculture 2022, 12, 926. [Google Scholar] [CrossRef]
  8. Lankford, B.; Pringle, C.; McCosh, J.; Shabalala, M.; Hess, T.; Knox, J.W. Irrigation area, efficiency and water storage mediate the drought resilience of irrigated agriculture in a semi-arid catchment. Sci. Total Environ. 2022, 859, 160623. [Google Scholar] [CrossRef]
  9. Han, C.; Zhang, B.; Han, S. Quantitative effects of changes in agricultural irrigation on potential evaporation. Hydrol. Process. 2021, 35, e14057. [Google Scholar] [CrossRef]
  10. Nakayama, T. Simulation of the effect of irrigation on the hydrologic cycle in the highly cultivated Yellow River Basin. Agric. For. Meteorol. 2010, 151, 314–327. [Google Scholar] [CrossRef]
  11. Wei, X.; Garcia-Chevesich, P.; Alejo, F.; García, V.; Martínez, G.; Daneshvar, F.; Bowling, L.C.; Gonzáles, E.; Krahenbuhl, R.; McCray, J.E. Hydrologic Analysis of an Intensively Irrigated Area in Southern Peru Using a Crop-Field Scale Framework. Water 2021, 13, 318. [Google Scholar] [CrossRef]
  12. Shu, Y.; Villholth, K.G.; Jensen, K.H.; Stisen, S.; Lei, Y. Integrated hydrological modeling of the North China Plain: Options for sustainable groundwater use in the alluvial plain of Mt. Taihang. J. Hydrol. 2012, 464–465, 79–93. [Google Scholar] [CrossRef]
  13. Liu, J.; Zhou, Z.; Yan, Z.; Gong, J.; Jia, L.; Xu, C.Y.; Wang, H. A new approach to separating the impacts of climate change and multiple human activities on water cycle processes based on a distributed hydrological model. J. Hydrol. 2019, 578, 124096. [Google Scholar] [CrossRef]
  14. Li, H.; Zhang, Q.; Singh, V.P.; Shi, P.; Sun, P. Hydrological effects of cropland and climatic changes in arid and semi-arid river basins: A case study from the Yellow River basin, China. J. Hydrol. 2017, 549, 547–557. [Google Scholar] [CrossRef]
  15. Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
  16. McDonald, M.; Harbaugh, A.W. A Modular Three-Dimensional Finite-Difference GroundWater Flow Model; U.S. Geological Survey: Reston, WV, USA, 1988.
  17. Guevara Ochoa, C.; Medina Sierra, A.; Vives, L.; Zimmermann, E.; Bailey, R. Spatio-temporal patterns of the interaction between groundwater and surface water in plains. Hydrol. Process. 2020, 34, 1371–1392. [Google Scholar] [CrossRef]
  18. George, A.; Hoang, T.L.; Takashi, G. A Review of SWAT Model Application in Africa. Water 2021, 13, 1313. [Google Scholar]
  19. Wagner, P.D.; Bieger, K.; Arnold, J.G.; Fohrer, N. Representation of hydrological processes in a rural lowland catchment in Northern Germany using SWAT and SWAT+. Hydrol. Process. 2022, 36, e14589. [Google Scholar] [CrossRef]
  20. Castellanos-Osorio, G.; López-Ballesteros, A.; Pérez-Sánchez, J.; Senent-Aparicio, J. Disaggregated monthly SWAT+ model versus daily SWAT+ model for estimating environmental flows in Peninsular Spain. J. Hydrol. 2023, 623, 129837. [Google Scholar] [CrossRef]
  21. Wen, J.; Wang, S.; Wang, H.; Cui, Y. Study on water cycle simulation model of multi-sources and multi-functional irrigation area based on SWAT model (II): Application of Wanyao irrigation area. IOP Conf. Ser. Earth Environ. Sci. 2020, 510, 032019. [Google Scholar] [CrossRef]
  22. Xu, X.Z. Assessment of runoff and sediment yield in the Miyun Reservoir catchment by using SWAT model. Hydrol. Process. 2009, 23, 3619–3630. [Google Scholar] [CrossRef]
  23. Rasmus, F.R.; Eugenio, M. The importance of subsurface drainage on model performance and water balance in an agricultural catchment using SWAT and SWAT-MODFLOW. Agric. Water Manag. 2021, 255, 107058. [Google Scholar]
  24. Fu, X. Optimization Management of Groundwater Resources and Modeling and Reme-diation of Nitrate Pollution in YangZhuang Basin; China University of Geosciences: Wuhan, China, 2019. [Google Scholar]
  25. Zheng, Z. Coupling Simulation of Surface Water and Groundwater in Beishan Reservoir Watershed Based on SWAT-MODFLOW; Nanjing University: Nanjing, China, 2021. [Google Scholar]
  26. Bailey, R.T.; Wible, T.C.; Arabi, M.; Records, R.M.; Ditty, J. Assessing regional-scale spatio-temporal patterns of groundwater–surface water interactions using a coupled SWAT-MODFLOW model. Hydrol. Process. 2016, 30, 4420–4433. [Google Scholar] [CrossRef]
  27. Molina-Navarro, E.; Bailey, R.T.; Andersen, H.E.; Thodsen, H.; Nielsen, A.; Park, S.; Jensen, J.S.; Jensen, J.B.; Trolle, D. Comparison of abstraction scenarios simulated by SWAT and SWAT-MODFLOW. Hydrol. Sci. J. 2019, 64, 434–454. [Google Scholar] [CrossRef]
  28. Liu, W.; Park, S.; Bailey, R.T.; Molina-Navarro, E.; Andersen, H.E.; Thodsen, H.; Nielsen, A.; Jeppesen, E.; Jensen, J.S.; Trolle, D. Quantifying the streamflow response to groundwater abstractions for irrigation or drinking water at catchment scale using SWAT and SWAT–MODFLOW. Environ. Sci. Eur. 2020, 32, 1–25. [Google Scholar] [CrossRef]
  29. Chunn, D.; Faramarzi, M.; Smerdon, B.; Alessi, D.S. Application of an Integrated SWAT–MODFLOW Model to Evaluate Potential Impacts of Climate Change and Water Withdrawals on Groundwater–Surface Water Interactions in West-Central Alberta. Water 2019, 11, 110. [Google Scholar] [CrossRef]
  30. Aliyari, F.; Bailey, R.T.; Tasdighi, A.; Dozier, A.; Arabi, M.; Zeiler, K. Coupled SWAT-MODFLOW model for large-scale mixed agro-urban river basins. Environ. Model. Softw. 2019, 115, 200–210. [Google Scholar] [CrossRef]
  31. Jafari, T.; Kiem, A.S.; Javadi, S.; Nakamura, T.; Nishida, K. Fully integrated numerical simulation of surface water-groundwater interactions using SWAT-MODFLOW with an improved calibration tool. J. Hydrol. Reg. Stud. 2021, 35, 100822. [Google Scholar] [CrossRef]
  32. Li, L. Spatial distribution and variation characteristics of soil salinity in the oasis of Weigan and Kuqa rivers. J. Arid Land Resour. Environ. 2022, 36, 136–142. [Google Scholar]
  33. Jiang, M. Interaction between Groundwater and Surface Water under Large-Scale Exploitation Conditions Based on SWAT-MODFLOW Model; Lanzhou University: Lanzhou, China, 2021. [Google Scholar]
  34. Yifru, B.A.; Chung, I.-M.; Kim, M.-G.; Chang, S.W. Assessment of Groundwater Recharge in Agro-Urban Watersheds Using Integrated SWAT-MODFLOW Model. Sustainability 2020, 12, 6593. [Google Scholar] [CrossRef]
  35. Park, S.; Nielsen, A.; Bailey, R.T.; Trolle, D.; Bieger, K. A QGIS-based graphical user interface for application and evaluation of SWAT-MODFLOW models. Environ. Model. Softw. 2018, 111, 493–497. [Google Scholar] [CrossRef]
  36. Wei, X.; Bailey, T.R. Assessment of System Responses in Intensively Irrigated Stream–Aquifer Systems Using SWAT-MODFLOW. Water 2019, 11, 1576. [Google Scholar] [CrossRef]
  37. Dangol, S.; Zhang, X.; Liang, X.Z.; Miralles-Wilhelm, F. Agricultural Irrigation Effects on Hydrological Processes in the United States Northern High Plains Aquifer Simulated by the Coupled SWAT-MODFLOW System. Water 2022, 14, 1938. [Google Scholar] [CrossRef]
  38. Chen, Z. Simulation of Interaction between Surface Water and Groundwater and Evaluation of Nitrate Load in Shaying River Sasin; Nanjing University: Nanjing, China, 2017. [Google Scholar]
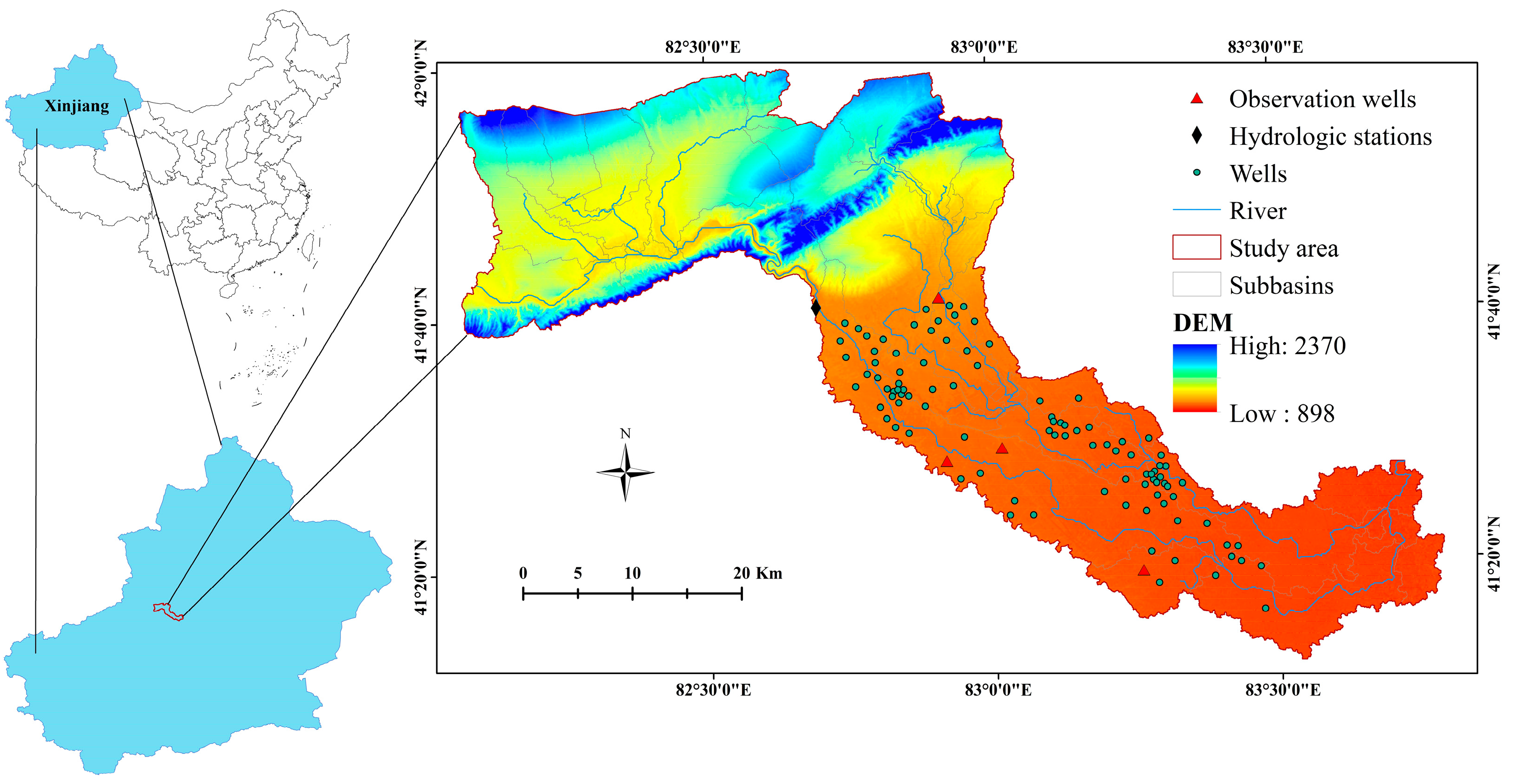
Water 15 03542 g001
Figure 1. Location of study area.
Figure 1. Location of study area.
Water 15 03542 g001
Water 15 03542 g002
Figure 2. (A) Digital elevation model with 12.5 m resolution, (B) land cover map, (C) modified soil map, and (D) slope map with 4 categories for the study area.
Figure 2. (A) Digital elevation model with 12.5 m resolution, (B) land cover map, (C) modified soil map, and (D) slope map with 4 categories for the study area.
Water 15 03542 g002
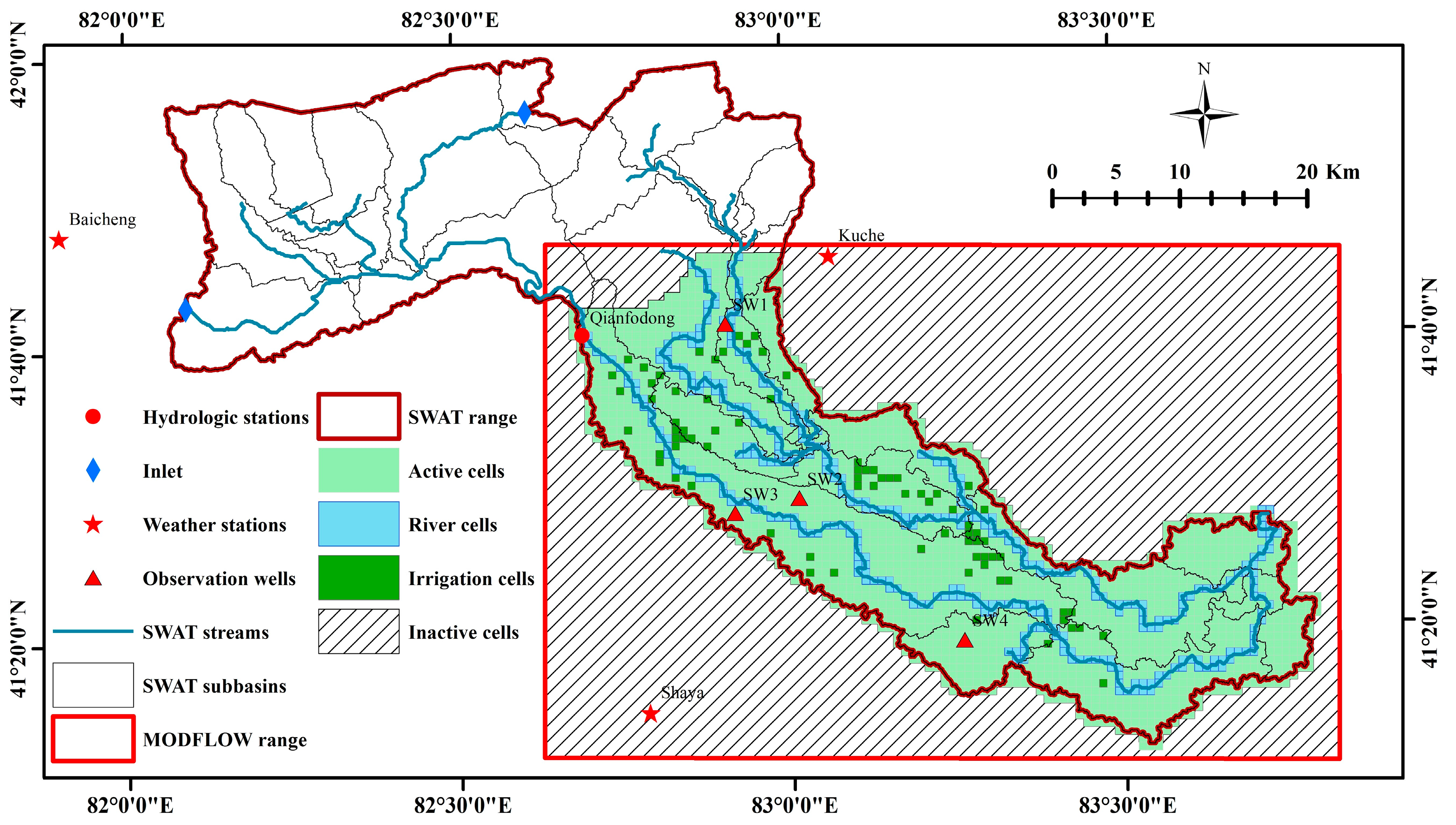
Water 15 03542 g003
Figure 3. Modeling domains for SWAT and MODFLOW.
Figure 3. Modeling domains for SWAT and MODFLOW.
Water 15 03542 g003
Water 15 03542 g004
Figure 4. Observed and specified groundwater head configurations 1 January 2002.
Figure 4. Observed and specified groundwater head configurations 1 January 2002.
Water 15 03542 g004
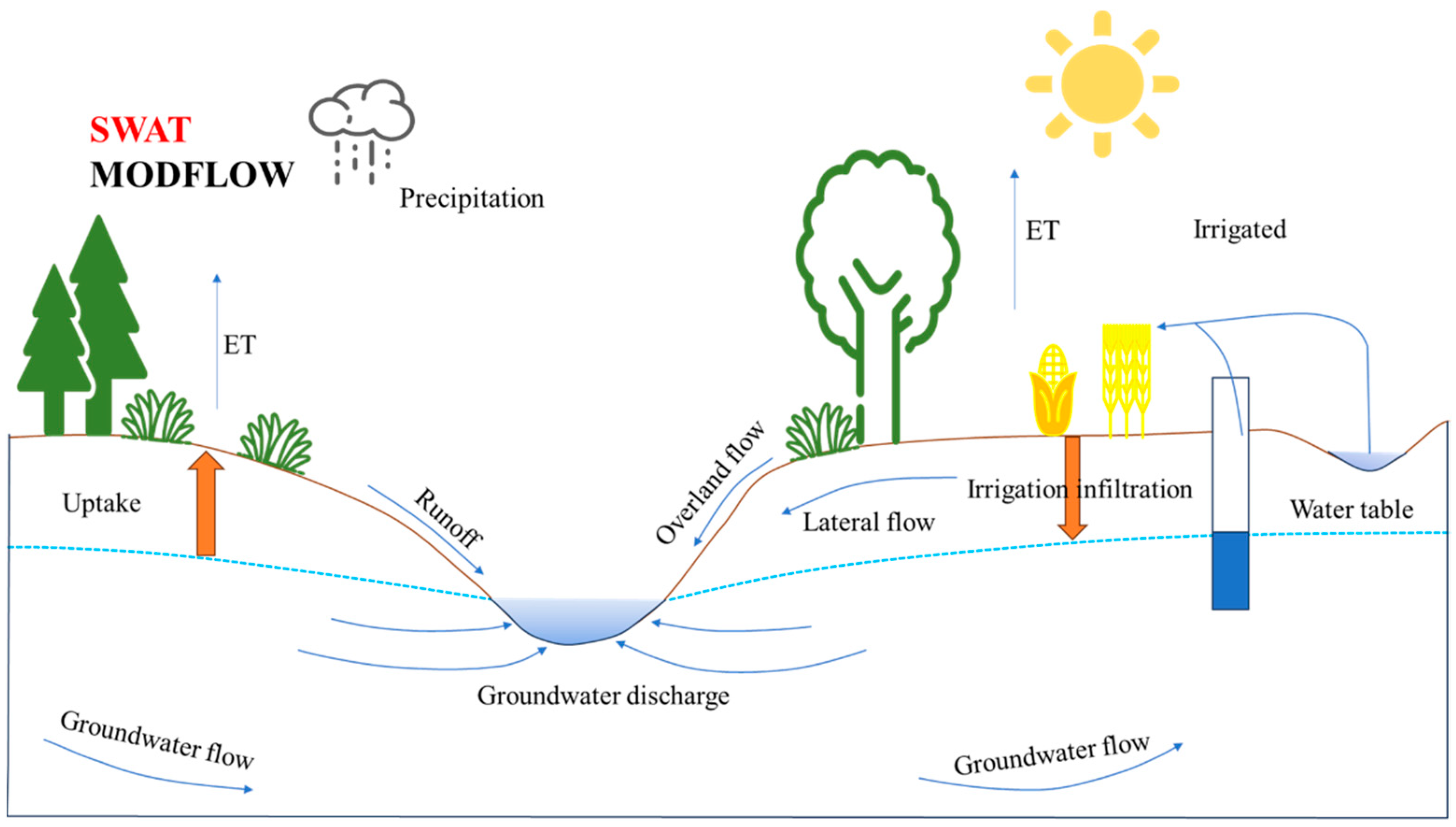
Water 15 03542 g005
Figure 5. Conceptual diagram of the SWAT-MODFLOW model cycle.
Figure 5. Conceptual diagram of the SWAT-MODFLOW model cycle.
Water 15 03542 g005
Water 15 03542 g006
Figure 6. Monthly observed and simulated streamflow comparison during calibration and validation periods (A), with corresponding coefficient of determination (B,C).
Figure 6. Monthly observed and simulated streamflow comparison during calibration and validation periods (A), with corresponding coefficient of determination (B,C).
Water 15 03542 g006
Water 15 03542 g007
Figure 7. Model evaporation data validation.
Figure 7. Model evaporation data validation.
Water 15 03542 g007
Water 15 03542 g008
Figure 8. Comparison between SWAT-MODFLOW calculated and measured transient groundwater level at selected measuring wells.
Figure 8. Comparison between SWAT-MODFLOW calculated and measured transient groundwater level at selected measuring wells.
Water 15 03542 g008
Water 15 03542 g009
Figure 9. Water budget scheme for the entire river basin.
Figure 9. Water budget scheme for the entire river basin.
Water 15 03542 g009
Water 15 03542 g010
Figure 10. Long-term (2002–2016) seasonal hydrological processes analysis of Weigan River Basin for irrigation scenario relative to no-irrigation scenario.
Figure 10. Long-term (2002–2016) seasonal hydrological processes analysis of Weigan River Basin for irrigation scenario relative to no-irrigation scenario.
Water 15 03542 g010
Water 15 03542 g011
Figure 11. Long-term (2002–2016) average mean annual recharge.
Figure 11. Long-term (2002–2016) average mean annual recharge.
Water 15 03542 g011
Water 15 03542 g012
Figure 12. Difference in annual recharge between irrigation and no-irrigation scenarios.
Figure 12. Difference in annual recharge between irrigation and no-irrigation scenarios.
Water 15 03542 g012
Water 15 03542 g013
Figure 13. (a) Long-term (2002–2016) average mean annual ET; (b) simulated mean annual difference in evapotranspiration.
Figure 13. (a) Long-term (2002–2016) average mean annual ET; (b) simulated mean annual difference in evapotranspiration.
Water 15 03542 g013
Water 15 03542 g014
Figure 14. Spatial distribution scale based on yearly average seepage to streams.
Figure 14. Spatial distribution scale based on yearly average seepage to streams.
Water 15 03542 g014
Water 15 03542 g015
Figure 15. Monthly average discharge at the model boundary.
Figure 15. Monthly average discharge at the model boundary.
Water 15 03542 g015
Water 15 03542 g016
Figure 16. Differences in surface water groundwater exchange compared with no irrigation.
Figure 16. Differences in surface water groundwater exchange compared with no irrigation.
Water 15 03542 g016
Table 1. Input datasets for the Soil Water Assessment Tool (SWAT) model.
Table 1. Input datasets for the Soil Water Assessment Tool (SWAT) model.
Data TypeScale or Spatial ResolutionData Sources
Elevation90 mSpatial geographic data cloud
Land-use map30 mGlobeLand30, LANDSAT8
Soil10 kmFAO Digital Soil Map of the World
Weather0.25° × 0.25°China Meteorological Data Network
Streamflowmonthly scaleXinjiang Water Conservancy and Hydropower Survey and Design Institute
Irrigation system field investigation
Table 2. Crop irrigation systems.
Table 2. Crop irrigation systems.
Crop typeManagement OperationsOperating TimeIrrigation Water Volume (mm)Irrigation Method
winter wheatplantation25 September
harvest28 May
irrigated15 March120diffusion irrigation
20 April120diffusion irrigation
20 May120diffusion irrigation
18 September120diffusion irrigation
20 November135diffusion irrigation
cottonplantation1 June
harvest15 September
irrigated10 June22.5drip irrigation
25 June37.5drip irrigation
10 July30drip irrigation
22 July30drip irrigation
25 August30drip irrigation
cornplantation20 March
harvest25 September
irrigated22 March120diffusion irrigation
25 May105diffusion irrigation
20 June97.4diffusion irrigation
27 July97.4diffusion irrigation
11 August90diffusion irrigation
Table 3. Selected SWAT parameters’ sensitivity and value range.
Table 3. Selected SWAT parameters’ sensitivity and value range.
Parameter NameDefinitiont-Statp-ValueValue Range
V__TRNSRCH.bsnFraction of transmission losses from main channel that enters deep aquifer−42.61 00–1
V__CH_K2.rteEffective hydraulic conductivity in main channel alluvium−11.900.01–150
IRR_EFF.mgtIrrigation efficiency−8.66 00–1
V__CNCOEF.bsnPlant ET curve number coefficient−1.86 0.06 0–2
V__ALPHA_BNK.rteBaseflow alpha factor for bank storage1.78 0.08 0–1.5
V__CH_N2.rteManning’s n value for the main channel−1.69 0.09 0–1
V__SOL_AWC.solAvailable water capacity of the soil layer−1.61 0.11 0.03–0.5
V__SOL_K.solSaturated hydraulic conductivity−1.50 0.13 1–100
V__DEP_IMP.hruDepth to impervious layer for modeling of perched water tables−1.36 0.17 0–1000
V__SURLAG.bsnSurface runoff lag time 1.26 0.21 1–10
V__EPCO.hruPlant uptake compensation factor1.22 0.22 0–1.5
V__CH_S1.subAverage slope of tributary channels−1.11 0.27 −0.2–0.2
V__ALPHA_BF.gwBaseflow alpha factor1.05 0.29 0–1
V__RCHRG_DP.gwDeep aquifer percolation fraction−1.03 0.30 0–30
V__CN2.mgtSoil conservation service (SCS) runoff curve number−0.970.33−0.2–0.2
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Liang, F.; Li, S.; Jie, F.; Ge, Y.; Liu, N.; Jia, G. The Development of a Coupled Soil Water Assessment Tool-MODFLOW Model for Studying the Impact of Irrigation on a Regional Water Cycle. Water 2023, 15, 3542. https://doi.org/10.3390/w15203542

AMA Style

Liang F, Li S, Jie F, Ge Y, Liu N, Jia G. The Development of a Coupled Soil Water Assessment Tool-MODFLOW Model for Studying the Impact of Irrigation on a Regional Water Cycle. Water. 2023; 15(20):3542. https://doi.org/10.3390/w15203542

Chicago/Turabian Style

Liang, Fuli, Sheng Li, Feilong Jie, Yanyan Ge, Na Liu, and Guangwei Jia. 2023. "The Development of a Coupled Soil Water Assessment Tool-MODFLOW Model for Studying the Impact of Irrigation on a Regional Water Cycle" Water 15, no. 20: 3542. https://doi.org/10.3390/w15203542

APA Style

Liang, F., Li, S., Jie, F., Ge, Y., Liu, N., & Jia, G. (2023). The Development of a Coupled Soil Water Assessment Tool-MODFLOW Model for Studying the Impact of Irrigation on a Regional Water Cycle. Water, 15(20), 3542. https://doi.org/10.3390/w15203542

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop