Optimizing the Flood Limit Water Level of Reservoirs in Sediment-Laden Rivers under Changing Water and Sediment Conditions: A Case Study of the Xiaolangdi Reservoir
Abstract
:1. Introduction
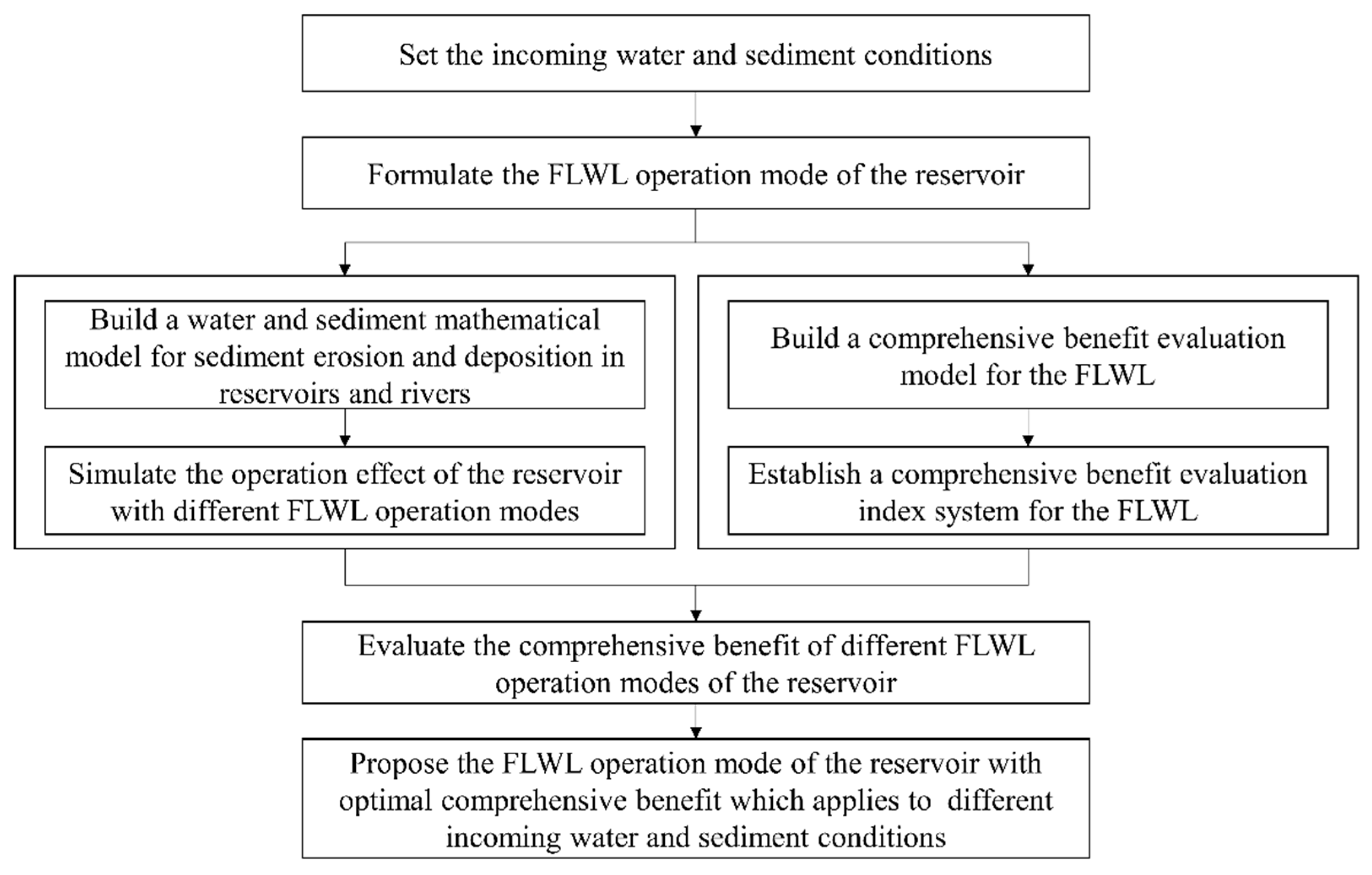
2. Methodology
2.1. Water–Sediment Mathematical Model
2.1.1. Model Principles and Control Equations
- Water flow movement control equationwhere denotes the direction of water flow (m); is time (s); represents the water flow (m3/s); is the water level (m); denotes the cross-sectional overflow area (m2); is the river width (m); is the inflow (or outflow) per unit time and per unit length (m2/s2); is the Manning roughness coefficient; and denotes the gravitational acceleration (m/s2).
- Non-equilibrium sediment transport equation
- 3.
- Riverbed deformation equationwhere is the dry bulk density of sediment (kN/m3).
- 4.
- Power generation equationwhere N is the hydropower generation (kW.h); is the hydropower station efficiency obtained by verification from the measured data; is the discharge flowing through the hydropower station turbine (m3/s); and is the net head of the hydropower station (m).
2.1.2. Solution Method
2.1.3. Constraining Conditions
2.1.4. Model Verification
2.2. Comprehensive Benefit Evaluation Model
2.2.1. Evaluation Indices
2.2.2. Evaluation Model
3. Case Study
3.1. Research Area and Data
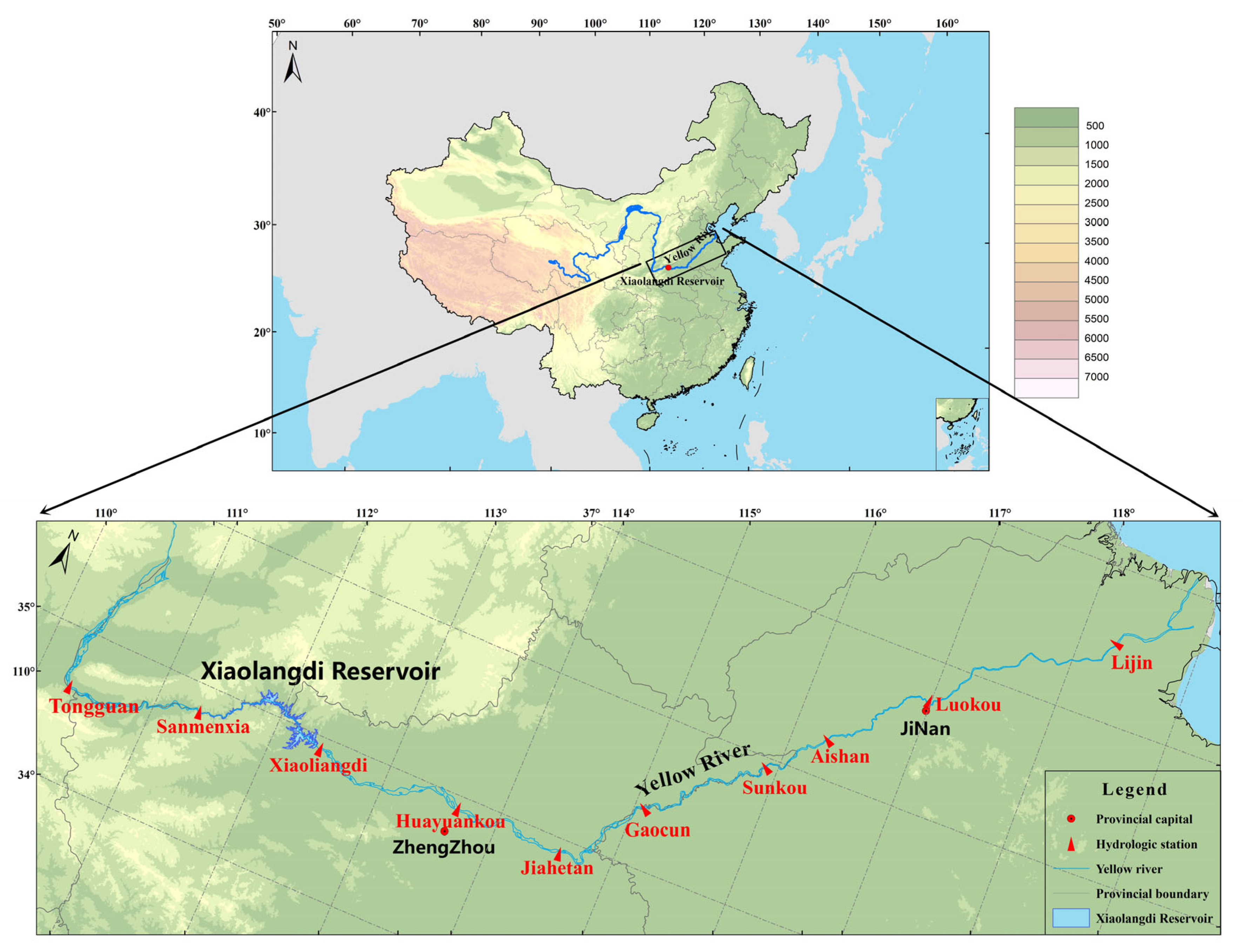
3.1.1. Research Area
3.1.2. Datasets
3.1.3. Minimum Discharge from the XLDR
3.2. Scenario Conditions
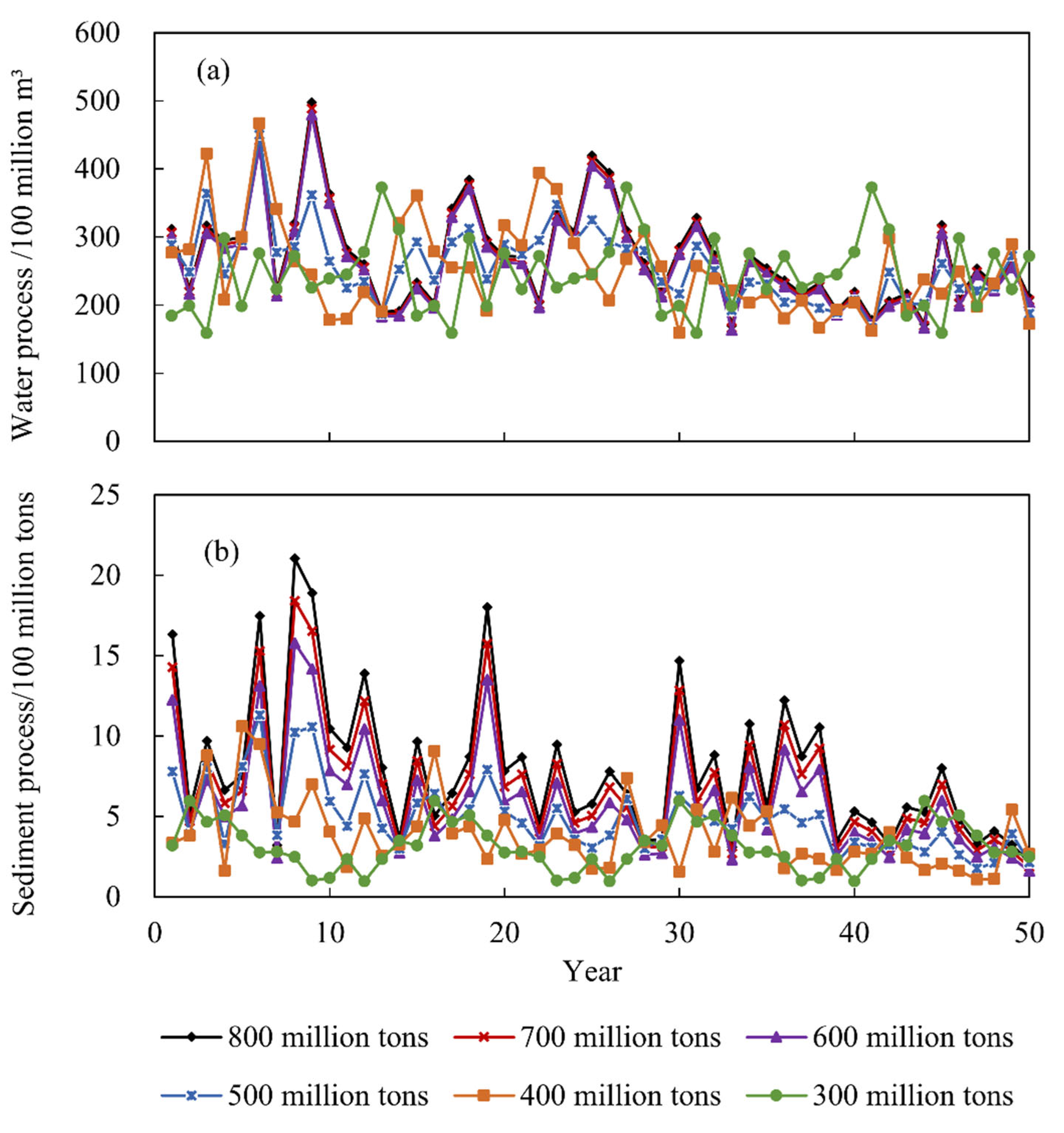
3.2.1. Scenario Conditions of Incoming Water and Sediment
3.2.2. Scenario Conditions of FLWL Operation Modes for the XLDR
3.3. Results
3.3.1. Analysis of Single Objective Effect
3.3.2. Analysis of Comprehensive Effects
3.3.3. Suggestions for Optimizing the FLWL of the XLDR during Flood Seasons
3.4. Discussion
4. Conclusions
- A mathematical model of water and sediment was established to simulate the water level, outflow, siltation, sediment retention period, and hydropower generation in the reservoir and siltation and minimum bank-full discharge in the river channel to study the FLWL operation modes of the reservoirs in sediment-laden rivers under changing water and sediment conditions. Considering the objectives of flood control, silt reduction, water resources supply, irrigation, hydropower generation, and ecological improvement, an index system for evaluating the comprehensive benefit of the FLWL was proposed. Furthermore, a comprehensive benefit evaluation model of the FLWL was established based on the fuzzy optimization theory and BP-ANN to evaluate the various FLWL operation modes’ effects.
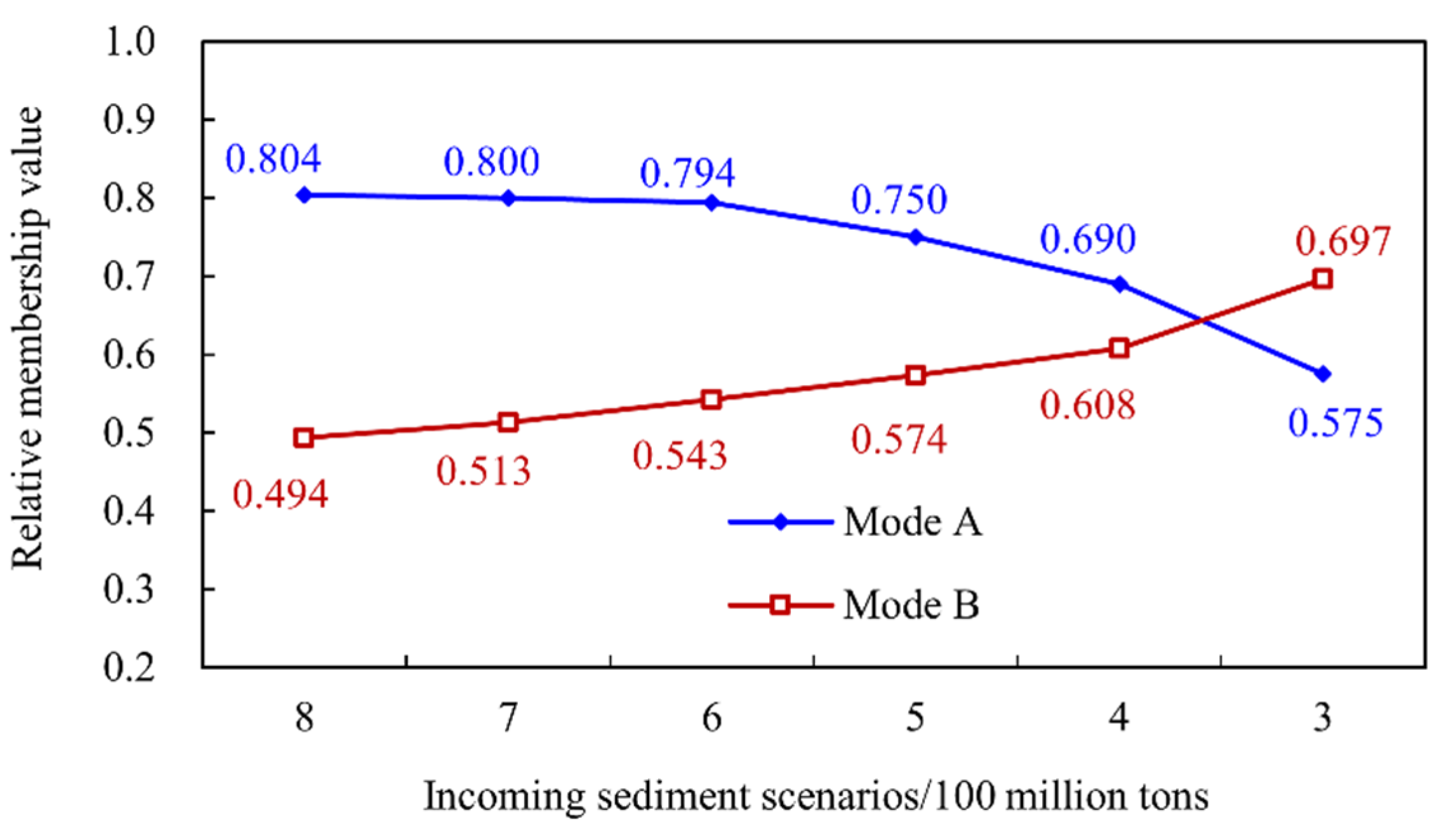
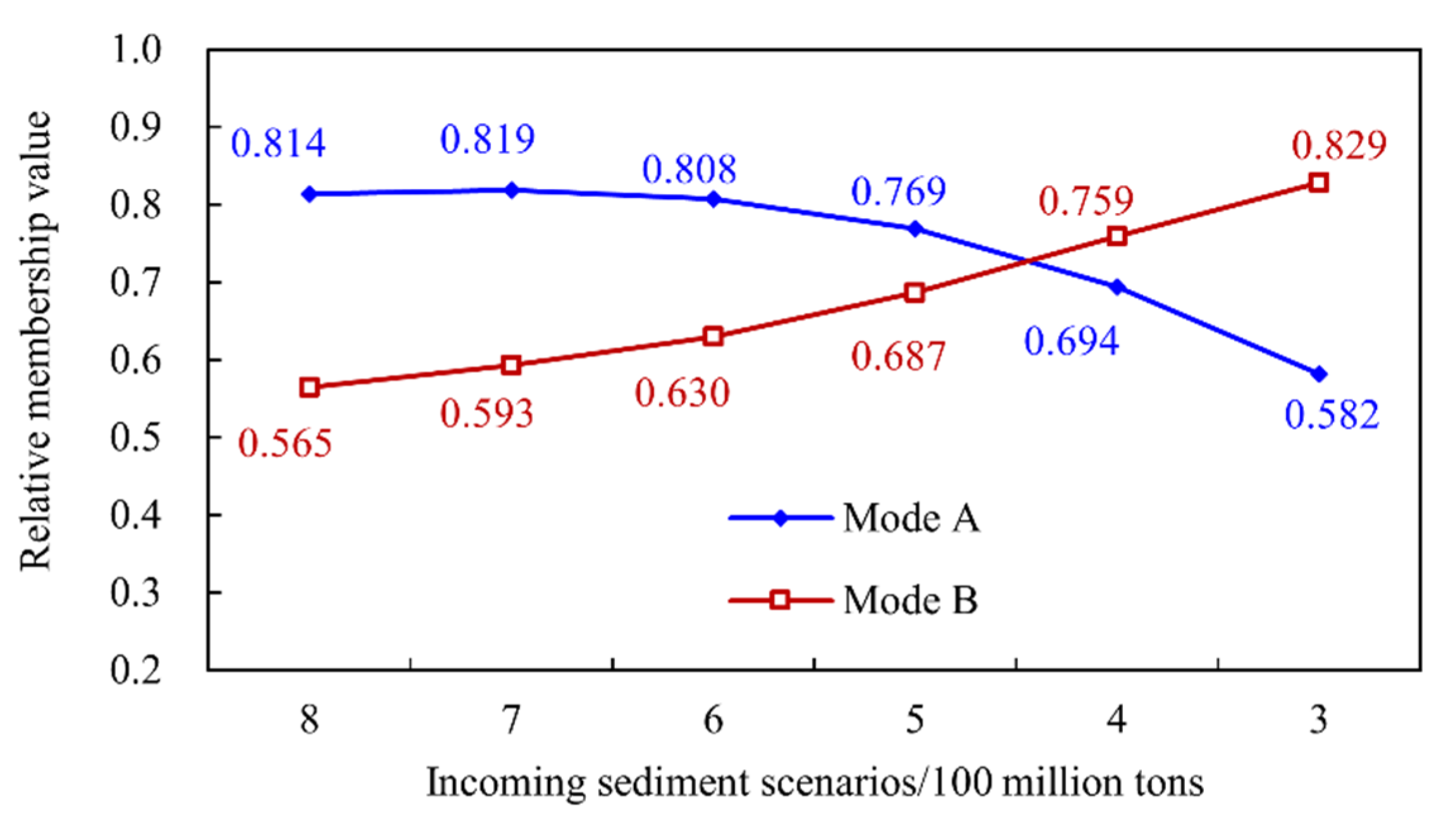
- Considering six scenarios of the incoming sediment amounts, which include 800, 700, 600, 500, 400, and 300 million tons, the water–sediment mathematical model was used to estimate the effect of the operation modes of raising the FLWL gradually or at one time during the XLDR’s sediment retention period. The former mode provided more sediment discharge opportunities and slowed XLDR’s sedimentation rate. Furthermore, the sediment retention period was 4–13 years longer, the average annual siltation in the LYR was lower, and the minimum bank-full discharge of the main channel after 50 years was larger by 150–260 m3/s. However, the mean annual number of days that did not meet the requirements for the downstream water resources supply, irrigation, and ecological improvement was larger by 0.64–2.16 days, average annual water level from July to August during the main flood period was lower by 6.79–8.35 m, and average annual hydropower generation was lower by 91–197 million kW.h. The above results indicated that the regulation mode of gradually raising the FLWL is good for sediment retention and siltation reduction but poor for economic and ecological improvements.
- The reservoir’s comprehensive benefit by raising the FLWL gradually decreases with the reduction in incoming sediment amounts in the Yellow River, while that of the reservoir with raising the FLWL at one time increases. The critical amount of incoming sediment for conversion of the two FLWL operation modes in the XLDR is about 350 million tons. It is suggested that the reservoir be operated in the current mode and gradually raise the FLWL during the flood season when the incoming sediment amount exceeds 350 million tons. However, the FLWL can be raised from the current level of 235 m during the pre-flood season and 248 m during the post-flood season to the designed FLWL of 254 m when the incoming sediment amount is <350 million tons. It is feasible to increase the water amount of the Yellow River by transferring water from the outer basin or reducing sediment into the downstream river channel by constructing large-scale water conservancy projects to improve the flexibility of reservoir operation. When the average annual incoming water volume increases by 2 billion m3, the critical amount of incoming sediment for converting the two FLWL operation modes will be ~450 million tons. This will increase to ~600 million tons after the Guxian Water Conservancy Project takes effect.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mekonnen, M.M.; Hoekstra, A.Y. Four billion people facing severe water scarcity. Sci. Adv. 2016, 2, 1500323. [Google Scholar] [CrossRef] [PubMed]
- Kong, D.X.; Miao, C.Y.; Li, J.H.; Zheng, H.Y. Full-stream erosion in the lower Yellow River: Feasibility, sustainability and opportunity. Sci. Total Environ. 2022, 807, 150810. [Google Scholar] [CrossRef] [PubMed]
- Chou, F.N.F.; Wu, C.W. Expected shortage-based pre-release strategy for reservoir flood control. J. Hydrol. 2013, 497, 1–14. [Google Scholar] [CrossRef]
- Dobson, B.; Wagener, T.; Pianosi, F. An argument-driven classification and comparison of reservoir operation optimization methods. Adv. Water Resour. 2019, 128, 74–86. [Google Scholar] [CrossRef]
- Xu, W.F.; Liu, P.; Guo, S.L.; Cheng, L.; Ming, B.; Gong, Y. Optimizing the reservoir operation for hydropower generation by using the flexibility index to consider inflow uncertainty. J. Water Resour. Plan. Manag. 2021, 147, 06021008. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Jiang, Z.Q.; Qin, H.; Song, Z.G. Monthly operation optimization of cascade hydropower reservoirs with dynamic programming and Latin hypercube sampling for dimensionality reduction. Water Resour. Manag. 2020, 34, 2029–2041. [Google Scholar] [CrossRef]
- Rani, D.; Mourato, S.; Moreira, M. A generalized dynamic programming modeling approach for integrated reservoir operation. Water Resour. Manag. 2020, 34, 1335–1351. [Google Scholar] [CrossRef]
- Mo, C.X.; Mo, G.Y.; Liu, P.; Zhong, H.H.; Wang, D.Y.; Huang, Y.; Jin, J.L. Reservoir operation by staging due to climate variability. Hydrol. Sci. J. 2018, 63, 926–937. [Google Scholar] [CrossRef]
- Chen, L.; Guo, S.L.; Yan, B.W.; Liu, P.; Fang, B. A new seasonal design flood method based on the bivariate joint distribution of flood magnitude and date of occurrence. Hydrol. Sci. J. 2010, 55, 1264–1280. [Google Scholar] [CrossRef]
- Eum, H.I.; Simonovic, S.P. Integrated reservoir management system for adaptation to climate change: The Nakdong river basin in Korea. Water Resour. Manag. 2010, 24, 3397–3417. [Google Scholar] [CrossRef]
- Ouyang, S.; Zhou, J.Z.; Li, C.L.; Liao, X.; Wang, H. Optimal design for flood limit water level of cascade reservoirs. Water Resour. Manag. 2015, 29, 445–457. [Google Scholar] [CrossRef]
- Ding, W.; Zhang, C.; Peng, Y.; Zeng, R.J.; Zhou, H.C.; Cai, X.M. An analytical framework for flood water conservation considering forecast uncertainty and acceptable risk. Water Resour. Res. 2015, 51, 4702–4726. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Wu, J.J.; Cheng, L.; Liu, K.; Wei, Y.M. Regional flood risk assessment via coupled fuzzy c-means clustering methods: An empirical analysis from China’s Huaihe River Basin. Nat. Hazards 2018, 93, 803–822. [Google Scholar] [CrossRef]
- Su, C.; Chen, X. Assessing the effects of reservoirs on extreme flows using nonstationary flood frequency models with the modified reservoir index as a covariate. Adv. Water Resour. 2019, 124, 29–40. [Google Scholar] [CrossRef]
- Mo, C.X.; Zhu, C.; Ruan, Y.L.; Lei, X.B.; Xing, Z.X.; Sun, G.K. Study on the staged operation of a multi-purpose reservoir in flood season and its effect evaluation. Water 2021, 13, 2563. [Google Scholar] [CrossRef]
- Mo, C.X.; Deng, J.; Lei, X.B.; Ruan, Y.L.; Lai, S.F.; Sun, G.K.; Xing, Z.X. Flood season staging and adjustment of limited water level for a multi-purpose reservoir. Water 2022, 14, 775. [Google Scholar] [CrossRef]
- Song, Y.; Wang, H.R. Study on stage method of reservoir flood season. In Proceedings of the 2021 6th International Conference on Clean, Shanghai, China, 10–12 September 2021; Energy Reports. Elsevier: Amsterdam, The Netherlands, 2022; Volume 8, pp. 138–146. [Google Scholar] [CrossRef]
- Liu, D.D.; Li, X.; Guo, S.L.; Rosbjerg, D.; Chen, H. Using a Bayesian probabilistic forecasting model to analyze the uncertainty in real-time dynamic control of the flood limiting water level for reservoir operation. J. Hydrol. Eng. 2015, 20, 04014036. [Google Scholar] [CrossRef]
- Liu, G.J.; Qin, H.; Shen, Q.; Tian, R.; Liu, Y.Q. Multi-Objective Optimal Scheduling Model of Dynamic Control of Flood LimitWater Level for Cascade Reservoirs. Water 2019, 11, 1836. [Google Scholar] [CrossRef]
- Zhang, J.; Min, Y.W.; Feng, B.F.; Duan, W.X. Research and application of key technologies for dynamic control of reservoir water level in flood season. Water 2021, 13, 3576. [Google Scholar] [CrossRef]
- Pan, J.B.; Xie, Y.; Liu, M.; Gao, Z.; Gao, Z.Z.; Xue, B.W. Dynamic control of water level in flood-limited reservoir based on intelligent calculation. Hindawi Math. Probl. Eng. 2022, 2022, 3683122. [Google Scholar] [CrossRef]
- Waylen, P.; Woo, M.K. Prediction of annual floods generated by mixed processes. Water Resour. Res. 1982, 18, 1283–1286. [Google Scholar] [CrossRef]
- Leclerc, G.; Marks, D.H. Determination of the discharge policy for existing reservoir networks under differing objectives. Water Resour. Res. 1983, 9, 1155–1165. [Google Scholar] [CrossRef]
- Colorni, A.; Fronza, G. Reservoir management via reliability programming. Water Resour. Res. 1976, 12, 85–88. [Google Scholar] [CrossRef]
- Miller, B.A.; Whitlock, A.; Hughes, R.C. Flood management—The TVA Experience. Water Int. 1996, 21, 119–130. [Google Scholar] [CrossRef]
- Black, A.R.; Werritty, A. Seasonality of flooding: A case study of North Britain. J. Hydrol. 1997, 195, 1–25. [Google Scholar] [CrossRef]
- Wurbs, R.A.; Cabezas, L.M. Analysis of reservoir storage reallocations. J. Hydrol. 1987, 92, 77–95. [Google Scholar] [CrossRef]
- Johnson, W.K.; Wurbs, R.A.; Beegle, J.E. Opportunities for reservoir-storage reallocation. J. Water Resour. Plan. Manag. 1990, 116, 550–566. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A.; Serinaldi, F.; Bales, J.; Bates, P.D.; Krajewski, W.F. Flood frequency analysis for nonstationary annual peak records in an urban drainage basin. Adv. Water Resour. 2009, 32, 1255–1266. [Google Scholar] [CrossRef]
- Shu, W.M.; Li, Q.P.; Cao, G.R.; Wang, H.T.; Li, P. Analysis of compensation benefits of Wudongde and Baihetan cascade reservoirs. Water Power 2018, 44, 74–77. [Google Scholar] [CrossRef]
- Liu, P.; Li, L.P.; Guo, S.L.; Xiong, L.H.; Zhang, W.; Zhang, J.W.; Xu, C.Y. Optimal design of seasonal flood limited water levels and its application for the Three Gorges Reservoir. J. Hydrol. 2015, 527, 1045–1053. [Google Scholar] [CrossRef]
- Chen, S.Y. The theory and application of fuzzy optimum selection for the multistage and multi-objective decision-making system. Shuilixuebao 1990, 1, 499–512. [Google Scholar]
- Hasebe, M.; Nagayama, Y. Reservoir operation using the neural network and fuzzy systems for dam control and operation support. Adv. Eng. Softw. 2002, 33, 245–260. [Google Scholar] [CrossRef]
- Deka, P.C.; Chandramouli, V. Fuzzy neural network modeling of reservoir operation. J. Water Resour. Plan. Manag. 2009, 135, 5–12. [Google Scholar] [CrossRef]
- Hadzima-Nyarko, M.; Rabi, A.; Sperac, M. Implementation of artificial neural networks in modeling the water-air temperature relationship of the river Drava. Water Resour. Manag. 2014, 28, 1379–1394. [Google Scholar] [CrossRef]
- Wambua, R.M.; Mutua, B.M.; Raude, J.M. Prediction of missing Hydro-meteorological data series using artificial neural networks (ANN) for upper Tana River Basin, Kenya. Am. J. Water Resour. 2016, 4, 35–43. [Google Scholar]
- Deweber, J.T.; Wagner, T. A regional neural network ensemble for predicting mean daily river water temperature. J. Hydrol. 2014, 517, 187–200. [Google Scholar] [CrossRef]
- Piccolroaz, S.; Calamita, E.; Majone, B.; Gallice, A.; Siviglia, A.; Toffolon, M. Prediction of river water temperature: A comparison between a new family of hybrid models and statistical approaches. Hydrol. Process. 2016, 30, 3901–3917. [Google Scholar] [CrossRef]
- Chen, C.X.; Fu, J.; Wu, M.X.; Gao, X.; Ma, L.M. High-efficiency sediment transport requirements for the operation of the Xiaolangdi Reservoir in the Lower Yellow River. Water Supply 2022, 22, 8572–8586. [Google Scholar] [CrossRef]
- Chen, L.; Sui, X.; Wang, D.S.; Yin, X.Y.; Ji, G.D. The ecological benefit-loss evaluation in a riverine wetland for hydropower projects—A case study of Xiaolangdi reservoir in the Yellow River, China. Ecol. Eng. 2016, 96, 34–44. [Google Scholar] [CrossRef]
- Zhao, Y.; Cao, W.H.; Hu, C.H.; Zhang, X.M.; Lv, X.Z.; Yin, X.L.; Hu, C.H.; Wang, Y.S.; Wang, Z.Y.; Zhang, X.M.; et al. Analysis of changes in characteristics of flood and sediment yield in typical basins of the Yellow River under extreme rainfall events. Catena 2019, 177, 31–40. [Google Scholar] [CrossRef]
- Hou, C.; Yi, Y.J.; Song, J.; Zhou, Y. Effect of water-sediment regulation operation on sediment grain size and nutrient content in the lower Yellow River. J. Clean. Prod. 2021, 279, 123533. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, C.H.; Zhang, X.M.; Lv, X.Z.; Yin, X.L.; Wang, Z.Y. Response of sediment discharge to soil erosion control in the middle reaches of the Yellow River. Catena 2021, 203, 105330. [Google Scholar] [CrossRef]
- Chen, Z.S.; Wang, H.M.; Qi, X.T. Pricing and water resource allocation scheme for the South-to-North Water Diversion Project in China. Water Resour. Manag. 2013, 27, 1457–1472. [Google Scholar] [CrossRef]
- Huang, H.; Niu, J.Y. Compensative operating feasibility analysis of the west route of the South-to-North Water Transfer Project dased on M-Copula Function. Water Resour. Manag. 2015, 29, 3919–3927. [Google Scholar] [CrossRef]
- Yang, T.; Zhang, Q.; Chen, Y.Q.D.; Tao, X.; Xu, C.Y.; Chen, X. A spatial assessment of hydrologic alteration caused by dam construction in the middle and lower Yellow River, China. Hydrol. Process. 2008, 22, 3829–3843. [Google Scholar] [CrossRef]
- Wang, S.; Fu, B.J.; Piao, S.L.; Lv, Y.H.; Ciais, P.; Feng, X.M.; Wang, Y.F. Reduced sediment transport in the Yellow River due to anthropogenic changes. Nat. Geosci. 2016, 9, 38–41. [Google Scholar] [CrossRef]





| Overall Objective | Primary Indices | Secondary Indices | Tertiary Indices | Types |
|---|---|---|---|---|
| The optimal regulation effect of comprehensive utilization of the reservoir | Flood control | Reservoir | Maximum water level for flood control | Cost |
| Downstream river channel | Cross-section flow capacity | Benefit | ||
| Siltation reduction | Reservoir | Sediment retention period | Benefit | |
| Downstream river channel | Siltation amount | Cost | ||
| Minimum bank-full discharge of main channel | Benefit | |||
| Water resources supply, Irrigation, ecological improvement | Downstream river channel | Number of days that do not meet the minimum discharge requirement | Cost | |
| Hydropower generation | Reservoir | Water level in front of the dam | Benefit (within the water level limit) | |
| Power Station | Hydropower generation | Benefit |
| Discharge Requirements | January | February | March | April | May | June | July | August | September | October | November | December |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a. Water resources supply and irrigation | 89 | 307 | 617 | 653 | 509 | 354 | 206 | 151 | 282 | 319 | 130 | 112 |
| b. Hydropower generation of a single station | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 |
| c. Minimum ecological discharge at sea entry control station | 100 | 100 | 100 | 75 | 75 | 75 | 220 | 220 | 220 | 220 | 100 | 100 |
| min(Qout) = max(a,b,c) | 300 | 307 | 617 | 653 | 509 | 354 | 300 | 300 | 300 | 319 | 300 | 300 |
| Operation Modes | Discharging When Filling Up | Discharging When Gathering Flow | Dispatching with High Sediment Concentration | Lowering the Water Level to Scour the Reservoir Area | |
|---|---|---|---|---|---|
| Gradually raising the flood limit water level | Starting condition | WXLD ≥ 1.3 billion m3 | Qin ≥ 2600 m3/s WXLD ≥ 600 million m3 | Qin ≥ 2600 m3/s Sin ≥ 200 kg/m3 | Qin ≥ 2600 m3/s ΔWsXLD ≥ 4.2 billion m3 |
| Scheduling command | QHYK ≥ 3700 m3/s T ≥ 5 d | QHYK ≥ 3700 m3/s T ≥ 5 d | Pre-discharge or storage water to 300 million m3 2 days in advance, Qout = Qin | QHYK = 4000 m3/s 2 days in advance until Qin < 2600 m3/s | |
| Raising the flood limit water level at one time | Starting condition | ZXLD ≥ 254 m | Same with gradually raising the flood limit water level | / | / |
| Scheduling command | QHYK ≥ 3700 m3/s T ≥ 5 d | Same with gradually raising the flood limit water level | Qout = min(Qout) | Qout = min(Qout) | |
| Evaluation Index | TSRP_XLDR | WS_LYR | Qbmin_LYR | Td | WLXLDR | NXLDR |
|---|---|---|---|---|---|---|
| relative membership weights | 0.19 | 0.20 | 0.24 | 0.16 | 0.12 | 0.09 |
| Options | Sample Input | Expected Output | Calculated Output | Simulation Errors |
|---|---|---|---|---|
| Best | (1.000, 1.000, 1.000, 1.000, 1.000, 1.000) | 1.00 | 1.000408 | 0.000408 |
| Intermediate 1 | (0.923, 0.974, 0.976, 0.971, 0.993, 0.996) | 0.75 | 0.750250 | 0.000250 |
| Intermediate 2 | (0.846, 0.948, 0.953, 0.942, 0.986, 0.992) | 0.50 | 0.500157 | 0.000157 |
| Intermediate 3 | (0.769, 0.922, 0.929, 0.912, 0.980, 0.989) | 0.25 | 0.249994 | −0.000006 |
| Worst | (0.692, 0.896, 0.906, 0.883, 0.973, 0.985) | 0.00 | 0.000071 | 0.000071 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Gao, X.; Wu, M.; Zhu, C.; An, C.; Li, D.; Liu, J. Optimizing the Flood Limit Water Level of Reservoirs in Sediment-Laden Rivers under Changing Water and Sediment Conditions: A Case Study of the Xiaolangdi Reservoir. Water 2023, 15, 3552. https://doi.org/10.3390/w15203552
Chen C, Gao X, Wu M, Zhu C, An C, Li D, Liu J. Optimizing the Flood Limit Water Level of Reservoirs in Sediment-Laden Rivers under Changing Water and Sediment Conditions: A Case Study of the Xiaolangdi Reservoir. Water. 2023; 15(20):3552. https://doi.org/10.3390/w15203552
Chicago/Turabian StyleChen, Cuixia, Xing Gao, Moxi Wu, Chenghao Zhu, Cuihua An, Da Li, and Junxiu Liu. 2023. "Optimizing the Flood Limit Water Level of Reservoirs in Sediment-Laden Rivers under Changing Water and Sediment Conditions: A Case Study of the Xiaolangdi Reservoir" Water 15, no. 20: 3552. https://doi.org/10.3390/w15203552
APA StyleChen, C., Gao, X., Wu, M., Zhu, C., An, C., Li, D., & Liu, J. (2023). Optimizing the Flood Limit Water Level of Reservoirs in Sediment-Laden Rivers under Changing Water and Sediment Conditions: A Case Study of the Xiaolangdi Reservoir. Water, 15(20), 3552. https://doi.org/10.3390/w15203552






