Navigational Safety Assessment of Ten-Thousand-Ton Vessels in Ship Tunnels by Ship Simulations
Abstract
:1. Introduction
2. Methodology
2.1. Theory of Simulation
2.2. Major Configurations
2.3. Simulations of the Scene and the Vessel
2.4. Validation
2.4.1. Validation of the Vessel Model
2.4.2. Added Debugging Conditions
3. Results
3.1. Forward Coasting Distance
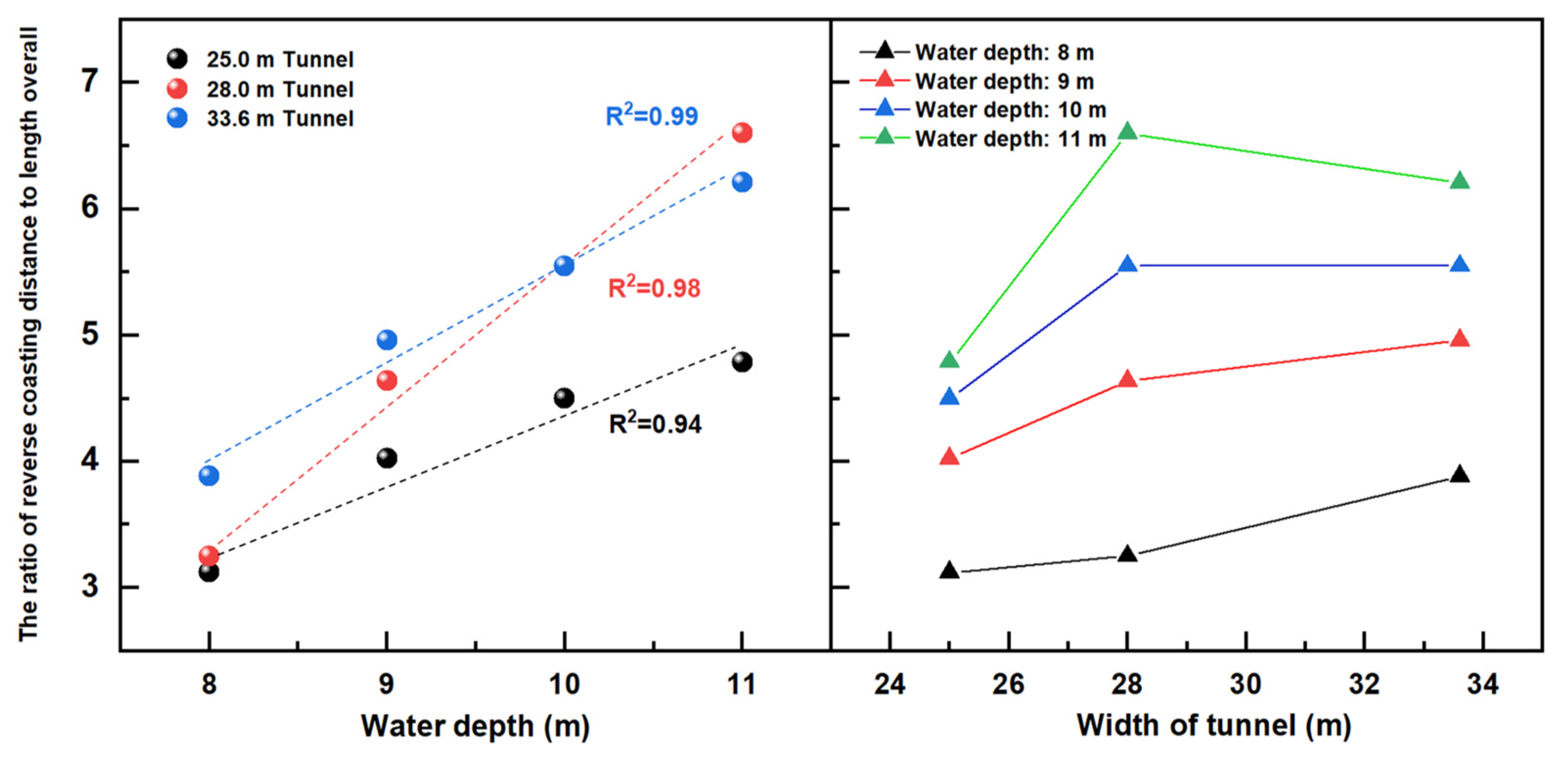
3.2. Reverse Coasting Distance
4. Discussion
4.1. Coasting Distance Characteristics
4.2. Following Distance
4.2.1. Vessel-Following Model
4.2.2. Quantitative Analysis
4.3. Handling Characteristics
5. Conclusions
- Ship simulation can effectively simulate vessel navigation in inland waterway ship tunnels and accurately reflect forward and reverse coasting characteristics.
- For a 10,000 DWT bulk carrier with a speed of 1.5 m/s, an increase of 1 m in water depth results in 16.5% (16.3% in reverse) average increase in forward coasting distance. An increase of 0.45 (0.31) times the vessel breadth leads to a one-time increase in the LOA for the forward (reverse) coasting distance. The forward and reverse coasting distances are positively correlated with the tunnel water depth or width. On average, the reverse coasting distance is 10% shorter than the forward distance.
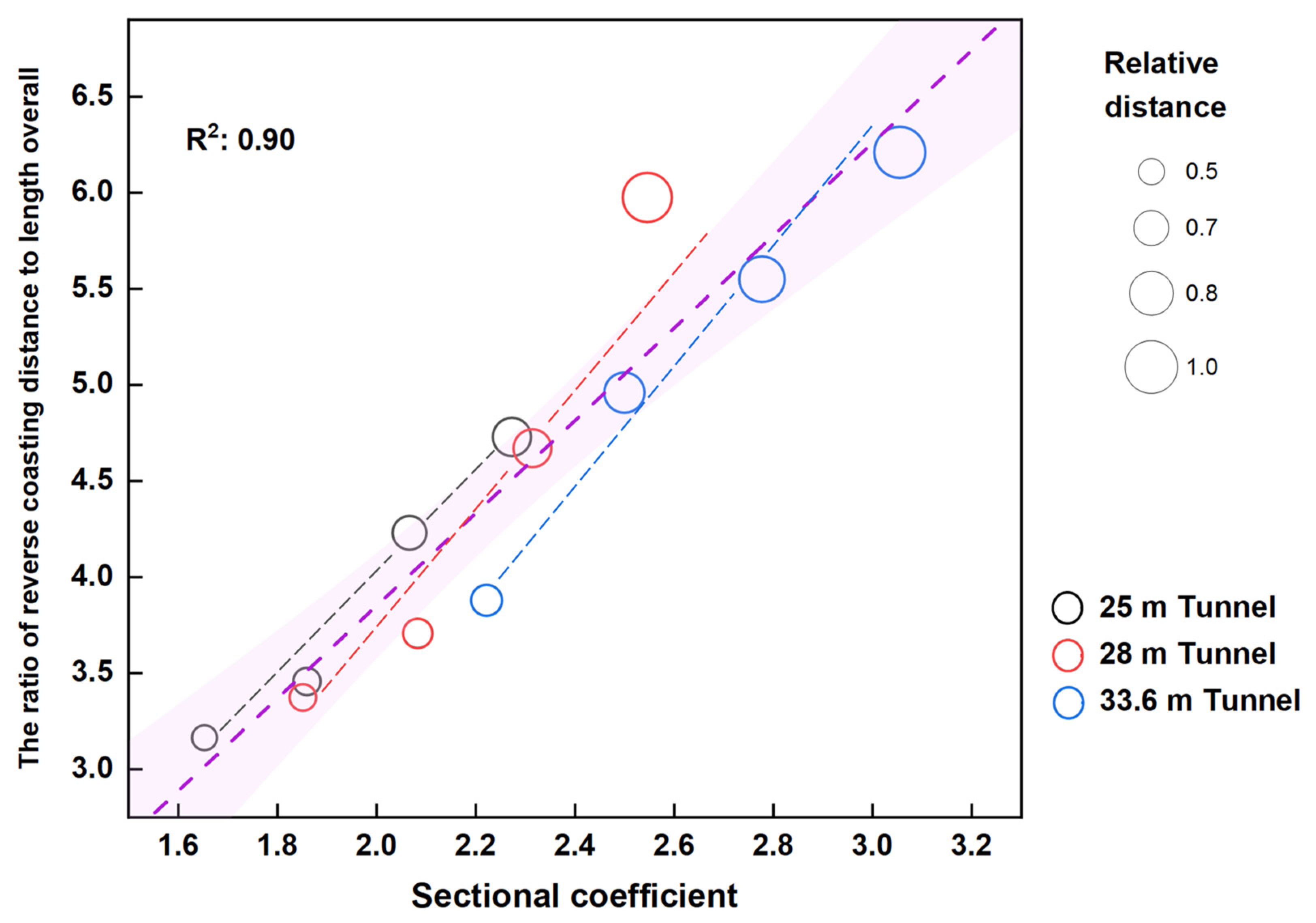
- The acceleration of the vessel during the initial phase of stopping is positively correlated with tunnel width. Forward and reverse coasting distances have a strong linear relationship with the sectional coefficient, with correlation coefficient values of 0.7 and 0.9, respectively.
- In forward motion, the MFD and AFD of 10,000 DWT bulk carriers’ fleet are 1.84–1.90 times the LOA and 5.79–5.96 times the LOA. And the GFD is 2.69 times the LOA. The SDDFD is slightly smaller than the AFD, ranging from 5.46 to 5.69 times the LOA. During reversing, the maximum MFD and SDDFD values are 1.47 and 5.56 times the LOA, respectively.
- Course deviation phenomena occur near the entrance and exit of the tunnel, and changes in lighting can affect the officer’s visual perception. Upon entering the tunnel, the vessel’s speed slightly reduces due to increased flow resistance, with a modest speed increase near the tunnel exit. The pilot and officer should control the speed and navigate along the centerline of the tunnel throughout the course. The implementation of distance and lighting markers indicating the tunnel center line is recommended for ship tunnels.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, C.; Aritua, B.; de Leijer, H.; van Liere, R.; Lee, P.T.-W. Exploring causes of growth in China’s inland waterway transport, 1978–2018: Documentary analysis approach. Transp. Policy 2023, 136, 47–58. [Google Scholar] [CrossRef]
- Zuo, D.; Liang, Q.; Zhan, S.; Huang, W.; Yang, S.; Wang, M. Using energy consumption constraints to control the freight transportation structure in China (2021–2030). Energy 2023, 262, 125512. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Y.; Wang, X.; An, J.; Dong, B.; Liao, Y. Influence of Unsteady Flow Induced by a Large-Scale Hydropower Station on the Water Level Fluctuation of Multi-Approach Channels: A Case Study of the Three Gorges Project, China. Water 2020, 12, 2922. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Y.; Cheng, L.; Wang, X.; Wang, B.; An, J. Investigating hydraulic operational schemes of a large-scale multi-lane lock group concerning water-level fluctuations in a branched approach channel system. Ocean Eng. 2022, 260, 111758. [Google Scholar] [CrossRef]
- Xiao, Y.; Wang, L.; Chen, S.; Jin, Y. Experimental study on influence of navigation performance of ship passing the inland navigation tunnel. In Proceedings of the 30th International Ocean and Polar Engineering Conference, Online, 11–16 October 2020; OnePetro: Richardson, TX, USA, 2020; Volume 20, p. 4260. [Google Scholar]
- Fell, J. In numbers. Eng. Technol. 2017, 12, 12–13. [Google Scholar]
- Ariansen, E.A. Accident Frequency Analysis for the Stad Ship Tunnel. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2018. [Google Scholar]
- Toerset, T.; Meland, S.; Bertelsen, D. Cost benefit analysis of Stad shipping tunnel. In Proceedings of the European Transport Conference, Leiden, The Netherlands, 6–8 October 2008; Association for European Transport: London, UK, 2008; pp. 1–14. [Google Scholar]
- Ash, E.H. Chandra Mukerji. Impossible Engineering: Technology and Territoriality on the Canal du Midi. Princeton Studies in Cultural Sociology. Renaiss. Q. 2010, 63, 676–678. [Google Scholar] [CrossRef]
- Patt, H.; Speerli, J.; Gonsowski, P.; Patt, H.; Speerli, J.; Gonsowski, P.; Stamm, J.; Verkehrswasserbau, S. Wasserbau: Grundlagen, Gestaltung von Wasserbaulichen Bauwerken und Anlagen; Springer Vieweg Wiesbaden: Berlin, Germany, 2021; pp. 419–464. [Google Scholar]
- Liu, X. Research on Ship Types and Comparison of Their Operation Modes in Navigable Tunnel of Wujiang River. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2020. [Google Scholar]
- Xiao, Y. Experimental Study on the Correlation between Wujiang Navigation Tunnel Size and Passing Ship Parameters. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2020. [Google Scholar]
- Gan, W.; Li, Y.; Qiao, H. Construction of risk assessment index system of ship in navigable tunnel. Ship Ocean Eng. 2021, 50, 122–125. [Google Scholar]
- Tani, H. On the reverse stopping of ships. J. Zosen Kiokai 1966, 1966, 81–86. [Google Scholar] [CrossRef]
- Liang-de, H.; Ye, J.; Zhao-jin, Y.; Bo, Z.; Hui, T. Following distance model of inland ship. J. Traffic Transp. Eng. 2012, 12, 55–62. [Google Scholar]
- Wu, B.; Cheng, Z. Safety opportunity of U-Turn model based on ship-following theory. In Proceedings of the 2011 International Conference on Future Wireless Networks and Information Systems, Macao, China, 30 November–1 December 2011; Springer: Berlin/Heidelberg, Germany, 2012; pp. 723–729. [Google Scholar]
- Yu, G.; Zhao, J. Research on hydraulic characteristics of navigable tunnels of high-dam navigable structures and ship navigation test. In Proceedings of the 2021 6th International Conference on Minerals Source, Geotechnology and Civil Engineering, Guangzhou, China, 9–11 April 2021; IOP (China) Publishing: Beijing, China, 2021; Volume 768, p. 012041. [Google Scholar]
- Zou, L.; Larsson, L. Numerical predictions of ship-to-ship interaction in shallow water. Ocean Eng. 2013, 72, 386–402. [Google Scholar] [CrossRef]
- Lo, D. Numerical simulation of hydrodynamic interaction produced during the overtaking and the head-on encounter process of two ships. Eng. Comput. Int. J. Comput.-Aided Eng. Softw. 2012, 29, 83–101. [Google Scholar] [CrossRef]
- Zheng, Z.; Zou, L.; Zou, Z. A numerical study of passing ship effects on a moored ship in confined waterways with new benchmark cases. Ocean Eng. 2023, 280, 114643. [Google Scholar] [CrossRef]
- Zhou, J.; Ren, J.; Bai, W. Survey on hydrodynamic analysis of ship–ship interaction during the past decade. Ocean Eng. 2023, 278, 114361. [Google Scholar] [CrossRef]
- Han, S. Application of car-following theory in calculation of safety distance between ships in restricted channel waters. J. Guangzhou Marit. Univ. 2021, 29, 16–19. [Google Scholar]
- Tani, H. On the Stopping Distances of Giant Vessels. J. Navig. 1970, 23, 196–211. [Google Scholar] [CrossRef]
- Jin, Z.; Chen, Z.; Xia, Z.; Peng, Y.; Wang, W. Influence of navigation rules on traffic situation of one-way fairway with multi-junction based on simulation and improved DEA approach. In Proceedings of the 6th International Conference on Transportation Information and Safety (ICTIS), Wuhan, China, 22–24 October 2021; IEEE: New York, NY, USA, 2021; pp. 1286–1293. [Google Scholar]
- Zhang, L.; Wang, H.; Meng, Q. Big data–based estimation for ship safety distance distribution in port waters. Transp. Res. Rec. 2015, 2479, 16–24. [Google Scholar] [CrossRef]
- Meng, Q.; Weng, J.; Li, S. Analysis with automatic identification system data of vessel traffic characteristics in the Singapore strait. Transp. Res. Rec. 2014, 2426, 33–43. [Google Scholar] [CrossRef]
- Wei, L. Research on Ship Distance Information Perception Based on Video. Master’s Thesis, Dalian Maritime University, Dalian, China, 2020. [Google Scholar]
- Yeo, D.J.; Cha, M.; Mun, D. Simulating ship and buoy motions arising from ocean waves in a ship handling simulator. Simulation 2012, 88, 1407–1418. [Google Scholar] [CrossRef]
- Johnston, M.M.; Kim, S.-C.; Allison, M.C. Mobile Harbor, Alabama Navigation Study: Ship Simulation Report; Technical Report; Army Engineer Research and Development Center: Vicksburg, MS, USA, 2021. [Google Scholar]
- Johnston, M.M.; Godsey, E. Multifaceted Approach of Assessing Channel Design through Ship Simulations in Mobile Harbor, Alabama. J. Waterw. Port Coast. Ocean Eng. 2021, 147, 04021027. [Google Scholar] [CrossRef]
- Martin, S.K.; Johnston, M.M.; Pazan, K.I.; Sanchez, M.J.; Allison, M.C.; Lynch, G. Screening Channel Design Alternatives Using Ship Simulation. J. Waterw. Port Coast. Ocean Eng. 2021, 147, 05021009. [Google Scholar] [CrossRef]
- Aydogdu; Volkan, Y. Utilization of full-mission ship-handling simulators for navigational risk assessment: A case study of large vessel passage through the Istanbul Strait. J. Mar. Sci. Eng. 2022, 10, 659. [Google Scholar] [CrossRef]
- Deng, J.; Liao, F.; Xie, C.; Guan, H.; Yan, Q. Ship handling simulation in research on safety of navigation in narrow and long tunnel. Navig. China 2021, 44, 7–12. [Google Scholar]
- GB/T 50139-2014; Navigation Standard of Inland Waterway. SAMR (State Administration for Market Regulation) & MOHURD (Ministry of Housing and Urban-Rural Development), Standardization Administration of China: Beijing, China, 2014.
- Gan, W.; Ma, D.; Li, Y.; Deng, J. Following model for ships in navigation tunnels. In Proceedings of the 8th International Conference onTraffic and Logistic Engineering, Shenzhen, China, 21–23 August 2020; MATEC Web of Conferences: Les Ulis, France, 2020; Volume 325, p. 04001. [Google Scholar]
- MSC.137(76); Standards for Ship Manoeuvrability. IMO (International Maritime Organization), Marine Safety Council: London, UK, 2002.
- Terziev, M.; Tezdogan, T.; Oguz, E. Numerical investigation of the behaviour and performance of ships advancing through restricted shallow waters. J. Fluids Struct. 2018, 76, 185–215. [Google Scholar] [CrossRef]
- Tang, J.; Kan, D. Economic analysis of navigable tunnel section of high dam. Port Waterw. Eng. 2017, 7, 141–144. [Google Scholar]
- Ma, G.; Ma, M.; Liang, S.; Wang, Y.; Zhang, Y. An improved car-following model accounting for the time-delayed velocity difference and backward looking effect. Commun. Nonlinear Sci. Numer. Simul. 2020, 85, 105221. [Google Scholar] [CrossRef]
- GB/T 20068-2017; Technical Requirements of Shipborne Automatic Identification System. SAMR (State Administration for Market Regulation), Standardization Administration of China: Beijing, China, 2017.
- Chandler, R.E.; Herman, R.; Montroll, E.W. Traffic dynamics: Studies in car following. Oper. Res. 1958, 6, 165–184. [Google Scholar] [CrossRef]
- Ming, L.; Liu, J.; Wang, X. Calculation model of safe longitudinal distance for very large vessels. Navig. China 2014, 37, 40–43. [Google Scholar]
- Niu, X.; Wu, J.; Wang, X. Study on section size of large navigation tunnel based on objective optimization. Hydro-Sci. Eng. 2021, 3, 1–8. [Google Scholar]
- Hou, H.; Zheng, B. Discussion on defining deep water shallow water and restricted channel. Port Waterw. Eng. 2006, 1, 53–58. [Google Scholar]
- Mehri, A.; Sajedifar, J.; Abbasi, M.; Naimabadi, A.; Mohammadi, A.A.; Teimori, G.H.; Zakerian, S.A. Safety evaluation of lighting at very long tunnels on the basis of visual adaptation. Saf. Sci. 2019, 116, 196–207. [Google Scholar] [CrossRef]
- Christelle, C.; Sandrine, C. Analysis of critical incidents in tunnels to improve learning from experience. Saf. Sci. 2019, 116, 222–230. [Google Scholar]
- Tian, Y.; Sun, X.; Chen, L. Risk assessment of nautical navigational environment based on grey fixed weight cluster. Promet-Traffic Transp. 2017, 29, 331–342. [Google Scholar] [CrossRef]
- Qiu, W.; Tang, C.; Tang, Q. Navigation environment risk assessment of uncertain inland waterway. Navig. China 2019, 42, 52–55. [Google Scholar]

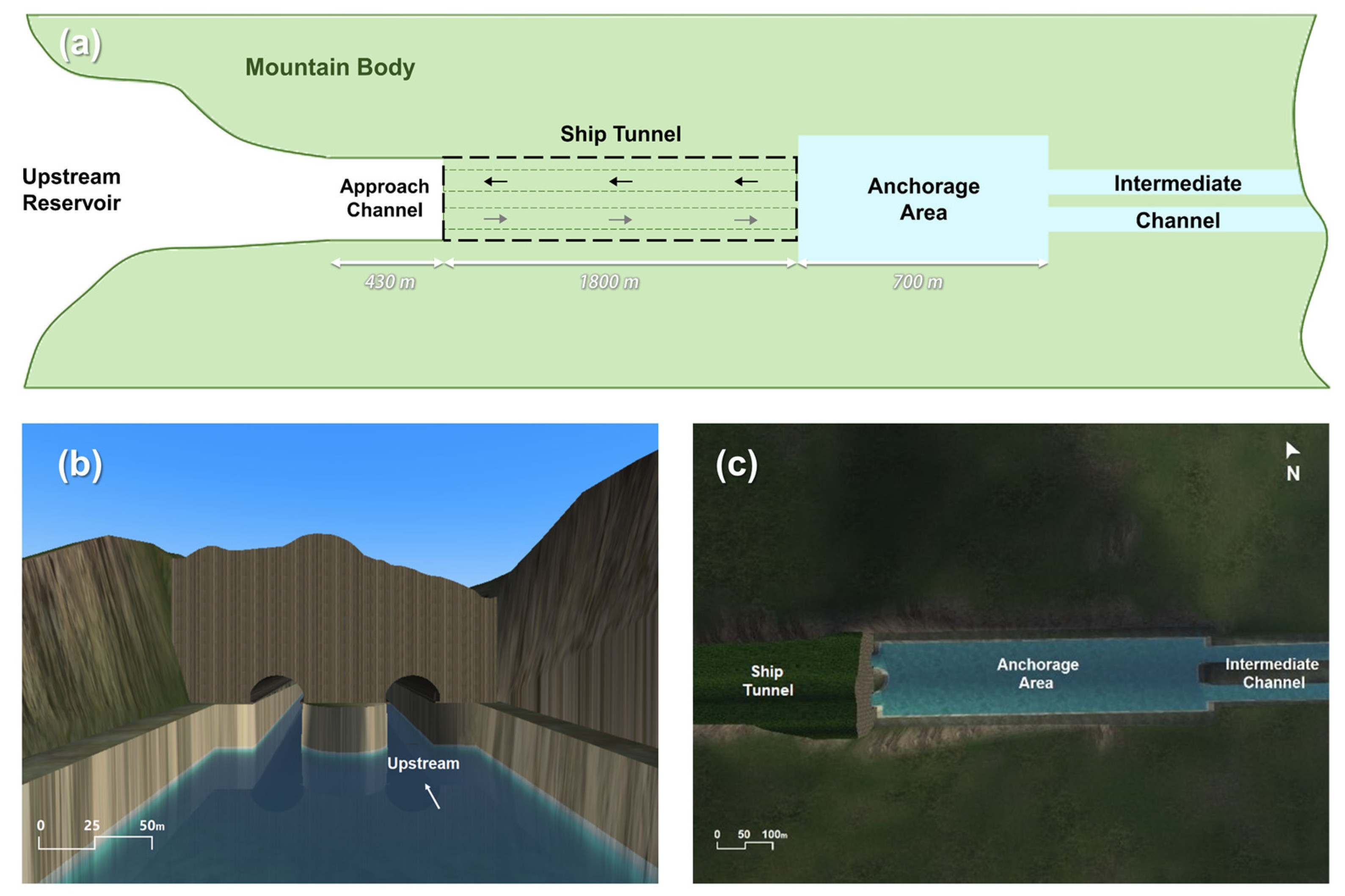
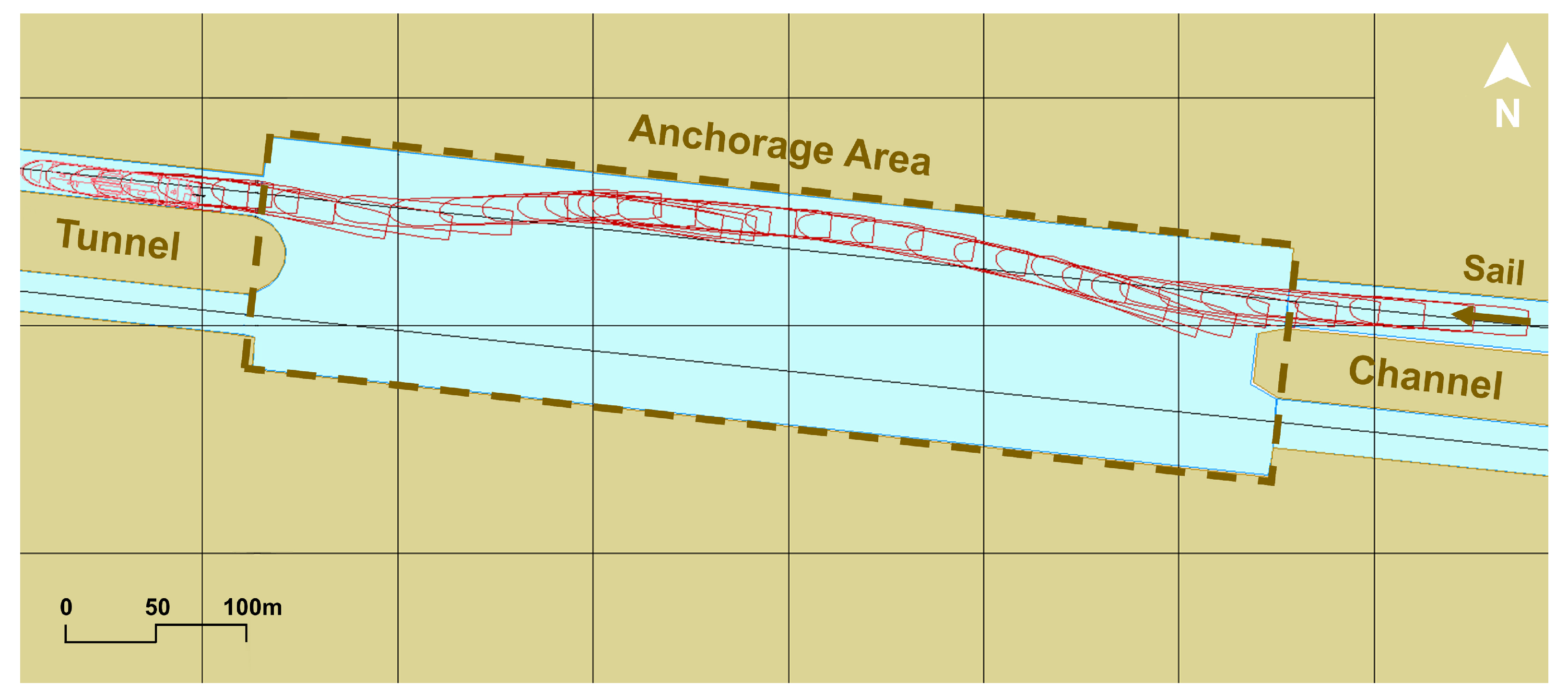
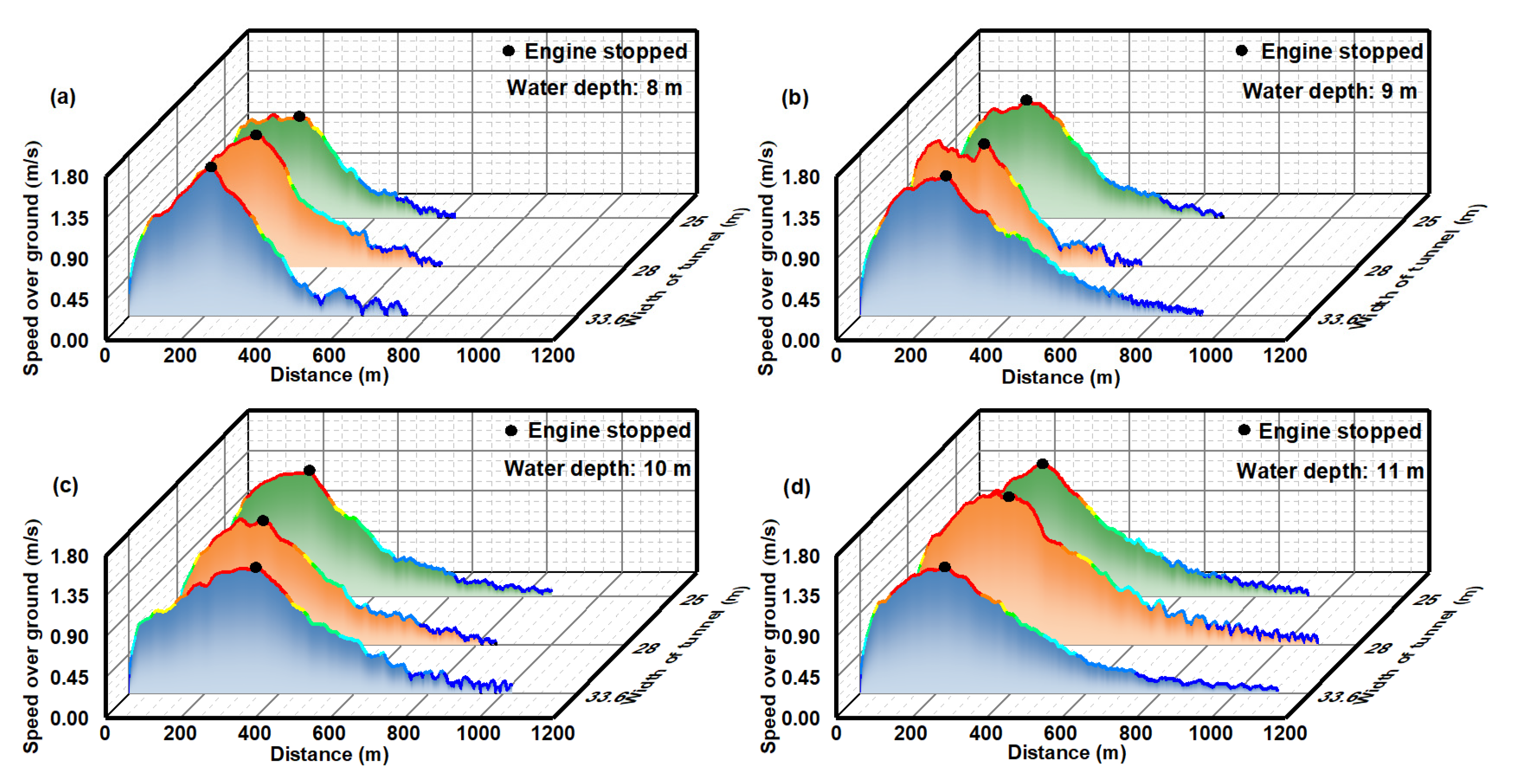

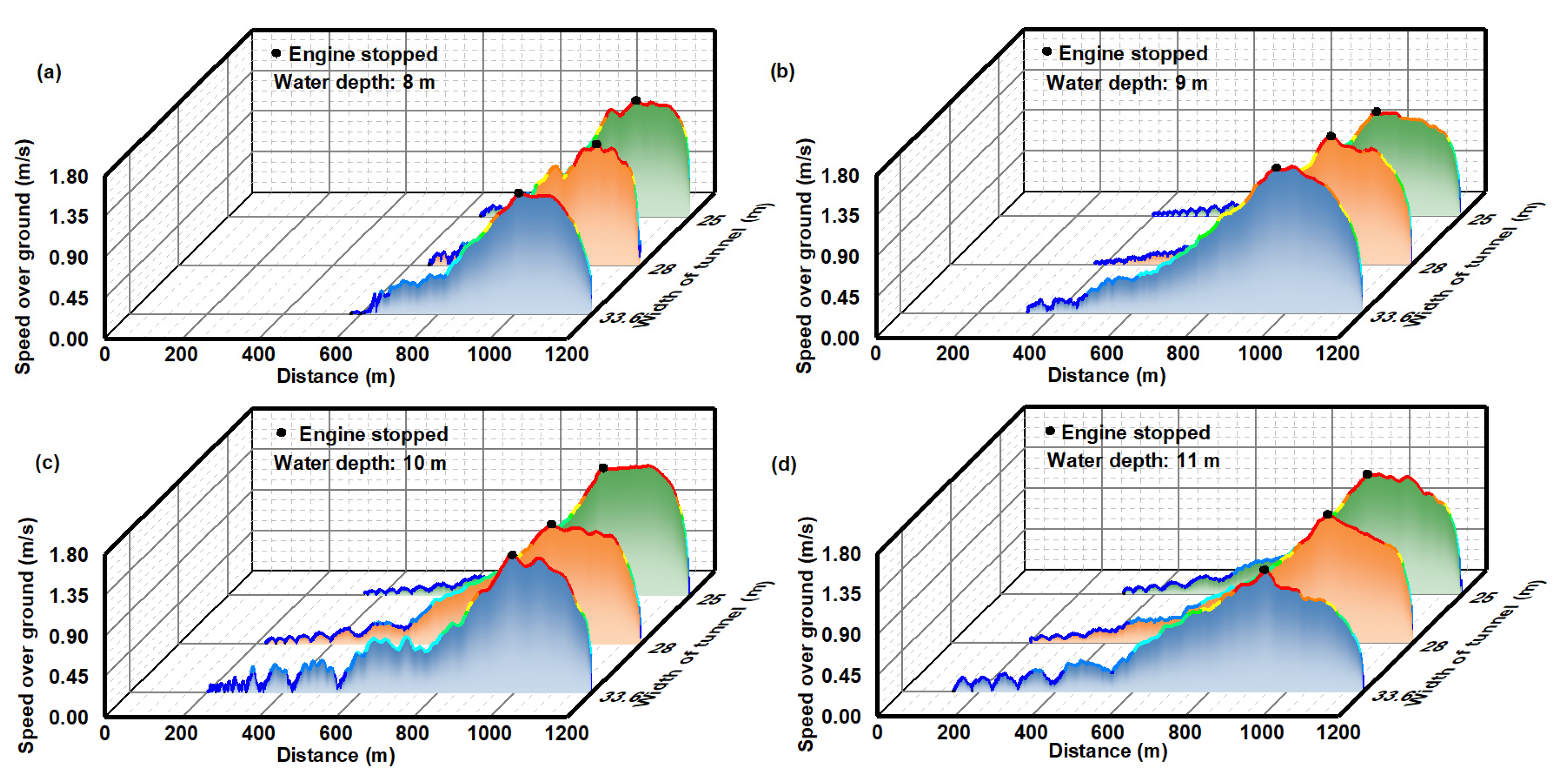


| Parameter | Value |
|---|---|
| Width | 25, 28, 33.6 m |
| Length | 1800 m |
| Water depth | 8, 9, 10, 11 m |
| Lighting level | 30 lx |
| Parameter | Value |
|---|---|
| Length overall (LOA) | 130 m |
| Breadth | 22 m |
| Draft (In ledge mode) | 5.5 m |
| Dead weight tonnage | 10,000 t |
| Type | Bulk carrier |
| Steering | VC (kn) | y090/LOA | x090/LOA | DC/LOA |
|---|---|---|---|---|
| Port | 5 | 1.17 | 3.1 | 2.41 |
| Starboard | 5 | 1.13 | 3 | 2.32 |
| Heading | Tunnel Width (m) | Water Depth (m) | Sectional Coefficient | SR (m) | SL (m) | MFD /LOA | GFD /LOA | SDDFD/LOA | AFD /LOA |
| Forward | 25 | 9 | 1.86 | 420 | 522 | 1.90 | 2.69 | 5.69 | 5.92 |
| 28 | 9 | 2.08 | 425 | 536 | 1.84 | 2.69 | 5.73 | 5.96 | |
| 28 | 8 | 1.85 | 390 | 487 | 1.94 | 2.69 | 5.46 | 5.69 | |
| 33.6 | 8 | 2.22 | 403 | 508 | 1.88 | 2.69 | 5.56 | 5.79 | |
| Heading | Tunnel Width (m) | Water Depth (m) | Sectional Coefficient | SRB (m) | SLB (m) | MFD /LOA | GFD /LOA | SDDFD /LOA | |
| Astern | 25 | 9 | 1.86 | 342 | 522 | 1.30 | 2.69 | 5.12 | |
| 28 | 9 | 2.08 | 399 | 599 | 1.15 | 2.69 | 5.56 | ||
| 28 | 8 | 1.85 | 264 | 422 | 1.47 | 2.69 | 4.52 | ||
| 33.6 | 8 | 2.22 | 330 | 504 | 1.35 | 2.69 | 5.03 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Cheng, H.; Deng, Z.; Mei, L.; Ding, L.; Guo, C.; Wang, X.; Zhao, G. Navigational Safety Assessment of Ten-Thousand-Ton Vessels in Ship Tunnels by Ship Simulations. Water 2023, 15, 3584. https://doi.org/10.3390/w15203584
Zhang S, Cheng H, Deng Z, Mei L, Ding L, Guo C, Wang X, Zhao G. Navigational Safety Assessment of Ten-Thousand-Ton Vessels in Ship Tunnels by Ship Simulations. Water. 2023; 15(20):3584. https://doi.org/10.3390/w15203584
Chicago/Turabian StyleZhang, Shouyuan, Hongyu Cheng, Ziming Deng, Lingqin Mei, Leyu Ding, Chao Guo, Xin Wang, and Gensheng Zhao. 2023. "Navigational Safety Assessment of Ten-Thousand-Ton Vessels in Ship Tunnels by Ship Simulations" Water 15, no. 20: 3584. https://doi.org/10.3390/w15203584
APA StyleZhang, S., Cheng, H., Deng, Z., Mei, L., Ding, L., Guo, C., Wang, X., & Zhao, G. (2023). Navigational Safety Assessment of Ten-Thousand-Ton Vessels in Ship Tunnels by Ship Simulations. Water, 15(20), 3584. https://doi.org/10.3390/w15203584






